Задача 1.
Даны три сигнала
male,
female и
bird.
Нужно их смешать, потом, используя ICA, разделить и сравнить с исходными.
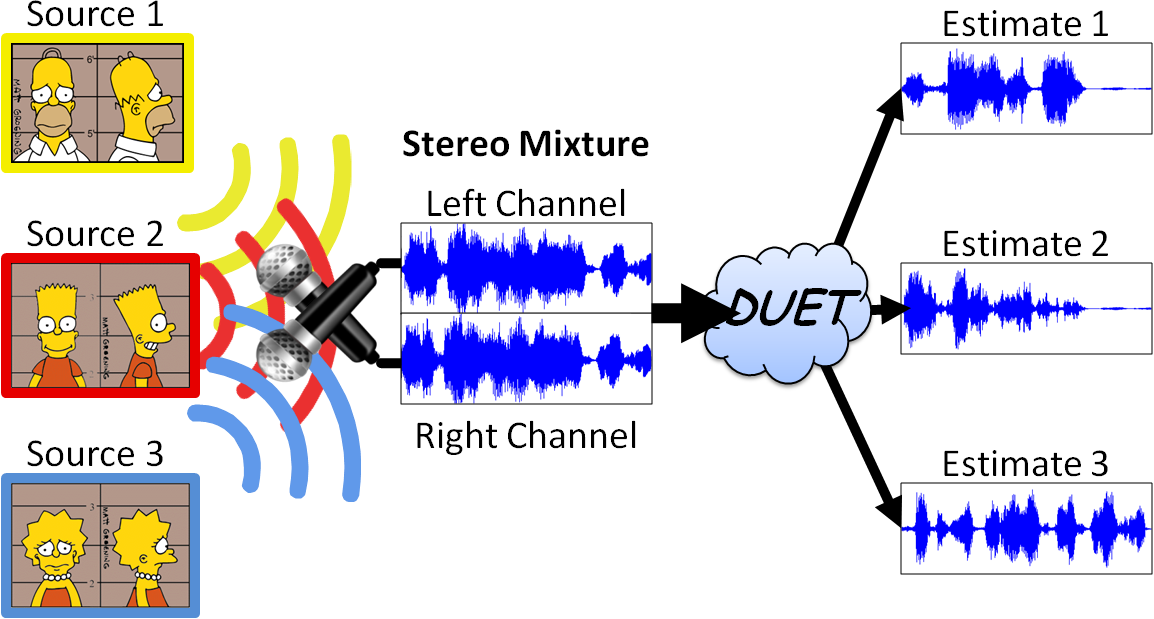
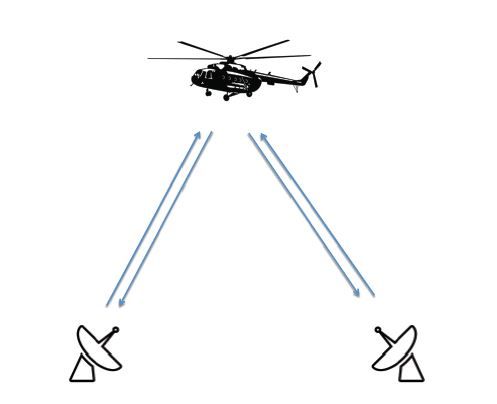
Задача 2.
Три сигнала
приняты двумя микрофонами
Требуется их снова разделить.
Задача 3.
Разделить смешанное изображение в градациях серого на два первоначальных
Задача 4.
Разделить смешанное цветное изображение на два первоначальных