Решение любой технической задачи, связанной с обработкой цифровых данных (сигнала), независимо от их природы, начинается с выделения полезной информации (информативных
признаков). Как правило исходная информация предоставляется нам с некоторой погрешностью. Случайные погрешности (шумы) при этом необходимо погасить тем или
иным фильтром. Далее, при решении конкретных задач информация, очищенная от помех, используется в виде исходной.
Если природа помех известна, то строятся цифровые фильтры, реагирующие именно на такие помехи. Если же природа помех не известна, т.е.
когда на информативный сигнал наложен "белый шум", то используют различные аппараты сглаживания, убирающие резкие изменения входящей информации.
В рассматриваемых нами задачах помехи, как правило, случайны, в частности, имеют характер "белого шума". Одним из наиболее распространенных видов снятия
информации в машиностроении, является обмер детали копиром. При этом снимаемая информация зашумлена случайными выбросами, что связано с механикой
самого копира. Конечно, искажение информации может быть связано и с регулярными изменениями данных, вызванными разбалансировкой механизмов или сбитой
градуировкой измерительного инструмента. В этом случае положение может исправить лишь изменение технологической оснастки.
Здесь мы рассмотрим некоторые простейшие алгоритмы сглаживания, которые наиболее эффективны в задачах, когда число единиц информации велико
(т.е. когда данные снимаются копиром, сканером и пр.).
Пусть дан набор из \(n+1\) точки
\[M_0(x_0,y_0),\,M_1(x_1,y_1),\,\ldots,M_n(x_n,y_n)\]
на плоскости, полученных в результате эксперимента или измерения.
Один из самых простых алгоритмов сглаживания данных основан на замене трех последовательных точек центром тяжести треугольника с вершинами в этих
точках.
Этот алгоритм изображен на рисунке, где исходные данные - это точки \(M_0\), \(M_1,\ldots,M_n\), а сглаженные точки - \(M_1^*,\ldots,M^*_{n-1}\).
То есть точки \(M_1^*,\ldots,M^*_{n-1}\) это точки пересечения медиан треугольников с вершинами в точках \(M_0\), \(M_1\) и \(M_2\); \(M_1\), \(M_2\) и \(M_3,\ldots\) \(M_{n-2}\),
\(M_{n-1}\) и \(M_n\). Ясно, что
\[
M_i^*=\frac{1}{3}(M_{i-1}+M_i+M_{i+1})\,\,\,\,\,\,(i=1,2,\ldots,n-1),
\]
т.е.
\begin{equation}\label{eq:(1.31)}
x_i^*=\frac{1}{3}(x_{i-1}+x_i+x_{i+1})\,\,\,\,\,\,(i=1,2,\ldots,n-1),
\end{equation}
\begin{equation}\label{eq:(1.32)}
y_i^*=\frac{1}{3}(y_{i-1}+y_i+y_{i+1})\,\,\,\,\,\,(i=1,2,\ldots,n-1).
\end{equation}
Равенства (\ref{eq:(1.31)}) и (\ref{eq:(1.32)}) можно переписать в эквивалентном виде
\begin{equation}\label{eq:(1.33)}
x_i^*=x_i+\frac{1}{3}\Delta^2x_i\,\,\,\,\,\,\,(i=1,2,\ldots,n-1),
\end{equation}
\begin{equation}\label{eq:(1.34)}
y_i^*=y_i+\frac{1}{3}\Delta^2y_i\,\,\,\,\,\,\,(i=1,2,\ldots,n-1).
\end{equation}
В процессе сглаживания количество данных (точек) уменьшилось на две.
Как правило, процесс сглаживания повторяют несколько раз. В результате мы
теряем часть информации, что приводит к потере точности при описании контура
у концов. Чтобы этого не произошло, необходимо пополнить разумным способом
исходные данные и пополненные данные сгладить.
Если данные \(M_0,M_1,\ldots,M_n\) описывают замкнутую кривую (в этом случае
\(M_0=M_n\)), то достаточно положить \(M_{-1}=M_{n-1}\) и \(M_{n+1}=M_1\)
(периодизировать данные). В этом случае будет
\[\Delta^2x_0=x_1-2x_0+x_{-1}=x_1-2x_0+x_{n-1},\]
\[\Delta^2x_n=x_{n+1}-2x_n+x_{n-1}=x_1-2x_n+x_{n-1}\]
и
\[\Delta^2y_0=y_1-2y_0+y_{-1}=y_1-2y_0+y_{n-1},\]
\[\Delta^2y_n=y_{n+1}-2y_n+y_{n-1}=y_1-2y_n+y_{n-1}\]
сглаженные данные определяются с помощью равенств (\ref{eq:(1.33)}) и
(\ref{eq:(1.34)}) для всех \(i=0,1,\ldots,n\).
Приведем два способа доопределения данных в случае, когда данные описывают
незамкнутую кривую.
Первый способ состоит следующем -
точки \(M_{-1}\) и \(M_{n+1}\) определяем из условия
\[M_{-1}M_0=M_0M_1,\,\,\, M_nM_{n-1}= M_{n+1}M_n,\] т.е.
\begin{equation}\label{eq:(1.35)}
x_{-1}=2x_0-x_1,\,\,\,\,\, x_{n+1}=2x_n-x_{n-1},
\end{equation}
\begin{equation}\label{eq:(1.36)}
y_{-1}=2y_0-y_1,\,\,\,\,\, y_{n+1}=2y_n-y_{n-1}.
\end{equation}
Второй способ изображен на рисунке
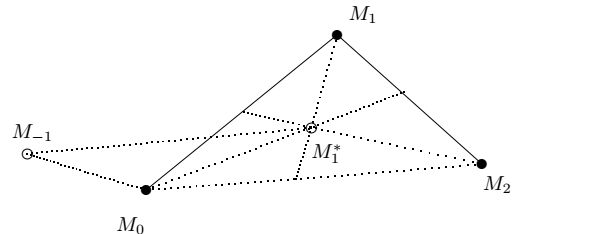
В этом случае точки \(M_{-1}\) и \(M_{n+1}\) мы выбираем из условий
\[M_2M_{-1}= M_2M^*_1+ M_2M_0,\,\,\,
M_{n-2}M_{n+1}= M_{n-2}M_{n-1}^*+ M_{n-2}M_n,\]
или, что то же,
\[x_2-x_{-1}=x_2-\frac{1}{3}(x_0+x_1+x_2)+x_2-x_0,\]
\[x_{n+1}-x_{n-2}=x_{n-2}-\frac{1}{3}(x_{n-2}+x_{n-1}+x_n)+x_n-x_{n-2}\]
и
\[y_2-y_{-1}=y_2-\frac{1}{3}(y_0+y_1+y_2)+y_2-y_0,\]
\[y_{n+1}-y_{n-2}=y_{n-2}-\frac{1}{3}(y_{n-2}+y_{n-1}+y_n)+y_n-y_{n-2}.\]
Находя из этих равенств \(x_{-1}, x_{n+1}\), \(y_{-1}\) и \(y_{n+1}\), получаем
формулы пополнения
\begin{equation}\label{eq:(1.37)}
x_{-1}=\frac{1}{3}(4x_0+x_1-2x_2),\,\,\,x_{n+1}=\frac{1}{3}
(4x_n+x_{n-1}-2x_{n-2}),
\end{equation}
\begin{equation}\label{eq:(1.38)}
y_{-1}=\frac{1}{3}(4y_0+y_1-2y_2),\,\,\,y_{n+1}=\frac{1}{3}
(4y_n+y_{n-1}-2y_{n-2}).
\end{equation}
Таким образом, мы пришли к следующему алгоритму сглаживания данных, описывающему
незамкнутую кривую.
Вычисляем значения \(x_{-1},y_{-1},x_{n+1},y_{n+1}\) в соответствии с равенствами
(\ref{eq:(1.37)}), (\ref{eq:(1.38)}) или (\ref{eq:(1.35)}),
(\ref{eq:(1.36)}) и вычисляем сглаженные данные \(x_i^*,y_i^*\) для
всех \(i=0,1,\ldots,n\) по формулам
\begin{equation}\label{eq:(1.39)}
x_i^*=x_i+\frac{1}{3}\Delta^2x_i,
\end{equation}
\begin{equation}\label{eq:(1.40)}
y_i^*=y_i+\frac{1}{3}\Delta^2y_i.
\end{equation}
Формулы (\ref{eq:(1.39)}), (\ref{eq:(1.40)}) дают хорошие результаты сглаживания в тех ситуациях,
когда ошибки измерения велики. В тех случаях когда ошибки очень большие, то используют
эти алгоритмы несколько раз. При малых ошибках алгоритм, приведенный выше, может
(даже при однократном применении) "перегладить" данные, исказив достоверную
информацию. В таких случаях обычно применяют (лучше несколько раз) более
"мягкие" алгоритмы сглаживания, которые отличаются от (\ref{eq:(1.39)}),
(\ref{eq:(1.40)}) меньшим коэффициентом при вторых разностях.
Точная формулировка такого алгоритма выглядит так:
\begin{equation}\label{eq:(1.41)}
x_{-1}=\frac{1}{3}(4x_0+x_1-2x_2),\,\,\,x_{n+1}=\frac{1}{3}
(4x_n+x_{n-1}-2x_{n-2}),
\end{equation}
\begin{equation}%\label{eq:(1.42)}
y_{-1}=\frac{1}{3}(4y_0+y_1-2y_2),\,\,\,y_{n+1}=\frac{1}{3}
(4y_n+y_{n-1}-2y_{n-2}),
\end{equation}
\begin{equation}%\label{eq:(1.43)}
x_i^*=x_i+\alpha\Delta^2x_i\,\,\,\,(i=0,1,\ldots,n),
\end{equation}
\begin{equation}\label{eq:(1.44)}
y_i^*=y_i+\alpha\Delta^2y_i\,\,\,\,(i=0,1,\ldots,n).
\end{equation}
Ясно, что если \(\alpha=0\), то \(x_i^*=x_i\) и \(y_i^*=y_i\), а если \(\alpha=1/3\),
то получим приведенный ранее алгоритм сглаживания (по центрам тяжести). Если же
\(0\lt \alpha \lt 1/3\), мы получаем "мостик" между наиболее "мягким" алгоритмом
(\(\alpha=0\)) и наиболее "жестким" (\(\alpha=1/3\)).
Можно показать, что при \(\alpha=1/8\) алгоритм (\ref{eq:(1.41)}) -
(\ref{eq:(1.44)}) тесно связан со сглаживанием данных с помощью параболических
сплайнов, а при \(\alpha=1/6\) с помощью кубических сплайнов. Эти связи мы не
будем изучать подробно (их можно найти почти во всех монографиях по сплайнам)
и укажем лишь на то, что их можно вывести из результатов последующих параграфов.
На практике обычно поступают так: выбирают параметр сглаживания \(\alpha\) (для
задач, связанных со сглаживанием данных снятых с показаний копира, достаточно,
как правило, полагать \(\alpha=1/10\)), сглаживают данные с помощью алгоритма
(\ref{eq:(1.41)}) - (\ref{eq:(1.44)}) и полученные данные принимают за исходные.
Затем сглаживают их тем-же алгоритмом повторно, и т.д.
Hа рисунках приведены примеры сглаживания при \(\alpha=1/3\).
Сглаживание периодических данных при 4 итерациях и\(\alpha=1/3\).
Сглаживание периодических данных при 7 итерациях и \(\alpha=1/3\).
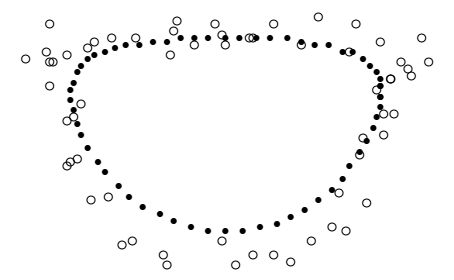Сглаживание периодических данных при 40 итерациях и \(\alpha=1/3\).
В приведенных примерах хорошо видно, что лучшие результаты получатся в случаях,
когда алгоритм сглаживания применяется 4 - 8 раз. Это типичная ситуация
в тех случаях, когда уровень ошибок велик.
Аналогичная картина будет и в случае сглаживания непериодических данных,
то есть данных, описывающих незамкнутую кривую. Вначале небольшое отличие
от предыдущего имеется лишь у концов кривой.
Сглаживание незамкнутой кривой при 5 итерациях и \(\alpha=1/3\).
Сглаживание незамкнутой кривой при 10 итерациях и \(\alpha=1/3\).
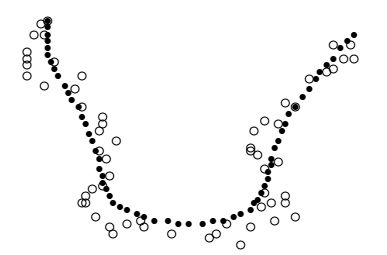Сглаживание незамкнутой кривой при 40 итерациях и \(\alpha=1/3\).
При многократном применении алгоритма сглаживания, в первом случае кривая вырождается в точку, а во
втором - в прямую. Примеры таких расчетов приведены на рисунках
Сглаживание периодических данных при 4 итерациях и \(\alpha=1/6\)
Сглаживание периодических данных при 10 итерациях и \(\alpha=1/6\)
Сглаживание периодических данных при 40 итерациях и \(\alpha=1/6\)
Сглаживание кривой при 5 итерациях и \(\alpha=1/6\).
Сглаживание кривой при 10 итерациях и \(\alpha=1/6\).
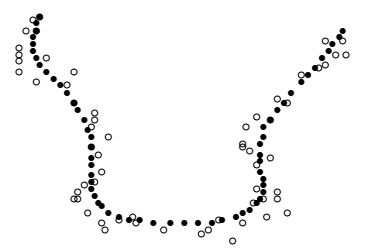Сглаживание кривой при 40 итерациях и \(\alpha=1/6\).
Условие окончания сглаживания данных
Естественно возникает вопрос: "Какое количество итераций будет достаточно для
завершения процесса сглаживания?"
То есть, до каких пор проводить процесс сглаживания?
Приведенные результаты наглядно демонстрируют, что многократное применение
алгоритма сглаживания может существенно исказить исходную информацию вплоть
до потери формы исходного контура.
Ясно, что это зависит от точности задания исходных данных или, что то же, от
уровня ошибок (шумов). Чем больше уровень ошибок, тем больше необходимо операций
сглаживания. С другой стороны, если число итераций слишком велико данные
"разгладятся" в отрезок прямой (если данные описывают незамкнутую кривую) или стянутся
в точку (в случае замкнутой кривой).
Алгоритм остановки сглаживания основан на следующем факте: если данные сглажены
не достаточно, то длины ломаных, последовательно соединяющих точки до и после
сглаживания, существенно различны (после сглаживания длина ломаной уменьшается),
а если данные сглажены достаточно - длины этих ломаных почти совпадают.
Формулировка этого факта такова:
Пусть \(M_0,M_1,\ldots,M_n\) - исходные данные, а \(M_0^*,M_1^*,\ldots,M^*_n\)
- сглаженные и \[\Theta_n=\sum_{i=1}^{n}{|M_iM_{i-1}|},\]
\[\Theta_n^*=\sum_{i=1}^{n}{|M^*_iM^*_{i-1}|}.\]
Тогда математическое ожидание величины \(|\Theta_n-\Theta_n^*|\) пропорционально
величине \(\alpha\cdot n\cdot \varepsilon\cdot \Theta_n\), где \(\varepsilon\) -
уровень ошибки.
Если же
\[x_i=x(a+ih),\,\,y_i=y(a+ih)\,\,\,\,(i=0,1,\ldots,n;\,\,\,\,\,h=(b-a)/n),\]
и, функции \(x(t)\) и \(y(t)\) четырежды непрерывно дифференцируемы на отрезке
\([a,b]\) (т.е. если данные снимаются равномерно с гладкой кривой), то
\begin{equation}\label{eq:(1.45)}
\Delta l_n=|\Theta_n-\Theta_n^*|\le A\alpha h^2+O(h^3),
\end{equation}
где \[A=\int_{a}^{b}{|\theta(t)|dt}\] и
\begin{equation}\label{eq:(1.46)}
\theta(t)=\frac{1}{2}\,\frac{x'(t)x'''(t)+y'(t)y'''(t)}
{\sqrt{(x'(t))^2+(y'(t))^2}},
\end{equation}
т.е. величина \(|\Theta_n-\Theta_n^*|\) стремится к нулю пропорционально \(1/n^2\).
На рисунках приведен пример поведения длин ломаных в процессе сглаживания.
Сглаживание данных в этом случае достаточно провести 6 - 7 раз.
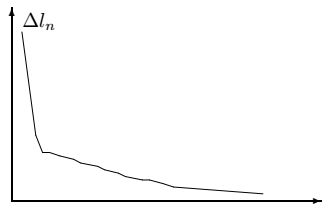
\(\alpha=1/3\)
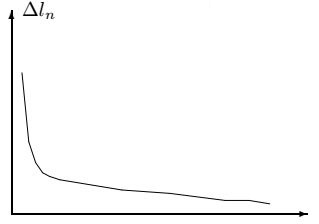
\(\alpha=1/6\)
Можно указать и критерий остановки процесса сглаживания. Для этого
достаточно записать дискретный аналог неравенства (\ref{eq:(1.45)}) (с
константой \(2A\) вместо \(A\) , чтобы
пренебречь погрешностью дискретизации, и величиной \(O(h^3)\)). Пусть
\[M_{i,k}(x_{i,k},y_{i,k})\,\,\,(i=0,1,\ldots,n)\]
- набор точек, полученных в результате \(k\)-го сглаживания,
\[\Theta_{n,k}=\sum_{i=1}^{n}{|M_{i,k}M_{i-1,k}|}\]
- длина ломаной, соединяющей точки, полученные в результате \(k\)-го
сглаживания, т.е.
\[\Theta_{n,k}=\sum_{i=1}^{n}\sqrt{\left(\Delta x_{i-1/2,k}\right)^2+
\left(\Delta y_{i-1/2,k}\right)^2}.\]
Если неравенство
\begin{equation}%\label{eq:(1.47)}
\Delta l_n=|\Theta_{n,k}-\Theta_{n.k-1}|\le2\alpha\Theta_{n,k}^2
\end{equation}
не выполняется, то сглаживание продолжаем, если выполняется - прекращаем.
Приведем доказательство основного в этом параграфе неравенства (\ref{eq:(1.45)}). Для
упрощения выкладок ограничимся случаем, когда данные описывают
замкнутую кривую. Для незамкнутой кривой добавляются лишь технические
трудности, связанные с доопределением точек у концов.
Итак, пусть \(x(t)\) и \(y(t)\) четырежды дифференцируемые на периоде \([0,T]\)
функции, \(h=T/n\) и \[x_i=x(ih),\,\,\,y_i=y(ih)\,\,\,\,(i\in Z),\]
\[x^*_i=x_i+\alpha \Delta^2x_i,\,\,\,\,y^*_i=y_i+\alpha \Delta^2y_i.\]
Кроме того, пусть
\[\theta_{n,i-1/2}=\sqrt{(x_i-x_{i-1})^2+(y_i-y_{i-1})^2},\]
\[\theta^*_{n,i-1/2}=\sqrt{(x^*_i-x^*_{i-1})^2+(y^*_i-y^*_{i-1})^2}\]
и\[\Theta_n=\sum_{i=1}^{n}{\theta_{n,i-1/2}},\,\,\,\,\,\,\,\,\,
\Theta^*_n=\sum_{i=1}^{n}{\theta^*_{n,i-1/2}}.\]
Тогда
\[(\theta^*_{n,i-1/2})^2=(x_i-x_{i-1}+\alpha(\Delta^2x_i-\Delta^2x_{i-1}))^2+
(y_i-y_{i-1}+\alpha(\Delta^2y_i-\Delta^2y_{i-1}))^2=
(\Delta^1x_{i-1/2}+\alpha\Delta^3x_{i-1/2})^2+
(\Delta^1y_{i-1/2}+\]
\[+\alpha\Delta^3y_{i-1/2})^2=
(\Delta^1x_{i-1/2})^2+(\Delta^1y_{i-1/2})^2+
\alpha^2\bigl((\Delta^3x_{i-1/2})^2+(\Delta^3y_{i-1/2})^2\bigr)+
\alpha\left(\Delta^1x_{i-1/2}\Delta^3x_{i-1/2}+
\Delta^1y_{i-1/2}\Delta^3y_{i-1/2}\right).\]
Таким образом, при \(h\to 0\) равномерно по \(i\) выполняется соотношение
\[(\theta^*_{n,i-1/2})^2=(\Delta^1x_{i-1/2})^2+(\Delta^1y_{i-1/2})^2+\alpha\left(x'_{i-1/2}x'''_{i-1/2}+y'_{i-1/2}y'''_{i-1/2}\right)h^4+O(h^6),\]
т.е.
\begin{equation}\label{eq:(1.48)}
(\theta^*_{n,i-1/2})^2=(\theta_{n,i-1/2})^2+\alpha\phi_{i-1/2}h^4+O(h^6),
\end{equation}
где \[\phi(t)=x'(t)x'''(t)+y'(t)y'''(t)\] и
\[\phi_{i-1/2}=\phi((2i-1)h/2).\]
Кроме того,
\[(\theta_{n,i-1/2})^2=((x'_{i-1/2})^2+(y'_{i-1/2})^2)h^2+O(h^4).\]
Отсюда и из (\ref{eq:(1.48)}) имеем
\[(\theta^*_{n,i-1/2})^2=
(\theta_{n,i-1/2})^2\left(1+\alpha\,\,\phi_{i-1/2}h^2/(\theta_{n,i-1/2})^2+O(h^4)\right)=\]
\[=(\theta_{n,i-1/2})^2\left(1+\alpha\,\,\psi_{i-1/2}h^2+O(h^4)\right),\]
где функция \(\psi(t)\) определена равенством
\[\psi(t)=\frac{\phi(t)}{(x'(t))^2+(y'(t))^2}.\]
Таким образом
\[\theta^*_{n,i-1/2}=\theta_{n,i-1/2}\sqrt{1+\alpha\,\,\psi_{i-1/2}h^2+O(h^4)}.\]
Кроме того, при \(\beta\to 0\)
\[\sqrt{1+\beta}=1+\frac{\beta}{2}+O(\beta^2).\]
Поэтому \[\sqrt{1+\alpha\,\,\psi_{i-1/2}h^2+O(h^4)}=
1+\frac{1}{2}\alpha\,\,\psi_{i-1/2}h^2+O(h^4).\]
Из этого и полученных ранее соотношений следует, что при \(h\to 0\) равномерно по
\(i\) выполняется асимптотическое равенство
\[\theta^*_{n,i-1/2}=\theta_{n,i-1/2}
\left(1+\frac{1}{2}\alpha\,\,\psi_{i-1/2}h^2+O(h^4)\right)=\theta_{n,i-1/2}+\alpha\,\,\theta_{n,i-1/2}\psi_{n,i-1/2}h^2+O(h^4).\]
Используя теперь равенство (\ref{eq:(1.46)}), получим
\[\theta^*_{n,i-1/2}-\theta_{n,i-1/2}=\alpha\,\,\theta_{n,i-1/2}h^3+O(h^4)\]
и, следовательно,
\[\Theta^*_n-\Theta_n=\alpha\,\, h^2
\left(h\sum_{i=1}^{n}{\theta_{n,i-1/2}}\right)+O(h^3).\]
Остается учесть, что
\[h\sum_{i=1}^{n}{\theta_{n,i-1/2}}=\int_{a}^{b}{\theta(t)dt}+O(h^2).\]
В заключение приведем формальный алгоритм сглаживания.
Даны массивы:
\[x_0,x_1,\ldots,x_n,\,\,\,\,\,\,\,y_0,y_1,\ldots,y_n.\]
Выбираем \(\alpha\,\,\in[0,1/3]\), и вычисляем величины
\[x_{-1}=\frac{1}{3}(4x_0+x_1-2x_2),\,\,\,\,\,\,\,x_{n+1}=\frac{1}{3}
(4x_n+x_{n-1}-2x_{n-2}),\]
\[y_{-1}=\frac{1}{3}(4y_0+y_1-2y_2),\,\,\,\,\,\,\,y_{n+1}=\frac{1}{3}
(4y_n+y_{n-1}-2y_{n-2}),\]
\[\Delta^2x_i=x_{i+1}-2x_i+x_{i-1}\,\,\,\,\,\,\,(i=0,1,\ldots,n),\]
\[\Delta^2y_i=y_{i+1}-2y_i+y_{i-1}\,\,\,\,\,\,\,(i=0,1,\ldots,n).\]
Найдем сглаженные данные
\[x_i^*=x_i+\alpha\,\, \Delta^2x_i\,\,\,\,\,\,\,(i=0,1,\ldots,n),\]
\[y_i^*=y_i+\alpha\,\, \Delta^2y_i\,\,\,\,\,\,\,(i=0,1,\ldots,n),\]
и вычислим величины
\[l_i=\sqrt{(x_i-x_{i-1})^2+(y_i-y_{i-1})^2}\,\,\,\,\,\,\,(i=1,2,\ldots,n),\]
\[l^*_i=\sqrt{(x^*_i-x^*_{i-1})^2+(y^*_i-y^*_{i-1})^2}\,\,\,\,\,\,\,(i=1,2,\ldots,n)\]
и\[L=\sum_{i=1}^{n}{l_{i}},\,\,\,\,\,\,\,\,\,\,L^*=\sum_{i=1}^{n}{l^*_{i}}.\]
Для того, чтобы определить достаточно ли сглажены данные, вычислим
\[qx_i=x_i-x_{i-1}\,\,\,\,\,\,\,\,\,\,\,(i=1,2,\ldots,n)\] и
\[px_i=qx_{i+1}-2qx_i+qx_{i-1}\,\,\,\,\,\,\,\,\,(i=1,2,\ldots,n)\]
и аналогичные величины для \(qy_i\) и \(py_i\). Тогда дискретным аналогом функции
\(\theta(t)\) является набор чисел
\[T_i=(qx_i\cdot px_i+qy_i\cdot py_i)/(2l^*_i),\]
а дискретным аналогом \(A\) - число
\[A=\sum_{i=1}^{n}{l^*_i\,\,T_i}.\]
Если будет выполняться условие
\[|L-L^*|\le A\alpha\,\,\left(\frac{L^*}{n}\right)^2,\]
то процесс сглаживания можно считать законченным. В противном случае все
нужно повторить, взяв в качестве исходной информации массивы
\[x^*_0,x^*_1,\ldots,x^*_n,\,\,\,\,\,\,y^*_0,y^*_1,\ldots,y^*_n.\]
Алгоритмы сглаживания повышенной точности
Приведенный в предыдущем параграфе алгоритм сглаживания является весьма
эффективным в случаях, когда данных много, например, когда они снимаются
с показаний копира или сканера.
Однако, при неумелом использовании его, в случае, когда число данных невелико,
мы можем перегладить данные в отрезок прямой, когда кривая незамкнутая и стянуть
в точку, если кривая замкнута. В этом параграфе мы приведем
более точный (но и более сложный) алгоритм сглаживания. В основе его лежит
формула
\begin{equation}\label{eq:(1.49)}
M_i^*=M_i-\beta\Delta^4M_i.
\end{equation}
Для того, чтобы алгоритм работал, необходимо выполнение следующий требований:
- обосновать равенство (\ref{eq:(1.49)}) и выбор \(\beta\);
- доопределить точки \(M_{-2}\), \(M_{-1}\), \(M_{n+1}\) и \(M_{n+2}\) (чтобы
было возможно найти величины \(\Delta^4M_0\), \(\Delta^4M_1\), \(\Delta^4M_{n-1}\),
\(\Delta^4M_n\)) и повторять сглаживание;
- найти критерий остановки алгоритма сглаживания.
Для того, чтобы ответить на первый вопрос, приведем сначала другой подход к
обоснованию алгоритма, описанного в предыдущем параграфе.
Пусть дан набор из \(n+1\) точки \(M_i(x_i,y_i)\) \((i=0,1,2,\ldots,n)\) на плоскости.
Этому набору поставим в соответствие два набора точек \[(0,x_0), (1,x_1),\ldots,(n,x_n)\] и
\[(0,y_0), (1,y_1),\ldots,(n,y_n).\]
Для каждой тройки чисел \((i-1,x_{i-1})\), \((i,x_i)\) и \((i+1,x_{i+1})\) определим
коэффициенты \(a\) и \(b\) прямой \(at+b\) так, чтобы сумма квадратов ошибок
\[\Phi(a,b)=(x_{i-1}-(a(i-1)+b))^2+(x_{i}-(ai+b))^2+(x_{i+1}-(a(i+1)+b))^2\]
была минимальной.
Пусть \(a^*\) и \(b^*\) решение этой задачи на минимум. Тогда мы полагаем
\[x_i^*=a^*i+b^*.\]
Необходимое и достаточное условие минимума в нашей задаче таково
\[
\cases{\partial \Phi/\partial a=0,\cr\cr
\partial \Phi/\partial b=0,}
\]
или, что то же,
\[\cases{a((i-1)^2+i^2+(i+1)^2)+b(i-1+i+i+1)=\cr\cr
\,\,\,\,\,\,\,\,=x_{i-1}(i-1)+x_ii+x_{i+1}(i+1),\cr\cr
a(i-1+i+i+1)+3b=x_{i-1}+x_i+x_{i+1}.}\]
Отсюда следует, что
\[a^*=\frac{x_{i+1}-x_{i-1}}{2},\,\,\,\,\,\,b^*=\frac{x_{i+1}+x_i+x_{i-1}}{3}-
\frac{x_{i+1}-x_{i-1}}{2}\,i\]
и, следовательно, \[x_i^*=\frac{x_{i+1}+x_i+x_{i-1}}{3}.\]
Применив ту же процедуру к данным \((i,y_i)\) \((i=0,1,\ldots,n)\), мы придем
к алгоритму сглаживания по "центрам тяжести треугольников".
Перейдем к построению алгоритма повышенной точности. Для каждой пятерки чисел
\[(i-2,x_{i-2}),\,\,(i-1,x_{i-1}),\,\,(i,x_{i}),\,\,\,\,
(i+1,x_{i+1}),\,\,(i+2,x_{i+2})\]
определим коэффициенты \(a\), \(b\) и \(c\) параболы \(at^2+bt+c\) из условия минимума
суммы квадратов ошибок
\[\sum_{k=i-2}^{i+2}{(x_k-(ak^2+bk+c))^2}\,\,\,\,(i=2,3,\ldots,n-2).\]
Если \(a^*\), \(b^*\) и \(c^*\) - решение этой задачи на минимум, то полагаем
\begin{equation}\label{eq:(1.50)}
x_i^*=a^*i^2+b^*i+c^*.
\end{equation}
Проведя необходимые в этом случае вычисления (находим и приравниваем к нулю
частные производные по \(a\), \(b\), \(c\,\) и решая полученную при этом систему
трех линейных уравнений с тремя неизвестными), находим значения \(a^*\), \(b^*\) и \(c^*\).
Затем, подставляя эти значения в (\ref{eq:(1.50)}), получаем
\begin{equation}\label{eq:(1.51)}
x^*_i=x_i-\frac{3}{35}\Delta^4x_i\,\,\,\,(i=2,3,\ldots,n-2).
\end{equation}
Аналогично получаем
\begin{equation}\label{eq:(1.52)}
y^*_i=y_i-\frac{3}{35}\Delta^4y_i\,\,\,\,(i=2,3,\ldots,n-2).
\end{equation}
Итак, алгоритм сглаживания повышенной точности состоит в том, что новые значения
\(x_i^*\) и \(y^*_i\) для всех \(i=0,1,2,\ldots,n\) вычисляются по формулам
\[
\cases{x_i^*=x_i-\beta\Delta^4x_i,\cr\cr
y_i^*=y_i-\beta\Delta^4y_i,},
\]
где \(0\lt\beta\lt3/35\).
Для того, чтобы алгоритм работал, необходимо доопределить точки
\[M_{-2}(x_{-2},y_{-2}),\,\,\,M_{-1}(x_{-1},y_{-1}),\,\,\,M_{n+1}(x_{n+1},
y_{n+1}),\,\,\,M_{n+2}(x_{n+2},y_{n+2}).\]
К задаче доопределения недостающих точек мы подойдем с тех же позиций.
Определим коэффициенты \(a\), \(b\) и \(c\) из условия минимума суммы квадратов ошибок
\[\Phi(a,b,c)=\sum_{i=0}^{4}{(x_i-p(i))^2},\]
где
\begin{equation}%\label{eq:(1.53)}
p(t)=at^2+bt+c
\end{equation}
и положим
\begin{equation}\label{eq:(1.54)}
x_{-1}=p(-1),\,\,\,x_{-2}=p(-2).
\end{equation}
Необходимые и достаточные условия экстремума имеют вид
\[\cases{\partial\Phi/\partial a=0;\cr\cr
\partial\Phi/\partial b=0;\cr\cr
\partial\Phi/\partial c=0}\]
или\[\sum_{i=0}^{4}{p(i)i^2}=\sum_{i=0}^{4}{x_i i^2},\]
\[\sum_{i=0}^{4}{p(i)i}=\sum_{i=0}^{4}{x_i i},\]
\[\sum_{i=0}^{4}{p(i)}=\sum_{i=0}^{4}{x_i}.\]
Решая эту систему, и, подставляя найденные значения \(a\), \(b\), \(c\) в (\ref{eq:(1.54)}), получим
\begin{equation}\label{eq:(1.55)}
x_{-1}=\frac{1}{70}(126x_0-56x_2-42x_3+42x_4),
\end{equation}
\begin{equation}%\label{eq:(1.56)}
x_{-2}=\frac{1}{35}(105x_0-14x_1-63x_2-42x_3+49x_4).
\end{equation}
Аналогично находим
\begin{equation}%\label{eq:(1.57)}
x_{n+1}=\frac{1}{70}(126x_n-56x_{n-2}-
42x_{n-3}+42x_{n-4}),
\end{equation}
\begin{equation}\label{eq:(1.58)}
x_{n+2}=\frac{1}{35}(105x_n-14x_{n-1}-63x_{n-2}-
42x_{n-3}+49x_{n-4}).
\end{equation}
Точно также доопределяем и значения \(y_{-1}\), \(y_{-2}\), \(y_{n+1}\), \(y_{n+2}\).
Таким образом мы пришли к следующему алгоритму сглаживания повышенной точности:
-
доопределяем точки \((x_i,y_i)\) для \(i=-2,-1,n+1,n+2\), исходя из равенств
(\ref{eq:(1.55)}) - (\ref{eq:(1.58)}) и аналогичных равенств для \(y_i\);
-
выбираем \(0\lt\beta\lt3/35\).
-
После этого вычисляем новые точки \((x_i^*,y_i^*)\) в соответствии с равенствами
(\ref{eq:(1.51)}) - (\ref{eq:(1.52)}).
Остался невыясненным вопрос сколько раз можно повторить процесс сглаживания без
ущерба для качества информации. Ответить на этот вопрос нам поможет следующее
утверждение, доказательство которого аналогично доказательству приведенному в
предыдущем параграфе. Иллюстрацией этого утверждения является рисунок:
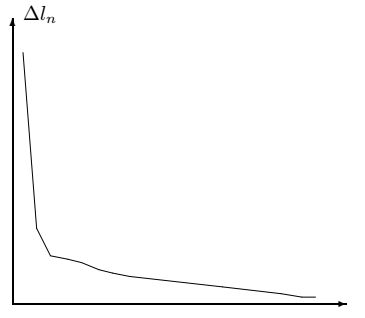
\(\alpha=-3/35\)
Пусть \(l_n\) - длина ломаной соединяющей точки \((x_i,y_i)\,\,\) \((i=0,1,\ldots,n)\), а
\(l_n^*\) - длина ломаной соединяющей точки \((x_i^*,y_i^*)\,\,\) \((i=0,1,\ldots,n)\).
Тогда математическое ожидание разности \(|l_n-l_n^*|\) пропорционально
величине \(n\,\,\beta\,\,\sigma \,\,l_n\). Если же \(x_i=x(\alpha+ih)\), \(y_i=y(\alpha+ih)\)
\((i=0,1,\ldots,n)\), где функции \(x(t)\) и \(y(t)\) имеют пять непрерывных
производных на отрезке \([a,b]\), то
\[
\Delta l_n=|l_n-l_n^*| \le B \beta h^4+O(h^6),
\]
где \[B=\int_{a}^{b}{|\Psi(t)|dt}\] и
\[\Psi(t)=\frac{1}{2}\frac{x'(t)x^{(5)}(t)+y'(t)y^{(5)}(t)}
{\sqrt{(x'(t))^2+(y'(t))^2}}.\]
Если исходные данные совсем редки (к примеру, если они снимаются с опорных точек
с помощью измерительной головки), то применять рассмотренные выше алгоритмы не
целесообразно.
В этих случаях применяют другие методы сглаживания исходных данных, например,
методы сплайн - сглаживания или способы сглаживания данных базирующиеся на
различных модификациях метода наименьших квадратов.
Возможна и другая крайность, когда при снятии информации погрешность превышает
длину звена ломаной между двумя соседними точками на снимаемой кривой. В этом
случае может получиться так, что большое значение параметра сглаживания \(\alpha\)
или \(\beta\) нельзя брать из- за вносимых при этом искажений, а малое значение
параметра не подходит ввиду необходимости в этом случае многократного
использования алгоритма сглаживания.
В таком случае используются либо алгоритмы, основанные на методах спектрального
анализа (методы анализа Фурье), либо алгоритмы, построенные на основе
интерполяционных или почти интерполяционных в среднем сплайнов.
В тех случаях, когда на исходную информацию налагаются регулярные знакопеременные
частоты (наведенные колебания), как правило применяют методы анализа Фурье и
различные демпферы.
