EM-алгоритм

Событие	Вероятность
\(x_1\in M_1\)	\(P(x_1)=\frac{1}{2}\)
\(x_2\in M_2\)	\(P(x_2)=u\)
\(x_3\in M_3\)	\(P(x_3)=2u\)
\(x_4\in M_4\)	\(P(x_4)=\frac{1}{2}-3u\)

Событие	Наблюдаемое явление
\(x_1\in M_1\)	\(a\)
\(x_2\in M_2\)	\(b\)
\(x_3\in M_3\)	\(c\)
\(x_4\in M_4\)	\(d\)

Событие	Наблюдаемое явление
\(x_1,x_2\in \{M_1 \|\| M_2\}\)	\(h\)
\(x_3\in M_3\)	\(c\)
\(x_4\in M_4\)	\(d\)

E-шаг: Опираясь на предыдущую оценку \(u\), вычислим скрытую переменную \(b\) \[ b^{(k)}=\frac{u^{(k-1)}}{\frac{1}{2}+u^{(k-1)}}h. \]

Графическая интерпретация одной итерации EМ-алгоритма.

Подробнее об ЕМ-алгоритме.

Рассмотрим один из методов решения задачи разделения смеси \[p(x) = \sum_{i=1}^k\omega _i p_i (x)\] в предположении, что известен только общий вид распределения вероятности и нужно оценить его параметры. Достаточно часто известно, что искомое распределение представляет собой линейную комбинацию, например, нормальных или биномиальных распределений. В этом случае говорят, что данное распределение представляет собой смесь нормальных, биномиальных (либо иных) распределений. В частности, если известно, что функция плотности вероятности каждого класса есть нормальное распределение \(N\left( {\mu _i ,\sigma _i^2 } \right)\), то нужно оценить параметры \(\mu _i ,\sigma _i\). Для байесовского классификатора эти параметры известны.
Пусть \(p\left( {x|\theta _i } \right)\) плотность вероятности того, что наблюдение \(x\) получено из компоненты \(p_i\) смеси распределений (\(\theta _i\) - параметры распределения).

Тогда \[ p\left( {x|\theta _i } \right) = p(x)P\left( {\left. {\theta _i } \right|x} \right) = \omega _i p_i (x). \] Апостериорную вероятность \(P\left( {\left. {\theta _i } \right|x} \right)\) того, что наблюдение \(x_j\) получено из i-й компоненты смеси, обозначим через \(g_{i,j}\). Из формулы полной вероятности выпишем условие нормировки \[ \sum_{i = 1}^k {g_{i,j} = 1,j = 1,...,n.} \] Тогда при известных \(\omega _i \) и \(p_i (x_j )\) из теоремы Байеса легко получить \[ g_{i,j} = \frac{\omega _i p_i (x_j )}{\sum\nolimits_{\nu = 1}^k {\omega _\nu p_\nu (x_j )} },i = 1,...k,j = 1,...,n. \] Функция \[ F\left( \Theta \right) = \prod_{j = 1}^n {p(x_j |\theta _i )} \] называется функцией правдоподобия от \(\Theta = \left\{ {\left( {\omega _i ,\theta _i } \right)} \right\}_{i = 1}^k \) по выборке \(X = \left\{ {x_1,...,x_n } \right\}\).
Традиционно через MLE (Maximum Likelihood Estimate) - метод максимального правдоподобия, называют метод, доставляющий \[ \hat {\Theta } = \arg \mathop {\max }_\Theta \left( {F\left( \Theta \right)} \right). \] Заметим, что в силу монотонности алгоритма \[ \hat {\Theta } = \arg \mathop {\max }_\Theta \left( {F\left( \Theta \right)} \right)= \arg \mathop {\max }_\Theta \left( {\ln \left( {F\left( \Theta \right)} \right)} \right). \] Покажем, что при известных \(g_{i,j}\), используя MLE, можно получить эффективный метод разделения параметров смеси. Запишем MLE в виде \[ \ln F\left( \Theta \right) = \ln \prod_{j = 1}^n {p(x_j |\theta _i )} = \sum_{j = 1}^n {\ln \sum_{i = 1}^k {\omega _i p_i \left( {x_j } \right)} } \to \mathop {\max }_\Theta \mbox{ при условии } \quad \sum_{i = 1}^k {\omega _i = 1.} \] Используя метод множителей Лагранжа, выпишем лагранжиан этой задачи \[ L\left( {\Theta ,\Omega } \right) = \sum_{j = 1}^n {\ln \sum_{i = 1}^k {\omega _i p_i \left( {x_j } \right)} } - \lambda \left( {\sum_{i = 1}^k {\omega _i } - 1} \right). \] Приравнивая частные производные по неизвестным параметрам нулю, получаем \begin{equation}\label{eq5.6} \frac{\partial }{\partial \omega _i }L\left( {\Theta ,\Omega } \right) =\sum_{j = 1}^n {\frac{p_i \left( {x_j } \right)}{\sum\nolimits_{\nu = 1}^k {\omega _\nu p_\nu (x_j )} }} - \lambda =0,i = 1,...,k.. \end{equation} Умножая обе части полученного соотношения на \(\omega _i\) и суммируя их по всем \(i\), получаем \[ \sum_{j = 1}^n {\sum_{i = 1}^k {\frac{\omega _i p_i \left( {x_j } \right)}{\sum\nolimits_{\nu = 1}^k {\omega _\nu p_\nu (x_j )} }} } =\lambda \sum_{i = 1}^k {\omega _i } . \] Замечая, что \[ \sum_{i = 1}^k {\frac{\omega _i p_i \left( {x_j } \right)}{\sum\nolimits_{\nu = 1}^k {\omega _\nu p_\nu (x_j )} }} = 1\mbox{ и } \quad \sum_{i = 1}^k {\omega _i } = 1, \] получаем \[ \sum_{j = 1}^n 1 = \lambda .\mbox{ и } \quad \lambda = n. \] Таким образом, умножая (\ref{eq5.6}) на \(\omega_i\), имеем \[ \omega _i = \frac{1}{n}\sum_{j = 1}^n {\frac{\omega _i p_i \left( {x_j } \right)}{\sum\nolimits_{\nu = 1}^k {\omega _\nu p_\nu (x_j )} }} =\frac{1}{n}\sum_{j = 1}^n {g_{i,j} } ,i = 1,...,k.. \] Теперь, замечая, что \(p_i (x)\) зависит от \(\theta _i \), возьмем частную производную лагранжиана от \(\theta _i\) и приравняем ее нулю \[ \frac{\partial }{\partial \theta _i }L\left( {\Theta ,\Omega } \right) =\sum_{j = 1}^n {\frac{\omega _i }{\sum\nolimits_{\nu = 1}^k {\omega _\nu p_\nu (x_j )} }\frac{\partial }{\partial \theta _i }p_i \left( {x_j }\right)} = 0,i = 1,...,k. \] Умножим числитель и знаменатель каждого слагаемого на \(p_i \left( {x_j } \right)\), соответственно \[ \frac{\partial }{\partial \theta _i }L\left( {\Theta ,\Omega } \right) =\sum_{j = 1}^n {\frac{\omega _i p_i \left( {x_j } \right)}{\sum\nolimits_{\nu = 1}^k {\omega _\nu p_\nu (x_j )} }\frac{\partial }{\partial \theta _i }\ln p_i \left( {x_j } \right)} = \sum_{j = 1}^n {g_{i,j} \frac{\partial }{\partial \theta _i }\ln p_i \left( {x_j } \right)} = 0,i = 1,...,k. \] Отсюда получаем \[ \frac{\partial }{\partial \theta _i }\sum_{j = 1}^n {g_{i,j} \ln p_i \left( {x_j } \right)} = 0,i = 1,...,k, \] что совпадает с необходимым условием максимума в задаче максимизации функции правдоподобия с весом \[ \sum_{j = 1}^n {g_{i,j} \ln p_i \left( {x_j } \right)} \to \mathop {\max }_\Theta ,i = 1,...,k. \]

Е-шаг (expectation).

M-шаг (maximization).

Заметим, что если известен вид функции плотности, то задачу MLE можно выписать в явном виде.

Рассмотрим случай, когда известно, что смесь состоит из нормальных распределений \(N\left( {\mu _i ,\sigma _i^2 } \right)\), где \(i= 1,...,k\).
Е-шаг будет выглядеть следующим образом \[ g_{i,j} = \frac{\omega _i p(x_j|\mu_j,\sigma_j)}{\sum_{\nu = 1}^k {\omega _\nu p_\nu (x_\nu|\mu_j,\sigma_j )} },i = 1,...k,j = 1,...,n, \] где \[ p(x|\mu_i,\sigma_i) = \frac{1}{\sigma_i \sqrt {2\pi } }\exp \left( { - \frac{\left( {x - \mu_i } \right)^2}{2\sigma_i^2}} \right). \] Для М- шага задача \[ \sum_{j = 1}^n {g_{i,j} \ln p_i \left( {x_j } \right)} \to \mathop {\max }_\Theta ,i = 1,...,k \] запишется в виде \[ \sum_{j = 1}^n {g_{i,j} \ln \left( {\frac{1}{\sigma _i \sqrt {2\pi } }\exp \left( { - \frac{\left( {x_j - \mu _i } \right)^2}{2\sigma _i^2 }} \right)} \right)} \to \mathop {\max }_\Theta ,i = 1,...,k, \] или, что то же, \[ G\left( {\left\{ {\mu _i ,\sigma _i } \right\}_{i = 1}^k } \right) = \sum_{j = 1}^n {g_{i,j} \left( { - \ln \left( {\sigma _i \sqrt {2\pi } } \right) - \frac{\left( {x_j - \mu _i } \right)^2}{2\sigma _i^2 }} \right)} \to \mathop {\max }_\Theta,\] \[i = 1,...,k. \] Приравнивая частные производные нулю, получаем \[ \frac{\partial }{\partial \mu _i }G\left( {\left\{ {\mu _\nu ,\sigma _\nu } \right\}_{\nu = 1}^k } \right) = - \sum_{j = 1}^n {g_{i,j} \frac{\left( {x_j - \mu _i } \right)}{\sigma _i^2 }} = 0, \] отсюда \[ \mu _i = \frac{\sum_{j = 1}^n {g_{i,j} x_j } }{\sum_{j = 1}^n {g_{i,j} } }. \] Аналогично, \[ \frac{\partial }{\partial \sigma _i }G\left( {\left\{ {\mu _\nu ,\sigma _\nu} \right\}_{\nu = 1}^k } \right) = - \sum_{j = 1}^n {g_{i,j} \left({\frac{1}{\sigma _i } - \frac{\left( {x_j - \mu _i } \right)^2}{\sigma _i^3}} \right)} = \] \[- \sum_{j = 1}^n {g_{i,j} \left( {\frac{\sigma _i^2 - \left( {x_j - \mu _i } \right)^2}{\sigma _i^3 }} \right) = } 0, \] таким образом, отсюда получаем \[ \sigma _i^2 = \frac{\sum_{j = 1}^n {g_{i,j} \left( {x_j - \mu _i } \right)^2} }{\sum_{j = 1}^n {g_{i,j} } }, \] что позволяет получить параметры распределения в явном виде.
Заметим, что для многомерного случая нормальное распределение описывается следующим соотношением \[ p\left( {x\left| {\mu _i ,\Sigma _i } \right.} \right) = \frac{1}{\left( {2\pi } \right)^{n / 2}\left| {\Sigma _i^{ - 1} } \right|^{1 / 2}}\exp \left( { - \frac{1}{2}\left( {x - \mu _i } \right)^T\Sigma _i^{ - 1} \left( {x - \mu _i } \right)} \right), \] где \(\Sigma \)-корреляционная матрица. Использование MLE позволяет оценить параметры распределения следующим образом \[ \mu _i = \frac{\sum_{j = 1}^n {g_{i,j} x_j } }{\sum_{j = 1}^n {g_{i,j} } }, \quad \Sigma _i = \frac{\sum_{j = 1}^n {g_{i,j} \left( {x_j - \mu _i } \right)\left( {x_j - \mu _i } \right)^T} }{\sum_{j = 1}^n {g_{i,j} } }. \] Значение весов определяется так же \[ \omega _i = \frac{1}{n}\sum_{j = 1}^n {g_{i,j} } ,i = 1,...,k, \] где \[ g_{i,j} = \frac{\omega _i p(x_j|\mu_j,\Sigma_j)}{\sum_{\nu = 1}^k {\omega _\nu p_\nu (x_\nu|\mu_j,\Sigma_j )} },i = 1,...k,j = 1,...,n, \]

Пример результата работы EM-алгоритма.

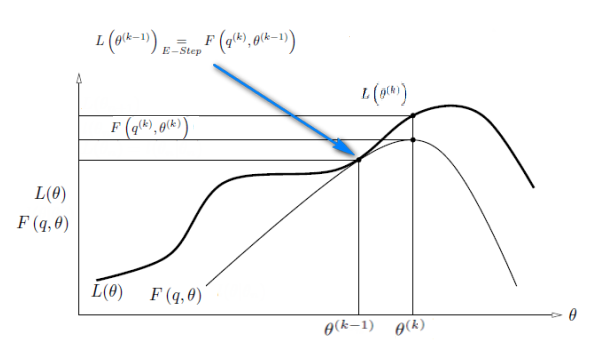
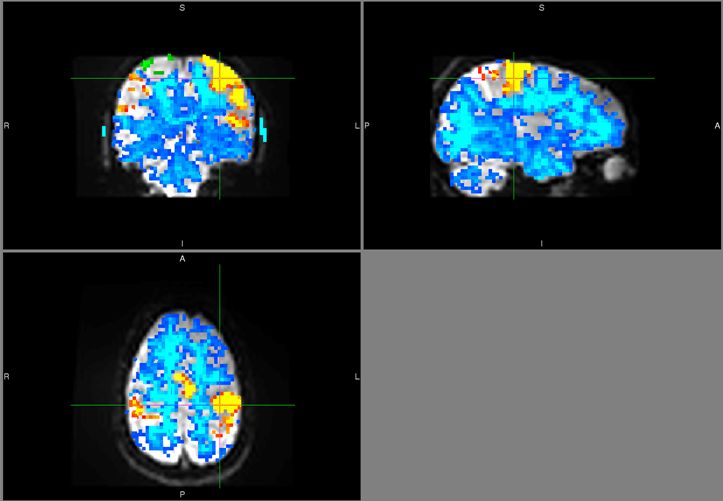
В качестве иллюстрации ЕМ-алгоритма используем пример, приведенный Andrew Moore’s tutorial:

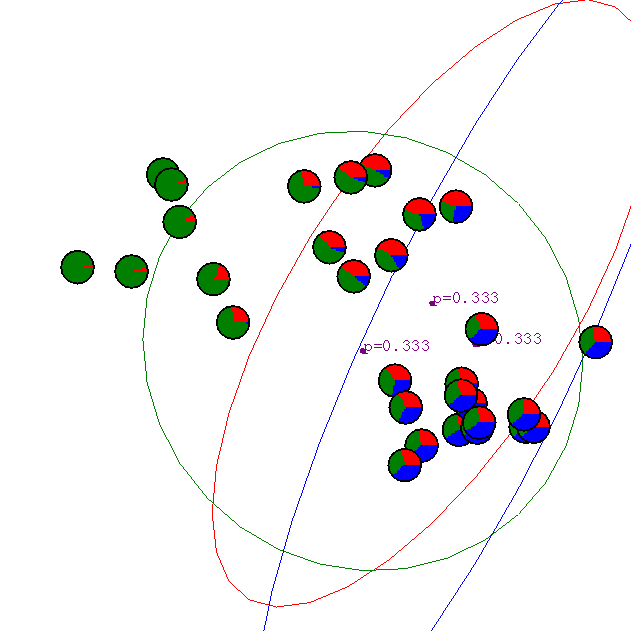
Начальное приближение.

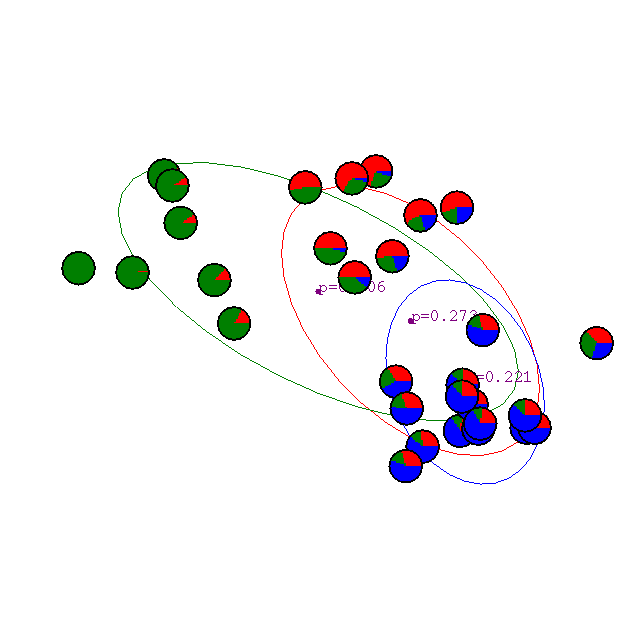
Результат первой итерации.

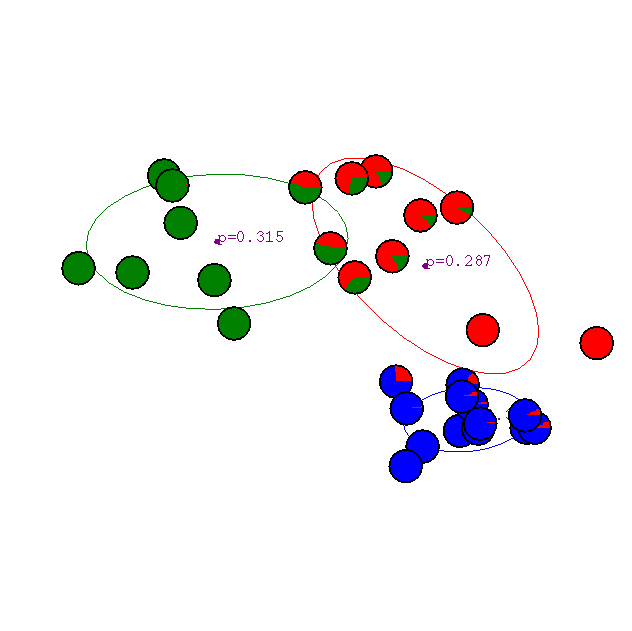
Что получилось после шестой итерации.

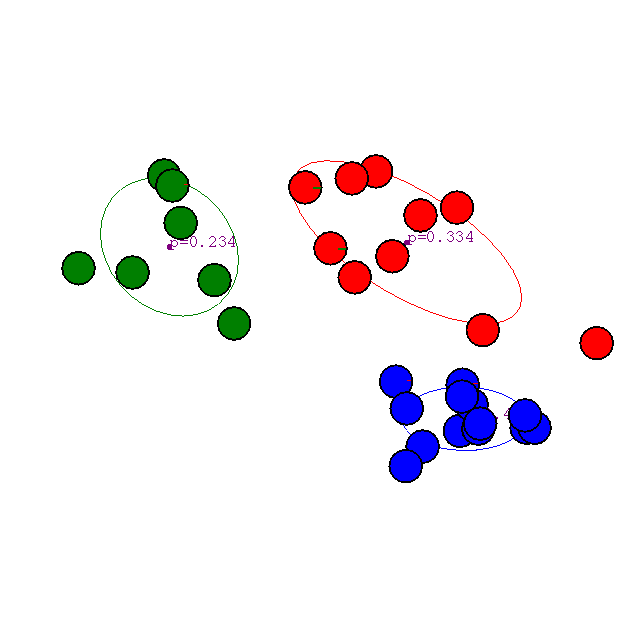
Результат применения двадцати итераций

Приведем простой пример применения EM-алгоритма для случая одной переменной.
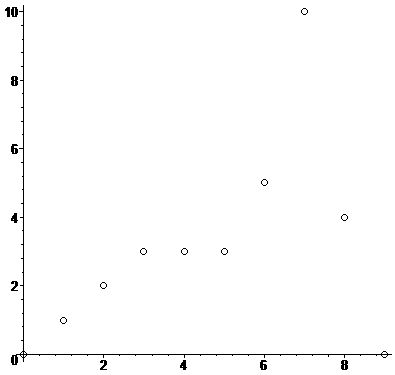
Для данных смеси \(x_i\) \(i=0,1,...,N\), где \(N=10\)

x	0	1	2	3	3	3	6	10	4	0
i	0	1	2	3	4	5	6	7	8	9

построим разделение этой смеси линейной комбинацией двух функций Гаусса \[ P(t)=\omega_0\frac{1}{\sqrt{2\pi}\sigma_0}\exp\left(-\frac{(t-\mu_0)^2}{2\sigma^2_0}\right)+ \omega_1\frac{1}{\sqrt{2\pi}\sigma_1}\exp\left(-\frac{(t-\mu_1)^2}{2\sigma^2_1}\right). \] Данная задача представляет собой задачу разделения гистограмм, постановка которой несколько отличается от классической задачи разделения смеси распределений вероятностей, поэтому используем модификацию ЕМ-алгоритма, с учетом этих особенностей.
Вначале проведем инициализацию \[ g_{0,i}=\left\{ \begin{array}{ll} 1, & \hbox{ для } i=0,...,N/2-1 \\ 0, & \hbox{ для } i=N/2,...,N-1, \end{array} \right. g_{1,i}=\left\{ \begin{array}{ll} 0, & \hbox{ для } i=0,...,N/2-1 \\ 1, & \hbox{ для } i=N/2,...,N-1. \end{array} \right. \]

g_0	1	1	1	1	1	0	0	0	0	0
g_1	0	0	0	0	0	1	1	1	1	1
i	0	1	2	3	4	5	6	7	8	9

M-шаг Вычислим веса \[ \omega_j=\frac{1}{N}\sum_{i=0}^{N-1}g_{j,i}x_i, j=0,1. \] Получаем \(\omega_0=0.9\) и \(\omega_1=2.3\), далее найдем матожидание и дисперсию \[ \mu_j=\frac{1}{N}\sum_{i=0}^{N-1}\frac{g_{j,i}i}{\omega_j}x_i, \sigma^2_j=\frac{1}{N}\sum_{i=0}^{N-1}\frac{g_{j,i}(i-\mu_i)^2}{\omega_j}x_i, j=0,1. \] \(\mu_0=\frac{26}{9}\), \(\mu_1=\frac{153}{23}\) и \(\sigma^2_0=\frac{80}{81}\), \(\sigma^2_1=\frac{442}{529}\).
На следующем шаге найдем приближенное значение смеси \[ P_i=\sum_{j=0}^1\omega_jp_{j,i},i=0,1,...,N-1, \] где \[ p_{j,i}=\frac{1}{\sqrt{2\pi}\sigma_j}\exp\left(-\frac{(i-\mu_j)^2}{2\sigma^2_j}\right),i=0,...,N-1,j=0,1. \] Отсюда

P	0.005283916006	0.05934794968	0.2421790495	0.3593770365	0.2338353195	0.2082958290	0.9337804754	0.7809344621	0.3384793202	0.03707425040
i	0	1	2	3	4	5	6	7	8	9

E-шаг Обновим значения \[ g_{j,i}=\frac{\omega_jp_{j,i}}{P_i} \]

g_0	0.9999999994	0.9999999158	0.9999901639	0.9990458670	0.9284007156	0.1618314989	0.003445026	0.0000744	0.00000193	0.00000006
g_1	0.0000000006	0.0000000842	0.00000983	0.0009541	0.07159928445	0.8381685009	0.9965549736	0.9999255828	0.9999980734	0.9999999401
i	0	1	2	3	4	5	6	7	8	9

Далее переходим к следующей итерации, проводя М-шаг, потом Е-шаг и так далее.
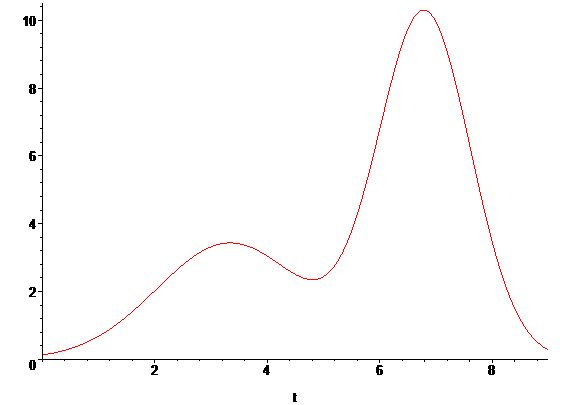
Уже после десятой итерации имеем \(\omega_0=1.114632089\), \(\omega_1=2.085367911\), \(\mu_0=3.340349207\), \(\mu_1=6.798195901\), \(\sigma^2_0=1.693040680\), \(\sigma^2_1=0.6711715483\). Получаем \[ P(t)=\omega_0\frac{1}{\sqrt{2\pi}\sigma_0}\exp\left(-\frac{(t-\mu_0)^2}{2\sigma^2_0}\right)+ \omega_1\frac{1}{\sqrt{2\pi}\sigma_1}\exp\left(-\frac{(t-\mu_1)^2}{2\sigma^2_1}\right)= 0.3417495181\exp\left(-\frac{(t-3.340349207)^2}{3.386081360}\right)+ 1.015490777\exp\left(-\frac{(t-6.798195901)^2}{1.342343097}\right). \] Остается провести масштабирование (так как мы восстанавливали не вероятности, а, по сути, гистограмму). Для этой цели найдем масштабирующий коэффициент S, который выбирается так, чтобы площадь полученной смеси была равна площади гистограммы, то есть \[ S=\frac{\sum_ix_i}{\int_0^NP(t)dt}=\frac{32}{3.186774135}=10.04150236, \] и получим результат \[ S\left(\omega_0\frac{1}{\sqrt{2\pi}\sigma_0}\exp\left(-\frac{(t-\mu_0)^2}{2\sigma^2_0}\right)+ \omega_1\frac{1}{\sqrt{2\pi}\sigma_1}\exp\left(-\frac{(t-\mu_1)^2}{2\sigma^2_1}\right)\right)= 3.431678591\exp\left(-\frac{(t-3.340349207)^2}{3.386081360}\right)+ 10.19705303\exp\left(-\frac{(t-6.798195901)^2}{1.342343097}\right). \]

Применение ЕМ-алгоритма к сегментации изображений.

Сегментация или разделение изображения на области, для которых выполняется определенный критерий однородности, является достаточно распростаненной задачей обработки и анализа изображений (Image Processing). Существует много различных методов сегментации изображений, продемонстрируем применение ЕМ-алгоритма к решению этой задачи.

Количество сегментов (от 2 до 16)

Для этой цели построим гистограмму цвета для каждой компоненты - красного, зеленого и синего. По оси \(x\) изменяется интенсивность цвета от 0 до 255, а по оси \(y\) - количество пикселей с данной интенсивностью.
Считая, что каждая гистограмма представляет собой смесь функций Гаусса \[ \sum_{i=1}^n\frac{w_i}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right), \] применим ЕМ-алгоритм с заданным количеством элементов смеси \(n\) (это же количество сегментов, на которое мы разбиваем каждую цветовую плоскость изображения). И как результат, пусть множество значений интенсивности \(X_j=[x_{j},x_{j+\nu_j})\) такое, что \[ \forall x\in X_j: \frac{w_j}{\sigma_j\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_j)^2}{2\sigma_j^2}\right)\ge \frac{w_i}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right) (i\ne j). \] Тогда всем точкам, интенсивность которых лежит в промежутке \(X_j\), поставим в соответствие значение \(\mu_j\) (при практической реализации - ее целую часть). Результатом работы алгоритма будет сегментация изображения на \(n\) сегментов по каждой цветовой компоненте.

ЕМ-алгоритм традиционно является наиболее используемым инструментом для разделения смеси распределений с известным числом компонентов. Определение числа компонент (кластеров) является нетривиальной задачей. Как правило, этот параметр выбирается исследователем из каких-то априорных предположений, что делает задачу автоматического выбора этого параметра актуальной. Наиболее популярными алгоритмами оценки количества элементов смеси являются –

метод скользящего контроля,
принцип минимальной длины описания,
использование информационного критерия Акаике,
метод релевантных векторов и пр.

Существующие подходы, как правило, отличаются сложностью реализации, интуитивными подходами или приближенными методами решения сложных аналитических задач, часто не ясно, как они вообще связаны с данной задачей. С другой стороны, по сути, ЕМ-алгоритм разделения смеси нормальных распределений, по сути, представляет собой восстановление имеющейся гистограммы линейной комбинацией функций Гаусса, поэтому, совершенно естественно, имея значение заданной погрешности восстановления ε, описать имеющуюся гистограмму обедненной гистограммой со свободными узлами, которая наилучшим образом (то есть восстанавлявающую исходную информацию с данной погрешностью и минимальным числом узлов). Полученное число узлов является оценкой числа компонентов смеси, восстанавливаемой линейной комбинацией функций Гаусса с заданной точностью ε. Более того, значения свободных узлов дают возможность получить стартовую оценку остальных параметров смеси.

Оценка числа компонентов смеси.

Обозначим через \(\Delta_n=\left\{ x_i \right\}_{i=0}^n \)- произвольное разбиение \(0=x_0\lt x_1\lt ...\lt x_n=T\), а также положим \(h_{i+1/2}=x_{i+1}-x_i\), \(h=\max_ih_{i+1/2}\) и \(x_{i+1/2}=(x_{i+1}+x_i)/2\) . Через \(S\left(\left\{a_{i+1/2}\right\}_{i=0}^{n-1},\Delta_n,x\right)\) обозначим кусочно-постоянную функцию со значениями \(a_{i+1/2}\) для \(x\in [x_i,x_{i+1})\).
Для функции \(y(x)\), непрерывной на \([0,T]\), рассмотрим задачу \begin{equation}\label{1} \varepsilon=\min_{x_i}\min_{a_{i+1/2}}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(a_{i+1/2}-y(x)\right)^2dx. \end{equation} Утверждение. Пусть \(y(x)\)- непрерывно дифференцируемая функция \(y\in C^2_{[0,T]}\) такая, что \(y'(x)\) на промежутке [0,T] имеет не более конечного числа нулей, тогда \begin{equation}\label{2} \varepsilon=\frac{1}{12n^2}\left(\int_{0}^{T}\left(y'(x)\right)^{2/3}dx\right)^3+O\left(\frac{1}{n^3}\right). \end{equation} и при этом минимум достигается для разбиения \(\Delta^*_n=\left\{ x^*_i\right\}_{i=0}^n\) такого, что \begin{equation}\label{3} \int_{x^*_i}^{x^*_{i+1}}\left(y'(x)\right)^{2/3}dx=\frac{1}{n} \int_{0}^{T}\left(y'(x)\right)^{2/3}dx, a^*_{i+1/2}=\frac{1}{h^*_{i+1/2}}\int_{x^*_i}^{x^*_{i+1}}y(x)dx. \end{equation} Покажем справедливость этого утверждения. Вначале рассмотрим следующую задачу \begin{equation}\label{4} \Phi\left(a_{i+1/2}\right)=\int_{x_i}^{x_{i+1}}\left(a_{i+1/2}-y(x)\right)^2dx\to\min. \end{equation} Тогда ввиду выпуклости задачи (\ref{4}), необходимое условие минимума является и достаточным, то есть решение этой задачи определяется из уравнения \[ \frac{d}{da_{i+1/2}}\Phi\left(a_{i+1/2}\right)= 2\int_{x_i}^{x_{i+1}}\left(a_{i+1/2}-y(x)\right)dx=0, \] и, следовательно, \[ a_{i+1/2}=\frac{1}{x_{i+1}-x_i}\int_{x_i}^{x_{i+1}}y(x)dx. \] Таким образом, задачу (\ref{1}) можно переписать в виде \[ \varepsilon=\min_{x_i}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(\frac{1}{h_{i+1/2}}\int_{x_i}^{x_{i+1}}y(x)dx-y(x)\right)^2dx. \] Используя формулу Тейлора \[ y(x)=y_{i+1/2}+y'_{i+1/2}\left(x-x_{i+1/2}\right)+O(h^2), \] где \(y_{i+1/2}=y(x_{i+1/2})\), получаем \[ \varepsilon=\min_{x_i}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(\frac{1}{h_{i+1/2}}\int_{x_i}^{x_{i+1}}y(x)dx-y(x)\right)^2dx= \min_{x_i}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left( y_{i+1/2}+y'_{i+1/2}\left(x-x_{i+1/2}\right)+O(h^2)- \frac{1}{h_{i+1/2}}\int_{x_i}^{x_{i+1}} \left(y_{i+1/2}+y'_{i+1/2}\left(x-x_{i+1/2}\right)+O(h^2)\right)\right)^2dx= \frac{1}{12}\min_{x_i}\sum_{i=0}^{n-1}\left(\left(y'_{i+1/2}\right)^2 h^3_{i+1/2}+O(h^4)\right). \] Из теоремы о среднем для интегралов следует, что найдется точка \(\theta_{i+1/2}\in [x_i,x_{i+1}]\) такая, что \[ \left(y'\left(\theta_{i+1/2}\right)\right)^2 h^3_{i+1/2}= \left(\left(y'\left(\theta_{i+1/2}\right)\right)^{2/3} h_{i+1/2}\right)^3= \left(\int_{x_i}^{x_{i+1}}\left(y'\left(x\right)\right)^{2/3}dx\right)^3, \] отсюда и из предыдущего сразу получаем \begin{equation}\label{5} \varepsilon=\frac{1}{12}\min_{x_i}\sum_{i=0}^{n-1}\left(\left(\int_{x_i}^{x_{i+1}}\left(y'(x)\right)^{2/3} dx\right)^3+O(h^4)\right). \end{equation} Выпишем следующее предположение.
Пусть \(\alpha\gt 0\) и \(C\gt 0\), тогда \[ \min\left\{\left.\sum_{i=0}^{n-1}C_i^\alpha\right|C_i^\alpha\ge 0,\sum_{i=0}^{n-1}C_i=C\right\}=n\left(\frac{C}{n}\right)^\alpha, \] и при этом минимум достигается тогда, когда все \(C_i\) равны между собой, то есть, \[ C^*_i=\frac{C}{n} (i=0,...,n-1). \] Для доказательства этого утверждения используем метод неопределенных множителей Лагранжа. Выпишем функцию цели \[ L=\lambda_0\sum_{i=0}^{n-1}C_i^\alpha+\lambda_1\left(\sum_{i=0}^{n-1}C_i-C\right), \] тогда \[ \frac{\partial L}{\partial C_i}=\lambda_0\alpha C^{\alpha-1}_i+\lambda_1=0, \] что то же \(\lambda_0\alpha \left(C^{\alpha-1}_i+\lambda_2\right)=0\), где \(\lambda_2=\frac{\lambda_1}{\lambda_0\alpha}\).
Таким образом, получаем \(C_i=-\lambda_2^{\frac{1}{\alpha-1}}\) и \[ \sum_{i=0}^{n-1}C_i=-\sum_{i=0}^{n-1}\lambda_2^{\frac{1}{\alpha-1}}=-n\lambda_2^{\frac{1}{\alpha-1}}=C. \] Следовательно, имеем \(\lambda_2^{\frac{1}{\alpha-1}}=-\frac{C}{n}\) , или, что то же \(C_i=\frac{C}{n} (i=0,...,n-1).\)
Предположение доказано.
Таким образом, из (\ref{4}) и доказанного предположения, получаем \[ \varepsilon=\frac{1}{12}\min_{x_i}\sum_{i=0}^{n-1}\left(\left(\int_{x_i}^{x_{i+1}}\left(y'(x)\right)^{2/3} dx\right)^3+O(h^4)\right)= \frac{1}{12}\sum_{i=0}^{n-1}\left(\left(\int_{x^*_i}^{x^*_{i+1}}\left(y'(x)\right)^{2/3} dx\right)^3+O(h^4)\right)= \frac{1}{12 n^2}\left(\int_{0}^{T}\left(y'(x)\right)^{2/3} dx\right)^3+O\left(\frac{1}{n^3}\right). \] и при этом минимум достигается для разбиения \(\Delta^*_n=\left\{ x^*_i\right\}_{i=0}^n\) такого, что \[ \int_{x^*_i}^{x^*_{i+1}}\left(y'(x)\right)^{2/3}dx=\frac{1}{n} \int_{0}^{T}\left(y'(x)\right)^{2/3}dx. \] Кроме того, заметим, что для заданной погрешности ε можно найти количество \(n\) звеньев кусочно-постоянной с асимптотически оптимальными узлами, выбираемыми из условия (\ref{2}) \[ n=\left[\sqrt{\frac{1}{12 \varepsilon}\left(\int_{0}^{T}\left(y'(x)\right)^{2/3} dx\right)^3}\right]+1, \] где [m] - целая часть числа m.
Полученное значение количества узлов может служить оценкой для числа элементов смеси нормальных распределений, а значения \(x^*_{i+1/2}\) - стартовыми значениями математического ожидания функций Гаусса.

В качестве примера, приведем определение, при заданной относительной точности, количества сегментов для примера, рассмотренного выше.

Относительная точность в процентах (от 1% до 100%)

Expectation maximization

Подробнее об ЕМ-алгоритме.

Е-шаг (expectation).

M-шаг (maximization).

Заметим, что если известен вид функции плотности, то задачу MLE можно выписать в явном виде.

Пример результата работы EM-алгоритма.

Иллюстрация работы метода EM-алгоритма.

Применение ЕМ-алгоритма к сегментации изображений.

Оценка числа компонентов смеси.

Пример использования сегментации изображений

Задачи для самостоятельной работы.

Задача 1.

Задача 2.

Задача 3.

Полезная литература. Книги.

Полезная литература. Статьи.

Вопрос-ответ.