Subdivision

Методы последовательного уплотнения (расщепления) данных (subdivision).

Методы subdivision относятся к рекурсивным методам, получившим широкое распространение в последнее время.
Идею метода последовательного уплотнения (subdivision) можно определить следующим образом: subdivision определяет гладкую кривую или поверхность как предел последовательности получаемую последующим уточнением первоначальных данных. Методы последовательного уплотнения используются в тех случаях, когда описываемый объект имеет сложную структуру, не позволяющую получить аналитическое описание с достаточной точностью. Такого рода задачи возникают, например, в компьютерной графике, при моделировании сложных объектов. Следующий пример является характерным для такого рода методов.

На приведенном рисунке, в результате применения метода subdivision треугольная решетка на каждом шаге становится все более мелкая. Тем самым на каждом шаге описание объекта становится более гладким.
Каким же условиям должны удовлетворять новые точки, получаемые в результате пополнения данных? Метод получения новых точек должен отвечать следующим условиям

Вычислительная эффективность. Вычисление значений новых точек должно использовать немного операций с плавающей точкой.
Локальность воздействия. Область влияния точки на форму кривой или поверхности должна быть ограничена и достаточно небольшой.
Локальность расположения. Геометрически новые точки не должны далеко лежать от точек их образующих.
Инвариантность к аффинным преобразованиям. Если оригинальные точки подверглись какой-нибудь трансформации, например, вращению или масштабированию, то результат применения пополнения до и после трансформации не должен измениться.
Простота реализации. Формула получения новых значений должна быть конструктивной.

Алгоритм Чайкина.

В 1974 Дж. Чайкин (George Chaikin) в курсе лекций прочитанных в университете штата Юта (University of Utah) описал процедуру конструирования кривой как предела последовательности полигонов. Нас этот алгоритм интересует как основополагающий алгоритм subdivision (алгоритм последующего уточнения кривой). В дальнейшем этот подход в геометрическом моделировании был забыт, так как приобретет в описании кривых был у аналитических методов, использующих, например, базисные сплайны. Однако со временем появился большой интерес к рекурсивным методам описания как кривых, так и поверхностей. Методы, которые стали определять как методы subdivision, основываются на основополагающей парадигме Чайкина:
- искомая кривая получается в результате последовательного усовершенствования первоначального контрольного полигона.
Сейчас этот подход используется для построения разнообразных методов генерирования как кривых, так и поверхностей.
Исследователи, начиная с Bezier работали с кривыми генерируемыми контрольными полигонами, но при этом они фокусировали исследования для получения аналитического описания этой кривой, основываясь, прежде всего, на полиномах Бернштейна.
Для Чайкина контрольные полигоны были интересны сами по себе. Его интересовало геометрическое моделирование. Он предложил схему "усечения углов", в результате чего, генерируется новый контрольный полигон, получаемый усечением углов оригинального полигона.
Эта идея проиллюстрирована на следующем рисунке.

Понятно, что мы можем на каждом шаге относится к полигону как к исходному, применить ту же процедуру ко второму полигону и "обрезать" его углы, и повторять эту процедуру далее. В результате предельного перехода мы получим кривую. В этом состоит идея Чайкина.

Опишем подробно эту процедуру. Имея контрольный полигон с вершинами \(\left\{ {\bf P}_0, {\bf P}_1, \ldots\right.\) \(\left.,{\bf P}_n \right\}\), построим новую последовательность точек \(\displaystyle \left\{ {\bf Q}_0, {\bf R}_0, {\bf Q}_1, {\bf R}_1, \ldots\right.\) \(\left., {\bf Q}_{n-1}, {\bf R}_{n-1} \right\}\), где каждая новая пара точек \({\bf Q}_i, {\bf R}_i\) получена как отношение \(\frac{1}{4}\) и \(\frac{3}{4}\) между концами отрезка прямой \(\overline{ {\bf P}_i {\bf P}_{i+1}}\)

то есть \begin{eqnarray*} {\bf Q}_i & = & \frac{3}{4} {\bf P}_i + \frac{1}{4} {\bf P}_{i+1} \\ {\bf R}_i & = & \frac{1}{4} {\bf P}_i + \frac{3}{4} {\bf P}_{i+1} \end{eqnarray*} Эти \( 2n\) новых точек образуют новый контрольный полигон, основанный на исправлении старого.
Приведем пример. Пусть дан следующий полигон.

Chaikin's алгоритм генерирует точки \({\bf Q}_i\) и \({\bf R}_i\) и использует эти точки для конструирования нового полигона.

Полученные точки позволяют провести следующий шаг итерации.

Последующее применение этого алгоритма позволяют получить искомую кривую.

Проиллюстрируем алгоритм построения кривой Chaikin's для случая замкнутого полигона.

После первой итерации получим следующую фигуру

Результат следующей итерации будет выглядеть следующим образом

Этот процесс можно продолжать, при этом полигон будет неуклонно приближаться к результирующей кривой.

Конструкция Чайкина не использует никакие аналитические представления и предоставляет простой и элегантный механизм построения кривых.

Масштабирующее свойство В-сплайнов.

Вначале приведем несколько определений необходимых нам в дальнейшем. Сверткой двух функций \(f(t)\) и \(g(t)\) будем называть функцию, определяемую следующим образом \[ (f\otimes g)(t)=f(t) \otimes g(t)=\int f(\tau)g(t-\tau)d\tau. \] Отметим некоторые свойства свертки функций, необходимые нам в дальнейшем:

Линейность \[ f(t)\otimes (g(t)+q(t))=f(t)\otimes g(t)+f(t)\otimes q(t). \]
Формула сдвига \[ f(t-i)\otimes g(t-j)=(f\otimes g)(t-i-j). \]
Формула подобия \[ f(\lambda t)\otimes g(\lambda t)=\frac{1}{|\lambda |}(f\otimes g)(\lambda t)\,\,\,\,(\lambda \in \mathbb{R},\lambda \ne 0). \]

Определение B-сплайнов, рассмотренное в разделе, посвященном сплайнам, можно переписать следующим образом:
В-сплайном порядка 0 будем называть функцию вида \begin{equation}\label{s.1} B_0(t)=\left\{ \begin{array}{ll} 1, & t\in [0,1] \\ 0, & \textrm{иначе}. \end{array} \right. \end{equation} то есть единичничный пульс

а В- сплайном порядка \(r\), где \(r=1,2,\ldots,\) будем называть функцию \begin{equation}\label{s.2} B_r(t)=(B_{r-1}\otimes B_0)(t)=\int B_{r-1}(\tau)B_{0}(t-\tau)d\tau. \end{equation} В частности, \begin{equation}\label{s.3} B_1(t)=(B_{0}\otimes B_0)(t)=\int B_{0}(\tau)B_{0}(t-\tau)d\tau= \end{equation} \[ = \left\{\begin{array}{lcc} {\displaystyle \int_{0}^{t}} d\tau & \textrm{ если}& 0 \leq t \leq 1 \\ {\displaystyle \int_{t-1}^{1}} d\tau & \textrm{ если}& 1 \leq t \leq 2\\ 0 &\textrm{ если}& t\notin [0,2] \end{array}\right. = \left\{\begin{array}{lcc} t \: \: & \textrm{ если}& \: 0 \leq t \leq 1 \\ 2-t \: \: & \textrm{ если}& \: 1 \leq t \leq 2\\ 0&\textrm{ если}& t\notin [0,2]. \end{array}\right.\] Если \(t_i=i\), то это соотношение можно переписать в виде \[ B_{1} (t) = \frac{t-t_0}{t_{1} - t_0} B_{0} (t) + \frac{t_{2} - t}{t_{2} - t_{1}} B_{0} (t-1) = t B_{0} (t) + (2-t) B_{0} (t-1) \] \[ = \left\{\begin{array}{lcc} t & \textrm{ если}& 0 \leq t \lt 1 \\ 2-t & \textrm{ если}& 1 \leq t \lt 2 \\ 0 & \textrm{ иначе.} \end{array} \right. \]

В-сплайн второго порядка представляет собой кусочно-параболическую функцию \begin{equation}\label{s.4} B_2(t)=(B_{0}\otimes B_1)(t)=\int B_{0}(\tau)B_{1}(t-\tau)d\tau= \end{equation} \[ = \left\{\begin{array}{lcc} {\displaystyle \int_{0}^{t}} B_{1}(\tau) d\tau \: \: & \textrm{ если}& \: 0 \leq t \leq 1 \\[.5em] {\displaystyle \int_{t-1}^{1}} B_{1}(\tau) d\tau \: \: + {\displaystyle \int_{1}^{t}} B_{1}(\tau) d\tau \: \: & \textrm{ если}& \: 1 \leq t \leq 2 \\[.5em] {\displaystyle \int_{t-2}^{1}} B_{1}(\tau) d\tau \: \: & \textrm{ если}& \: 2 \leq t \leq 3 \end{array}\right.\] \[= \left\{\begin{array}{lcc} {\displaystyle \int _{0}^{t}} \tau d\tau \: \: & \textrm{ если}& \: 0 \leq t \leq 1 \\[.5em] {\displaystyle \int _{t-1}^{1}} (2 - \tau) d\tau \: \: + {\displaystyle \int _{1}^{t}} \tau d\tau \: \: & \textrm{ если}& \: 1 \leq t \leq 2 \\[.5em] {\displaystyle \int }_{t-2}^{1} (2 - \tau) d\tau \: \: & \textrm{ если}& \: 2 \leq t \leq 3 \end{array}\right.\] \[ \left\{ \begin{array}{ll} {\displaystyle \frac{1}{2}t^2}, & t\in [0,1] \\ {\displaystyle \frac{1}{2}(6t-2t^2-3)}, & t\in [1,2] \\ {\displaystyle \frac{1}{2}(t-3)^2}, & t\in [2,3] \\ 0, & \textrm{иначе}. \end{array} \right. \]

В этом случае для \(t_i=i\) имеем \[ B_{2} (t) = \frac{t-t_0}{t_{2} - t_0} B_{1} (t) + \frac{t_{3} - t}{t_{3} - t_{1}} B_{1} (t-1) = \frac{t}{2} B_{1} (t) + \frac{3-t}{2} B_{1} (t-1) \] \[= \left\{\begin{array}{lcc} {\displaystyle\frac{t^2}{2}} & \textrm{ если}& 0 \leq t \lt 1 \\ {\displaystyle\frac{t^2}{2} ( 2-t) + \frac{3-t}{2} (t-1) }& \textrm{ если}& 1 \leq t \lt 2 \\ {\displaystyle\frac{(3-t)^2}{2}} & \textrm{ если}& 2 \leq t \lt 3 \\ 0 & \textrm{ иначе} \end{array}\right. \] \[= \left\{\begin{array}{lcc} {\displaystyle \frac{t^2}{2}} & \textrm{ если}& 0 \leq t \lt 1 \\ {\displaystyle\frac{-3 + 6t - 2t^2}{2}} & \textrm{ если}& 1 \leq t \lt 2 \\ {\displaystyle\frac{(3-t)^2}{2}} & \textrm{ если}& 2 \leq t \lt 3 \\ 0 & \textrm{ иначе}. \end{array}\right. \] Нормализованный В-сплайн удовлетворяет следующим свойствам

Нормализация: \[ \sum_{i\in Z}B_r(t-i)=1. \]
Положительность: \(B_r(t)\ge 0\).
Локальность: \(B_r(t-i)=0\) если \(t\ne [i,i+r+1]\).
Непрерывность: \(B_r(t)\) есть \((r-1)\) раз непрерывно дифференцируемая функция.
Рекурсивность: \[ B_r(t-i)=\frac{t-i}{r}B_{r-1}(t-i)+\frac{i+r+1-t}{r}B_{r-1}(t-i-1). \]

Функция \begin{equation}\label{s.5} S_r(t)=\sum_{i\in Z}P_iB_r(t-i) \end{equation} есть сплайн порядка \(r\) минимального дефекта. Вследствие того, что В-сплайн имеет конечный носитель, соотношение (\ref{s.5}) имеет лишь конечное число слагаемых. Например, если \(S_r(t)=S_{r,i}(t)\), то для \(r=2\) \begin{equation}\label{s.6} S_{2,i}(t)=P_{i}\frac{1}{2}(1-t)^2+P_{i+1}\frac{1}{2}(1+2t-2t^2)+P_{i+2}\frac{1}{2}t^2= \end{equation} \[ =\left[ \begin{array}{ccc} 1 & t & t^2 \end{array} \right] M \left[ \begin{array}{c} P_{i} \\P_{i+1} \\P_{i+2} \end{array} \right], \] где \(M\) есть матрица размера \(3 \times 3\) \[ M \: = \: \frac{1}{2} \left[ \begin{array}{rrr} 1 & 1 & 0 \\ -2 & 2 & 0 \\ 1 & -2 & 1 \end{array} \right] \] и для \(i = 0, 1, ..., n-2\) и \(0 \leq t \leq 1\)
Для кубических сплайнов имеет место равенство \[ S_{3,i}(t) \: = \: \left[ \begin{array}{cccc} 1 & t & t^2 & t^3 \end{array} \right] M \left[ \begin{array}{c} {P}_i \\{P}_{i+1} \\{P}_{i+2} \\{P}_{i+3} \\ \end{array} \right] \] для \(i = 0, 1, ..., n-3\) и \(0 \leq t \leq 1\), где \[ M \: = \: \frac{1}{6}\left[ \begin{array}{rrrr} 1 & 4 & 1 & 0 \\ -3 & 0 & 3 & 0 \\ 3 & -6 & 3 & 0 \\ -1 & 3 & -3 & 1 \end{array} \right]. \] Для набора контрольных точек \(\mathbb{P}=\mathbb{P}^0=\left\{ {\bf P} _0 , {\bf P} _1 , ..., {\bf P} _n \right\}\) и множества узлов \(\left\{ t_0 , t_1 , ..., t_{n+r+1} \right\}\) В-сплайновую кривую порядка \( r\) \begin{equation}\label{s.7} {\bf S}_r(t)=\sum_{i\in Z}{\bf P}_iB_r(t-t_i) \end{equation} можно определить рекурсивно \begin{equation} {\bf S}_r(t) = {\bf S}_{r,i}(t) \textrm{ если } t \in [ t_i , t_{i+1} ) \end{equation} где \begin{equation} {\bf S}_{k,i}(t) = \left\{ \begin{array}{lc} {(1 - \tau_i^k )} { {\bf S} _{k-1,i-1}(t) } + {\tau_i^k} { {\bf S} _{k-1,i}(t)} & \textrm{ если } k > 0, \\ {\bf P} _i & \textrm{ если } k = 0. \end{array} \right. \end{equation} и \begin{equation} \tau_i^k = \frac{t - t_i}{t_{i+r+1-k} - t_i} \end{equation} Геометрически это соотношение можно представить в виде пирамиды \begin{equation} \begin{array}{ccccccc} \vdots & & & & & & \\ {\bf P} _{i-r} & & & & & & \\ & {\bf S} _{1,i-r+1} & & & & & \\ {\bf P} _{i-r+1} & & {\bf S} _{2,i-r+2} & & & & \\ & {\bf S} _{1,i-r+2} & & \cdot & & & \\ {\bf P} _{i-r+2} & & \cdot & & & & \\ & & & & & & \\ {\bf P} _{i-r+3} & & & & & & \\ \cdot & & & & & {\bf S} _{r-1,i-1} & \\ \cdot & & & & & & {\bf S} _{r,i} \\ \cdot & & & & & {\bf S} _{r-1,i} \\ \cdot & & & & & & \\ {\bf P} _{i-2} & & {\bf S} _{2,i-1} & & & & \\ & {\bf S} _{1,i-1} & & \cdot & & & \\ {\bf P} _{i-1} & & {\bf S} _{2,i} & & & & \\ & {\bf S} _{1,i} & & & & & \\ {\bf P} _i & & & & & & \\ \vdots & & & & & & \end{array} \end{equation} Из определения В-сплайна нулевого порядка видно, что его можно записать в виде суммы В-сплайнов того же порядка \begin{equation}\label{s.8} B_0(t)=B_0(2t)+B_0(2t-1). \end{equation} Отсюда, используя определение В-сплайна порядка \(r\), сразу получаем \[ B_r(t)=\bigotimes_{i=0}^rB_0(t)=\bigotimes_{i=0}^r\left(B_0(2t)+B_0(2t-1)\right). \] В частности, для \(r=1\) получаем \[ B_1(t)=(B_{0}\otimes B_0)(t)=\left(B_0(2t)+B_0(2t-1)\right)\otimes \left(B_0(2t)+B_0(2t-1)\right). \] Отсюда и из линейности оператора свертки сразу получаем \[ B_1(t)=B_0(2t)\otimes B_0(2t)+B_0(2t)\otimes B_0(2t-1)+B_0(2t-1)\otimes B_0(2t)+B_0(2t-1)\otimes B_0(2t-1). \] Используя свойство сдвига и подобия, отсюда сразу получаем \[ B_1(t)=\frac{1}{2}B_1(2t)+\frac{1}{2}B_1(2t-1)+\frac{1}{2}B_1(2t-1)+\frac{1}{2}B_1(2t-1-1), \] или, что тоже \[ B_1(t)=\frac{1}{2}\left(B_1(2t)+{2}B_1(2t-1)+\frac{1}{2}B_1(2t-2)\right)=\frac{1}{2}\sum_{i=0}^2 { 2 \choose i } B_1(2t-i). \] Покажем, что справедливо соотношение \begin{equation}\label{s.9} B_r(t)=\frac{1}{2^r}\sum_{i=0}^{r+1}{ r+1 \choose i }B_r(2t-i). \end{equation}

Пусть, как обычно, \(\hat{f}(\omega)\) есть преобразование Фурье \( f(t)\), тогда \[ \hat{B}_r(\omega) \: = \: \int_{-\infty}^{\infty} e^{-\imath \omega x} B_r(x) dx. \] Отсюда и из (\ref{s.2}) сразу получаем \[ \hat{B}_r(\omega) \: = \: \widehat{( B_{r-1} \otimes B_0 )}(\omega) \: = \: \hat{B}_{r-1}(\omega) \hat{B}_0(\omega). \] Замечая, что преобразование Фурье от свертки функций есть произведение преобразований Фурье от этих функций, а также того факта, что \[ \hat{B}_0(\omega) \: = \: \frac{1 - e^{-\imath \omega}}{\imath \omega} \] сразу получаем \[ \hat{B}_r(\omega) \: = \: \left( \frac{1 - e^{-\imath \omega}}{\imath \omega} \right) ^ {r+1} \] Применяя преобразование Фурье к обеим частям равенства \[ B_r(t) \: = \: \sum_{j=-\infty}^{\infty} p_j B_r(2t-j) \] получаем \[ \hat{B}_r(\omega) \: = \: \frac{1}{2} \left( \sum_{j=-\infty}^{\infty} p_j e^{-\frac{\imath j \omega}{2}} \right) \hat{B}_r \left( \frac{\omega}{2} \right), \] или, что то же, \[ \left( \frac{1 - e^{-\imath \omega}}{\imath \omega} \right) ^ {r+1} \: = \: \frac{1}{2} \left( \sum_{j=-\infty}^{\infty} p_j e^{-\frac{\imath j \omega}{2}} \right) \left( \frac{1 - e^{-\imath \frac{\omega}{2}}}{\imath \frac{\omega}{2}} \right) ^ {r+1} \] таким образом \[ \frac{1}{2} \left( \sum_{j=-\infty}^{\infty} p_j e^{-\frac{\imath j \omega}{2}} \right) = \left( \frac{1 - e^{-\imath \omega}}{\imath \omega} \right) ^ {r+1} \left( \frac{\imath \frac{\omega}{2}}{1 - e^{-\imath \frac{\omega}{2}}} \right) ^ {r+1} = \left( \frac{1 - e^{-\imath \frac{\omega}{2}}}{2} \right) ^ {r+1} = 2^{-r-1} \sum_{j=0}^{r+1} {r+1 \choose j} e^{-\frac{\imath j \omega}{2}}. \] Отсюда и из бинома Ньютона сразу получаем \[ p_j \: = \: \left\{\begin{array}{lccc} \frac{1}{2^{r}} { r+1 \choose j } & \textrm{ если}& 0 \leq j \leq r \\ 0 &\textrm{ иначе}. \end{array}\right. \] что и доказывает равенство (\ref{s.9}).

Методы последовательного уплотнения (subdivision) кривых.

Если \(\textbf{B}_r(t)\) есть вектор \[ \textbf{B}_r(t)=\left(\ldots B_r(t-2), B_r(t-1), B_r(t), B_r(t+1), B_r(t+2),\ldots\right), \] то равенство (\ref{s.9}) запишется в виде \begin{equation}\label{s.10} \textbf{B}_r(t)=\textbf{B}_r(2t)\mathbb{S}, \end{equation} где \(\mathbb{S}\) матрица у которой лишь коэффициенты \begin{equation}\label{s.11} s_{2k+i,i}=\frac{1}{2^r}{ r+1 \choose i } \end{equation} отличны от нуля. Любую сплайновую кривую (\ref{s.5}) можно записать в виде \begin{eqnarray*} \textbf{S}_r(t) & = & \textbf{B}_r(t){\mathbb{P}}^0 \\ & = & \textbf{B}_r(2t){\mathbb{P}}^1 = \textbf{B}_r(2t)\mathbb{S}{\mathbb{P}}^0\\ & & \ldots\\ & = & \textbf{B}_r(2^{j+1}t){\mathbb{P}}^{j+1} = \textbf{B}_r(2^{j+1}t)\mathbb{S}{\mathbb{P}}^{j}= \textbf{B}_r(2^jt)\mathbb{S}^j{\mathbb{P}}^0, \end{eqnarray*} откуда сразу получаем соотношения \[ {\mathbb{P}}^{j+1} = \mathbb{S}{\mathbb{P}}^j, \] где \(\mathbb{S}\) матрица c коэффициентами (\ref{s.11}).
Полученное соотношение называется формулами subdivision.
В координатной форме формулы subdivision будут иметь вид \begin{equation}\label{s.12} P^{j+1}_k=\sum_{i}s_{k,i}P^j_i, \end{equation} или, что то же \begin{equation}\label{s.13} P^{j+1}_{2k+1}=\sum_{i}s_{2k+1,i}P^j_i \end{equation} и \begin{equation}\label{s.14} P^{j+1}_{2k}=\sum_{i}s_{2k,i}P^j_i. \end{equation}

Сходимость метода subdivision.

Для полученного метода последовательного бинарного уточнения важно знать сходится ли последовательность полученная в результате полученной рекурсии к исходной функции.
Этот вопрос является очень важным и требует отдельного обсуждения.
Будем говорить что последовательность функция \(f_i\) определенная на промежутке \([a,b]\) равномерно сходится к \(f\), если для любого \(\varepsilon>0\) существует такое \(n_0>0\), что для всех \(n>n_0\) \[ \max_{t\in [a,b]}|f(t)-f_n(t)|\lt\varepsilon. \] Введем необходимые в дальнейшем обозначения \[ \|f\|=\sup_{t}|f(t)|, \] \[ \|\mathbb{P}\|=\sup_{i}|P_i|, \] \[ \|\mathbb{S}\|=\sup_{i}\sum_{k}|s_{i,k}|. \] Каждую последовательность контрольных точек \(\mathbb{P}^j\) будем ассоциировать с кусочно-линейной функцией с узлами в этих точках, то есть \[ \mathbb{P}^j(t)=\textbf{B}_1(2^jt)\mathbb{P}^j. \] Положим \(\left(\Delta P^j\right)_i=P^j_{i+1}-P^j_{i}\). В работе Joe Warren показано, что если для некоторых \(c>0\) и \(\gamma\in (0,1)\) существует \(j_0>0\) такие что для всех \(j>j_0\) имеет место неравенство \(\|\Delta \mathbb{P}^j\|\lt c\gamma^j\), то последовательность функций \(\mathbb{P}^j(t)\) сходится равномерно по \(t\) \[ \mathbb{P}^\infty(t)=\lim_{j\to\infty}\mathbb{P}^j(t) \] и при \(j\to \infty\) \[ \|\mathbb{P}^\infty-\mathbb{P}^j\|\le \frac{\widetilde{c}}{1-\gamma}\gamma^j, \] где \(\widetilde{c}\) постоянная зависящая от метода subdivision.

Конкретные методы subdivision кривых

Для примера рассмотрим формулы subdivision подробнее.
Если \(Z/2=\left\{\ldots,-1,-\frac{1}{2},0,\frac{1}{2},1,\ldots\right\}\), то поставим в соответствие множеству \(\textbf{P}^j_i\) (\(i\in Z\)) множество \(\textbf{p}^j_i\) (\(i\in Z/2\)) согласно правилу \[ \textbf{P}^j_i=\textbf{p}^j_{2i}. \] Тогда \begin{equation}\label{s.15} \textbf{S}_r(t)=\sum_{i\in Z/2}\textbf{p}^1_iB_r(2(t-i)) \end{equation} и при этом, \begin{equation}\label{s.16} B_r(t)=\sum_{i\in Z/2}c_{r,i}B_r(2(t-i)), \end{equation} где \begin{equation}\label{s.17} c^r_{i}=\frac{1}{2^{r}} { r+1 \choose 2i }. \end{equation} Отсюда и из (\ref{s.5}) получаем \begin{equation}\label{s.18} \textbf{S}_r(t)=\sum_{i\in Z}\textbf{P}^0_i\sum_{j\in Z/2}c^r_{j-i}B_r(2(t-j))= \sum_{j\in Z/2}\sum_{i\in Z}c^r_{j-i}\textbf{P}^0_iB_r(2(t-j)). \end{equation} Используя (\ref{s.9}), имеем \begin{equation}\label{s.19} \textbf{p}^1_j=\sum_{i\in Z}c^r_{j-i}\textbf{P}^0_i. \end{equation} Для \(r=2\) получаем \[ \textbf{p}^1_0=\ldots+0\cdot \textbf{P}^0_{-2}+\frac{3}{4}\textbf{P}^0_{-1}+\frac{1}{4}\textbf{P}^0_{0}+0\cdot \textbf{P}^0_{1}+\ldots \] и, соответственно, \[ \textbf{p}^1_{\frac{1}{2}}=\ldots+0\cdot \textbf{P}^0_{-2}+\frac{1}{4}\textbf{P}^0_{-1}+\frac{3}{4}\textbf{P}^0_{0}+0\cdot \textbf{P}^0_{1}+\ldots. \] Заметим, что \(\textbf{p}^1_j\) есть выпуклая комбинация близких значений \(\textbf{P}^0_i\). Для \(r=2\) узлы нового полигона (полигона де Бора) есть концы отрезков делящих отрезки определяемые исходными точками в пропорции \(1:3\) и \(3:1\) \[ \textbf{P}^{j+1}_{2k}=\textbf{p}^{j+1}_{k}=\frac{1}{4}\left(3\textbf{P}^{j}_{k}+\textbf{P}^{j}_{k+1}\right), \] \[ \textbf{P}^{j+1}_{2k+1}=\textbf{p}^{j+1}_{k+1/2}=\frac{1}{4}\left(\textbf{P}^{j}_{k}+3\textbf{P}^{j}_{k+1}\right). \] Как видно, в результате получили алгоритм Чайкина.
Заметим, что если значения опорных точек снимаются с искомой кривой, то порядок аппроксимации кривой полученным методом subdivision совпадает с порядком приближения ломаной, то есть при \(n-\)й итерации с точностью \(O(n^{-2})\).
Для заданных значений кривой в точках \(i+0.5\) опорные точки можно уточнить так, что формулы для subdivision примут вид \[ \textbf{P}^{j+1}_{2k}=\frac{1}{32}\left(-3\textbf{P}^{j}_{k-1}+29\textbf{P}^{j}_{k}+7\textbf{P}^{j}_{k+1}- \textbf{P}^{j}_{k+2}\right), \] \[ \textbf{P}^{j+1}_{2k+1}=\frac{1}{32}\left(-\textbf{P}^{j}_{k-1}+7\textbf{P}^{j}_{k}+29\textbf{P}^{j}_{k+1}- 3\textbf{P}^{j}_{k+2}\right). \] Полученные формулы позволяют получить значения искомой кривой при \(n-\)й итерации с точностью \(O(n^{-3})\).

Схема Catmull-Clark.

Для случая кубических сплайнов формулы subdivision примут вид \begin{equation}\label{s.20} \textbf{P}^{j+1}_{2k+1}=\textbf{p}^{j+1}_{k+1/2}=\frac{1}{8}\left(4\textbf{P}^{j}_{k}+4\textbf{P}^{j}_{k+1}\right), \end{equation} и \begin{equation}\label{s.21} \textbf{P}^{j+1}_{2k}=\textbf{p}^{j+1}_{k}=\frac{1}{8}\left(\textbf{P}^{j}_{k-1}+6\textbf{P}^{j}_{k}+\textbf{P}^{j}_{k+1}\right). \end{equation} Метод subdivision порожденный кубическими В-сплайнами называют методом Catmull-Clark. В этом случае процедура последовательного уточнения опирается на вычисление вершин и угловых точек полигона на каждой итерации.

Полагаем, что мы имеем контрольный полигон \(\left\{ {\bf P}_0, {\bf P}_1, {\bf P}_2, {\bf P}_3 \right\}\)

Используя метод последовательного улучшения, основывающийся на бинарном subdivision кривой, мы генерируем новый контрольный полигон следующим образом

Три новые точки располагаются в серединах соответствующих отрезках полигона. Эти точки классифицируются как "угловые точки". Остальные точки ("вершины") генерируются в соответствии с методом subdivision. В целом новый полигон определяется точками \(\left\{ {\bf E}_0, {\bf V}_0, {\bf E}_1, {\bf V}_1, {\bf E}_2 \right\}\) которые в матричном виде вычисляются следующим образом \[ \left[ \begin{array}{r} {\bf E}_0 \\{\bf V}_0 \\{\bf E}_1 \\{\bf V}_1 \\{\bf E}_2 \end{array} \right] \: = \: \frac{1}{8} \left[ \begin{array}{cccc} 4 & 4 & 0 & 0 \\ 1 & 6 & 1 & 0 \\ 0 & 4 & 4 & 0 \\ 0 & 1 & 6 & 1 \\ 0 & 0 & 4 & 4 \end{array} \right] \left[ \begin{array}{r} {\bf P}_0 \\{\bf P}_1 \\{\bf P}_2 \\{\bf P}_3 \end{array} \right] \] то есть угловые точки \({\bf E}_0\), \({\bf E}_1\), \({\bf E}_2\) вычисляются следующим образом \begin{eqnarray*} {\bf E}_0 & = & \frac{1}{8}(4 {\bf P}_0 + 4 {\bf P}_1) \\ & = & \frac{ {\bf P}_0 + {\bf P}_1}{2} \\ & & \\ \end{eqnarray*} \begin{eqnarray*} {\bf E}_1 & = & \frac{1}{8}(4 {\bf P}_1 + 4 {\bf P}_2) \\ & = & \frac{ {\bf P}_1 + {\bf P}_2}{2} \\ & & \\ \end{eqnarray*} \begin{eqnarray*} {\bf E}_2 & = & \frac{1}{8}(4 {\bf P}_2 + 4 {\bf P}_3) \\ & = & \frac{ {\bf P}_2 + {\bf P}_3}{2} \\ \end{eqnarray*} а вершины \({\bf V}_0\) и \({\bf V}_1\) определяются следующим образом \begin{eqnarray*} {\bf V}_0 & = & \frac{1}{8} ( {\bf P}_0 + 6 {\bf P}_1 + {\bf P}_2 ) \\ & = & \frac{1}{8} ( ( {\bf P}_0 + {\bf P}_1 ) + 4 {\bf P}_1 + ( {\bf P}_1 + {\bf P}_2 )) \\ & = & \frac{1}{4} \left( \frac{ {\bf P}_0 + {\bf P}_1}{2} + 2 {\bf P}_1 + \frac{ {\bf P}_1 + {\bf P}_2}{2} \right) \\ & = & \frac{1}{4} ( {\bf E}_0 + 2 {\bf P}_1 + {\bf E}_1 ) \\ & = & \frac{\displaystyle{\frac{ {\bf E}_0 + {\bf P}_1}{2} + \frac{ {\bf P}_1 + {\bf E}_1}{2}}}{2} \\ & & \\ \end{eqnarray*} \begin{eqnarray*} {\bf V}_1 & = & \frac{1}{8} ( {\bf P}_1 + 6 {\bf P}_2 + {\bf P}_3 ) \\ & = & \frac{1}{8} ( ( {\bf P}_1 + {\bf P}_2 ) + 4 {\bf P}_2 + ( {\bf P}_2 + {\bf P}_3 )) \\ & = & \frac{1}{4} \left( \frac{ {\bf P}_1 + {\bf P}_2}{2} + 2 {\bf P}_2 + \frac{ {\bf P}_2 + {\bf P}_3}{2} \right) \\ & = & \frac{1}{4} ( {\bf E}_1 + 2 {\bf P}_2 + {\bf E}_2 ) \\ & = & \frac{\displaystyle{\frac{ {\bf E}_1 + {\bf P}_2}{2} + \frac{ {\bf P}_2 + {\bf E}_2}{2}}}{2} \\ \end{eqnarray*}

Как видно, это средние значения отрезков соединяющих угловые точки и вершины предыдущего контрольного полигона.
Проиллюстрируем алгоритм улучшения на следующих рисунках. Пусть исходный полигон имеет вид

Вычислим углы и вершины полигона первой итерации.

Смонтируем на основании этих точек новый полигон и вновь повторим процесс - вычислим новые вершины и углы.

Предел этой последовательности существует и сходится к искомой кривой.

Заметим, что как и в случае метода Doo-Sabin, так и для метода Catmull-Clark, если значения опорных точек снимаются с искомой кривой, то порядок аппроксимации кривой полученным методом subdivision совпадает с порядком приближения ломаной, то есть при \(n-\)й итерации с точностью \(O(n^{-2})\).
Как и в предыдущем случае, формулы subdivision полученные на основе кубических сплайнов можно уточнить. В этом случае формулы subdivision примут вид \[ \textbf{P}^{j+1}_{2k+1}=\frac{1}{12}\left(-\textbf{P}^{j}_{k-1}+7\textbf{P}^{j}_{k}+7\textbf{P}^{j}_{k+1} -\textbf{P}^{j}_{k+2}\right), \] и \[ \textbf{P}^{j+1}_{2k}=\frac{1}{48}\left(-\textbf{P}^{j}_{k-2}+2\textbf{P}^{j}_{k-1}+46\textbf{P}^{j}_{k} +2\textbf{P}^{j}_{k+1}-\textbf{P}^{j}_{k+2}\right). \] Полученные формулы позволяют получить значения искомой кривой при \(n-\)й итерации с точностью \(O(n^{-4})\).

Subdivision поверхностей.

Subdivision поверхностей использует похожесть на локальных местах с полиномиальным представлением и предполагает описание поверхности с помощью последовательности полиномиальных поверхностей. Как правило поверхность называют subdivision поверхностью, если она основывается на бинарном представлении однородных (uniform) B-сплайновых кривых (поверхностей). В общем случае определим полиномиальный метод, соответствующую subdivision оператору (оператору улучшения), который генерирует новое множество с большим числом полиномиальных элементов, что позволяет надеяться на достаточно полное описание исходной поверхности. Поверхность \(S_{r,s}(\mathbf{u})\) описываемая тензорным произведением В-сплайнов по прямоугольной решетке имеет вид \begin{equation}\label{s.22} \textbf{S}_{r,s}(\mathbf{u})=\sum_{\mathbf{i}\in Z^2}\textbf{P}_{\mathbf{i}} N_{r,s}(\mathbf{u}-\mathbf{i}), \end{equation} где \(\mathbf{u}=(u,v)\in R^2\) и \(N_{r,s}(\mathbf{u}-\mathbf{i})\equiv B_r(u-i)B_s(v-j)\) нормализованное тензорное произведение В-сплайнов порядка \(rs\) по решетке с узлами \(\mathbf{i}=(i,j)\).

Реализация метода subdivision поверхности образованной тензорным произведением В-сплайнов аналогична subdivision В- сплайновой кривой.
Положим \(\mathbf{j}\in Z^2/2\), если \(\mathbf{j}=\left\{\left(\left.\frac{i}{2},\frac{j}{2}\right)\right|(i,j)\in Z^2\right\}\), тогда для тензорного произведения В-сплайнов будет иметь место равенство \begin{equation}\label{s.23} N_{r,s}(\mathbf{u}-\mathbf{i})=\sum_{\mathbf{j}\in Z^2/2}c^{r,s}_{\mathbf{j}-\mathbf{i}}N_{r,s}(2(\mathbf{u}-\mathbf{j})). \end{equation} Отсюда и из (\ref{s.22}) сразу получаем \begin{equation}\label{s.24} \textbf{S}_{r,s}(\mathbf{u})=\sum_{\mathbf{i}\in Z^2}\textbf{P}_{\mathbf{i}}\sum_{\mathbf{j}\in Z^2/2}c^{r,s}_{\mathbf{j}-\mathbf{i}}N_{r,s}(2(\mathbf{u}-\mathbf{j})), \end{equation} откуда сразу получаем \[ \textbf{p}^1_{\mathbf{j}}=\sum_{\mathbf{i}\in Z^2}c^{r,s}_{\mathbf{j}-\mathbf{i}}\textbf{P}_{\mathbf{i}}, \mathbf{j}\in Z^2/2. \] Значения \(\textbf{p}^1_{\mathbf{j}}\) формируют решетку де Бора. К тому же \[ c^{r,s}_{\mathbf{j}}\equiv c^r_ic^s_j, \] или, что тоже \begin{equation}\label{s.25} c^{r,s}_{\mathbf{j}}=2^{-r+s}C_{r+1}^{2i}C_{s+1}^{2j}. \end{equation} В случае \(r=s=2\) отсюда получаем \[ \textbf{p}^1_{0,0}=\ldots+\frac{9}{16}\textbf{P}_{-1,-1}+\frac{3}{16}\textbf{P}_{0,-1}+\ldots +\frac{3}{16}\textbf{P}_{-1,0}+\frac{1}{16}\textbf{P}_{0,0}+\ldots \] Поверхности, полученные в результате последовательного применения таких масок, называют поверхностями Doo-Sabin.

Схема Doo-Sabin.

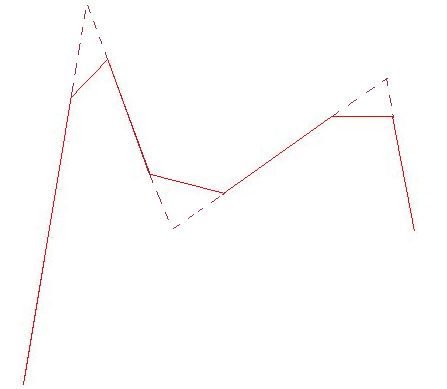
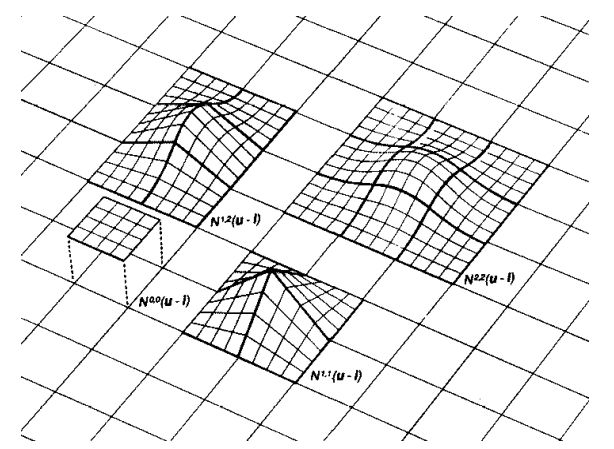
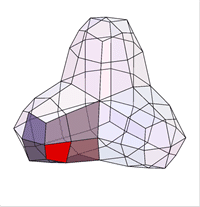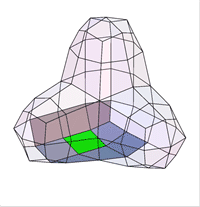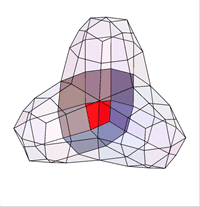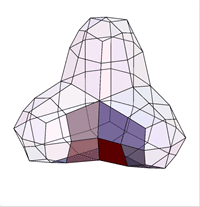
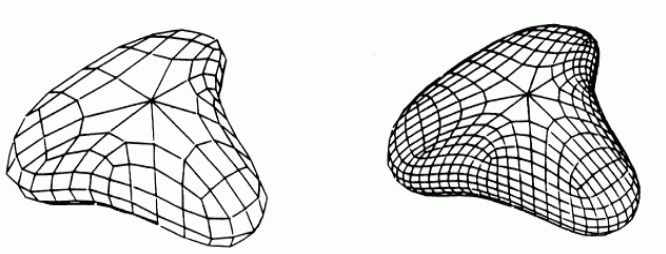
Daniel Doo и Malcolm Sabin развили идею последовательного улучшения предложенную George Chaikin и адаптировали эту технологию для B-сплайновых поверхностей, что позволило получить новую конструкцию поверхности.

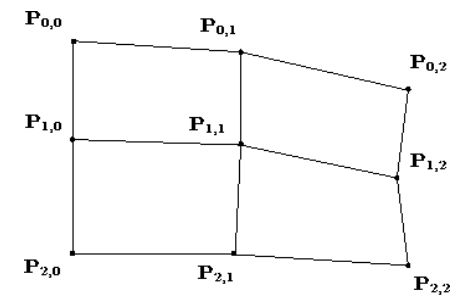
Считаем, что биквадратные однородные В-сплайн поверхности \({\bf P} (u,v)\) определены \(3 \times 3\) массивом контрольных точек \[ P \: = \: \left[ \begin{array}{ccc} {\bf P} _{0,0} & {\bf P} _{0,1} & {\bf P} _{0,2} \\ {\bf P} _{1,0} & {\bf P} _{1,1} & {\bf P} _{1,2} \\ {\bf P} _{2,0} & {\bf P} _{2,1} & {\bf P} _{2,2} \end{array} \right] \]

и следующее уравнение (в матричной форме) \[ {\bf P} (u,v) \: = \: \left[ \begin{array}{ccc} 1 & u & u^2 \end{array} \right] M P M^T \left[ \begin{array}{c} 1 \\v \\v^2 \end{array} \right] \] где \( M\) есть \(3 \times 3\) матрица \[ M \: = \: \frac{1}{2} \left[ \begin{array}{rrr} 1 & 1 & 0 \\ -2 & 2 & 0 \\ 1 & -2 & 1 \end{array} \right] \] Каждую фиксированную заплатку мы разобьем на четыре заплатки, которые дадут 16 новых контрольных точек. Обсудим subdivision схему только для одной из четырех (этой подзаплатке соответствует \(0 \leq u,v \leq \frac{1}{2}\), остальные легко определить аналогичным образом.

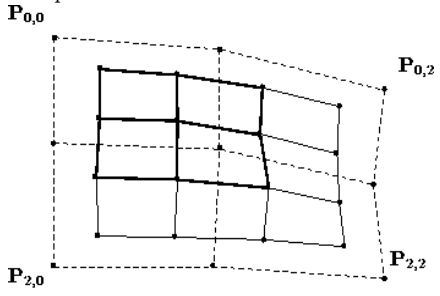
Разбивая поверхность, вводим новый параметр \(u'=\frac{u}{2}\) и \(v'=\frac{v}{2}\) и определяем новую поверхность \({\bf P}'(u,v)\). После замены получаем \[ {\bf P} '(u,v) = {\bf P} \left( \frac{u}{2}, \frac{v}{2} \right) \] \[ =\left[ \begin{array}{ccc} 1 & \frac{u}{2} & \left(\frac{u}{2}\right)^2 \end{array} \right] M P M^T \left[ \begin{array}{c} 1 \\ \frac{v}{2} \\ \left(\frac{v}{2}\right)^2 \end{array} \right] \] \[ = \left[ \begin{array}{ccc} 1 & u & u^2 \end{array} \right] \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] M P M^T \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] ^T \left[ \begin{array}{c} 1 \\v \\v^2 \end{array} \right] \] \[ = \left[ \begin{array}{ccc} 1 & u & u^2 \end{array} \right] M M^{-1} \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] M P M^T \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] ^T (M^{-1})^T M^T \left[ \begin{array}{c} 1 \\v \\v^2 \end{array} \right] \] \[ = \left[ \begin{array}{ccc} 1 & u & u^2 \end{array} \right] M \left( M^{-1} \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] M \right) P \left( M^T \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] ^T (M^{-1})^T \right) M^T \left[ \begin{array}{c} 1 \\v \\v^2 \end{array} \right] \] \[ = \left[ \begin{array}{ccc} 1 & u & u^2 \end{array} \right] M \left( M^{-1} \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] M \right) P \left( M^{-1} \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] M \right) ^T M^T \left[ \begin{array}{c} 1 \\v \\v^2 \end{array} \right] \] \[ = \left[ \begin{array}{ccc} 1 & u & u^2 \end{array} \right] M P' M^T \left[ \begin{array}{c} 1 \\v \\v^2 \end{array} \right] \] где \(P' = S P S^T\) и \[ S \: = \: M^{-1} \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] M \] Таким образом получаем поверхность \[ {\bf P} '(u,v) \: = \: \left[ \begin{array}{ccc} 1 & u & u^2 \end{array} \right] M S M^T \left[ \begin{array}{c} 1 \\v \\v^2 \end{array} \right] \] для любых \(3 \times 3\) массива контрольных точек \( S\). Таким образом \({\bf P} '(u,v)\) есть однородная биквадратная B-сплайновая поверхность. Матрица \( S\) называется матрицей дробления \begin{eqnarray*} S & = & \frac{1}{2} \left[ \begin{array}{rrr} 2 & -1 & 0 \\ 2 & 1 & 0 \\ 2 & 3 & 4 \end{array} \right] \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & \frac{1}{4} \end{array} \right] \frac{1}{2} \left[ \begin{array}{rrr} 1 & 1 & 0 \\ -2 & 2 & 0 \\ 1 & -2 & 1 \end{array} \right] \\ & = & \frac{1}{4} \left[ \begin{array}{rrr} 3 & 1 & 0 \\ 1 & 3 & 0 \\ 0 & 3 & 1 \end{array} \right] \end{eqnarray*} и контрольные точки \( P'\) соответствующие подзаплатке определяются из условия \[ P' \: = \: S P S^T \] или, что то же, \begin{eqnarray*} P' & = & \frac{1}{4} \left[ \begin{array}{rrr} 3 & 1 & 0 \\ 1 & 3 & 0 \\ 0 & 3 & 1 \end{array} \right] \left[ \begin{array}{ccc} {\bf P} _{0,0} & {\bf P} _{0,1} & {\bf P} _{0,2} \\ {\bf P} _{1,0} & {\bf P} _{1,1} & {\bf P} _{1,2} \\ {\bf P} _{2,0} & {\bf P} _{2,1} & {\bf P} _{2,2} \\ \end{array} \right] \frac{1}{4} \left[ \begin{array}{rrr} 3 & 1 & 0 \\ 1 & 3 & 0 \\ 0 & 3 & 1 \end{array} \right] ^T \\ & = & \frac{1}{16} \left[ \begin{array}{ccc} 3 {\bf P} _{0,0} + {\bf P} _{1,0} & 3 {\bf P} _{0,1} + {\bf P} _{1,1} & 3 {\bf P} _{0,2} + {\bf P} _{1,2} \\ {\bf P} _{0,0} + 3 {\bf P} _{1,0} & {\bf P} _{0,1} + 3 {\bf P} _{1,1} & {\bf P} _{0,2} + 3 {\bf P} _{1,2} \\ 3 {\bf P} _{1,0} + {\bf P} _{2,0} & 3 {\bf P} _{1,1} + {\bf P} _{2,1} & 3 {\bf P} _{1,2} + {\bf P} _{2,2} \end{array} \right] \left[ \begin{array}{rrr} 3 & 1 & 0 \\ 1 & 3 & 3 \\ 0 & 0 & 1 \end{array} \right] \\ & = & \frac{1}{16} \left[ \begin{array}{ccc} {\bf P} _{0,0}' & {\bf P} _{0,1}' & {\bf P} _{0,2}' \\ {\bf P} _{1,0}' & {\bf P} _{1,1}' & {\bf P} _{1,2}' \\ {\bf P} _{2,0}' & {\bf P} _{2,1}' & {\bf P} _{2,2}' \\ \end{array} \right] \end{eqnarray*} где \({\bf P} '_{i,j}\) может быть записана следующим образом \[ {\bf P} _{0,0}' = \frac{1}{16} \left( 3 ( 3 {\bf P} _{0,0} + {\bf P} _{1,0} ) + ( 3 {\bf P} _{0,1} + {\bf P} _{1,1} ) \right) \] \[ {\bf P} _{0,1}' = \frac{1}{16} \left( ( 3 {\bf P} _{0,0} + {\bf P} _{1,0} ) + 3 ( 3 {\bf P} _{0,1} + {\bf P} _{1,1} ) \right) \] \[ {\bf P} _{0,2}' = \frac{1}{16} \left( 3 ( 3 {\bf P} _{0,1} + {\bf P} _{1,1} ) + ( 3 {\bf P} _{0,2} + {\bf P} _{1,2} ) \right) \] \[ {\bf P} _{1,0}' = \frac{1}{16} \left( 3 ( {\bf P} _{0,0} + 3 {\bf P} _{1,0} ) + ( {\bf P} _{0,1} + 3 {\bf P} _{1,1} ) \right) \] \[ {\bf P} _{1,1}' = \frac{1}{16} \left( ( {\bf P} _{0,0} + 3 {\bf P} _{1,0} ) + 3 ( {\bf P} _{0,1} + 3 {\bf P} _{1,1} ) \right) \] \[ {\bf P} _{1,2}' = \frac{1}{16} \left( 3 ( {\bf P} _{0,1} + 3 {\bf P} _{1,1} ) + ( {\bf P} _{0,2} + 3 {\bf P} _{1,2} ) \right) \] \[ {\bf P} _{2,0}' = \frac{1}{16} \left( 3 ( 3 {\bf P} _{1,0} + {\bf P} _{2,0} ) + ( 3 {\bf P} _{1,1} + {\bf P} _{2,1} ) \right) \] \[ {\bf P} _{2,1}' = \frac{1}{16} \left( ( 3 {\bf P} _{1,0} + {\bf P} _{2,0} ) + 3 ( 3 {\bf P} _{1,1} + {\bf P} _{2,1} ) \right) \] \[ {\bf P} _{2,2}' = \frac{1}{16} \left( 3 ( 3 {\bf P} _{1,1} + {\bf P} _{2,1} ) + ( 3 {\bf P} _{1,2} + {\bf P} _{2,2} ) \right) \] 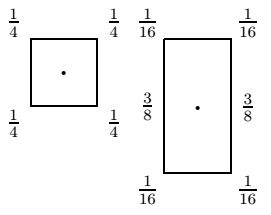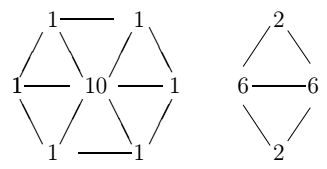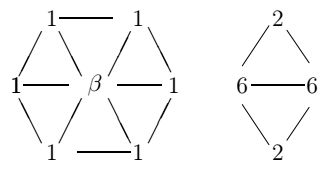Это равенство может быть рассмотрено с двух сторон:

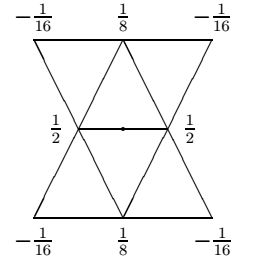
Каждая из точек \({\bf P} _{i,j}\) использует четыре точки первоначальной прямоугольной решетки в соотношении 9-3-3-1. Таким образом получаем маску subdivision схемы для генерации новой точки
Каждое из этих равенств строит взвешенную точку от угла в пропорции 3:1 и новую взвешенную точку от полученной в пропорции 3:1. Это в точности совпадает с пропорцией кривой Чайкина, что дает возможность рассматривать этот метод как обобщение метода Чайкина на случай поверхностей.

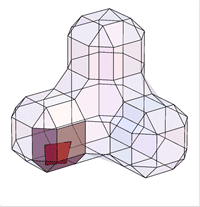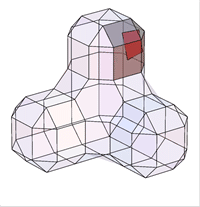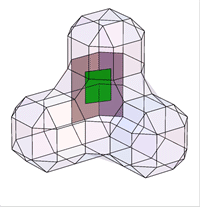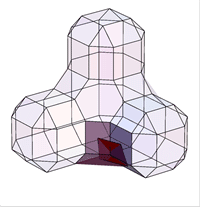
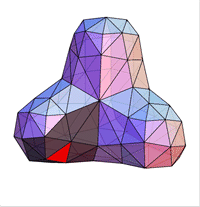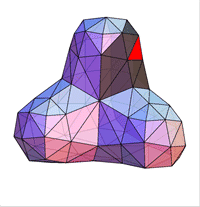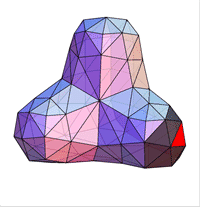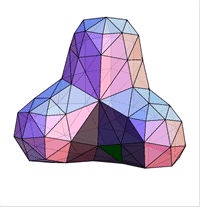
Описанный метод предложен Donald Doo и Malcolm Sabin и носит название Doo-Sabin поверхностей.
Doo и Sabin построили точки как взвешенные средние значения четырех точках полигона - в его вершинах:

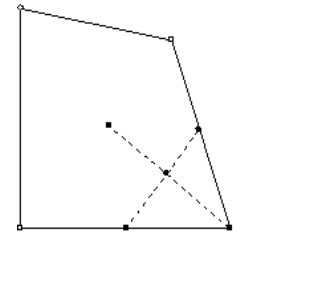
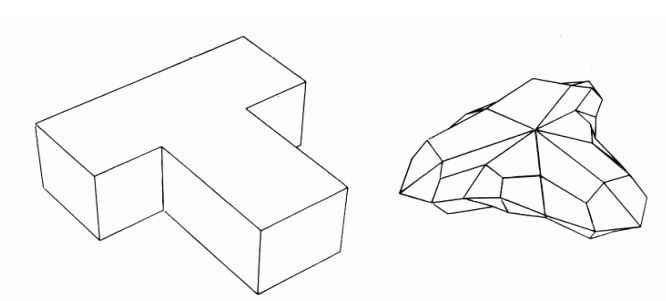
Легко видеть, что в этом случае однородный B-сплайн дает новую точку (на рисунке Face Point). Таким образом генерируя новые четыре точки мы получаем новую четырехугольную решетку. Последовательно повторяя этот процесс, получаем описание исходной поверхности.
Таким образом для каждой вершины \({\bf P} _i\) генерируем новую точку \({\bf P} _i'\) как среднее значение вершин соответствующей клетки.

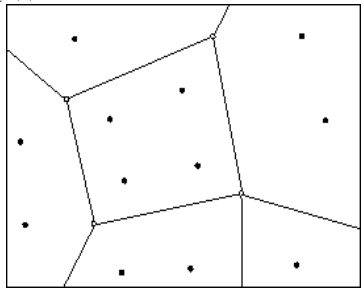
Для каждой клетки получаются четыре новые точки, дающие вложенный полигон с вершинами в этих точках.

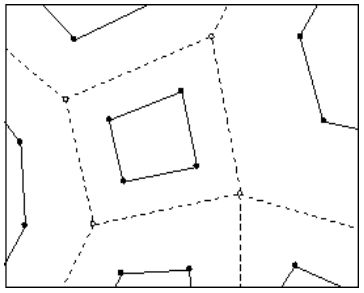
Соединяя эти точки между собой, получаем новую решетку.

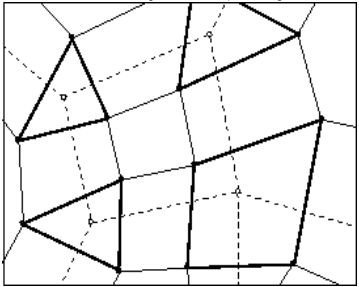
Построенная решетка является исходной для следующего шага.
Описанный метод называется "cutting off the corners" (разрезание углов).

Как правило, для построения поверхностей Doo-Sabin в качестве опорных точек \({\bf P} _{i,j}\) используются значения, снятые с поверхности. При этом качество описания поверхности методом Doo-Sabin совпадает с качеством описания полигональной функцией, то есть поверхностью, совпадающей на каждом шаге с некоторой плоскостью.

Схема Doo-Sabin.

Если для построения метода subdivision использовать сплайны, то метод Doo-Sabin можно существенно уточнить. Для элемента \({\bf P}' _{0,0}\) маска subdivision будет иметь вид \[ S=(s_{\nu,\mu})_{\nu,mu=-1}^2= \frac{1}{1024} \left[ \begin {array}{rrrr} -3&-19&-9&-1\\ -27&213&47&-9\\ -57&791&213&-19\\ -9&-57&-27 &-3 \end {array} \right] \] то есть \[ {\bf P}' _{0,0}=\frac{1}{1024}(-27\,{\bf P}_{{1,-1}}+213\,{\bf P}_{{1,0}}+47\,{\bf P}_{{1,1}} -9\,{\bf P}_{{1,2}}-9\,{\bf P}_{{-1,-1}}-3\,{\bf P}_{{2,-1}}\] \[-19\,{\bf P}_{{2,0}}-9\,{\bf P}_{{2,1}}-{\bf P}_{{2,2}}-3\,{\bf P}_{{-1,2}}-57 \,{\bf P}_{{0,-1}}+ 791\,{\bf P}_{{0,0}}+213\,{\bf P}_{{0,1}}\] \[-19\,{\bf P}_{{0,2}}-57\,{\bf P}_{{-1,0} }-27\,{\bf P}_{{-1,1}} ), \] \[ {\bf P}' _{1,0}=\frac{1}{1024}(-9\,{\bf P}_{{2,-1}}-57\,{\bf P}_{{2,0}}-27\,{\bf P}_{{2,1}} -3\,{\bf P}_{{2,2}}-57\,{\bf P}_{{1,-1}}+791\,{\bf P}_{{1,0}}\] \[+213\,{\bf P}_{{1,1}}-19\,{\bf P}_{{1,2}}-27\,{\bf P}_{{0,-1}}+213\,{\bf P}_{{0 ,0}} +47\,{\bf P}_{{0,1}}-9\,{\bf P}_{{0,2}}-3\,{\bf P}_{{-1,-1}}\] \[-19\,{\bf P}_{{-1,0}}-9\,{\bf P}_{{- 1,1}}-{\bf P}_{{-1,2}} ), \] \[ {\bf P}' _{0,1}=\frac{1}{1024}(-{\bf P}_{{2,-1}}-9\,{\bf P}_{{2,0}}-19\,{\bf P}_{{2,1}}-3\,{\bf P}_{{2,2}}- 9\,{\bf P}_{{1,-1}}+47\, {\bf P}_{{1,0}}+213\,{\bf P}_{{1,1}}\] \[-27\,{\bf P}_{{1,2}}-19\,{\bf P}_{{0,-1}}+213\,{\bf P}_{{0,0}}+ 791\,{\bf P}_{{0,1}}-57\,{\bf P}_{{0,2}} -3\,{\bf P}_{{-1,-1}}-27\,{\bf P}_{{-1,0}}\] \[-57\,{\bf P}_{{-1,1}}-9\,{\bf P}_{{-1,2}} ), \] \[ {\bf P}' _{1,1}=\frac{1}{1024}(-3\,{\bf P}_{{2,-1}}-27\,{\bf P}_{{2,0}}-57\,{\bf P}_{{2,1}}-9\,{\bf P}_{{2,2}} -19\,{\bf P}_{{1,-1}}+213\,{\bf P}_{{1,0}}\] \[+791\,{\bf P}_{{1,1}}-57\,{\bf P}_{{1,2}}-9\,{\bf P}_{{0,-1}}+47\,{\bf P}_{{0,0 }}+213\,{\bf P}_{{0,1}} -27\,{\bf P}_{{0,2}}-{\bf P}_{{-1,-1}}\] \[-9\,{\bf P}_{{-1,0}}-19\,{\bf P}_{{-1,1}}-3\,{\bf P}_{{-1,2}} ). \]

Поверхности Catmull-Clark.

Используя subdivision для бикубических B-сплайновых поверхностей (для \(r=s=3\) ), Ed Catmull и Jim Clark получили следующие маски

В дальнейшем они развили методологию Doo и Sabin отметив, что она годится не только для прямоугольных решеток, но и для разбиений с произвольной топологией. Это обобщение было реализовано введением новой узловой точки, модификацией метода для вычисления точек вершин и методики присоединения точки в решетку.
Опишем этот алгоритм.
Для каждого набора узловых точек генерируются новые точки - которые представляют собой среднее всех оригинальных точек определяющих данную грань.
Граничные точки (точки лежащие на ребре) генерируются как средние значения оригинальных концов ребра и двух новых точек смежных к этому ребру.
Вычисление новых вершин определяется как среднее от \( {\bf Q} \), \( 2 {\bf R}\) и \(\frac{(n-3) {\bf S} }{n}\), где \( {\bf Q} \) есть среднее от новых узловых точек смежных с оригинальной узловой точкой, \( {\bf R} \) есть среднее от средин всех ребер соединеных с оригинальной вершиной и \( {\bf S} \) есть оригинальная вершина.
Присоединение к сетке происходит следующим образом.
Каждая новая узловая точка соединяется с новыми краевыми точками, ограничивающими новое ребро.
Каждая новая вершина соединяется с новыми краевыми точками порожденными оригинальной вершиной.

Схема Catmull-Clark.

Пример.

Для примера проиллюстрируем этот процесс на сетке состоящей из четырех треугольников.

Сначала мы создаем узловые точки как средние значения точек, описывающих оригинальную грань. Эти точки на рисунке обозначены \( {\bf F} \).

Далее мы создаем краевые точки, которые вычисляются как среднее число четырех точек - две оригинальные, которые определяют край, и две новые, которые смежны к краю. Эти точки обозначены \( {\bf E} \).

Теперь создаем единственную точку вершины. Эта точка, по крайней мере в двух измерениях совпадает с оригинальным центром.

Наконец, мы соединяем края к точкам, которые сгенерировали. Сначала соединяем узловую точку которая соответствует краю грани и потом соединяем точку вершины с краями.

Заметим, что каждая грань новой решетки имеет четыре ребра и можно использовать алгоритм для четырехугольной решетки.
Для последующего описания этого примера рассмотрим следующую решетку.

Вначале создаем узловые точки, как средние оригинальных узлов. Эти точки на рисунке обозначены через \( {\bf F} \).

Теперь создаем граничные точки, вычисляемые как среднее четырех точек - две оригинальные, определяющие ребро и две новые, смежные с этим ребром. Эти точки обозначены через \( {\bf E} \) (Узловые точки на предшествующем шаге указаны как точки с белым центром).

Перейдем к конструированию вершин. Эти точки показаны ниже с узловыми и краевыми точками с помощью белых центров.

И, наконец, соединяем узлы краев с точками, которые мы получили. Вначале соединим узловую точку которая соответствует краю и соединим вершины с краями.

Отметим, что, как и в предыдущем случае, новая сетка имеет четыре ребра и, фактически, во всех случаях это будет справедливо не зависимо от вида первоначальной решетки.

На следующей иллюстрации продемонстрированы четыре шага применения схемы Catmull-Clark.

При этом грани соответствующие оригинальным контрольным точкам сохраняют валентность (количество ребер смежных вершине).
Заметим, что грани, соответствующие оригинальным точкам сохраняют валентность. Обратите внимание на точку с валентностью 8 на вершине тела.

Любая часть поверхности, где к нас массив \(4 \times 4\) контрольных точек с прямоугольной топологией, представляет собой бикубическую В-сплайн поверхность. В течение процесса subdivision единственно, где это условие не выполняется - в особых точках, где валентность не кратна четырем. Если в оригинале все грани имели валентность четыре, то в результате получим бикубическую В-сплайн поверхность.

Методы subdivision по треугольной решетке.

Тензорное произведение В-сплайнов можно определять не обязательно по прямоугольной решетке. Другой широко используемой модификацией В-сплайнов на случай двух переменных является поверхность вида \begin{equation}\label{s.26} \textbf{S}_{r,s,t}(\mathbf{u})=\sum_{\mathbf{i}\in Z^2}\textbf{P}_{\mathbf{i}} N_{r,s,t}(\mathbf{u}-\mathbf{i}), \end{equation} где \(\mathbf{u}\in R^2\) и \(\mathbf{i}\in Z^2\) узлы треугольной решетки определяемой векторами \(u\), \(v\), \(w\).
Сплайн по треугольной решетке строится как выпуклая оболочка В-сплайнов порядка \(r\), \(s\) и \(t\) с центром в точке \(\mathbf{i}\) построенных вдоль направлений \(u\), \(v\), \(w\).

Процедура subdivision сплайнами по треугольной решетке совершенно аналогична той же процедуре по прямоугольной решетке. Решетка с узлами \(\mathbf{i}\) определяет решетку с узлами в точках \(\mathbf{j}=\mathbf{i}/2\).
Тогда поверхность (\ref{s.26}) можно записать в виде \begin{equation}\label{s.27} \textbf{S}_{r,s,t}(\mathbf{u})=\sum_{\mathbf{j}\in Z^2}\textbf{P}_{\mathbf{j}} N_{r,s,t}(2(\mathbf{u}-\mathbf{j})). \end{equation} Замечая, что для базисного сплайна имеет место равенство \begin{equation}\label{s.28} N_{r,s,t}(\mathbf{u})=\sum_{\mathbf{j}\in Z^2}{c}^{r,s,t}_{\mathbf{j}} N_{r,s,t}(2(\mathbf{u}-\mathbf{j})), \end{equation} имеем \begin{equation}\label{s.29} \textbf{p}^1_{\mathbf{j}}=\sum_{\mathbf{i}\in Z^2}{c}^{r,s,t}_{\mathbf{j}-\mathbf{i}}\textbf{P}_{\mathbf{i}}. \end{equation} и \begin{equation}\label{s.30} c_{\mathbf{j}}=2^{-(r+s+t)}\sum_{k=0}^{t}C_r^{2i-k}C_s^{2j-k}C_t^{k}. \end{equation} Отсюда, для каждого конкретного случая, сразу получаем формулы subdivision. В частности, для сплайны \(N_{2,2,2}(\mathbf{u})\) порождают следующие маски

Последовательное применение таких масок образует поверхность Loop.
Основываясь на треугольной решетке и развивая идею subdivision, С. Loop предложил схему генерации двух вершин и углов.
Маска генерирования вершины позволяет сгенерировать контрольные точки для каждой вершины и граничные маски генерируют новые контрольные точки для каждого ребра треугольной решетки.
Краевые маски позволяют найти граничные точки как среднее трех величин: два центра смежных граней и средину ребра. Маска для вершины определяется как выпуклая комбинация точек \( {\bf V} \), оригинальной вершины и \( {\bf Q} \) среднего значения оригинальных точек на границе \( {\bf V} \). Эта выпуклая комбинация должна быть таковой, что: если \({\bf V} ^1\) есть новая точка вершины, то \begin{eqnarray*} {\bf V} ^1 & = & \frac{10 {\bf V} + {\bf Q} _1 + {\bf Q} _2 + {\bf Q} _3 + {\bf Q} _4 + {\bf Q} _5 + {\bf Q} _6}{16} \\ & = & \frac{5}{8} {\bf V} + \frac{ {\bf Q} _1 + {\bf Q} _2 + {\bf Q} _3 + {\bf Q} _4 + {\bf Q} _5 + {\bf Q} _6}{16} \\ & = & \frac{5}{8} {\bf V} + \frac{6 {\bf Q} }{16} \\ & = & \frac{5}{8} {\bf V} + \frac{3}{8} {\bf Q} \end{eqnarray*} Для произвольной треугольной решетки мы можем использовать те же правила генерирования новых краевых точек и новой вершины. Тем не менее Loop отмечал, что относительно определения вершины, поверхность дает некоторые точки в которых касательная поверхность изменяется дискретно. В дальнейшем он заметил, что если использовать subdivision определяемый следующим образом \[ {\bf V} ^1 \: = \: \alpha_n {\bf V} + ( 1 - \alpha_n ) {\bf Q} \] где \[ \alpha_n \: = \: \left( \frac{3}{8} + \frac{1}{4} \cos\frac{2\pi}{n} \right) ^ 2 + \frac{3}{8} \] то получим поверхность с непрерывно изменяющейся касательной плоскостью. (Отметим, что когда \(n=\frac{1}{2}\), то \( \alpha_n=\frac{5}{8}\), как требовалось).
Такие поверхности называют поверхностями Loop и для их генерирования используют маски

где для вершины с \( n\) углами параметр \( \beta\) используется для определения новой вершины. Это \[ \alpha_n {\bf V} + ( 1 - \alpha_n ) {\bf Q} \: = \: \frac{\beta {\bf V} + n {\bf Q} }{\beta+n} \] или \[ \alpha_n \: = \: \frac{\beta}{\beta+n} \] или \[ \beta \: = \: \frac{n \alpha_n}{1 - \alpha_n}. \]

Схема Loop.

Для треугольных решеток Dyn, N., Levin, D., и Gregory, J. A. в 1990 году предложили другую схему, известную как схема "бабочка" (Butterfly)

Вычисление формул subdivision из условия точности.

Заметим, что формулы subdivision можно получить из других соображений, например, из условия точности.
Проиллюстрируем этот факт для равномерных решеток.
Пусть \(f_{i,j}=f(ih,jh)\), где \(h\) шаг решетки. Имея значения \(f_{i,j}\), \(f_{i+1,j}\), \(f_{i,j+1}\), \(f_{i+1,j+1}\), найдем приближенное значение функции в точке \(((i+1/4)h,(j+1/4)h)\). Используя параллельный перенос, совместим точку \)((i+1/4)h,(j+1/4)h)\) с началом координат. Используя формулу Тейлора в окрестности нуля, получаем, что если \(f\in C^3(\mathbb{R}^2)\), то искомые данные можно записать в виде \[ f\left(-\frac{1}{4}h,-\frac{1}{4}h\right)=f-\frac{h}{4}\left(f'_x+f'_y\right)+\frac{h^2}{32}\left(f''_{xx}+2f''_{xy}+f''_{yy}\right)+O(h^3), \] \[ f\left(-\frac{1}{4}h,\frac{3}{4}h\right)=f+\frac{h}{4}\left(-f'_x+3f'_y\right)+\frac{h^2}{32}\left(f''_{xx}-6f''_{xy}+9f''_{yy}\right)+O(h^3), \] \[ f\left(\frac{3}{4}h,\frac{3}{4}h\right)=f+\frac{3h}{4}\left(f'_x+f'_y\right)+\frac{9h^2}{32}\left(f''_{xx}+2f''_{xy}+f''_{yy}\right)+O(h^3), \] \[ f\left(\frac{3}{4}h,-\frac{1}{4}h\right)=f+\frac{h}{4}\left(3f'_x-f'_y\right)+\frac{h^2}{32}\left(9f''_{xx}-6f''_{xy}+f''_{yy}\right)+O(h^3), \] где \(f=f(0,0)\) и \[ \left.f^{(n+m)}_{x^ny^m}=\frac{\partial^{n+m}f}{\partial x^{n}\partial y^{m}}\right|_{(0,0)}. \] Будем искать приближенное значение \(f=f(0,0)\) в виде линейной комбинации \[ f\approx\alpha f\left(-\frac{1}{4}h,-\frac{1}{4}h\right)+\beta f\left(-\frac{1}{4}h,\frac{3}{4}h\right)+\gamma f\left(\frac{3}{4}h,\frac{3}{4}h\right)+\delta f\left(\frac{3}{4}h,-\frac{1}{4}h\right)= \] \[ =f(\alpha+\beta+ \gamma+\delta)+\frac{h}{4}f'_x\left(-\alpha-\beta+3\gamma+3\delta \right)+ \frac{h}{4}f'_y\left(-\alpha+3\beta+3\gamma-\delta \right)+\] \[ \frac{h^2}{32}f''_{xx}\left(\alpha+\beta+ 9\gamma+9\delta\right)+ \frac{h^2}{16}f''_{xy}\left(\alpha-3\beta+ 9\gamma-3\delta\right)+ \] \[\frac{h^2}{32}f''_{yy}\left(\alpha+9\beta+ 9\gamma+\delta\right)+O(h^3).\] Если не давать предпочтения какому-либо направлению, то исходя из наиболее высокой точности формулы subdivision, получаем систему уравнений \[ \left\{ \begin{array}{c} \alpha+\beta+ \gamma+\delta=1, \\ \alpha+\beta-3\gamma-3\delta=0, \\ \alpha-3\beta-3\gamma+\delta=0, \\ \alpha-3\beta+9\gamma-3\delta=0. \end{array} \right. \] Отсюда сразу получаем \[ \alpha=\frac {9}{16},\beta=\frac{3}{16},\gamma=\frac{1}{16},\delta=\frac{3}{16}.\] Таким образом мы получили формулы subdivision Doo-Sabin. При этом заметим, что если \(f\in C^3(\mathbb{R}^2)\), то ошибка subdivision в точке \((0,0)\) будет равна \[ \frac{3h^2}{32}\left(f''_{xx}+f''_{yy}\right)+O(h^3). \] Аналогично получаются формулы subdivision для схемы Catmull-Clark, а также Loop и "Butterfly".
Заметим, что если \(f\in C^3(\mathbb{R}^2)\), то для схемы Catmull-Clark ошибка subdivision для точки на грани будет равна \[ \frac{h^2}{8}\left(f''_{xx}+f''_{yy}\right)+O(h^3), \] а для точки на ребре \[ \frac{h^2}{2}\left(f''_{xx}+f''_{yy}\right)+O(h^3). \] Для схемы Loop ошибка subdivision равна \[ \frac{3h^2}{8}\left(f''_{xx}+f''_{yy}\right)+O(h^3). \] Аналогично, но технически сложнее получается схема "Butterfly". Если \(f\in C^4(\mathbb{R}^2)\), то ошибка в этом случае имеет порядок \(O(h^4)\).
Идея алгебраической точности метода subdivision привела к появлению другого подхода к уплотнению данных. Это идея интерполяционного subdivision.

В следующем скрипте продемонстрированы возможности subdivision по отрисовке различных поверхностей.