|
|
Interpolation Subdivision
|
|
Схема интерполяционного subdivision.
Идея интерполяционного subdivision.
Идея метода состоит в том, что по некоторому алгоритму пополняем
таблицу \(y_{i,0}\) \((i=0,\ldots,n)\) значениями в срединах, получая новую таблицу \(y_{i,1}\) \((i=0,\ldots,2n)\). Далее,
рассматривая в качестве исходной таблицу \(y_{i,1}\) \((i=0,\ldots,2n)\) по тому же правилу получаем таблицу данных уже
вчетверо гуще и так далее.
Рассмотрим вспомогательную задачу: через точки \((x_{\nu,0},y_{\nu})\) \((\nu=i-1,i,i+1,i+2)\) проведем интерполяционную
кубическую параболу
\[
y=-\frac{y_{i-1}}{6h^3}(x-x_{i,0})(x-x_{i+1,0})(x-x_{i+2,0})+
\frac{y_{i}}{2h^3}(x-x_{i-1,0})(x-x_{i+1,0})(x-x_{i+2,0})-
\]
\[
-\frac{y_{i+1}}{2h^3}(x-x_{i-1,0})(x-x_{i,0})(x-x_{i+2,0})+ \frac{y_{i+2}}{6h^3}(x-x_{i-1,0})(x-x_{i,0})(x-x_{i+1,0})
\]
и через \(\hat{y}_{i+1/2,0}\) обозначим значение этой параболы в точке \(x_{i+1/2,0}\). Ясно, что
\begin{equation}\label{s.31}
\hat {y}_{i+1/2,0}=\frac{1}{16}\left(-y_{i-1,0}+9y_{i,0}+9y_{i+1,0}-y_{i+2,0}\right)=
\frac{y_{i+1,0}+y_{i,0}}{2}-\frac{1}{8}\Delta^2 \left(\frac{y_{i+1,0}+y_{i,0}}{2}\right),
\end{equation}
где \(\Delta^2z_i=z_{i+1}-2z_i+z_{i-1}\) вторая центральная разность в точке \(i\).
Обозначим
\begin{equation}\label{s.32} y_{2i,1}=y_{i,0}\,\,\,\,\,\,\,\,\,\,(i=0,\ldots,n), \end{equation}
\begin{equation}\label{s.33} y_{2i+1,1}=\hat{y}_{i+1/2,0}\,\,\,\,\,\,\,\,\,\,(i=0,\ldots,n-1). \end{equation}
Таким образом мы получим значения функции \(y_{i,1}\) \((i=0,1,\ldots,2n)\). Этих данных вдвое больше исходных.
Последовательно повторяя эту процедуру, получаем
\begin{equation}\label{s.33_1} \hat{y}_{i+1/2,1}=\frac{y_{i+1,1}+y_{i,1}}{2}-\frac{1}{8}\Delta^2\left(\frac{y_{i+1,1}+y_{i,1}}{2}\right) \end{equation}
и по аналогии с (\ref{s.32}) - (\ref{s.33}) находим
\(y_{i,2}\) \((i=0,\ldots,2^2n)\).
Поступая далее таким же образом, получаем рекуррентное соотношение
\begin{equation}\label{s.34}
\hat{y}_{i+1/2,k-1}=\frac{y_{i+1,k-1}+y_{i,k-1}}{2}-\frac{1}{8}\Delta^2 \left(\frac{y_{i+1,k-1}+y_{i,k-1}}{2}\right),
\end{equation} и
\begin{equation}\label{s.34_1} y_{2i,k}=y_{i,k-1}\,\,\,\,\,\,\,\,\,\,(i=0,\ldots,2^{k-1}n), \end{equation}
\begin{equation}\label{s.34_2}
y_{2i+1,k}=\hat{y}_{i+1/2,k-1}\,\,\,\,\,\,\,\,\,\,(i=0,\ldots,2^{k-1}n-1),
\end{equation}
где \(k\) любое натуральное число.
Заметим, что если вместо кубической интерполяционной параболы мы возьмем кубическую В-сплайновую функцию, то получим те же формулы subdivision.
Схематически формула интерполяционного subdivision порожденного кубическими В-сплайнами будет иметь вид

Заметим, что для традиционной схемы subdivision порожденного кубическими В-сплайнами (схема Catmull-Clark) аналогичная схема будет иметь вид
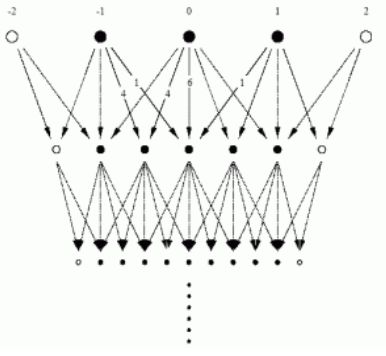
Схема интерполяционного subdivision. Общая постановка.
Через \(\ell_{\infty}(\mathbb{R})\) обозначим пространство ограниченных числовых последовательностей
\({\textstyle\it\bf{f}}=\{f_i\}_{i\in Z}\) с нормой \( \|{\textstyle\it\bf{f}}\|= \sup_{i\in Z}|f_i|. \)
Пусть, вначале, \( {\it\bf x}_0=\{x_{i}\}_{i\in Z}=\{x_{i,0}\}_{i\in Z}=\{ih\}_{i\in Z} \) - равномерное разбиение оси с
шагом \(h>0\) и \( {\textstyle\it\bf{f}}={\textstyle\it\bf{f_0}} =\{f_{\nu}\}_{\nu\in Z}=\{f_{\nu,0}\}_{\nu\in Z} \)
последовательность из \(\ell_{\infty}(\mathbb{R})\).
Пусть дано \(m\) линейных функционалов \(A_\mu({\textstyle\it\bf{f}})\) (\(\mu=1,\ldots,m\)) и зафиксирована система точек
\(\xi_\mu\in (0,1)\) (\(\mu=1,\ldots,m\)) такая, что \(0\lt\xi_1\lt\xi_2\lt\ldots\lt\xi_m\lt 1\). Полагаем
\({\textstyle\it\bf{f_0}}=A_0({\textstyle\it\bf{f}})\) и \(\hat{{\textstyle\it\bf{f}}}^{0,\nu}_{\mu}=
A_\mu({\textstyle\it\bf{f}}^{\nu}_0)\) (\(\mu=0,1,\ldots,m\)), где \({\textstyle\it\bf{f}}^{\nu}_0\) сдвиг
последовательности \({\textstyle\it\bf{f_0}}\), то есть \({\textstyle\it\bf{f}}^{\nu}_0=\{f_{i-\nu}\}_{i\in Z}\). Построим
новые последовательности \({\textstyle\it\bf{x}}_1=\{x_{i,1}\}_{i\in Z}\) и
\({\textstyle\it\bf{f_{1}}}=\{f_{\nu,1}\}_{\nu\in Z} \) полагая
\[
x_{mi+\mu,1}=x_{i,0}+\xi_{\mu}(x_{i+1,0}-x_{i,0})= x_{i,0}+\xi_{\mu}h,\,\,\,\,\,\, \mu=0,\ldots,m,
\]
и, аналогично,
\[
f_{mi+\mu,1}=\hat{f}^0_{\mu,i}=A_\mu({\textstyle\it\bf{f}}^{i}_0),\,\,\,\,\,\, \mu=0,\ldots,m.
\]
Упорядоченный по возрастанию набор чисел \(x_{mi+\mu,1}\) образует новое разбиение оси, которое обозначим через \({\it\bf
x_{1}}\), а его элементы - через \(x_{\nu,1}\) \(\nu\in Z\). Соответственно числа \(f_{mi+\mu,1}\) будем обозначать через
\(f_{\nu,1}\) и полагаем \({\textstyle\it\bf{f_{1}}}= \{f_{\nu,1}\}_{\nu\in Z}\).
Полученный набор будем использовать в качестве исходного и повторяем процедуру пополнения данных, что приводит к
рекуррентным формулам для \({\it\bf x_{k}}=x_{\nu,k}\) \(\nu\in Z\) и \({\textstyle\it\bf{f_{k}}}=\{f_{\nu,k}\}_{\nu\in Z}\):
\begin{equation}\label{s.35} x_{mi+\mu,k}=x_{i,k-1}+\xi_{\mu}(x_{i+1,k-1}-x_{i,k-1}),\,\,\,\,\,\, \mu=0,\ldots,m, \end{equation}
\begin{equation}\label{s.36} f_{mi+\mu,k}=A_\mu({\textstyle\it\bf{f}}^{i}_{k-1}),\,\,\,\,\,\, \mu=0,\ldots,m. \end{equation}
Для \(m=1\) (в этом случае задан один функционал \(A({\textstyle\it\bf{f}})= A_1({\textstyle\it\bf{f}})\)) метод пополнения
называют бинарным пополнением и формулы пополнения (\ref{s.35}) - (\ref{s.36}) выглядят проще: \begin{equation}\label{s.37}
x_{2i,k}=x_{i,k-1},\,\,\,\,f_{2i,k}=f_{i,k-1}\,\,\,\,\,\,\,\,\,\,(i\in Z, k\in\mathbb{N}), \end{equation} и \begin{equation}\label{s.38}
x_{2i+1,k}=\frac{x_{i,k-1}+x_{i+1,k-1}}{2}, f_{2i+1,k}=A({\textstyle\it\bf{f^i_{k-1}}})\,\,\,\,\,(i\in Z, k\in\mathbb{N}).\end{equation}
Через 2r точек \((x_\nu,f_\nu)\) \((\nu=-r+1,\ldots,r)\) проведем интерполяционный полином Бесселя порядка \(2r-1\) и
вычислим его значение \(\hat{f}^{0}_{1,0}\) в точке \(x_{1/2}=h/2\). Это приводит к формуле
\begin{equation}\label{s.39}
A({\textstyle\it\bf{f}})=\hat{f}^{0}_{1,0}= \frac{f_{1,0}+f_{0,0}}{2}+\sum_{n=1}^{r-1}
(-1)^n\frac{(2n-1)!!}{(2n)!!2^{2n}} \Delta^{2n}\left(\frac{f_{1,0}+f_{0,0}}{2}\right), \end{equation} где \(\Delta^{2n}z_i\) \(2n\)-я
центральная разность \(z_i\).
Алгоритм subdivision в этом случае будет иметь вид
\begin{equation}\label{s.40}
x_{2i,k}=x_{i,k-1},\,\,\,\,f_{2i,k}=f_{i,k-1}\,\,\,\,\,\,\,\,\,\,(i\in Z, k\in\mathbb{N}), \end{equation} и \begin{equation}\label{s.40_1}
x_{2i+1,k}=\frac{x_{i,k-1}+x_{i+1,k-1}}{2}, \end{equation}
\[f_{2i+1,k}=
\frac{f_{i+1,k-1}+f_{i,k-1}}{2}+\sum_{n=1}^{r-1} (-1)^n\frac{(2n-1)!!}{(2n)!!2^{2n}}
\Delta^{2n}\left(\frac{f_{i+1,k-1}+f_{i,k-1}}{2}\right),\]
\[
i\in Z, k\in\mathbb{N}.
\]
Для \(r=2\), то есть формула (\ref{s.31}) была получена в работе S.Dubuc
и позже изучалась достаточно часто.
Для каждого фиксированного \(k\) построим ломаную \(g_{r,k,h}({\textstyle\it\bf{f}},x)\), принимающую значения \(f_{i,k}\) в
узлах \(x_{i,k}\).
Пусть
\[
\Delta
g_{r,k,h}({\textstyle\it\bf{f}},x)=g_{r,k,h}({\textstyle\it\bf{f}},x+x_{i,k})-g_{r,k,h}({\textstyle\it\bf{f}},x)=
g_{r,k,h}\left({\textstyle\it\bf{f}},x+\frac{h}{2^{k}}\right)-g_{r,k,h}({\textstyle\it\bf{f}},x),
\]
\[
\Delta^k g_{r,k,h}({\textstyle\it\bf{f}},x)=\Delta\left(\Delta^{k-1}
g_{r,k,h}({\textstyle\it\bf{f}},x)\right)\,\,\,\,k\ge 2.
\]
Заметим, что \begin{equation}\label{s.41} \|\Delta^{2n} g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\le 2^{2n-2}\|\Delta^{2}
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\le 2^{2n-1}\|\Delta g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}. \end{equation}
Лемма 1.
Для любой последовательности \({\textstyle\it\bf{f}}\in\ell_{\infty}(\mathbb{R})\) и произвольных фиксированных \(k,\mu\in\mathbb{N}\)
имеют место неравенства \begin{equation}\label{s.43} \|\Delta^2 g_{r,k+1,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\le \varepsilon_r
\|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}, \end{equation} и \begin{equation}\label{s.44}
\|g_{r,k+\mu}({\textstyle\it\bf{f}})-g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\lt \frac{\varepsilon_r^{2}}{2}
\frac{1-\varepsilon_r^{\mu}}{1-\varepsilon_r} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}. \end{equation} где
\begin{equation}\label{s.45} \varepsilon_r=\sum_{n=1}^{r-1}\frac{(2n-1)!!}{(2n)!!2}.\end{equation}
Доказательство. Рассмотрим величину
\[
\left|\Delta^2 g_{r,k+1,h}({\textstyle\it\bf{f}},x_{\nu,k+1})\right|.\]
Пусть, вначале, \(\nu=2\mu+1\), тогда
\[
\left|\Delta^2 g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu+1,k+1})\right|=\]
\[=\left|
g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu,k+1})- 2g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu+1,k+1})+
g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu+2,k+1})\right|=
\]
\[
=\left|g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu,k})+ g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu+1,k})-
2\left(\frac{g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu,k})+
g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu+1,k})}{2}+\right.\right.\]
\[\left.\left.+\sum_{n=1}^{r-1}
(-1)^n\frac{(2n-1)!!}{(2n)!!2^{2n}}\Delta^{2n}\left(\frac{1}{2}\left(
g_{r,k,h}\left({\textstyle\it\bf{f}},x_{\mu+1,k}\right) +
g_{r,k,h}\left({\textstyle\it\bf{f}},x_{\mu,k}\right)\right)\right)\right) \right|\le\]
\[
\le 2\sum_{n=1}^{r-1}\frac{(2n-1)!!}{(2n)!!2^{2n}} \|\Delta^{2n} g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.
\]
Отсюда, из (\ref{s.41}) сразу получаем
\[
\left|\Delta^2 g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu+1,k+1})\right|
\le 2\sum_{n=1}^{r-1}\frac{(2n-1)!!}{(2n)!!2^{2n}}2^{2n-2} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}=
\varepsilon_r\|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.
\]
Пусть, теперь, \(\nu=2\mu\), тогда
\[
\left|\Delta^2 g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu,k+1})\right|=\]
\[=\left|
g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu-1,k+1})- 2g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu,k+1})+
g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu+1,k+1})\right|=
\]
\[
=\left|\frac{g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu-1,k})+ g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu,k})}{2} -
2g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu,k+1})+\right.\]
\[
+\frac{g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu+1,k})+ g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu,k})}{2}+
\frac{1}{2}\sum_{n=1}^{r-1}
(-1)^n\frac{(2n-1)!!}{(2n)!!2^{2n}}\Delta^{2n}\left(g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu-1,k})+ \right.\]
\[+\left.\left.
2g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu-1,k})+ g_{r,k,h}({\textstyle\it\bf{f}},x_{\mu+1,k})\right)\right|\le \]
\[
\le \frac{1}{4}\|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}+ \sum_{n=2}^{r-1}
\frac{(2n-1)!!}{(2n)!!2^{2n}}\|\Delta^{2n} g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.\]
Используя соотношение (\ref{s.41}) отсюда имеем
\[
\left|\Delta^2 g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\mu,k+1})\right| \le \varepsilon_r\|\Delta^2
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.
\]
Неравенство (\ref{s.43}) доказано.
Из полученного соотношения и того факта, что
\[
\|\Delta^2 g_{r,0,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}= \|\Delta^2 ({\textstyle\it\bf{f}})\|_{\ell_{\infty}(\mathbb{R})},
\]
сразу получаем, что для любой последовательности \({\textstyle\it\bf{f}}\in\ell_{\infty}(\mathbb{R})\) и \(k\in \mathbb{N}\) имеет
место неравенство
\begin{equation}\label{s.46} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\le \varepsilon_r^k\|\Delta^2
({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}. \end{equation}
Докажем теперь неравенство (\ref{s.44}). Пусть, вначале, \(\mu=1\). По построению, \(g_{r,k+1,h}({\textstyle\it\bf{f}},x)\)
есть ломаная с узлами в точках \(x_{\nu,k+1}\), принимающая значения \(f_{\nu,k+1}\) в узлах, а
\(g_{r,k,h}({\textstyle\it\bf{f}},x)\) есть ломаная с узлами в точках \(x_{\nu,k}\) с значениями в узлах, равными
\(f_{\nu,k}\). Отсюда и из того факта, что \(f_{2\nu,k+1}=f_{\nu,k}\), сразу следует что разность
\(g_{r,k+1,h}({\textstyle\it\bf{f}},x)-g_{r,k,h}({\textstyle\it\bf{f}},x)\) есть ломаная с узлами в точках \(x_{\nu,k+1}\),
обращающаяся в ноль в точках \(x_{\nu,k}=x_{2\nu,k+1}\). Таким образом для доказательства неравенства (\ref{s.44}) при
\(\mu=1\) достаточно показать, что для всех \(\nu\in Z\).
\[
|g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1})- g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1})|\le
\frac{\varepsilon_r^2}{2} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.
\]
Действительно,
\[
g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1})= \frac{g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu+2,k+1})+
g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu,k+1})}{2}+
\]
\[
+\sum_{n=1}^{r-1} (-1)^n\frac{(2n-1)!!}{(2n)!!2^{2n}}\Delta^{2n}\left(
\frac{g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu+2,k+1})+g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu,k+1})}{2}\right).\] С
другой стороны, так как для \(x\in [x_{2\nu,k+1},x_{2\nu+2,k+1}]\) график функции \(g_{r,k,h}\) есть отрезок прямой, то
\[
g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1}) =\frac{g_{r,k,h}\left({\textstyle\it\bf{f}},x_{2\nu+2,k+1}\right)+
g_{r,k,h}\left({\textstyle\it\bf{f}},x_{2\nu,k+1}\right)}{2}.
\]
Таким образом,
\[
g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1})-g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1})=
\]
\begin{equation}\label{s.47} =\sum_{n=1}^{r-1} (-1)^n\frac{(2n-1)!!}{(2n)!!2^{2n}}\Delta^{2n}\left(
\frac{g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu+2,k+1})+g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu,k+1})}{2}\right). \end{equation}
Следовательно,
\[
|g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1})-g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1})|
\le \frac{\varepsilon_r}{2} \|\Delta^{2} g_{r,k+1,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.
\]
Отсюда и из (\ref{s.43}) сразу получаем
\[
|g_{r,k+1,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1})-g_{r,k,h}({\textstyle\it\bf{f}},x_{2\nu+1,k+1})|\le
\frac{\varepsilon_r^2}{2}\|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})},\] что и доказывает (\ref{s.44}) при
\(\mu=1\).
Пусть, теперь, \(\mu>1,\) тогда
\[
\|g_{r,k+\mu}({\textstyle\it\bf{f}})-g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\le
\|g_{r,k+1,h}({\textstyle\it\bf{f}})-g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})} +\]
\[+\|g_{r,k+2}({\textstyle\it\bf{f}})-g_{r,k+1,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}+\ldots
\|g_{r,k+\mu}({\textstyle\it\bf{f}})-g_{r,k+\mu-1}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\le
\]
\[
\le \frac{\varepsilon_r^2}{2} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}+ \frac{\varepsilon_r^2}{2}
\|\Delta^2 g_{r,k+1,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}+\ldots\]
\[\ldots
+\frac{\varepsilon_r^2}{2} \|\Delta^2 g_{r,k+\mu-1}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\le
\]
\[
\le \frac{\varepsilon_r^2}{2} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}+ \frac{\varepsilon_r^3}{2}
\|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}+\ldots + \frac{\varepsilon_r^{\mu+1}}{2} \|\Delta
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}=
\]
\[
= \frac{\varepsilon_r^{2}}{2} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\left(1+ \varepsilon_r+\ldots +
\varepsilon_r^{\mu-1}\right)\lt \frac{\varepsilon_r^{2}}{2} \frac{1-\varepsilon_r^{\mu}}{1-\varepsilon_r} \|\Delta^2
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.
\]
Лемма доказана.
Нетрудно видеть, что
\[
\varepsilon_2=\frac{3}{16},\varepsilon_3=\frac{11}{32}\,\,\,\, {\rm и}\,\,\,\,\, \varepsilon_2\lt\ldots\lt\varepsilon_7=
0.96630859375.
\]
Следовательно, для \(r=2,\ldots,7\) выполняются неравенства
\begin{equation}\label{s.48} \|g_{r,k+\mu,h}({\textstyle\it\bf{f}})-
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\lt \frac{\varepsilon_r^{2}}{2(1-\varepsilon_r)} \|\Delta^2
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}
\le \frac{\varepsilon_r^{k+2}}{2(1-\varepsilon_r)}
\|\Delta^2({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}, \end{equation}
то есть в этом случае последовательность
\(g_{r,k,h}({\textstyle\it\bf{f}})\) сходится в себе. Нетрудно видеть, что \(g_{r,k,h}({\textstyle\it\bf{f}},x)\)
ограничена (более того, далее мы покажем, что норма оператора \(g_{r,k,h}({\textstyle\it\bf{f}},x)\) ограничена в
совокупности и невелика). Отсюда следует, что поточечный предел \(g_{r,k,h}({\textstyle\it\bf{f}},x)\) при \(k\to\infty\)
существует. Обозначим этот предел через \(g_{r,h}({\textstyle\it\bf{f}},x)\).
Переходя к пределу по \(\mu\to\infty\) из леммы 1 немедленно получаем следующее утверждение.
Теорема 1.
Для любой последовательности \({\textstyle\it\bf{f}}\in \ell_\infty(\mathbb{R})\), \(k\in\mathbb{N}\) и \(r=2,\ldots,7\) имеет место
неравенство
\[
\|g_{r,h}({\textstyle\it\bf{f}})-g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\le
\frac{\varepsilon_r^{2}}{2(1-\varepsilon_r)} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\lt
\frac{\varepsilon_r^{k+2}}{2(1-\varepsilon_r)} \|\Delta^2 ({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.
\]
Как обычно, через \(L_{p[a,b]}\) \((p\in [1,\infty))\) обозначим множество всех измеримых суммируемых в \(p\)-й степени на
отрезке \([a,b]\) вещественных функций таких, что
\[\|f\|_{p[a,b]}=\left(\int_a^b{|f(x)|^pdx}\right)^{1/p}\lt \infty,\]
а через \(L_{\infty\,[a,b]}\) множество всех измеримых существенно ограниченных на \([a,b]\) функций с конечной нормой
\(\|f\|_{\infty[a,b]}=\mbox{supvrai}\{|f(x)|\bigm|t\in [a,b]\}.\)
Следствие.
Пусть \(p\in [1,\infty)\), числа \(k\in\mathbb{N}\), \(r=2,\ldots,7\) и \(a\lt b\). Для любой последовательности
\({\it\bf f}\in\it \ell_\infty(\mathbb{R})\) имеют место неравенства
\begin{equation}\label{s.51}
\left|\|g_{r,h}({\textstyle\it\bf{f}})\|_{p[a,b]}-\|g_{r,k,h}({\textstyle\it\bf{f}})\|_{p[a,b]}\right|\le (b-a)^{1/p}
\frac{\varepsilon_r^{2}}{2(1-\varepsilon_r)} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})} \end{equation} и
\begin{equation}\label{s.52} \|g_{r,k,h}({\textstyle\it\bf{f}})\|_{C[a,b]}\le\|g_{r,h}({\textstyle\it\bf{f}})\|_{C[a,b]}\le
\|g_{r,k,h}({\textstyle\it\bf{f}})\|_{C[a,b]}+
\frac{\varepsilon_r^{2}}{2(1-\varepsilon_r)} \|\Delta^2 g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.
\end{equation}
Соотношение (\ref{s.51}) верно и для случая, когда \(a=-\infty\) и \(b=\infty\).
Действительно, для всех \(x\in\mathbb{R}\)
\begin{equation}\label{s.53}
|g_{r,k,h}({\textstyle\it\bf{f}},x)|- \frac{\varepsilon_r^{2}}{2(1-\varepsilon_r)} \|\Delta^2
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}\le |g_{r,h}({\textstyle\it\bf{f}},x)|\le
|g_{r,k,h}({\textstyle\it\bf{f}},x)|+ \frac{\varepsilon_r^{2}}{2(1-\varepsilon_r)} \|\Delta^2
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})}.
\end{equation}
Отсюда и из очевидных неравенств
\[
\|g\|_{p[a,b]}-\|\varphi\|_{p[a,b]}\le\|g-\varphi\|_{p[a,b]} \le\|g\|_{p[a,b]}+\|\varphi\|_{p[a,b]},
\]
верных для любых \(p\in [1,\infty)\) и \(g,\varphi\in L_{p[a,b]}\), сразу получаем следующие неравенства
\[
\|g_{r,k,h}({\textstyle\it\bf{f}})\|_{p\,[a,b]}- (b-a)^{1/p} \frac{\varepsilon_r^{2}}{2(1-\varepsilon_r)} \|\Delta^2
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})} \le \|g_{r,h}({\textstyle\it\bf{f}})\|_{p\,[a,b]}\le\]
\[\le
\|g_{r,k,h}({\textstyle\it\bf{f}})\|_{p\,[a,b]}+ (b-a)^{1/p} \frac{\varepsilon_r^{2}}{2(1-\varepsilon_r)} \|\Delta^2
g_{r,k,h}({\textstyle\it\bf{f}})\|_{C(\mathbb{R})},
\]
что и доказывает соотношение (\ref{s.51}).
В соотношении (\ref{s.52}) оценка снизу вытекает из того факта, что норма интерполяционной ломаной
\(g_{r,k,h}({\textstyle\it\bf{f}},x)\) не превышает нормы интерполируемой функции \(g_{r,h}({\textstyle\it\bf{f}},x)\).
Базисная функция метода интерполяционного subdivision
Далее нам понадобится одна функция специального вида, которая в дальнейшем будет играть роль базисной функции,
являющейся аналогом B-сплайнов и фундаментальных сплайнов в теории сплайн-аппроксимации.
Пусть \(h=1\) и последовательность \({\it\bf f}^*= {\it\bf f}^{*0}=\{f^*_{0,i}\}_{i\in Z}\), где
\(f^*_{0,i}=\delta_{0,i}\)
\[
\delta_{\nu,\mu}= \left\{
\begin{array}{lc}
1,\nu=\mu\\ 0,\nu\ne\mu
\end{array}
\right.
\]
- символ Кронекера.
Положим
\(
G_{r,k}(x)=g_{r,k,1}({\textstyle \it\bf f}^*,x)
\)
и
\(
G_r(x)=g_{r,1}({\textstyle \it\bf f}^*,x).
\)
Для любого \(k\in\mathbb{N}\) оператор \(f\to g_{r,k,h}({\textstyle \it\bf f})\) есть линейный оператор, отображающий
пространство \(\ell_{\infty}(\mathbb{R})\) в пространство ограниченных на всей оси ломаных с узлами в точках \(x_{i,k}\), а
оператор \(f\to g_{r,h}({\textstyle \it\bf f})\) есть линейный оператор, отображающий пространство \(\ell_{\infty}(\mathbb{R})\)
в пространство \(C(\mathbb{R})\).
Ясно, что
\(
g_{r,k,h}({\textstyle \it\bf f^*})=G_{r,k}\left(\frac{x}{h}\right)
\)
и если \({\textstyle \it\bf f^{*i}}\) сдвиг последовательности \({\textstyle \it\bf f^{*}}\), то
\(
g_{r,k,h}({\textstyle \it\bf f^{*i}})=G_{r,k}\left(\frac{x}{h}-i\right).
\)
Отсюда и из линейности оператора \(g_{r,k,h}\) следует
\begin{equation}\label{s.54}
g_{r,k,h}({\textstyle \it\bf f},x)=
g_{r,k,h}\left(\sum_{i\in Z}{f}_{i,0}{\textstyle \it\bf f^{*i}},x \right)=
\sum_{i\in Z}f_{i,0} g_{r,k,h}\left({\textstyle \it\bf f^{*i}},x \right)=
\sum_{i\in Z}{f}_{i,0}G_{r,k}\left(\frac{x}{h}-i\right).
\end{equation}
Следовательно, для любой последовательности \({\it\bf f}\in\ell_\infty(\mathbb{R})\), любого \(x\in\mathbb{R}\) и \(h>0\)
имеет место равенство
\begin{equation}\label{s.55} g_{r,h}({\textstyle\it\bf{f}},x)=\sum_{i\in Z}f_{i,0}G_r\left(\frac{x}{h}-i\right).
\end{equation}
Из построения функции \(G_{r,k}(x) (k\ge 2)\), вытекает, что она имеет конечный носитель
\([-2r+1+\frac{1}{2^{k-2}},2r-1-\frac{1}{2^{k-2}}]\), а функция \(G_r(x)\) имеет конечный носитель \([-2r+1,2r-1]\). Отсюда
следует, что для \(x\in [x_i,x_{i+1}]\), \(i\in Z\) в равенствах (\ref{s.54}) и (\ref{s.55}) лишь \(4r-2\) слагаемых отличны
от нуля, то есть для \(x\in [x_i,x_{i+1}]\) выполняются равенства
\begin{equation}\label{s.56}
g_{r,h}({\textstyle\it\bf{f}},x)=\sum_{\nu=i-2r+2}^{i+2r-1}f_{\nu,0} G_{r}\left(\frac{x}{h}-\nu\right) \end{equation} и
\begin{equation}\label{s.57} g_{r,k,h}({\textstyle\it\bf{f}},x)=\sum_{\nu=i-2r+2}^{i+2r-1}f_{\nu,0}
G_{r,k}\left(\frac{x}{h}-\nu\right). \end{equation}
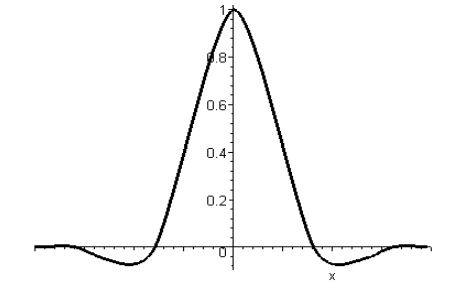
Отметим, что для любого \(k\in\mathbb{N}\) функции \(G_{r,k}(x)\) четные, следовательно, и функция \(G_{r}(x)\) четная.
Ниже приведен график функции \(G_{2}(x)\)
Каждой ломаной \(g_{r,k,h}({\textstyle \it\bf f},x)\) поставим в соответствие последовательность ее значений \(f_{i,k}\) в
узлах \(x_{i,k}\).
Если \(f\in C(\mathbb{R})\), то положим
\(
g_{r,k,h}(f,x)=g_{r,k,h}({\textstyle \it\bf f},x),
\)
где
\(
{\textstyle \it\bf f}=\{f_{i}\}_{i\in Z}=\{f(ih)\}_{i\in Z}.
\)
Заметим, что из построения оператора \(g_{r,k,h}({\textstyle \it\bf f})\) вытекает, что для любых \(k,\nu=0,1,2,\ldots\)
имеет место равенство \begin{equation}\label{s.58} g_{r,k,h2^{-\nu}}({\textstyle \it\bf f}_\nu,x)=
g_{r,k,h2^{-\nu}}(g_{r,\nu,h}({\textstyle \it\bf f}),x)=g_{r,k+\nu,h}({\textstyle \it\bf f},x). \end{equation} Переходя к пределу
при \(k\to\infty\), получаем \begin{equation}\label{s.59} g_{r,h2^{-\nu}}({\textstyle \it\bf f}_\nu,x)=g_{r,h}({\textstyle \it\bf
f},x). \end{equation}
Из метода построения вытекает следующая цепочка равенств
\[
g_{h/2^k}\left(g_h(f),x\right)= g_{h/2^k}\left(\left\{g_h\left(f,\frac{ih}{2^k}\right)\right\}_{i\in Z},
x\right)=g_h(f,x),
\]
то есть
\begin{equation}\label{s.60} g_{h/2^k}\left(g_h(f),x\right)=g_h(f,x). \end{equation}
Положим
\[
\alpha_{0,r}= \frac{1}{2}+\sum_{n=1}^{r-1}\frac{(2n-1)!!}{(2n)!!2^{2n+1}}C^n_{2n}
\]
и для \(\mu=1,\ldots,n\)
\[
\alpha_{\mu,r}= \sum_{n=1}^{r-1}(-1)^{\mu} C^{n-\mu}_{2n}\frac{(2n-1)!!}{(2n)!!2^{2n+1}}.
\]
Теорема 2.
Для всех \(x\) имеет место соотношение
\[
G_r(x)=G_r(2x)+\sum_{\mu=0}^{r-1}\alpha_{\mu,r} \left(G_r(2x+2\mu+1)+G_r(2x-2\mu-1)\right).
\]
Действительно, из (\ref{s.59}) имеем равенство
\(g_{r,h}({\textstyle \it\bf f_0},x)=g_{r,h/2}({\textstyle \it\bf f_1},x),\)
в частности,
\(g_{r,1}({\textstyle \it\bf f^{*}},x)=g_{r,1/2}({\textstyle \it\bf f^{*}_1},x)\)
или, что то же
\begin{equation}\label{s.62} G_{r}(x)= \sum_{i=-2r+2}^{2r-1}f^*_{i,1} G_{r}(2x-i).\end{equation}
Непосредственные вычисления показывают, что
\[
G_r(\pm i)=0,\,\,\,\,\,i\in\mathbb{N},
\]
\[
f^*_{\pm 1,1}=G_r\left(\pm \frac{1}{2}\right)=\alpha_{0}=
\frac{1}{2}+\sum_{n=1}^{r-1}\frac{(2n-1)!!}{(2n)!!2^{2n+1}}C^n_{2n}
\]
и
\[
f^*_{\pm (2\mu+1),1}=G_r\left(\pm \frac{2\mu+1}{2}\right)=\alpha_{\mu,r}
\]
при \(\mu\in\mathbb{N} (\mu\le n)\).
Отсюда сразу получаем требуемое утверждение.
В частности, следует что для бинарного пополнения использующего интерполяционный полином степени 3 и 5 для всех
\(x\) имеют место соотношения
\[
G_2(x)=G_2(2x)+\frac{9}{16}\left(G_2(2x+1)+G_2(2x-1)\right)- \frac{1}{16}\left(G_2(2x+3)+G_2(2x-3)\right)\] и
\[
G_3(x)=G_3(2x)+\frac{75}{128}\left(G_3(2x+1)+G_3(2x-1)\right)- \frac{25}{256}\left(G_3(2x+3)+\right.\]
\[\left.+G_3(2x-3)\right)+\frac{3}{256}\left(G_3(2x-5)+G_3(2x+5)\right).
\]
Аппроксимативные свойства интерполяционного subdivision
Положим для \(x\in [0,1]\)
\[
K_{r}(x)=x^{2r}-\sum_{i=-2r+2}^{2r-1}i^{2r}G_{r}\left(x-i\right)
\]
и
\[
K_{r,k}(x)=x^{2r}-\sum_{i=-2r+2}^{2r-1}i^{2r}G_{r,k}\left(x-i\right).
\]
Теорема 3.
Пусть функция \(f\) такова, что \(f^{(\nu)}\in C(\mathbb{R})\), \(\nu=0,2r\), \(r=2,\ldots,7\), тогда для \(x\in [ih,(i+1)h]\)
равномерно по \(i\in Z\) выполняется соотношение
\begin{equation}\label{s.64}
f(x)-g_{r,h}(f,x)=\frac{h^{2r}}{(2r)!}f^{(2r)}_{i}K_r\left(\frac{x}{h}-i\right)+o(h^{2r}), \end{equation} кроме того,
\[
\|K_{r,k}\|_{C(\mathbb{R})} \le\frac{(2r)!}{h^{2r}}\sup_{f\in W^{2r}_{C(\mathbb{R})}}\|f-g_{r,h}(f)\|_{C(\mathbb{R})}
\le\|K_{r,k}\|_{C(\mathbb{R})}+ \frac{r\varepsilon_r^{2}}{1-\varepsilon_r} \|\Delta^2 K_{r,k}\|_{C(\mathbb{R})}
\]
и
\[
\|K_{r,k}\|_{p[0,1]}- \frac{r\varepsilon_r^{2}}{1-\varepsilon_r} \|\Delta^2 K_{r,k}\|_{C(\mathbb{R})}
\le\frac{(2r)!}{h^{2r}}\sup_{f\in W^{2r}_{C[0,1]}}\|f-g_{r,h}(f)\|_{p[0,1]}\le\]
\[
\le\|K_{r,k}\|_{p[0,1]}+ \frac{r\varepsilon_r^{2}}{1-\varepsilon_r} \|\Delta^2 K_{r,k}\|_{C(\mathbb{R})}.
\]
Доказательство. Доказательству предпошлем одно вспомогательное утверждение.
Лемма 2.
Для \(x\in [0,1]\) и \(\nu=0,\ldots,2r-1\) справедливы равенства \begin{equation}\label{s.65} x^\nu=\sum_{i=-2r+2}^{2r-1}i^\nu
G_{r}(x-i). \end{equation}
Доказательство. Пусть \(h=1\) и \(\widetilde{\textstyle \it\bf f}^0=\{\widetilde{f}_{i,0}\}_{i\in Z}\), где
\(\widetilde{f}_{i,0}=1\), \(i\in Z\). Ясно, что в этом случае
\[
g_{r,h}(\widetilde{\textstyle \it\bf f}^0,x)=1.
\]
С другой стороны, как следует из (\ref{s.57}), для \(x\in [0,1]\)
\[
g_{r,h}(\widetilde{\textstyle \it\bf f}^0,x)=\sum_{i=-2r+2}^{2r-1}G_{r}(x-i).
\]
Утверждение для \(\nu=0\) доказана.
Пусть, теперь, \(\nu=1,\ldots,2r-1\) и \(\widetilde{\textstyle \it\bf f}_\nu= \{\widetilde{f}_{i,\nu}\}_{i\in Z}\), где
\(\widetilde{f}_{i,\nu}=i^\nu\), \(i=-2r+2,\ldots,2r-1\) и \(\widetilde{f}_{i,\nu}=0\), \(i\in Z\setminus \{-2r+1,\ldots,2r-2\}\).
Тогда в силу построения метода \(g\), для \(x\in [0,1]\) выполняется равенство
\[
g_{r,h}(\widetilde{\textstyle \it\bf f}_\nu,x)=x^\nu.
\]
Замечая, что из (\ref{s.57}) следует равенство
\[
g_{r,h}(\widetilde{\textstyle \it\bf f}_\nu,x)=\sum_{i=-2r+2}^{2r-1}i^\nu G_{r}(x-i),
\]
сразу получаем утверждение (\ref{s.65}).
Перейдем к доказательству нашего утверждения.
Используя разложения по формуле Тейлора в окрестности точки \(ih\) равенство (\ref{s.57}) перепишем в виде
\[
g_{r,h}(f,x)=\sum_{\nu=i-2r+2}^{i+2r-1}\sum_{\mu=0}^{2r}\frac{((\nu-i)h)^{\mu}}{\mu !} f^{(\mu)}_\nu
G_{r}\left(\frac{x}{h}-\nu\right) +o(h^{2r}).\]
Отсюда получаем
\[
f(x)-g_{r,h}(f,x)=\sum_{\nu=i-2r+2}^{i+2r-1}\sum_{\mu=0}^{2r} \frac{h^{\mu}}{\mu !} f^{(\mu)}_\nu
\left(x^{(\mu)}-(\nu-i)^{\mu} G_{r}\left(\frac{x}{h}-\nu\right)\right) +o(h^{2r}).\]
Таким образом из (\ref{s.65}) вытекает (\ref{s.64}).
Кроме того,
\[
\|K_{r,k}\|_{C(\mathbb{R})}\le\|K_r\|_{C(\mathbb{R})} \le\|K_{r,k}\|_{C(\mathbb{R})}+ \frac{r\varepsilon_r^{2}}{1-\varepsilon_r}
\|\Delta^2 K_{r,k}\|_{C(\mathbb{R})}
\]
и
\[
\|K_{r,k}\|_{p[0,1]}- \frac{r\varepsilon_r^{2}}{1-\varepsilon_r} \|\Delta^2 K_{r,k}\|_{C(\mathbb{R})}
\le\|K_r\|_{p[0,1]}\le\]
\[
\le\|K_{r,k}\|_{p[0,1]}+ \frac{r\varepsilon_r^{2}}{1-\varepsilon_r} \|\Delta^2 K_{r,k}\|_{C(\mathbb{R})}.
\]
Отсюда сразу получаем требуемое утверждение.
Рассмотрим другой подход к определению ошибки subdivision, изложенный в работе.
Пусть \(f\in C(\mathbb{R})\) и \(\|g_{r,h}\|_{C(\mathbb{R})\to C(\mathbb{R})}-\) норма оператора \(g_{r,h}\), то есть
\[\|g_{r,h}\|_{C(\mathbb{R})\to C(\mathbb{R})}=
\sup_{\|f\|_{C(\mathbb{R})}\le 1}\|g_{r,h}(f)\|_{C(\mathbb{R})}.\]
Положим \begin{equation}\label{s.66} N_r(x)=\sum_{i\in Z}\left|G_{r}\left(x-i\right)\right|\end{equation} и для \(k\in\mathbb{N}\)
\[
N_{r,k}(x)=\sum_{i\in Z}\left|G_{r,k}\left(x-i\right)\right|.\]
Заметим, что так как \(N(x)\) непрерывная 1-периодическая функция, то
\[\|N_r\|_{L_\infty(\mathbb{R})}=\|N_r\|_{C[0,1]}.\]
Теорема 4.
Для \(r=2,\ldots,7\) справедливо равенство
\begin{equation}\label{s.68} \|g_{r,h}\|_{C(\mathbb{R})\to C(\mathbb{R})}=\|N_r\|_{C[0,1]}. \end{equation}
Кроме того, для любого \(k\in\mathbb{N}\)
\begin{equation}\label{s.69} \|N_{r,k}\|_{C[0,1]} \le\|g_{r,h}\|_{C(\mathbb{R})\to C(\mathbb{R})}\le
\|N_r\|_{C[0,1]}+ \frac{r\varepsilon_r^2}{(1-\varepsilon_r)} \|\Delta^2 N_{r,k}\|_{C[0,1]}. \end{equation}
Доказательство. Пусть \(f\) произвольная функция из \(C(\mathbb{R})\), такая, что \(\|f\|_{C(\mathbb{R})}\le 1\), тогда из
(\ref{s.57}) вытекает
\[
\|g_{r,h}(f)\|_{C(\mathbb{R})}\le\left\|\sum_{i\in Z}f_{i,0}G_{r}\left(\frac{(\cdot)}{h}- i\right)\right\|_{C(\mathbb{R})}=
\sup_{x\in\mathbb{R}}\left|\sum_{i\in Z}f_{i,0}G_{r}\left(\frac{x}{h}- i\right)\right|\le
\]
\begin{equation}\label{s.70} \le\sup_{x\in\mathbb{R}}\sum_{i\in Z}\left|f_{i,0}G_{r}\left(\frac{x}{h}-
i\right)\right|=\sup_{x\in\mathbb{R}}\sum_{i\in Z}\left|f_{i,0}G_{r}\left(x- i\right)\right|\le\end{equation} \[\le
\sup_{x\in\mathbb{R}}\sum_{i\in Z}\left|G_{r}\left(x-i\right)\right|= \sup_{x\in\mathbb{R}}N_r(x). \]
Так как \(N_r(x)\) непрерывная 1-периодическая функция, то существует точка \(x_0\) такая, что
\(N_r(x_0)=\max_{x\in\mathbb{R}}N(x).\)
Через \(f_0(x)\) обозначим непрерывную функцию, принимающую значения
\[
{\rm sgn\,} G_{r}\left(\frac{x_0}{h}-i\right)
\]
в точках \(\frac{x_0}{h}-i\) и любые значения \(f_0(x) (|f_0(x)|\lt 1)\) в остальных точках из \(\mathbb{R}\). Тогда
\[
\|g_{r,h}\|_{C(\mathbb{R})\to C(\mathbb{R})}\ge \frac{\|g_{r,h}(f_0)\|_{C(\mathbb{R})}}{\|f_0\|_{C(\mathbb{R})}}=
\|g_{r,h}(f_0)\|_{C(\mathbb{R})}=\sup_{(x,y)\in\mathbb{R}}N_r(x),
\]
что вместе с (\ref{s.70}) доказывает равенство (\ref{s.68}).
Для завершения доказательства заметим, что из (\ref{s.53}) и (\ref{s.57}) сразу следует соотношение
\[
\|N_{r,k}\|_{C[0,1]}\le\|N_r\|_{C[0,1]}\le \|N_{r,k}\|_{C[0,1]}+ \frac{r\varepsilon_r^2}{(1-\varepsilon_r)} \|\Delta^2
N_{r,k}\|_{C[0,1]}.
\]
Пусть, теперь \(n\in \mathbb{N}\) фиксировано и \({\it\bf f}- 2n\)-периодическая последовательность, то есть
\[
f_{i+2n}=f_i\,\,\,(i\in Z)
\]
и \(h=\pi/n\).
Через \(\widetilde{G}_{r}(x)\) обозначим \(2\pi\)-периодическое продолжение функции \(G_{r}\left({x}/{h}\right)\) и
\(\widetilde{G}_{r,k}(x)\)- \(2\pi\)-периодическое продолжение функции \(G_{r,k}\left({x}/{h}\right)\).
Ясно, что для любой последовательности \(f_i=f(ih)\) имеет место представление
\[
g_{r,h}(f,x)=\sum_{i=1}^{2n}f_i\widetilde{G}_{r}\left(\frac{x}{h}-i\right)
\]
и
\[
g_{r,k,h}(f,x)=\sum_{i=1}^{2n}f_i\widetilde{G}_{r,k}\left(\frac{x}{h}-i\right).
\]
Для каждого \(x\in [ih,(i+1)h]\) \(i=0,\ldots,2n\) в этих представлениях присутствуют только \(4r-2\) слагаемых, то есть
\[
g_{r,h}(f,x)=\sum_{\nu=i-2r+2}^{i+2r-1}f_i\widetilde{G}_{r,n}\left(\frac{x}{h}-\nu\right)
\]
и
\[
g_{r,k,h}(f,x)=\sum_{\nu=i-2r+2}^{i+2r-1}f_i\widetilde{G}_{r,n,k}\left(\frac{x}{h}-\nu\right).
\]
Естественно, в этом случае верны аналоги всех утверждений приведенных выше.
Тот факт, что оператор восстановления \(g_{r,h}(f,x)\) можно записать в виде (\ref{s.57}) (вместе со свойствами функции
\(G_{r}(x)\)) позволяет построить метод послойного кодирования и передачи информации.
Для фиксированного \(\varepsilon>0\) положим
\[
z^+_\varepsilon= \left\{
\begin{array}{lc}
z,\,\,\,\,|z|\ge \varepsilon,\\ 0,\,\,\,\,|z|\lt \varepsilon
\end{array}
\right.
\]
и \begin{equation}\label{s.71} z^-_\varepsilon=z-z^+_\varepsilon. \end{equation}
Использование метода бинарного пополнения (интерполяционного subdivision) для послойного восстановления
данных
Назовем \(\mathfrak{G}_{r,1,h}(f,x)=g_{r,h}(f,x)\) восстановлением функции \(f(x)\) по первому слою информации. Пусть
\(f(x)-\mathfrak{G}_{r,1,h}(f,x) \) погрешность восстановления по первому слою.
Для \(k>1\) восстановление на \(k-\)м слое информации определим рекуррентными соотношениями \begin{equation}\label{s.72}
\mathfrak{G}_{r,k,h}(f,x)=\mathfrak{G}_{r,k-1,h}(f,x)+g_{r,h/2^{k-1}}\left(\left(f-\mathfrak{G}_{r,k-1,h}(f)\right)^+_\varepsilon,x\right). \end{equation}
Ясно, что
\[
f(x)-\mathfrak{G}_{r,k,h}(f,x)=f(x)- \mathfrak{G}_{r,k-1,h}(f,x)+g_{r,h/2^{k-1}}\left(\left(f- \mathfrak{G}_{r,k-1,h}(f)\right)-
-\left(f- \mathfrak{G}_{r,k-1,h}(f)\right)^-_\varepsilon,x\right).
\]
Из линейности метода \(g_{r,h/2^{m}}\) следует, что
\[
f(x)-\mathfrak{G}_{r,k,h}(f,x)=f(x)- \mathfrak{G}_{r,k-1,h}(f,x)+g_{r,h/2^{k-1}}\left(\left(f- \mathfrak{G}_{r,k-1,h}(f)\right),x\right)-
g_{r,h/2^{k-1}}\left(\left(f- \mathfrak{G}_{r,k-1,h}(f)\right)^-_\varepsilon,x\right)=
\]
\[
=f(x)- \mathfrak{G}_{r,k-1,h}(f,x)+g_{r,h/2^{k-1}}(f,x)- g_{r,h/2^{k-1}}\left(\mathfrak{G}_{r,k-1,h}(f),x\right)-
g_{r,h/2^{k-1}}\left(\left(f- \mathfrak{G}_{r,k-1,h}(f)\right)^-_\varepsilon,x\right).
\]
Отсюда, из (\ref{s.72}), свойства (\ref{s.57}) сразу получаем
\[
f(x)-\mathfrak{G}_{r,k,h}(f,x)= f(x)-g_{r,h/2^{k-1}}(f,x)+\theta_k\varepsilon \|N_r\|_{C[0,1]},
\]
где \(\theta_k=\theta_k(r,f,h)\in [-1,1]\) и величина \(N_r(x)\) определена соотношением (\ref{s.66}).
Таким образом, с учетом \(k-\)го слоя информации метод \(\mathfrak{G}_{r,k,h}(f)\) восстанавливает искомую функцию с точностью до
\(\theta_k\varepsilon \|N_r\|_{C[0,1]}\) так же, как и первоначальный метод с шагом \(h/2^{k-1}\). При этом в реальных
задачах количество ненулевых единиц информации, которое требуется для этого, гораздо меньше, чем \(2^{k-1}n\) единиц
информации отличной от нуля, необходимой для метода \(g_{r,h/2^{k-1}}(f)\).
О восстановлении кривых методами интерполяционного subdivision
Приведенный метод бинарного пополнения достаточно эффективен для восстановления функций. К сожалению непосредственное
использование этого метода для восстановления кривых - баролиний, изолиний, геодезических и пр. невозможно.
Данный параграф посвящен адаптации метода основанного на бинарном subdivision (\ref{s.34}) - (\ref{s.34_2}) для
восстановления кривых.
Пусть дан набор точек \(\Gamma_i=\Gamma_{i,0}\) \((i=0,1,\ldots,n)\), лежащих на кривой \(\Gamma\). Если кривая не замкнута, то этот
набор пополним точками \begin{equation}\label{s.73} \Gamma_{-1}=\Gamma_{-1,0}=4\Gamma_{0}-6\Gamma_{1}+4\Gamma_{2}-\Gamma_{3}, \end{equation}
\[
\Gamma_{-2}=\Gamma_{-2,0}=10\Gamma_{0}-20\Gamma_{1}+15\Gamma_{2}-4\Gamma_{3},
\]
и \begin{equation}\label{s.74} \Gamma_{n+1}=\Gamma_{n+1,0}=4\Gamma_{n}-6\Gamma_{n-1}+4\Gamma_{n-2}-3\Gamma_{n-3}, \end{equation}
\[
\Gamma_{n+2}=\Gamma_{n+2,0}=10\Gamma_{n}-20\Gamma_{n-1}+15\Gamma_{n-2}-4\Gamma_{n-3}.
\]
Эти формулы берутся из соображений алгебраической экстраполяции. Используя алгоритм пополнения (subdivision)
(\ref{s.34}) - (\ref{s.34_2}), приходим к рекуррентным формулам \begin{equation}\label{s.75}
\Gamma_{2i,k}=\Gamma_{i,k-1}\,\,\,\,\,\,\,\,\,\,(i=-1,\ldots,n+1; k\in\mathbb{N}), \end{equation} и \begin{equation}\label{s.76} \Gamma_{2i+1,k}=
\frac{\Gamma_{i+1,k-1}+\Gamma_{i,k-1}}{2}-\frac{1}{8}\Delta^2 \left(\frac{\Gamma_{i+1,k-1}+\Gamma_{i,k-1}}{2}\right) \end{equation}
\[i=-1,\ldots,n; k\in\mathbb{N}.\]
Для каждого фиксированного \(k\) построим ломаную \(g_k(\Gamma,t)\), принимающую значения \(\Gamma_{i,k}\) в узлах и для каждого
фиксированного \(t\) положим
\[
g(\Gamma,t)=\lim_{k\to\infty}g_k(\Gamma,t).
\]
Существование этой функции следует из существования функции \(g(f,x)\).
Таким образом можно записать
\begin{equation}\label{s.77} g(\Gamma,t)=\sum_{\nu=-2}^{n+2}\Gamma_\nu G\left(t-\nu\right). \end{equation}
Нетрудно видеть, что полученный аппарат интерполирует данные значения \(\Gamma_i\).
Если кривая замкнута, то в использовании экстраполяционных формул (\ref{s.75}) - (\ref{s.76}) нет необходимости.
Достаточно учесть, что \(\Gamma_{i}=\Gamma_{n+i}\).
Ясно, что качество восстановления кривой \(\Gamma\) зависит от выбора значений \(\Gamma_{i}\). Если кривая задана в естественной
параметризации, то значения \(\Gamma_{i}\) делят кривую на дуги с одинаковой длиной. В этом случае алгоритм восстановления
основанный на рекуррентных формулах (\ref{s.34}) - (\ref{s.34_2}) будет наиболее эффективен.
Для кривой в естественной параметризации при достаточно больших \(n\) получем погрешность восстановления достаточно
гладкой кривой \(\Gamma(t)\) методом \(g(\Gamma)\) в метрике Хаусдорфа. В этом случае \(\Gamma_i=\Gamma(ih) (i=0,\ldots,n)\). На практике
это нетрудно реализовать, вписывая в данную кривую ломаную с большим числом звеньев.
Определим, как обычно, хаусдорфово расстояние между двумя множествами
\(\Gamma\) и L равенством:
\[
\mathcal{R}(L,\Gamma)=\max\{\sup\{\inf\{\vert MN\vert;N\in L\};M\in\Gamma\};\sup\{\inf\{\vert MN\vert;N\in\Gamma\};M\in L\}\},
\]
где \(\vert MN\vert\) - евклидово расстояние между точками M и N .
В силу интерполяции, достаточно найти Хаусдорфово расстояние между \(\Gamma\) и \(g(\Gamma)\) на каждом промежутке между
точками \(\Gamma_i\) и \(\Gamma_{i+1}\).
Ясно, что если \(u,t\in [ih,(i+1)h]\), то
\[\Gamma(u)-g(\Gamma,t)=\Gamma(t)-g(\Gamma,t)+\Gamma(u)-\Gamma(t).\]
Положим \(\xi=(u-ih)/h\) и \(\tau=(t-ih)/h\).
Используя (\ref{s.64}) равномерно по \(i\) получаем
\[\Gamma(t)-g(\Gamma,t)=\frac{h^4}{4!}\Gamma^{(4)}_{i+1/2}K\left(\frac{t}{h}-i\right)+O(h^5),
\]
где \(\Gamma^{(\nu)}_{i+1/2}=\Gamma^{(\nu)}((i+1/2)h)\).
Кроме того для \(u,t\in [ih, (i+1)h]\)
\[\Gamma(u)-\Gamma(t)=\Gamma'h(\xi-\tau)+\Gamma''\frac{h^2}{2}((1/2-\xi)^2-(1/2-\tau)^2)+
\Gamma^{(3)}\frac{h^3}{6}((1/2-\xi)^3-(1/2-\tau)^3)
+\Gamma^{(4)}\frac{h^4}{24}((1/2-\xi)^4-(1/2-\tau)^4)+O(h^5).\]
Таким образом, равномерно по \(i\)
\begin{equation}\label{s.78}
\Gamma(u)-g(\Gamma,t)=\frac{h^4}{4!}\Gamma^{(4)}_{i+1/2}K\left(\frac{t}{h}-i\right)+ \Gamma'h(\xi-\tau)+O(h^2(\tau-\xi))+O(h^5).
\end{equation}
С другой стороны
\[
\mathcal{R}(\Gamma,g(\Gamma))\le \sqrt{\|x-g(x)\|^2_C+\|y-g(y)\|^2_C+\|z-g(z)\|^2_C}\le
\frac{h^4}{4!}\Gamma^{(4)}_{i+1/2}\|K\|_{C} \sqrt{\|x^{(4)}\|^2_C+\|y^{(4)}\|^2_C+\|z^{(4)}\|^2_C}=O(h^4).
\]
Отсюда и из (\ref{s.78}) следует,что при оценках величины \(\mathcal{R}(\Gamma,g(\Gamma))\) достаточно рассматривать лишь те \(\tau\) и
\(\xi\) для которых \(\tau-\xi=O(h^3)\).
В этом случае
\[
{\mathcal{R}}=\max\left\{\min\{|\Gamma(u)-g(\Gamma,t)|; u\in [ih,(i+1)h]\}; t\in[ih, (i+1)h]\right\}=
\max\left\{\min\left\{\frac{h^4}{4!}\Gamma^{(4)}_{i+1/2}
K\left(\frac{t}{h}-i\right)-\Gamma'h(\tau-\xi)|; \xi\in [0,1]\right\};\tau\in [0,1]\right\}(1+O(h))=\]
\[\max\left\{\tau^2(1-\tau)^2h^4{\Phi}^{(1/2}\left|1+\alpha\,\frac{h}{2}+
(2\tau-1)\beta\,\frac{h}{10}+O(h^2)\right|;\tau\in[0,1]\right\},\]
где
\[{\Phi}=(|\Gamma^{(4)}|^2|\Gamma'|^2-(\Gamma^{(4)}\Gamma')^2)/|\Gamma'|^2,\]
\[\alpha=(\Gamma^{(4)}\Gamma')|\Gamma'|^{-3}((\Gamma^{(4)}\Gamma')|\Gamma''|-
(\Gamma^{(4)}\Gamma'')^2|\Gamma'|)/{\Phi},\]
\[\beta=|\Gamma'|^{-3}((\Gamma^{(4)}\Gamma')|\Gamma^{(5)}|-
(\Gamma^{(4)}\Gamma^{(5)})|\Gamma'|)/{\Phi}.\]
Отсюда следует, что
\[{\mathcal{R}}=\frac{h^4}{384}\Phi_{k-1/2,n}(1+O(h^2)),\]
поэтому
\begin{equation}
\mathcal{R}(\Gamma,g(\Gamma))=\max_{k}\frac{h^4_{k,n}}{384}\Phi_{k-1/2,n}(1+C_{k,n}h^2_{k,n}),
\end{equation}
где \(|C_{k,n}|\le C\lt\infty\) и константа \(С\) зависит разве,что от \(\Gamma\).
Интерполяционный subdivision поверхностей
Интерполяционный subdivision по треугольной решетке
Через \(\ell_{\infty}(\mathbb{R}^2)\) обозначим линейное
пространство всех ограниченных массивов \( F=\{f_{i,j}\}_{i,j\in Z} \) с нормой
\[
\|F\|_{\ell_{\infty}(\mathbb{R}^2)}=\sup_{i,j\in Z}|f_{i,j}|.
\]
Пусть \(\mathbf{\ell}=\{\mathbf{\ell}_0, \mathbf{\ell}_1\}\) пара неколлинеарных радиус-векторов
на плоскости \(XOY\).
Пусть \(\Delta^0=\Delta^0(\mathbf{\ell})= \{i\mathbf{\ell}_0+j\mathbf{\ell}_1\}_{i,j\in Z}\)
- решетка порожденная этими векторами и \(M_{i,j}\) ее узлы.
Зададим на множестве ограниченных массивов \(F^0\) линейные функционалы \(B_1\), \(B_2\), \(B_3\) и положим \({\bf
B}=\{B_1,B_2,B_3\}\).
Обозначим через \(F^{0}_{\nu,\mu}=\{f_{i+\nu,j+\mu,0}\}_{i,j\in Z}\) сдвиг массива \(F^0\) и определим узлы решетки
\(\Delta^k\) и массив \(F^k=\{f_{i,j,k}\}_{i,j\in Z}\), \(k\in\mathbb{N}\) рекуррентными соотношениями
\begin{equation}\label{s.79}
\begin{array}{llll}
M_{2i,2j,k} & =M_{i,j,k-1},& f_{2i,2j,k} & =f_{i,j,k-1},\\
M_{2i+1,2j,k} & =0.5(M_{i,j,k-1}+M_{i+1,j,k-1}),&
f_{2i+1,2j,k} & =B_1(F^{k-1}_{i,j}),\\
M_{2i,2j+1,k} & =0.5(M_{i,j,k-1}+M_{i,j+1,k-1}),&
f_{2i,2j+1,k} & =B_2(F^{k-1}_{i,j}),\\
M_{2i+1,2j+1,k} &=0.5(M_{i+1,j,k-1}+M_{i,j+1,k-1}),&
f_{2i+1,2j+1,k} & =B_3(F^{k-1}_{i,j}).\\
\end{array}
\end{equation}
Непрерывную на \(\mathbb{R}^2\) функцию двух переменных назовем k-полигоном с узлами в точках \(M_{i,j,k}\), если для всех
\(i,j\in Z\) на каждом треугольнике \(\mathbb{T}^+_{i,j+1,k}\) с вершинами в точках \(M_{i+1,j,k},\) \(M_{i,j,k},\) \(M_{i,j+1,k}\) и
треугольнике \(\mathbb{T}^-_{i+1,j,k}\) с вершинами в точках \(M_{i,j+1,k},\) \(M_{i+1,j,k},\) \(M_{i+1,j+1,k}\) она совпадает с
некоторой плоскостью (своей для каждого треугольника).
Через \(g_{k}(F,{\bf B},{\bf \ell},x,y)\) обозначим k-полигон интерполирующий в узлах \(M_{i,j,k}\) значения
\(f_{i,j,k}\). Для любого \(k\in\mathbb{N}\) \(g_{k}(F,{\bf B},{\bf \ell})\) есть линейный оператор, отображающий
пространство \(\ell_{\infty}(\mathbb{R}^2)\) в пространство ограниченных на всей плоскости k-полигонов.
Если при \(k\to\infty\) предел последовательности \(g_{k}(F,{\bf B},{\bf \ell},x,y)\) существует, то будем
обозначать его через \(g(F,{\bf B},{\bf \ell},x,y)\). В дальнейшем будем рассматривать лишь те функционалы
\(B_\nu\) \((\nu=1,2,3)\), для которых \(g(F,{\bf B},{\bf \ell},x,y)\) существует.
Если функция \(f\) определена в точках \(M_{i,j}\) и \(f_{i,j}=f(M_{i,j})\) \(i,j\in Z\), то вместо \(g_k(F,{\bf
B},{\bf \ell})\) и \(g(F,{\bf B},{\bf \ell})\) будем писать \(g_k(f,{\bf B},{\bf \ell})\) и \(g(f,{\bf B},{\bf \ell})\), соответственно.
Из способа построения оператора \(g_k({\bf B},{\bf \ell})\) следует, что для любых \(k,\nu=0,1,2,\ldots\)
имеет место равенство
\begin{equation}\label{s.80} g_k\left(F^\nu,{\bf B},2^{-\nu}{\bf \ell}\right)=
g_{k+\nu}\left(F,{\bf B},{\bf \ell}\right) \end{equation} и для \(\nu\le k\)
\begin{equation}\label{s.81} g_k\left(F,{\bf B},{\bf \ell}\right)=
g_k\left(g_{\nu}(F,{\bf B},{\bf \ell}),{\bf B}, {\bf \ell}\right). \end{equation}
Переходя к пределу при \(k\to\infty\) в (\ref{s.80}), получаем
\begin{equation}\label{s.82} g\left(F^\nu,{\bf
B},2^{-\nu}{\bf \ell}\right)= g\left(F,{\bf B},{\bf \ell}\right), \end{equation}
а предельный переход в (\ref{s.82}) дает равенство
\begin{equation}\label{s.83} g\left(F,{\bf B},{\bf \ell}\right)= g\left(g\left(F,{\bf
B},{\bf \ell}\right), {\bf B},{\bf \ell}\right). \end{equation}
Кроме того \begin{equation}\label{s.84} g\left(F_{\nu,\mu},{\bf B},{\bf \ell},x,y\right)= g\left(F,{\bf
B},{\bf \ell},x-\nu|{\bf \ell}_0|,y-\mu |{\bf \ell}_1|\right) \end{equation} и если
\(\alpha= (\alpha_0,\alpha_1)\) \((\alpha_0,\alpha_1\in\mathbb{R})\) и
\(\ell(\alpha)=\{\alpha_0\ell_0, \alpha_1\ell_1\}\), то
\begin{equation}\label{s.85} g\left(F,{\bf B},{\bf \ell},x,y\right)= g\left(F,{\bf
B},\ell(\alpha),\frac{\alpha_0} {|\ell_0|}x,\frac{\alpha_1}{|\ell_1|}y\right). \end{equation}
Положим \begin{equation}\label{s.86} B_1(F^0)=\frac{f_{1,0,0}+f_{0,0,0}}{2}-\frac{1}{8}\Delta_x^2
\left(\frac{f_{1,0,0}+f_{0,0,0}}{2}\right), \end{equation} \begin{equation}\label{s.87}
B_2(F^0)=\frac{f_{0,0,0}+f_{0,1,0}}{2}-\frac{1}{8}\Delta^2_{y} \left(\frac{f_{0,0,0}+f_{0,1,0}}{2}\right), \end{equation}
\begin{equation}\label{s.88} B_3(F^0)=\frac{f_{1,0,0}+f_{0,1,0}}{2}-\frac{1}{8}\Delta^2_{x,y}
\left(\frac{f_{1,0,0}+f_{0,1,0}}{2}\right), \end{equation} где
\[
\Delta_x^2Z_{i,j}=Z_{i+1,i}-2Z_{i,j}+Z_{i-1,i},
\]
\[
\Delta^2_{y}Z_{i,j}=Z_{i,j+1}-2Z_{i,j}+Z_{i,j-1},
\]
\[
\Delta^2_{x,y}Z_{i,j}=Z_{i-1,j+1}-2Z_{i,j}+Z_{i+1,j-1}.
\]
В этом случае вместо \(g_{k}(F,{\bf B},{\bf \ell},x,y)\) будем писать \(g_{k}(F,{\bf \ell},x,y)\).
Пусть
\[
\Delta_xg_{k}(F,{\bf \ell},x,y) =g_{k}(F,{\bf \ell},x+2^{-k}|\ell_0|,y)-
g_{k}(F,{\bf \ell},x,y),
\]
\[
\Delta_y g_{k}(F,{\bf \ell},x,y)= g_{k}(F,{\bf \ell},x,y+2^{-k}|\ell_1|)-
g_{k}(F,{\bf \ell},x,y),
\]
\[
\Delta_{x,y}g_{k}(F,{\bf \ell},x,y)= g_{k}(F,{\bf \ell},x-2^{-k}|\ell_0|,y+
2^{-k}|\ell_1|)- g_{k}(F,{\bf \ell},x,y)
\]
и \begin{equation}\label{s.89} \|\delta g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}= \max\{
\|\Delta_xg_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}, \|\Delta_yg_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)},
\|\Delta_{x,y}g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\}, \end{equation}
где, как обычно,
\[\|Z\|_{C(\mathbb{R}^2)}=\sup_{(x,y)\in \mathbb{R}^2}|Z(x,y)|.\]
Теорема 5.
Для любого массива \(F\in\ell_{\infty}(\mathbb{R}^2)\) и произвольных фиксированных \(k,\mu\in\mathbb{N}\) имеет место неравенство
\begin{equation}\label{s.91} \|g_{k+\mu}(F,{\bf \ell})-g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\lt \frac{5}{24}\|\delta g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}. \end{equation}
Доказательство. Из определения (\ref{s.89}), соотношения (\ref{s.43}), конструкции метода и очевидного равенства
\[
\|\delta g_0(F,{\bf \ell})\|_{C(\mathbb{R}^2)}= \|\delta (F)\|_{\ell_{\infty}(\mathbb{R}^2)},
\]
следует, что для любого массива \(F\in\ell_{\infty}(\mathbb{R}^2)\) и произвольных фиксированного \(k\in\mathbb{N}\) имеет место
неравенство \begin{equation}\label{s.97} \|\delta g_{k+1}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\le
\left(\frac{5}{8}\right)^{k+1}\|\delta (F)\|_{\ell_{\infty}(\mathbb{R}^2)},\end{equation} где
\[
\|\delta (F)\|_{\ell_{\infty}(\mathbb{R}^2)}= \max\{ \|\Delta_x F\|_{\ell_{\infty}(\mathbb{R}^2)},\,\,\|\Delta_y
F\|_{\ell_{\infty}(\mathbb{R}^2)}, \|\Delta_{x,y}F\|_{\ell_{\infty}(\mathbb{R}^2)}\},
\]
и
\[
\|\Delta_x F\|_{\ell_{\infty}(\mathbb{R}^2)}=\max_{i,j\in Z}|f_{i+1,j,0}-f_{i,j,0}|, \|\Delta_y
F\|_{\ell_{\infty}(\mathbb{R}^2)}=\max_{i,j\in Z}|f_{i,j+1,0}-f_{i,j,0}|,
\]
\[
\|\Delta_{x,y} F\|_{\ell_{\infty}(\mathbb{R}^2)}=\max_{i,j\in Z}|f_{i+1,j,0}-f_{i,j+1,0}|.
\]
Пусть \(\mu=1\) и, например, \((x,y)\in \mathbb{T}^+_{i,j,k}\). Ясно, что
\(g_{k+1}(F,{\bf \ell},x,y)-g_{k}(F,{\bf \ell},x,y)\) является (k+1)-полигоном. Отсюда и из того
факта, что
\(g_{k+1}(F,{\bf \ell},x_{i,j,k},y_{i,j,k})-g_{k}(F,
{\bf \ell},x_{i,j,k},y_{i,j,k})=0,\) имеем
\[
\sup_{(x,y)\in\mathbb{T}^+_{i,j,k}}\| g_{k+1}(F,{\bf \ell})-g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}=\]
\[= \max\{
|g_{k+1}(F,{\bf \ell},M_{2i+1,2j-2,k+1})-g_{k}(F,{\bf \ell},M_{2i+1,2j-2,k+1})|,
|g_{k+1}(F,{\bf \ell},M_{2i+1,2j-1,k+1})-g_{k}(F,{\bf \ell},M_{2i+1,2j-1,k+1})|,
|g_{k+1}(F,{\bf \ell},M_{2i,2j-1,k+1})-g_{k}(F,{\bf \ell},M_{2i,2j-1,k+1})|\}.
\]
Отсюда и из (\ref{s.44}) получаем
\[
\sup_{(x,y)\in\mathbb{T}^+_{i,j,k}}\|
g_{k+1}(F,{\bf \ell},x,y)-g_{k}(F,{\bf \ell},x,y)\|_{C(\mathbb{R}^2)}\le \frac{5}{64}\|\delta
g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}.\] Для \((x,y)\in \mathbb{T}^-_{i,j,k}\) доказательство проводится аналогично.
Пусть, теперь, \(\mu>1,\) тогда
\[
\|g_{k+\mu}(F,{\bf \ell})-g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\le
\|g_{k+1}(F,{\bf \ell})-g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)} +\]
\[+\|g_{k+2}(F,{\bf \ell})-g_{k+1}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}+\ldots
+\|g_{k+\mu}(F,{\bf \ell})-g_{k+\mu-1}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\le
\]
\[
\le \frac{5}{64}\|\delta g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}+ \frac{5}{64}\|\delta
g_{k+1}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}+\ldots +\frac{5}{64}\|\delta
g_{k+\mu-1}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}.
\]
Отсюда и из (\ref{s.43}) следует, что
\[
\|g_{k+\mu}(F,{\bf \ell})-g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\le
\]
\[
\le\frac{5}{64}\|\delta g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\left(1+
\frac{5}{8}+\left(\frac{5}{8}\right)^2+\ldots+\left(\frac{5}{8}\right)^{\mu-1}\right)\lt
\frac{5}{64}\|\delta g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\frac{8}{3}= \frac{5}{24}\|\delta
g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}.
\]
Требуемое утверждение доказано.
Отсюда и неравенства (\ref{s.43}) получаем \begin{equation}\label{s.98}
\|g_{k+\mu}(F,{\bf \ell})-g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\lt \frac{5}{24}
\left(\frac{5}{8}\right)^{k}\|\delta (F)\|_{\ell_{\infty}(\mathbb{R}^2)}.\end{equation}
Следовательно, последовательность \(g_{k}(F,{\bf \ell},x,y)\) сходится в себе. Нетрудно видеть, что
\(g_{k}(F,{\bf \ell},x,y)\) ограничена (более того, далее мы покажем, что нормы операторов
\(g_{k}({\bf \ell})\) действующих из \(\ell_{\infty}(\mathbb{R}^2)\) в \(C(\mathbb{R}^2)\) по правилу \(F\to
g_{k}(F,{\bf \ell})\) ограничены в совокупности и невелики). Отсюда
следует, что равномерный предел \(g_{k}(F,{\bf \ell},x,y)\) при \(k\to\infty\) существует. Обозначим этот
предел через \(g(F,{\bf \ell},x,y)\).
Переходя к пределу по \(\mu\to\infty\) в (\ref{s.98}), получаем следующее утверждение.
Теорема 6.
Для любого массива \(F\in \ell_\infty(\mathbb{R}^2)\) и \(k\in\mathbb{N}\) имеет место неравенство
\[
\|g(F,{\bf \ell})-g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}\lt \frac{5}{24}\|\delta
g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)} \lt \frac{5}{24} \left(\frac{5}{8}\right)^{k}\|\delta
(F)\|_{\ell_{\infty}(\mathbb{R}^2)}.
\]
Если \(\mathfrak{S}\in\mathbb{R}^2\) множество конечной меры, то положим
\[\|f\|_{p(\mathfrak{S}S)}=\left(\int_{\mathfrak{S}S}|f(x,y)|^pdxdy\right)^{1/p},
\|f\|_{C(\mathfrak{S}S)}=\max_{(x,y)\in\mathfrak{S}S}|f(x,y)|.
\]
Следствие.
Пусть \(p\in [1,\infty)\), \(k\in\mathbb{N}\). Для любого массива \(F\in \ell_\infty(\mathbb{R}^2)\) имеют место неравенства
\begin{equation}\label{s.101}
\left|\|g(F,{\bf \ell})\|_{p(\mathfrak{S}S)}-\|g_{k}(F,{\bf \ell})\|_{p(\mathfrak{S}S)}\right|\le (mes(\mathfrak{S}))^{1/p} \frac{5}{24}\|\delta g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)} \end{equation} и \begin{equation}\label{s.102}
\|g_{k}(F,{\bf \ell})\|_{C(\mathfrak{S}S)}\le\|g(F,{\bf \ell})\|_{C(\mathfrak{S}S)}\le
\|g_{k}(F,{\bf \ell})\|_{C(\mathfrak{S}S)}+ \frac{5}{24}\|\delta g_{k}(F,{\bf \ell})\|_{C(\mathbb{R}^2)}.
\end{equation} Соотношение (\ref{s.101}) верно и для случая, когда \(\mathfrak{S}=\mathbb{R}^2\).
Левая часть неравенства (\ref{s.101}) следует из того факта, что \(g_k(F,{\bf \ell})\) есть полигон
интерполирующий \(g(F,{\bf \ell})\) в узлах.
Всюду далее будем считать, что \(\ell_0=(h,0)\) и \(\ell_1=(h/2,h^*)\), где
\(h^*=h\sqrt{3}/2\). В этом случае вместо \(g_{k}(F,{\bf \ell})\) и \(g(F,{\bf \ell})\) будем писать
\(g_{k,h}(F)\) и \(g_{h}(F)\) соответственно.
Пусть \(h=1\) и \(F^*=F^{*,0}=\{f^*_{i,j}\}_{i,j\in Z}\) такова, что \(f^*_{i,j}=\delta_{|i|+|j|,0}\) \delta_{\nu,\mu}-\)
символ Кронекера). Положим
\[
G_{k}(x,y)=g_{k,1}(F^*,x,y),\,\,\,\,\, G(x,y)=g_1(F^*,x,y).
\]
Из линейности операторов \(g_{k,h}\) и \(g_h\) следует, что
для любого массива \(F\in\ell_\infty(\mathbb{R}^2)\), любых \((x,y)\in\mathbb{R}^2\) и \(h>0\) имеют место равенства \begin{equation}\label{s.103}
g_h(f,x,y)=\sum_{i,j\in Z}f_{i,j}G\left(\frac{x}{h}-i,\frac{y}{h^*}-j\right) \end{equation} и \begin{equation}\label{s.104}
g_{k,h}(f,x,y)=\sum_{i,j\in Z}f_{i,j}G_{k}\left(\frac{x}{h}-i,\frac{y}{h^*}-j\right). \end{equation} Ясно, что носителем функции
\)G_{k}(x,y)\) является шестиугольник \(\mathfrak{D}_k\) с вершинами в точках
\[
M^k_1\left(\left(-3+\frac{1}{2^k}\right),0\right),\,\,\,\,\, M^k_2\left(\frac{-3+\frac{1}{2^k}}{2},
\left(-3+\frac{1}{2^k}\right)\frac{\sqrt{3}}{2}\right),\,\,\,\,\,
\]
\[
M^k_3\left(\frac{3-\frac{1}{2^k}}{2},\left(3-\frac{1}{2^k}\right) \frac{\sqrt{3}}{2}\right),\,\,\,\,\,
M^k_4\left(\left(3-\frac{1}{2^k}\right),0\right),\,\,\,\,\,
\]
\[
M^k_5\left(\frac{3-\frac{1}{2^k}}{2},\left(-3+\frac{1}{2^k}\right) \frac{\sqrt{3}}{2}\right),\,\,\,\,\,
M^k_6\left(\frac{-3+\frac{1}{2^k}}{2},\left(-3+\frac{1}{2^k}\right) \frac{\sqrt{3}}{2}\right)
\]
и, следовательно, носителем функции \(G(x,y)\) является правильный шестиугольник \(\mathfrak{D}\) с вершинами в точках \((\pm
3,0),\) \((\pm 3/2,\pm 3\sqrt{3}/2)\).
Таким образом для \((x,y)\in \mathbb{T}^{\pm}_{i,j,k}\) выполняются равенства \begin{equation}\label{s.105}
g_{k,h}(f,x,y)=\sum_{\nu,\mu:(\nu-i,\mu-j)\in\mathfrak{D}_k}f_{\nu,\mu} G_{k}\left(\frac{x}{h}-\nu,\frac{y}{h^*}-\mu\right)
\end{equation} и \begin{equation}\label{s.106} g_h(f,x,y)=\sum_{\nu,\mu:(\nu-i,\mu-j)\in\mathfrak{D}}f_{\nu,\mu}
G\left(\frac{x}{h}-\nu,\frac{y}{h^*}-\mu\right). \end{equation}
Теорема 7.
Для всех \((x,y)\in\mathbb{R}^2\) имеет место равенство
\begin{equation}\label{s.108}
G(x,y)=G(2x,2y)+ \frac{1}{16}\sum_{\nu=0}^5\left(9G\left(2x-\cos\frac{\pi}{3}\nu,2y-\sin\frac{\pi}{3}\nu\right)-
G\left(2x-3\cos\frac{\pi}{3}\nu,2y-3\sin\frac{\pi}{3}\nu\right)\right).
\end{equation}
Доказательство. Из (\ref{s.105}) и (\ref{s.80}) следует, что
\[
G(x,y)=g_1(F^{*,0},x,y)=g_{1/2}(F^{*,1},x,y)
=g_{1/2}\left(\sum_{(\nu,\mu)\in\mathfrak{D}}f^{*,1}_{\nu,\mu} F^{*,0}_{\nu,\mu},x,y\right)=
\sum_{(\nu,\mu)\in\mathfrak{D}}f^{*,1}_{\nu,\mu} g_{1/2}\left(F^{*,0}_{\nu,\mu},x,y\right).
\]
Теперь последовательно используя равенства (\ref{s.84}) и (\ref{s.85}), получаем
\[
G(x,y)= \sum_{(\nu,\mu)\in\mathfrak{D}}f^{*,1}_{\nu,\mu} g_{1/2}\left(F^{*,0},x-\nu h,y-\mu h^*\right)
=\sum_{(\nu,\mu)\in\mathfrak{D}}f^{*,1}_{\nu,\mu} g_{1}\left(F^{*,0},2x-\nu h,2y-\mu h^*\right)
\]
или, что то же \begin{equation}\label{s.109} G(x,y)= \sum_{\nu,\mu\in\mathfrak{D}}f^*_{\nu,\mu,1}
G\left(2x-\nu\frac{1}{2},2y-\mu\frac{\sqrt{3}}{2}\right). \end{equation} Непосредственно вычисляя значения \(f^*_{\nu,\mu,1}\),
отсюда получаем требуемое утверждение.
Пусть \(f\in C(\mathbb{R}^2)\) и \(\|g_h\|_{C(\mathbb{R}^2)\to C(\mathbb{R}^2)}-\) норма оператора \(g\), действующего из пространства
\)C(\mathbb{R}^2)\) в пространство \(C(\mathbb{R}^2)\), то есть
\[\|g_h\|_{C(\mathbb{R}^2)\to C(\mathbb{R}^2)}=
\sup_{\|f\|_{C(\mathbb{R}^2)}\le 1}\|g_h(f)\|_{C(\mathbb{R}^2)}.\]
Положим
\[
N_k(x,y)=\sum_{i,j\in Z}\left|G_k\left(x-i\frac{1}{2},y-j\frac{\sqrt{3}}{2}\right)\right|\] и \begin{equation}\label{s.110}
N(x,y)=\sum_{i,j\in Z}\left|G\left(x-i\frac{1}{2},y-j\frac{\sqrt{3}}{2}\right)\right|. \end{equation}
Теорема 8.
Справедливо равенство \begin{equation}\label{s.112} \|g_h\|_{C(\mathbb{R}^2)\to C(\mathbb{R}^2)}=\|N\|_{C(\mathbb{R}^2)}. \end{equation}
Кроме того, для любого
\(k\in\mathbb{N}\) и \(h>0\)
\begin{equation}\label{s.113} \|N_k\|_{C(\mathbb{R}^2)} \le\|g_h\|_{C(\mathbb{R}^2)\to C(\mathbb{R}^2)}\le \|N_k\|_{C(\mathbb{R}^2)}+
{12}\|\delta N_{k}\|_{C(\mathbb{R}^2)}. \end{equation}
Доказательство. Пусть \(f\) произвольная функция из \(C(\mathbb{R}^2)\), такая, что \(\|f\|_{C(\mathbb{R}^2)}\le 1\), тогда в силу
(\ref{s.103})
\[
\|g_h(f)\|_{C(\mathbb{R}^2)}\le\left\|\sum_{i,j\in Z}f_{i,j}
G\left(\frac{(\cdot)}{h}-i,\frac{(\cdot\cdot)}{h^*}-j\right)\right\|_{ C(\mathbb{R}^2)}=\]
\[=
\sup_{(x,y)\in\mathbb{R}^2}\left|\sum_{i,j\in Z}f_{i,j} G\left(\frac{x}{h}-i,\frac{y}{h^*}-j\right)\right|\le
\]
\[
\le\sup_{(x,y)\in\mathbb{R}^2}\sum_{i,j\in Z}\left|f_{i,j}G\left(\frac{x}{h}- i,\frac{y}{h^*}-j\right)\right|\le\]
\[\le \sup_{i,j\in Z}|f_{i,j}|\sup_{(x,y)\in\mathbb{R}^2}\sum_{i,j\in Z}
\left|G\left(x-i\frac{1}{2},y-j\frac{\sqrt{3}}{2}\right)\right|\le\] \begin{equation}\label{s.114} \le
\sup_{(x,y)\in\mathbb{R}^2}\sum_{i,j\in Z}\left|G\left(x-i\frac{1}{2},y-j\frac{\sqrt{3}}{2}\right)\right|=
\sup_{(x,y)\in\mathbb{R}^2}N(x,y). \end{equation}
Из 1-периодичности функции \(N(x,y)\) по переменной \(x\) и \(\sqrt{3}\)-периодичности по переменной \(y\), а также из ее
непрерывности следует, что существует точка \((x_0,y_0)\in \mathbb{T}_{0,0,0}^{+}\) такая, что
\(N\left({x_0},{y_0}\right)=\max_{(x,y)\in\mathbb{R}^2}N(x,y).\)
Через \(f_0(x,y)\) обозначим непрерывную функцию, принимающую значения
\[
{\rm sgn\,} G\left({x_0}-i,{y_0}-j\right)
\]
в точках \((ih,jh^*)\) и любые значения из \((-1,1)\)
в остальных точках из \(\mathbb{R}^2\). Тогда
\[
\|g_h\|_{C(\mathbb{R}^2)\to C(\mathbb{R}^2)}\ge \frac{\|g_h(f_0)\|_{C(\mathbb{R}^2)}}{\|f_0\|_{C(\mathbb{R}^2)}}= \|g_h(f_0)\|_{C(\mathbb{R}^2)}\ge\]
\[
\ge |f_0(x_0h,y_0h^*)|= \sum_{i,j\in Z}{\rm sgn\,} G\left({x_0}-i,{y_0}-j\right) G\left({x}-i,{y}-j\right) =\]
\[=\sup_{(x,y)\in\mathbb{R}^2}N(x,y),
\]
что вместе с (\ref{s.114}) доказывает равенство (\ref{s.112}).
Для доказательства равенства (\ref{s.113}) достаточно учесть равенство (\ref{s.102}) и тот факт, что в соотношении
(\ref{s.103}) не более чем 54 слагаемых отличны от нуля.
Отметим, что функция \(N(x,y)\) обладает более сильной симметрией, чем периодичность по каждой переменной, а именно, если
через \((x_{\varphi},y_{\varphi})\) обозначим точку \((x,y)\in \mathbb{T}_{i,j,k}^{\pm}\), полученную поворотом на угол \(\varphi\)
(в положительном направлении) вокруг центра треугольника \(\mathbb{T}_{i,j,k}^{\pm}\), то для любых \(n_0,n_1,n_2\in\mathbb{N}\) имеет
место равенство
\[
N(x,y)=N\left(x_{n_0\pi/3}\pm n_1h,y_{n_0\pi/3}\pm n_2h^*\right).
\]
Положим для \((x,y)\in \mathbb{T}^\pm_{0,0,0}\)
\[
K_{n,m}(x,y)=x^ny^m- \sum_{\nu,\mu:(\nu,\mu)\in\mathfrak{D}}\nu^n\left(\mu\frac{\sqrt{3}}{2}\right)^m
G\left(\frac{x}{h}-\nu,\frac{y}{h^*}-\mu\right),
\]
где \(n,m\ge 0: n+m=4.\)
Для функции \(f\) такой, что
\[\frac{\partial f^{\nu+\mu}}{\partial x^\nu\partial y^\mu}
\in C(\mathbb{R}^2) \,\,\,\,\,\nu,\mu=0,1,\ldots,4,\,\,\,\,\nu+\mu=4\] введем модуль непрерывности
\[
\omega\left(f^{IV},t\right)= \max_{\nu+\mu=4}\sup_{|M'-M''|\lt t}\left| \frac{\partial f^{\nu+\mu}}{\partial x^\nu\partial
y^\mu}(M')- \frac{\partial f^{\nu+\mu}}{\partial x^\nu\partial y^\mu}(M'')\right|.
\]
Теорема 9.
Пусть функция \(f\) такова, что
\[\frac{\partial f^{\nu+\mu}}{\partial x^\nu\partial y^\mu}
\in C(\mathbb{R}^2) \,\,\,\,\,\nu,\mu=0,1,\ldots,4,\,\,\,\,\nu+\mu\le 4,\] тогда для \((x,y)\in \mathbb{T}^{\pm}_{i,j,k}\) равномерно
по \(i,j\in Z\) и \((x,y)\in\mathbb{R}^2\) выполняется соотношение \begin{equation}\label{s.116} |f(x,y)-g_h(f,x,y)|=\end{equation}
\[=
\frac{h^4}{24}\left|\sum_{n,m\ge 0: n+m=4}C^n_4 \frac{\partial^4f}{\partial x^n\partial y^m}\Big|_{(ih,jh^*)}
K_{n,m}(x,y)\right|+O(h^4\omega\left(f^{IV},h\right)).\]
Доказательство. Без потери общности можно считать, что \((x,y)\in \mathbb{T}^\pm_{0,0,0}\).
Ранее была доказана точность соответствующего одномерного метода subdivision на кубических полиномах.
Отсюда и из того факта, что след полинома двух переменных на любую прямую есть полином одной переменной той же степени
и из конструкции метода \(g_h(f)\) следует, что если \(P_3(x,y)\) кубический полином по переменным \(x\) и \(y\), то
\(g_h(P_3,x,y)=P_3(x,y)\).
Таким образом для \(n,m=0,1,\ldots\), \(n+m\le 3\) и \((x,y)\in \mathbb{T}^\pm_{0,0,0}\) имеем \begin{equation}\label{s.117}
x^ny^m=g_h(x^ny^m,x,y)=\sum_{\nu,\mu:(\nu,\mu)\in\mathfrak{D}}\nu^n \left(\mu\frac{\sqrt{3}}{2}\right)^m
G\left(\frac{x}{h}-\nu,\frac{y}{h^*}-\mu\right). \end{equation}
Если непустое множество \(\Re\) лежит в круге радиуса \(Mh\) (\)M\) абсолютная константа), то для \((x,y)\in\Re\) формулу
Тейлора для функции двух переменных \(f\) можно записать в виде
\[
f(x,y)=\sum_{n,m\ge 0: n+m\le 4}C^{n+m}_4\frac{h^{n+m}}{(n+m)!} \frac{\partial^4f}{\partial x^n\partial
y^m}\Bigg|_{(0,0)}x^ny^m \]\[+\alpha(x,y)h^4\omega\left(f^{IV},hM\right),
\]
где \(|\alpha(x,y)|\le M^4/24\).
Отсюда, из линейности оператора \(g_h\), соотношения (\ref{s.117}), из того факта, что равенство (\ref{s.103}) содержит
не более чем 54 слагаемых отличных от нуля, что носитель базисной функции содержится в круге радиуса 3, имеем
\[
g_h(f,x,y)= \sum_{n,m\ge 0: n+m\le 4}C^{n+m}_4\frac{h^{n+m}}{(n+m)!} \frac{\partial^4f}{\partial x^n\partial
y^m}\Bigg|_{(0,0)} g_h\left(x^ny^m,x,y\right)+\]
\[+\beta(x,y)h^4\omega\left(f^{IV},hM\right)=
\sum_{n,m\ge 0: n+m\le 3}C^{n+m}_4\frac{h^{n+m}}{(n+m)!} \frac{\partial^4f}{\partial x^n\partial y^m}\Bigg|_{(0,0)}x^n
y^m +\]
\[+
\sum_{n,m\ge 0: n+m=4}\frac{h^{4}}{4!} \frac{\partial^4f}{\partial x^n\partial y^m}\Bigg|_{(0,0)}
g_h\left(x^ny^m,x,y\right) +\beta(x,y)h^4\omega\left(f^{IV},4h\right),
\]
где \(|\beta(x,y)|\le \|N\|_{C(\mathbb{R}^2)}4\cdot 4^4\cdot 54/24\).
Отсюда и из равенства (\ref{s.103}) следует, что
\[g_h(f,x,y)=
\sum_{n,m\ge 0: n+m\le 3}C^{n+m}_4\frac{h^{n+m}}{(n+m)!} \frac{\partial^4f}{\partial x^n\partial
y^m}\Bigg|_{(0,0)}x^ny^m +\]
\[+
\sum_{n,m\ge 0: n+m= 4}\frac{h^{4}}{4!} \frac{\partial^4f}{\partial x^n\partial y^m}\Bigg|_{(0,0)}
\sum_{\nu,\mu:(\nu,\mu)\in\mathfrak{D}} \nu^n\left(\mu\frac{\sqrt{3}}{2}\right)^m
G\left(\frac{x}{h}-\nu,\frac{y}{h^*}-\mu\right)+ \beta(x,y)h^4\omega\left(f^{IV},4h\right).
\]
Таким образом имеем
\[
|f(x,y)-g_h(f,x,y)|=
\frac{h^4}{24}\left|\sum_{n,m\ge 0: n+m=4}
C^n_4\left(x^ny^m-
\sum_{\nu,\mu:(\nu,\mu)\in\mathfrak{D}}\nu^n\left(\mu\frac{\sqrt{3}}{2}\right)^m
G\left(\frac{x}{h}-\nu,\frac{y}{h^*}-\mu\right)\right)\times\right.\]
\[\left.\times
\frac{\partial^4f}{\partial x^n\partial y^m}\Bigg|_{(0,0)} \right|+O(h^4\omega\left(f^{IV},h\right))=
\]
\[
=\frac{h^4}{24}\left|\sum_{n,m\ge 0: n+m=4} C^n_4 \frac{\partial^4f}{\partial x^n\partial y^m}\Bigg|_{(0,0)}
K_{n,m}(x,y)\right|+O(h^4\omega\left(f^{IV},h\right)).
\]
Соотношение (\ref{s.116}) доказано.
Положим
\[
|||f^{IV}|||=\max_{n,m\ge 0: n+m=4}\left\{\left\| \frac{\partial^4f}{\partial x^n\partial y^m}
\right\|_{C(\mathbb{R}^2)}\right\}
\]
и
\[
\mathbb{K}=\max_{(x,y)\in \mathbb{T}^\pm_{0,0,0}}\left\{\sum_{n,m\ge 0: n+m=4}
C^n_4 |K_{n,m}(x,y)|\right\}.
\]
Следствие.
Пусть функция \(f\) такова, что
\[\frac{\partial f^{\nu+\mu}}{\partial x^\nu\partial y^\mu}
\in C(\mathbb{R}^2) \,\,\,\,\,\nu,\mu=0,1,\ldots,4,\,\,\,\,\nu+\mu\le 4,\] тогда
\[
\|f-g_h(f)\|_{C(\mathbb{R}^2)}= \mathbb{K}\frac{h^4}{24}|||f^{IV}|||+o(h^4).
\]
Приведем пример триангуляции фрагмента русла Днепра с использованием метода пополнения (subdivision).

Интерполяционный subdivision по четырехугольной решетке
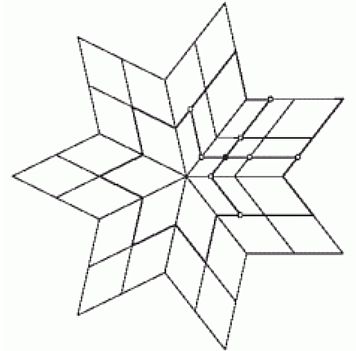
Основываясь на интерполяционной формуле, Leif Kobbelt предложил следующую схему subdivision поверхностей
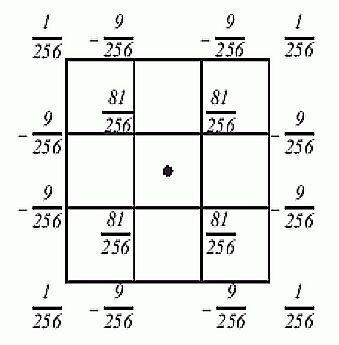
Схема Kobbelt двухпроходная. Вначале вычисляются краевые значения, а уже используя полученные новые значения, находим
новые значения в средине.
Формулы subdivision в этом случае имеют вид
\[
p^{j+1}_{i,1}=\left(\frac{1}{2}-\omega\right)p^j_0+\left(\frac{1}{2}-\omega\right)p^j_{i,1}+\omega p^j_i+\omega
p^j_{i,3},
\]
\[
v^j_i=\frac{4}{k}\sum_{i=0}^{k-1}p^j_{i,1}-\left(p^j_{i-1,1}+p^j_{i,1}+p^j_{i+1,1}\right)-
\frac{\omega}{\frac{1}{2}-\omega}\left(p^j_{i-2,2}+p^j_{i-1,2}+p^j_{i,2}+p^j_{i+1,2}\right)+
\frac{4\omega}{k\left(\frac{1}{2}-\omega\right)}\sum_{i=0}^{k-1}p^j_{i,2},
\]
где для регулярного случая \(\omega=-1/16\).
Заметим, что используя методику описанную в предыдущем параграфе, для методов пополнения по квадратной решетке можно
получить аналогичные результаты.
Интерполяционные в среднем методы subdivision





