Задача оптимального выбора узлов при приближении сплайнами и ее связь с оптимальными квадратурами
Положим
\begin{equation}\label{2.1}
\varepsilon(x,S_{r-1,1}(\Delta_n))_p=\inf\left\{\|x-s\|_p | s\in S_{r-1,1}(\Delta_n),\right.
\left.x^{(\nu)}(a)-s^{(\nu)}(a)=x^{(\nu)}(b)-s^{(\nu)}(b) (\nu=0,1,\ldots,r-1)\right\},
\end{equation}
\begin{equation}\label{2.2}
e(x,S_{r-1,1}(\Delta_n))_p=\inf\left\{\|x-s\|_p | s\in S_{r-1,1}(\Delta_n),\right.
\left.
x^{(\nu)}(i)=s^{(\nu)}(i) (\nu=0,1,\ldots,r-1, i=a,b)\right\}
\end{equation}
и величины \(\varepsilon_{n,r-1}(x)_p\), \(e_{n,r-1}(x)_p\), которые вводятся аналогично \(E_{n,r-1}(x)_p\) (см. список основных обозначений), то есть
\[
\varepsilon_{n,r-1}(x)_p=\inf\left\{\varepsilon(x,S_{r-1,1}(\Delta_n))_p|\Delta_n\right\},
\]
\[
e_{n,r-1}(x)_p=\inf\left\{e(x,S_{r-1,1}(\Delta_n))_p|\Delta_n\right\}.
\]
Непосредственно из определения следует
\[
E(x,S_{r-1,1}(\Delta_n))_p\le \varepsilon(x,S_{r-1,1}(\Delta_n))_p\le e(x,S_{r-1,1}(\Delta_n))_p.
\]
Введем, теперь, в рассмотрение весовые квадратурные формулы (формулы приближенного вычисления интегралов).
Пусть
\[
A_n=\left\{a_i\right\}_{i=1}^n,B_n=\left\{b_i\right\}_{i=1}^n,C_n=\left\{c_i\right\}_{i=1}^n,D_n=\left\{d_i\right\}_{i=1}^n
\]
и
\[
\mathfrak{I} (x,C_n,\Delta_n)=\sum_{i=1}^nc_ix(t_{i,n}),
\mathfrak{J} _a (x,A_r)=\sum_{i=1}^{r-1}a_ix^{(i)}(a),\]
\[
\mathfrak{J} _b (x,B_r)=\sum_{i=1}^{r-1}b_ix^{(i)}(b),
\mathfrak{J} _d (x,D_r)=\sum_{i=1}^{r-1}a_i\left(x^{(i)}(a)-x^{(i)}(b)\right).
\]
Квадратурную формулу
\begin{equation}\label{2.3}
\int_a^bz(t)x(t)dt=\mathfrak{I} (x,C_n,\Delta_n)+R(x,z,C_n,\Delta_n)
\end{equation}
принято называть открытой весовой квадратурной формулой. Формулу
\begin{equation}\label{2.4}
\int_a^bz(t)x(t)dt=\mathfrak{I} (x,C_n,\Delta_n)+\mathfrak{J} _a (x,A_r)+\mathfrak{J} _b (x,B_r)+r(x,z,A_r,B_r,C_n,\Delta_n)
\end{equation}
будем называть замкнутой весовой квадратурной формулой и
\begin{equation}\label{2.5}
\int_a^bz(t)x(t)dt=\mathfrak{I} (x,C_n,\Delta_n)+\mathfrak{J} _D (x,D_r)+\rho(x,z,D_r,C_n,\Delta_n)
\end{equation}
формулой типа Эйлера-Макларена.
Обозначим через \(R(\mathfrak{M} ,z,C_n,\Delta_n)\), \(r(\mathfrak{M} ,z,A_r,B_r,C_n,\Delta_n)\) и \(\rho(\mathfrak{M} ,z,D_r,C_n,\Delta_n)\) погрешности квадратурных формул (\ref{2.3}) - (\ref{2.5}) на классе \(\mathfrak{M} \)
\[
R(\mathfrak{M} ,z,C_n,\Delta_n)=\sup\left\{R(x,z,C_n,\Delta_n)|x\in\mathfrak{M} \right\},
\]
\[
r(\mathfrak{M} ,z,A_r,B_r,C_n,\Delta_n)=\sup\left\{r(x,z,A_r,B_r,C_n,\Delta_n)|x\in\mathfrak{M} \right\},
\]
\[
\rho(\mathfrak{M} ,z,D_r,C_n,\Delta_n)=\sup\left\{\rho(x,z,D_r,C_n,\Delta_n)|x\in\mathfrak{M} \right\},
\]
и, кроме того,
\(
R(\mathfrak{M} ,z,\Delta_n)=\inf{R(\mathfrak{M} ,z,C_n,\Delta_n)|C_n}
\)
и
\(
R_n(\mathfrak{M} ,z)=\inf{R(\mathfrak{M} ,z,\Delta_n)|\Delta_n}.
\)
Аналогично вводятся величины \(r(\mathfrak{M} ,z,\Delta_n)\), \(R_n(\mathfrak{M} ,z)\) и \(\rho(\mathfrak{M} ,z,\Delta_n)\), \(\rho_n(\mathfrak{M} ,z)\).
Теорема 2.
При всех \(n,r=1,2,\ldots,p\in [1,\infty]\) и любого \(z(t)\in L\) выполняются неравенства
\begin{equation}\label{2.6}
\rho_n(W^r_p,z)=\varepsilon_{n,r-1}(z_r)_{p'},
\end{equation}
\begin{equation}\label{2.7}
R_n(W^r_p,z)=e_{n,r-1}(z_r)_{p'},
\end{equation}
\begin{equation}\label{2.8}
r_n(W^r_p,z)=E_{n,r-1}(z_r)_{p'},
\end{equation}
где \(\frac{1}{p}+\frac{1}{p'}=1\) и \(z_r-\)й интеграл (любой) от функции \(z(t)\).
Доказательство. Напомним, что квадратурная формула вида (\ref{2.3}) называется точкой на множестве \(\mathfrak{N} \), если для \(x\in\mathfrak{N} \) выполняется равенство
\(
R(x,z,C_n)=0.
\)
Если квадратурная формула вида (\ref{2.2}) не точна на множестве алгебраических полиномов степени не выше \(r-1\), то найдется такой полином \(P^*\in \mathbb{P}_{r-1}\) из этого множества, что \(R(P^*)\ne 0\). Тогда
\[
\sup_{x\in W^r_p}R(x)\ge \sup\{R(x)|x\in \mathbb{P}_{r-1}\}\ge \sup_{\lambda}R(\lambda P^*)=\sup_{\lambda}|\lambda | R(P^*)=\infty.
\]
Поэтому в дальнейшем будем рассматривать только те квадратурные формулы, которые точны на множестве алгебраических полиномов степени не выше \(r-1\).
Аналогично определяется точность квадратурных формул вида (\ref{2.4}) и (\ref{2.5}).
Рассмотрим квадратурную формулу вида (\ref{2.3}), точную на множестве алгебраических полиномов степени не выше \(r-1\).
Согласно формуле Тейлора, для любой функции \(x\in L^r\) выполняется равенство
\[
x(t)=\sum_{\nu=0}^{r-1}\frac{x^{(\nu)}(a)}{\nu !}(t-a)^\nu+\frac{1}{(r-1)!}\int_a^b(t-u)^{r-1}_+x^{(r)}(u)du.
\]
Следовательно,
\begin{equation}\label{2.9}
x(t_{i,n})=\sum_{\nu=0}^{r-1}\frac{x^{(\nu)}(a)}{\nu !}(t_{i,n}-a)^\nu+\frac{1}{(r-1)!}\int_a^b(t_{i,n}-u)^{r-1}_+x^{(r)}(u)du,
\end{equation}
где \(z^r_+-\) усеченная степенная функция.
Тогда, интегрируя по частям, получаем
\begin{equation}\label{2.10}
\int_a^bz(t)x(t)dt=\int_a^bz_r(t)x^{(r)}(t)dt+\sum_{\nu=0}^{r-1}z_\nu(a)x^{(\nu)}(a),
\end{equation}
где
\[
z_\nu(t)=\frac{1}{(\nu-1)!}\int_t^b(t-u)^{\nu-1}z(u)du.
\]
Используя (\ref{2.9}) и (\ref{2.10}), из (\ref{2.3}) получаем
\begin{equation}\label{2.11}
R(x,x,C_n,\Delta_n)=
\int_a^b x^{(r)}(u)\left(z_r(u)-\sum_{i=1}^nc_i\frac{(t_{i,n}-a)^{r-1}_+}{(r-1)!}\right)du+\sum_{\nu=0}^{r-1}x^{(\nu)}(a)\ell_\nu,
\end{equation}
где
\[
\ell_\nu=z_\nu(a)-\sum_{i=1}^nc_i\frac{(t_{i,n}-a)^\nu}{\nu !}.
\]
Ясно, что для того, чтобы формула (\ref{2.3}) была точна на алгебраических полиномах степени не выше \(r-1\), необходимо и достаточно, чтобы \(\ell_\nu=0 (\nu=0,\ldots,r-1)\). Кроме того, видно, что
\[
\frac{1}{(r-1)!}\sum_{i=1}^nc_i(t_{i,n}-u)^{r-1}_+
\]
является сплайном порядка \(r-1\) минимального дефекта по разбиению \(\Delta_n=\left\{t_{i,n}\right\}_{i=0}^n\). Обозначим его через \(s(C_n,\Delta_n)\). Покажем, что этот сплайн интерполирует \(r-1\) раз функцию \(z_r(t)\) в точках \(a\) и \(b\)
\[
s^{(\nu)}(C_n,\Delta_n,i)=z_r^{(\nu)}(i) (i=a,b;\nu=0,\ldots,r-1),
\]
где под \(s^{(r-1)}(C_n,\Delta_n,a)\) и \(s^{(r-1)}(C_n,\Delta_n,b)\) будем понимать \(s^{(r-1)}(C_n,\Delta_n,a+0)\) и \(s^{(r-1)}(C_n,\Delta_n,b-0)\) соответственно.
Используя далее формулу интегрирования по частям, легко убедиться в том, что
\begin{equation}\label{2.12}
\int_a^b x^{(r)}(u)\sigma_r(u)du=(-1)^r\mathfrak{I} (x,C_n,\Delta_n)+
\sum_{\nu=0}^{r-1}(-1)^{r-\nu-1}x^{(\nu)}(a)\sigma^{(r-\nu-1)}_r(a)+\sum_{\nu=0}^{r-1}(-1)^{r-\nu-1}x^{(\nu)}(b)\sigma^{(r-\nu-1)}_r(b)+
(-1)^rR(x,z,C_n,\Delta_n),
\end{equation}
где \(\sigma_r(t)=z_r(t)-s(C_n,\Delta_n,t)\).
Из (\ref{2.12}) следует, что для того, чтобы для произвольной функции \(x\in W^r_p\) эта формула была формулой вида (\ref{2.3}), необходимо, чтобы выполнялись условия
\[
\sum_{\nu=0}^{r-1}(-1)^{r-\nu-1}x^{(\nu)}(a)\sigma^{(r-\nu-1)}_r(a)=0,
\sum_{\nu=0}^{r-1}(-1)^{r-\nu-1}x^{(\nu)}(b)\sigma^{(r-\nu-1)}_r(b)=0,
\]
что эквивалентно выполнению соотношений
\begin{equation}\label{2.13}
\sigma^{(\nu)}_r(a)=0,\sigma^{(\nu)}_r(b)=0 (\nu=0,1,\ldots,r-1).
\end{equation}
Таким образом, какова бы ни была квадратурная формула (\ref{2.3}), найдется сплайн \(s=s(C_n,\Delta_n)\in S_{r-1,1}(\Delta_n)\) такой, что если
\begin{equation}\label{2.14}
\sigma_r(t)=z_r(t)-s(t),
\end{equation}
то выполняются равенства (\ref{2.13}) и
\begin{equation}\label{2.15}
\left|R(x,z,C_n,\Delta_n)\right|=\left|\int_a^bx^{(\nu)}(u)\sigma_r(u)du\right|
\end{equation}
и наоборот, какой бы ни был сплайн \(s\in S_{r-1,1}(\Delta_n)-\) таков, что выполняются условия (\ref{2.13}), где \(\sigma_r(t)\) определено равенством (\ref{2.14}), найдется квадратурная формула вида (\ref{2.3}) такая, что выполняется равенство (\ref{2.15}).
Переходя к точной верхней грани по \(x\in W^r_p\) в (\ref{2.15}) и учитывая, что (см. [14] с.301)
\begin{equation}\label{2.16}
\sup_{\|y\|_{p}\le 1}\int_a^bx(t)y(t)dt=\|x\|_{p'},
\end{equation}
получаем
\(
R(W^r_p,z,C_n,\Delta_n)=\|\sigma_r\|_{p'}.
\)
Отсюда и из предыдущего, получаем
\[
\inf_{C_n}R(W^r_p,z,C_n,\Delta_n)=
\inf\{\|z_r-s\|_{p'}|s\in S_{r-1,1}(\Delta_n),s^{(\nu)}(i)=z_r^{(\nu)}(i) (i=a,b;\nu=0,1,\ldots,r-1)\}=
e(z_r,S_{r-1,1}(\Delta_n))_{p'}.
\]
Тогда из произвольности разбиения \(\Delta_n\) сразу получаем равенство (\ref{2.7}).
Соотношения (\ref{2.6}) и (\ref{2.8}) устанавливаются аналогично.
Определение 1.
Пусть \(\left\{\mathbb{P}_{r,k}(\cdot,\Delta_n)\right\}_{n=1}^\infty\) - некоторая последовательность операторов, отображающая пространство \(C^\rho (\rho\ge r-k)\) в \(S_{r,k}(\Delta_n)\). При фиксированных \(r\) и \(\rho\) последовательность разбиений \(\left\{\Delta^*_n\right\}_{n=1}^\infty\) назовем асимптотически оптимальной для функции \(x\) и последовательности операторов \(\left\{\mathbb{P}_{r,k}(x,\Delta_n)\right\}_{n=1}^\infty\), если при \(n\to\infty\)
\[
\inf_{\Delta_n}\|x-\mathbb{P}_{r,k}(x,\Delta_n)\|_p=\|x-\mathbb{P}_{r,k}(x,\Delta^*_n)\|_p(1+o(1)).
\]
Определение 2.
Будем говорить, что последовательность разбиений \(\left\{\Delta^*_n\right\}_{n=1}^\infty\) является асимптотически оптимальной для квадратурных формул вида (\ref{2.3}) и класса \(\mathfrak{M} \), если при \(n\to\infty\)
\[
R_n(\mathfrak{M} ,z)=R(\mathfrak{M} ,z,\Delta^*_n)(1+o(1)).
\]
Аналогично определяется асимптотически оптимальная последовательность разбиений для квадратурных формул вида (\ref{2.4}) и (\ref{2.5}).
Замечание 1.
Теорема 2 устанавливает связь между задачей наилучшей и асимптотически наилучшей квадратурной формулой и асимптотически наилучшем выборе узлов при приближении конкретной функции (\)r-\)го интеграла от веса) сплайнами наилучшего приближения (с ограничениями на концах или без таковых). Из доказательства теоремы следует, что если \(\left\{\Delta^*_n\right\}_{n=1}^\infty\) последовательность разбиений асимптотически наилучшая для сплайна наилучшего приближения порядка \(r-1\) минимального дефекта для функции \(z_r\) в метрике пространства \(L_{p'}\), то эта последовательность разбиений будет асимптотически наилучшей для квадратурной формулы (\ref{2.4}) на классе \(W^r_p\) и веса \(z\).
Аналогичный случай имеет место и для квадратурных формул вида (\ref{2.3}) и (\ref{2.5}), только вместо наилучшего приближения с соответствующими ограничениями (\ref{2.1}) и (\ref{2.2}).
Покажем теперь, что при \(n\to\infty\) для "хороших" классов функций \(\mathfrak{M} \) главный член асимптотики величин \(r_n(\mathfrak{M} ,z)\), \(\rho_n(\mathfrak{M} ,z)\) и \(R_n(\mathfrak{M} ,z)\) будет один и тот же.
Отсюда и из теоремы 2 и замечания 1 будет следовать и асимптотическое равенство величин \(E_{n,r-1}(z_r)_p\), \(\varepsilon_{n,r-1}(z_r)_p\) и \(e_{n,r-1}(z_r)_p\). Следовательно, для выяснения поведения асимптотики граничные условия не играют никакой роли, другими словами, они несущественны.
Теорема 3.
Для произвольного класса \(\mathfrak{M} \subset C^r\) и веса \(z\in L\) справедливо
\begin{equation}\label{2.17}
r_n(\mathfrak{M} ,z)\le \rho_n(\mathfrak{M} ,z)\le R_n(\mathfrak{M} ,z),
\end{equation}
и если класс \(\mathfrak{M} \) функций \(x\) таков, что производная от \(x\) любого порядка \(\nu (\nu=0,1,\ldots,r)\) с любой степенью точности
приближается разделенными разностями на этом классе, то есть, для произвольного
\(\nu=0,1,\ldots,r\) и любой точки \(t\in [a,b]\) и \(\forall \varepsilon>0\) существует система чисел \(q_{i,\nu}\) и точки
\(\tau_i\in (t+t+\varepsilon)\) (\)\tau_i\in (t-\varepsilon,t)\)) такие, что
\[
\sup \left\{\left|x^{(\nu)}(t)-\sum_{i=0}^rq_{i,\nu}x(\tau_i)\right| \left|x\in\mathfrak{M} \right.\right\}\lt \varepsilon,
\]
то будет справедливо неравенство
\begin{equation}\label{2.18}
R_{n+2r+2}(\mathfrak{M} ,z)\le r_n(\mathfrak{M} ,z).
\end{equation}
Доказательство. Неравенства (\ref{2.17}) вытекают непосредственно из определения соответствующих величин и того факта, что множество всех квадратурных формул вида (\ref{2.3}) содержится в множестве всех квадратурных формул вида (\ref{2.5}), которое, в свою очередь, включается в множество всех квадратурных формул вида (\ref{2.4}).
Перейдем к доказательству неравенства (\ref{2.18}). Предположим, что это неравенство неверно, то есть, что выполняется соотношение
\begin{equation}\label{2.19}
R_{n+2r+2}(\mathfrak{M} ,z)> r_n(\mathfrak{M} ,z).
\end{equation}
Тогда найдется квадратурная формула вида (\ref{2.4}) (то есть найдутся \(\Delta^\star_n\), \(A^\star_r\), \(B^\star_r\) и \(C^\star_n\)) такие, что
\begin{equation}\label{2.20}
r(\mathfrak{M} ,z, A^\star_r, B^\star_r, C^\star_n,\Delta^\star_n)+\varepsilon\lt R_{n+2r+2}(\mathfrak{M} ,z).
\end{equation}
Из условия теоремы \ref{2.5} следует, что для любого положительного \(\varepsilon\) найдутся точки
\(
a\lt \tau_0(a)\lt\ldots\lt\tau_r(a)\lt t^\star_{1,n}
\) и
\(
t^\star_{n-1,n}\lt\tau_0(b)\lt\ldots\lt\tau_r(b)\lt b,
\)
и числа \(q_{\mu,\nu}^j (\mu,\nu=0,1,\ldots,r; j=a,b)\) такие, что
\begin{equation}\label{2.21}
\sup \left\{\left|x^{(\nu)}(j)-\sum_{\mu=0}^rq_{\mu,\nu}^jx(\tau_\mu^j)\right| \left|x\in\mathfrak{M} \right.\right\}\lt\frac{\varepsilon}{M},
\end{equation}
где
\[
M=\sum_{\nu=0}^r|a_\nu|+\sum_{\nu=0}^r|b_\nu|.
\]
Таким образом, формула
\begin{equation}\label{2.22}
\int_a^bz(t)x(t)dt\approx \sum_{\nu=0}^ra^\star_\nu x^{(\nu)}(a)+ \mathfrak{I} (x,C^\star_n,\Delta^\star_n)+\sum_{\nu=0}^rb^\star_\nu x^{(\nu)}(b)\approx
\sum_{\mu=0}^r\left(\sum_{\nu=0}^ra^\star_\nu q^a_{i,\nu}\right) x(\tau_\mu(a))+ \mathfrak{I} (x,C^\star_n,\Delta^\star_n)+\sum_{\mu=0}^r\left(\sum_{\nu=0}^rb^\star_\nu q^b_{i,\nu}\right)x(\tau_\mu(b))
\end{equation}
есть формула вида (\ref{2.3}) с \(n+2r+2\) узлами и, следовательно, погрешность ее на классе \(\mathfrak{M} \) будет не меньше, чем погрешность наилучшей на классе \(\mathfrak{M} \) квадратурной формулы вида (\ref{2.3}), то есть не меньше
\(R_{n+2r+2}(\mathfrak{M} ,z).\)
Учитывая, что
\[
r(x,z, A^\star_r, B^\star_r, C^\star_n,\Delta^\star_n)=
\left|\int_a^bz(t)x(t)dt - \sum_{\nu=0}^ra^\star_\nu x^{(\nu)}(a)- \mathfrak{I} (x,C^\star_n,\Delta^\star_n)-\sum_{\nu=0}^rb^\star_\nu x^{(\nu)}(b)\right|,
\]
из (\ref{2.21}) заключаем, что погрешность квадратурной формулы (\ref{2.22}) строго меньше левой части (\ref{2.19}), что вместе с (\ref{2.20}) приводит к противоречию.
Учитывая тот факт, что при любом \(p\in[1,\infty]\) множество \(W^r_p\) удовлетворяет условию теоремы 3, из теоремы 2 и замечания 1 (при \(\mathfrak{M} =W^r_p\)) немедленно вытекает справедливость следующего утверждения.
Следствие 1.
Пусть \(z-\) произвольная функция из \(L^r\) и \(p\in [1,\infty]\). Тогда для \(r=0,1,\ldots;n=2r+3,\ldots\) имеет место цепочка неравенств
\(
E_{n,r}(z)_p\le \varepsilon_{n,r}(z)_p\le e_{n,r}(z)_p\le E_{n-2r-2,r}(z)_p.
\)
В дальнейшем нам понадобится один глубокий факт из теории квадратурных формул. Доказательство этого утверждения выходит за пределы интересов данной книги, поэтому ограничимся лишь формулировкой.
Теорема 4 (Моторный В.П., Лигун А.А., Женсыкбаев А.А.)
Пусть \(z\equiv 1\). Тогда квадратурная формула вида (\ref{2.5}) на классе \(W^r_p\) существует и единственна, причем
\(
\rho_n(W^r_p,1)=\frac{B_{r,p'}}{n^r}(b-a)^\frac{r+1}{p'},
\)
где
\(
B_{r,p}=\inf\left\{\|D_r-\lambda\|_{p[0,1]}|\lambda\in \mathbb{R}^1\right\}
\)
и \(D_{r+1}(t)\) \(r-\)й 1-периодический, в среднем равный нулю на периоде, интеграл от функции \(D_1(t)=t-1/2\) для \(t\in [0,1]\).
Из теорем 3 и 4 следует, что
\(
\varepsilon_{n,r-1}\left(\frac{(\cdot)^r}{r !}\right)_p=\frac{B_{r,p}}{n^r}(b-a)^\frac{r+1}{p}.
\)
Отсюда и из следствия 1 получаем
Следствие 2.
Пусть \(r=1,2,\ldots;n=2r+3,\ldots\), тогда
\[
\frac{B_{r,p}}{(n+2r+2)^r}(b-a)^\frac{r+1}{p}\le E_{n,r-1}\left(\frac{(\cdot)^r}{r !}\right)_p\le\frac{B_{r,p}}{n^r}(b-a)^\frac{r+1}{p},
\]
\[
\frac{B_{r,p}}{n^r}(b-a)^\frac{r+1}{p}\le e_{n,r-1}\left(\frac{(\cdot)^r}{r !}\right)_p\le\frac{B_{r,p}}{(n-2r-2)^r}(b-a)^\frac{r+1}{p}.
\]
Оптимальный выбор узлов при приближении функций эрмитовыми сплайнами
Далее мы рассмотрим вопрос выбора последовательности асимптотически оптимальных разбиений (см. определение 1) при приближении функций эрмитовыми сплайнами. Отметим как положительные, так и отрицательные стороны этих сплайнов. Большим преимуществом эрмитовых сплайнов является тот факт, что их можно записать в явном виде на каждом промежутке, что существенно упрощает работу с ними. Основным недостатком является их малая гладкость и то, что явный вид некоторых эрмитовых сплайнов предполагает знание производной приближаемой функции в узлах. Заметим, что этот недостаток можно компенсировать, рассмотрев вместо производной функции в узлах, ее разделенные разности.
Теорема 5.
Пусть \(r=1,2,3\), \(p\in (0,\infty]\) и \(x\in L^{r+1}_\infty\) такова, что \(x^{(r+1)}\) обращается в ноль на конечном числе отрезков или точек из \([a,b]\). Тогда при \(n\to\infty\)
\[
EP_{r,n}(x)_p=\frac{\Theta_{r,p}}{n^{r+1}}\|x^{(r+1)}\|_\alpha+o\left(\frac{1}{n^{r+1}}\right),
\]
где для \(p\in(0,\infty)\)
\[
\Theta_{r,p}=\cases{
\frac{1}{2!}\left(\int_0^1t^p(1-t)^pdt\right)^\frac{1}{p} (r=1),\cr
\frac{1}{3!}\left(\int_0^1t^p(1-t)^p(1/2-t)^pdt\right)^\frac{1}{p} (r=2),\cr
\frac{1}{4!}\left(\int_0^1t^{2p}(1-t)^{2p}dt\right)^\frac{1}{p} (r=3),
}
\]
и для \(p=\infty\) эта константа равна
\(
\Theta_{r,\infty}=\frac{1}{2^{r+1}(r+1)!},
\)
здесь
\[
\alpha=\cases{
(r+1+1/p)^{-1} (p\in (0,\infty)),\cr
(r+1)^{-1} (p=\infty).
}
\]
Доказательство. Из (\ref{1.8}) ясно, что для \(t\in [t_{i-1,n},t_{i,n}]\)
\[
x(t)-P_1(x,\Delta_n,t)=x(t)-x_{i-1,n}(1-\tau)-x_{i,n}\tau=
(x(t)-x_{i-1,n})(1-\tau)+(x(t)-x_{i,n})\tau=
\]
\[
=(1-\tau)\int_{t_{i-1,n}}^tx'(u)du-\tau\int^{t_{i,n}}_tx'(u)du=\int_{t_{i-1,n}}^{t_{i,n}}\mathcal{K}(t,u)x'(u)du,
\]
где
\[
\mathcal{K} (t,u)=\cases{
(1-\tau),(u\in [t_{i-1,n},t]),\cr
-\tau, (u\in (t,t_{i,n}]).
}
\]
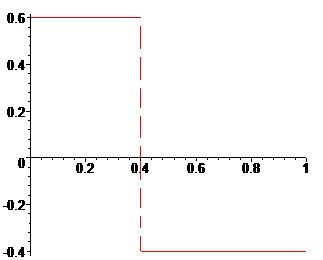График \(\mathcal{K} (t,u)\) для \(\tau=0.4.\)
Интегрируя последнее соотношение по частям и учитывая, что \(\mathcal{K} (t,u)\) (как функция от \(u\)) в среднем равна нулю на \([t_{i-1,n},t_{i,n}]\), убеждаемся, что для \(t\in [t_{i-1,n},t_{i,n}]\)
\[
x(t)-P_1(x,\Delta_n,t)=\int_{t_{i-1,n}}^{t_{i,n}}\mathcal{K}_1(t,u)x''(u)du,
\]
где
\[
\mathcal{K}_1 (t,u)=\cases{
(u-t_{i-1,n})(1-\tau),(u\in [t_{i-1,n},t]),\cr
-(u-t_{i,n})\tau, (u\in (t,t_{i,n}]).
}
\]
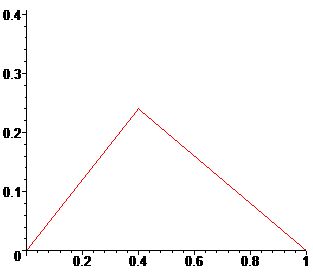
График \(\mathcal{K}_1 (t,u)\) для \(\tau=0.4.\)
Аналогично, с помощью интегрирования по частям, легко проверить, что для \(t\in [t_{i-1,n},t_{i,n}]\) при \(r=1,2,3\)
\begin{equation}\label{3.1}
\delta_{r,i}(t)
\stackrel{\mathrm{\Delta}}{=}
x(t)-P_r(x,\Delta_n,t)=\int_{t_{i-1,n}}^{t_{i,n}}\mathcal{K}_r(t,u)x^{(r+1)}(u)du,
\end{equation}
где, в случае, когда \(t\in[t_{i-1/2,n},t_{i,n}]\)
\[
\mathcal{K}_2(t,u)=\cases{
(\tau-1/2)(\tau-1)(u-t_{i-1,n})^2, (u\in [t_{i-1,n},t_{i-1/2,n}]),\cr
(1-\tau)(\tau+1/2)(u-t_{i,n})^2+(\tau-1/2)(\tau-1)(u-t_{i,n})h_{i-1/2,n}+\frac{1}{4}(\tau-1/2)(\tau-1)h^2_{i-1/2,n}, (u\in[t_{i-1/2,n},t)),\cr
(\tau-1/2)\tau(u-t_{i,n})^2, (u\in [t,t_{i,n}]),
}
\]
а для \(t\in[t_{i-1,n},t_{i-1/2,n}]\) ядро \(\mathcal{K}_2(t,u)\) определяется аналогично и
\[
\mathcal{K}_3(t,u)=\cases{
\frac{1}{3!}(1-\tau)^2(1+2\tau)(u-t_{i-1,n})^3-\frac{1}{2}h_{i-1/2,n}\tau(1-\tau)^2(u-t_{i-1,n})^2, (u\in [t_{i-1,n},t]),\cr
\frac{1}{3!}(2\tau-3)\tau^2(u-t_{i,n})^3-\frac{1}{2}h_{i,n}\tau^2(1-\tau)(u-t_{i,n})^2, (u\in (t,t_{i,n}]),
}
\]
где \(\tau\) определено в (\ref{1.5}).
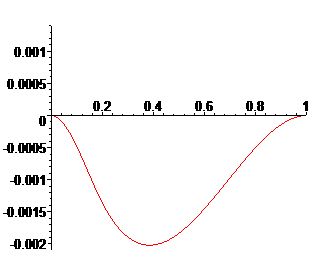
График \(\mathcal{K}_3(t,u)\) для \(\tau=0.2.\)
Эти же ядра можно выписать, используя формулу Тейлора.
Непосредственно поверяется, что для любого \(t\in[t_{i-1,n},t_{i,n}]\) функция \(\mathcal{K}_r(t,u)\) \((r=1,2,3)\) знакопостоянна на промежутке \([t_{i-1,n},t_{i,n}]\) и, следовательно,
\begin{equation}\label{3.2}
m^-_{i,r}|\mathcal{K}_r(t)|\le|\delta_{i,r}(t)|\le m^+_{i,r}|\mathcal{K}_r(t)|,
\end{equation}
где
\[
\mathcal{K}_r(t)=\int_{t_{i-1,n}}^{t_{i,n}}\mathcal{K}_r(t,u)du
\]
и
\[
m^-_{i,r}=\min\left\{\left|x^{(r+1)}(t)\right| |t\in[t_{i-1,n},t_{i,n}]\right\},
\]
\[
m^+_{i,r}=\max\left\{\left|x^{(r+1)}(t)\right| |t\in[t_{i-1,n},t_{i,n}]\right\}.
\]
Полагая в равенстве (\ref{3.1}) \(x(t)=\frac{t^{r+1}}{(r+1)!}\), получим
\begin{equation}\label{3.3}
\mathcal{K}_r(t)=\int_{t_{i-1,n}}^{t_{i,n}}\mathcal{K}_r(t,u)du=\frac{t^{r+1}}{(r+1)!}-P_r\left(\frac{(\cdot)^{r+1}}{(r+1)!},\Delta_n,t\right).
\end{equation}
Легко убедиться в том, что
\begin{equation}\label{3.4}
\mathcal{K}_r(t)=\cases{
\frac{1}{2!}(t-t_{i-1,n})(t_{i,n}-t), (r=1),\cr
\frac{1}{3!}(t-t_{i-1,n})(t-t_{i-1/2,n})(t_{i,n}-t), (r=2),\cr
\frac{1}{4!}(t-t_{i-1,n})^2(t_{i,n}-t)^2, (r=3).
}
\end{equation}
 |  |  |
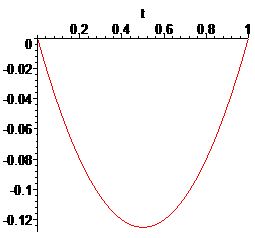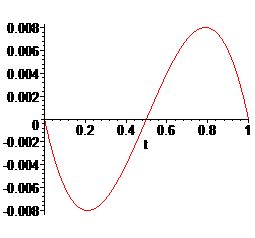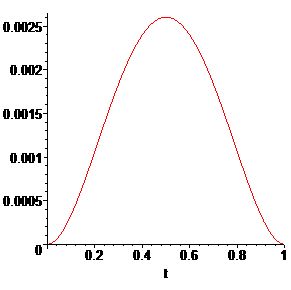| График \(\mathcal{K}_1(t)\) | График \(\mathcal{K}_2(t)\) | График \(\mathcal{K}_3(t)\) |
Используя замену переменных, \(z=t-t_{i-1,n}\), получаем
\(
\|\mathcal{K}_r(\cdot)\|_{p[t_{i-1,n},t_{i,n}]}=\Theta_{r,p}h^{1/\alpha}_{i-1/2,n}.
\)
Отсюда и из (\ref{3.2}) имеем
\begin{equation}\label{3.5}
\Theta_{r,p}m^-_{i,r}h^{1/\alpha}_{i,n}\le\|\delta_{i,r}\|_{p[t_{i-1,n},t_{i,n}]}\le \Theta_{r,p}m^+_{i,r}h^{1/\alpha}_{i-1/2,n}.
\end{equation}
Следовательно, для \(p\in (0,\infty)\)
\[
\|x-P_r(x,\Delta_n)\|^p_p\ge \Theta^p_{r,p}\sum_{i=1}^n\left|m^-_{i,n}h^{1/\alpha}_{i-1/2,n}\right|^p=
\Theta^p_{r,p}\sum_{i=1}^n\left(\int_{t_{i-1,n}}^{t_{i,n}}\left|y^-_{i,n}(t)\right|^\alpha dt\right)^{p/\alpha},
\]
где \(y^-_{i,n}(t)\) - кусочно-постоянная функция, равная \(m^-_{i,n}\) для \(t\in[t_{i-1,n},t_{i,n}]\).
Далее нам нужно следующее вспомогательное утверждение.
Лемма 2.
Для любого \(n=1,2,\ldots\) и \(\alpha\gt 1\) при условиях
\begin{equation}\label{3.6}
A_i\ge 0,\sum_{i=1}^nA_i=\mathcal{A}
\end{equation}
справедливо соотношение
\[
\min\left\{\sum_{i=1}^nA^\alpha_i|A_i\right\}=\frac{\mathcal{A}^\alpha}{n^{\alpha-1}},
\]
причем минимум правой части достигается при \(A^*_i=\frac{\mathcal{A}}{n}\).
Доказательство леммы будем проводить с использованием метода неопределенных множителей Лагранжа (см., например, [15]).
Составим функцию Лагранжа
\[
\mathcal{L}(\lambda,A_1,\ldots,A_n)=\sum_{i=1}^nA^\alpha_i-\lambda\left(\sum_{i=1}^nA_i-\mathcal{A}\right).
\]
Дифференцируя ее по \(A_i\) \((i=1,\ldots,n)\) и приравнивая нулю, получим систему уравнений
\[
\frac{\partial}{\partial A_i}\mathcal{L}(\lambda,A_1,\ldots,A_n)=-\lambda+\alpha A^{\alpha-1}_i=0, (i=1,\ldots,n).
\]
Решением этой системы является
\(
A^*_i=\left(\frac{\lambda}{\alpha}\right)^{\frac{1}{\alpha-1}} (i=1,\ldots,n).
\)
Отсюда, используя условие (\ref{3.6}), получаем, что
\(
A^*_i=\frac{\mathcal{A}}{n} (i=1,\ldots,n)
\)
и тогда экстремальное значение задачи будет равно
\[
\sum_{i=1}^n\left(A^*_i\right)^\alpha=\sum_{i=1}^n\frac{\mathcal{A}}{n^\alpha}=\frac{\mathcal{A}}{n^{\alpha-1}},
\]
что и является минимумом рассматриваемой величины.
Из этой леммы следует, что для любой функции \(y\in C\) и произвольного набора \(t_i\in [a,b]\), для любого \(\beta\in (0,\infty)\) выполняется неравенство
\begin{equation}\label{3.7}
\sum_{i=1}^n\left(\int_{t_{i-1}}^{t_{i}}\left|y(t)\right|dt\right)^{\beta+1}\ge \frac{1}{n^\beta}\left(\int_a^b\left|y(t)\right|dt\right)^{\beta+1},
\end{equation}
следовательно, для любого разбиения \(\Delta_n\)
\begin{equation}\label{3.8}
\|x-P_r(x,\Delta_n)\|_p\ge \Theta_{r,p}\frac{1}{n^{r+1}}\left(\int_a^b\left|y^-_{n,r}(t)\right|^\alpha dt\right)^{1/\alpha}.
\end{equation}
Пусть, теперь \(p=\infty\). Из (\ref{3.5}) получаем
\[
\|x-P_r(x,\Delta_n)\|_\infty\ge
\Theta_{r,\infty}\max\left\{\left(h_{i-1/2,n}\left|m^-_{i,r}\right|^{\frac{1}{r+1}}\right)^{r+1}|i=1,\ldots,n\right\}=
\Theta_{r,\infty}\max\left\{\left(\int_{t_{i-1,n}}^{t_{i,n}}\left|y^-_{n,r}(t)\right|^\alpha dt\right)^{1/\alpha}|i=1,\ldots,n\right\},
\]
где функция \(y^-_{n,r}(t)\) определена ранее.
Очевидно следующее экстремальное соотношение.
Лемма 3.
Для любого \(n=1,2,\ldots\) и \(\alpha>1\) при условиях
\(
A_i\ge 0,\sum_{i=1}^nA_i=\mathcal{A}
\)
справедливо соотношение
\(
\min\left\{\max\left\{A^\alpha_i|i=1,\ldots,n\right\}|A_i\right\}=\frac{\mathcal{A}^\alpha}{n^{\alpha}},
\)
причем минимум правой части достигается при \(A^*_i=\frac{\mathcal{A}}{n}\).
Отсюда и из предыдущего, имеем
\[
\|x-P_r(x,\Delta_n)\|_\infty\ge
\frac{\Theta_{r,\infty}}{n^{r+1}}\left(\int_a^b\left|y^-_{n,r}(t)\right|^\alpha dt\right)^{1/\alpha}.
\]
Таким образом, неравенство (\ref{3.8}) справедливо для \(p\in (0,\infty]\).
Ясно, что если при \(n\to\infty\)
\[
\int_a^b\left|y^-_{n,r}(t)\right|^\alpha dt \not{\to} \int_a^b\left|x^{(r+1)}(t)\right|^\alpha dt,
\]
то
\(
\|x-P_r(x,\Delta_n)\|_p \not{\to} 0 (p\in (0,\infty]).
\)
Учитывая это замечание, перейдем в (\ref{3.8}) к нижней грани по всем разбиениям, в результате чего, получим
\begin{equation}\label{3.9}
EP_{r,n}(x)_p\ge \frac{\Theta_{r,p}}{n^{r+1}}\|x^{(r+1)}\|_\alpha (1+o(1)).
\end{equation}
Этим неравенством заканчивается доказательство оценки снизу.
Перейдем к доказательству оценки сверху.
Пусть \(z_n(t) - \) произвольная последовательность функций, такая, что при \(n\to\infty\)
\begin{equation}\label{3.10}
\|z_n-x^{(r+1)}\|_\infty\le\sigma_n,
\end{equation}
где
\[
\sigma_n=\frac{1}{n^\gamma}\left(1-\frac{2\mathcal{A}\|x^{(r+2)}\|_C}{n^{(r+1)\alpha+2}}\right), \mathcal{A}=\int_a^b|x^{(r+1)}(t)|^\alpha dt,\gamma=((r+2)\alpha+2)^{-1}.
\]
Выберем узлы \(t^*_{i,n}\) из условия
\begin{equation}\label{3.11}
\int_a^{t^*_{i,n}}\left(|z_n(t)|+\frac{1}{n^\gamma}\right)^\alpha dt=\frac{i}{n}\mathcal{A}_n, (i=0,\ldots,n),
\end{equation}
где
\[
\mathcal{A}_n=\int_a^b\left(|z_n(t)|+\frac{1}{n^\gamma}\right)^\alpha dt.
\]
Тогда
\begin{equation}\label{3.12}
\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|z_n(t)|+\frac{1}{n^\gamma}\right)^\alpha dt=\frac{i}{n}\mathcal{A}_n, (i=0,\ldots,n),
\end{equation}
Учитывая, что \(\mathcal{A}_n\to \mathcal{A}\) при \(n\to\infty\), получаем, что при достаточно больших \(n\) будут выполняться неравенства
\begin{equation}\label{3.13}
h_{i+1/2,n}\le\frac{\mathcal{A}_n}{n^{1-\alpha\gamma}}\le \frac{2\mathcal{A}}{n^{1-\alpha\gamma}}.
\end{equation}
Из (\ref{3.5}), используя (\ref{3.10}) и (\ref{3.13}), получаем для \(p\in (0,\infty)\)
\[
\delta_{i,r,p}
\stackrel{\mathrm{\Delta}}{=}
\int_{t^*_{i-1,n}}^{t^*_{i,n}}|x(t)-P_r(x,\Delta^*_n,t)|^pdt\le \Theta^p_{r,p}\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}|m^+_{i,r}|dt\right)^{\frac{p}{\alpha}}.
\]
Отсюда и из того, что
\(
m^+_{i,r}=\max\left\{\left|x^{(r+1)}(t)\right| |t\in [t^*_{i-1,n},t^*_{i,n}]\right\}=\left|x^{(r+1)}(t)+x^{(r+2)}(\xi)(t^*_{i,n}-t)\right|,
\)
получаем
\[
\delta_{i,r,p}\le
\Theta^p_{r,p}\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|x^{(r+1)}(t)|+\|x^{(r+2)}\|_\infty h^*_{i-1/2,n}\right)^\alpha dt\right)^{\frac{p}{\alpha}}\le
\Theta^p_{r,p}\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|z_n(t)|+\sigma_n+\frac{2\mathcal{A}\|x^{(r+2)}\|_\infty}{n^{1-\alpha\gamma}}\right)^\alpha dt\right)^{\frac{p}{\alpha}}=
\Theta^p_{r,p}\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|z_n(t)|+\frac{1}{n^\gamma}\right)^\alpha dt\right)^{\frac{p}{\alpha}}.
\]
Используя (\ref{3.12}), отсюда получаем
\(
\delta_{i,r,p}\le \Theta^p_{r,p}\left(\frac{\mathcal{A}_n}{n}\right)^{\frac{p}{\alpha}},
\)
cледовательно,
\begin{equation}\label{3.14}
\|x-P_r(x,\Delta^*_n)\|_p=\left(\sum_{i=1}^n\delta_{i,r,p}\right)^{\frac{1}{p}}\le
\Theta_{r,p}\frac{\mathcal{A}^{\frac{1}{\alpha}}}{n^{r+1}}
\end{equation}
и для \(p=\infty\)
\[
\|x-P_r(x,\Delta^*_n)\|_\infty\le
\Theta_{r,p}\max_i\left\{\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|x^{(r+1)}(t)|+\|x^{(r+2)}\|_\infty h^*_{i-1/2,n}\right)^\alpha dt\right)^{\frac{1}{\alpha}}\right\}\le
\Theta_{r,\infty}\max_i\left\{\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|z_n(t)|+\sigma_n+\frac{2\mathcal{A}\|x^{(r+2)}\|_\infty}{n^{1-\alpha\gamma}}\right)^\alpha dt\right)^{\frac{1}{\alpha}}\right\}=
\Theta_{r,\infty}\max_i\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|z_n(t)|+\frac{1}{n^\gamma}\right)^\alpha dt.
\]
Отсюда и из (\ref{3.12}) получаем
\begin{equation}\label{3.15}
\|x-P_r(x,\Delta^*_n)\|_\infty\le \Theta_{r,\infty}\max_i\left\{\left(\frac{\mathcal{A}_n}{n}\right)^\alpha |i=1,\ldots,n\right\}=\frac{\Theta_{r,\infty}}{n^{r+1}}\mathcal{A}_n^{1/\alpha}.
\end{equation}
Из (\ref{3.14}) и (\ref{3.15}) с учетом того, что при \(n\to\infty\) будет \(\mathcal{A}_n\to \mathcal{A}\) и для всех \(p\in (0,\infty]\) следует
\[
EP_{r,n}(x)_p\le \|x-P_r(x,\Delta^*_n)\|_\infty\le \frac{\Theta_{r,\infty}}{n^{r+1}}\|x^{(r+1)}\|_\alpha (1+o(1)).
\]
Отсюда и из (\ref{3.9}) сразу получаем утверждение теоремы.
Следующая теорема дает простой алгоритм асимптотически оптимального выбора узлов при приближении функций, у которых \(x^{(r+1)}(t)\) отделена от нуля, то есть \(|x^{(r+1)}(t)|>\varepsilon>0\) \(t\in [a,b]\).
Теорема 6.
Пусть \(r=1,2,3\), \(p\in (0,\infty]\) и функция \(x\in L^{r+2}_\infty\) такова, что \(x^{(r+1)}\ne 0\) \((t\in [a,b])\).
Тогда последовательность разбиений \(\left\{\Delta^*_n\right\}_{n=1}^\infty=\left\{\left\{t^*_{i,n}\right\}_{i=0}^n\right\}_{n=1}^\infty\), определяемая из равенств
\begin{equation}\label{3.16}
\int_a^{t^*_{i,n}}|z_n(t)|^\alpha dt=\frac{i}{n}\int_a^b|z_n(t)|^\alpha dt (i=0,\ldots,n),
\end{equation}
где \(z_n - \) произвольная последовательность функций, сходящихся к \(x^{(r+1)}\) в метрике пространства \(L_\infty,\) будет асимптотически оптимальной, причем
\[
\|x-P_r(x,\Delta^*_n)\|_p =\frac{\Theta_{r,p}}{n^{r+1}}\|x^{(r+1)}\|_\alpha (1+o(1)),
\]
где \(\alpha\) и \(\Theta_{r,p}\) те же, что и в теореме 5.
Доказательство. Ясно, что для доказательства достаточно провести оценку сверху. Пусть, сначала, \(p\in (0.\infty)\) и \(y'_{n,r}(t)\) кусочно-постоянная
функция, равная \(\max\left\{|x^{(r+1)}(t)| |t\in [t^*_{i-1,n},t^*_{i,n}]\right\}\) для \(t\in [t^*_{i-1,n},t^*_{i,n}]\).
Положим
\(
\omega_n=\|y^+_{n,r}-x^{(r+1)}\|_\infty+\|x^{(r+1)}-z_n\|_\infty.
\)
Тогда из (\ref{3.5}) легко получаем
\[
\delta_{i,r,p}
\stackrel{\mathrm{\Delta}}{=}
\int_{t^*_{i-1,n}}^{t^*_{i,n}}|x(t)-P_r(x,\Delta^*_n,t)|^pdt\le \Theta^p_{r,p}\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}|y^+_{n,r}(t)|^\alpha dt\right)^{\frac{p}{\alpha}}\le
\Theta^p_{r,p}\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(z_n(t)+\omega_n\right)^\alpha dt\right)^{\frac{p}{\alpha}}.
\]
Отсюда и из неравенства Минковского (см., например, [20] с.178) для всех \(q\in (0,1)\), \(x,y\in L\)
\begin{equation}\label{3.17}
\int_a^b|x(t)+y(t)|^qdt\le\int_a^b\left(|x(t)|^q+|y(t)|^q\right)dt
\end{equation}
получаем
\begin{equation}\label{3.18}
\delta_{i,r,p}\le \Theta^p_{r,p}\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}|z_n(t)|^\alpha dt+h^*_{i-1/2,n}\omega_n^\alpha \right)^{\frac{p}{\alpha}}.
\end{equation}
Из (\ref{3.16}) следует, что
\begin{equation}\label{3.19}
\int_{t^*_{i-1,n}}^{t^*_{i,n}}|z_n(t)|^\alpha dt=\frac{\mathcal{A}_n}{n}\stackrel{\mathrm{\Delta}}{=}\frac{1}{n}\int_a^b|z_n(t)|^\alpha dt,
\end{equation}
кроме того, при \(n\to\infty\) имеем
\(
\|z_n-x^{(r+1)}\|_\infty\to 0.
\)
Следовательно, найдется такое число \(\zeta\), что почти всюду на \([a,b]\) будет выполняться неравенство
\begin{equation}\label{3.20}
|z_n(t)|^\alpha>\zeta>0.
\end{equation}
Отсюда и из (\ref{3.19}) получаем
\begin{equation}\label{3.21}
h^*_{i-1/2,n}\le\frac{\mathcal{A}_n}{n\zeta} (i=1,\ldots,n).
\end{equation}
С учетом этого неравенства из (\ref{3.18}) следует
\[
\delta_{i,r,p}\le\Theta^p_{r,p}\left(\frac{\mathcal{A}_n}{n}+\frac{\mathcal{A}_n}{n\zeta}\omega_n^\alpha\right)^{\frac{p}{\alpha}}=
\Theta^p_{r,p}\left(\frac{\mathcal{A}_n}{n}\right)^{\frac{p}{\alpha}}\left(1+\frac{\omega_n^\alpha}{\zeta}\right)^{\frac{p}{\alpha}},
\]
следовательно,
\[
EP_{r,n}(x)_p\le\|x-P_r(x,\Delta^*_n)\|_p\le \left(\sum_{i=1}^n\delta_{i,r,p}\right)^{\frac{1}{p}}=
n^{\frac{1}{p}}\Theta_{r,p}\left(\frac{\mathcal{A}_n}{n}\right)^{\frac{1}{\alpha}}\left(1+\frac{\omega_n^\alpha}{\zeta}\right)^{\frac{1}{\alpha}}=
\Theta_{r,p}\frac{\mathcal{A}^{\frac{1}{\alpha}}_n}{n^{r+1}}\left(1+\frac{\omega_n^\alpha}{\zeta}\right)^{\frac{1}{\alpha}}.
\]
Остается заметить, что в силу условия теоремы при \(n\to\infty\) имеем
\(
\mathcal{A}^{\frac{1}{\alpha}}_n\to\|x^{(r+1)}\|_\alpha,\omega_n\to 0,
\)
что вместе с утверждением теоремы 5 и завершает доказательство теоремы 6 для \(p\in (0,\infty)\). Для \(p=\infty\) доказательство проводится
аналогично (см. оценку сверху в теореме 5).
Данная теорема позволяет строить численные алгоритмы асимптотически оптимальной последовательности разбиений при приближении функций эрмитовыми сплайнами.
Приведем один из таких алгоритмов для интерполяционных ломаных.
Выберем \(N\ll n\) и \(N\to\infty\). Вычислим значения функции \(x(t)\) в точках разбиения \(\Delta^0_n=\left\{\tau_{i,N}\right\}_{i=0}^N\), где \(\tau_{i,N}=a+iH\) и \(H=\frac{b-a}{N}\), затем найдем вторые разделенные разности от функции \(x\) в точках \(\tau_{i,N}\)
\[
\Delta^2x_i=\frac{1}{H^2}(x(\tau_{i-1,N})-2x(\tau_{i,N})+x(\tau_{i+1,N})),
\]
а через \(z_N(t)\) обозначим кусочно-постоянную функцию, принимающую значения
\[
z_N(t)=\cases{
\Delta^2x_1,\left(t\in \left[a,a+\frac{3}{2}H\right]\right),\cr
\Delta^2x_i,\left(t\in \left[\tau_{i,N}-\frac{1}{2}H,\tau_{i,N}+\frac{1}{2}H\right]\right),i=1,\ldots,N-2\cr
\Delta^2x_{N-1},\left(t\in \left[b-\frac{3}{2}H,b\right]\right).}
\]
Ясно, что \(z_N(t)\) является формальной производной от \(s_1(x,\Delta^0_N)\), где \(s_1(x,\Delta^0_N)=P_1(x,\Delta^0_N)\), то есть, ломаная с узлами \(\tau_{i,N}\) \((i=0,\ldots,N)\), интерполирующая функцию \(x\) в узлах.
Затем выберем узлы \(t^*_{i,n}\) из условия (\ref{3.16}). Тогда последовательность ломаных \(\left\{s_1(x,\Delta^*_n)\right\}_{n=1}^\infty\) будет асимптотически оптимальной для функции \(x\) (такой, что \(x''(t)\ne 0\) \(t\in [a,b]\)) в метрике пространства \(L_p(p\in (0,\infty])\).
Можно показать, что если \(x(t)\) такова, что \(x''(t)\) имеем на \([a,b]\) лишь простые нули, то этот алгоритм будет давать также асимптотически
оптимальную последовательность ломаных. В том случае, когда \(x''(t)\) имеет либо нули большой кратности, либо \(x''(t)\) близка к нулю на
множестве меры отличной от нуля, то можно рекомендовать (см. теорему 5) делать выбор узлов не по функции \(z_N\), а по \(z^*_N(t)\stackrel{\mathrm{\Delta}}{=} z_N(t)+n^{-\gamma}\).
Теорема 7.
Пусть \(p\in (0,\infty)\) и функция \(x\in C^4\) такова, что \(x''(t)\ne 0\) \((t\in [a,b])\).
Тогда при \(n\to\infty\) последовательность разбиений, определяемая из равенств
\begin{equation}\label{3.22}
\int_a^{t^*_{i,n}}|x''(t)|^\alpha dt=\frac{i}{n}\int_a^b|x''(t)|^\alpha dt, i=0,\ldots,n;\alpha=\left(2+p^{-1}\right)^{-1},
\end{equation}
будет асимптотически оптимальной, причем
\[
\|x-P_1(x,\Delta^*_n)\|_p =\frac{\Theta_{1,p}}{n^2}\|x''\|_\alpha +O\left(\frac{1}{n^4}\right).
\]
Доказательство. Используя формулу Тейлора, получаем
\[
x(t)=x_{i-1/2,n}+x'_{i-1/2,n}h_{i-1/2,n}\left(\frac{1}{2}-\tau\right)+\frac{1}{2}x''_{i-1/2,n}h^2_{i-1/2,n}\left(\frac{1}{2}-\tau\right)^2+
\frac{1}{6}x'''_{i-1/2,n}h^3_{i-1/2,n}\left(\frac{1}{2}-\tau\right)^3+O\left(h^4_{i-1/2,n}\right),
\]
\[
x_{i-1,n}=x_{i-1/2,n}+x'_{i-1/2,n}\frac{h_{i-1/2,n}}{2}+\frac{1}{8}x''_{i-1/2,n}h^2_{i-1/2,n}+\frac{1}{48}x'''_{i-1/2,n}h^3_{i-1/2,n}+O\left(h^4_{i-1/2,n}\right),
\]
\[
x_{i,n}=x_{i-1/2,n}-\frac{1}{2}x'_{i-1/2,n}h_{i-1/2,n}+\frac{1}{8}x''_{i-1/2,n}h^2_{i-1/2,n}-\frac{1}{48}x'''_{i-1/2,n}h^3_{i-1/2,n}+O\left(h^4_{i-1/2,n}\right).
\]
Отсюда и из (\ref{1.8}) имеем
\[
x(t)-P_1(x,\Delta_n,t)=
\frac{1}{2}x''_{i-1/2,n}h^2_{i-1/2,n}\tau(\tau-1)-\frac{1}{12}x''_{i-1/2,n}h^3_{i-1/2,n}\tau(1-3\tau+2\tau^2)+O(h^4_{i-1/2,n})=
\]
\[
=\frac{1}{12}x''_{i-1/2,n}h^2_{i-1/2,n}\tau(\tau-1)\left(1+\frac{1}{6}a_{i,n}h_{i-1/2,n}(1-2\tau)\right)\left(1+O(h^2_{i-1/2,n})\right),
\]
где \(a_{i,n}=\frac{x'''_{i,n}}{x''_{i,n}}\lt \infty.\)
Следовательно,
\begin{equation}\label{3.23}
\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left|x(t)-P_1(x,\Delta^*_n,t)\right|^pdt=
\frac{1}{2^p}\left(x''_{i-1/2,n}\right)^ph^{2p+1}_{i-1/2,n}\int_0^1\tau^p(\tau-1)^p
\left(1+\frac{1}{6}a_{i,n}h_{i-1/2,n}(1-2\tau)\right)^pdt\times\left(1+O(h^2_{i-1/2,n})\right)^p.
\end{equation}
Кроме того,
\[
\left(1+\frac{1}{6}a_{i,n}h_{i-1/2,n}(1-2\tau)\right)^p=1+\frac{p}{6}a_{i,n}h_{i-1/2,n}(1-2\tau)+O(h^2_{i-1/2,n}),
\]
а так как \(x''(t)\ne 0 \) при \(t\in [a,b]\), то
\[
|x''_{i-1/2,n}|^\alpha h_{i-1/2,n}=\int_{t_{i-1,n}}^{t_{i,n}}|x''(t)|^\alpha dt+O(h^3_{i-1/2,n}).
\]
Отсюда и из (\ref{3.23}) получаем
\[
\delta_{i,1,p}=\Theta^p_{1,p}\left(\int_{t_{i-1,n}}^{t_{i,n}}|x''(t)|^\alpha dt\right)^{\frac{p}{\alpha}}\left(1+O(h^2_{i-1/2,n})\right)^{p+2}.
\]
Замечая, что
\(
\int_0^1\tau^p(\tau-1)^p(1-2\tau)dt=0,
\)
получаем
\[
\|x-P_1(x,\Delta^*_n)\|_p=\Theta_{1,p}\left(\sum_{i=1}^n\left(\int_{t_{i-1,n}}^{t_{i,n}}|x''(t)|^\alpha dt\right)^{\frac{p}{\alpha}}\right)^{\frac{1}{p}}\left(1+O(h^2_{i-1/2,n})\right).
\]
Для завершения доказательства остается учесть выбор узлов (\ref{3.22}) и тот факт, что \(h_{i-1/2,n}=O\left(\frac{1}{n}\right)\).
Некоторые сведения об интерполяционных сплайнах.
В этом разделе мы получим оценки уклонения интерполяционных сплайнов минимального дефекта от эрмитовых сплайнов, рассмотренных ранее, а также, приведем оценки уклонения интерполяционных сплайнов и его производных от приближаемой функции и, соответственно, от ее производных.
Результаты этого раздела носят, в основном, вспомогательный характер, хотя имеют и самостоятельный интерес.
Теорема 8.
Пусть \(r=2,3\), \(\nu=0,\ldots,r\) и разбиение \(\Delta_n\) таково, что \(|h_{i+1/2,n}-h_{i-1/2,n}|\lt \varepsilon_nh_{i-1/2,n}\) \((\varepsilon_n\in (0,1))\) и пусть
\begin{equation}\label{4.1}
\epsilon_{r,n}=(1+\varepsilon_n)\left(\varepsilon_n\|x^{(r+1)}\|_{C(t_{i-1,n},t_{i,n})}+(2+\varepsilon_n)\|x^{(r+2)}\|_Ch_{i-1/2,n}\right).
\end{equation}
Тогда
\[
\left\|s^{(\nu)}_r(x,\Delta_n)-P^{(\nu)}_r(x,\Delta_n)\right\|_{C(t_{i-1,n},t_{i,n})}\le C_{r,\nu}\epsilon_{r,n}h^{r+1-\nu}_{i-1/2,n},
\]
где \(C_{r,\nu}\) сведены в таблицу
| 0 | 1 | 2 | 3 |
|---|
| 2 | \(\frac{1}{192}\) | \(\frac{1}{6}\) | \(\frac{1}{3}\) | - |
|---|
| 3 | \(\frac{1}{324}\) | \(\frac{1}{72}\) | \(\frac{1}{12}\) | \(\frac{1}{4}\) |
|---|
Доказательство. Рассмотрим, для начала, параболические сплайны с граничными условиями (\ref{1.14}). Ранее была получена система
(\ref{1.23}) для определения коэффициентов интерполяционного параболического сплайна. Если положим
\begin{equation}\label{4.2}
c_{i,n}=m_{i,n}-x_{i,n} (i=0,\ldots,n),
\end{equation}
то эта система запишется в виде
\begin{equation}\label{4.3}
\cases{
3c_{0,n}=0,\cr
\lambda_{i,n}c_{i-1,n}+3c_{i,n}+\mu_{i,n}c_{i+1,n}=d_{i,n} (i=1,\ldots,n-1),\cr
3c_{n,n}=0,
}
\end{equation}
где
\[
d_{i,n}=4\mu_{i,n}x_{i+1/2,n}+4\lambda_{i,n}x_{i-1/2,n}-\lambda_{i,n}x_{i-1,n}-3x_{i,n}-\mu_{i,n}x_{i+1,n}.
\]
Так как \(3-\lambda_{i,n}-\mu_{i,n}=2 (i=1,\ldots,n)\), то система (\ref{4.3}) имеет диагональное преобладание. Отсюда и из леммы Адамара имеем
\(
|c_{i,n}|\le\frac{1}{2}\max\left\{|d_{i,n}||i=1,\ldots,n-1\right\}.
\)
Интегрируя по частям, легко убедиться в том, что
\(
d_{i,n}=\int_{t_{i-1,n}}^{t_{i,n}}\mathcal{K}_2(u)x'''(u)du,
\)
где
\[
\mathcal{K}_2(u)=\cases{
-\frac{1}{2}\lambda_{i,n}(u-t_{i-1,n})^2,(u\in[t_{i-1,n},t_{i-1/2,n}]),\cr
\frac{3}{2}\lambda_{i,n}(u-t_{i-1,n}-\frac{2}{3}h_{i-1/2,n})^2-\frac{1}{6}\lambda_{i,n}h^2_{i-1/2,n},(u\in[t_{i-1/2,n},t_{i,n}]),\cr
-\frac{3}{2}\mu_{i,n}(u-t_{i,n}-\frac{1}{3}h_{i+1/2,n})^2+\frac{1}{6}\mu_{i,n}h^2_{i+1/2,n},(u\in[t_{i,n},t_{i+1/2,n}]),\cr
\frac{1}{2}\mu_{i,n}(u-t_{i+1,n})^2,(u\in[t_{i+1/2,n},t_{i+1,n}]).
}
\]
 |  |
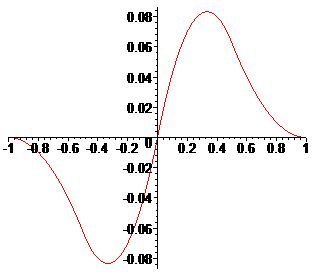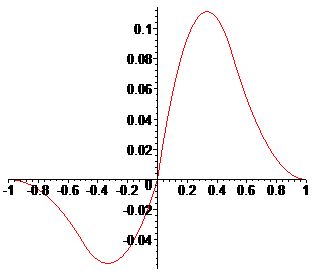| График \(\mathcal{K}_2(u)\) для \(\lambda_{i,n}=\frac{1}{2}\) | График \(\mathcal{K}_2(u)\) для \(\lambda_{i,n}=\frac{1}{3}\) |
Так как для \(u\in [t_{i-1,n},t_{i,n}]\) выполняется соотношение
\(
{\rm sign }{\mathcal{K}_2(u)}={\rm sign }(u-t_{i,n}),
\)
то найдутся точки \(\xi_{i,n}\in [t_{i-1,n},t_{i,n}]\), \(\eta_{i,n}\in [t_{i,n},t_{i+1,n}]\) \((i=1,\ldots,n-1)\) такие, что
\begin{equation}\label{4.4}
d_{i,n}=x'''(\xi_{i,n})\int_{t_{i-1,n}}^{t_{i,n}}\mathcal{K}_2(u)du+x'''(\eta_{i,n})\int_{t_{i,n}}^{t_{i+1,n}}\mathcal{K}_2(u)du=
-\frac{1}{12}\lambda_{i,n}x'''(\xi_{i,n})h^3_{i-1/2,n}+\frac{1}{12}\mu_{i,n}x'''(\eta_{i,n})h^3_{i+1/2,n}\le
\end{equation}
\[
\le\frac{h_{i-1/2,n}h_{i+1/2,n}}{12(h_{i-1/2,n}+h_{i+1/2,n})}\left(|x'''_{i,n}||h^2_{i-1/2,n}-h^2_{i+1/2,n}|+(h^2_{i-1/2,n}+\right.
\left.h^2_{i+1/2,n})h_{i-1/2,n}\|x^{(4)}\|_C\right)\le
\frac{1}{12}\epsilon_{2,n}h^3_{i-1/2,n}.
\]
Далее нам понадобится следующее простое утверждение.
Лемма 4.
Пусть
\[
\Phi_r(a,b,t)=\cases{
a(1-t)(0.5-t)+bt(t-0.5),r=2,\cr
a(1-t)^2t-bt^2(1-t),r=3,
}
\]
тогда справедливы неравенства
\[
\max\left\{\left.\|\Phi^{(\nu)}_2(a,b,\cdot)\|_C\right||a|,|b|\le\delta\right\}\le 12\delta C_{2,\nu}, (\nu=0,1,2)
\]
и
\[
\max\left\{\left.\|\Phi^{(\nu)}_3(a,b,\cdot)\|_C\right||a|,|b|\le\delta\right\}\le 24\delta C_{3,\nu}, (\nu=0,1,2,3),
\]
где \(C_{r,\nu}\) определены в теореме 8.
Для доказательства леммы достаточно решить задачу нахождения экстремума функции \(\Phi^{(\nu)}_r(a,b,t)\) в области
\(
|a|,|b|\le\delta, 0\le t\le 1.
\)
Для завершения доказательства теоремы 8 в случае \(r=2\) достаточно заметить, что из (\ref{1.9}) и (\ref{1.21}) следует
\[
\left\|s^{(\nu)}_2(x,\Delta_n)-P^{(\nu)}_2(x,\Delta_n)\right\|_{C(t_{i-1,n},t_{i,n})}=h^{-\nu}_{i-1/2,n}\|\Phi^{(\nu)}_2(2c_{i-1,n},2c_{i,n},\cdot)\|_C,
\]
и учесть утверждение леммы 4 и соотношение (\ref{4.4}).
Пусть, теперь, \(r=3\). Дальнейшие рассуждения аналогичные предыдущим.
Положим \(c_{i,n}=M_{i,n}-x'_{i,n}\). Тогда систему (\ref{1.25}) можно записать в виде
\begin{equation}\label{4.5}
\cases{
c_{0,n}=0,\cr
\lambda_{i,n}c_{i-1,n}+2c_{i,n}+\mu_{i,n}c_{i+1,n}=d_{i,n} (i=1,\ldots,n-1),\cr
c_{n,n}=0,
}
\end{equation}
где
\[
d_{i,n}=3\left(\mu_{i,n}\frac{x_{i+1,n}-x_{i,n}}{h_{i+1/2,n}}+\lambda_{i,n}\frac{x_{i,n}-x_{i-1,n}}{h_{i-1/2,n}}\right)-\lambda_{i,n}x'_{i-1,n}-2x'_{i,n}-\mu_{i,n}x'_{i+1,n}.
\]
Интегрируя по частям, легко проверить справедливость равенства
\(
d_{i,n}=\int_{t_{i-1,n}}^{t_{i,n}}\mathcal{K}_3(u)x^{(4)}(u)du,
\)
где
\[
\mathcal{K}_3(u)=\cases{
\frac{1}{2h_{i-1/2,n}}\lambda_{i,n}(u-t_{i-1,n})^2(t_{i,n}-u),(u\in[t_{i-1,n},t_{i,n}]),\cr
-\frac{1}{2h_{i+1/2,n}}\mu_{i,n}(u-t_{i,n})(t_{i+1,n}-u)^2,(u\in[t_{i,n},t_{i+1,n}]).
}
\]
 |  |
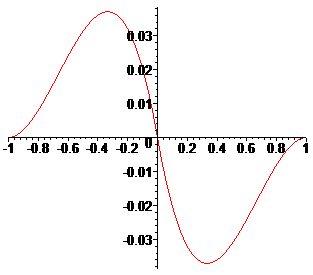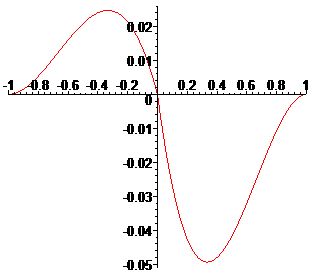| График \(\mathcal{K}_3(u)\) для \(\lambda_{i,n}=\frac{1}{2}\) | График \(\mathcal{K}_3(u)\) для \(\lambda_{i,n}=\frac{1}{3}\) |
Используя далее, так же как для параболических сплайнов, теорему о среднем, получаем
\[
d_{i,n}=\frac{1}{24}\frac{h_{i+1/2,n}h_{i-1/2,n}}{h_{i-1/2,n}+h_{i+1/2,n}}\left(h^2_{i-1/2,n}x^{(4)}(\xi_{i,n})-h^2_{i+1/2,n}x^{(4)}(\eta_{i,n})\right)\le
h_{i+1/2,n}h_{i-1/2,n}\left(|h_{i+1/2,n}-h_{i-1/2,n}||x^{(\nu)}_{i,n}|+
(h_{i+1/2,n}+h_{i-1/2,n})\max\{h_{i+1/2,n},h_{i-1/2,n}\}\|x^{(5)}\|_C\right).
\]
Из равенств (\ref{1.24}) и (\ref{1.11}) следует
\[
\|P_3^{(\nu)}(x,\Delta_n)-s_3^{(\nu)}(x,\Delta_n)\|_{C(t_{i-1,n},t_{i,n})}=h^{-\nu}_{i-1/2,n}\left\|\Phi^{(\nu)}_3(c_{i-1,n},c_{i,n},\cdot)\right\|_C.
\]
Отсюда, из предыдущего и из леммы 4 сразу следует утверждение теоремы.
Докажем еще одну теорему, которая будет нам нужна в дальнейшем.
Теорема 9.
Пусть \(\Delta^0_n=\left\{t^0_i\right\}_{i=0}^n=\left\{a+\frac{b-a}{n}i\right\}_{i=0}^n\). Тогда для любой функции \(x\in C^4\)
\[
\|x^{(\nu)}-s_3^{(\nu)}(x,\Delta^0_n)\|_\infty=O\left(\frac{1}{n^{4-\nu}}\right) (\nu=0,1,2,3).
\]
Доказательство. Сплайн \(s_3(x,\Delta^0_n)\), как было указано ранее, представим в виде (\ref{1.24}), и если \(c_{i,n}=M_{i,n}-x'_{i,n}\), то \(c_{i,n}\) удовлетворяют системе (\ref{4.5}), причем \(h_{i-1/2,n}=\frac{b-a}{n}\) и \(\mu_{i,n}=\lambda_{i,n}=0.5\) для \(i=1,\ldots,n\), кроме того, \(d_{i,n}\) можно записать в виде
\(
d_{i,n}=-\int_{t^0_{i-1}}^{t^0_{i+1}}\mathcal{K}'_3(u)x'''(u)du,
\)
причем
\(
\int_{t^0_{i-1}}^{t^0_{i+1}}\mathcal{K}'_3(u)du=0.
\)
Тогда
\[
d_{i,n}=\int_{t^0_{i-1}}^{t^0_{i+1}}\mathcal{K}'_3(u)(x'''(u)-x'''(t^0_i))du\le
\frac{b-a}{n}\|x^{(4)}\|_C\int_{t^0_{i-1}}^{t^0_{i+1}}|\mathcal{K}'_3(u)|du=\frac{4(b-a)^4}{27n^4}\|x^{(4)}\|_C.
\]
Отсюда и из леммы Адамара сразу получаем
\(
|c_{i,n}|\le\frac{4(b-a)^4}{27n^4}\|x^{(4)}\|_C.
\)
Тогда, используя лемму 4, имеем
\begin{equation}\label{4.8}
\|P_3^{(\nu)}(x,\Delta^0_n)-s_3^{(\nu)}(x,\Delta^0_n)\|_{C(t_{i-1,n},t_{i,n})}=O\left(\frac{1}{n^{4-\nu}}\right).
\end{equation}
Для завершения доказательства остается показать
\(
\|x^{(\nu)}-P_3^{(\nu)}(x,\Delta^0_n)\|_{C(t_{i-1,n},t_{i,n})}=O\left(\frac{1}{n^{4-\nu}}\right).
\)
Докажем это утверждение. Так как функция \(\delta(t)\stackrel{\mathrm{\Delta}}{=}x(t)-P_3(x,\Delta^0_n)\) имеет два кратных нуля в точках \(t_{i-1}\) и \(t_i\), то \(\delta^{(\nu)}(t)\) \((\nu=0,1,2,3)\) имеет, по крайней мере, один нуль на \((t_{i-1},t_i)\) и, следовательно, получаем
\(
\|\delta\|_{C(t_{i-1},t_i)}\le\|\delta'\|_{C(t_{i-1},t_i)}h_{i-1/2,n},
\)
то есть
\(
\|\delta^{(\nu)}\|_{C(t_{i-1},t_i)}\le h^{4-\nu}_{i-1/2,n}\|\delta^{(4)}\|_{C(t_{i-1},t_i)}\le h^{4-\nu}_{i-1/2,n}\|x^{(4)}\|_C.
\)
Отсюда, из (\ref{4.8}) и неравенства треугольника, получаем
\[
\|x^{(\nu)}-s_3^{(\nu)}(x,\Delta^0_n)\|_{C(t_{i-1,n},t_{i,n})}\le \|x^{(\nu)}-P_3^{(\nu)}(x,\Delta^0_n)\|_{C(t_{i-1,n},t_{i,n})}+
\|P_3^{(\nu)}(x,\Delta^0_n)-s_3^{(\nu)}(x,\Delta^0_n)\|_{C(t_{i-1,n},t_{i,n})}=O\left(\frac{1}{n^{4-\nu}}\right).
\]
Оптимальный выбор узлов при приближении функций параболическими сплайнами минимального дефекта
Ранее была рассмотрена задача асимптотически оптимального выбора узлов при приближении функций сплайнами, но при этом были рассмотрены эрмитовые сплайны, которые при всех своих преимуществах (прежде всего это их явный вид и свойство локальности) имеют присущие им недостатки, основным из которых является малая гладкость. Интерполяционный сплайны минимального дефекта избавлены от этого недостатка, но решение задачи асимптотически оптимального выбора узлов для них значительно сложнее, чем для локальных сплайнов.
Теорема 10.
Пусть \(p\in [1,\infty], \alpha=(3+p^{-1})^{-1}\) и \(\gamma=0.2\alpha+3\). Тогда для любой функции \(x\in L^4_\infty\) при \(n\to\infty\) последовательность разбиений \(\left\{\Delta^*_n\right\}_{n=1}^\infty=\left\{\left\{t^*_{i,n}\right\}_{i=0}^n\right\}_{n=1}^\infty\), определяемая из равенств
\begin{equation}\label{5.1}
\int_a^{t^*_{i,n}}\left(|x'''(t)|+\frac{1}{n^\gamma} \right)^\alpha dt=\frac{i}{n}\int_a^b\left(|x'''(t)|+\frac{1}{n^\gamma} \right)^\alpha dt (i=0,\ldots,n),
\end{equation}
будет асимптотически оптимальной для интерполяционных параболических сплайнов и параболических сплайнов наилучшего приближения, при этом
\begin{equation}\label{5.2}
E_{n,2}(x)_p=ES_{2,n}(x)_p(1+o(1))=\frac{B_{3,p}}{n^{3}}\|x'''\|_\alpha (1+o(1))
\end{equation}
где \(B_{3,p}\) введено в теореме 4.
Кроме того, если \(x\in C^4\) такова, что \(|x'''(t)|>0\) \(t\in [a,b]\), то последовательность разбиений, определяемая равенствами
\begin{equation}\label{5.3}
\int_a^{t^*_{i,n}}\left|z_n(t)\right|^\alpha dt=\frac{i}{n}\int_a^b\left|z_n(t)\right|^\alpha dt (i=0,\ldots,n),
\end{equation}
где \(\left\{z_n\right\}_{n=1}^\infty\) любая последовательность функций, такая, что
\(
\|x'''-z_n\|_\infty\to 0,
\)
будет асимптотически оптимальной для интерполяционных параболических сплайнов и параболических сплайнов наилучшего приближения
(то есть, лучшие среди всех параболических сплайнов!!!).
Доказательство. Так как
\(
E_{n,2}(x)_p\le ES_{2,n}(x)_p,
\)
и
\(
ES_{2,n}(x)_p\le \|x-s_2(x,\Delta^*_n)\|_p,
\)
то ясно, что для доказательства соотношения (\ref{5.2}) достаточно показать, что
\begin{equation}\label{5.4}
E_{n,2}(x)_p\ge\frac{B_{3,p}}{n^3}\|x'''\|_\alpha (1+o(1))
\end{equation}
и
\begin{equation}\label{5.5}
\|x-s_2(x,\Delta^*_n)\|_p\le\frac{B_{3,p}}{n^3}\|x'''\|_\alpha (1+o(1)).
\end{equation}
Докажем вначале, соотношение (\ref{5.5}). Пусть узлы выбраны из условия (\ref{5.1}). Тогда для \(i=0,\ldots,n\)
\begin{equation}\label{5.6}
\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|x'''(t)|+\frac{1}{n^\gamma} \right)^\alpha dt=\frac{\mathcal{A}}{n} (i=1,\ldots,n),
\end{equation}
где
\(
\mathcal{A}=\int_a^b\left(|x'''(t)|+\frac{1}{n^\gamma} \right)^\alpha dt,
\)
следовательно,
\(
\int_{t^*_{i-1,n}}^{t^*_{i,n}}n^{-\alpha\gamma}dt\le \frac{\mathcal{A}}{n}.
\)
Тогда
\begin{equation}\label{5.7}
h^*_{i-1/2,n}\le\frac{\mathcal{A}}{n^{1-\gamma\alpha}},
\end{equation}
и для достаточно больших \(n\) выполняется неравенство
\(
\int_{t^*_{i-1,n}}^{t^*_{i,n}}(2\|x'''\|_\infty)^\alpha dt\ge \frac{\mathcal{A}}{n}.
\)
Отсюда имеем
\begin{equation}\label{5.8}
{h^*_{i-1/2,n}}(2\|x'''\|_\infty)^\alpha \ge \frac{\mathcal{A}}{n}.
\end{equation}
Кроме того, из (\ref{5.6}), используя теорему о среднем, получаем, что найдется точка \(\xi_{i,n}\in [t^*_{i-1,n},t^*_{i,n}]\) такая, что
\[
h^*_{i-1/2,n}\left(|x'''(\xi_{i,n})|+\frac{1}{n^\gamma} \right)^\alpha dt=\frac{\mathcal{A}}{n},
\]
и, следовательно,
\begin{equation}\label{5.9}
\left|h^*_{i-1/2,n}-h^*_{i+1/2,n}\right|=\frac{\mathcal{A}}{n}\left|\frac{1}{(|x'''(\xi_{i,n})|+n^{-\gamma})^{\alpha}}-\frac{1}{(|x'''(\xi_{i+1,n})|+n^{-\gamma})^{\alpha}}\right|\le
(2\|x'''\|_\infty)^\alpha h^*_{i-1/2,n}\left|(|x'''(\xi_{i,n})|+n^{-\gamma})^{\alpha}-(|x'''(\xi_{i+1,n})|+n^{-\gamma})^{\alpha}\right|n^{2\gamma\alpha}.
\end{equation}
Для продолжения доказательства нам понадобится следующее простое утверждение:
Для всех \(A\), \(B\), \(C>0\) и \(\alpha\in (0,1]\) справедливо неравенство
\begin{equation}\label{5.10}
(A+B)^\alpha-(C+B)^\alpha\le(|A-C|+B)^\alpha-B^\alpha.
\end{equation}
Не ограничивая общности рассуждений, можно считать, что \(A>C\). Тогда, для того, чтобы доказать неравенство (\ref{5.10}), достаточно показать, что функция
\(
\varphi(t)=(A+B-t)^\alpha-(C+B-t)^\alpha
\)
достигает своего максимума на отрезке в точке \(t=C\).
Из неравенства (\ref{5.10}) и из (\ref{5.9}) следует, что
\[
\left|h^*_{i-1/2,n}-h^*_{i+1/2,n}\right|\le (2\|x'''\|_\infty)^\alpha h^*_{i-1/2,n}n^{2\gamma\alpha}\left(\left(\left|x'''(\xi_{i+1,n})-x'''(\xi_{i,n})\right|+n^\gamma\right)^\alpha-n^{-\alpha\gamma}\right).
\]
Так как \(x'''\in L^1_\infty\), то
\[
\left|x'''(\xi_{i+1,n})-x'''(\xi_{i,n})\right|=\left|\int_{\xi_{i,n}}^{\xi_{i+1,n}}x^{(4)}(t)dt\right|\le \|x^{(4)}\|_\infty(h_{i+1/2,n}+h_{i-1/2,n}).
\]
Отсюда и из (\ref{5.7}) получаем
\[
\left|x'''(\xi_{i+1,n})-x'''(\xi_{i,n})\right|\le \frac{2\mathcal{A}}{n^{1-\alpha\gamma}}\|x^{(4)}\|_\infty.
\]
Следовательно,
\[
\left|h^*_{i-1/2,n}-h^*_{i+1/2,n}\right|\le (2\|x'''\|_\infty)^\alpha h^*_{i-1/2,n}n^{2\gamma\alpha}\left(\left(
\frac{2\mathcal{A}\|x^{(4)}\|_\infty}{n^{1-\gamma\alpha}}-\frac{1}{n^\gamma}\right)^\alpha-n^{-\alpha\gamma}\right)=
\]
\[
=(2\|x'''\|_\infty)^\alpha h^*_{i-1/2,n}n^{\gamma\alpha}\left(\left(1+
\frac{2\mathcal{A}\|x^{(4)}\|_\infty}{n^{1-\gamma\alpha}}-\frac{1}{n^\gamma}\right)^\alpha-1\right)\le
C h^*_{i-1/2,n}\frac{n^{\alpha\gamma}}{n^{1-\alpha\gamma-\gamma}}=C h^*_{i-1/2,n}n^{(2\alpha+1)\gamma-1},
\]
где \(C\equiv const\).
Отсюда и из выбора \(\gamma\) имеем
\begin{equation}\label{5.11}
\left|h^*_{i-1/2,n}-h^*_{i+1/2,n}\right|\le h^*_{i-1/2,n}\varepsilon_n,
\end{equation}
где
\(
\varepsilon_n\le \frac{C}{n^\frac{3\alpha+1}{5\alpha+2}}.
\)
Пусть \(\epsilon_{2,n}\) задано равенством (\ref{4.1}), тогда из (\ref{5.11}) и (\ref{5.7}) следует
\(
\epsilon_{2,n}= O\left(\frac{1}{n^\frac{3\alpha+1}{5\alpha+2}}\right).
\)
Отсюда и из (\ref{5.7}), используя теорему 8, имеем
\[
\|s_2(x,\Delta^*_n)-P_2(x,\Delta^*_n)\|_\infty=\frac{C}{n^\frac{3\alpha+1}{5\alpha+2}}\cdot \frac{1}{n^{3(1-\alpha\gamma)}}=O\left(\frac{1}{n^{3+\frac{1}{5\alpha+2}}}\right).
\]
Это неравенство вместе с теоремой 5 и с учетом того, что
\(
\Theta_{2,p}=B_{3,p},
\)
и завершает доказательство неравенства (\ref{5.5}).
Приведем доказательство оценки снизу, то есть, неравенства (\ref{5.4}).
Пусть \(N=\left[n^{\frac{7}{8}}\right]+1\), где \([z]-\) целая часть числа \(z\). и обозначим через \(x_N\) интерполяционный кубический сплайн по разбиению
\(
\Delta^0_N=\left\{t^0_i\right\}_{i=0}^N
\stackrel{\mathrm{\Delta}}{=}
\left\{a+\frac{b-a}{N}i\right\}_{i=0}^N,
\)
то есть, \(x_N=s_3(x,\Delta^0_m)\).
В силу теоремы 9
\(
\|x-x_N\|_\infty=O\left(\frac{1}{N^4}\right)=O\left(\frac{1}{n^{3,5}}\right)
\)
и
\(
\|x'''-x'''_N\|_\infty=O\left(\frac{1}{N}\right)=O\left(\frac{1}{n^{\frac{7}{8}}}\right).
\)
Отсюда следует, что для \(p\in [1,\infty]\) имеем
\(
\|x-x_N\|_p=O\left(\frac{1}{n^{3,5}}\right)
\)
и
\(
\left|\|x'''\|_\alpha-\|x'''_N\|_\alpha\right|=O\left(\frac{1}{n^{\frac{7}{8}}}\right).
\)
Кроме того,
\(
\left|E_{n,r}(x)_p-E_{n,r}(y)_p\right|\le \|x-y\|_p.
\)
Из этих соотношений следует, что для доказательства неравенства (\ref{5.4}) достаточно показать, что
\begin{equation}\label{5.12}
E_{n,2}(x_N)_p\ge \frac{B_{3,p}}{n^3}\|x'''_N\|_\alpha (1+o(1)).
\end{equation}
Пусть \(\Delta_N\) - произвольное разбиение отрезка \([a,b]\) и \(s_2\in S_2(\Delta_n)\). Тогда
\begin{equation}\label{5.13}
\|x_N-s_2\|^p_p=\sum_{i=1}^N\int_{t_{i-1}}^{t_i}|x_N(t)-s_2(t)|^pdt\ge
\sum_{i=1}^N\inf\left\{\left.\|x_N-s\|^p_{p[t_{i-1},t_t]}\right|s\in S_2(\Delta_n)\right\}=
\sum_{i=1}^NE(x_N,S_2(\Delta_{n,i}))^p_{p[t_{i-1},t_t]}
\end{equation}
для \(p\in [1,\infty)\) и
\begin{equation}\label{5.14}
\|x_N-s_2\|_\infty=\max\left\{\left.E(x_N,S_2(\Delta_{n,i}))_{\infty[t_{i-1},t_t]}\right|i=1,\ldots,N\right\},
\end{equation}
где \(\Delta_{n,i}=\left(\Delta_n\bigcap [t_{i-1},t_i]\right)\bigcup t_{i-1}\bigcup t_{i}\).
Так как для \(t\in [t_{i-1},t_i]\) имеем
\(
x_N(t)=\frac{a_i}{3!}t^3+P_2(t),
\)
то для всех \(p\in [1,\infty]\)
\[
E(x_N,S_2(\Delta_{n,i}))_{p[t_{i-1},t_i]}=\frac{|a_i|}{3!}E\left((\cdot)^3,S_2(\Delta_{n,i})\right)_{p[t_{i-1},t_i]}=
\frac{|a_i|}{3!N^{3+1/2}}E\left((\cdot)^3,S_2(\Delta'_{n,i})\right)_p,
\]
где
\(
\Delta'_{n,i}=\{t|t=(\tau-t_{i-1})N,\tau\in \Delta_{n,i}\}.
\)
Следовательно, для любого \(p\in [1,\infty]\)
\begin{equation}\label{5.15}
E(x_N,S_2(\Delta_{n,i}))_{p[t_{i-1},t_i]}\ge
\frac{|a_i|}{3!N^{3+1/2}}E_{n_i,2}\left(\frac{(\cdot)^3}{3!}\right)_p,
\end{equation}
где \(n_i\) число узлов разбиения \(\Delta_{n,i}\).
Отсюда и из следствия 2 получаем
\[
E(x_N,S_2(\Delta_{n,i}))_{p[t_{i-1},t_i]}\ge
\frac{|a_i|}{N^{3+1/p}}\frac{B_{3,p}}{(n_i+6)^3}(b-a)^{3+1/p}.
\]
что вместе с (\ref{5.13}) дает
\[
\|x_N-s_2\|^p_p\ge\left(\frac{B_{3,p}}{N^{3+1/p}}\right)^p\sum_{i=1}^N\frac{|a_i|^p}{(n_i+6)^{3p}}(b-a)^{3p+1}
\]
для \(p\in [1,\infty)\) и
\[
\|x_N-s_2\|_\infty\ge\frac{B_{3,\infty}}{N^{3}}\max\left\{\left.\frac{|a_i|}{(n_i+6)^{3}}(b-a)^{3}\right|i=1,\ldots,N\right\}.
\]
Отметим, что
\(
\sum_{i=1}^N(n_i+6)\le n+6N.
\)
Используя теперь леммы 2 и 3, приходим к соотношениям
\[
\|x_N-s_2\|^p_p\ge \frac{B^p_{3,p}}{N^{\frac{p}{\alpha}}}\left(\sum_{i=1}^N|a_i|^\alpha\right)^{\frac{p}{\alpha}}\frac{(b-a)^{\frac{p}{\alpha}}}{(n+6N)^{3p}}
\]
для \(p\in [1,\infty)\) и
\[
\|x_N-s_2\|_\infty\ge\frac{B_{3,\infty}}{N^{\frac{1}{\alpha}}}\left(\sum_{i=1}^N|a_i|^\alpha\right)^{\frac{1}{\alpha}}\frac{(b-a)^{\frac{1}{\alpha}}}{(n+6N)^{3}},
\]
то есть, для \(p\in [1,\infty]\) выполняется неравенство
\(
\|x_N-s_2\|_p\ge\frac{B_{3,p}}{(n+6N)^3}\|x'''_N\|_\alpha.
\)
Отсюда и из выбора числа \(N\) получаем неравенство (\ref{5.12}), а вместе с ним и неравенство (\ref{5.4}) и, следовательно, соотношение (\ref{5.2}).
Для доказательства второй части теоремы остается доказать, что
\[
\|x-s_2(x,\Delta^*_n)\|_p\le\frac{B_{3,p}}{n^3}\|x'''\|_\alpha (1+o(1)).
\]
Докажем это соотношение. Из (\ref{5.3}) следует, что
\[
\int_{t^*_{i-1,n}}^{t^*_{i,n}}|z_n(t)|^\alpha dt=\frac{\mathcal{A}}{n},
\]
где
\(
\mathcal{A}=\int_a^b|z_n(t)|^\alpha dt.
\)
Следовательно, учитывая, что \(x'''(t)\ne 0\) \((t\in [a,b])\), получаем
\(
h^*_{i-1/2,n}=O\left(\frac{1}{n}\right).
\)
Кроме того, из (\ref{5.3}) и из теоремы о среднем, следует, что
\[
\left|h^*_{i-1/2,n}-h^*_{i+1/2,n}\right|=\frac{\mathcal{A}}{n}\left(\frac{1}{|z_n(\xi_{i,n})|^\alpha}-\frac{1}{|z_n(\xi_{i-1,n})|^\alpha}\right)=O\left(\frac{1}{n}\right).
\]
Сопоставляя эти соотношения с утверждением теоремы 8, получаем
\[
\left\|s_2^{(\nu)}(x,\Delta^*_n)-P_2^{(\nu)}(x,\Delta^*_n)\right\|_\infty=o\left(\frac{1}{n^{3-\nu}}\right),
\]
что вместе с теоремой 5 и завершает доказательство теоремы.
