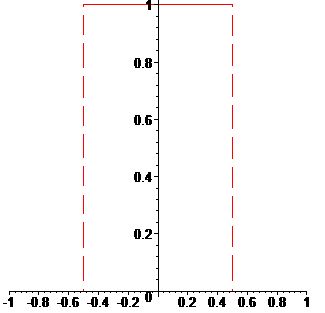
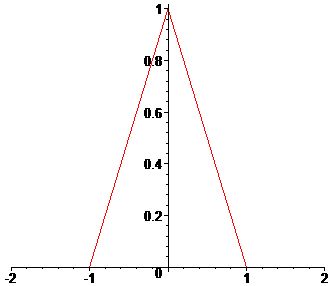
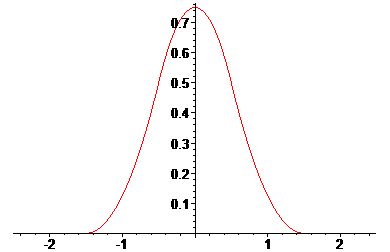
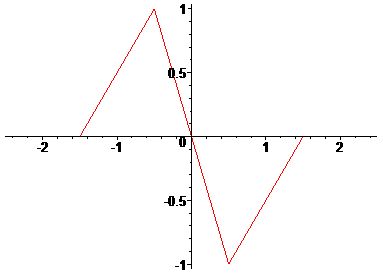
На практике, как правило, используют интерполяционные сплайны и близкие к ним. То есть сплайны, совпадающие с данной функцией \(x(t)\) в заданной системе точек.
Для простоты изложения мы будем считать, что функция \(x(t)\) и все сплайны, описывающие ее, имеют период \(T\).
Это избавит нас от необходимости рассматривать различные виды задания краевых условий для сплайнов, чему мы
уделим внимание позже.
Как было отмечено ранее, любой сплайн \(s_3(t)\) третьего порядка с узлами в точках \(ih\), \(i=0,1,\ldots,n\) \((h=T/n)\) для
\(t\in [0,T]\) однозначно представим в виде:
\begin{equation}\label{eq:(1.99)}
s_3(t)=\sum_{i=-1}^{n+1}{c_iB_{3,h}(t-ih)}.
\end{equation}
Если \(c_{-1}=c_{n-1}\), \(c_0=c_{n}\) и \(c_1=c_{n+1}\), то функция \(s_3(t)\) есть
периодический (с периодом \(T=nh\)) сплайн. Задавая различными способами коэффициенты \(c_i=c_i(x)\), мы получим различные виды сплайнов, описывающих
функцию \(x(t)\). Остановимся на некоторых способах задания \(c_i\).
Пусть, как обычно, \(x_i=x(ih)\), \(i=0,\pm1,\pm2,\ldots\) и
\begin{equation}\label{eq:(1.100)}
c_i=c_i(x)=\sum_{\nu=0}^{\infty}{\left(-\frac{1}{6}\right)^{\nu}
\Delta^{2\nu}x_i}.
\end{equation}
Здесь и далее мы считаем, что для всех \(i\) выполняются соотношения \(x_{i+n}=x_i\) и \(c_{i+n}=c_i\). Из равенства (\ref{eq:(1.89)}) следует, что
\begin{equation}\label{eq:(1.101)}
s_3(ih)=\frac{c_{i+1}+4c_i+c_{i-1}}{6}=c_i+\frac{1}{6}\Delta^2c_i.
\end{equation}
Отсюда и из (\ref{eq:(1.100)}) получаем
\[
s_3(ih)=\sum_{\nu=0}^{\infty}{\left(-\frac{1}{6}\right)^{\nu}\Delta^{2\nu}x_i}+\frac{1}{6}\Delta^2\left(
\sum_{\nu=0}^{\infty}{\left(-\frac{1}{6}\right)^{\nu}\Delta^{2\nu}x_i}\right)=\sum_{\nu=0}^{\infty}{\left(-\frac{1}{6}\right)^{\nu}\Delta^{2\nu}x_i}-
\sum_{\nu=0}^{\infty}{\left(-\frac{1}{6}\right)^{\nu+1}\Delta^{2\nu+2}x_i}==\sum_{\nu=0}^{\infty}{\left(-\frac{1}{6}\right)^{\nu}\Delta^{2\nu}x_i}-
\sum_{\nu=1}^{\infty}{\left(-\frac{1}{6}\right)^{\nu}\Delta^{2\nu}x_i}=
\Delta^0x_i=x_i.\]
Таким образом, если коэффициенты сплайна \(c_i\) определены равенствами (\ref{eq:(1.100)}), то для всех \(i\) выполняются равенства
\[s_3(ih)=x_i,\]
т.е. при задании коэффициентов равенствами (\ref{eq:(1.100)}) сплайн \(s_3(t)\) интерполирует
функцию \(x(t)\) в равноотстоящих точках \(ih\) \((i=0,\pm 1,\pm 2,\ldots)\).
Из неравенства
\[|\Delta^{2\nu}x_i|\le 4^{\nu-3}\max_{k}{|\Delta^6x_k|}\]
следует, что для \(\nu\ge 3\) имеет место следующая цепочка соотношений
\[\left|\sum_{\nu=3}^{\infty}
{\left(-\frac{1}{6}\right)^{\nu}\Delta^{2\nu}x_i}\right|\le
\sum_{\nu=3}^{\infty}
{\left|\left(-\frac{1}{6}\right)^{\nu}\Delta^{2\nu}x_i\right|}\le\max_{k}{|\Delta^6x_k|}
\sum_{\nu=3}^{\infty}{\frac{4^{\nu-3}}{6^{\nu}}}=\max_{k}{|\Delta^6x_k|}
\frac{1}{64}\frac{(2/3)^3}{1-2/3},\]
т.е.
\begin{equation}%\label{eq:(1.7.4)}
\left|\sum_{\nu=3}^{\infty}
{\left(-\frac{1}{6}\right)^{\nu}\Delta^{2\nu}x_i}\right|\le
\frac{1}{72}\max_{k}{|\Delta^6x_k|}.
\end{equation}
Кроме того, если функция \(x(t)\) имеет шесть непрерывных производных на
периоде, то \[\max_{k}{|\Delta^6x_k|}=O(h^6).\]
Отсюда и из (\ref{eq:(1.100)}) следует, что для гладких функций
\[c_i=x_i-\frac{1}{6}\Delta^2x_i+\frac{1}{36}\Delta^4x_i+O(h^6).\]
Это говорит о том, что в большинстве случаев при задании коэффициентов \(c_i\)
с помощью равенств (\ref{eq:(1.100)}) нет нужды выписывать ряды полностью, а достаточно брать
лишь несколько слагаемых. Подробнее этот вопрос мы обсудим позже.
Коэффициенты \(c_i\) интерполяционных сплайнов можно найти и из других соображений.
Действительно, из равенства (\ref{eq:(1.93)}) следует, что если сплайн \(s_3(t)\)
интерполирует функцию \(x(t)\) в точках \(ih\), то
\[s_3(ih)=\frac{c_{i+1}+4c_i+c_{i-1}}{6}=x_i\,\,\,\,\,(i=1,2,\ldots,n).\]
С учетом того, что \(c_{-1}=c_{n-1}\) , \(c_0=c_n\) и \(c_1=c_{n+1}\) имеем
\begin{equation}\label{eq:(1.102)}
\cases{4c_0+c_1\,\,\,\,\,\,\,\,+c_{n-1}=6x_0,\cr\cr
c_0+4c_1+c_2\,\,\,\,\,\,\,\,\,\,\,\,=6x_1,\cr\cr
\,\,\,\,\,\,\,\,\,\,\,c_1+4c_2+c_3\,\,\,\,\,\,=6x_2,\cr\cr
..........................................\cr\cr
\,\,\,\,\,\,c_{n-3}+4c_{n-2}+c_{n-1}=6x_{n-2},\cr\cr
c_0\,\,\,\,\,\,\,\,\,\,\,+c_{n-2}+4c_{n-1}=6x_{n-1}}.
\end{equation}
Матрица этой системы имеет диагональное преобладание и, следовательно, система
имеет одно и только одно решение (см. лемму Адамара). Это решение
легко найти с помощью одной из разновидностей алгоритма прогонки.
Непосредственной проверкой можно убедиться, что решение системы
(\ref{eq:(1.102)}) можно записать в виде (\ref{eq:(1.100)}).
Вернемся к методам задания интерполяционных сплайнов с помощью равенств
(\ref{eq:(1.99)}) - (\ref{eq:(1.100)}).
Как уже отмечалось, на практике используют не весь ряд (\ref{eq:(1.100)}), а несколько его
слагаемых. Остановимся на этом подробнее.
Пусть \[c_{i,1}=x_i\,\,\,\,(i=0,\pm 1,\ldots),\]
\[c_{i,2}=x_i-\frac{1}{6}\Delta^2x_i\,\,\,\,(i=0,\pm 1,\ldots),\]
\[c_{i,3}=x_i-\frac{1}{6}\Delta^2x_i+\frac{1}{36}\Delta^4x_i\,\,\,\,
(i=0,\pm 1,\ldots)\]
и
\[s_{3,k}(t)=\sum_{i=-1}^{n+1}{c_{i,k}B_{3,h}(t-ih)} \,\,\,(k=1,2,3).\]
Или, что то же,
\begin{equation}%\label{eq:(1.103)}
s_{3,1}(t)=\sum_{i=-1}^{n+1}{x_iB_{3,h}(t-ih)},
\end{equation}
\begin{equation}%\label{eq:(1.104)}
s_{3,2}(t)=\sum_{i=-1}^{n+1}{\left(x_i-
\frac{1}{6}\Delta^2x_i\right)B_{3,h}(t-ih)},
\end{equation}
\begin{equation}\label{eq:(1.105)}
s_{3,3}(t)=\sum_{i=-1}^{n+1}{\left(x_i-\frac{1}{6}\Delta^2x_i
+\frac{1}{36}\Delta^4x_i\right)B_{3,h}(t-ih)}.
\end{equation}
Каждый из этих сплайнов задается явно и, следовательно, легко программируется. Кроме того, каждый из них локальный, т.е. при изменении значения функции
\(x(t)\) в одной точке \(t\), каждый из них меняется лишь на нескольких соседних
промежутках. Далее, из равенства (\ref{eq:(1.101)}) следует, что
\begin{equation}\label{eq:(1.106)}
s_{3,1}(x,ih)-x_i=\frac{1}{6}\Delta^2x_i,
\end{equation}
\begin{equation}\label{eq:(1.107)}
s_{3,2}(x,ih)-x_i=-\frac{1}{36}\Delta^4x_i,
\end{equation}
\begin{equation}%\label{eq:(1.108)}
s_{3,3}(x,ih)-x_i=\frac{1}{216}\Delta^6x_i.
\end{equation}
Отсюда следует, что для гладких функций \(x(t)\) сплайны
\(s_{3,2}(x,t)\) интерполируют функцию \(x(t)\) с точностью до \(O(h^4)\), а сплайны
\(s_{3,3}(x,t)\) - с точностью до \(O(h^6)\). Это обстоятельство и обусловило их
название.
Сплайны \(s_{3,2}(x,t)\) называют локальными сплайнами, совпадающими с
интерполяционными по порядку, а сплайны \(s_{3,3}(x,t)\) - локальными сплайнами
асимптотически совпадающими с интерполяционными или почти интерполяционными
сплайнами.
Пусть, как и ранее, функция \(x(t)\) и все сплайны, восстанавливающие ее, имеют период \(T\).
Обозначим \[x_{i+0.5}=x((i+0.5)h)\,\,\,\,(i=0,\pm 1,\pm 2,\ldots,\,\,h=T/n).\]
Тогда для всех \(i\) \[x_{i+n+0.5}=x_{i+0.5}.\]
Пусть
\begin{equation}\label{eq:(1.124)}
b_i=b_i(x)=\sum_{\nu=0}^{\infty}{\left(-\frac{1}{8}\right)^{\nu}
\Delta^{2\nu}x_{i+0.5}}
=x_{i+0.5}-\frac{1}{8}\Delta^2x_{i+0.5}+\ldots\,\, .
\end{equation}
Как уже отмечалось выше, любой \(T\) - периодический параболический сплайн с
узлами в точках \(ih\) \((i=0,1,\ldots,n)\) для \(t\in [0,T]\) однозначно представим
в виде
\[s_2(t)=\sum_{i=-1}^{n}{\theta_iB_{2,h}(t-(i+0.5)h)}.\]
Рассмотрим сплайн
\begin{equation}%\label{eq:(1.125)}
s_2(x,t)=\sum_{i=-1}^{n}{b_iB_{2,h}(t-(i+0.5)h)},
\end{equation}
где коэффициенты \(b_i\) определены равенствами (\ref{eq:(1.124)}).
Тогда
\[s_2(x,(i+0.5)h)=\sum_{j=-1}^{n}{b_jB_{2,h}((i+0.5)h-(j+0.5)h)}=(b_{i-1}+b_{i+1})B_{2,h}(h)+b_iB_{2,h}(0)=
\frac{1}{8}(b_{i-1}+6b_i+b_{i+1})=b_i+\frac{1}{8}\Delta^2b_i.\]
Таким образом,
\begin{equation}\label{eq:(1.126)}
s_2(x,(i+0.5)h)=b_i+\frac{1}{8}\Delta^2b_i.
\end{equation}
Подставляя в (\ref{eq:(1.126)}) значения, определенные равенствами
(\ref{eq:(1.124)}), получаем для всех
\(i\) \[s_2(x,(i+0.5)h)=x_{i+0.5}.\]
Следовательно, сплайны \(s_2(x,t)\) интерполируют функцию \(x(t)\) в точках
\((i+0.5)h\).
Рассмотрим теперь сплайны близкие к интерполяционным
\[s_{2,1}(x,t)=\sum_{i=-1}^{n}{x_{i+0.5}B_{2,h}(t-(i+0.5)h)}\]
и
\[s_{2,2}(x,t)=\sum_{i=-1}^{n}{\left(x_{i+0.5}-
\frac{1}{8}\Delta^2x_{i+0.5}\right)B_{2,h}(t-(i+0.5)h)}.\]
Из равенств (\ref{eq:(1.126)}) следует, что
\[s_{2,1}(x,(i+0.5)h)=x_{i+0.5}+\frac{1}{8}\Delta^2x_{i+0.5}\] и
\[s_{2,2}(x,(i+0.5)h)=x_{i+0.5}-\frac{1}{64}\Delta^4x_{i+0.5}.\]
Кроме того, так как
\[\max_{i}{|\Delta^4x_{i+0.5}|}\le h^4\max_{t}{|x^{(4)}(t)|}=O(h^4)\]
и сплайны \(s_2(x,t)\) приближают гладкую функцию \(x(t)\) с
порядком \(O(h^3)\), то с точностью до \(O(h^4)\) сплайны \(s_{2,2}(x,t)\) совпадают с
интерполяционными сплайнами \(s_2(x,t)\). Этим и обусловлено их название -
асимптотически ("почти") интерполяционные параболические сплайны.