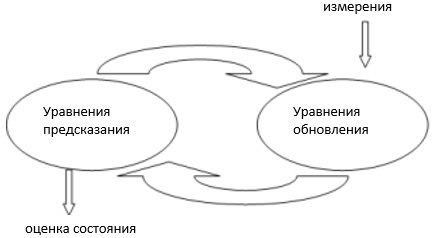
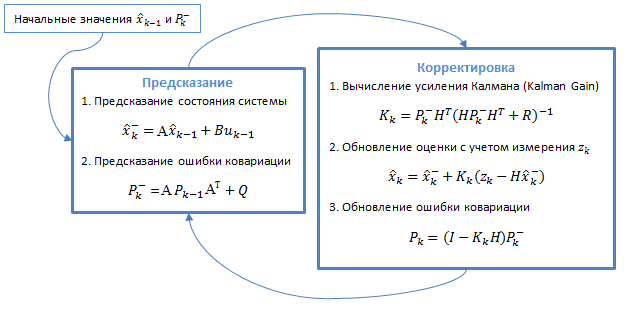
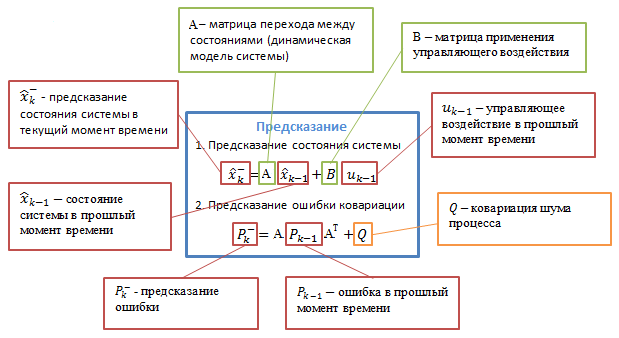
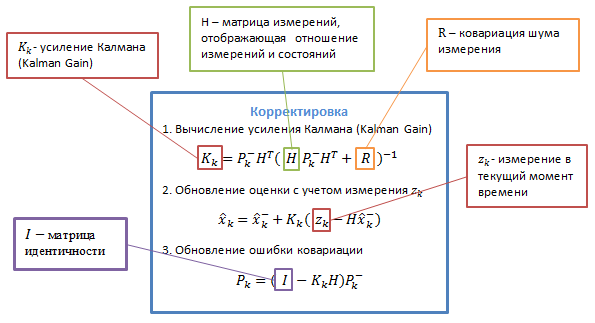
Приведем алгоритм.
Задача 1.
Имея наблюдение \(z_i=x+\varepsilon_i\) текущей координаты \(x\) сигнала GPS с \(i-\)го спутника (где \(\varepsilon_i\) погрешность
измерения с известной дисперсией \(\sigma^2_i\) и нулевым матожиданием), найти значение \(x\) и показать как меняется точность в зависимости от
количества спутников, с которых получаем сигнал.
Задача 2.
Зная курс гривна-доллар в банках, рассчитать функцию предсказания для прогноза валютного курса.
|
20 апреля 2019 г. | 27 апреля 2019 г. | 2 мая 2019 г. |
8 мая 2019 г. | 17 мая 2019 г. |
|---|
| Курс НБУ | 26.8377 | 26.6193 | 26.4927 |
26.3400 | 26.3429 |
|---|
| Покупка | / | Продажа |
Покупка | / | Продажа |
Покупка | / | Продажа |
Покупка | / | Продажа |
Покупка | / | Продажа |
|---|
| Приватбанк | 26.800 | / | 27.200 | 26.350 | / | 26.750 |
26.350 | / | 26.750 | 26.250 | / | 26.600 | 26.150 | / | 26.460 |
Райффайзен Банк Аваль | 26.800 | / | 27.150 | 26.300 | / | 26.700 |
26.300 | / | 26.700 | 26.200 | / | 26.600 | 26.150 | / | 26.550 |
| Альфа-Банк | 26.850 | / | 27.200 | 26.300 | / | 26.650 |
26.450 | / | 26.800 | 26.150 | / | 26.450 | 26.200 | / | 26.450 |
|---|
| Кредобанк | 26.900 | / | 27.200 | 26.350 | / | 26.800 |
26.350 | / | 26.800 | 26.200 | / | 26.500 | 26.200 | / | 26.500 |
|---|
| Таскомбанк | 26.750 | / | 27.150 | 26.200 | / | 27.000 |
26.550 | / | 26.750 | 26.200 | / | 26.400 | 26.280 | / | 26.420 |
|---|
| Альянс Банк | 26.850 | / | 27.200 | 26.350 | / | 26.750 |
26.350 | / | 26.750 | 26.250 | / | 26.600 | 26.200 | / | 26.500 |
|---|
| Укргазбанк | 26.500 | / | 27.100 | 26.000 | / | 26.600 |
26.000 | / | 26.600 | 26.000 | / | 26.500 | 26.000 | / | 26.500 |
|---|
| Индустриалбанк | 26.800 | / | 27.100 | 26.450 | / | 26.650 |
26.450 | / | 26.800 | 26.250 | / | 26.500 | 26.250 | / | 26.450 |
|---|