К сожалению, описанный алгоритм реализуем только для линейно разделимых множеств, что само по себе встречается достаточно нечасто. Приведем
модернизацию этого алгоритма для случая линейно неразделимых множеств.
Введем дополнительные переменные \(\xi _i \), которые характеризуют величину ошибки на каждом объекте \(x_{i}\), Введем в функционал цели штраф за суммарную
ошибку:
\begin{equation}\label{eq7.2}
\left\{ {{\begin{array}{*{20}c}
{\frac{1}{2}\left\| w \right\|^2 + \lambda \sum\limits_{i = 1}^n
{\xi _i } \to \min ,} \hfill \\
{u_i \left( {w^tx_i + w_0 } \right) \ge 1 - \xi _i ,i = 1,...,n,}
\hfill \\
{\xi _i \ge 0_i ,i = 1,...,n,} \hfill \\
\end{array} }} \right.
\end{equation}
здесь \(\lambda \)- параметр настройки метода, который позволяет регулировать отношение между максимизацией ширины разделяющей полосы и минимизацией
суммарной ошибки.
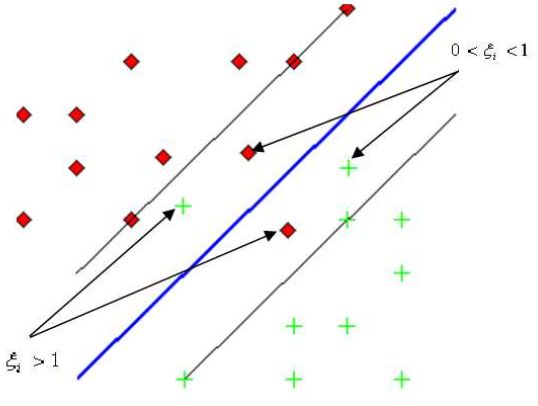
Величина штрафа \(\xi _i \) для соответствующего объекта \(x_{i} \) зависит от расположения объекта \(x_{i } \) относительно разделяющей полосы. Так, если
\(x_{i} \) лежит с противоположной стороны дискриминантной функции, то будем считать величину штрафа \(\xi _i > 1\), если \(x_{i} \) лежит в разделяющей
полосе, но со стороны своего класса, то соответствующий вес будет \(0\lt \xi _i \lt 1\), Для идеального случая будем считать \(\xi _i \lt 0.\)
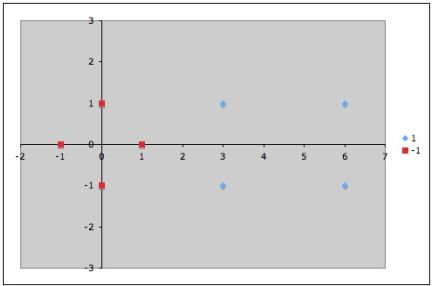
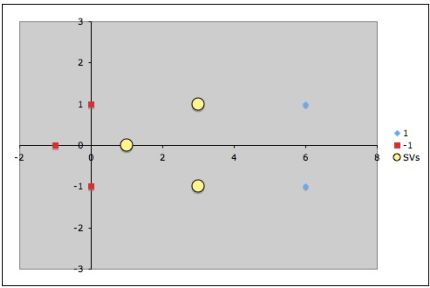
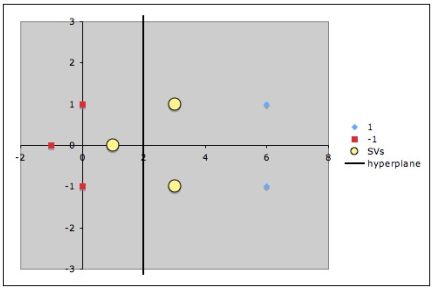
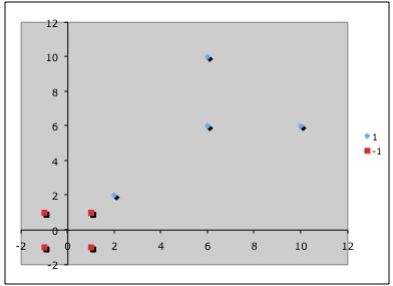
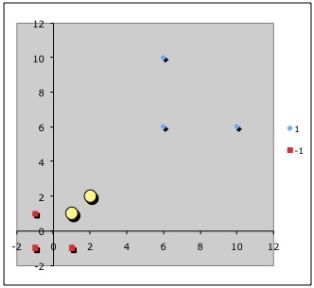
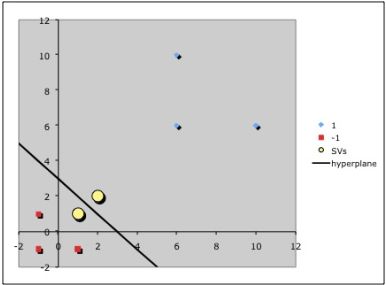
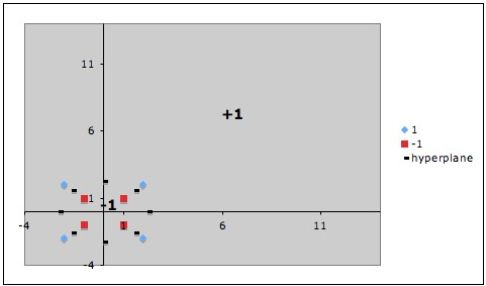
 Точки, к которым применяются штрафы.
Точки, к которым применяются штрафы.
Тогда полученную задачу можно переписать в виде
\[
J(w,\xi _1 ,...,\xi _n ) = \frac{1}{2}\left\| w
\right\|^2 + \beta \sum\limits_{i = 1}^n {I\left( {\xi _i > 0} \right)} \to
\min ,
\]
то есть в процессе минимизации участвуют элементы, которые не представляют собой идеальный случай. Здесь
\[
I\left( {\xi _i > 0} \right) = \left\{ {{\begin{array}{*{20}c}
{1,} \hfill & {\xi _i > 0,} \hfill \\
{\mbox{0,}} \hfill & {\xi _i \le 0,} \hfill \\
\end{array} }} \right.
\]
при выполнении условий \(u_i \left( {w^tx_i + w_0 } \right) \ge 1 - \xi _i \) и \(\xi _i \ge \mbox{0}\), Здесь постоянная \(\beta \) является весом,
учитывающим ширину полосы. Если \(\beta \) мало, то мы позволяем расположить относительно много элементов в неидеальной позиции, то есть, в разделяющей
полосе. Если \(\beta \) велико, то мы требуем наличия малого количества элементов в неидеальной позиции, то есть в разделяющей полосе.
К сожалению, задача минимизации является достаточно сложной, ввиду разрывности \(I\left( {\xi _i } \right)\), Вместо этого мы рассмотрим
минимизацию величины \(J(w,\xi_1 ,...,\xi _n) =\frac{1}{2}\left\| w \right\|^2 + \beta \sum\limits_{i = 1}^n {\xi _i }\)
при ограничениях \(\forall i \)
\[
\left\{ {{\begin{array}{*{20}c}
{u_i \left( {w^tx_i + w_0 } \right) \ge 1 - \xi _i ,} \hfill \\
{\xi _i \ge 0.} \hfill \\
\end{array} }} \right.
\]
Используя теорему Куна-Таккера, отсюда получаем
\begin{equation}
\label{eq7.3}
L\left( \alpha \right) = \sum\limits_{i = 1}^n {\alpha _i -
\frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\alpha _i \alpha _j
u_i u_j x_i^T x_j } } } \to \max
\end{equation}
при условии, что \(0 \le \alpha _i \le \beta ,\forall i \) и \(\sum\limits_{i =
1}^n {\alpha _i u_i = 0} \).
Найдем \(w\) из соотношения \(w = \sum\limits_{i = 1}^n {\alpha _i u_i x_i } \).
Значение \(w_0 \) также можно найти, учитывая, что для любого \(0 \le \alpha _i \le \beta \) и \(\alpha _i \left[ {u_i \left( {w^tx_i + w_0 } \right) - 1} \right] = 0\).
Другой идеей метода опорных векторов (в случае невозможности линейного разделения классов), является переход в пространство большей размерности, в
котором такое разделение возможно.
Для решения задачи нелинейной классификации с помощью линейного классификатора нужно:
- Спроектировать данные x в пространство более высокой размерности с помощью
отображения \(\varphi \left( x \right)\).
- Найти линейную дискриминантную функцию для данных \(\varphi \left( x\right)\).
- Окончательная нелинейная дискриминантная функция может быть записана в виде
\[
g(x) = w^t\varphi (x) + w_0 .
\]
В 2D дискриминантная функция линейная
\[
g\left( {\left[ {{\begin{array}{*{20}c}
{x^{(1)}} \hfill \\
{x^{(2)}} \hfill \\
\end{array} }} \right]} \right) = \left[ {{\begin{array}{*{20}c}
{w_1 } \hfill & {w_1 } \hfill \\
\end{array} }} \right]\mbox{ }\left[ {{\begin{array}{*{20}c}
{x^{(1)}} \hfill \\
{x^{(2)}} \hfill \\
\end{array} }} \right] + w_0 .
\]
В 1D дискриминантная функция нелинейная
\[
g(x) = w_1 x + w_2 x^2 + w_0 .
\]
Для перевода данных в пространство более высокой размерности используют так называемые ядерные функции.
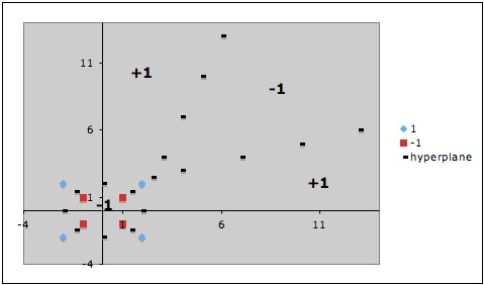
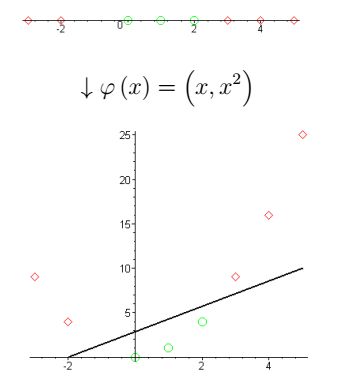 Пример линейного разделения множеств при переходе в пространство более высокой размерности.
Пример линейного разделения множеств при переходе в пространство более высокой размерности.
Запишем экстремальную задачу метода опорных векторов в виде (\ref{eq7.3})
\[
L\left( \alpha \right) = \sum\limits_{i = 1}^n {\alpha _i -
\frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\alpha _i \alpha _j
u_i u_j x_i^T x_j } } } \to \max .
\]
Заметим, что оптимизация зависит от произведения \(x_i^T x_j\) . Если мы переведем \( x_{i} \) в пространство более высокой размерности используя
отображение \(\varphi \left( x \right)\), то нужно вычислять
аналогичное произведение в пространстве более высокой размерности \(\varphi
(x_i )^T\varphi (x_j )\).
Идея метода состоит в том, что нужно найти ядерную функцию \(K\left(x_i,x_j \right) = \varphi (x_i )^T\varphi (x_j ) \) и максимизировать целевую
функцию
\[
L\left( \alpha \right) = \sum\limits_{i = 1}^n {\alpha _i -
\frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\alpha _i \alpha _j
u_i u_j K(x_i ,x_j )} } } \to \max .
\]
Рассмотрим пример и возьмем ядерную функцию в виде \(K(x,y) = (x^ty)^2\). Выясним какое отображение \(\varphi
\left( x \right) \) соответствует этой ядерной функции.
\[
K(x,y) = (x^ty)^2 = \left( {\left[
{{\begin{array}{*{20}c}
x^{(1)} \hfill & x^{(2)} \hfill \\
\end{array} }} \right]\mbox{ }\left[ {{\begin{array}{*{20}c}
y^{(1)} \hfill \\
y^{(2)} \hfill \\
\end{array} }} \right]} \right)^2 = \left( x^{(1)}y^{(1)} +
x^{(2)}y^{(2)} \right)^2 =
\]
\[
= \left( x^{(1)}y^{(1)} \right)^2 + 2\left(
x^{(1)}y^{(1)} \right)\left( x^{(2)}y^{(2)}
\right) + \left( x^{(2)}y^{(2)} \right)^2 =
\]
\[
= \left[\begin{array}{*{20}c}
{\left( x^{(1)} \right)^2} \hfill & \sqrt 2
x^{(1)}x^{(2)} \hfill & \left( x^{(2)} \right)^2
\hfill \\
\end{array} \right]\mbox{ }\left[ {{\begin{array}{*{20}c}
{\left( y^{(1)} \right)^2} \hfill & {\sqrt 2
y^{(1)}y^{(2)}} \hfill & {\left( y^{(2)} \right)^2}
\hfill \\
\end{array} }} \right]^T.
\]
Таким образом, \(\varphi \left( x \right) = \left[ {{\begin{array}{*{20}c}
{\left( {x^{(1)}} \right)^2} \hfill & {\sqrt 2
x^{(1)}x^{(2)}} \hfill & {\left( {x^{(2)}} \right)^2}
\hfill \\
\end{array} }} \right]\).
Выбор ядерной функции является достаточно сложным.
Рассмотрим пример.
Класс[1]: \(x_{1} =[1,-1], x_{2}=[-1,1].\)
Класс[2]: \(x_{3}=[1,1], x_{4}=[-1,-1].\)
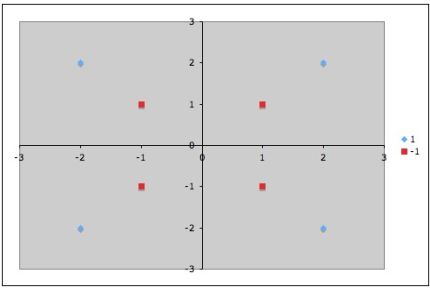
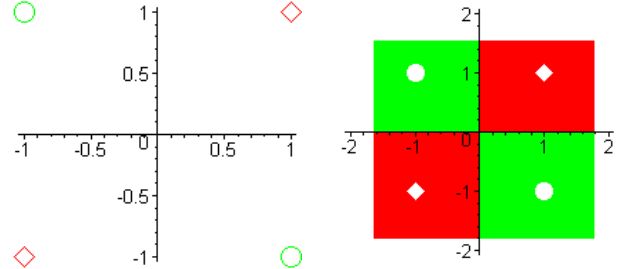 Пример линейно неразделимых множеств.
Пример линейно неразделимых множеств.
Для построения нелинейной дискриминантной функции используем ядерную функцию вида
\[
K\left( {x_i ,x_j } \right) = \left( {x_i^T x_j + 1}
\right)^2.
\]
Отображение, соответствующее этой функции имеет вид
\[
\varphi (x) = \left[ {{\begin{array}{*{20}c}
1 \hfill & {\sqrt 2 x^{(1)}} \hfill & {\sqrt 2 x^{(2)}} \hfill & {\sqrt 2
x^{(1)}x^{(2)}} \hfill & {\left( {x^{(1)}} \right)^2} \hfill & {\left(
{x^{(2)}} \right)^2} \hfill \\
\end{array} }} \right].
\]
Далее нужно максимизировать функцию
\[
L\left( \alpha \right) = \sum\limits_{i = 1}^n {\alpha _i -
\frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\alpha _i \alpha _j
u_i u_j \left( {x_i^T x_j + 1} \right)^2} } } \to \max
\]
при выполнении ограничений
\[
\alpha _i \ge 0,\alpha _1 + \alpha _2 - \alpha _3 - \alpha _4 = 0.
\]
Перепишем задачу в виде
\[
L(\alpha) = \sum\limits_{i =1}^4{\alpha _i - \frac{1}{4}\alpha ^TH\alpha ,}
\]
где \(\alpha = \left[ {{\begin{array}{*{20}c}
{\alpha _1 } \hfill & {\alpha _2 } \hfill & {\alpha _3 } \hfill & {\alpha
_4 } \hfill \\
\end{array} }} \right]^T \) и \(H = \left( {{\begin{array}{*{20}r}
9 \hfill & 1 \hfill & { - 1} \hfill & { - 1} \hfill \\
1 \hfill & 9 \hfill & { - 1} \hfill & { - 1} \hfill \\
{ - 1} \hfill & { - 1} \hfill & 9 \hfill & 1 \hfill \\
{ - 1} \hfill & { - 1} \hfill & 1 \hfill & 9 \hfill \\
\end{array} }} \right)\).
Для нахождения максимума, найдем производную по неизвестным и приравнивая нулю эти производные, найдем значения неизвестных, на которых достигается максимум целевой функции.
\[
\frac{\mbox{d}}{\mbox{d}\alpha }L(\alpha ) = \left( {{\begin{array}{*{20}c}
1 \hfill \\
1 \hfill \\
1 \hfill \\
1 \hfill \\
\end{array} }} \right) - \left( {{\begin{array}{*{20}c}
9 \hfill & 1 \hfill & { - 1} \hfill & { - 1} \hfill \\
1 \hfill & 9 \hfill & { - 1} \hfill & { - 1} \hfill \\
{ - 1} \hfill & { - 1} \hfill & 9 \hfill & 1 \hfill \\
{ - 1} \hfill & { - 1} \hfill & 1 \hfill & 9 \hfill \\
\end{array} }} \right)\alpha = 0.
\]
Решая эту систему, получаем \(\alpha _1 = \alpha _2 = \alpha _3 = \alpha _4 = \frac{1}{4} \) ,
\[
w = \sum_{i = 1}^4 {\alpha _i u_i \varphi \left( {x_i }
\right) = \frac{1}{4}\left( {\varphi \left( {x_i } \right) + \varphi \left(
{x_2 } \right) - \varphi \left( {x_3 } \right) - \varphi \left( {x_4 }
\right)} \right)} = \left[ {{\begin{array}{*{20}c}
0 \hfill & 0 \hfill & 0 \hfill & { - \sqrt 2 } \hfill & 0 \hfill & 0 \hfill
\\
\end{array} }} \right]
\]
и, наконец, нелинейная дискриминантная функция будет иметь вид
\[
\mbox{g(x)} = w\varphi (x) = \sum_{i =1}^6w_i \varphi_i(x) =
- \sqrt{2} \left( {\sqrt{2} x^{(1)}x^{(2)}} \right) = -
2x^{(1)}x^{(2)}.
\]
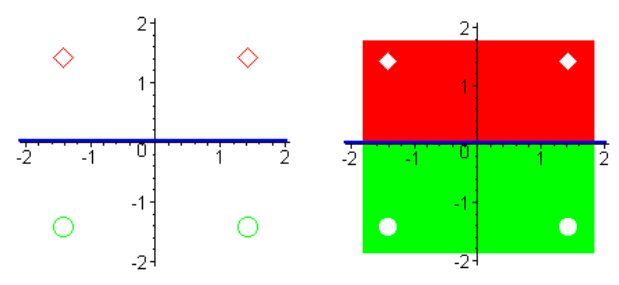 Линейная разделимость множеств, полученная в результате использования полиномиального неоднородного ядра.
Линейная разделимость множеств, полученная в результате использования полиномиального неоднородного ядра.
В заключение приведем несколько наиболее распространенных ядер, используемых для разделения кластеров:
-
Полиномиальное однородное ядро \(\mbox{K}\left( {x_i ,x_j }
\right) = \left( {x_i^T x_j } \right)^d\).
-
Полиномиальное неоднородное ядро \(\mbox{K}\left( {x_i ,x_j }
\right) = \left( {x_i^T x_j + 1} \right)^d\).
-
Радиальная функция Гаусса \(\mbox{K}\left( {x_i ,x_j } \right)
= \exp \left( { - \gamma\left\| {x_i - x_j } \right\|^2}\right). \)
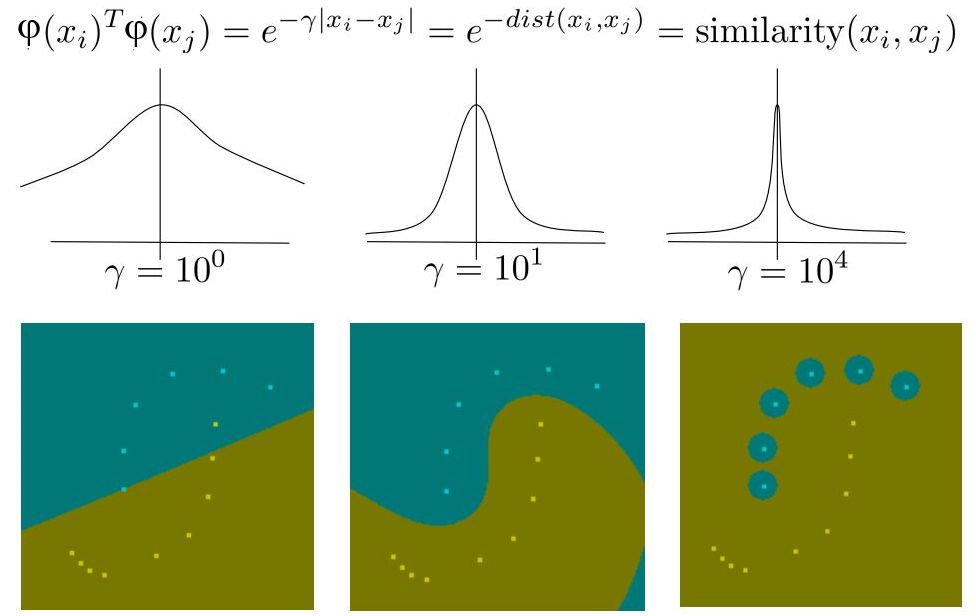 Использование экспонентциального ядра - в первом случае "почти" линейная дискриминантная функция, в последнем, "почти" метод ближайшего соседа.
Использование экспонентциального ядра - в первом случае "почти" линейная дискриминантная функция, в последнем, "почти" метод ближайшего соседа.