Через \(L^2(R^n)\) будем обозначать гильбертово пространство функций с конечной нормой \(\|f\|_2=\int_{R^n}|f(x)|^2dx,\) порожденное скалярным произведением \(\left\lt f,g\right>=\int_{R^n}f(x)\overline{g(x)}dx.\) Для функции \(f\in L^1(R)\) через \(\widehat{f}\) обозначим преобразование Фурье \(\widehat{f}(\omega)=\int_{-\infty}^{\infty}f(x)e^{-ix\omega}dx.\)
Под термином всплеск или wavelet будем понимать произвольную функцию \(\psi\), сдвиги и растяжения \(\{2^{j/2}\psi(2^jx-n)\}_{j,n\in Z}\) которой образуют ортонормированный базис пространства \(L^2(R)\).
Фундаментальным понятием теории всплесков является понятие кратномасштабного анализа (КМА). На современном этапе КМА является основным инструментом для построения всплесков.
Кратномасштабный анализ (КМА) в \(L^2(R^n)\) это последовательность замкнутых подпространств \( \ldots\subset V^{-1}\subset V^{0}\subset V^{1}\subset \ldots \) для которых выполняются условия

1. \(\overline{\cup_{j\in Z}{V^j}}=L^2(R^n);\)
2. \(\cap_{j\in Z}{V^j}=\{0\};\)
3. \(f(x)\in V^j\Longleftrightarrow f(2^{-j}\cdot)\in V^0;\)
4. найдется такая функция \(\varphi\in V^0\) (масштабирующая функция), что множество ее сдвигов \(\varphi(x-n)\) образует ортонормированный базис пространства \(V^0\).

Данная последовательность пространств (в силу первого условия) гарантирует что для любой суммируемой функции \(f\) и наперед заданного числа \(\varepsilon >0\) существует пространство \(V^k\) и элемент \(f_k\in V^k\), что \(\|f-f_k\|\lt \varepsilon\). Замечая, что в евклидовом пространстве наилучшим приближением функции является ортогональная проекция функции на это пространство, в качестве \(f_k\) будем брать ортогональную проекцию \(f\) на это пространство.
Второе и четвертое свойство КМА приводят к выводу, что для любого \(j\in Z\) набор функций \(\varphi^j_k(x)=2^{j/2}\varphi(2^jx-k)\) \(k=0,\pm 1, \ldots\) образуют ортонормированный базис. Множитель \(2^{j/2}\) появляется вследствие того, что при замене переменной \(x\) на \(2x\) норма функции уменьшается в \(2^{1/2}\) раз.
Поскольку \(V^0\subset V^1\), то функция \(\varphi\) является линейной комбинацией функций \(\{\varphi^1_n\}\). Таким образом найдется набор коэффициентов \(\{h_n\}\) такой что \begin{equation}\label{w.1} \varphi(x)=\sqrt{2}\sum_{n\in Z}h_n\varphi(2x-n), \end{equation} (масштабирующее уравнение). Это равенство является основополагающим.
Из равенства Парсеваля сразу следует, что \(\sum_nh^2_n=1\).
Выполняя преобразование Фурье выражения (\ref{w.1}), получаем \begin{equation}\label{w.2} \widehat{\varphi}(\omega)=\frac{1}{\sqrt{2}}\sum_{n\in Z}h_ne^{-in\omega/2}\widehat{\varphi} \left(\frac{\omega}{2}\right), \end{equation} или, что то же \begin{equation}\label{w.3} \widehat{\varphi}(\omega)=m\left(\frac{\omega}{2}\right) \widehat{\varphi}\left(\frac{\omega}{2}\right), \end{equation} где \begin{equation}\label{w.4} m(\omega)=\frac{1}{\sqrt{2}}\sum_{n\in Z}h_ne^{-in\omega/2}. \end{equation} Таким образом функция \(\varphi\) полностью определяется \(2\pi-\) периодической функцией \(m(\omega)\).
Функция \(\varphi\) является ортонормированной, то есть \begin{equation}\label{w.5} \int_R\varphi(x)\overline{\varphi(x-n)}dx=\delta_{n,0}, \end{equation} где \(\delta_{n,0}\) символ Кронекера.
С другой стороны, преобразование Фурье этого интеграла равно \[ \frac{1}{\sqrt{2\pi}}\int_R\int_R\varphi(x)\overline{\varphi(x-n)}dx e^{-in\omega}dn= \frac{1}{\sqrt{2\pi}}\int_Re^{-ix\omega}\varphi(x)dx\int_R\overline{\varphi(x-n)} e^{i(x-n)\omega}dn= \] \[ =\widehat{\varphi}(\omega)\overline{\int_R\varphi(x-n) e^{-i(x-n)\omega}dn}= \widehat{\varphi}(\omega)\overline{\int_R\varphi(z) e^{-iz\omega}dz}=\sqrt{2\pi}\widehat{\varphi}(\omega) \overline{\widehat{\varphi}(\omega)}=\sqrt{2\pi}|\widehat{\varphi}(\omega)|^2. \] Выполняя обратное преобразование Фурье, получаем \[ \int_R\varphi(x)\overline{\varphi(x-n)}dx= \int_R |\widehat{\varphi}(\omega)|^2e^{in\omega}d\omega= \sum_{j\in Z}\int_{2\pi j}^{2\pi(j+1)} |\widehat{\varphi}(\omega)|^2e^{in\omega}d\omega \] \[ =\sum_{j\in Z}\int_{0}^{2\pi} |\widehat{\varphi}(\omega+2\pi j)|^2e^{in(\omega+2\pi j)}d\omega= \int_{0}^{2\pi}\sum_{j\in Z} |\widehat{\varphi}(\omega+2\pi j)|^2e^{in\omega}d\omega \] Отсюда и из (\ref{w.5}) следует, что все коэффициенты Фурье кроме нулевого \(2\pi\) периодической функции \(\sum_{j\in Z} |\widehat{\varphi}(\omega+2\pi j)|^2\) равны нулю, то есть \[ \sum_{j\in Z} |\widehat{\varphi}(\omega+2\pi j)|^2=\frac{1}{2\pi}. \] Сделаем замену \(\omega\) на \(2\omega\) и используя \(2\pi\)-периодичность и соотношение (\ref{w.3}), получаем \[ \frac{1}{2\pi}=\sum_{j\in Z} |\widehat{\varphi}(2\omega+2\pi j)|^2= \sum_{j\in Z} |m(\omega+\pi j)\widehat{\varphi}(\omega+\pi j)|^2= \sum_{j\in Z} |m(\omega+2\pi j)\widehat{\varphi}(\omega+2\pi j)|^2+ \sum_{j\in Z} |m(\omega+\pi+2\pi j)\widehat{\varphi}(\omega+\pi+2\pi j)|^2= \] \[ =\sum_{j\in Z} |m(\omega)\widehat{\varphi}(\omega+2\pi j)|^2+ \sum_{j\in Z} |m(\omega+\pi)\widehat{\varphi}((\omega+\pi)+2\pi j)|^2= \frac{1}{2\pi}|m(\omega)|^2+|m(\omega+\pi)|^2. \] Отсюда следует, что почти всюду имеет место равенство \( |m(\omega)|^2+|m(\omega+\pi)|^2=1. \)
Пусть пространства \(\{V^j\}\) образуют КМА пространства \(L^2(R)\), тогда ортогональное дополнение \(W^j\) пространства \)V^j\) до пространства \(V^{j+1}\) называется пространством всплесков, то есть пространство \(V^{j+1}\) представимо в виде прямой суммы \( V^{j+1}=V^{j}\oplus W^{j},\,\,\,\,j\in Z. \) Таким образом учитывая второе свойства КМА имеем \( V^{j+1}=\bigoplus_{k=-\infty}^j W^{k} \) и, соответственно, из первого свойства КМА, получаем \( L^2(R)=\overline{\bigoplus_{k=-\infty}^\infty W^{k}}. \)
Далее в пространствах \(W^j\) построим ортогональный базис, состоящий из сдвигов одной функции.
Ясно, что для функции \(f\in V^1\) существует набор коэффициентов \(c_n\) такой, что \begin{equation}\label{w.6} f(x)=\sqrt{2}\sum_{n\in Z}c_n\varphi(2x-n), \end{equation} и \begin{equation}\label{w.7} \widehat{f}(\omega)=m_f\left(\frac{\omega}{2}\right) \widehat{\varphi}\left(\frac{\omega}{2}\right), \end{equation} где \(m_f\) \(2\pi\)-периодическая функция определяемая соотношением \begin{equation}\label{w.8} m_f(\omega)=\frac{1}{\sqrt{2}}\sum_{n\in Z}c_ne^{-in\omega}. \end{equation} Функция \(m_f\) имеет смысл спектра функции \(f\).
Пусть теперь функций \(f\) из пространства \(W^0\), то есть ортогональна всем функциям базиса \(\{\varphi(x-n)\}\). Проведя построения аналогичные приведенным выше, получаем \[ 0=\int_Rf(x)\overline{\varphi(x-n)}dx= \int_R\widehat{f}(\omega)\overline{\widehat{\varphi}(\omega)}e^{in\omega}d\omega= \int_0^{2\pi}\left( \sum_{k\in Z}\widehat{f}(\omega+2k\pi) \overline{\widehat{\varphi}(\omega+2k\pi)}\right) e^{in\omega}d\omega. \] Отсюда, из (3) и (7) следует \begin{equation}\label{w.9} m_f(\omega)\overline{m(\omega)}+ m_f(\omega+\pi)\overline{m(\omega+\pi)}=0. \end{equation} При фиксированном \(\omega\) это равенство имеет смысл скалярного произведения векторов \( \left( m_f(\omega),m_f(\omega+\pi)\right) \) и \( \left( m(\omega),m(\omega+\pi)\right). \) Если второй вектор не нулевой, то в равенство (\ref{w.9}) выполняется только в том случае, когда почти всюду \( m_f(\omega)=\xi(\omega)\overline{m(\omega+\pi)}. \) Здесь \(\xi(\omega)\) произвольная \(2\pi\) периодическая функция такая, что \(\xi(\omega+\pi)=-\xi(\omega)\), или, что тоже \( \xi(\omega)=e^{i\omega}\zeta(\omega), \) где \(\zeta(\omega)\) \(\pi\) периодическая функция.
Отсюда и из (\ref{w.7}) получаем \[ \widehat{f}(\omega)=\zeta(\omega/2)e^{i\omega/2}\overline{m(\omega/2+\pi)} {\varphi}(\omega/2). \] Повторяя предыдущие выкладки (используя вместо \(\varphi\) функцию \(f\)) получаем, что целочисленные сдвиги образуют ортонормированный базис в том и только том случае, когда имеет место равенство \( |m_f(\omega)|^2+|m_f(\omega+\pi)|^2=1 \) или, что то же \[ 1=\left|\zeta(\omega)e^{i\omega}\overline{m(\omega+\pi)}\right|^2+ \left|\zeta(\omega+\pi)e^{i(\omega+\pi)}\overline{m(\omega+2\pi)}\right|^2= |\zeta(\omega)|^2\left(|m(\omega+\pi)|^2+ m(\omega)|^2\right)=|\zeta(\omega)|^2. \] Таким образом все возможные функции порождающие ортогональные базисы сдвигов в \(W^0\) порождаются функцией \(\zeta\) равной по модулю единице. Если в качестве \(\zeta\) взять единицу, то получаем \( m_\psi(\omega)=e^{i\omega}\overline{m(\omega+\pi)} \) и, следовательно, \begin{equation}\label{w.10} \widehat{\psi}(\omega)=e^{i\omega/2}\overline{m(\omega/2+\pi)} \widehat{\varphi}(\omega/2)=m_1(\omega/2)\widehat{\varphi}(\omega/2), \end{equation} или что то же \begin{equation}\label{w.11} \psi(x)=\sqrt{2}\sum_{n\in Z}g_n\varphi(2x-n), \end{equation} где \(g_n=(-1)^{1-n}\overline{h}_{1-n}\).

Рассмотрим пространство \(V^0\). Прежде всего отметим, что из теоремы двойственности следует, что для евклидовой нормы наилучшим приближением функции \(f\) является ортогональная проекция \(\overline{f}\) на пространство \(L^2(R)\): \begin{equation}\label{w.12} \overline{f}=\sum_{n\in Z}c_n\varphi^0_n(x)=\sum_{n\in Z}c_n\varphi(x-n), \end{equation} где \[ c_n=\left\lt f,\varphi^0_n\right>=\int_Rf(x)\overline{\varphi(x-n)}dx. \] Выбор коэффициентов \(c_n\) можно провести исходя из других соображений, например, условия интерполяции \begin{equation}\label{w.13} \overline{f}(k)=\sum_{n\in Z}c_n\varphi(k-n)=f_k. \end{equation} В этом случае если \(\varphi\) имеет конечный носитель, то эта задача сводится к решению системы линейных уравнений с ленточной матрицей.
Самым простым, но в большинстве случаев приемлемым способом проектирования на пространство \(V^0\) является проектор задаваемый равенством \(c_n=f_n\). Например, если взять \( \varphi(x)=\frac{\sin{\pi x}}{\pi x}, \) то эта проекция не только обеспечивает интерполяцию в целочисленных точках, то и точное восстановление сигналов со спектрами из отрезка \([-\pi,\pi]\).
Приведем спектры функции \(\overline{f}\) для различных методов проектирования на пространство \(V^0\):
ортогональная проекция \begin{equation}\label{w.14} \widehat{\overline{f}}(\omega)=\widehat{\varphi}(\omega) \sum_{n\in Z}\widehat{f}(\omega+2\pi n)\overline{\widehat{\varphi}(\omega+2\pi n)}; \end{equation} интерполяционная проекция \begin{equation}\label{w.15} \widehat{\overline{f}}(\omega)=\widehat{\varphi}(\omega) \frac{\sum_{n\in Z}\widehat{f}(\omega+2\pi n)} {\sum_{n\in Z}\widehat{\varphi}(\omega+2\pi n)}; \end{equation} проектор \(f_n\to c_n\) \begin{equation}\label{w.16} \widehat{\overline{f}}(\omega)=\widehat{\varphi}(\omega) \sum_{n\in Z}\widehat{f}(\omega+2\pi n). \end{equation}
В дальнейшем будем рассматривать коэффициенты вида (\ref{w.12}) и получим равенство \begin{equation}\label{w.17} V^{-1}\oplus W^{-1}=V^0. \end{equation} В качестве всплеска определяющего базисы сдвигов в пространствах \(W^j\) возьмем функцию \(\psi\) определяемую равенством (\ref{w.11}) и положим \( \psi^j_n(x)=2^{j/2}\psi(2^jx-n). \)
В этом случае соотношение (\ref{w.17}) запишется в виде \begin{equation}\label{w.18} \sum_{n\in Z}c_n^{-1}\varphi_n^{-1}(x)+ \sum_{n\in Z}d_n^{-1}\psi_n^{-1}(x)= \sum_{n\in Z}c_n^{0}\varphi_n^{0}(x). \end{equation} Здесь и далее \(c_n=c^0_n\).
Для определения коэффициентов разложения \(c_n^{-1}\) и \(d_n^{-1}\) нам понадобятся два важных в дальнейшем равенства \begin{equation}\label{w.19} \varphi^j_k(x)=\sum_{n\in Z} h_{n-2k}\varphi^{j+1}_n(x) \end{equation} и \begin{equation}\label{w.20} \psi^j_k(x)=\sum_{n\in Z} g_{n-2k}\varphi^{j+1}_n(x), \end{equation} где \( g_n=(-1)^{1-n}\overline{h}_{1-n}. \)
Действительно, согласно соотношению (\ref{w.1}) получаем \[ \varphi^j_k(x)= 2^{j/2}\varphi(2^jx-k)= 2^{j/2}\sum_{n\in Z}h_n2^{1/2}\varphi(2^{j+1}x-n-2k)= \sum_{n\in Z} h_{n}\varphi^{j+1}_{n+2k}(x) =\sum_{n\in Z} h_{n-2k}\varphi^{j+1}_n(x). \] Равенство (\ref{w.19}) доказано. Аналогично доказывается соотношение (\ref{w.20}).
Применяя операцию скалярного умножения (\ref{w.18}) на \(\varphi^{-1}_k(x)\), получаем \[ c^{-1}_k=\sum_{n\in Z}c_n^0\left\lt \varphi^0_n(x),\varphi^{-1}_k(x)\right>= \sum_{n\in Z}c_n^0\left\lt \varphi^0_n(x), \sum_{m\in Z}h_{m-2k}\varphi^{-1}_m(x)\right>= \sum_{n\in Z}c_n^0\overline{h_{n-2k}}. \] Найдем скалярное произведение (\ref{w.18}) на \(\psi^{-1}_k\), то есть \(d^{-1}_k= \sum_{n\in Z}c_n^0\overline{g_{n-2k}}.\)
Таким образом в общем случае разложение \( V^{j}\oplus W^{j}=V^{j+1} \) примет вид \begin{equation}\label{w.21} \sum_{n\in Z}c_n^{j}\varphi_n^{j}(x)+ \sum_{n\in Z}d_n^{j}\psi_n^{j}(x)= \sum_{n\in Z}c_n^{j+1}\varphi_n^{j+1}(x). \end{equation} Отсюда сразу получаем общие формулы декомпозиции \begin{equation}\label{w.22} c^{j}_k= \sum_{n\in Z}c_n^{j+1}\overline{h_{n-2k}}, \end{equation} \begin{equation}\label{w.23} d^{j}_k= \sum_{n\in Z}c_n^{j+1}\overline{g_{n-2k}}. \end{equation} Процесс разложения пространства \(V^0\) в ортогональную сумму \( V^0=W^{-1}\oplus W^{-2}\oplus \ldots W^{-k}\oplus V^{-k} \) для конкретного элемента пространства \(V^0\) с координатами \(\{c^0_n\}\) заключается в последовательном выполнении операций (\ref{w.22}), (\ref{w.23}) для \(j=-1,-2,\ldots,-k\).
Теперь рассмотрим обратную задачу -- реконструкции функции по известным коэффициентам разложения по базису всплесков, то есть по известным коэффициентам \(\{c_n^j\}\), \(\{d_n^j\}\) \((j=-1,-2,\ldots -k), n\in Z\) нужно восстановить \(\{c^0_n\}\).
Соотношение (\ref{w.21}) умножим скалярно на \(\varphi_k^{j+1}\), в результате получим \[ c^{j+1}_k= \sum_{n\in Z}c_n^{j}\left\lt \varphi_n^{j},\varphi_k^{j+1}\right>+ \sum_{n\in Z}d_n^{j}\left\lt \psi_n^{j},\varphi_k^{j+1}\right>= \sum_{n\in Z}c_n^{j} \left\lt \sum_{m\in Z}h_{m-2n}\varphi_m^{j+1},\varphi_k^{j+1}\right>+ \sum_{n\in Z}d_n^{j} \left\lt \sum_{m\in Z}g_{m-2n}\varphi_m^{j+1},\varphi_k^{j+1}\right>= \sum_{n\in Z}c_n^{j}h_{k-2n}+ \sum_{n\in Z}d_n^{j}g_{k-2n}. \] Таким образом формула реконструкции имеет вид \begin{equation}\label{w.24} c^{j+1}_k= \sum_{n\in Z}c_n^{j}h_{k-2n}+\sum_{n\in Z}d_n^{j}g_{k-2n}. \end{equation}
Приведенный алгоритм называется каскадным. Если в последовательности \(\{h_n\}\) только \(N\) отличны от нуля, то зная коэффициенты \(\{c_n^j\}\) для нахождения одного коэффициента \(d_n^{j-1}\) требуется \(N\) операций умножения и \(N-1\) сложения. В то же время, если вычислять исходя из последовательности \(\{c_n^0\}\), то учитывая увеличение носителя базисных всплесков вдвое при уменьшении индекса \(j\) на единицу, получаем, что затраты при вычислении одного коэффициента возрастают вдвое.

Пусть \(\varphi\) есть ортогональная функция на решетке с шагом 2, то есть \[ \left\lt \varphi,\varphi(\cdot-2k)\right>=\delta_{0,k} \] или, что тоже, \begin{equation}\label{w.o.1} \sum_ih_ih_{i-2k}=\delta_{0,k}. \end{equation} Известно , что если ортогональная функция имеет компактный носитель, то этот носитель четный.
Легко видеть, что в простейшем случае носитель равен двум и при этом \[ h_0=\frac{1}{\sqrt{2}},h_1=\frac{1}{\sqrt{2}}. \] Соответствующая базисная функция называется функцией Хаара. На рисунке приведена иллюстрация функции Хаара и ее всплеска. Для получения более сложных масштабирующих функций условия ортогональности не достаточно. В частности, Ингрид Добеши предложила использовать условие обнуления моментов соответствующих всплесков до \(n-1\) порядка включительно, то есть \( \int x^k\psi(x)=0, k=0,1,\ldots,n-1. \)
Учитывая (\ref{w.11}), условие обнуления моментов эквивалентно соотношению \( \sum_i i^k(-1)^{i}h_{i}=0, k=0,1,\ldots,n-1. \)
В случае, если длина носителя равна четырем, условия ортогональности будут иметь вид \[ \begin{array}{l} h_0^2+h_1^2+h_2^2+h_3^2=1, \\ h_0h_2+h_1h_3=0. \end{array} \] Для разрешимости системы добавим два условия обнуления моментов для всплесков \[ \begin{array}{l} h_0-h_1+h_2-h_3=0, \\ -h_1+2h_2-3h_3=0. \end{array} \] Решая полученную систему получаем \begin{equation}\label{w.Dob} h_0=\frac{1+\sqrt{3}}{4\sqrt{2}}, h_1=\frac{3+\sqrt{3}}{4\sqrt{2}}, h_2=\frac{3-\sqrt{3}}{4\sqrt{2}}, h_3=\frac{1-\sqrt{3}}{4\sqrt{2}}.\end{equation} Соответствующая масштабирующая функция (функция Добеши) приведена ниже. В случае \(n=6\) получаем \[ h_0=\frac{1}{16\sqrt{2}}\left(1+\sqrt{10}+\sqrt{5+2\sqrt{10}}\right), h_1=\frac{1}{16\sqrt{2}}\left(5+\sqrt{10}+3\sqrt{5+2\sqrt{10}}\right), \] \[ h_2=\frac{1}{16\sqrt{2}}\left(10-2\sqrt{10}+2\sqrt{5+2\sqrt{10}}\right), h_3=\frac{1}{16\sqrt{2}}\left(10-2\sqrt{10}-\sqrt{5+2\sqrt{10}}\right), \] \[ h_4=\frac{1}{16\sqrt{2}}\left(5+\sqrt{10}-3\sqrt{5+2\sqrt{10}}\right), h_5=\frac{1}{16\sqrt{2}}\left(1+\sqrt{10}-\sqrt{5+2\sqrt{10}}\right), \] Пусть \(v^j\) есть последовательность конечной длины \(c^j_n\). Этот вектор преобразуется в вектор \(v^{j-1}\) содержащий последовательности \(c^{j-1}_n\) и \(d^{j-1}_n\) каждая из которых половинной длины. Это преобразование может быть записано в виде \[ v^{j-1}=M_jv^{j}, \] где \(M_j\) состоит из нулей и элементов \(h_n\). Она является ортонормированной, то есть обратная матрица равна транспонированной.
Для иллюстрации возьмем фильтр длиной 4 (то есть фильтр Добеши). Тогда формулы декомпозиции (\ref{w.22}), (\ref{w.23}) можно записать в матричном виде \begin{equation}\label{w.33} \left[ \begin{array}{c} c^{-1}_{0}\\c^{-1}_{1}\\c^{-1}_{2}\\c^{-1}_{3}\\ d^{-1}_{0}\\d^{-1}_{1}\\d^{-1}_{2}\\d^{-1}_{3} \end{array} \right] = \left[ \begin{array}{cccccccc} h_0&h_1&h_2&h_3\\ &&h_0&h_1&h_2&h_3\\ &&&&h_0&h_1&h_2&h_3\\ h_2&h_3&&&&&h_0&h_1\\ h_3&-h_2&h_1&-h_0\\ &&h_3&-h_2&h_1&-h_0\\ &&&&h_3&-h_2&h_1&-h_0\\ h_1&-h_0&&&&&h_3&-h_2 \end{array} \right] \left[ \begin{array}{c} c^{0}_{0}\\c^{0}_{1}\\c^{0}_{2}\\c^{0}_{3}\\ c^{0}_{4}\\c^{0}_{5}\\c^{0}_{6}\\c^{0}_{7} \end{array} \right] \end{equation} и обратное преобразование (то есть формулы реконструкции (\ref{w.24})) имеет вид \begin{equation}\label{w.34} \left[ \begin{array}{c} c^{0}_{0}\\c^{0}_{1}\\c^{0}_{2}\\c^{0}_{3}\\ c^{0}_{4}\\c^{0}_{5}\\c^{0}_{6}\\c^{0}_{7} \end{array} \right] = \left[ \begin{array}{cccccccc} h_0&&&h_2&h_3&&&h_1\\ h_1&&&h_3&-h_2&&&-h_0\\ h_2&h_0&&&h_1&h_3&&\\ h_3&h_1&&&-h_0&-h_2&&\\ &h_2&h_0&&&h_1&h_3&\\ &h_3&h_1&&&-h_0&-h_2&\\ &&h_2&h_0&&&h_1&h_3\\ &&h_3&h_1&&&-h_0&-h_2 \end{array} \right] \left[ \begin{array}{c} c^{-1}_{0}\\c^{-1}_{1}\\c^{-1}_{2}\\c^{-1}_{3}\\ d^{-1}_{0}\\d^{-1}_{1}\\d^{-1}_{2}\\d^{-1}_{3} \end{array} \right] \end{equation} Условие ортогональности является достаточно жестким. Ортонормированность функций \(\varphi(\cdot-n)\) может быть ослаблена, для этого достаточно чтобы эти функции образовывали базис Рисса.
Для того, чтобы построить последовательность ортонормированных масштабирующих функций \(\varphi^*(\cdot-n)\) для \(V^0\) заметим, что они образуют базис Рисса тогда и только тогда, когда для любых \(\{c_n\}_{n\in Z}\) \begin{equation}\label{w.35} A\sum_{n}|c_n|^2\le \left\|\sum_{n}c_n\varphi\left({\cdot}-n\right)\right\|^2_{2(R)}\le B\sum_{n}|c_n|^2, \end{equation} где \(A,B\) не зависят от \(c_n\).
С другой стороны, \[ \left\|\sum_{n}c_n\varphi\left({\cdot}-\nu\right)\right\|^2_{2(R)}= \int_{R}\left|\sum_{n} e^{-in\omega} \widehat{\varphi}(\omega)\right|^2d\omega= \int_{0}^{2\pi}\left|\sum_{n}c_n e^{-in\omega} \right|^2\sum_{k}|\widehat{\varphi}(\omega+2\pi k)|^2d\omega \] и \[ \sum_{n}|c_n|^2=(2\pi)^{-1} \int_{0}^{2\pi}\left|\sum_{n}c_n e^{-in\omega} \right|d\omega. \] Отсюда и из (\ref{w.35}) следует, что почти всюду имеет место соотношение \( 0\lt (2\pi)^{-1}A\le\sum_{n}|\widehat{\varphi}(\omega+2\pi n)|^2\le (2\pi)^{-1}B. \)
Положим \begin{equation}\label{w.36} \widehat{\varphi}^*(\omega)=(2\pi)^{-1/2}\left( \sum_{n}|\widehat{\varphi}(\omega+2\pi n)|^2\right)^{-1/2} \widehat{\varphi}(\omega). \end{equation}
Ясно, что почти всюду \( \sum_{n}|\widehat{\varphi}^*(\omega+2\pi n)|^2=(2\pi)^{-1}, \) то есть \(\varphi^*(\cdot-n)\) являются ортогональными.
Понятно, что при построении конкретных функций в сумме \({\sum_n{|\widehat{\varphi}(\omega+2\pi k )}|^2}\) нужно брать индекс суммирования \(n\) из конечного множества. В этом случае получаем тригонометрический полином, который называется полиномом Эйлера-Фробениуса для данной масштабирующей функции. В зависимости от того, насколько много слагаемых в этом полиноме мы возьмем, настолько точно получим ортогональную функцию.
Наряду с ортогональными масштабирующими функциями широкое применение нашли биортогональные и полуортогональные базисы всплесков.
Масштабирующая функция называется полуортогональной, если порожденный ею базис Рисса удовлетворяет неравенству \( \left\lt \varphi^i_k, \varphi^j_m\right>=0,\,\,\,\,\,i\ne j\,\, (i,j,k,m\in\mathbb{Z}). \)
Пара масштабирующих функций \((\varphi, \widetilde{\varphi})\) обладает свойством биортогональноcти, если \( \left\lt \varphi^i_k, \widetilde{\varphi}^j_m\right>=\delta_{i,j}\delta_{k,m}\,\,\,\, (i,j,k,m\in\mathbb{Z}). \)
Заметим, что каждая полуортогональная масштабирующая функция порождает, согласно соотношению (\ref{w.36}), ортогональный базис.
Более того, для каждой полуортогональной масштабирующей функции существует единственная биортогональная функция \(\widetilde{\varphi}\), у которой преобразование Фурье определяется равенством \begin{equation}\label{w.36.1} \widehat{\widetilde{\varphi}}(\omega)=\frac{\widehat{\varphi}(\omega)}{\displaystyle {\sum_{k\in \mathbb{Z}}{|\widehat{\varphi}(\omega+2\pi k )}|^2}}. \end{equation} Действительно, для каждого \(m\in \mathbb{Z}\) \[ \left\lt \varphi, \widetilde{\varphi}(\cdot-m)\right>=\frac{1}{2\pi}\int_{-\infty}^\infty \widehat{\varphi}(\omega)\overline{\widehat{\widetilde{\varphi}}(\omega)}e^{im\omega}d\omega =\sum_{k=-\infty}^\infty{\frac{1}{2\pi}\int_{2\pi k}^{2\pi(k+1)} \widehat{\varphi}(\omega)\overline{\widehat{\widetilde{\varphi}}(\omega)}e^{im\omega}d\omega} =\frac{1}{2\pi}\int_{0}^{2\pi}\left(\sum_{k=-\infty}^\infty \widehat{\varphi}(\omega+2\pi k )\overline{\widehat{\widetilde{\varphi}}(\omega+2\pi k)}\right)e^{im\omega}d\omega. \] Замечая, что из (\ref{w.36.1}) следует, что почти всюду \( \sum_{k=-\infty}^\infty \widehat{\varphi}(\omega+2\pi k )\overline{\widehat{\widetilde{\varphi}}(\omega+2\pi k)}=1, \) то отсюда сразу получаем \( \left\lt \varphi, \widetilde{\varphi}(\cdot-m)\right>=\delta_{0,m}. \)
Из полученного равенства и условия полуортогональности следует, что полученная пара функций обладает свойством биортогональности.
Приведем несколько примеров.
Сплайнами Баттла-Лемарье (Battle-Lemarie) называются ортогональные функции порожденные В-сплайнами. Сплайн Баттла-Лемарье первого порядка определяется следующим образом \[ \widehat{\phi}(\omega)=\sqrt{\frac{2}{3\pi}}e^{-i\omega}\frac{\displaystyle{4\sin^2\frac{\omega}{2}}} {\displaystyle{\omega^2\left(1+2\cos^2\frac{\omega}{2}\right)^{1/2}}}, \] а сплайн Баттла-Лемарье второго порядка \[ \widehat{\phi}(\omega)=e^{-3i\omega/2}\frac{\displaystyle{8\sin^3\frac{\omega}{2}}} {\displaystyle{\omega^3\left(1+2\cos^2\frac{\omega}{2}\right)^{1/2}}} \left(\frac{8}{15}+\frac{13}{30}\cos{\omega}+\frac{1}{30}\cos^2{\omega}\right)^{-\frac{1}{2}}. \] Кроме того, используя В-сплайн в качестве масштабирующей функции, можно построить биортогональную пару.
Для кубических В-сплайнов фильтр для анализа данных имеет вид \[ \widetilde{h}_0=\frac{5}{4}, \widetilde{h}_1=\widetilde{h}_{-1}=\frac{5}{32}, \widetilde{h}_2=\widetilde{h}_{-2}=-\frac{3}{8}, \widetilde{h}_3=\widetilde{h}_{-3}=\frac{3}{32}, \] \[ \widetilde{g}_0=\frac{3}{8}, \widetilde{g}_1=\widetilde{g}_{-1}=-\frac{1}{4}, \widetilde{g}_2=\widetilde{g}_{-2}=\frac{1}{16}, \] фильтр для синтеза \[ {h}_0=\frac{3}{4}, {h}_1={h}_{-1}=\frac{1}{2}, {h}_2={h}_{-2}=\frac{1}{8}. \] \[ {g}_0=\frac{5}{2}, {g}_1={g}_{-1}=-\frac{5}{16}, {g}_2={g}_{-2}=-\frac{3}{4}, {g}_3=\widetilde{h}_{-3}=-\frac{3}{16}. \] На рисунке приведены биортогональная пара соответствующая В-сплайнам вместе с их всплесками.

В данном разделе рассмотрим метод быстрого всплеск-преобразования, основанный на биортогональной системе всплесков.
Введем необходимые в дальнейшем обозначения. Обозначим через \( Z^+=\{2i|i\in Z\}\) множество четных индексов, а через \( Z^-=\{2i+1|i\in Z\}\) множество нечетных.
Массив \(F=\{f_{i}\}_{i\in Z}\) будем называть массивом с конечным носителем, если \( \exists N>0:|i|>N \Longrightarrow f_{i}=0. \) В дальнейшем все рассматриваемые массивы имеют конечный носитель.
Пусть, далее, \(\Re\) множество массивов \(A=\{a_{i}\}_{i\in Z}\)(с конечным носителем) с симметричными коэффициентами \begin{equation}\label{w.25} a_{-i}=a_{i},\,\,\,\,(i\in Z). \end{equation} Сдвиг массива \(A\) на \(\nu\) будем обозначать через \( A_{\nu}=\left\{a_{i-\nu}\right\}_{i\in Z}. \)
Положим \( \left\lt A,B_{\nu}\right>=\sum_{i\in Z}a_{i}b_{i-{\nu}} \) и \( A\times B_{\nu}=\sum_{i\in Z}a_{i}b_{{\nu}-i}. \)
Для массива \(H\in\Re\) положим \[ H^+= \left\{ \begin{array}{lc} h_{i}, & i\in Z^+, \\ 0, & i\in Z^- \end{array} \right. \hbox{ и } H^-=\left\{ \begin{array}{lc} 0, & i\in Z^+, \\ h_{i}, & i\in Z^-, \end{array} \right. \] кроме того, пусть \( \mathbb{H}^+=H^++H^-=\{h^+_{i}\}_{i\in Z} \) и \( \mathbb{H}^-=H^+-H^-=\{h^-_{i}\}_{i\in Z}. \)

Лемма 1. Для всех \(\nu\in Z\) имеет место равенство \begin{equation}\label{w.26} \left\lt \mathbb{H}^+,\mathbb{H}^-_{\nu}\right>=0. \end{equation}

Доказательство. Пусть, вначале, \(\nu\in Z^-\). Ясно, что \[ \left\lt \mathbb{H}^+,\mathbb{H}^-_{\nu}\right>=\sum_{i\in Z^+}h_{i}h^-_{i-\nu}+ \sum_{i\in Z^-}h_{i}h^-_{i-\nu}. \] Замечая, что если \(i\in Z^+\) и \(\nu \in Z^-\), то \((i-\nu)\in Z^-\) и, соответственно, если \(i\in Z^-\) и \(\nu \in Z^-\), то \((i-\nu)\in Z^+\), таким образом имеем равенство \[ \left\lt \mathbb{H}^+,\mathbb{H}^-_{\nu}\right>=-\sum_{i\in Z^+}h_{i}h_{i-\nu}+ \sum_{i\in Z^-}h_{i}h_{i-\nu},\] которое после замены переменных в первом слагаемом можно переписать в виде \[\left\lt \mathbb{H}^+,\mathbb{H}^-_{\nu}\right>=-\sum_{i\in Z^-}h_{i}h_{i+\nu}+ \sum_{i\in Z^-}h_{i}h_{i-\nu}. \] Отсюда, в силу условия (\ref{w.25}) сразу следует справедливость соотношения (\ref{w.26}). Для \(\nu \in Z^+\) доказательство аналогично.
Будем говорить, что массивы \(\mathbb{H}^+\) и \(\mathbb{G}^+\) образуют биортогональную пару, если для всех \(n,\nu \in Z^+\) имеет место соотношение \begin{equation}\label{w.27} \left\lt \mathbb{H}^+_{n},\mathbb{G}^+_{\nu}\right>= \left\{ \begin{array}{lc} 1, & n=\nu, \\ 0, & \textrm{иначе}. \end{array} \right. \end{equation}

Лемма 2. Если массивы \(\mathbb{H}^+\) и \(\mathbb{G}^+\) образуют биортогональную пару, то для всех \(n,\nu \in Z^-\) имеет место соотношение \begin{equation}\label{w.28} \left\lt \mathbb{H}^-_{n},\mathbb{G}^-_{\nu}\right>= \left\{ \begin{array}{lc} 1, & n=\nu, \\ 0, & \textrm{иначе}. \end{array} \right. \end{equation}

Доказательство. Действительно, \[ \left\lt \mathbb{H}^-_{n},\mathbb{G}^-_{\nu}\right> =\sum_{i\in Z^+}h^-_{i-n}g^-_{i-\nu}+ \sum_{i\in Z^-}h^-_{i-n}g^-_{i-\nu}. \] Замечая, что для \(i\in Z^+\) \[ h^-_{i-n}=-h_{i-n} \hbox{ и } g^-_{i-\nu}=-g_{i-\nu} \] а для \(i\in Z^-\) \[ h^-_{i-n}=h_{i-n} \hbox{ и } g^-_{i-\nu}=g_{i-\nu} \] сразу получаем \[ \left\lt \mathbb{H}^-_{n},\mathbb{G}^-_{\nu}\right> =\sum_{i\in Z^+}h_{i-n}g_{i-\nu}+ \sum_{i\in Z^-}h_{i-n}g_{i-\nu}=\sum_{i\in Z}h_{i-n}g_{i-\nu}=\sum_{i\in Z}h_{i}g_{i-\nu+n}. \] Отсюда, из того факта, что \((-\nu+n)\in Z^+\) и из (\ref{w.27}) сразу следует утверждение леммы.
Положим \begin{equation}\label{w.29} \mathbb{H}_{\nu}=\left\{{\bf h}_{i-\nu}\right\}_{i\in Z}= \left\{ \begin{array}{lc} \mathbb{H}^+_{\nu}, & \nu \in Z^+, \\ \mathbb{G}^-_{\nu} & \nu \in Z^- \end{array} \right. \hbox{ и } \mathbb{G}_{\nu}=\left\{{\bf g}_{i-\nu}\right\}_{i\in Z}= \left\{ \begin{array}{lc} \mathbb{G}^+_{\nu}, & \nu \in Z^+, \\ \mathbb{H}^-_{\nu} & \nu \in Z^-. \end{array} \right. \end{equation} Для биортогональной пары \(H,G\in\Re\) положим \[ \mathbb{U}_\nu= \left\{ \begin{array}{lc} G^+_\nu-H^-_\nu, & \nu\in Z^+, \\ H^+_\nu+G^-_\nu, & \nu\in Z^-, \end{array} \right. \hbox{ и } \mathbb{V}_\nu= \left\{ \begin{array}{lc} H^+_\nu-G^-_\nu, & \nu\in Z^+, \\ G^+_\nu+H^-_\nu, & \nu\in Z^-. \end{array} \right. \]

Теорема 1. Если \(F\) массив конечным носителем, то \[ f_\nu=\mathbb{C}\times \mathbb{G}_\nu=\mathbb{D}\times \mathbb{H}_\nu, \] где \[ \mathbb{C}=\left\{\left\lt F,\mathbb{H}_{n}\right>\right\}, \mathbb{D}=\left\{\left\lt F,\mathbb{G}_{n}\right>\right\}. \]

Доказательство. Действительно, \[ \mathbb{C}\times \mathbb{G}_\nu=\sum_{n\in Z}\left\lt F,\mathbb{H}_{n}\right>{\bf g}_{{\nu}-n}= \sum_{n\in Z}\left(\sum_{k\in Z}f_k{\bf h}_{k-n}\right){\bf g}_{{\nu}-n}=\sum_{k\in Z}f_k\left\lt \mathbb{H}_{-k},\mathbb{G}_{-\nu}\right>. \] Пусть \(\nu,k\in Z^+\),тогда из (\ref{w.27}) сразу получаем \[ \left\lt \mathbb{H}_{-k},\mathbb{G}_{-\nu}\right>=\left\lt \mathbb{H}^+_{-k},\mathbb{G}^+_{-\nu}\right>= \left\{ \begin{array}{lc} 1, & k=\nu, \\ 0, & \textrm{иначе} \end{array} \right. \] если \(\nu\in Z^+\) и \(k\in Z^-\), то в силу (\ref{w.26}) имеем \[ \left\lt \mathbb{H}_{-k},\mathbb{G}_{-\nu}\right>=\left\lt \mathbb{G}^-_{-k},\mathbb{G}^+_{-\nu}\right>=0 \] и, следовательно, для \(\nu\in Z^+\) \[ \mathbb{C}\times \mathbb{G}_\nu=\sum_{k\in Z^+}f_k\left\lt \mathbb{H}_{-k},\mathbb{G}_{-\nu}\right>+\sum_{k\in Z^-}f_k\left\lt \mathbb{H}_{-k},\mathbb{G}_{-\nu}\right>=f_\nu. \] Пусть, теперь \(\nu\in Z^-\) \[ \mathbb{C}\times \mathbb{G}_\nu=\sum_{k\in Z^+}f_k\left\lt \mathbb{H}_{-k},\mathbb{G}_{-\nu}\right>+\sum_{k\in Z^-}f_k\left\lt \mathbb{H}_{-k},\mathbb{G}_{-\nu}\right>= \sum_{k\in Z^+}f_k\left\lt \mathbb{H}^+_{-k},\mathbb{H}^-_{-\nu}\right>+\sum_{k\in Z^-}f_k\left\lt \mathbb{G}^-_{-k},\mathbb{H}^-_{-\nu}\right>. \] Отсюда, из (\ref{w.26}) и (\ref{w.28}) сразу получаем \[ \mathbb{C}\times \mathbb{G}_\nu=f_\nu. \] Вторая часть доказывается аналогично.
Таким образом, если у нас построена биортогональная пара массивов, то результаты теоремы 1 предоставляют формулы декомпозиции и реконструкции для любого массива с конечным носителем.

Теорема 2. Если \(F\) массив с конечным носителем, то \[ F=\left\{\left\lt \left\lt F,\mathbb{H}_\nu\right>,\mathbb{U}_\nu\right>\right\}_{\nu\in Z}=\left\{\left\lt \left\lt F,\mathbb{G}_\nu\right>,\mathbb{V}_\nu\right>\right\}_{\nu\in Z}. \]

Действительно, пусть, вначале, \(\nu \in Z^+\), тогда из результатов теоремы 1 имеем \[ f_\nu=\sum_{n\in Z}\left\lt F,\mathbb{H}_{n}\right>{\bf g}_{{\nu}-n}= \sum_{n\in Z^+}\left\lt F,\mathbb{H}_{n}\right>{\bf g}_{{\nu}-n}+\sum_{n\in Z^-}\left\lt F,\mathbb{H}_{n}\right>{\bf g}_{{\nu}-n}= \sum_{n\in Z^+}\left\lt F,\mathbb{H}_{n}\right>g_{{\nu}-n}+\sum_{n\in Z^-}\left\lt F,\mathbb{H}_{n}\right>(-h_{\nu-n})= \left\lt \left\lt F,\mathbb{H}_{\nu}\right>,\mathbb{U}_{\nu}\right>. \] Если \(\nu\in Z^-\), то \[ f_{\nu}=\sum_{i\in Z^+}\left\lt F,\mathbb{H}_{i-\nu}\right>g^+_{i-\nu}+ \sum_{i\in Z^-}\left\lt F,\mathbb{H}_{i-\nu}\right>g^-_{i-\nu}= \sum_{i\in Z^+}\left\lt F,\mathbb{H}_{i-\nu}\right>g_{i-\nu}+ \sum_{i\in Z^-}\left\lt F,\mathbb{H}_{i-\nu}\right>h_{i-\nu}=\left\lt \left\lt F,\mathbb{H}_{\nu}\right>,\mathbb{U}_{\nu}\right>. \] Аналогично доказывается вторая часть.
Таким образом, при таком подходе алгоритм обратного хода отличается от алгоритма прямого хода только конструкцией фильтра. Следовательно, число вычислений для обратного хода всплеск-преобразований равно числу вычислений при прямом ходе.
В реальных задачах при построении цифровых фильтров используются методы точные на тех или иных тестовых множествах. Как правило, используются методы точные на алгебраических полиномах.
Дальнейшие наши рассуждения посвящены задаче построения масштабирующих функций точных на полиномах. Базисы порожденные такими функциями называются койфлетами.
Для \(n=0,1,\ldots\) положим \( M^\pm_{n}(H)=\sum_{i\in Z^\pm}i^nh_{i}, \) и \( M_{n}(H)=\sum_{i\in Z}i^nh_{i}=M^+_{n}(H)+M^-_{n}(H), \)
Заметим, что после замены \(i=-k\) в силу условия (\ref{w.25}), получаем \[ M^\pm_{2n-1}(H)= \sum_{k\in Z^\pm}(-k)^{2n-1}h_{-k}= -\sum_{k\in Z^\pm}k^{2n-1}h_{k}=-M^\pm_{2n-1}(H), \] таким образом, \( M^\pm_{2n-1}(H)=0. \)
Отсюда сразу получаем, что если хотя бы одно из значений \(n\) или \(m\) нечетное, то \( M^\pm_{n}(H)=0. \)
Кроме того, пусть \( P^{n}=\{i^n\}_{i\in Z}\,\,\,\,\,(0^0=1). \)

Теорема 3. Если \(H,G\in\Re\) таковы, что \( M^\pm_{0}(H)=M^\pm_{0}(G)=\frac{1}{\sqrt{2}} \) и для \(n=0,1,2,\ldots\) \(0\lt n+m\lt N\) выполняется равенство \( M^\pm_{n}(H)=M^\pm_{n}(G)=0, \) то для \(\nu \in Z^-\) \[ \left\lt P^{n},\mathbb{H}_{\nu}\right>= \left\lt P^{n},\mathbb{G}_{\nu}\right>=0. \]

Доказательство. Из определения (\ref{w.29}) следует, что для \(\nu \in Z^-\) \[ \left\lt P^{n},\mathbb{H}_{\nu}\right>= \left\lt P^{n},\mathbb{G}^-_{\nu}\right>= \sum_{i\in Z}i^ng^-_{i-\nu}= \sum_{i\in Z}(i+\nu)^ng^-_{i}= \nu^n\sum_{i\in Z^+}g_{i}+ n\nu^{n-1}\sum_{i\in Z^+}ig_{i}+\ldots+ \sum_{i\in Z^+}i^ng_{i} -\nu^n\sum_{i\in Z^-}g_{i}- n\nu^{n-1}\sum_{i\in Z^-}ig_{i}-\ldots- \sum_{i\in Z^-}i^ng_{i}. \] Отсюда и из условия теоремы 3 сразу получаем для \(\nu\in Z^-\) \[ \left\lt P^{n},\mathbb{H}_{\nu}\right>=\nu^nM^+_{0}(G)-\nu^nM^-_{0}(G)=0. \] Вторая часть доказывается аналогично.

Следствие 1. Если \(H,G\in\Re\) удовлетворяют условию теоремы 3, то \[ P^{n}=\sum_{i\in Z^+}\left\lt P^{n},\mathbb{H}_{i}\right>\mathbb{G}_{i}= \sum_{i\in Z^+}\left\lt P^{n},\mathbb{G}_{i}\right>\mathbb{H}_{i}. \]

Доказательство. Пусть, вначале, \(n=0\), тогда \(P^{0}_{\nu}=1\) для всех \(\nu \in Z\).
С другой стороны, \[ \left\lt P^{0},\mathbb{H}_{\nu}\right>=\sum_{i\in Z}h_{i-\nu}= \sum_{i\in Z}h_{i}=M_{0}(H), \] и \[ \sum_{i\in Z^+}M_{0}(H)\mathbb{G}_{i-\nu}= M_{0}(H)\sum_{i\in Z^+}\mathbb{G}_{i-\nu}. \] Если \(\nu \in Z^+\), то для \(i\in Z^+\) будет выполняться условие \((i-\nu)\in Z^+\) и, следовательно, \[ \sum_{i\in Z^+}M_{0}(H)\mathbb{G}_{i-\nu}= M_{0}(H)\sum_{i\in Z^+}\mathbb{G}_{i}=M_{0}(H)M^+_{0}(G)=1. \] Если же \(\nu \in Z^-\), то для \(i\in Z^+\) будет \((i-\nu)\in Z^-\) и, \[ \sum_{i\in Z^+}M_{0}(H)\mathbb{G}_{i-\nu}= M_{0}(H)\sum_{i\in Z^-}\mathbb{G}_{i}=M_{0}(H)M^-_{0}(G)=1. \] Пусть, далее, \(n\) таковы, что \(n+m>0\), тогда \[ \left\lt P^{n},\mathbb{H}_{\nu}\right>= \sum_{i\in Z}i^nh_{i-\nu}= \sum_{i\in Z}(i+\nu)^nh_{i}= \sum_{i\in Z}\left( \sum_{\xi=0}^nC_n^\xi i^\xi\nu^{n-\xi}\right)h_{i}= \sum_{i\in Z}\left( \nu^n+n\nu^{n-1}i+\ldots+i^n \right)h_{i}= \] \[ =\nu^n\sum_{i\in Z}h_{i}+ n\nu^{n-1}\sum_{i\in Z}ih_{i}+\ldots+ \sum_{i\in Z}i^nh_{i}= \nu^n\sum_{i\in Z^+}h_{i}+ n\nu^{n-1}\sum_{i\in Z^+}ih_{i}+\ldots+ \sum_{i\in Z^+}i^nh_{i}+ \nu^n\sum_{i\in Z^-}h_{i}+ n\nu^{n-1}\sum_{i\in Z^-}ih_{i}+\ldots+ \sum_{i\in Z^-}i^nh_{i}. \] В силу условия отсюда сразу получаем \[ \left\lt P^{n},\mathbb{H}_{\nu}\right>= \nu^n\sum_{i\in Z}h_{i}=\nu^nM_{0}(H). \] Далее, \[ \sum_{i\in Z^+}\left\lt P^{n},\mathbb{H}_{\nu}\right>\mathbb{G}_{i-\nu}= \sum_{i\in Z^+}\nu^nM_{0}(H)\mathbb{G}_{i-\nu} \] и если \(\nu \in Z^+\), то \[ \sum_{i\in Z^+}\left\lt P^{n},\mathbb{H}_{\nu}\right>\mathbb{G}_{i-\nu}= \nu^nM_{0}(H)M^+_{0}(G)=\nu^n=P^{n}_{\nu} \] а если \(\nu \in Z^-\), то \[ \sum_{i\in Z^+}\left\lt P^{n},\mathbb{H}_{\nu}\right>\mathbb{G}_{i-\nu}= \nu^nM_{0}(H)M^-_{0}(G)=\nu^n=P^{n}_{\nu}. \] В качестве примера приведем расчет классической биортогональной пары 3-5 Коэна-Добеши- Фово.
Пусть \(n=1\) и потребуем точности фильтра на константе. Тогда, следуя теоереме 3, коэффициенты \(a_i\) \((i=0,1)\) фильтра удовлетворяют условию \[\left\{ \begin{array}{c} a_0=\frac{1}{\sqrt{2}},\\ 2a_1=\frac{1}{\sqrt{2}}, \end{array} \right. \hbox{ а для } n=2 \hbox{ } \left\{ \begin{array}{c} b_0+2b_2=\frac{1}{\sqrt{2}},\\ 2b_1=\frac{1}{\sqrt{2}}, \end{array} \right. \hbox{ то есть } b_1 = \frac{\sqrt{2}}{4}, b_0 = -2b_2+\frac{\sqrt{2}}{2}. \] В этом случае условие биортогональности имеет вид \[ \frac{1}{8}+\frac{b_2\sqrt{2}}{2}=0 \hbox{ и } \frac{3}{4} -\sqrt{2}b_{{2}}=1. \] Таким образом, отсюда сразу получаем биортогональную пару \[ a_{-1}=\frac{\sqrt{2}}{4},a_0=\frac{\sqrt{2}}{2},a_1=\frac{\sqrt{2}}{4}, \] \[ b_{-2}=-\frac{\sqrt{2}}{8}, b_{-1}=\frac{\sqrt{2}}{4},b_0=\frac{3\sqrt{2}}{4},b_1=\frac{\sqrt{2}}{4},b_2=-\frac{\sqrt{2}}{8}. \]

Использование кратномасштабного анализа не является единственным методом для построения базиса всплесков. Принципиально иным методом для построения биортогональных всплесков явилось введение Wim Sweldens конструкции лифтинг-схемы.
Формально лифтинг-схема для построения биортогональных всплесков мажет быть сформулирована в следующем виде:

Теорема 3. Пусть \(\{H^{old},\widetilde{H}^{old}\}\) и \(\{G^{old},\widetilde{G}^{old}\}\) пара биортогональных фильтров, тогда фильтры \(\{H^{new},\widetilde{H}^{new}\}\) и \(\{G^{new},\widetilde{G}^{new}\}\) определяемые из условия \[ \begin{array}{l} h^{new}_{\textbf{i}}=h^{old}_{\textbf{i}}, \\ \widetilde{h}^{new}_{\textbf{i}}=\widetilde{h}^{old}_{\textbf{i}}+\sum_{\textbf{j}}s_{\textbf{j}}{g}^{old}_{\textbf{j} -\textbf{i}},\\ {g}^{new}_{\textbf{i}}={g}^{old}_{\textbf{i}}-\sum_{\textbf{j}}s_{\textbf{j}}\widetilde{h}^{old}_{\textbf{j} -\textbf{i}},\\ \widetilde{g}^{new}_{\textbf{i}}=\widetilde{g}^{old}_{\textbf{i}}. \end{array} \] также будут биортогональными.

Ключевым моментом лифтинга является выбор коэффициентов \(s_{\textbf{i}}\). Как правило, их выбор определяется требованием обнуления моментов у полученных всплесков.
Кроме того, \(\textbf{i}\) есть мультииндекс - лифтинг-схема может быть использована для построения базиса всплесков для случая нескольких переменных.
Приведем пример использования лифтинга для построения пары биортогональных всплесков.
В качестве стартовой биортогональной пары возьмем всплески Хаара, то есть масштабирующие функции \[H(x)=G(x)=\chi(x),\] где \[ \chi(x)=\left\{ \begin{array}{cc} 1, & x\in [0,1] \\ 0, & \textrm{иначе} \end{array} \right. \] и соответствующие всплески \( \widetilde{H}(x)=\widetilde{G}(x)=\widetilde{\chi}(x)=\chi(2x)-\chi(2x-1). \)
Следуя приведенной схеме, запишем новый всплеск в виде \[ \widetilde{H}^{new}(x)=\widetilde{H}(x)+s_{-1}{G}(x+1)+s_{0}{G}(x)+s_{1}{G}(x-1) =\widetilde{\chi}(x)+s_{-1}{\chi}(x+1)+s_{0}{\chi}(x)+s_{1}{\chi}(x-1). \] Коэффициенты \(s_i\) выберем из условия обнуления моментов \( \int_0^1x^n\widetilde{H}^{new}(x)dx=0. \)
Для этого случая максимальное число нулевых моментов равно трем и при этом \( s_{-1}=-\frac{1}{8},s_{0}=0,s_{1}=\frac{1}{8}. \)
Таким образом новый всплеск имеет вид \( \widetilde{H}^{new}(x)=\widetilde{\chi}(x)-\frac{1}{8}\chi(x+1)+\frac{1}{8}\chi(x-1), \) соответственно новая биортогональная масштабирующая функция имеет вид \[ {G}^{new}(x)=G(x)-s_{-1}\widetilde{H}(x+1)-s_{0}\widetilde{H}(x)-s_{1}\widetilde{H}(x-1)= {\chi}(x)-\frac{1}{8}\widetilde{\chi}(x+1)+\frac{1}{8}\widetilde{\chi}(x-1) \] \[ ={\chi}(2x)+{\chi}(2x-1)-\frac{1}{8} {\chi}(2x+2)+ \frac{1}{8}{\chi}(2x+1) +\frac{1}{8}\chi(2x-2)-\frac{1}{8}\chi(2x-3). \] Коэффициенты соответствующего фильтра равны \( -\frac{1}{8},\frac{1}{8},1,1,\frac{1}{8},-\frac{1}{8}, \) то есть, получили фильтр, порожденный интерполяционным в среднем методом subdivision.
Для конструкции с помощью лифтинга интерполяционных схем всплеск- преобразований, в качестве стартовой биортогональной пары (начального приближения) можно использовать "ленивые" всплески, которые всего лишь разделяют исходные данные по четным и нечетным индексам, то есть базис "ленивых" всплесков определен значениями \(\delta-\) функции Дирака: \( H(x)=G(x)=\delta(x). \)
Еще немного об идеологии лифтинга.
Идея лифтинга состоит в реализации метода предсказания - уточнения (predict- update) данных. Обрабатываемые данные разбиваются на две группы, например, с четными и нечетными индексами. Значения декомпозиции с нечетными номерами прогнозируются по значениям элементов с четными номерами. После этого находится ошибка прогноза и в соответствии с этой ошибкой производится коррекция значений элементов с четными номерами. Для прогноза, как правило, используются интерполяционные формулы, например, интерполяционные полиномы (чаще всего кубические).
Идеология "предсказание-уточнение" является итерационным методом построения фильтров. Используя в качестве стартового набор простых фильтров, можно, последовательно применяя к этим фильтрам шаги лифтинга, получать новые фильтры обладающие заданными свойствами.
С другой стороны, применяя идеологию лифтинга непосредственно к обрабатываемым данным, получаем лифтинговую (пошаговую) схему обработки данных.
Формально один шаг лифтинг-схемы может быть записан в виде \begin{equation}\label{lift} \begin{array}{l} c_{2n}^{i}=c^{i-1}_{2n}-\sum_{\nu}\alpha_\nu^{i}c^{i-1}_{2\nu+1}, \\ c_{2n+1}^{i}=c^{i-1}_{2n+1}-\sum_{\nu}\beta_\nu^{i}c^{i-1}_{2\nu} \end{array} \end{equation} с последующим масштабированием полученных коэффициентов \( c_{2n}^{i}=kc_{2n}^{i},\,\,\,\,c_{2n+1}^{i}=\frac{1}{k}c_{2n+1}^{i}. \)
Результатом использования этой схемы будет два новых набора коэффициентов \(c_{2n}^{i}\) (низкочастотная составляющая) и \(c_{2n+1}^{i}\) (высокочастотная составляющая сигнала). Обратное преобразование реализуется теми же формулами записанными в обратном порядке и с обратными знаками.
Лифтинг позволяет конструировать новые схемы всплеск- преобразований, в том числе и такие, которые другим способом получить сложно (в частности, преобразования, базисные функции которых не являются сдвигами и сжатиями одной функции, то есть без использования кратномасштабного анализа).
Важным достоинством лифтинг-схемы является возможность построения такой конструкции, что если исходные значения даны в целых числах, то всплеск-преобразование также будет целочисленным. При этом обратное преобразование является точным.
Лифтинг-схема одного шага целочисленного (integer-to-integer) всплеск-преобразования имеет вид \begin{equation}\label{lift_I} \begin{array}{l} c_{2n}^{i}=c^{i-1}_{2n}-\left[\sum_{\nu}\alpha_\nu^{i}c^{i-1}_{2\nu+1}+\frac{1}{2}\right], \\ c_{2n+1}^{i}=c^{i-1}_{2n+1}-\left[\sum_{\nu}\beta_\nu^{i}c^{i-1}_{2\nu}+\frac{1}{2}\right] \end{array} \end{equation} В качестве примера приведем лифтинговые схемы реализованные в формате JPEG2000.
Целочисленное преобразование для сжатия без потерь имеет следующий вид.
Декомпозиция \[ c_{2n}^{1}=c^{0}_{2n}-\left[\frac{c^{0}_{2n-1}+c^{0}_{2n+1}+2}{4}\right], c_{2n+1}^{1}=c^{0}_{2n+1}+\left[\frac{c^{1}_{2n}+c^{1}_{2n+2}}{2}\right]. \] Реконструкция \[ c_{2n+1}^{0}=c^{1}_{2n+1}-\left[\frac{c^{1}_{2n}+c^{1}_{2n+2}}{2}\right], c_{2n}^{0}=c^{1}_{2n}+\left[\frac{c^{0}_{2n-1}+c^{0}_{2n+1}+2}{4}\right]. \] Для высоких степеней сжатия JPEG2000 использует биортогональную пару 7-9. В этом случае лифтиноговая схема для декомпозиции выглядит следующим образом \[ \left\{ \begin{array}{llll} c_{2n}^{1}&\longleftarrow & k c_{2n}^{0}, & \textrm{первый шаг}, \\ c_{2n+1}^{1}&\longleftarrow & -\frac{1}{k} c_{2n+1}^{0}, & \textrm{второй шаг}, \\ c_{2n}^{1}&\longleftarrow & c_{2n}^{1}-\delta (c_{2n-1}^{1}+c_{2n+1}^{1}), & \textrm{третий шаг}, \\ c_{2n+1}^{1}&\longleftarrow & c_{2n+1}^{1}-\gamma (c_{2n}^{1}+c_{2n+2}^{1}), & \textrm{четвертый шаг}, \\ c_{2n}^{1}&\longleftarrow & c_{2n}^{1}-\beta (c_{2n-1}^{1}+c_{2n+1}^{1}), & \textrm{пятый шаг}, \\ c_{2n+1}^{1}&\longleftarrow & c_{2n+1}^{1}-\alpha (c_{2n}^{1}+c_{2n+2}^{1}), & \textrm{шестой шаг}. \end{array} \right. \] где \[ \alpha=-1.586 134 342,\beta=-0.052 980 118 , \gamma=0.882 911 075,\delta=0.443 506 852,\] и масштабирующий коэффициент \(k=1.230 174 105.\)
Реконструкция сигнала производится следующим образом \[ \left\{ \begin{array}{llll} c_{2n+1}^{0}&\longleftarrow &c_{2n+1}^{1}+\alpha (c_{2n}^{1}+c_{2n+2}^{1}), & \textrm{первый шаг},\\ c_{2n}^{0}&\longleftarrow &c_{2n}^{1}+\beta (c_{2n-1}^{0}+c_{2n+1}^{0}), & \textrm{второй шаг}\\ c_{2n+1}^{0}&\longleftarrow &c_{2n+1}^{0}+\gamma (c_{2n}^{0}+c_{2n+2}^{0}), & \textrm{третий шаг}\\ c_{2n}^{0}&\longleftarrow &c_{2n}^{0}+\delta (c_{2n-1}^{0}+c_{2n+1}^{0}), & \textrm{четвертый шаг}, \\ c_{2n+1}^{0}&\longleftarrow &-\frac{1}{k} c_{2n+1}^{0}, &\textrm{пятый шаг}, \\ c_{2n}^{0}&\longleftarrow &k c_{2n}^{0}, &\textrm{шестой шаг}. \end{array} \right. \]

Для исследования случая двух переменных обобщим естественным образом понятие кратномасштабного анализа на случай двух переменных.
Через \(L^2(R^n_2)\) будем обозначать гильбертово пространство функций с конечной нормой \(\|f\|_2=\int_{R^n_2}|f(x,y)|^2dxdy,\) порожденное скалярным произведением \(\left\lt f,g\right>=\int_{R^n_2}f(x,y)\overline{g(x,y)}dxdy.\)

Определение 2. Кратномасштабный анализ (КМА) в \(L^2(R^n_2)\) это последовательность замкнутых подпространств \( \ldots\subset \textbf{V}^{-1}\subset \textbf{V}^{0}\subset \textbf{V}^{1}\subset \ldots \) для которых выполняются условия

1. \(\overline{\cup_{j\in Z}{\textbf{V}^j}}=L^2(R^n_2);\)
2. \(\cap_{j\in Z}{\textbf{V}^j}=\{0\};\)
3. \(f(x,y)\in \textbf{V}^j\Longleftrightarrow f(2\cdot,2\cdot\cdot)\in \textbf{V}^{j+1};\)
4. найдется такая функция \(\varphi\in \textbf{V}^0\) (масштабирующая функция), что множество ее сдвигов \(\varphi(x-n,y-m)\) образует ортонормированный базис пространства \(L^2(R^n_2)\).

Наиболее простой способ построения многомерного КМА конструируется как тензорное произведение одномерных. Такие КМА называются сепарабельными, общий случай КМА, не распадающийся в тензорное произведение, называется несепарабельным.
Внвчвле уделим внимание сепарабельному случаю.
Пусть \(\textbf{V}^j\) есть тензорное произведение пространства \(V^j\) само на себя, то есть \( \textbf{V}^j=V^j\otimes V^j=\textrm{Span}\{f(x)g(y)|f,g\in V^j\}. \)
Здесь \(\textrm{Span} \{S\}\) есть линейная оболочка множества \(S\).
Опишем один из наиболее популярных методов построения сепарабельных всплесков. Этот метод был предложен S.Mallat и называется схемой Малла.
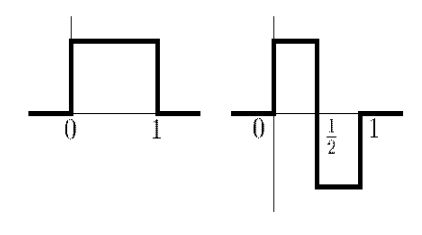
В качестве базиса пространства \(\textbf{V}^0\) возьмем совокупность функций \(\varphi(x-n)\varphi(y-m)\).
Таким образом в этом пространстве базис порожден функцией \(\varphi(x,y)=\varphi(x)\varphi(y)\), а в качестве функций порождающих базис ортогонального дополнения \(\textbf{W}^0\) можно взять функции \(\psi_1(x,y)=\varphi(x)\psi(y)\), \(\psi_2(x,y)=\psi(x)\varphi(y)\), \(\psi_3(x,y)=\psi(x)\psi(y)\).
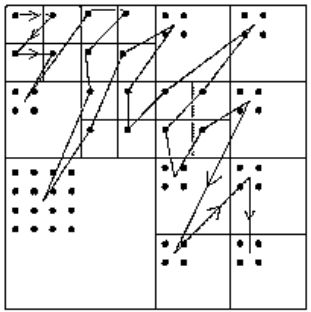
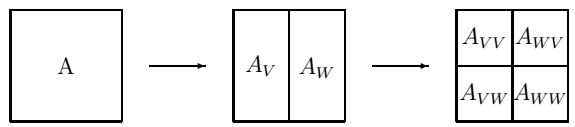
Схематически процедура вейвлет-преобразования двумерных данных пространства \(\textbf{V}^1\) проиллюстрирована на следующем рисунке. То есть, на первом этапе распределяем коэффициенты разложения по сдвигам масштабирующей функции пространства \(\textbf{V}^1\) в виде матрицы (в общем случае бесконечной). Применяя последовательно к коэффициентам каждой строки одномерный алгоритм разложения на пространство \(V\) и ортогональное дополнение \(W\), получаем две матрицы \(A_V\) (низкочастотный домен) и \(A_W\) (высокочастотный домен), которые соответствуют этим пространствам. На втором этапе этот же алгоритм применяется к столбцам каждой из полученных матриц. В результате из каждой матрицы вновь получается две. Результат применения масштабирующего фильтра к матрице \(A_V\) даст матрицу \(A_{VV}\), всплеского фильтра - матрицу \(A_{VW}\). Результатом аналогичного преобразования матрицы \(A_{W}\) есть матрицы \(A_{WV}\) и \(A_{WW}\). Пространство всплесков в этом случае можно записать в виде \[ \textbf{W}^0=\left(W^0\otimes W^0\right)\oplus \left(W^0\otimes V^1\right)\oplus\left(V^0\otimes W^1\right). \] Применяя последовательно описанный алгоритм к \(A_{VV}\), получаем каскадный алгоритм вейвлет преобразования двумерных данных. 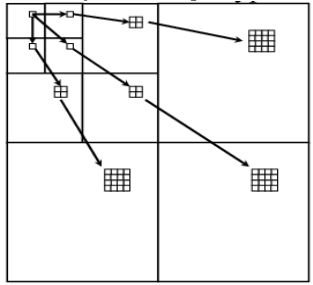Описанная схема не является единственной. Среди большого набора методов обработки двумерных данных приведем еще один - использование вейвлет пакетов. В отличие от каскадного алгоритма, при использовании вейвлет-пакетов одномерное вейвлет-пребразование применяется к каждому частотному домену (то есть к каждой из матриц \(A_{VV}\), \(A_{VW}\), \(A_{WV}\) и \(A_{WW}\)).
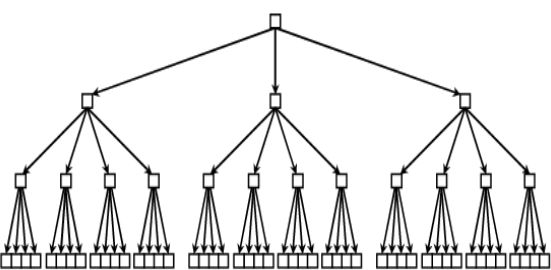
Схема полного пакета может быть проиллюстрирована следующим образом. Как правило, на практике к каждому последующему высокочастотному домену применяется базис другого КМА. Кроме того, полный пакет всплесков редко используется ввиду больших временных и вычислительных затрат. Целесообразно использовать выборочную, а не полную пакетную схему. Заметим, что в этом случае схема восстановлнгия существенно усложняется, так как при восстановлении значения с каждого частотного домена нужно брать разное число коэффициентов. Например для схемы восстановление будет проходить следующим образом

Построение несепарабельных зеркально- квадратурных всплесков

Несмотря на простоту реализации КМА образованного тензорным произведением базиса всплесков, безусловно для обработки двумерных данных более эффективным является использование существенно двумерных, то есть несепарабельных всплесков.
В данном параграфе мы рассмотрим конструкцию несепарабельного базиса всплесков.
Пусть имеет место масштабирующее свойство \begin{equation}\label{w.40} \varphi(x,y)=\varphi^0(x,y)=\sum_{(\nu,\mu)\in Z^2} h_{\nu,\mu} \varphi^1\left(x-\frac{\nu}{2},y-\frac{\mu}{2}\right). \end{equation}
Для преобразования Фурье соотношение (\ref{w.40}) можно записать в виде \[ \hat{\varphi}(\omega_1,\omega_2)=\sum_{(\nu,\mu)\in Z^2} h_{\nu,\mu} \exp{\left(- \frac{i}{2}(\nu\omega_1+\mu\omega_2)\right)} \hat{\varphi}^1(\omega_1,\omega_2)= m_{\varphi\varphi^1}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right)\hat{\varphi}^1(\omega_1,\omega_2). \] При этом в силу равенства Парсеваля имеет место тождество \[ 1=\sum_{(\nu,\mu)\in Z^2}|\hat{\varphi}(\omega_1+2\pi\nu,\omega_2+2\pi\mu)|^2= \sum_{(\nu,\mu)\in Z^2}\left|m_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi\nu,\frac{\omega_2}{2}+\pi\mu\right)\right|^2 \left|\hat{\varphi}^1(\omega_1+2\pi\nu,\omega_2+2\pi\mu,)\right|^2=\] \[ =\sum_{(\nu,\mu)\in Z^2}\left(\left|m_{\varphi\varphi^1} \left(\frac{\omega_1}{2}+2\pi\nu, \frac{\omega_2}{2}+2\pi\mu\right)\right|^2+\right. \left|m_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+2\pi\nu, \frac{\omega_2}{2}+\pi(2\mu+1)\right)\right|^2 +\left|m_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi(2\nu+1), \frac{\omega_2}{2}+2\pi\mu\right)\right|^2+\] \[\left. +\left|m_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi(2\nu+1), \frac{\omega_2}{2}+\pi(2\mu+1)\right)\right|^2\right) \sum_{(\nu,\mu)\in Z^2}|\hat{\varphi}^1(\omega_1+2\pi\nu,\omega_2+2\pi\mu)|^2, \] что влечет выполнение почти всюду соотношения \[ \left|m_{\varphi\varphi^1}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right)\right|^2+ \left|m_{\varphi\varphi^1}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\pi\right)\right|^2 +\left|m_{\varphi\varphi^1}\left(\frac{\omega_1}{2}\pi,\frac{\omega_2}{2}\right)\right|^2+ \left|m_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi,\frac{\omega_2}{2}+\pi\right)\right|^2=1. \] Далее, для \(f\in V_1\) выполняется соотношение \[ f(x,y)=\sum_{(\nu,\mu)\in Z^2}f_{\nu,\mu} \varphi^1\left(x-\frac{\nu}{2},y-\frac{\mu}{2}\right) \] и соответственно, для преобразования Фурье \[ \hat{f}(\omega_1,\omega_2)=\sum_{(\nu,\mu)\in Z^2}f_{\nu,\mu}\exp{\left(-i\frac{\nu\omega_1+\mu\omega_2}{2}\right)} \hat{\varphi}^1\left(\omega_1,\omega_2\right)= m_f\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right)\hat{\varphi}^1\left(\omega_1,\omega_2\right). \] Из того, что \(f\perp V_0\), то есть \(f\perp \overline{\varphi}(x-k) \forall k\in Z^2\) или что то же \[ 0=\int_{R^2}f(x,y)\overline{\varphi}(x-n,y-m)dxdy =\frac{1}{(2\pi)^2}\int_{R^2}\hat{f}(\omega)\overline{\hat{\varphi}}(\omega_1,\omega_2)\exp{\left(i(n\omega_1+m\omega_2) \right)}d\omega_1d\omega_2=\] \[=\frac{1}{4\pi^2}\int_0^{2\pi}\int_0^{2\pi}\exp{\left(i(n\omega_1+m\omega_2)\right)}\sum_{(\nu,\mu\in Z^2)} \hat{f}(\omega_1+2\pi\nu,\omega_2+2\pi\mu) \overline{\hat{\varphi}}(\omega_1+2\pi\nu,\omega_2+2\pi\mu)d\omega_1d\omega_2. \] Таким образом имеем \[ \sum_{(\nu,\mu)\in Z^2}\hat{f}(\omega_1+2\pi\nu,\omega_2+2\pi\mu)\overline{\hat{\varphi}}(\omega_1+2\pi\nu,\omega_2+2\pi\mu)=0 \] и \[ \sum_{(\nu,\mu)\in Z^2}m_f\left(\frac{\omega_1}{2}+\pi\nu,\frac{\omega_2}{2}+\pi\mu\right)\hat{\varphi}^1(\omega_1+2\pi\nu,\omega_2+2\pi\mu) \overline{m}_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi\nu,\frac{\omega_2}{2}+\pi\mu\right) \overline{\hat{\varphi}}^1(\omega_1+2\pi\nu,\omega_2+2\pi\mu)= \] \[ =\sum_{(\nu,\mu)\in Z^2}m_f\left(\frac{\omega_1}{2}+\pi\nu,\frac{\omega_2}{2}+\pi\mu\right) \overline{m}_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi\nu,\frac{\omega_2}{2}+\pi\mu\right) \left|\hat{\varphi}^1(\omega_1+2\pi\nu,\omega_2+2\pi\mu)\right|^2=0. \] Следовательно, \[ m_f\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right) \overline{m}_{\varphi\varphi^1}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right)+ m_f\left(\frac{\omega_1}{2}+\pi,\frac{\omega_2}{2}\right) \overline{m}_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi,\frac{\omega_2}{2}\right)+ \] \[ +m_f\left(\frac{\omega_1}{2},\frac{\omega_2}{2}+\pi\right) \overline{m}_{\varphi\varphi^1}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}+\pi\right) +m_f\left(\frac{\omega_1}{2}+\pi,\frac{\omega_2}{2}+\pi\right) \overline{m}_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi,\frac{\omega_2}{2}+\pi\right)=0. \] Положим \[ m_{\psi^1}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right)= \exp{\left(i\frac{\omega_1+\omega_2}{2}\right)}\overline{m}_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi,\frac{\omega_2}{2} \right)=\exp{\left(i\left\lt \left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right),(1,0)\right>\right)}\overline{m}_{\varphi\varphi^1} \left(\frac{\omega_1}{2}+\pi,\frac{\omega_2}{2}\right), \] \[ m_{\psi^2}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right)= \exp{\left(i\left\lt \left(\frac{\omega_1}{2},\frac{\omega_2}{2}+\pi\right),(1,1)\right>\right)} \overline{m}_{\varphi\varphi^1}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}+\pi\right), \] \[ m_{\psi^3}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right)= \exp{\left(i\left\lt \left(\frac{\omega_1}{2},\frac{\omega_2}{2}+\pi\right),(0,1)\right>\right)} \overline{m}_{\varphi\varphi^1}\left(\frac{\omega_1}{2}+\pi,\frac{\omega_2}{2}+\pi\right). \] Всплесками назовем функции, у которых преобразования Фурье имеют вид \[ \hat{\psi}^i(\omega_1,\omega_2)=m_{\psi^i}\left(\frac{\omega_1}{2},\frac{\omega_2}{2}\right)\hat{\varphi}^1(\omega_1,\omega_2) \] или, что то же \[ \hat{\psi}^1(\omega_1,\omega_2)=\hat{\varphi}^1(\omega_1,\omega_2)\exp{\left(i\frac{\omega_1+\omega_2}{2}\right)} \sum_{(\nu,\mu)\in Z^2)}h_{\nu,\mu} \exp{\left(i\left(\nu\left(\frac{\omega_1}{2}+\pi\right)+\mu\frac{\omega_2}{2}\right)\right)}, \] \[ \hat{\psi}^2(\omega_1,\omega_2)=\hat{\varphi}^1(\omega_1,\omega_2)\exp{\left(i\frac{\omega_1+\omega_2}{2}+i\pi\right)} \sum_{(\nu,\mu)\in Z^2}h_{\nu,\mu} \exp{\left(i\left(\nu\frac{\omega_1}{2}+\mu\left(\frac{\omega_2}{2}+\pi\right)\right)\right)}, \] \[ \hat{\psi}^3(\omega_1,\omega_2)=\hat{\varphi}^1(\omega_1,\omega_2)\exp{\left(i\frac{\omega_2}{2}+i\pi\right)} \sum_{(\nu,\mu)\in Z^2}h_{\nu,\mu} \exp{\left(i\left(\nu\left(\frac{\omega_1}{2}+\pi\right)+\mu\left(\frac{\omega_2}{2}+\pi\right)\right)\right)}. \] Перепишем эти соотношения в виде \begin{equation}\label{w.41} \hat{\psi}^1(\omega_1,\omega_2)=\hat{\varphi}^1(\omega_1,\omega_2) \sum_{(\nu,\mu)\in Z^2}h_{\nu,\mu} \exp{\left(i\left(\frac{\omega_1}{2}+\frac{\omega_1\nu}{2}+\pi\nu+ \frac{\omega_2\mu}{2}\right)\right)}= \hat{\varphi}^1(\omega_1,\omega_2)\sum_{(\nu,\mu)\in Z^2}(-1)^{\nu}h_{\nu.\mu} \exp{\left(i\left(\frac{\omega_1(\nu+1)}{2}+\frac{\omega_2\mu}{2}\right)\right)}, \end{equation} \begin{equation}\label{w.42} \hat{\psi}^2(\omega_1,\omega_2)=\hat{\varphi}^1(\omega_1,\omega_2)\sum_{(\nu,\mu)\in Z^2 }(-1)^{\mu+1}h_{\nu,\mu} \exp{\left(i\left(\frac{\omega_1(\nu+1)}{2}+\frac{\omega_2(\mu+1)}{2}\right)\right)}, \end{equation} \begin{equation}\label{w.43} \hat{\psi}^3(\omega_1,\omega_2)=\hat{\varphi}^1(\omega_1,\omega_2)\sum_{(\nu,\mu)\in Z^2 }(-1)^{\nu+\mu+1}h_{\nu,\mu} \exp{\left(i\left(\frac{\omega_1\nu}{2}+\frac{\omega_2(\mu+1)}{2}\right)\right)}. \end{equation} В соотношении (\ref{w.41}) сделаем замену, полагая \(\nu+1=\nu\) получаем \[ \hat{\psi}^1(\omega_1,\omega_2)=\hat{\varphi}^1(\omega_1,\omega_2)\sum_{(\nu,\mu)\in Z^2 }(-1)^{\nu-1}h_{\nu-1,\mu} \exp{\left(i\frac{\omega_1\nu+\omega_2\mu}{2}\right)}, \] полагая в (\ref{w.42}) \(\nu_1+1=\nu_1\) и \(\mu+1=\mu\) получаем \[ \hat{\psi}^2(\omega_1,\omega_2)=\hat{\varphi}^1(\omega_1,\omega_2)\sum_{(\nu,\mu)\in Z^2 }(-1)^{\mu}h_{\nu-1,\mu-1} \exp{\left(i\frac{\omega_1\nu+\omega_2\mu}{2}\right)}, \] и, наконец, полагая в (\ref{w.43}) \(\mu+1=\mu\) приходим к соотношению \[ \hat{\psi}^3(\omega_1,\omega_2)=\hat{\varphi}^1(\omega_1,\omega_2)\sum_{(\nu,\mu)\in Z^2 }(-1)^{\nu+\mu}h_{\nu_1,\mu_2-1} \exp{\left(i\frac{\omega_1\nu+\omega_2\mu}{2}\right)}. \] Отсюда сразу получаем \begin{equation}\label{w.44} \psi^1(x,y)=\sum_{(\nu,\mu)\in Z^2 }(-1)^{\mu}h_{\nu-1,\mu}\varphi^1\left(x-\frac{\nu}{2},y-\frac{\mu}{2}\right), \end{equation} \begin{equation}\label{w.45} \psi^2(x,y)=\sum_{(\nu,\mu)\in Z^2}(-1)^{\nu}h_{\nu,1-\mu}\varphi^1\left(x-\frac{\nu}{2},y-\frac{\mu}{2}\right), \end{equation} \begin{equation}\label{w.46} \psi^3(x,y)=\sum_{(\nu,\mu)\in Z^2}(-1)^{\nu+\mu}h_{\nu-1,1-\mu}\varphi^1\left(x-\frac{\nu}{2},y-\frac{\mu}{2}\right), \end{equation} и \begin{equation}\label{w.47} \varphi(x,y)=\sum_{(\nu,\mu)\in Z^2}h_{\nu,\mu}\varphi^1\left(x-\frac{\nu}{2},y-\frac{\mu}{2}\right). \end{equation} Опишем алгоритм декомпозиции и реконструкции для такого рода всплесков.
Пусть известны числа \[ c^1_{\nu,\mu}=\left\lt f,\varphi^1\left(\cdot-\frac{\nu}{2},\cdot\cdot-\frac{\mu}{2}\right)\right>, (\nu,\mu)\in Z^2. \] Отсюда и из (\ref{w.47}) сразу получаем \[ c^0_{n,m}=\left\lt f,\varphi\left(\cdot-n,\cdot\cdot-m\right)\right>= \left\lt f,\sum_{(\nu,\mu)\in Z^2 }h_{\nu,\mu}\varphi^1\left(\cdot-n-\frac{\nu}{2},\cdot\cdot-m-\frac{\mu}{2}\right)\right>= \sum_{(\nu,\mu)\in Z^2}h_{\nu,\mu}\left\lt f,\varphi^1\left(\cdot-n-\frac{\nu}{2},\cdot\cdot-m-\frac{\mu}{2}\right)\right>= \] \[ =\sum_{(\nu,\mu)\in Z^2}h_{\nu,\mu}\left\lt f,\varphi^1\left(\cdot-\frac{2n+\nu}{2},\cdot\cdot-\frac{2m+\mu}{2}\right)\right>= \sum_{(\nu,\mu)\in Z^2}h_{\nu,\mu}c^1_{2n+\nu,2m+\mu}. \] Отсюда сразу получаем \begin{equation}\label{w.48} c^0_{n,m}=\left\lt f,\varphi\left(\cdot-n,\cdot\cdot-m\right)\right>= \sum_{(\nu,\mu)\in Z^2 }h_{\nu-2n,\mu-2m}\left\lt f,\varphi^1\left(\cdot-\frac{\nu}{2},\cdot\cdot-\frac{\mu}{2}\right)\right> =\sum_{(\nu,\mu)\in Z^2}h_{\nu-2n,\mu-2m}c^1_{\nu,\mu}. \end{equation} Проведем аналогичные построения для \(\psi^i\) \((i=1,2,3)\), \[ d^{0,1}_{n,m}=\left\lt f,\psi^1\left(\cdot-n,\cdot\cdot-m\right)\right>= \left\lt f,\sum_{(\nu,\mu)\in Z^2}(-1)^{\nu-1}h_{\nu-1,\mu}\varphi^1\left(\cdot-n+\frac{\nu}{2},\cdot\cdot-n+\frac{\mu}{2}\right)\right>= \] \[ =\sum_{(\nu,\mu)\in Z^2}(-1)^{\nu-1}h_{\nu-1,\mu}\left\lt f,\varphi^1\left(\cdot-n+\frac{\nu}{2},\cdot\cdot-m+\frac{\mu}{2}\right)\right>= \sum_{(\nu,\mu)\in Z^2}(-1)^{\nu-1}h_{\nu-1,\mu}\left\lt f,\varphi^1\left(\cdot-\frac{2n-\nu}{2},\cdot\cdot-\frac{2m-\mu}{2}\right)\right>. \] Используя в последнем соотношении замену переменных приходим к равенству \[ d^{0,1}_{n,m}=\left\lt f,\psi^1\left(\cdot-n,\cdot\cdot-m\right)\right>= \sum_{(\nu,\mu)\in Z^2}(-1)^{2n-\nu-1}h_{2n-\nu-1,2m-\mu}\left\lt f,\varphi^1\left(\cdot-\frac{\nu}{2},\cdot\cdot-\frac{\mu}{2}\right)\right>= \] \begin{equation}\label{w.49} =\sum_{(\nu,\mu)\in Z^2}(-1)^{2n-\nu-1}h_{2n-\nu-1,2m-\mu}c^1_{\nu,\mu}. \end{equation} Далее, \[ d^{0,2}_{n,m}=\left\lt f,\psi^2\left(\cdot-n,\cdot\cdot-m\right)\right>= \left\lt f,\sum_{(\nu,\mu)\in Z^2}(-1)^{\mu}h_{\nu-1,\mu-1)}\varphi^1\left(\cdot-n+\frac{\nu}{2},\cdot\cdot-m+\frac{\mu}{2}\right)\right>= \] \[ =\sum_{(\nu,\mu)\in Z^2}(-1)^{\mu}h_{\nu-1,\mu-1}\left\lt f,\varphi^1\left(\cdot-\frac{2n-\nu}{2},\cdot\cdot-\frac{2m-\mu}{2}\right)\right>. \] Отсюда получаем равенство \begin{equation}\label{w.50} d^{0,2}_{n,m}=\left\lt f,\psi^2\left(\cdot-n,\cdot\cdot-m\right)\right>= \sum_{(\nu,\mu)\in Z^2}(-1)^{2m-\mu}h_{2n-\nu-1,2m-\mu-1}\left\lt f,\varphi^1\left(\cdot-\frac{\nu}{2},\cdot-\frac{\mu}{2}\right)\right>= \sum_{(\nu,\mu)\in Z^2}(-1)^{2m-\mu}h_{2n-\nu-1,2m-\mu-1}c^1_{\nu,\mu} \] \end{equation} и, наконец, \[ d^{0,3}_{n,m}=\left\lt f,\psi^3\left(\cdot-n,\cdot\cdot-m\right)\right>=\left\lt f,\sum_{(\nu,\mu)\in Z^2}(-1)^{\nu+\mu}h_{\nu,\mu-1}\varphi^1\left(\cdot-n+\frac{\nu}{2},\cdot\cdot-m+\frac{\mu}{2}\right)\right>= \sum_{(\nu,\mu)\in Z^2}(-1)^{\nu+\mu}h_{\nu,\mu-1}\left\lt f,\varphi^1\left(\cdot-\frac{2n-\nu}{2},\cdot\cdot-\frac{2m-\mu}{2}\right)\right>. \] и, следовательно, \begin{equation}\label{w.51} d^{0,3}_{n,m}=\left\lt f,\psi^3\left(\cdot-n,\cdot\cdot-m\right)\right>= \sum_{(\nu,\mu)\in Z^2}(-1)^{2m-\mu}h_{2n-\nu,2m-\mu-1}\left\lt f,\varphi^1\left(\cdot-\frac{\nu}{2},\cdot\cdot-\frac{\mu}{2}\right)\right> =\sum_{(\nu,\mu)\in Z^2}(-1)^{2m-\mu}h_{2n-\nu,2m-\mu-1}c^1_{\nu,\mu}. \end{equation} По полученному набору чисел \[ \left\{c^0_{\nu,\mu},d^{0,1}_{\nu,\mu},d^{0,2}_{\nu,\mu},d^{0,3}_{\nu,\mu}\right\}_{(\nu,\mu)\in Z^2} =\left\{\left\lt f,\varphi(\cdot-n,\cdot\cdot-m)\right>\right\}_{({\nu,\mu})\in Z^2}, \left\{\left\lt f,\psi^k(\cdot-n,\cdot\cdot-m)\right>\right\}_{({\nu,\mu})\in Z^2} (k=1,2,3) \] однозначно восстанавливается набор \[ \left\{c^1_{\nu,\mu}\right\}_{(\nu,\mu)\in Z^2}=\left\{\left\lt f,\varphi^1\left(\cdot-\frac{\nu}{2},\cdot\cdot-\frac{\mu}{2}\right)\right>\right\}_{(\nu,\mu)\in Z^2}. \] Для этого достаточно воспользоваться равенством \begin{equation}\label{w.52} c^1_{\nu,\mu}=\left\lt f,\varphi^1\left(\cdot-\frac{\nu}{2},\cdot\cdot-\frac{\mu}{2}\right)\right>= \left\lt \sum_{(n,m)\in Z^2}\left\lt f,\varphi(\cdot -n,\cdot\cdot-m)\right>\varphi(\cdot -n,\cdot\cdot-m)+\right. \end{equation} \[ \left. +\sum_{j=1}^3\sum_{(n,m)\in Z^2}\left\lt f,\psi^j(\cdot -n,\cdot\cdot-m)\right>\psi^j(\cdot -n,\cdot\cdot-m),\varphi^1\left(\cdot-\frac{\nu}{2},\cdot\cdot-\frac{\mu}{2}\right) \right>= \sum_{(n,m)\in Z^2}\left\lt f,\varphi(\cdot -n,\cdot\cdot -m)\right>\left\lt \varphi(\cdot -n,\cdot\cdot -m), \varphi^1\left(\cdot-\frac{\nu}{2},\cdot\cdot-\frac{\mu}{2}\right)\right>+\] \[ +\sum_{j=1}^3\sum_{(n,m)\in Z^2}\left\lt f,\psi^j(\cdot -n,\cdot\cdot-m)\right> \left\lt \psi^j(\cdot -n,\cdot\cdot-m),\varphi^1\left(\cdot-\frac{\nu}{2},\cdot\cdot-\frac{\mu}{2}\right)\right>. \]

Традиционные сферы приложения всплесков в компьютерной графике и обработке изображений:

1. Сжатие и коррекция изображений.
2. Восстановление, сжатие, коррекция кривых и поверхностей.
3. Решение задачи моделирования освещенности (radiosity).

Эти вопросы можно рассмотреть с другой точки зрения, соответственно~-- приложения всплесков к растровой графике, векторной графике и к решению дифференциальных и интегральных уравнений. Рассмотрим первую из перечисленных проблем.
Широкое использование цифровых средств коммуникации привело к необходимости уменьшения объема сохраненной (и передаваемой) информации, что породило новое направление научных исследований -- сжатие данных без потерь и с потерями. Беспотерьные методы сжатия применяются, прежде всего, к текстовой информации, а сжатие с потерями - к информации основанной на восприятии человеком, например, визуальной или акустической. Визуальная информация, как статическая так и динамическая (видео- или аудио-ряд), обладают свойством избыточности. Это может быть обусловлено наличием резких границ, высокой глубины цветопередачи и пр., что не воспринимается адекватно человеком. Таким образом, уменьшая избыточность данных, можно без существенного ухудшения (с точки зрения восприятие чувствами человека) уменьшить объем информации, описывающей данный объект.
В средине восьмидесятых годов для решения задачи сжатия полноцветных изображений был разработан формат JPEG (Joint Photographic Experts Group). Схема работы метода сжатия положенного в основу JPEG состоит в следующем. После перевода полноцветного изображения из цветового пространства RGB (red, green, blue) в цветовое пространство YСrCb (Y-люминисцкентная составляющая, Cr- хроматический красный, то есть теплые тона и Cb- хроматический синий- холодные тона), изображение разбивается на квадраты размера \(8\times 8\) пикселов. К каждому из этих квадратов применяется дискретное косинус-преобразование Фурье. Дальнейшая обработка заключается в квантовании полученных коэффициентов с требуемой степенью сжатия (компрессии) и последующим сжатии без потерь при помощи кода Хаффмана. Благодаря большой коллекции вариантов кодирования (фиксированные таблицы квантования, z-обход, различные методы группирования коэффициентов Фурье для различных цветовых компонентов) этот формат достаточно эффективен. Однако для высоких степеней сжатия (более 25 раз) сжатое изображение визуально распадается на квадратные участки постоянности интенсивности, что затрудняет восприятие образа. Кроме того, в виду фиксированности таблиц квантования, получить изображение с заданной степенью сжатия в формате JPEG сложно.
Эти и другие сопутствующие причины привели к необходимости разработки принципиально новых методов сжатия полноцветных изображений.
Среди методов сжатия, конкурирующих на право создания преемника JPEG, прежде всего, рассматривались методы, основанные на фрактальном и на всплесковом (wavelets) сжатии данных.
Фрактальные методы основаны на выделении и группировании фрагментов изображения со схожей структурой.Основной сложностью фрактальных методов является выбор геометрического примитива, на котором сравнивается структура данных и возможность его вращения. Для реализации фрактальных методов требуются не только большие вычислительные затраты, но и, самое главное, они требуют достаточно большого времени.
Всплесковые методы сжатия являются продолжением и развитием классического анализа Фурье. В основе wavelet-методов сжатия лежит частотный анализ характеристик изображения. При этом, для низких частот используется более аккуратная обработка, а для высоких - более грубая. Всплесковые методы сжатия показывают более высокие показатели, как по качеству сжатия, так и по времени работы. Этот факт обусловил использование именно всплесковых методов для разработки преемника JPEG.
В общем случае сжатие изображения сводится к следующим шагам

1. Выбор базиса. Прежде всего это может быть сепарабельный или несепарабельный всплесковый базис, обладающий теми или иными требуемыми свойствами. Прежде всего это условия на гладкость, симметричность, количество обнуляющихся моментов и пр.
2. Процедура фильтрации. На данном этапе важно определиться со схемой фильтрации. Это может быть каскадная, пакетная или гибридная схема фильтрации.
3. Квантование коэффициентов. На этом этапе каждому коэффициенту ставится в соответствие целое число. Простейшим квантованием является округление (по модулю) числа.
4. Кодирование. На этом этапе используется метод группового кодирования в сочетании с энтропийным сжатием.

Использование всплесков к сжатию изображений, породило направление связанное с прогнозом всплековых коэффициентов нижней иерархии коэффициентами более высокой иерархии. Первый шаг в этом направлении был сделан в работе Шапиро. Он отметил, что в случае если низкочастотный коэффициент равен нулю, то достаточно часто соответствующие высокочастотные коэффициенты также равны нулю. Дальнейшие исследования в этом направлении привели к алгоритмам подрезания нуль-деревьев. Схематически идея нуль-дерева может быть проиллюстрирована следующим образом. что соответствует графу Таким образом, указав в коде лишь координату корня дерева нулей, кодируется все "дерево".
Многочисленные исследования в этом направлении вылились в конце концов в принятие нового стандарта - JPEG2000. Разработка JPEG2000 началась в 1996 году. Как раз к этому времени стало ясно существенное преимущество алгоритмов сжатия на основе вейвлетов перед ДКП, использованным в JPEG. При создании нового стандарта наряду с достижением большей эффективности сжатия ставились еще и следующие цели:

1. Устойчивость алгоритма к ошибкам канала связи при передаче сжатого изображения. Здесь видна нацеленность нового стандарта на мобильные приложения, на передачу изображений по радиоканалу.
2. Унифицированная архитектура декодера. В JPEG имеется порядка 44 различных режимов декодирования, в зависимости от приложения. Конструкция JPEG2000 такова, что в независимости от применяемого способа кодирования используется один и тот же декодер.
3. Масштабируемость. В зависимости от потребности, это может быть масштабируемость по размеру, разрешению. частотному содержанию, количеству цветов.
4. Обработка отдельных областей на изображении (Region Of Interest). Например, пользователя может интересовать не все изображение, а лишь некоторый фрагмент, например, лицо. В таком случае он выделяет его (мышью), и декодер с высоким качеством восстанавливает этот фрагмент.
5. Сжатие изображений больших размеров.

Локальная, масштабированная структура вейвлет-функций позволила решить вышеперечисленные задачи.
Основные блоки, входящие в структурную схему алгоритма сжатия JPEG2000.

1. Предварительная обработка. Изображение, как правило представляет собой набор неотрицательных целых чисел. На этапе предварительной обработки из него вычитают среднее. Кроме того, если изображение большого размера, то оно может быть разбито на части. Тогда каждая часть сжимается отдельно, а для предотвращения появления заметных линий на стыке восстановленных частей применяются специальные меры.
2. Вейвлет-преобразование. В JPEG2000 в качестве фильтра используется тензорное произведение одномерных фильтров. В первой части стандарта определены два вейвлет-фильтра - фильтр Добеши (9-7) для сжатия с потерями и тоже биортогональный фильтр с целочисленными коэффициентами (5, 3) для сжатия без потерь.
3. Квантование. JPEG 2000 использует равномерное квантование.
4. Энтропийное кодирование. Применяется адаптивный арифметический кодер (а в JPEG был кодер Хаффмана).