|
|
Векторизація елементів растрового зображення
|
У даному розділі розглянемо підходи до вилучення із растрового представлення прошарку ліній, замінюючи їх на векторний опис.
Підходи до вирішення цієї проблеми ґрунтуються на методах витягання ліній із зображення і подальшим автоматичним вибором аналітичного опису між прямою, ламаною і сплайном Без’є.
Спектр задач, в яких використовується вектризація досить широкий, це аналіз дистанційного зондування поверхні Землі з метою виявлення елементів штучного походження – аеродроми,
дороги, аналіз сільськогосподарських угідь та ін., розпізнавання на растрових зображеннях різного роду об’єктів, які представляють інтерес, наприклад, наявність на фотографіях
зброї і так інше.
Класично для виявлення контурів використовується згортка матриці яскравості \(Y=\left\{y_{i,j}\right\}_{i=1,j=1}^{W,H}\) з оператором Собела:
\begin{equation}\label{1}
G^S_x=\left(
\begin{array}{ccc}
-1 & 0& 1 \\
-2 & 0 & 2 \\
-1 & 0 & 1 \\
\end{array}
\right)\otimes Y,
G^S_y=\left(
\begin{array}{ccc}
1 & 2& 1 \\
0 & 0 & 0 \\
-1 & -2 & 1 \\
\end{array}
\right)\otimes Y.
\end{equation}
або з оператором Превіта:
\begin{equation}\label{2}
G^P_x=\left(
\begin{array}{ccc}
-1 & 0& 1 \\
-1 & 0 & 1 \\
-1 & 0 & 1 \\
\end{array}
\right)\otimes Y,
G^P_y=\left(
\begin{array}{ccc}
1 & 1& 1 \\
0 & 0 & 0 \\
-1 & -1 & 1 \\
\end{array}
\right)\otimes Y.
\end{equation}
Позначимо через \(G=\left\{g_{i,j}\right\}_{i=1,j=1}^{W,H}\) ( W, H – розміри матриці) матрицю для вибраного оператора, елементи якої мають вид:
\begin{equation}\label{3}
g_{i,j}=\|grad(i,j)\|=\sqrt{\left(g^x_{i,j}\right)^2+\left(g^y_{i,j}\right)^2}.
\end{equation}
Для того, щоб знайти особливо контрастні місця, які належать символам, до матриці G застосовується бінаризація по порогу.
Таким чином, знаходимо бінарну матрицю \(Bin=\left\{b_{i,j}\right\}_{i=1,j=1}^{W,H}\), у якої
\begin{equation}\label{4}
b_{i,j}=
\left\{
\begin{array}{ll}
1, & \hbox{ якщо }g_{i,j}\gt \varepsilon, \\
0, & \hbox{ у протилежному випадку.}
\end{array}
\right.
\end{equation}
де \(\varepsilon\)– поріг бінаризації.
Кожен елемент матриці Bin додатково аналізується на предмет належності до регіону інтересу (ROI-Region Of Interest)– наприклад, видаляються ізольовані точки, які, швидше за все, відносяться до шумів.
Однією з головних проблем даного підходу є вибір порогу бінаризації (один з яких розглянутий у розділі, присвяченому просторовій фільтрації зображень). Особливо ця проблема стає актуальною, якщо на зображенні присутні елементи з різним рівнем освітлення.
Аналіз зв'язних компонент.
Даний метод полягає в сегментуванні бінарного зображення на зв'язані регіони і їх подальший аналіз. Зазвичай бінарним зображенням є матриця Bin, отримана внаслідок побудови границь об’єктів.
Будемо називати точки \((x_1,y_1)\) та \((x_2,y_2)\) сусідніми, якщо вони задовольняють умові зв'язності, а саме, для 4-х зв'язної області умова зв'язності має вигляд:
\[
x_1-x_2=0,|y_1-y_2|=1
\]
або
\[
|x_1-x_2|=1,y_1-y_2=0.
\]
Для 8-ми зв’язної:
\begin{equation}\label{5}
|x_1-x_2|\le 1,|y_1-y_2|\le 1
\end{equation}
На рис. 1 наочно проілюстровано поняття зв'язності.
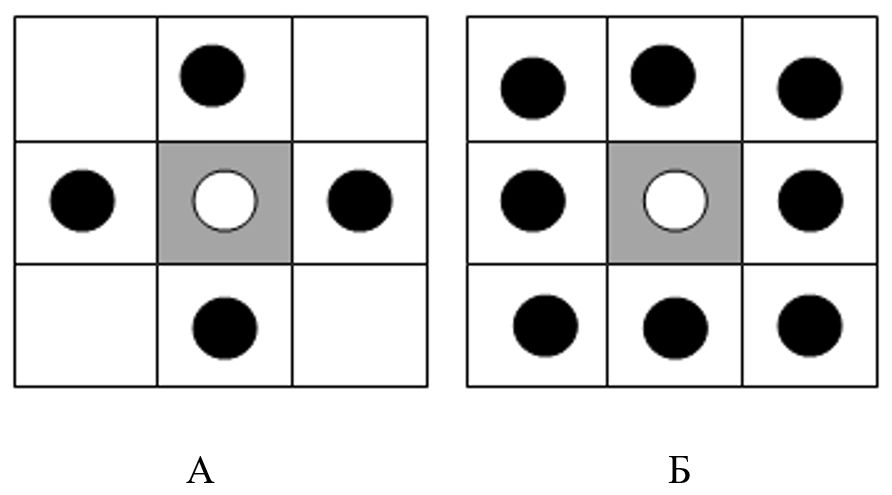
Рис. 1 А) 4-х зв'язана область; Б) 8-ми зв'язана область.
Множину S будемо назвати зв’язною, якщо \(\forall (x_1,y_1)\in S\) и \((x_n,y_n)\in S \) \(\exists \left\{ (x_1,x_2),...,(x_i,y_i),(x_{i+1},y_{i+1}),...,(x_n,y_n)\right\}
(x_i,y_i)\in S\), де \((x_i,y_i),(x_{i+1},y_{i+1})\) – сусідні точки.
Існують різні алгоритми побудови зв'язних множин, наприклад, такі як: алгоритм заповнення з «затравкою» (розглянутий у розділі,
присвяченому сегментації зображень), порядковий лінійний алгоритм та ін.
Кінцевим кроком роботи алгоритму є аналіз різних характеристик, якими володіють отримані зв'язані множини: відсікання шуму, відсікання таких графічних елементів, як внутрішні зображення і т.д. Очевидно, що в даному підході багато залежить від того бінарного зображення, яке передається для побудови зв'язних компонент.
Вилучення ліній із зображення.
Контуром будемо називати області зображення з високою концентрацією інформації, що мало залежить від кольору і яскравості. Виявлення контурів дозволяє перейти з двовимірного простору зображення до простору контурів, що дозволяє знизити обчислювальну та алгоритмічну складність аналізу зображення, підвищити якість відновленого зображення при менших розмірах, а також провести більш детальний аналіз об’єкту, описаного контуром.
Традиційно для виявлення контурів використовуються підходи, які спираються на інформацію про компоненти градієнта та на збіги із шаблоном. Обидві методики оцінюють локальне значення
градієнта і його проекції. Відмінність в тому, що для компонента градієнта зазвичай використовуються фільтри, які дозволяють відловлювати перепади в двох ортогональних напрямках,
наприклад, фільтри Собела (\ref{1}), Превіта (\ref{2}), а також фільтр Робертса:
\[
G^R_x=\left(
\begin{array}{cc}
0 & 1 \\
-1 & 0 \\
\end{array}
\right)\otimes Y,
G^R_y=\left(
\begin{array}{cc}
1 & 0 \\
0 & -1 \\
\end{array}
\right)\otimes Y.
\]
де \(Y=\left\{y_{i,j}\right\}_{i=1,j=1}^{W,H}\) матриця освітленності.
Для підходу збігу із шаблоном характерне використання фільтрів, які проявляють потрібні критерії і дають необхідну похибку збігу.
Контрастні перепади на зображенні знаходяться в точках максимального значення градієнта \(\|grad(i,j)\|\) (див. рис. 3).
Зазвичай для відділення контрастних точок використовується деяке порогове значення \(\varepsilon\)
\[
\|grad(i,j)\|\gt \varepsilon.
\]
Вибір порога – важлива частина визначення перепадів, від якої залежить товщина і неперервність контурів. На даний момент серед подібних методів виділяють фільтр Кенні.
Основні етапи алгоритму Кенні:
- Згладжування. Фільтр Кенні чутливий до шумів на зображенні, тому первісна матриця згладжується за допомогою фільтра Гаусу:
\[
Gauss=
\left(
\begin{array}{ccccc}
2 & 4 & 5& 4 & 2 \\
4 & 9 & 12 & 9 & 4 \\
5 & 12 & 15 & 12 & 5 \\
4 & 9 & 12 & 9 & 4 \\
2 & 4 & 5 & 4 & 2 \\
\end{array}
\right)\otimes Y.
\]
- Пошук градієнтів. Знаходимо градієнти, згідно вибраним фільтрам (Собела, Прeвіта, Робертса). Для того щоб відстежити лінії з нахилом, фільтри розширюються діагональними
операторами, щоб виявити лінії під відповідним кутом: \(0,\pi/4,\pi/2,3\pi/4\).
- Заглушення немаксимумів. В якості контурів відзначаються тільки ті точки, в яких знаходиться локальний максимум градієнта в напрямку вектора градієнта.
- Подвійна порогова фільтрація. Високий поріг використовується для виявлення сильних контурів, низький поріг – для приєднання до сильних контурів, менш чітких, але які є їх частиною.
- Трасування областей неоднозначності. Заглушуються слабкі контури, що не пов'язані з сильними.
Метод Кенні є досить універсальним апаратом вилучення контурів, але, як і більшість універсальних підходів, в спеціалізованих ситуаціях може бути не настільки ефективний.
Наприклад, у випадку нечітких ліній, втрата яких буде помітна людському оку. Особливо гостро ця ситуація проявляється, коли нечіткі лінії не пов'язані з чіткими
(червоні блоки на рис. 2).
 |  |
| А | Б |
| Рис.2. Застосування фільтра Кенні до тестового зображенню "Bicycle". |
| А) Оригінальне тестове зображення; | Б) Зображення після застосування фільтра Кенні. |
Векторний опис ліній.
Для того щоб виділені контури поліпшили свою структуру і краще піддавалися аналітичному опису, класично до отриманого контуру застосовують морфологічні операції виду – нарощування, ерозія, замикання, розмикання (див. розділ, присвячений просторовим фільтрам).
Кінцевою метою обробки контурів є векторизація. Під векторизацією ми будемо розуміти спосіб представлення об'єктів і зображень, заснований на використанні елементарних геометричних об'єктів: точки, лінії, ламані, сплайни, багатокутники.
Перетворення Хафа.
Одним з найвідоміших методів виявлення прямої є перетворення Хафа. Зазначимо, що перетворення Хафа можна узагальнити на випадок пошуку інших примітивів, таких як дуг кіл, та ін.
У перетворенні Хафа використовується представлення прямої у вигляді: \(r=x\cos\theta+y\sin\theta\), де \(\theta\in [0,\pi],r\in \mathbb{R}\).
Тоді, функція, що задає сімейство прямих: \(F(r,\theta,x,y)=x\cos\theta+y\sin\theta\).
Через кожну точку \((x,y)\) зображення можна провести безліч прямих з різними параметрами \(r,\theta\). Кожній точці на зображенні \(r_0,\theta_0\) простору \(r,\theta\)
можна поставити у відповідність лічильник, що відповідає кількості точок (x,y), що лежать на прямій \(r_0=x\cos\theta_0+y\sin\theta_0\). Точка \(r_0,\theta_0\),
в якій досягається максимальне значення лічильника, описує параметри шуканої прямої (на рис. 3 найбільш темна точка – негатив максимального значення лічильника).
Щоб описати комп'ютерну реалізацію, перейдемо до дискретного випадку простору \(r,\theta\). Таким чином, введемо сітку на \(r,\theta\) просторі та поставимо у відповідність
кожній клітині \([r_i,\theta_i]\times [r_{i+1},\theta_{i+1}]\) лічильник кількості точок (x,y), що задовольняють рівнянню
\[
r=x\cos\theta+y\sin\theta,\theta\in [\theta_i,\theta_{i+1}],r\in [r_i,r_{i+1}].
\]
 |  |
| А | Б |
| Рис. 3. Демонстрація перетворення Хафа; |
| А) Оригінальний набір точок; | Б) Негатив відображення простору Хафа –
чим темніше точка, тим більше значення
відповідного лічильника. |
Важливий аспект алгоритму – вибір розміру клітини. Розмір клітини потрібно вибирати з міркувань, щоб в якості прямої не був сприйнятий розрізнений набір точок і щоб клітини не були настільки малі, що призведе до відсутності різко вираженого максимального значення лічильника. Другий важливий аспект методу – швидкість його роботи.
Якщо на зображенні наявні кілька прямих, їх можна отримати за допомогою перестановки величин лічильників. Однак якщо прямі на зображенні повинні скластися в ламану лінію, після перетворення Хафа можуть з'явитися розриви, так як безперервність ланок ламаної в перетворенні ніяк не враховується. Тому для цього випадку переважний варіант безпосереднього наближення множини точок ламаними. У цьому випадку ми маємо справу з кусково-лінійною апроксимацією.
Метод кусково-лінійної апроксимації полягає в заміні заданої множини точок ламаною з однією або декількома вузлами.
Опишемо побудову «майже» оптимального відновлення кривої в метриці Хаусдорфа (візуальної метриці) (див.[19]).
Опис асимптотично оптимальної ламаної.
Нехай задана впорядкована множина зв’язаних точок \((x_i,y_i)\), тоді для заданого порога \(\varepsilon\gt 0\) число ланок асимптотично оптимальної інтерполяційної ламаної обчислюється за формулою:
\[
m=\left[\frac{1}{4\sqrt{2\varepsilon}}\sum_{i=0}^{n-1}\Delta\ell_{i+1/2}(K_i+K_{i+1})\right]+1,
\]
де [α] - ціла частина числа α,
\[
K_i=\sqrt{\frac{|x_i''y_i'-x_i'y_i''|}{\sqrt{\left(x_i'\right)^2+\left(y_i'\right)^2}}},\\
x_{i+1/2}'=\frac{x_{i+1}-x_i}{\Delta\ell_{i+1/2}}, y_{i+1/2}'=\frac{y_{i+1}-y_i}{\Delta\ell_{i+1/2}},\\
\Delta\ell_{i+1/2}=\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2},\\
x_i'=\frac{x_{i+1/2}'+x_{i-1/2}'}{2},y_i'=\frac{y_{i+1/2}'+y_{i-1/2}'}{2},\\
x_i''=2\frac{x_{i+1/2}'-x_{i-1/2}'}{\Delta\ell_{i+1/2}+\Delta\ell_{i-1/2}}, y_i''=2\frac{y_{i+1/2}'-y_{i-1/2}'}{\Delta\ell_{i+1/2}+\Delta\ell_{i-1/2}},\\
x'_{-1/2}=2x'_{1/2}-x'_{3/2},y'_{-1/2}=2y'_{1/2}-y'_{3/2},
x'_{n+1/2}=2x'_{n-1/2}-x'_{n-3/2}, y'_{n+1/2}=y'_{n-1/2}-y'_{n-3/2}.
\]
А координати вузлів ламаної \(t_j,j=0,1,...,m\) вибираються з умови:
\[
\sum_{i=0}^{t_j}\Delta\ell_{i+1/2}(K_i+K_{i+1}+m^{-2/3})\le
\frac{j}{m}\sum_{i=0}^{m}\Delta\ell_{i+1/2}(K_i+K_{i+1}+m^{-2/3})\le
\sum_{i=0}^{t_j+1}\Delta\ell_{i+1/2}(K_i+K_{i+1}+m^{-2/3}).
\]
Таким чином, маємо асимптотично оптимальну інтерполяційну ламану з таким числом вузлів та їхнім розташуванням, що забезпечити задану похибку \(\varepsilon\) наближення.
Очевидно, що не всі криві можуть бути ефективно наближені ламаною с досить малою кількістю вузлів. Для опису складних кривих розроблена методика наближення сплайнами.
Функція S(t), визначена на відрізку [a,b], називається поліноміальних сплайном порядку m с вузлами \(a\le x_0\lt ...\lt x_n\le b\), якщо на кожному з
відрізків \([x_{j-1},x_j]\), \(S(t)\) є алгебраїчним поліномом ступеня, який не перевищує m. Якщо в точці \(x_j,(j=0,...,n)\) функції \(S(t),S'(t),..,S^{(m-k)}(t)\)
неперервні, а похідна \(S^{(m-k+1)}\) в точці \(x_j\) має розрив, число \(k\) називають дефектом сплайну. Множина \(\{x_0,x_1,...,x_n\}\) називається сіткою вузлів сплайну,
а точки \(x_j\) – вузлами або точками склейки сплайну.
Приклад сплайну 2-го порядку (параболічний сплайн) наведений на рисунку.
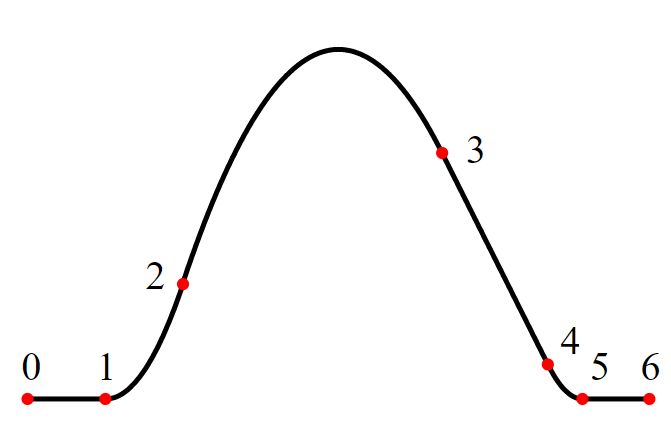
Рис.4. Приклад наближення функції сплайном 2-го порядку.
В комп’ютерних програмах обробки обробки графічних об’єктів прийнято використовувати сплайни Без’є. Це зумовлено, поперед всього, простотою їх реалізації.
Для рівномірного розбиття \(a\le h\lt 2h\lt ...\lt (n-1)h\le b\) для точок \(M_{i},M_{i+1/2},M_{i+1}\) квадратичний сплайн Без’є буде мати вигляд:
\[
sb\left(\left\{M_{i},M_{i+1/2},M_{i+1}\right\},t\right)=M_i(1-\tau)^2+2\,M_{i+1/2}\tau(1-\tau)+M_{i+1}\tau^2,
\]
де \(\tau=(t-ih)h^{-1},t\in [ih,(i+1)h]\).
Однак у сплайнів Без’є зворотною стороною їх простоти є достатньо висока помилка наближення. Якість наближення сплайнами Без’є така ж, як у інтерполяційних ламаних.
Локалізація слабоконтрастних ліній.
Як вже було зазначено, проблема локалізації ліній, чітко виражених на зображенні, досить добре вивчена і існують алгоритми побудовані, наприклад, на фільтрах Собела, Превітта,
Кенні, для виявлення таких ліній. Складність визначення прошарку ліній зростає з ускладненням фону, на яких ці лінії знаходяться.
Розглянемо задачу виділення в окремий прошарок слабоконтрастних ліній з нечіткою структурою щодо фону прилеглих точок. Такі лінії, можна побачити на рис. 5.

Рис.5. Тестовий приклад "Bicycle". На рис 5 А та рис. 5.Б наведені приклади ліній,
контрастних на навколишньому фоні, на рис. 5. В і рис. 5 Г приклади ліній,
слабоконтрастних на навколишньому фоні.
Виділення слабо контрастних ліній складається з 2-х етапів:
Етап 1. Формування множини точок фону;
Етап 2. Формування множин контрастних щодо фону.
Тепер більш докладно.
Етап 1. Формування точок фону.
Поняття локального фону є ключовим і інтуїтивно під фоном розуміється множина точок зображення, кожна з яких має достатнє число сусідів зі схожою освітленістю. При цьому не дуже помітні лінії на зображенні складаються з точок, які по своїй освітленості дуже близькі до яскравості сусідніх точок фону. Надалі в рамках опису алгоритму, це поняття буде формалізовано.
Будемо працювати з освітленістю зображення, що представляє собою числову матрицю \(Y=\left\{y_{i,j}\right\}_{i=1,j-1}^{W,H}\).
Через \(C^R_{i,j}=\left\{(\nu,\mu):(i-\nu)^2+(j-\mu)^2\le R^2\right\}\) позначимо окіл точки (i,j) радіусом R (у нашому випадку розглядалося R=3) і кожній точці зображення поставимо у відповідність середню освітленість околу
\begin{equation}\label{6}
b^R_{i,j}=\frac{1}{\sum\left\{1\left|(\nu,\mu)\in C^R_{i,j}\right.\right\}}\sum\left\{y_{\nu,\mu}\left|(\nu,\mu)\in C^R_{i,j}\right.\right\}
\end{equation}
Для заданого \(\delta\gt 0\) визначимо множину
\[
\Re(\delta)=\left\{(i,j):\left||y_{i,j}-b^R_{i,j}|\lt \delta\right.\right\}.
\]
Всі точки цієї множини будемо називати первинними точками фону по порогу \(\delta\). При визначенні множини первинних точок фону, використовувалися точки, які в подальшому не
увійшли в цю множину, тому треба перевизначити поняття околу, спираючись на інформацію тільки про точки з \(\Re(\delta)\)
\[
\tilde{C}^R_{i,j}=\left\{(\nu,\mu)\left|(\nu,mu)\in C^R_{i,j},(\nu,\mu)\in \Re(\delta)\right.\right\}.
\]
Використовуючи уточнене поняття околу первинної точки фону, заново знайдемо значення освітленості фону в точці \((i,j)\)
\[
\tilde{b}^R_{i,j}=\frac{1}{\sum\left\{1\left|(\nu,\mu)\in \tilde{C}^R_{i,j}\right.\right\}}\sum\left\{y_{\nu,\mu}\left|(\nu,\mu)\in \tilde{C}^R_{i,j}\right.\right\}
\]
Значення освітленості точок, що належать лініям, слабоконтрастним щодо навколишнього фону, більш істотно відрізняються від значень яскравості фону, ніж значення точок, що не лежать на подібних місцях. При виділенні ліній природно вимагати, щоб точки, які можуть їм належати, не брали участь у формуванні освітленості фону. Для цієї мети побудуємо наступну процедуру.
Для кожної точки околу \(\tilde{C}^R_{i,j}\) знайдемо помилку опису її освітленості середнім значенням фону
\[
e^{(i,j)}_{\nu,\mu}=\left|y_{\nu.\mu}-\tilde{b}^R_{i,j}\right|,(\nu,\mu)\in \tilde{C}^R_{i,j}
\]
та побудуємо множину точок \(M^R_{i,j}\), яка складається з Θ відсотків точок \((\nu,\mu)\in \tilde{C}^R_{i,j}\), для яких значення помилок \(e^{(i,j)}_{\nu,\mu}\)
максимальні (наприклад, \(\Theta\approx 20\%\) ). Обчислимо нові середні значення, видаливши точки з максимальним відхиленням:
\[
\tilde{b}^M_{i,j}=\frac{1}{\sum\left\{1\left|(\nu,\mu)\in \tilde{C}^R_{i,j}\setminus M^R_{i,j}\right.\right\}}\sum\left\{y_{\nu,\mu}\left|(\nu,\mu)\in \tilde{C}^R_{i,j}\setminus M^R_{i,j}\right.\right\}
\]
Аналогічно попередньому твердженню, власне фоновими точками будемо вважати точки, що задовольняють умові:
\begin{equation}\label{7}
\left|y_{i,j}-\tilde{b}_{i,j}^{M^R_{i,j}}\right|\lt\varepsilon,(i,j)\in\Re(\delta),
\end{equation}
де \(\varepsilon\gt 0\) – параметр, що регулює кількість точок фону.
Всі точки, що задовольняють умові (\ref{7}), утворюють множину точок фону \(\tilde{\Re}(\Theta,\delta)\).
Етап 2. Формування множин точок, контрастних на фоні.
Точки, які належать множині \(P^\delta=\Re(\delta)\setminus\tilde{\Re}(\Theta,\delta)\), будемо називати точками, контрастними на фоні.
Всі ці точки "підозрілі" на предмет формування ліній. Через \(\left\{P_k^\delta\right\}_{k=1}^m\) позначимо множини зв'язаних точок зображення, тобто точок,
для яких виконується умова 8-ми зв'язності (\ref{5}) двох точок \((i,j)\) та \(\nu,\mu\).
Мірою множини A будемо називати величину
\[
mes(A)=\sum\left\{1|(i,j)\in A\right\}
\]
Зазначимо, що у множину \(P^\delta\) можуть потрапити точки, що містять шум. Тому перш ніж, приступити до формування ліній на базі множини
\(\left\{P_k^\delta\right\}_{k=1}^n\), необхідно провести очистку зображення від шумів.
Не зупиняючись на цьому питанні детально, зауважимо, що фільтрація даних від шуму є важливою і цікавою задачею.
Існують різні алгоритми очищення, в даному випадку можна скористатися методом видалення елементів з малою мірою.
Таким чином, в результаті отримуємо множину \(\left\{P_k^\delta\right\}_{k=1}^m\) зв’язаних точок, які будемо називати слабо контрастними (нечіткими) лініями щодо фону.
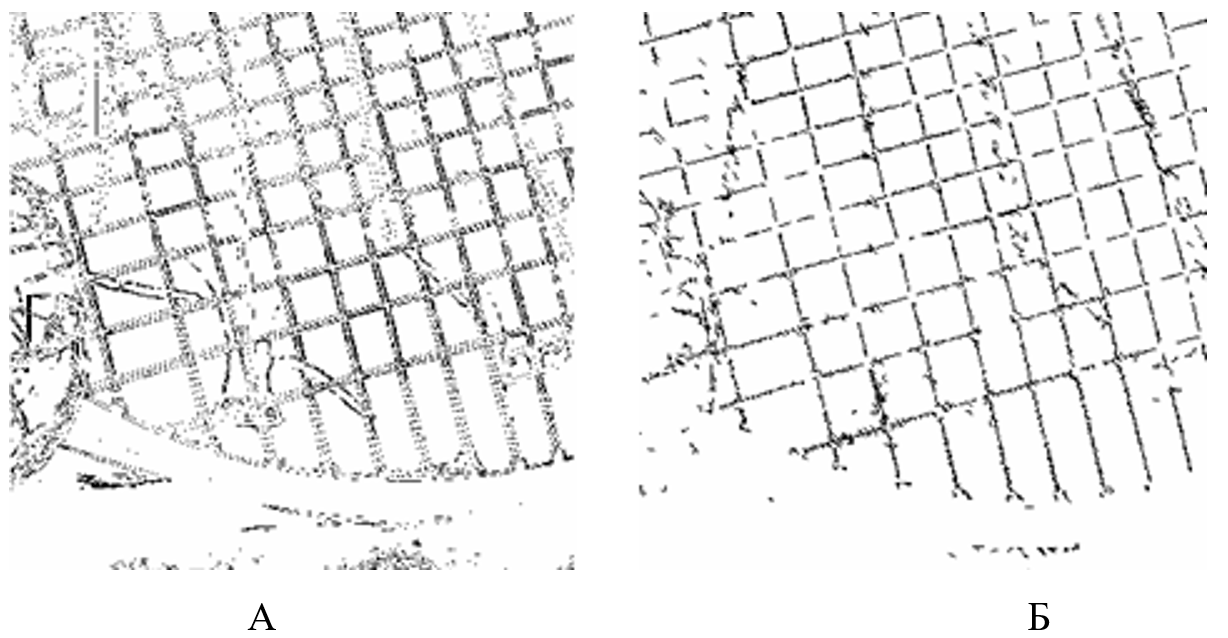
6. А) Виділення нечітких ліній за допомогою фільтрів Собела;
Б) Виділення нечітких ліній за допомогою описаного підходу.
Наступним кроком є формування з множин \(\left\{P_k^\delta\right\}_{k=1}^m\) безпосередньо ліній.
Формування суперліній.
Складність топологічної структури множин \(\left\{P_k^\delta\right\}_{k=1}^m\) не дозволяє реалізувати їх ефективну обробку, тому є актуальним опис множин
\(\left\{P_k^\delta\right\}_{k=1}^n\) об'єктами більш простої конструкції – суперлініямі, чому присвячені подальші побудови.
Так як будь-яка зв'язна множина може бути представлена у вигляді підмножини об'єднання кіл, то \(P^\delta_k\subset\bigcup_{(i,j)\in B_k}C^{R_{i,j}}_{i,j}\).
Зв'язну множину \(B(B^\delta_k)=\left\{(i_\nu,j_\nu)\right\}_{\nu=1}^{N_k}\) будемо називати каркасом множини \(P^\delta_k\), якщо воно дає рішення наступної екстремальної задачі
\begin{equation}\label{8}
\left\{
\begin{array}{l}
\sum_{(i,j)\in B_k}mes\left(C^{R_{i,j}}_{i,j}\right)\to\min,\\
P^\delta_k\subset\bigcup_{(i,j)\in B_k}C^{R_{i,j}}_{i,j}.
\end{array}
\right.
\end{equation}
Каркас множини описує геометричну поведінку множини в цілому, тому для опису \(\left\{P_k^\delta\right\}_{k=1}^m\) скористаємося їх представленням через каркаси.
Зауважимо, що отримання каркаса множини з використанням рішення задачі (\ref{8}) трудомістке і, взагалі кажучи, не потрібне для коректного опису множини.
Тому далі розглянемо спосіб побудови множини, близької до каркаса, конструювання якої істотно простіше.
Граничною точкою множини будемо називати точку, з якої граничить, хоча б одна точка, яка не належить цій множині.
Контуром будемо називати впорядковану замкнуту послідовність граничних точок, у якої ν и (ν+1)-я точка зв'язні, але кожна точка межує не більше ніж з двома граничними точками.
Під однопіксельною лінією будемо розуміти зв'язну множину, кожна точка (піксель) якої має не більш ніж 3 сусідів із множини (рис. 7Б).
Під строго однопіксельною лінією будемо розуміти таку однопіксельну лінію, у якої видалення будь-якої точки, крім кінцевої, призводить до втрати зв'язності (рис. 7А).
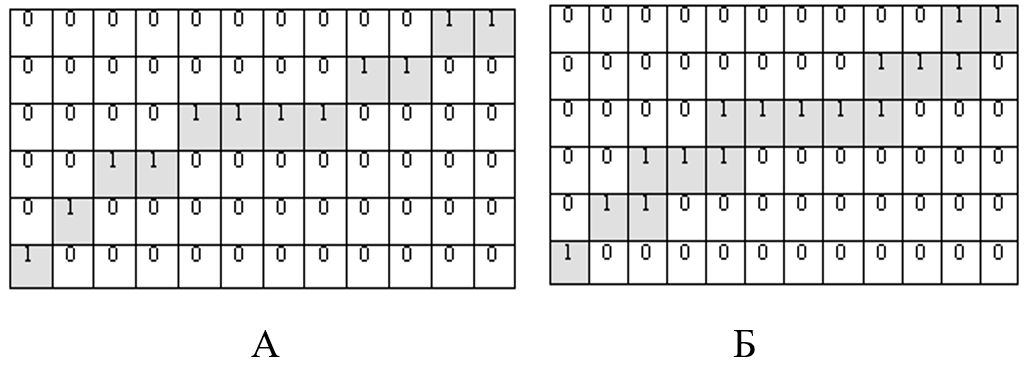
Рис. 7. А) Строго однопіксельна лінія; Б) Однопіксельна лінія.
Операцією депіляції (див. розділ "Обробка растрових зображень") над множиною A для заданого околу \(D^N_{i,j}\) будемо називати
приєднання до множини всіх точок околу \(D^N_{i,j}\), побудованого навколо кожної точки (a,b) множини A.
\[
Dep(A)=A\bigcup\left\{(\nu.\mu)\left|(\nu,mu)\in D^N_{i,j},\forall (i,j)\in A\right.\right\}.
\]
Операцією епіляції \(Epl(A)\) над множиною A будемо називати вилучення із множини A всіх граничних точок, які не порушують зв'язність A.
Застосування операції депіляції дозволяє з'єднати декілька множин в одну зв'язну. Таким чином, послідовне застосування епіляції і депіляції покращує структуру множин, що є підготовкою множини до побудови каркасів
\[
A=Epl(Dep(A)).
\]
Наведемо алгоритм побудова каркасу для множини точок A.
Етап 1. Побудова маски множини.
Поставимо у відповідність множині точок A матрицю \(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\), де
\[
a_{i,j}=\left\{
\begin{array}{ll}
1, & \hbox{ } (i,j)\in A;\\
0, & \hbox{ } (i,j)\notin A.
\end{array}
\right.
\]
Етап 2. Знаходження контуру множини.
Задаємо правило обходу граничних точок. Для побудови контуру будемо обходити кожну граничну точку у фіксованому напрямку, наприклад, у додатному, і при цьому кожен елемент
контуру \(p_k\) будемо характеризувати парою точок \(V(p_k)\) і \(U(p_k)\), де \(V(p_k)\) координати k-ої точки контуру, а \(U(p_k)\)– координати точки, з якої при
заданому обході була додана k-та точка, тобто \(U(p_k)=V(p_{k-1})\).
Побудова контуру починається з довільної граничної точки множини A. Просуваючись по напрямку контуру, приєднуємо черговий елемент. Матриця \(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\)
відображає вплив кожної точки на формування контуру. Додаючи k-й елемент в контур, збільшуємо на одиницю значимість точки в матриці \(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\) з
координатами \(V(p_k)_x,V(p_k)_y\). За визначенням контур є замкнутим, тому процес повинен завершитися, коли в контур буде доданий елемент, що співпадає з першим, тобто
\(V(p_k)=V(p_1)\). Але для коректної обробки ситуації петель цього порівняння не достатньо, тому необхідно порівнювати всі характеристики елементу, тобто і \(U(p_k)\).
З огляду на те, що перший елемент не володіє інформацією про \(U(p_1)\), будемо вважати, що контур побудований, якщо виконано наступні умови:
\[
V(p_k)=V(p_2),\\U(p_k)=U(p_2).
\]
Останні два доданих елемента необхідні для алгоритмізації зупинки формування контуру, тобто не повинні впливати на формування \(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\).
Етап 3. Вилучення множини контуру з зображення.
Після побудови контуру аналізуємо вплив кожної граничної точки на формування контуру. Зауважимо, що одна і та ж гранична точка може бути присутня в декількох елементах
контуру, в цьому випадку вона істотна для зв'язності множини А і не може бути видалена.
Для того щоб ефективно аналізувати входження кожної граничної точки в елементи контуру, не використовуючи додатковий пошук, була введена матриця
\(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\). Виходячи з її значень, легко проаналізувати вплив граничних точок на формування контуру.
Елементи \(a_{i,j}\) можуть приймати значення:
1 – якщо точка не входить в контур;
>2 – якщо точка входить у контур не один раз, а, значить, її видалення призводить до порушення зв'язності множини A.
2 – якщо точка, вимагає додаткового аналізу на видалення.
Видалення точки (i,j) супроводжується установкою значення елемента матриці \(a_{i,j}=0\). Точки, відповідні значенням 2, які мають серед сусідів одиниці –
видаляються. При цьому, можливий розпад множини А на незв'язні підмножини. Підмножини приводяться до строго однопіксельних лінії.
Зауважимо, що для строго однопіксельної лінії легко знаходяться кінці – це точки, які мають тільки одного сусіда, що належить лінії. Очевидно, що розрив зв'язності може
відбуватися в околі кінцівок строго однопіксельних підмножин. Для того щоб уникнути розриву лінії, кожен кінець отриманих фрагментів поміщається в окіл розміру 5×5.
Якщо в цьому околі лежить хоча б одна точка, значення якої дорівнює 1, то повертаємо в окіл ту точку, яка відновить зв'язність.
Одночасно відновлюємо точки, які мали в своїх сусідах більше трьох віддалених точок із значенням 2.
Контур видаляється до тих пір, поки множина А не буде являти собою строго однопіксельну лінію. Рис. 8 ілюструє даний алгоритм.

Рис.8. Приклад поетапного видалення контуру множини.
Таким чином, отримуємо каркас ліній \(B_k=\{P_k\}_{k=1}^m\). На рис. 9Б наведено приклад побудови каркасу для множини точок, зображених на рис. 9 А.
 |  |
| A | Б |
|
Рис.9. А) Фрагмент нечітко виражених ліній; | Б) Цей же фрагмент після обробки. |
Кінцевою точкою будемо назвати таку точку , для якої виконується умова:
\[
\sum\left\{1\left|(x_i,y_i)\in D^1_{x_k,y_k},(x_i,y_i)\in\{P_k\}_{k=1}^m\right.\right\}\le 2.
\]
Суттєвою точкою множини \(\{P_k\}_{k=1}^m\) будемо називати таку точку \((x_k,y_k)\), яка або є кінцевою або її видалення призводить до порушення зв'язності множини \(\{P_k\}_{k=1}^m\).
Однак каркас в чистому вигляді ще не є тією лінією, яку зручно наближати аналітично. У каркасі зазвичай присутні перетини, і візуально виділяються довгі лінії, з яких він складається.
Суперлінією будемо називати множину строго однопіксельних ліній, об'єднаних в місцях перетину.
Першим кроком побудови є отримання місць перехрещень.
Будемо називати вузловою точкою строго однопіксельної лінії таку точку \(x_k,y_k\), для якої виконується умова:
\[
\sum\left\{1\left|(x_i,y_i)\in D^1_{x_k,y_k},(x_i,y_i)\in\{P_k\}_{k=1}^m\right.\right\}\gt 3.
\]
Як показала практика для формалізації перетинів каркасу недостатньо спиратися лише на визначення вузлових точок. На рис. 10. представлені «гарні» вузлові точки – в цьому
випадку перетин явно виражається в одній вузловій точці. На рис. 11. ситуація інакша – один перетин характеризується 4-ма вузловими точками.

Рис. 10. Приклади «гарних» вузлових точок.
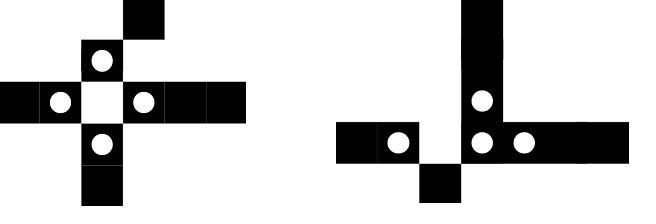
Рис. 11. Приклади «поганих» вузлових точок.
Щоб описати усі варіанти введемо поняття вузла.
Вузлом будемо називати зв'язану множину точок, що спирається на вузлові точки і містять не більше ніж K не вузлових точок. Параметр K регулює допустиме
поширення вузла. Зазвичай K=3.
З кожного вузла виходять фрагменти каркаса.
Фрагментом будемо називати строго однопіксельну лінію, яка не є вузлом, і має або дві вузлові точки, або дві кінцеві точки, або один вузол та одну кінцеву точку:
\(F_i=\left\{p^i_k\right\}_{k=1}^{N_i}\),
де \(N_i\)– кількість точок у фрагменті, \(p_1^i,...,p_{N_i}^i\) вузлові або кінцеві точки.
Таким чином, каркас може бути представлений з вузлів і фрагментів каркаса, що є строго однопіксельними лініями:
\[\bigcup_i^{N_f}F_i\subset \{P_k\}_{k-1}^m,\]
де \(N_f\)– кількість фрагментів каркасу.
Будемо вважати, що в одну лінію можуть бути об'єднані два фрагменти, які виходять з одного вузла, якщо вони схожі по градієнту. Формалізуємо це твердження.
Нехай з вузла виходять m фрагментів \(\{F_k\}_{k=1}^m\). Вважаємо, що точки кожного фрагмента впорядковані від поточного до наступного вузла або кінцевої точки.
Це не представляє складності, враховуючи те, що фрагменти – строго однопіксельні лінії. Перші N ( рекомендоване значення N=5) точок кожного фрагмента апроксимуємо за допомогою прямої. Таким чином, порівняння градієнта фрагментів зведемо до порівняння параметрів відповідних прямих.
Так як відстань від точки \((x_i,y_i)\) до прямої \(x\cos\varphi+y\sin\varphi+c=0\) дорівнює
\[\varepsilon_i=\left|x_i\cos\varphi+y_i\sin\varphi+c\right|,\]
то пряму, найбільш близьку до точок \(\left\{(x_i,y_i)\right\}_{i=1}^N\), будемо шукати з умови:
\begin{equation}\label{9}
\sum_{i=1}^N\left|x_i\cos\varphi+y_i\sin\varphi+c\right|^2\to\min_{\varphi,c}.
\end{equation}
Не зупиняючись докладно, випишемо рішення \(\tilde{\varphi}\) цієї екстремальної задачі
\[
\tilde{\varphi}=\frac{1}{2}\mathrm{arctg}\left(2\frac{\sum_{\nu=1}^Nx_\nu y_\nu-\frac{1}{N}\sum_{\nu=1}^Nx_\nu \sum_{\nu=1}^Ny_\nu}
{\sum_{\nu=1}^Ny_\nu^2-\frac{1}{N}\left(\sum_{\nu=1}^N y_\nu\right)^2-\sum_{\nu=1}^Nx_\nu^2+\frac{1}{N}\left(\sum_{\nu=1}^N x_\nu\right)^2}\right)+\frac{\pi k}{4}.
\]
Таким чином, кожному фрагменту \(F_k\) поставимо у відповідність \(\tilde{\varphi}_k\). Для того щоб упорядкувати ступені подібності всіх можливих пар фрагментів у вузлі,
введемо відстань \(d(\varphi_1,\varphi_2)\) з врахуванням того, що \(\tilde{\varphi}+\pi\) також є рішенням екстремальної задачі.
Відкладемо кожен кут на одиничному колі.
Нехай функція \(\mathrm{Pos}(\varphi)\) повертає координати кута на одиничному колі в декартовій системі координат. Таким чином, відстань між параметрами двох прямих знаходимо за формулою
\[
d(\varphi_1,\varphi_2)=\min\left\{d_E(\mathrm{Pos}(\varphi_1),\mathrm{Pos}(\varphi_2)),d_E(\mathrm{Pos}(\varphi_1),\mathrm{Pos}(\varphi_2+\pi))\right\},
\]
де функція \(d_E\)– евклідова відстань, тобто
\[
d_E((x_1,y_1),(x_2,y_2))=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}.
\]
Побудуємо наступну матрицю відстаней між усіма можливими парами фрагментів
\[
W=\left(
\begin{array}{cccc}
\infty & d(\varphi_1,\varphi_2) & \cdots & d(\varphi_1,\varphi_m) \\
d(\varphi_2,\varphi_1) & \infty& \cdots & d(\varphi_2,\varphi_m) \\
\vdots & \vdots & \infty & \vdots \\
d(\varphi_m,\varphi_1) & d(\varphi_m,\varphi_2) & \cdots & \infty \\
\end{array}
\right)
\]
Значення елементів по діагоналі встановимо рівними нескінченності, так на цих місцях розташовано значення відстані між однією і тією ж прямою, а нас цікавлять тільки можливі пари.
Пара фрагментів \(F_i\) і \(F_j\) об'єднується в одну суперлінію, якщо
\[w_{i,j}=\min_{i,j=1,...,m}(W).\]
Вважаючи, що \(F_i\) і \(F_j\) знайшли пару, встановлюємо у відповідних стовпцях і рядках матриці значення елементів рівними нескінченності.
І знову будуємо нову пару. І так до тих пір, поки не залишиться елементів матриці, не рівних нескінченності або такий елемент буде один.
Об’єднуємо всі фрагменти в лінію, якщо вони утворюють пари і мають спільний вузол.
Зауважимо, що отримані лінії носять явно дискретний характер, тому наступним етапом буде їх згладжування, що дозволить знаходити їх диференціальні характеристики.
Для простоти подальшого розгляду, наступні викладки будемо розглядати на прикладу однієї суперлінії, яка має собою множину \(\{p_i\}_{i=1}^n\).
Поповнимо вихідні дані \(p_i=(x_i,y_i),i=1,...,n\) точками, щоб алгоритми працювали коректно для всіх точок лінії
\begin{equation}\label{10}
p_0=\frac{1}{3}(4\,p_1+p_2-2\,p_3),
p_{n+1}=\frac{1}{3}(4\,p_n+p_{n-1}-2\,p_{n-2}
\end{equation}
і обчислимо згладжені значення
\begin{equation}\label{11}
p^*_i=p_i+\alpha\Delta^2p_i=p_i+\alpha(p_{i-1}-2\,p_i+p_{i+1}),
\end{equation}
де \(\alpha\in (0,1/3]\) (якщо \(\alpha=1/3\), то отримаємо медіанне згладжування).
Після того, як будуть перебрані всі точки, проведемо переприсвоєння \(p_i=p^*_i,i=1,2,...,n\) і повторимо процес згладжування до тих пір поки
заданого \(\varepsilon\gt 0\) та \(\forall i=1,2,...,n\) не виконається умова:
\[
\left(x'_{i+1/2}\right)^2+ \left(y'_{i+1/2}\right)^2=1+\varepsilon,
\]
де
\begin{equation}\label{12}
x'_{i+1/2}=\frac{x_{i+1}-x_i}{\Delta\ell_{i+1/2}},y'_{i+1/2}=\frac{y_{i+1}-y_i}{\Delta\ell_{i+1/2}},\\
\Delta\ell_{i+1/2}=\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2},\\
x'_{-1/2}=2\,x'_{1/2}-x'_{3/2},x'_{n+1/2}=2\,x'_{n-1/2}-x'_{n-3/2},\\
y'_{-1/2}=2\,y'_{1/2}-y'_{3/2},y'_{n+1/2}=2\,y'_{n-1/2}-y'_{n-3/2}.
\end{equation}
Таким чином, результатом роботи даного етапу є набір згладжених суперліній.
Аналітичний опис суперліній.
Суперлінію \(\{p_i\}_{i=1}^n\) будемо описувати в залежності від її геометричної форми. Будемо використовувати такі типи суперліній, як прямі, ламані, криві.
Для визначення належності суперлінії до того чи іншого типу будемо застосовуати дискретний аналог кривизни в кожній точці.
Позначимо через \(\Phi_i\) дискретне значення кривизни у точці \(x_i,y_i\), яка обчислюється за формулою:
\[
\Phi_i=\frac{\left|x''_iy'_i-x'_iy''_i\right|}{\left((x'_i)^2-(y'_i)^2\right)^{3/2}},i=0,1,...,n,
\]
де
\[
x_i'=\frac{x_{i+1/2}'+x_{i-1/2}'}{2},y_i'=\frac{y_{i+1/2}'+y_{i-1/2}'}{2},\\
x_i''=2\frac{x_{i+1/2}'-x_{i-1/2}'}{\Delta\ell_{i+1/2}+\Delta\ell_{i-1/2}}, y_i''=2\frac{y_{i+1/2}'-y_{i-1/2}'}{\Delta\ell_{i+1/2}+\Delta\ell_{i-1/2}},
\]
а відсутні значення похідних визначаються відповідно з формулами (\ref{12}).
Таким чином, для точок \(\{p_i\}_{i=1}^n\), які утворюють собою суперлінію, отримуємо набір \(\{\Phi_i\}_{i=1}^n\), який буде критерієм вибору апарату наближення.
Етап 1. Апроксимація прямою.
Будемо вважати, що якщо для заданого порогу δ>0 виконується нерівність \(\max_i\Phi_i\le\delta\), то лінія достатньо добре описується прямою \(x\cos\varphi+y\sin\varphi+c=0\), яка знаходиться з умови регресії.
У цьому випадку:
\[
\varphi=\frac{1}{2}\mathrm{arctg}\left(2\frac{\sum_{\nu=1}^Nx_\nu y_\nu-\frac{1}{N}\sum_{\nu=1}^Nx_\nu \sum_{\nu=1}^Ny_\nu}
{\sum_{\nu=1}^Ny_\nu^2-\frac{1}{N}\left(\sum_{\nu=1}^N y_\nu\right)^2-\sum_{\nu=1}^Nx_\nu^2+\frac{1}{N}\left(\sum_{\nu=1}^N x_\nu\right)^2}\right)+\frac{\pi k}{4}.
\]
та
\[
c=-\frac{1}{n+1}\left(\sum_{\nu=0}^nx_\nu\cos\varphi+\sum_{\nu=0}^ny_\nu\sin\varphi\right).\]
Якщо умова \(\max_i\Phi_i\le\delta\) не виконується, то на наступному кроці зробимо спробу описати суперлінію ламаною.
Етап 2. Апроксимація ламаною.
При використанні ламаних потрібно, щоб необхідна точність опису лінії давала ламана з малим числом ланок, наприклад, не більше 10 ланок для опису ламаними.
Тобто якщо для множини точок \(p^*_i,i=1,2,...,n\) не достатньо ламаної не більше ніж з 10 ланками, значить, для наближення потрібно використовувати інший апарат.
Для побудови такої ламаної використовувався алгоритм асимптотично оптимального відновлення кривої в метриці Хаусдорфа (візуальної метриці).
Наведемо алгоритм побудови оптимальної ламаної (з точки зору мінімізації вузлів при заданій похибці). Цей алгоритм дозволяє гарантовано отримати ламану з найменшим числом вузлів.
Нехай \((x_i,y_i), i=1,2,...,n\) впорядковані точки, які відповідають деякому контуру Γ, який необхідно описати та ε- допустима помилка.
Через \((x_1,y_1)\) позначимо стартову точку, в ролі якої візьмемо будь-яку точку з ε-околу точки \((x_1,y_1)\), наприклад, саме цю точку.
Побудуємо наступний ітераційний процес - нехай, спочатку, i=2 та ν=1. Через точки \((x_i,y_i)\) і \((x_\nu,y_\nu)\) побудуємо пряму та знайдемо точку
\((x_j,y_j)\) , віддалену від цієї прямої на відстань, яка дорівнює допустимої похибці, тобто
\[
\frac{|(y_j-y_i)(x_\nu-x_i)-(x_j-x_i)(y_\nu-y_i)|}{\sqrt{(x_\nu-x_i)^2+(y_\nu-y_i)^2}}\le\varepsilon\le
\frac{|(y_{j+1}-y_i)(x_\nu-x_i)-(x_{j+1}-x_i)(y_\nu-y_i)|}{\sqrt{(x_\nu-x_i)^2+(y_\nu-y_i)^2}}.
\]
Проекцію точки \((x_j,y_j)\) на пряму \((y-y_j)(x_\nu-x_i)=(x-x_j)(y_\nu-y_i)\) позначимо через \((x^*,y^*)\) і довжина ланки ламаної буде дорівнює
\[
h_\nu=\sqrt{(x^*-x_\nu)^2+(y^*-y_\nu)^2}.
\]
Далі вважаємо i = i +1 і повторюємо цей процес, поки не знайдемо максимальне значення \(h_\nu\). Після цього, в ролі стартової точки візьмемо \(x_\nu,y_\nu\)
і цей процес будемо повторювати до тих пір, поки \(j\le n\). В результаті отримаємо ламану, яка описує дану криву із заданою похибкою ε і з найменшим числом ланок (тобто з найменшим числом інформативних характеристик).
Якщо в результаті отримане число ланок досить мале, наприклад, не більше десяти, то замість шуканої кривої будемо використовувати цю ламану.
Якщо ж точок \(x_\nu,y_\nu\) багато, то для опису кривої використовуємо більш складний апарат.
Етап 3. Апроксимація сплайнами Бєз’є.
Для аналітичного опису суперлінії, яка не може бути наближена прямою чи ламаною з даною точністю, будемо використовувати апарат наближення Без’є - кривими. Розглянемо одну конструкцію сплайнів Без’є, яка, не змінюючи локальних властивостей апроксимації Без’є, для рівномірного розбиття дозволяє одержати інструмент наближення, що асимптотично співпадає з інтерполяційним сплайном мінімального дефекту.
Відомо, що для \(t\in [ih,(i+1)h]\) будь-який параболічний сплайн мінімального дефекту по розбиттю \(ih,i\in Z\) можна записати у вигляді (див.[17])
\begin{equation}\label{13}
s_2(t)=\sum_ic_iB_{2,h}\left(t-h\frac{2i+1}{2}\right)=
c_{i-1}B_{2,h}\left(t-h\frac{2i-1}{2}\right)+c_iB_{2,h}\left(t-h\frac{2i+1}{2}\right)+c_{i+1}B_{2,h}\left(t-h\frac{2i+3}{2}\right),
\end{equation}
де \(B_{2,h}(t)\)– параболічний B- сплайн по решітці із кроком h (див., наприклад тут).
Для неперервної функції \(f\) покладемо \(f_{i+1/2}=f((i+0.5)h)\) й \(f_i=f(ih)\). У даному розділі показано, що якщо
\[
\tilde{c}_i=f_{i+1/2}-\frac{1}{8}\Delta^2f_{i+1/2},
\]
то сплайн
\begin{equation}\label{14}
\tilde{s}_2(f,t)=\sum_{i=-1}^n\tilde{c}_iB_{2,h}\left(t-h\frac{2i+1}{2}\right)
\end{equation}
асимптотично співпадає з інтерполяційним сплайном, тобто
\[
\tilde{s}_2(f,(i+0.5)h)=f_{i+1/2}-\frac{1}{64}\Delta^4f_{i+1/2},
\]
і при цьому, якщо \(f\in C^3\), то для \(t\in [ih,(i+1)h]\)
\begin{equation}\label{15}
f(t)-\tilde{s}_2(f,t)=\frac{h^3}{3}\tau(1-\tau)(\tau-0.5)f^{(3)}(t)+O(h^3),
\end{equation}
де \(\tau=\frac{t-ih}{h}\).
Сплайни виду (\ref{14}) досить зручні й прості, однак у ряді програмних засобів для графічного відображення використовуваються параболічні сплайни Без’є.
Побудуємо таку конструкцію сплайнов Без’є, які будуть співпадать з майже інтерполяційними сплайнами (\ref{14}).
Одержання такої конструкції сплайнів Без’є дозволяє підвищити ефективність вбудованих графічних функцій.
Розрахунок опорних точок Без’є кривої.
Для \(t\in [ih,(i+1)h]\) та точок \(M_i,M_{i+1/2},M_{i+1}\) сплайн Без’є має вигляд
\[
sb(\{M_i,M_{i+1/2},M_{i+1}\},t)=M_i(1-\tau)^2+2\,M_{i+1/2}\tau (1-\tau)^2+M_{i+1}\tau^2.
\]
Тоді похідна має вигляд
\[
sb'(\{M_i,M_{i+1/2},M_{i+1}\},t)=\frac{2}{h}(-M_i(1-\tau)+M_{i+1/2}(1-2\,\tau)+M_{i+1}\tau)
\]
та
\[
sb'(\{M_i,M_{i+1/2},M_{i+1}\},ih)=\frac{2}{h}(-M_i+M_{i+1/2}),\\
sb'(\{M_i,M_{i+1/2},M_{i+1}\},(i+1)h)=\frac{2}{h}(M_{i+1}-M_{i+1/2}).
\]
Крім того,
\[
sb(\{M_i,M_{i+1/2},M_{i+1}\},(i+0.5)h)=\frac{1}{4}(M_i+2\,M_{i+1/2}+M_{i+1}).
\]
Зауважуючи, що
\[
\tilde{s}'_2(f,ih)=\frac{1}{8\,h}(11\,f_{i+1/2}-f_{i+3/2}-11\,f_{i-1/2}+f_{i-3/2}),\\
\tilde{s}'_2(f,(i+1)h)=\frac{1}{8\,h}(11\,f_{i+3/2}-f_{i+5/2}-11\,f_{i+1/2}+f_{i-1/2}),
\]
та
\[
\tilde{s}'_2(f,(i+0.5)h)=\frac{1}{16}f_{i+3/2}-\frac{1}{64}f_{i+5/2}+\frac{29}{32}f_{i+1/2}+\frac{1}{16}f_{i-1/2}-\frac{1}{64}f_{i-3/2},
\]
випишемо умови неперервності сплайну та його похідної, що призводять до системи:
\[
\left\{
\begin{array}{l}
sb'(\{M_i,M_{i+1/2},M_{i+1}\},ih)= \tilde{s}'_2(f,ih);\\
sb'(\{M_i,M_{i+1/2},M_{i+1}\},(i+1)h)= \tilde{s}'_2(f,(i+1)h);\\
sb'(\{M_i,M_{i+1/2},M_{i+1}\},(i+1/2)h)= \tilde{s}'_2(f,(i+1/2)h).
\end{array}
\right.
\]
Розв’язуючи цю систему, одержуємо
\[
\tilde{M}_i=-\frac{1}{16}f_{i-3/2}+\frac{9}{16}f_{i-1/2}+\frac{9}{16}f_{i+1/2}-\frac{1}{16}f_{i+3/2},\\
\tilde{M}_{i+1/2}=-\frac{1}{8}f_{i+3/2}+\frac{5}{4}f_{i+1/2}-\frac{1}{8}f_{i-1/2},\\
\tilde{M}_{i+1}=-\frac{1}{16}f_{i-1/2}+\frac{9}{16}f_{i+1/2}+\frac{9}{16}f_{i+3/2}-\frac{1}{16}f_{i+5/2}.
\]
Сплайн Без’є \(sb(\{M_i,M_{i+1/2},M_{i+1}\},t)\) буде співпадати з майже інтерполяційним параболічним сплайном мінімального дефекту.
Наведемо один приклад використання векторизації растрових зображень з метою зменшення розміру даних. Нижче наведено фрагмент векторного прошарку, на якому алгоритм автоматично вибрав відповідні варіанти наближення фрагментів ліній.
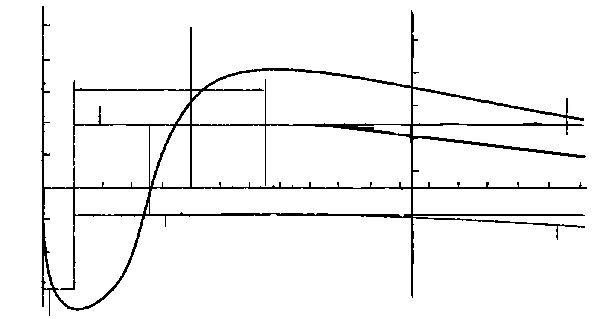
Рис. 12. Оригінальний фрагмент у форматі TIF (3530 байт).
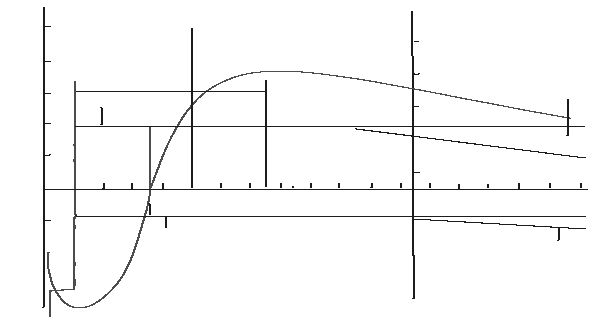
Рис. 13. Векторизований фрагмент (800 байт).
Корисна література.
- Asymptotically Optimum Recovery of Smooth Contours by Bezier Curve / A.A.Ligun, A.A.Shumeiko, S.P.Radzevich, E.D.Goodman // Computer Aided Geometric Design .— 1998 .— №15 .— C.495-506.
- Canny John, A Computational Approach to Edge Detection, Pattern Analysis and Machine Intelligence / John Canny // IEEE Transactions on .– Nov. 1986 .– 679 – 698 p.
- Deriche R. Using Canny's criteria to derive a recursively implemented optimal edge detector / R. Deriche // Int. J. Computer Vision .− 1987 .− Vol. 1 .− P. 167–187.
- Duda R.O. Use Of The Hough Trasformtion To Detect Lines And Curves In Pictures / Richard O. Duda, Peter E. Hart // The Communications of ACM .− 1972 .− Vol 15, No. 1 .− P. 11-15.
- Fisher, Perkins, Walker & Wolfart (2003). "Spatial Filters - Laplacian of Gaussian". Retrieved 2010-09-13 : [Electronic resource] .– http://homepages.inf.ed.ac.uk/rbf/HIPR2/log.htm.
- Prewitt J.M.S. Object Enhancement and Extraction / J.M.S. Prewitt // Picture processing and Psychopictorics .– NY:Academic Press,1970 .– P. 75-149
- Guil N. A fast Hough transform for segment detection, Image Processing / N. Guil, J. Villalba, Zapata // IEEE Transactions .− Nov 1995 .− P. 1541–1548.
- Rad Ali A. Fast Circle Detection Using Gradient Pair Vectors / Ali Ajdari Rad, Karim Faez, Navid Qaragozlou // Proc. VIIth Digital Image Computing .− Sydney, Australia, 2003.− P. 879-887.
- Sobel vs. Prewitt Masks for Edge Detection: [Electronic resource] .– http://the-evan.com/files/eel5820/project%2004/eel5802_pr04-05_turner_evan.pdf.
- Trajkovich M. Fast corner detection / M. Trajkovich, M. Handley // Image and Vision Computing .−1998 .− 16 .− P. 75-87.
- Ziou D, Tabbone S. Edge Detection Techniques - An Overview: [Electronic resource] .– http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.27.1821&rep=rep1&type=pdf
- Введение в контурный анализ / Я.А. Фурман, А.В. Кревецкий, А.К. Передреев и др.; Под ред. Я.А. Фурмана .− М.: ФИЗМАТЛИТ, 2003 .− 392 с.
- Гонсалес Р. Цифровая обработка изображений / Р. Гонсалес, Р. Вудс . – М.: Техносфера, 2005 .– 1070 с.
- Гонсалес Р. Цифровая обработка изображений в среде MATLAB/ Р. Гонсалес, Р. Вудс, С. Эддингс . – М.: Техносфера, 2006 .– 616 с.
- Денисюк В. С. Применение и оптимизация преобразования Хафа для поиска объектов на изображении / В.С. Денисюк // Международный конгресс по информатике: информационные системы и технологии: материалы международного научного конгресса 31 окт.– 3 нояб. 2011 г. .− Минск: БГУ, 2011.− Ч. 2.– C. 162-165.
- Лигун А.О. ALLDocument – технологія нового покоління для збереження, передачі та відображення електронних документів / А.О. Лигун, О.О. Шумейко, Д.В. Тимошенко // Вісник Східноукраїнського національного університету імені Володимира Даля .− 2006 .− №9 (103) Частина 1 .− C. 83-85.
- Лигун А.О. Про побудову майже інтерполяційних сплайнів Без’є / А.О. Лигун, О.О. Шумейко, Д.В. Тимошенко // Актуальні проблеми автоматизації та інформаційних технологій. Збірник наукових праць .– Дніпропетровськ, 2008 .– Том 12 .– С. 125-133.
- Лигун А.А. Локализация и формирование линий на изображении / А.А. Лигун, А.А. Шумейко, Д.В. Тимошенко // Системные технологии. Региональный межвузовский сборник научных трудов .− Днепропетровск, 2007 .− № 3(50) .− С. 5-14.
- Лигун А.А. Асимптотические методы восстановления кривых / А.А.Лигун, А.А.Шумейко .— К.: Изд. Института математики НАН Украины, 1997 .— 358 с.
- Прэтт У. Цифровая обработка зображений. Кн. 2 / У. Прэтт .− М.: Мир, 1982 .− 480 с.
- Роджерс Д. Математические основы машинной графики / Д. Роджерс, Дж. Адамс .– М.: Мир,2001 .– 357 c.
- Ту Дж. Принципы распознавания образов / Дж. Ту, Р. Гонсалес .− М., 1978 .− 410 с.