Обробка растрових зображень |
У останньому випадку компонентами сигналу можуть бути кольори – червоний (R), зелений (G), синій (B), або хроматичні складові Y - освітленість, Cr- теплі відтінки, Cb-холодні відтінки, або елементи простору HSV, головні компоненти PCA простору кольорів, або компоненти іншого простору кольорів.
Переходячи до розгляду теми розділу, треба зазначити, що в реальних сигналах шум так чи інакше присутній. Цей факт обумовлений як апаратною складовою, за допомогою якої отримане зображення, так і впливом стану атмосфери, рухом відносно об'єкта з'йомки, та ін. Компоненти шуму зображень \(n [k_1, k_2]\) можуть об'єднуватися з корисним сигналом \(s [k_1, k_2]\) адитивно: \[ f [k_1, k_2] = s [k_1, k_2] + n [k_1, k_2], \] або мультиплікативно: \[ f [k_1, k_2] = s [k_1, k_2] * n [k_1, k_2]. \] Типовий приклад мультиплікативної взаємодії сигналу з шумом - зв'язок між освітленістю відеооб'єктиву (корисний сигнал) і світловим потоком, відбитим від місцевих об'єктів (шум).До аддитивних відносяться, в основному, шуми, обумовлені властивостями чутливих елементів відео або фотокамер. Ці шуми виникають з наступних причин:

 |  |  |
| а | б | в |
 |  |  |
| г | д | е |
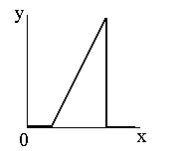 |  |  |
| ж | з | и |
Безумовно, ключовим у бінарізації є вибір порогу. Існує багато різних підходів до вибору порогу бінарізації, але найбільш популярним є метод Оцу (大津展之 ŌtsuNobuyuki).
Ідея методу Оцу полягає в тому, щоб виставити поріг між класами таким чином, щоб кожен з них був якомога більш «щільним». Якщо виражатися математичною мовою, то це зводиться до мінімізації внутрішньокласової дисперсії, яка визначається як зважена сума дисперсій двох класів: \[ \sigma_W^2=w_1 \sigma_1^2+w_2 \sigma_2^2, \] де для будь якого фіксованого \(k=0,1,…,255\) \[ w_1=\frac{\sum_{i=0}^kh_i}{H\times W}, \mu_1=\frac{\sum_{i=0}^kih_i}{\sum_{i=0}^kh_i}, \sigma_1=\frac{\sum_{i=0}^k(i-\mu_1)h_i}{\sum_{i=0}^kh_i}, \] \[ w_2=\frac{\sum_{i=k+1}^{255}h_i}{H\times W}, \mu_2=\frac{\sum_{i=k+1}^{255}ih_i}{\sum_{i=k+1}^{255}h_i}, \sigma_2=\frac{\sum_{i=k+1}^{255}(i-\mu_2)h_i}{\sum_{i=k+1}^{255}h_i}, \] і \(\{h_i \}_{i=0}^{255}\) –гістограма інтерсивності освітлення (компоненти Y). |  |
| Оригінальне зображення Lena | Бінарізація зображення Lena методом Оцу. |
У загальному випадку просторова обробка зображення описується рівнянням:
\[G(x,y)=T(I(x,y)),\]
де \(G(x,y)\)- зображення на виході процедури обробки;
\(I(x,y)\) - вхідне зображення для обробки;
\(T\) - оператор системи обробки.
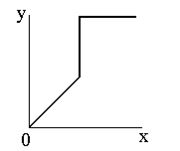
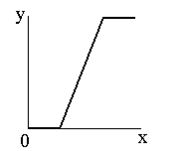
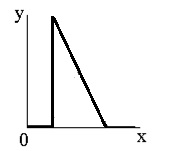
Соляризація полягає в тому, що ділянки вхідного зображення, що мають рівень білого або близького до нього рівень яскравості, після обробки мають відповідний рівень чорного. При цьому зберігається рівень чорного і ділянки, що мають його на оригінальному зображенні.
Функція перетворення має вигляд: \(y=k\cdot x\cdot(x_\max-x)\), де \(x_\max\) - максимальне значення вихідного сигналу, а \(k\)- константа, що дозволяє управляти динамічним діапазоном перетвореного зображення. Функція, що описує дане перетворення, є квадратичною параболою. При \(y_\max =x_\max \) динамічні діапазони зображень збігаються, що може бути досягнуто при \(k=4/x_\max.\)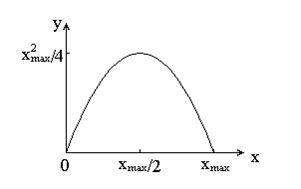 |
| Функція, яка описує солярізацію. |
 |
| Солярізація зображення Lena. |
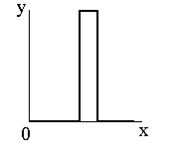
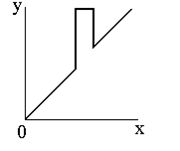
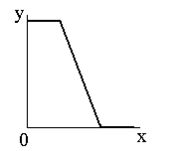
Гамма-корекція яскравості.
Наші очі сприймають зображення не так, як цифрові пристрої. Гамма-корекція зображень - це процес, за допомогою якого цифрове кодування зображення приводиться у відповідність з нашим сприйняттям зображення. Цей метод зміни яскравості зображення відноситься до статичних перетворень і описується виразом: \[ s_{вих}=c\cdot s^\gamma_{вх}, \] де \(с\) та \(\gamma\) – додатні константи, а \(s_{вх}\) і \(s_{вих}\) - відповідно значення яскравості на вході і виході процедури її зміни. Вигляд відповідних співвідношень наведений на зображені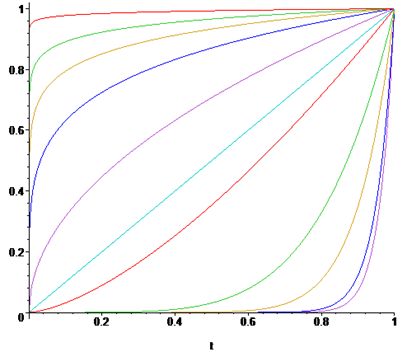 |
| По горизонталі - яскравість на вході, по вертикалі - на виході. |
 |
| По горизонталі - яскравість на вході, по вертикалі - на виході. |
 |  |
 |
| Оригінальне зображення Lena. | Зображення після \(\gamma\)-корекції для \(\gamma=0.5\). | Зображення після сплайн-корекції. |
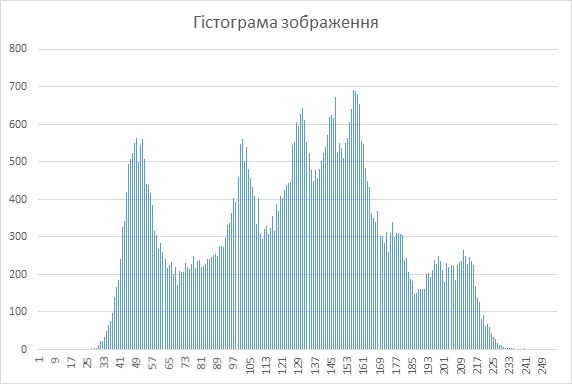
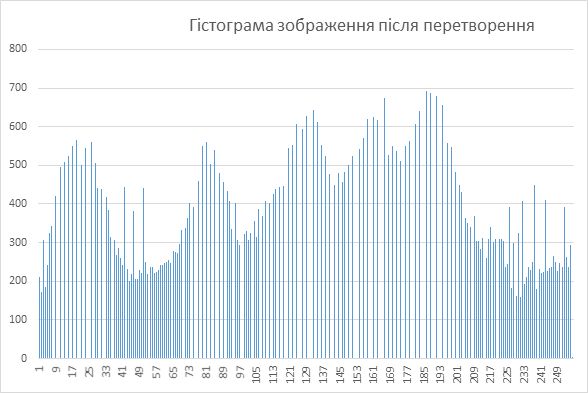
Гістограми є вихідним матеріалом для багатьох методів обробки зображень в просторовій області. Гістограма є характеристикою кількості пікселів в заданому діапазоні освітленості. Оскільки цю кількість ділять на загальну кількість пікселів, то таким чином, значення нормалізованої гістограми показують ймовірності появи в зображенні пікселів у цьому діапазоні освітленості. Очевидно, що сума ймовірностей повинна дорівнювати одиниці.
З вигляду гістограми можна зробити деякі висновки і про саме оригінальне зображення. Наприклад, гістограми дуже темних зображень характеризуються тим, що ненульові значення гістограми сконцентровано близько нульових рівнів яскравості, а для дуже світлих зображень навпаки - все ненульові значення сконцентровані в правій частині гістограми.Розглянемо методи покращення зображень шляхом корекції їх гістограм.


 |
| Алгоритм медіанної фільтрації. |
Лінійна фільтрація зображень в просторовій області полягає в обчисленні лінійної комбінації значень яскравості пікселів у вікні фільтрації з коефіцієнтами матриці ваг, званої маскою або ядром лінійного фільтру.
Найпростішим видом лінійної віконної фільтрації в просторовій області є ковзаюче вікно середніх значень. Результатом такої фільтрації є значення математичного очікування, обчислене по всім пікселям вікна. Математично це еквівалентно згортці з ядром, всі елементи якої дорівнюють 1 / n, де n - число елементів ядра, тобто для випадку ядра розміром \(3\times 3\) має вигляд: \[ \frac{1}{9} \left( \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\ \end{array} \right). \] |  |
| Оригінальне зображення Cougar. | Згладжене зображення Cougar. |
Візуально підвищення різкості призводить до підкреслення дрібних деталей і контурів зображення або поліпшення розрізнення тих його деталей, які опинилися розфокусованими з якоїсь причини.
У подальшому нам знадобиться перша дискретна різниця - аналог першої похідної: \[ \frac{\partial s}{\partial x}\to \Delta s[x+1]=s[x+1]-s[x], \] та друга дискретна різниця – аналог другої похідної: \[ \frac{\partial^2 s}{\partial x^2}\to \Delta^2 s[x+1]=\Delta s[x+1]-\Delta s[x]=s[x+1]-2s[x]+s[x-1], \] які широко застосовуються в методах посилення різкості зображень. Зокрема, на їх використанні заснований оператор Лапласа (лапласіан), який для функції двох змінних для аналогових сигналів визначається як \[ \nabla^2s=\frac{\partial^2 s}{\partial x^2}+\frac{\partial^2 s}{\partial y^2}. \] У простійшому випадку лапласіан дає ядро згортки \[ \left( \begin{array}{ccc} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \\ \end{array} \right) \] але для підвищення різкості краще використовувати ядро \[ \left( \begin{array}{ccc} -1 & -1 & -1 \\ -1 & 9 & -1 \\ -1 & -1 & -1 \\ \end{array} \right) \] або ядро \(5\times 5\) \[ \left( \begin{array}{ccccc} -1 & -3 & -4 & -3 & -1 \\ -3 & 0 & 6 & 0 & -3 \\ -4 & 6 & 20 & 6 & -4 \\ -3 & 0 & 6 & 0 & -3 \\ -1 & -3 & -4 & -3 & -1 \\ \end{array} \right). \] В цілому алгоритм використання лапласіану для підвищення різкости зображення має вигляд: \[ \bar{s}[x,y]= \left\{ \begin{array}{lll} s[x,y]-\nabla^2s[x,y]/k, & \hbox{ якщо } & w[0,0]\le 0, \\ s[x,y]+\nabla^2s[x,y]/k, & \hbox{ якщо } & w[0,0]\gt 0. \\ \end{array} \right. \] Результат обробки зображення із застосуванням оператора Лапласу, тут \(w[0,0]\) - значення центрального коефіцієнта маски Лапласіану. |  |
| Оригінальне зображення Cougar. | Результат застосування Лапласіана. |
Принцип роботи градієнтних операторів зручно розглянути на прикладі алгоритму Собеля. Оператор обчислює градієнт яскравості зображення в кожній точці. Так знаходиться напрямок найбільшого збільшення яскравості і величина її зміни в цьому напрямку. Результат показує, наскільки різко або плавно змінюється яскравість зображення в кожній точці, а значить, ймовірність знаходження точки на границі і орієнтацію границі.
Градієнт функції двох змінних для кожної точки зображення (зокрема і функції яскравості) - двовимірний вектор, компонентами якого є похідні яскравості зображення по горизонталі і вертикалі. У кожній точці зображення вектор орієнтований в напрямку найбільшої зміни яскравості, а його довжина відповідає величині зміни яскравості. Оператор використовує ядро \(3\times 3\) і з ним згортається вихідне зображення. Нехай А- вхідне зображення, а Gx і Gy - дві матриці такого ж розміру як і зображення, кожна точка яких є похідні по x і y \[ Gx=\left( \begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0& 1 \\ \end{array} \right)\otimes A, Gy=\left( \begin{array}{ccc} -1 & -2 & -1 \\ 0 &0 & 0 \\ 1 & 2 & 1 \\ \end{array} \right)\otimes A, \] |  |  |
| Оригінальне зображення Cougar. | Мапа змінності освітлення по горизонталі. | Мапа змінності освітлення по вертикалі. |
 |  |
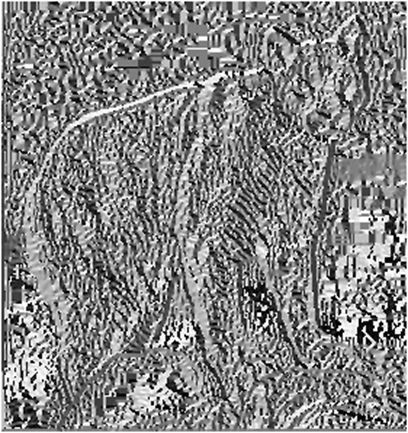 |
| Оригінальне зображення Cougar. | Інверсне зображення величини градієнта Cougar. | Мапа нормованного направлення градієнта Cougar. |
Фільтрація з підйомом високих частот є узагальненням процедури нерізкого маскування. Ця операція зводиться до застосування правила контрастування виду \[ h(x, y)= k\cdot f (x, y) -\nabla^2f (x, y), \] за умови, що ваговий коефіцієнт у центрі фільтру менше нуля, інакше знак перед лапласіаном змінюється на протилежний. У такій ситуації підвищення різкості зображення може проводитися із застосуванням фільтрів \[ \left( \begin{array}{ccc} 0 & -1 & 0 \\ -1 &4+k & -1 \\ 0 & -1 & 0 \\ \end{array} \right) \hbox{ або } \left( \begin{array}{ccc} -1 & -1 & -1 \\ -1 &8+k & -1 \\ -1 & -1 & -1 \\ \end{array} \right). \]
 |  |
 |
| Оригінальне зображення Cougar. | Застосування нерізкого маскування з маскою М1. | Застосування нерізкого маскування з маскою М2. |
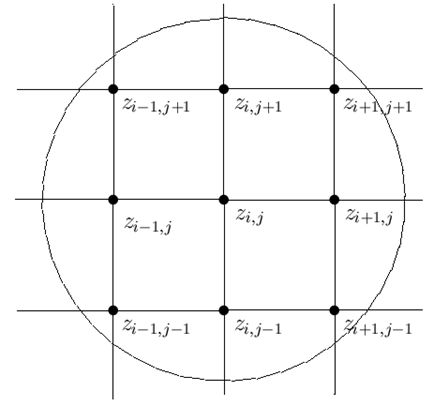
Через \(\ell^2_2\) позначимо лінійний простір всіх обмежених двовимірних послідовностей (масивів) \(A=\{a_{i,j}\}_{(i,j)\in Z^2}\) з нормою \(\|A\|=\left(\sum_{i,j\in Z}a^2_{i,j}\right)^{1/2}\) і покладемо \(|A|=\left|\sum_{i,j\in Z}a_{i,j}\right|\).
Хай \(L\) лінійний оператор, який відображає простір \(X\) у простір \(Y\). Традиційно, нормою оператора \(L\) будемо називати величину \[ \|L\|_{X\to Y}=\sup \frac{\|L(F)\|_Y}{\|F\|_X\le 1}. \] Позначимо через \(C=A\otimes B\) згортку масивів (матриць) \(A\) і \(B\), тобто масив \(C\) такий, що \[ c_{i,j}=\sum_{\nu,\mu}a_{\nu,\mu}b_{\nu-i,\mu-j}. \] Розглянемо рівняння \(E\otimes X=F\), де |E|≠ 0, тоді \(\frac{E}{|E|}\otimes X=\frac{F}{|E|}\), або, що те ж, \(\tilde{E}\otimes X=\Phi\), де \(\tilde{E}=\frac{E}{|E|}\) і \(\Phi = \frac{F}{|E|}\).Основою для побудови відновлюючих фільтрів є наступне твердження:
Теорема. Якщо для будь-якого натурального n виконується нерівність \begin{equation}\label{1} \|I-\tilde{E}\|_{\ell^2_2\to\ell^2_2}\lt 1, \end{equation} то має місце співвідношення \begin{equation}\label{2} X_n=C^1_n\Phi-C^2_n\tilde{E}\otimes \Phi+C^3_n\tilde{E}^2\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^n\otimes \Phi+\varepsilon_n \end{equation} де \(\varepsilon_n\) таке, що \begin{equation}\label{3} \tilde{E}\otimes \varepsilon_n=\left(I-\tilde{E}\right)^{n+1}\otimes \Phi. \end{equation} Дійсно, якщо \[ X_n=C^1_n\Phi-C^2_n\tilde{E}\otimes \Phi+C^3_n\tilde{E}^2\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^n\otimes \Phi+\varepsilon_n \] то \[ \tilde{E}\otimes X_n=\tilde{E}\otimes\left(C^1_n\Phi-C^2_n\tilde{E}\otimes \Phi+C^3_n\tilde{E}^2\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^n\otimes \Phi+\varepsilon_n\right)= \tilde{E}\otimes C^1_n\Phi-C^2_n\tilde{E}^2\otimes \Phi+C^3_n\tilde{E}^3\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^{n+1}\otimes \Phi+ \tilde{E}\otimes \varepsilon_n. \] Звідси, і з (\ref{3}) відразу одержуємо \[ \tilde{E}\otimes X_n=\tilde{E}\otimes C^1_n\Phi-C^2_n\tilde{E}^2\otimes \Phi+C^3_n\tilde{E}^3\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^{n+1}\otimes \Phi+ \left(I-\tilde{E}\right)^{n+1}\otimes \Phi= \] \[ \tilde{E}\otimes C^1_n\Phi-C^2_n\tilde{E}^2\otimes \Phi+C^3_n\tilde{E}^3\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^{n+1}\otimes \Phi+ \Phi-\tilde{E}\otimes C^1_n\Phi+C^2_n\tilde{E}^2\otimes \Phi-C^3_n\tilde{E}^3\otimes \Phi+...+(-1)^{n+1}C^n_n\tilde{E}^{n+1}\otimes \Phi=\Phi. \] Зазначимо, що, якщо виконується умова (\ref{1}), то \[ \|\varepsilon_n\|\le |\tilde{E}^{-1}|\|I-\tilde{E}\|^{n+1}|\Phi|, \] і, в цьому випадку, рішення можна записати в операторному вигляді \[ X=\lim_{n\to \infty}\left(I-\left(I-\tilde{E}\right)^n\right)\Phi. \] Використовуємо цей результат для побудови оператора контрастування, що повертає зображення, змінене в результаті застосування оператора згладжування.Як приклад розглянемо побудову контрастуючого фільтру псевдозворотного до згладжуючого фільтру S, побудованого раніше: \[ S=[s_{i,j}]_{i,j=-1}^1=\frac{1}{9}\left( \begin{array}{ccc} -1 & 2 & -1 \\ 2 &5 & 2 \\ -1 & 2 & -1 \\ \end{array} \right). \]
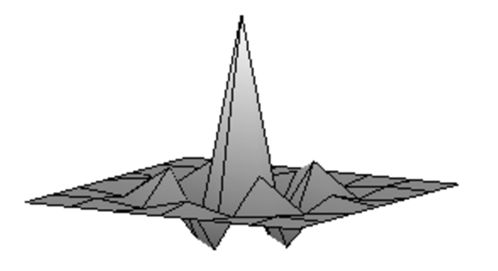
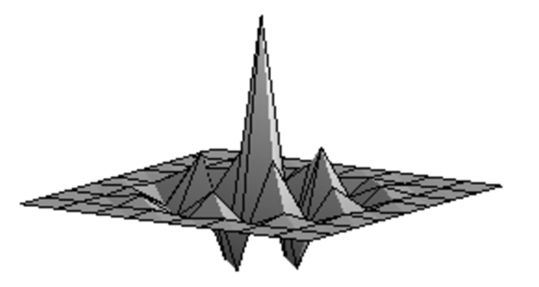
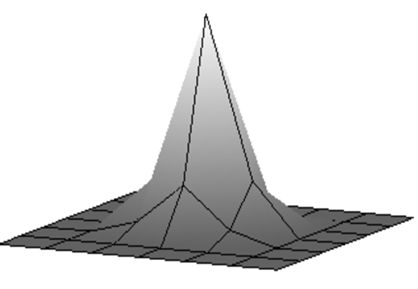

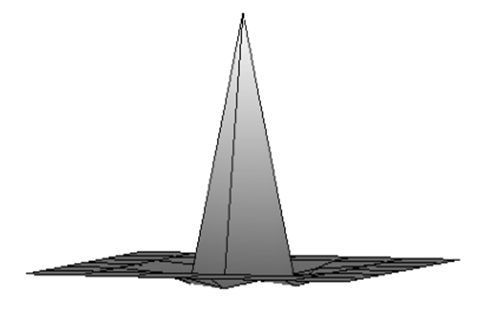

| Згладжене зображення. | Результат після застосування зворотного фільтру першої ітерації. | Результат після застосування зворотного фільтру другої ітерації. |
Результат після застосування зворотного фільтру третьої ітерації. |
 |  |
 |  |
| PSNR=27.26. | PSNR=32.08. | PSNR=35.53. | PSNR=37.96. |
PSNR найчастіше використовується для вимірювання якості реконструкції зображень. Сигнал у цьому випадку є вихідними даними, а шум - це помилка.
Типові значення PSNR для порівняння зображень лежать в межах від 30 до 40 dB. Чим вище значення PSNR, тим менша різниця між зображеннями, що порівнюються.Для монохромних зображень I та K розміру H×W, одне з яких вважається зашумленими наближенням іншого, обчислюється наступним чином: \[ PSNR=20\times \rm{lg} \frac{\max \{I\}}{\sqrt{MSE}}, \] де \[ MSE=\frac{1}{H\times W}\sum_{i=1}^W\sum_{j=1}^H|I_{i,j}-K_{i,j}|^2. \] У разі порівняння повнокольорових зображень, використовуємо суму MSE по кожній кольоровій компоненті і поділемо на 3.
На завершення параграфа, присвяченого створенню просторових фільтрів, розглянемо реалізацію ефекту акварелізації. Акварельний фільтр перетворить зображення, і, після обробки воно виглядає так, як ніби написано аквареллю. Для отримання такого ефекту використовується метод медіанного усереднення кольору в кожній точці. Значення кольору кожного піксела і його 24 сусідів поміщаються в список і сортуються від меншого до більшого. Медіанне (тринадцяте)значення кольору в списку привласнюється центральному пікселу. Після цього, для виділення межі переходів кольорів, до одержаного зображення застосовується контрастуючий фільтр. Результуюче зображення нагадує акварельний живопис.


 |
 |
| A | B |
 |
 |
 |  |
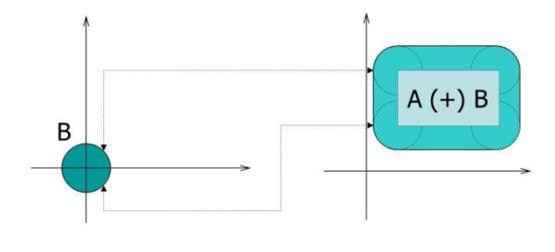
| \(А\oplus В\) Розширення (dilation) |
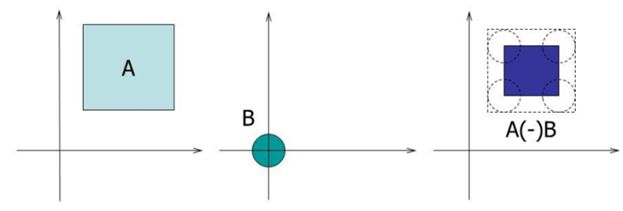
\(А\ominus В\) Звуження (erosion) |
\((А\oplus В)\ominus В\) Відкриття (open) |
\((А\ominus В) \oplus В\) Закриття (close) |
 |
| Костел святого Миколая (м.Кам'янське) кінець ХІХ ст. |
 |
 |
| A | B |
 |
 |
| \(А\oplus В\) Розширення (dilation) |
\(А\ominus В\) Звуження (erosion) |
 |
 |
| \((А\oplus В)\ominus В\) Відкриття (open) |
\((А\ominus В) \oplus В\) Закриття (close) |
Використання морфологічної обробки для знаходження контуру.
Формування внутрішнього контуру \( C^-=A-(A\ominus B) \)


 |
 |
| \(А\oplus В\) Розширення (dilation) |
\(А\ominus В\) Звуження (erosion) |
 |
 |
| \((А\oplus В)\ominus В\) Відкриття (open) |
\((А\ominus В) \oplus В\) Закриття (close) |
Мета морфологічної обробки:
В основі даного підходу лежить метод кластеризації k-середніми (k-means) (див., наприклад, тут).
Ідея методу k-середніх полягає в наступному - спочатку вибирається k довільних початкових центрів з множини \(\mathfrak{T}\). Далі всі об'єкти розбиваються на k груп, найбільш близьких до відповідного центру. На наступному кроці обчислюються центри знайдених кластерів. Процедура повторюється ітераційно до тих пір, поки центри кластерів не стабілізуються.Алгоритм розбиття об'єктів \(x_i (i=0,1,…,n)\) заснований на мінімізації межкластерної відстані, у разі, якщо в якості відстані використовується середньоквадратична норма \(\ell_2\), тобто цільовою функцією є \[ J=\sum_{j=1}^k\sum\left\{\left.\|x_i-\mu_j\|^2\right|x_i\in C_j\right\}, \] де \(x_i\)-i -й об'єкт, а \(C_j\) являє собою j -й кластер із центром \(\mu_j\).
Структура алгоритму полягає в наступному:
У нашому випадку для двох пікселів \(X(X_{red},X_{green}, X_{blue} )\) та \(Y(Y_{red},Y_{green}, Y_{blue} )\) відстань між ними дорівнює \[ \|X-Y\|^2=(X_{red}-Y_{red})^2+(X_{green}-Y_{green})^2+(X_{blue}-Y_{blue})^2 \] і колір пікселів всього кластеру \(C_j\) співпадає з кольором центру кластера \(\mu_j\).
Для тестового зображення Lena у випадку k=8 маємо

Для вирішення цієї задачі використовується ЕМ-алгоритм (див., наприклад, тут). ЕМ-алгоритм для відомого фіксованого числа компонентів суміші можна записати в наступному вигляді.
Нехай \(X=\{x_1,…,x_n \}\) вибірка спостережень, k число компонентів суміші, \(\Theta=\{(w_i,\theta_i )\}_{i=1}^k\)- початкове наближення параметрів суміші, і ε число, що визначає зупинку алгоритму.ЕМ-алгоритм складається з послідовного застосування двох кроків.
Е-крок (expectation) \[ g_{i,j}^0=g_{i,j}, \] \[ g_{i,j}=\frac{\omega_ip_i(x_j)}{\sum_{\nu=1}^k\omega_\nu p_\nu(x_j)},i=1,…,k,j=1,…,n. \] \[ \delta=\max\{|g_{i,j}^0-g_{i,j} |\}. \] M-крок (maximization) \[\sum_{j=1}^ng_{i,j}\rm{ln } p_i(x_j)\to \max_\Theta,i=1,…,k, \] \[ w_i=\frac{1}{n}\sum_{j=1}^ng_{i,j} ,i=1,…,k. \] Якщо δ>ε, то переходимо до Е-кроку, якщо δ≤ ε, то повертаємо знайдені параметри суміші, \(\Theta=\{(w_i,\theta_i )\}_{i=1}^k\).У разі суміші нормальних розподілів \(N(\mu_i,\sigma_i^2)\) Е-крок буде виглядати наступним чином \[ g_{i,j}=\frac{\omega_ip_i(x_j)}{\sum_{\nu=1}^k\omega_\nu p_\nu(x_j)},i=1,…,k,j=1,…,n. \] де \[ p(x|\mu_i,\sigma_i)=\frac{1}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right). \] Для М-кроку задача \[ \sum_{j=1}^ng_{i,j}\ln p_i(x_j)\to \max_{\Theta}, i=1,...,k, \] запишеться у наступному вигляді \[ \sum_{j=1}^ng_{i,j}\ln \left(\frac{1}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right)\right)\to \max_{\Theta}, i=1,...,k, \] або,що теж саме \[ G\left(\left\{\mu_i,\sigma_i\right\}_{i=1}^k\right)=\sum_{j=1}^ng_{i,j} \left(-\ln\left(\sigma_i\sqrt{2\pi}\right)-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right)\to \max_{\Theta}, i=1,...,k. \] Знайдемо похідні та прирівняємо їх до нуля \[ \frac{\partial}{\partial \mu_i}G\left(\left\{\mu_i,\sigma_i\right\}_{i=1}^k\right)=-\sum_{j=1}^ng_{i,j}\frac{x-\mu_i}{\sigma_i^2}=0, \] звідси \[ \mu_i=\frac{\sum_{j=1}^ng_{i,j}x_j}{\sum_{j=1}^ng_{i,j}}. \] Аналогічно, \[ \frac{\partial}{\partial \sigma_i}G\left(\left\{\mu_i,\sigma_i\right\}_{i=1}^k\right)= -\sum_{j=1}^ng_{i,j} \left(\frac{1}{\sigma_i}-\frac{(x-\mu_i)^2}{\sigma_i^3}\right)= -\sum_{j=1}^ng_{i,j} \left(\frac{\sigma_i^2-(x-\mu_i)^2}{\sigma_i^3}\right)=0, \] таким чином, \[ \sigma_i^2=\frac{\sum_{j=1}^ng_{i,j}(x-\mu_i)^2}{\sum_{j=1}^ng_{i,j}}, \] що дозволяє отримати параметри у явному вигляді.
Вважаючи, що кожна гістограма являє собою суміш функцій Гаусса \[ \sum_{i=1}^n\frac{\omega_i}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right) \] застосуємо ЕМ-алгоритм із заданою кількістю елементів суміші n (це ж кількість сегментів, на яке ми розбиваємо кожну колірну площину зображення). І як результат, нехай множина значень інтенсивності \(X_j=(x_j,x_{j+v_j }\) ) така, що \[ \forall x\in X_j: \frac{\omega_j}{\sigma_j\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_j)^2}{2\sigma_j^2}\right)\ge \frac{\omega_i}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right) (i\ne j). \] Тоді всім точкам, інтенсивність яких лежить в проміжку \(X_j\). Поставимо у відповідність значення \(\mu_j\) (при практичній реалізації - її цілу частину). Результатом роботи алгоритму буде сегментація зображення на n сегментів по кожній колірної компоненті.
Для зображення Lena при \(k=3\) маємо

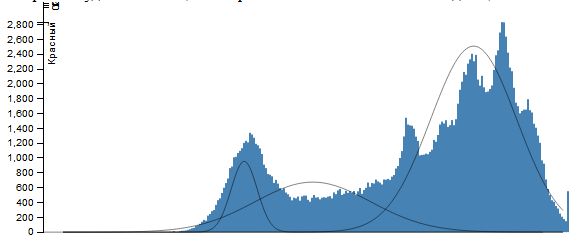
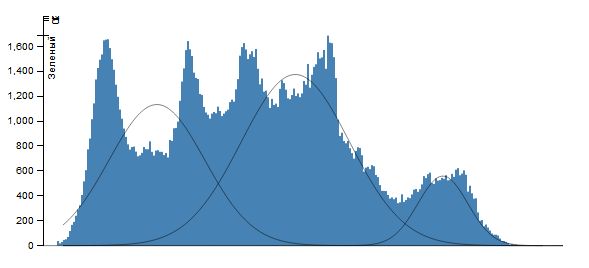
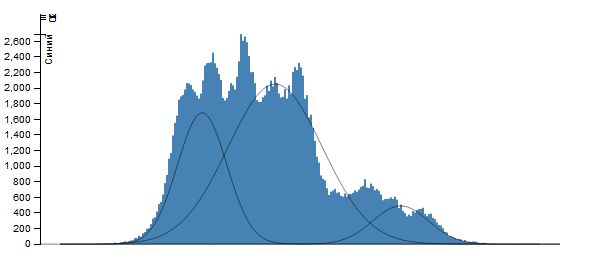
Як видно з розглянутого ЕМ-алгоритму, у разі використання даних двох змінних (i,j,r_(i,j) ), (i,j,g_(i,j) ), (i,j,b_(i,j) ) кожну з множин можна описати лінійною комбінацією двовимірних функцій Гауса \[ \frac{1}{2\pi|\Sigma_i^{-1}|^{1/2}}\exp\left(-\frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)\right) \] за допомогою ЕМ-алгоритму аналогічно тому, як було зроблено у одновимірному випадку.
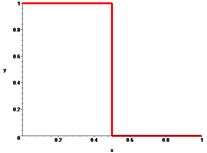
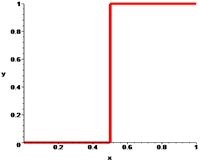
Зазначимо, що для двовимірного випадку нормальний розподіл визначається наступним чином \[ p\left(x|\mu_i,\Sigma_i\right)=\frac{1}{2\pi|\Sigma_i^{-1}|^{1/2}}\exp\left(-\frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)\right) \] де \(\Sigma_i\)-кореляційна матриця і параметри дорівнюють \[ \mu_i=\frac{\sum_{j=1}^ng_{i,j}x_j}{\sum_{j=1}^ng_{i,j}} \] та \[ \Sigma_i=\frac{\sum_{j=1}^ng_{i,j}(x_j-\mu_i)(x_j-\mu_i)^T}{\sum_{j=1}^ng_{i,j}}. \]Порогова сегментація виконується наступним чином: \[ Bin_{i,j}= \left\{ \begin{array}{ll} 1, & \hbox{якщо }I_{i,j}\ge T,\\ 0, & \hbox{якщо }I_{i,j}\lt T, \end{array} \right. \] де \(Bin_{i,j}\) - елемент результуючого бінарного зображення, \(I_{i,j}\)- елемент вихідного зображення.
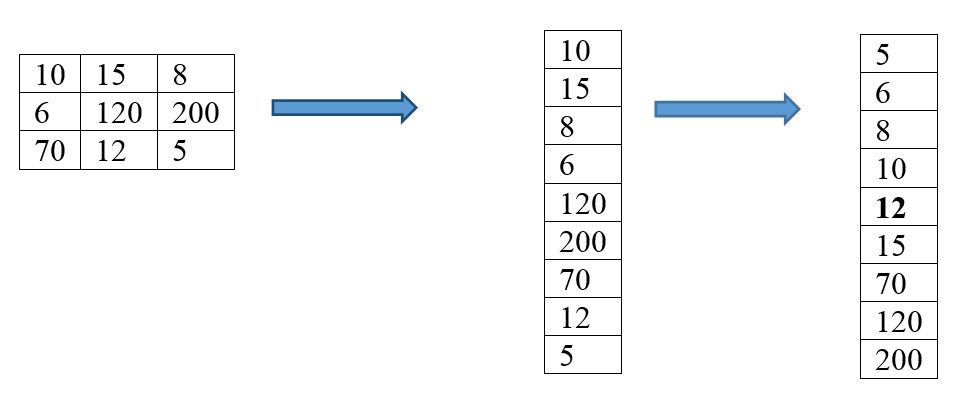
Успіх порогової сегментації залежить від способу вибору порогу \(T\). У разі використання методу Оцу, зображення розбивається на передній і на задній план, тобто, проводиться бінарізація зображення.Нехай \(X_1,X_2,...,X_N\)-вибірка заданого розподілу, розбиття \(\Delta_n=\{-\infty\lt x_0\lt x_1\lt ...\lt x_n\lt \infty\}\) із кроком \(h_{i-1/2}=x_i-x_{i-1}\) і \(m_i=\sum_{i=1}^N\left\{1\left|X_k\in (x_{i-1},x_{i}]\right.\right\},i=1,...,n\) число елементів вибірки з i-го інтервалу. Тоді кусково-постійна функція \(H:R\to R\) \[ H(x)=H(\Delta_n,x)=m_i,x\in (x_{i-1},x_i],i=1,2,...,n \] називається гістограмою вибірки \(X_1,X_2,...,X_N\), якщо ж кусочно-постійна функція \(\hat{H}:R\to R\) така, що \[ \hat{H}(x)=\hat{H}(\Delta_n,x)=\frac{m_i}{Nh_{i-1/2}},x\in (x_{i-1},x_i],i=1,2,...,n, \] то вона називається нормалізованою гістограмою. Помітимо, що нормалізована гістограма є функцією щільності ймовірності, тому що \[ \hat{H}(t)\ge 0 \hbox{ при } t\in R \hbox{ і, крім того, }\int_{-\infty}^\infty \hat{H}(t)dt=1. \] Для абсолютно неперервних розподілів випадкових величин із щільністю ймовірності \(f(x)\) для нормалізованих гістограм при \(N\to\infty\) \[ \forall x\in (x_{i-1},x_i], \hat{H}(x)=\frac{m_i}{Nh_{i-1/2}}\to P\left(X\in (x_{i-1},x_i]\right)\equiv \int_{x_{i-1}}^{x_i}f(x)dx,i=1,2,...,n. \] Таким чином, для неперервної випадкової величини, гістограма на кожній ділянці свого постійного значення повинна зберігати середнє значення. Традиційно розглядаються гістограми з рівновіддаленими вузлами, але вибір вузлів гістограмы істотно впливає на якість опису випадкового процесу. Розглянемо задачу побудови гістограми з асимптотично оптимальними вузлами.
Позначимо через \(\Delta_n=\{x_i\}_{i=0}^n\) - довільне розбиття \(\Delta_n=\{0= x_0\lt x_1\lt ...\lt x_n=T\}\) , і покладемо \(h_{i+1/2}=x_{i+1}-x_i\), \(h=\max_ih_{i+1/2}\) і \(x_{i+\frac{1}{2}}=\frac{x_{i}+x_{i+1}}{2}\). Через \(S\left(\left\{a_{i+\frac{1}{2}}\right\}_{i=1}^{n-1},\Delta_n,x\right)\) позначимо кусково-постійну функцію зі значеннями \(a_{i+\frac{1}{2}}\) для \(x\in [x_i,x_{i+1})\).Для функції \(y(x)\) , неперервної на [0,T], розглянемо задачу \[ \varepsilon=\min_{x_i}\min_{a_{i+\frac{1}{2}}}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(a_{i+\frac{1}{2}}-y(x)\right)^2dx. \] Теорема 1. Нехай \(y(x)\)- неперервно диференційована функція \(y\in C^2_{[0,T]}\) така, що \(y'(x)\) на проміжку \([0,T]\) має не більше скінченного числа нулів, тоді \[ \varepsilon=\frac{1}{12n^2}\left(\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O\left(\frac{1}{n^3}\right) \] і при цьому мінімум досягається для розбиття \(\Delta^*_n=\{x^*_i\}_{i=0}^n\) такого, що \[ \int_{x^*_i}^{x^*_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx=\frac{1}{n}\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx \hbox{ і } a_{i+\frac{1}{2}}^*=\frac{1}{h^*_{i+\frac{1}{2}}}\int_{x^*_i}^{x^*_{i+1}}y(x)dx. \] Доведемо це твердження. На початку розглянемо наступну задачу \[ \Phi\left(a_{i+\frac{1}{2}}\right)=\int_{x_i}^{x_{i+1}}\left(a_{i+\frac{1}{2}}-y(x)\right)^2dx\to\min_{a_{i+\frac{1}{2}}}. \] Тоді зважаючи на опуклість задачі, необхідна умова мінімума є і достатньою, тобто, розв’язок цієї задачі знаходиться з рівняння \[ \frac{d}{da_{i+\frac{1}{2}}}\Phi\left(a_{i+\frac{1}{2}}\right)=2\int_{x_i}^{x_{i+1}}\left(a_{i+\frac{1}{2}}-y(x)\right)dx=0, \] і тоді, \[ a_{i+\frac{1}{2}}=\frac{1}{h_{i+\frac{1}{2}}}\int_{x_i}^{x_{i+1}}y(x)dx. \] Таким чином, первісну задачу можна переписати у вигляді \[ \varepsilon=\min_{x_i}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(y(x)-\frac{1}{h_{i+\frac{1}{2}}}\int_{x_i}^{x_{i+1}}y(x)dx\right)^2dx. \] Використовуючи формулу Тейлора \[ y(x)=y_{i+\frac{1}{2}}+y'_{i+\frac{1}{2}}\left(x-x_{i+\frac{1}{2}}\right)+O(h^2), \] де \(h=\max_ih_{i+\frac{1}{2}}\), отримуємо \[ \varepsilon=\min_{x_i}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(y_{i+\frac{1}{2}}+y'_{i+\frac{1}{2}}\left(x-x_{i+\frac{1}{2}}\right)+O(h^2) -\frac{1}{h_{i+\frac{1}{2}}}\int_{x_i}^{x_{i+1}}\left(y_{i+\frac{1}{2}}+y'_{i+\frac{1}{2}}\left(x-x_{i+\frac{1}{2}}\right)+O(h^2)\right)dx\right)^2dx= \] \[ =\min_{x_i}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(y_{i+\frac{1}{2}}+y'_{i+\frac{1}{2}}\left(x-x_{i+\frac{1}{2}}\right)- y_{i+\frac{1}{2}}+O(h^2)\right)^2dx= \min_{x_i}\frac{1}{12}\sum_{i=0}^{n-1}\left(\left(y'_{i+\frac{1}{2}}\right)^2h^3_{i+\frac{1}{2}}+O(h^4)\right). \] Із теореми про середнє для інтегралів маємо, що знайдеться точка \(\xi_{i+\frac{1}{2}}\in [x_i,x_{i+1}]\) така, що \[ \left(y'\left(\xi_{i+\frac{1}{2}}\right)\right)^2h^3_{i+\frac{1}{2}}= \left(\left(y'\left(\xi_{i+\frac{1}{2}}\right)\right)^{\frac{2}{3}}h_{i+\frac{1}{2}}\right)^3= \left(\int_{x_i}^{x_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3, \] Звідси і із попереднього одразу маємо \[ \varepsilon=\min_{x_i}\frac{1}{12}\sum_{i=0}^{n-1}\left(\left(y'_{i+\frac{1}{2}}\right)^2h^3_{i+\frac{1}{2}} +\left(y'\left(\xi_{i+\frac{1}{2}}\right)\right)^2h^3_{i+\frac{1}{2}}- \left(y'\left(\xi_{i+\frac{1}{2}}\right)\right)^2h^3_{i+\frac{1}{2}} +O(h^4)\right)=\min_{x_i}\frac{1}{12}\sum_{i=0}^{n-1}\left(\left( \int_{x_i}^{x_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O(h^4)\right). \] Лема. Нехай \(\alpha\gt 0\) і \(C\gt 0\), тоді \[ \min\left\{\sum_{i=0}^{n-1}C^\alpha_i|C_i\ge 0,\sum_{i=0}^{n-1}C_i=C\right\}=n\left(\frac{C}{n}\right)^\alpha, \] і при цьому мінімум досягається тоді, коли всі \(C_i\) рівні між собою, тобто, \[ C^*_i=\frac{C}{n},i=0,...,n-1. \] Для доведення цього твердження використаємо метод невизначених множників Лагранжу.
Випишемо функцію мети \[ \mathfrak{L}=\lambda_0\sum_{i=0}^{n-1}C_i^\alpha+\lambda_1\left(\sum_{i=0}^{n-1}C_i-C\right), \] тоді \[ \frac{\partial\mathfrak{L}}{\partial C_i}=\lambda_0\alpha C_i^{\alpha-1}+\lambda_1=0, \] і \(\lambda_0\alpha(C_i^{\alpha-1}+\lambda_2)=0,\) де \(\lambda_2=\frac{\lambda_1}{\lambda_0\alpha}\).
Таким чином, маємо \(C_i=-\lambda_2^{\frac{1}{\alpha-1}}\) і \[ \sum_{i=0}^{n-1}C_i=-\sum_{i=0}^{n-1}\lambda_2^{\frac{1}{\alpha-1}}=-n\lambda_2^{\frac{1}{\alpha-1}}=C. \] Звідси \(\lambda_2^{\frac{1}{\alpha-1}}=-\frac{C}{n}\), або, шо те ж саме, \(C_i=\frac{C}{n}, i=0,...,n-1.\).Лема доведена.
Таким чином, повертаючись до доведення теореми із доведеної леми маємо \[ \varepsilon=\min_{x_i}\frac{1}{12}\sum_{i=0}^{n-1}\left(\left( \int_{x_i}^{x_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O(h^4)\right)= \frac{1}{12}\sum_{i=0}^{n-1}\left(\left( \int_{x^*_i}^{x^*_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O(h^4)\right)= \frac{1}{12}\left(\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O\left(\frac{1}{n^3}\right) \] і при цьому мінімум досягається для разбиття \(\Delta^*_n=\{x^*_i\}_{i=0}^n\) такого, що \[ \int_{x^*_i}^{x^*_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx=\frac{1}{n}\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx. \] Крім того, зазначимо, що для заданої похибки \(\varepsilon\) можна знайти кількість вузлів n кусково-постійної функції \(S\left(\left\{a_{i+\frac{1}{2}}\right\}_{i=1}^{n-1},\Delta_n,x\right)\) з асимптотично оптимальними вузлами, які вибираються із умови вище \[ n=\left[\sqrt{\frac{1}{12\varepsilon}\left(\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3}\right]+1, \] де \([\cdot]\) - ціла частина числа.Ідея отриманого результату складається в тому, що вузли розподіляються таким чином, щоб похибки наближення на кожному відрізку функції \(x(t)\) кусково-постійною функцією \(S\left(\left\{a_{i+\frac{1}{2}}\right\}_{i=1}^{n-1},\Delta_n,x\right)\) будуть рівні між собою.
Розподіл вузлів \(S\left(\left\{a_{i+\frac{1}{2}}\right\}_{i=1}^{n-1},\Delta_n,x\right)\) у разі наближення гістограми зображення може служити множиною порогів для сегментації даного зображення.Ясно, что кожен сегмент буде складатися з декількох не зв'язаних з собою областей. Наступним кроком буде злиття областей, тобто, якщо кількість точок, з яких складається область, менше заданого числа К, то дану область будемо об'єднувати з тією сусідньою областю, рівень сегментації якої найбільш схожий з рівнем поточної області.
Для визначення точок, які належать області, в тому числі, а також знайти кількість точок області, треба використати той чи інший алгоритм заповнення однозв'язаної області. Розглянемо один з них.Простий алгоритм заповнення Затравка(х, у) видає затравочний піксел. Push - процедура, яка вкладає піксел в стек. Pop - процедура, яка виймає піксел зі стека. Піксел(х, у) = Затравка(х, у) Push Піксел(х, у) ; ініціалізація стеку While (стек не пустий) Pop Пиксел(х, у) ; виймаємо піксел зі стека If Пиксел(х, у) <> Нов_значенняthen Пиксел(х, у) = Нов_значення End if Перевірка, чи треба вкладати сусідні пікселі у стек If (Піксел(х + 1, у) <> Нов_значення and Піксел(х + 1, у) <> Гран-значення)then Push Піксел (х + 1, у) If (Піксел(х, у + 1) <> Нов_значення and Піксел(х, у + 1) <> Гран_значення)then Push Пиксел (х, у + 1) If (Піксел(х - 1, у) <> Нов_значення and Піксел(х - 1, у) <> Гран_значення)then Push Піксел (х - 1, у) If (Піксел(х, у - 1) <> Нов_значення and Піксел(х, у - 1) <> Гран_значення)then PushПіксел (х, у - 1) End If EndWhile
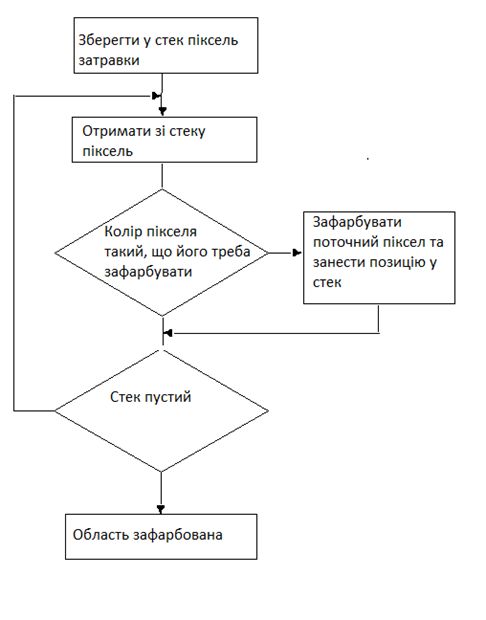
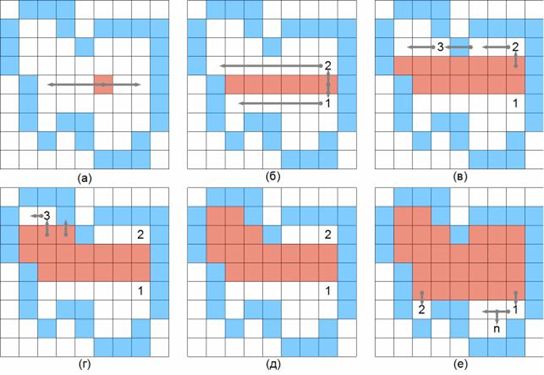


Крок перший – бінарізація.


Даний процес є представлення собою співставлення переднього плану бінарного зображення з відстанню від найближчої перешкоди або фонового пікселя. Цей процес дозволяє прибрати невеличкі або витягнуті області, зберігаючи регіональні центри.



Проста лінійна ітераційна кластеризація (SLIC) є адаптацією k-середніх для генерації суперпікселів з двома важливими відмінностями:
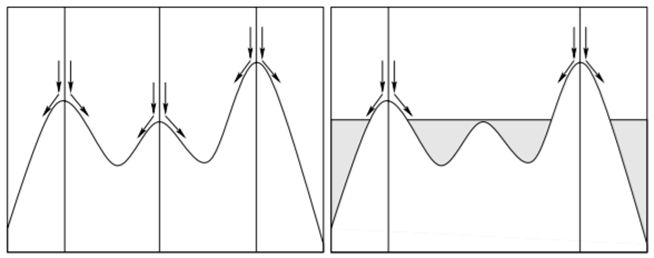
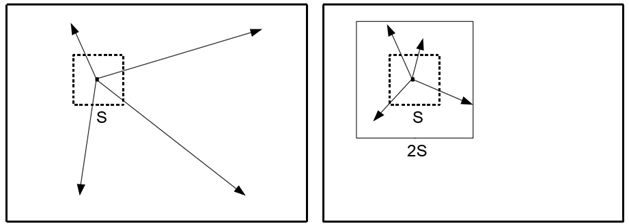
SLIC простий у використанні та розумінні. За замовчуванням єдиним параметром алгоритму є параметр k - бажана кількість суперпікселів приблизно рівного розміру. Для кольорових зображень у колірному просторі CIELAB процедура кластеризації починається з етапу ініціалізації, де k стартових центрів кластерів \(C_i = [l_i a_i b_i x_i y_i]^T\) вибираються на регулярній сітці, з кроком на S пікселів. Для отримання приблизно однакових розмірів суперпікселів, інтервал сітки вибираємо \(S=\sqrt{\frac{N}{k}}\). На кожній ітерації центри переміщуються на місце, що відповідає найменшій позиції градієнта в околі 3 × 3 пікселя \[ G(x,y)=\|I(x+1,y)-I(x-1,y)\|^2+\|I(x,y+1)-I(x,y-1)\|^2, \] де \(I(x,y)\) lab вектор, що відповідає пікселю з позицією (x,y) та \(\|\cdot\|\) норма \(L_2\).
Це робиться для того, щоб уникнути центрування суперпікселя по краю, і щоб зменшити ймовірність співпадання суперпікселів з зашумленим пікселем. Оскільки очікувана просторова протяжність суперпікселя є областю приблизно розміру S × S, пошук подібних пікселів здійснюється в області 2S × 2S навколо центру суперпікселів.Як тільки кожен піксель асоціюється з найближчим центром кластера, крок оновлення регулює центри кластера як середнього вектору \([l a b x y]^Т\) всіх пікселів, що належать кластеру.
Норма \(L_2\) використовується для обчислення залишкової помилки E між новими місцями центру кластера і попередніми центрами кластера. Кроки призначення та оновлення можна повторювати ітераційно, поки помилка не збігається, але для більшості зображень достатньо 10 ітерацій.
Алгоритм SLIC суперпіксельної сегментації / Ініціалізація / Ініціалізація центрів кластерів Ck = [lk ak bk xk yk]T - вибірка пікселів на регулярній сітці з кроком S. Перемістити центри кластера в найнижчу позицію градієнта в околі 3 × 3. Встановити мітку l (i) = −1 для кожного пікселя i. Встановити відстань d (i) = ∞ для кожного пікселя i. repeat / Призначення / for кожного кластерного центру Ck do for кожного пікселя i в області 2S × 2S навколо Ck do Обчислити відстань D між Ck та i. if D < d (i) then множина d (i) = D множина l (i) = k end if end for end for / Оновлення / Обчислити нові центри кластерів. Обчислення залишкової помилки E. until E ≤ порогу
Просто визначення D як п'ятивимірної евклідової відстані у просторі labxy призведе до невідповідності у кластеризації. Для великих суперпікселів просторові відстані перевершують колірну близькість, надаючи більш відносне значення просторовій близькості, ніж колір. Це продукує компактні суперпікселі, які не добре дотримуються меж зображення. Для дрібних суперпікселів є вірним зворотне.
Щоб об'єднати дві відстані в єдину міру, необхідно нормалізувати близькість кольору і просторову близькість за їх відповідними максимальними відстанями в межах кластера.Нехай \[ d_c=\sqrt{(l_j-l_i)^2+(a_j-a_i )^2+(b_j-b_i )^2 }, \] \[ d_s=\sqrt{(x_j-x_i )^2+(y_j-y_i )^2 }, \] \[ D'=\sqrt{\left(\frac{d_c}{N_c} \right)^2+\left(\frac{d_s}{N_s} \right)^2 }. \] Максимальна просторова відстань, що очікується в межах даного кластера повинна відповідати інтервалу вибірки, \(N_s=S=\sqrt{\frac{N}{K}}\). Визначення максимальної відстані кольору \(N_c\) не так просте, оскільки кольорові відстані можуть істотно відрізнятися від кластера до кластера і від зображення до зображення. Цієї проблеми можна уникнути, замінивши \(N_c\) на константу m, тоді \[ D'=\sqrt{\left(\frac{d_c}{m} \right)^2+\left(\frac{d_s}{S} \right)^2 }. \] що спрощує вимірювання відстані. На практиці використовується значення відстані \[ D=\sqrt{\left(d_c \right)^2+m^2\left(\frac{d_s}{S} \right)^2 }. \] Визначаючи D таким чином, m також дозволяє зважувати відносну важливість між колірною подібністю і просторовою близькістю. Коли m є великим, просторова близькість є більш важливою і результуючі суперпікселі є більш компактними (тобто вони мають більш низьке співвідношення області до периметра). Коли m є малим, отримані суперпікселі щільніше прилипають до меж зображення, але мають менший розмір і форму. При використанні колірного простору CIELAB параметр m змінюється у діапазоні \(m\in [1; 40]\), але, як правило, вибирається значення m=20.
В деяких випадках в якості характеристики відстані використовується значенния \[ D=d_c+\frac{d_s}{S} m,m\in [1,20]. \] Рівняння може бути пристосовано для зображень у градаціях сірого шляхом налаштування \[ d_c=\sqrt{(l_j-l_i )^2 }. \] Наведемо приклади суперпіксельної сегментації для різних параметрів.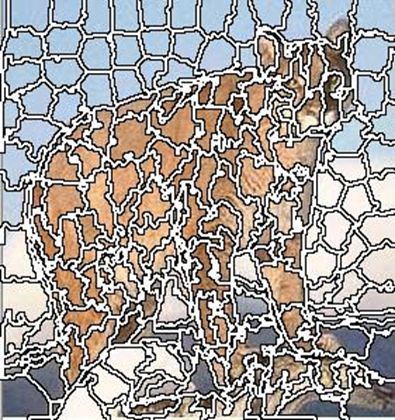 |  | |
| Кількість сегментів 200, m=10. | Кількість сегментів 200, m=40. |
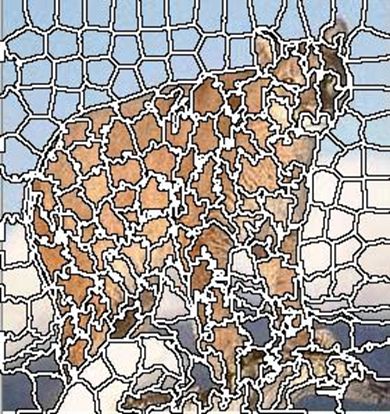 |  | |
| Кількість сегментів 200, m=20. | Кількість сегментів 20, m=20. |
У найпростішому випадку невелика частина фракталу містить інформацію про весь фрактал. Строге визначення самоподібних множин було дано Дж. Хатчинсоном (J. Hutchinson) в 1981 році. Він назвав множину самоподібною, якщо воно складається з декількох компонентів, подібних всій цій множині, тобто компонент одержуваних афінними перетвореннями.
Однак самоподобність – це хоча й необхідне, але далеко не достатня властивість фракталів. Адже не можна ж, справді, уважати фракталом точку, або площину, розкреслену клітками. Головна особливість фрактальних об'єктів полягає в тому, що для їхнього опису недостатньо «стандартної» топологічної розмірності, що, як відомо, для лінії дорівнює 1, для поверхні 2, і т.д. Фракталам характерна геометрична «ізрізаність». Тому використовується спеціальне поняття фрактальної розмірності, що введене Ф. Хаусдорфом (F. Hausdorf) і А.С. Безиковичем. Стосовно до ідеальних об'єктів класичної евклідової геометрії вона давала ті ж чисельні значення, що й топологічна розмірність, однак нова розмірність мала більш тонку чутливість до всякого роду недосконалостям реальних об'єктів, дозволяючи розрізняти й індивідуалізувати те, що колись було безлике й нерозрізнене. Розмірність Хаусдорфа - Безиковича саме й дозволяє вимірювати ступінь «ізрізаності». Розмірність фрактальних об'єктів не є цілим числом, характерним для звичних геометричних об’єктів. Разом з тим, у більшості випадків фрактали нагадують об'єкти, що щільно займають реальний простір, але не використовують його повністю.Нехай є множина G в евклідовому просторі розмірності r. Ця множина покривається кубиками тієї ж розмірності, при цьому довжина ребра будь-якого кубика не перевищує деякого значення δ , тобто \(\delta_i\lt \delta\).
Уводиться залежна від деякого параметра d і δ сума по всіх елементах покриття: \[ \ell_d(\delta)=\sum_i\delta_i^d. \] Визначимо нижню грань даної суми: \[ L_d=\inf\sum_i\left\{\left.\delta_i^d\right|\delta_i\lt\delta\right\} \] При зменшенні максимальної довжини δ, якщо параметр d буде досить великий, мабуть, буде виконуватися \[ \lim_{\delta\to 0}L_d(\delta)\to \infty. \] При деякому досить малому значенні параметра d буде виконуватися: \[ \lim_{\delta\to 0}L_d(\delta)\to 0. \] Проміжне, критичне значення \(\sigma\), для якого виконується: \[ \lim_{\delta\to 0}L_d(\delta)= \left\{ \begin{array}{ll} 0, & \hbox{якщо }d\gt \sigma,\\ \infty, & \hbox{якщо }d\lt \sigma, \end{array} \right. \] і називається розмірністю Хаусдорфа-Безиковича (або фрактальною розмірністю). Для простих геометричних об'єктів розмірність Хаусдорфа-Безиковича збігається з топологічною (для відрізка 1, для квадрата 2, для куба 3 і т.д.)Незважаючи на те, що розмірність Хаусдорфа-Безиковича з теоретичної точки зору визначена бездоганно, для реальних фрактальних об'єктів розрахунок цієї розмірності єдосить скрутним. Тому вводиться трохи спрощений показник - ємнісна розмірність \(d_c\).
При визначенні цієї розмірності використовуються кубики із гранями однакового розміру. У цьому випадку, природно, справедливо: \(L_d(\delta)=N(\delta)\delta^{dc}\),де N(δ) - кількість кубиків, що покриває область G. Шляхом логарифмування й переходу до межі при зменшенні грані кубика одержуємо: \[ d_c=-\lim_{\delta\to 0}\frac{\log{N(\delta)}}{\log{\delta}}, \] якщо ця межа існує. Слід зазначити, що в більшості чисельних методів визначення фрактальної розмірності використовується саме \(d_c\), при цьому необхідно враховувати, що завжди справедливо умову: \(\sigma\le d_c\). Для регулярних само подібних фракталів ємнісна розмірність і розмірність Хаусдорфа-Безиковича збігаються, тому термінологічно їх часто не розрізняють і говорять просто про фрактальну розмірність об'єкта. На жаль класичний підхід дозволяє оцінити фрактальний розмір об’єктів на площині, наприклад, берегову лінію, а з тим, щоб оцінити двовимірний об’єкт, такий я зображення, є великі проблеми. Але все не так погано, існують деякі підходи, які ми і розглянемо.Метод Triangular Prism Surface Area.
Метод TPSA призначений для обробки напівтонових (grayscale) зображень.
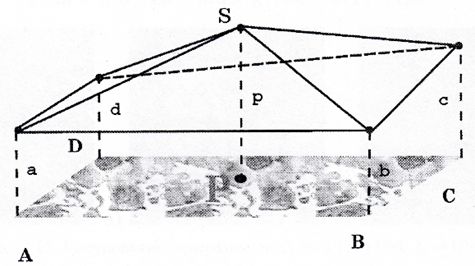
Алгоритм полягає в наступному.
Розглядається центральний пиксель Р и його оточення - квадрат ABCD, лінії між величинами a, b, с, d, р - утворять 4 трикутники з вершиною S та площею: \[ S_p=\sum_{i=1}^4Str_i,Str_i=F(x_i,y_i,r), \] де \(S_p\) - площа фігури, \(Str_i\)- площа і-го трикутника \(i = 1..4, x_i, y_i\) - координати пікселів (вершини і-го трикутника), r - сторона квадрата ABCD.Подібна процедура повторюється для всіх пікселів зображення. Для фіксованого r площі всіх фігур формують одну загальну площу A.
Потім r збільшується, і процедура повторюється. Нахил s графіка A(r) у логарифмічному масштабі використовується для визначення фрактальной розмірності: \(D_{tP}=2-s\).Даний метод, при дослідженні кольорових зображень дозволяє оцінювати розмірність кожного колірного каналу RGB та окремо розмірність його “яркісного” зображення.
Meтод 2D Variation Procedure.Метод 2D Variation призначений для обробки бінарних (binary) і напівтонових (grayscale) зображень.
Знаходимо мінімальний і максимальний рівні сірого в межах кожної квадратної області зі стороною r. Таким чином, визначаються двомірна мінімальна й максимальна функції для кожного кроку решітки. Потім для всього зображення визначається різниця об'єму між мінімальними й максимальними функціями.
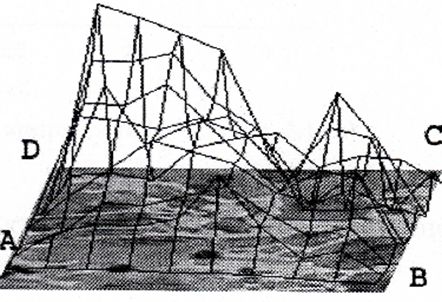
Тоді \(V(r)=r^sconst\), де V - «різницевий» об'єм фігури r - крок сітки, S- фрактальна розмірність.
Подібна процедура повторюється для всіх пикселів зображення, потім r збільшується, і процедура повторюється.Нахил s графіка V(r) у логарифмічному масштабі використовується для визначення фрактальної розмірності: \[ D_{2D}=3-\frac{s}{2}. \] Даний метод при роботі з кольоровими зображеннями також як і TPSA дозволяє оцінювати як розмірність кожного колірного каналу RGB окремо, так і розмірність "яркостного” зображення.
Броуновска розмірність.Ще одним методом оцінювання фрактальной розмірності напівтонових зображень є броуновская розмірність, що пропорційна експоненті Херста (Hurst`s exponent) D=3-H.
Параметр Н можна обчислити статистично із закону дисперсії, використовуючи властивості броуновского руху: \[ H=-\frac{\log\left(\sigma_{\Delta R}(\Delta I)\right)}{\log(\Delta R)} \] \(\sigma_{\Delta R}(\Delta I)\) - середньоквадратичне відхилення приростів, тобто різниця яскравості в точках \(R+\Delta R\) і \(R\), \(\Delta I=I(R+\Delta R)-I(R)\), \(R\) - координати точки.Алгоритм обчислень виглядає в такий спосіб: для всіх точок обчислюються прирости яскравості \(\Delta I\) в \(\Delta R\)-околі, для отриманого масиву приростів обчислюється середньоквадратичне відхилення \(\sigma_{\Delta R}(\Delta I)\), потім змінюємо \(\Delta R\) і повторюємо попередні кроки.
Нахил графіка залежності \(\sigma_{\Delta R}(\Delta I)\) від \(\Delta R\) у логарифмічних координатах дає нам величину Н.Даний метод при роботі з кольоровими зображеннями також як і TPSA і 2D Variation Procedure дозволяє оцінювати як розмірність кожного кольору RGB окремо, так і розмірність "яркісного" зображення.
Таким чином, після того, як кожному пікселю поставимо у відповідність фрактальну розмірність, після фрагментації шкали фрактальної розмірності можна провести відповідну сегментацію зображення.
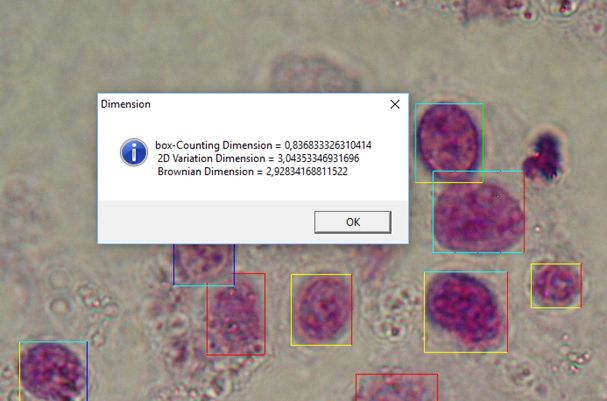
Що до практичного використання фрактальних характеристик, то це можна знайти тут.
 |
| Найпопулярніша жінка у фахівців з комп’ютерної графіки – Lena Soderberg (з обкладинки журналу Playboy за листопад 1972 р.) |
 |
| Костел святого Миколая (Кам'янське) кінець ХІХ ст. |
 |
| Cougar. Кугуар або пума. Кішка, красива до смерті. |
 |
| Зображення Superfood. Мрія вегана. |
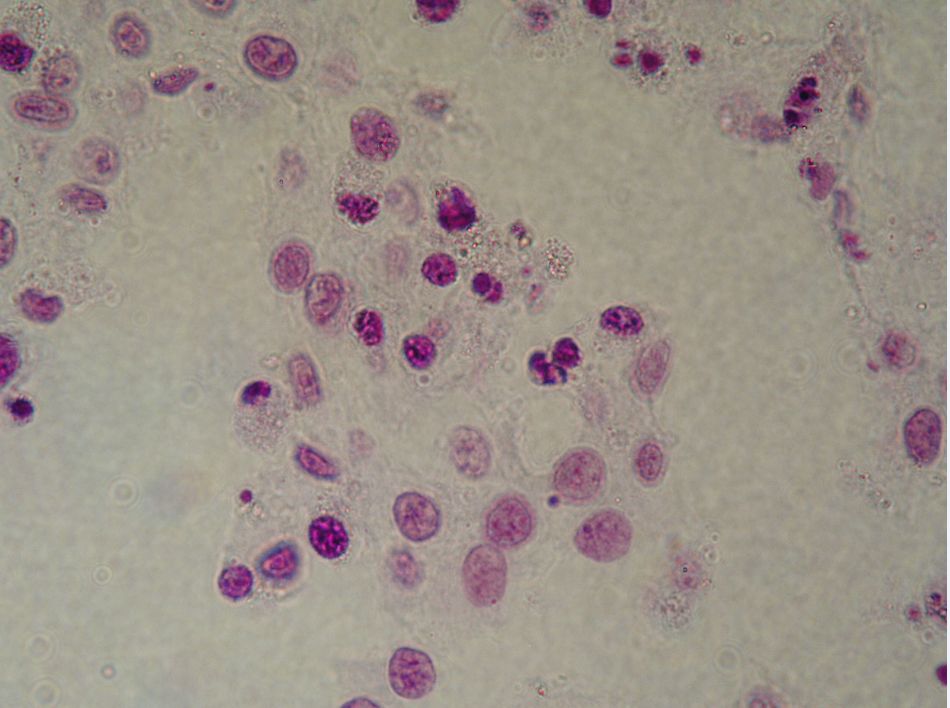 |
| Клітини букального епітелію. (Архів цитопрепаратів крові та кісткового мозку, відділ онкогематології ІЕПОР НАНУ). |