Спектральні методи обробки зображень
Цифрова обробка зображень не обмежується задачами трансформації, які були розглянуті у попередньому розділі. Важливою складовою є кодування інформації, тобто представлення зображення у вигляді, який дозволяє ефективне зберігання та передачу графічної інформації, виділити ті чи інші характеристики, які потрібні під час аналізу об’єктів на даному зображенні, визначити найбільш інформативні характеристики та інше. Для цієї мети використовуються частотні методи аналізу, поперед всього це аналіз Фур’є і аналіз головних компонент. Аналіз Фур’є може використовувати тригонометричний базис, або базис з компактним носієм, що призведе до вейвлет-методів.
Пряме дискретне перетворення Фур'є (ДПФ) і зворотне йому перетворення, мають стандартну форму \[ F(\nu)=N^{-1}\sum_{\tau=0}^{N-1}f(\tau)\exp\left(-i\frac{2\pi\nu \tau}{N}\right), f(\tau)=\sum_{\nu=0}^{N-1}F(\nu)\exp\left(i\frac{2\pi\nu \tau}{N}\right). \] Часто треба виконати перетворення тільки в дійсній області, без використання комплексних змінних. У цьому випадку традиційним методом, який розділяє частотні характеристики сигналу є дискретне косинус перетворення (ДКП), з якого ми і почнемо.
Розглянемо одновимірне ДКП для N=8. Вибір такого значення N не випадковий, у форматі Jpeg зображення розбивається на квадрати 8×8, що і призвело до того, що говорячи про використання частотних методів у обробці зображень використовують як раз таке число складових дискретного перетворення.
Пряме дискретне косинус перетворення має вигляд \[ F_\nu=\frac{1}{\sqrt{2}}C_\nu\sum_{i=0}^7p_i\cos\frac{(2i+1)\nu\pi}{16},\\ C_i=\left\{ \begin{array}{ll} \frac{1}{\sqrt{2}}, & \hbox{i=0;} \\ 1, & \hbox{ i>0}. \end{array} \right. \] Зворотне дискретне косинус перетворення \[ p_i=\frac{1}{\sqrt{2}}C_i\sum_{\nu=0}^7F_\nu\cos\frac{(2i+1)\nu\pi}{16}. \] Ясна річ, що окрім ДКТ існують інші тригонометричні перетворення, наприклад ДСП – дискретне синус перетворення або ДПХ - перетворення Хартлі.
Цей вид перетворення названий на честь Р. Хартлі, що опублікував в 1942 р. статтю про пару інтегральних перетворень - пряму і зворотну, що використовують введену ним функцію \(\mathrm{cas } \theta=\sin\theta+\cos\theta\). До початку 1980-х років ці результати залишалися в забутті, поки до них не привернув увагу дослідників Р. Брейсуэлл, що розробив основи теорії як неперервного, так і дискретного перетворення Хартлі.
Дискретне перетворення Хартлі (ДПХ) дійсної функції f(τ) і відповідне зворотне перетворення визначаються співвідношеннями \[ H(\nu)=\frac{1}{N}\sum_{\tau=0}^{N-1}f(\tau)\mathrm{cas } \frac{2\pi\nu\tau}{N}, \] \[ f(\tau)=\sum_{\nu=0}^{N-1}H(\nu)\mathrm{cas } \frac{2\pi\nu\tau}{N}, \] де використовується позначення cas θ= cos θ+sin θ, введене Хартлі.
Для доведення даного факту скористаємося властивістю ортогональності \[ \sum_{\nu=0}^{N-1}\mathrm{cas } \frac{2\pi\nu\tau}{N}\mathrm{cas } \frac{2\pi\nu t}{N} =\left\{ \begin{array}{ll} N, & \tau=t;\\ 0, & \tau\ne t. \end{array} \right. \] Підставляючи величину \[ \frac{1}{N}\sum_{\tau=0}^{N-1}f(\tau)\mathrm{cas } \frac{2\pi\nu\tau}{N}, \] яка визначає перетворення H(v), у вираз \[ \sum_{\nu=0}^{N-1}H(\nu)\mathrm{cas } \frac{2\pi\nu\tau}{N}, \] отримаємо \[ \sum_{\nu=0}^{N-1}H(\nu)\mathrm{cas } \frac{2\pi\nu\tau}{N}= \sum_{\nu=0}^{N-1}\frac{1}{N}\sum_{t=0}^{N-1}f(t)\mathrm{cas } \frac{2\pi\nu t}{N}\mathrm{cas } \frac{2\pi\nu\tau}{N}= \frac{1}{N}\sum_{t=0}^{N-1}f(t)\sum_{\nu=0}^{N-1}\mathrm{cas } \frac{2\pi\nu t}{N}\mathrm{cas } \frac{2\pi\nu\tau}{N}= \frac{1}{N}\sum_{t=0}^{N-1}f(t)\times \left\{ \begin{array}{ll} N, & \tau=t;\\ 0, & \tau\ne t \end{array} \right. =f(\tau). \] що підтверджує справедливість зворотного перетворення.
Коефіцієнт \(N^{-1}\) в ДПХ запозичується з практики використання ДПФ, для якого величина F(0) дорівнює сталій складовій функції \(f(\tau)\), іншими словами, ДПХ є симетричною процедурою. Окрім цього, ДПХ є дійсним перетворенням, оскільки дійсною є функція \(f(\tau)\).
Проведемо порівняння приведених дискретних перетворень на прикладі множини точок p={12,10,8,10,12,10,8,11}. Знайдемо ДКТ, ДСТ та ДПХ цієї множини. Проведемо наступний експеримент - відквантуємо отримані результати з точністю до десятків, а для синус перетворення, навіть удвічі точніше.

dct={30,0,0,0,0,0,0,0}- чорний колір,
dst={0,25,0,10,0,10,0,10}- червоний колір,
dht={80,0,10,0,0,0,10,0}- зелений колір.

Застосовуючи зворотні перетворення, відновимо дані і знайдемо помилку, яка візуалізована нижче

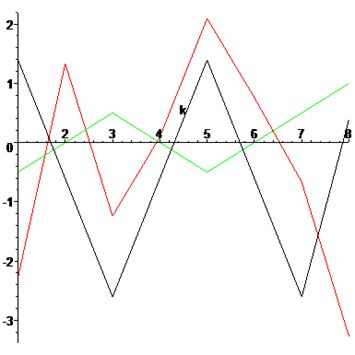Помилка відновлення даних по відквантованим частотним коефіцієнтам.
Як видно навіть з наведеного простого прикладу, найгіршу якість показує синус перетворення, а найкращу – перетворення Хартлі. Але не все так просто, тому що кількість ненульових коефіцієнтів ДКП менша за кількість перетворення Хартлі.
Отримані результати говорять про перспективність перетворення Хартлі. Для того, щоб перевірити і переконатися в ефективності дискретного перетворення Хартлі перед косинус - і синус-перетворенням,побудуємо норми частотних доменів, отриманих з використанням відповідних перетворень.
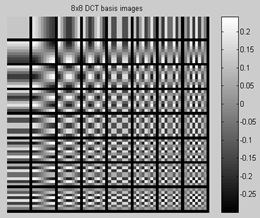
Використовуючи ідеологію JPEG, розіб’ємо зображення на квадрати із стороною у вісім пікселів і на кожному квадраті обчислимо відповідні частотні коефіцієнти. Для ДКП це \[ c^k_{i,j}=\frac{1}{4}C_iC_j\sum_{x=0}^7\sum_{y=0}^7p_{x,y}\cos\frac{(2x+1)i\pi}{16}\cos\frac{(2y+1)j\pi}{16}, \] де \[ C_i=\left\{ \begin{array}{ll} \frac{1}{\sqrt{2}}, & i=0;\\ 1, & i\gt 0. \end{array} \right. \] для ДСП \[ s^k_{i,j}=\frac{1}{4}C_iC_j\sum_{x=0}^7\sum_{y=0}^7p_{x,y}\sin\frac{(2x+1)i\pi}{16}\sin\frac{(2y+1)j\pi}{16}, \] і для ДПХ \[ h^k_{i,j}=\sum_{x=0}^7\sum_{y=0}^7p_{x,y}\mathrm{cas }\frac{2xi\pi}{16}\mathrm{cas }\frac{2yj\pi}{16}, \] де k - номер квадрата.
Множину відповідних частотних коефіцієнтів \(D(q_{i,j})=\left\{q^k_{i,j}|k=0,1,...\right\}\) будемо називати частотним доменом. Норма частотного домену обчислюється за правилом \(\|D(q_{i,j})\|=\sqrt{\sum_k\left(q^k_{i,j}\right)^2}\). По суті, норма, це енергія, що відповідає коефіцієнтам відповідного домену. Чим більше значення норми, тим більше інформації акумулює цей домен. 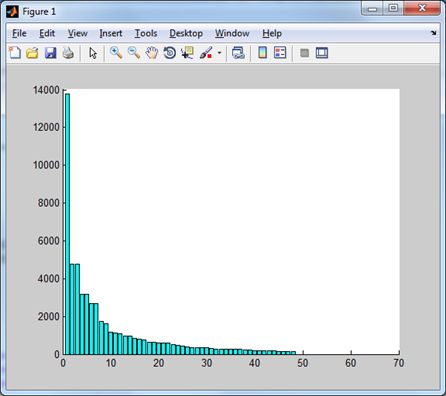Тому, про ефективність того або іншого перетворення можна судити по тому, наскільки швидко спадають норми частотних доменів. Для тестового зображення Lena маємо наступні результати

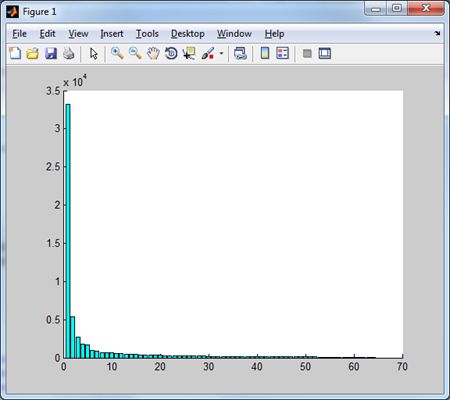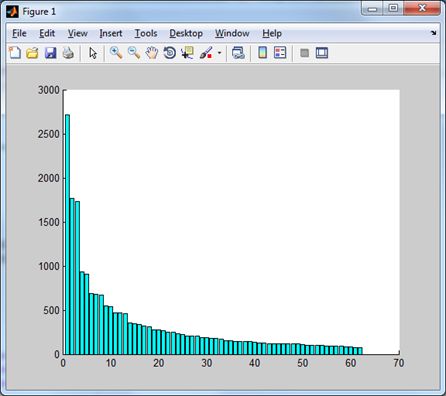Дискретне косинус-перетворення дає
наступний розподіл норм частотних доменів.		Цей же розподіл, але без першого
(низькочастотного) домену.
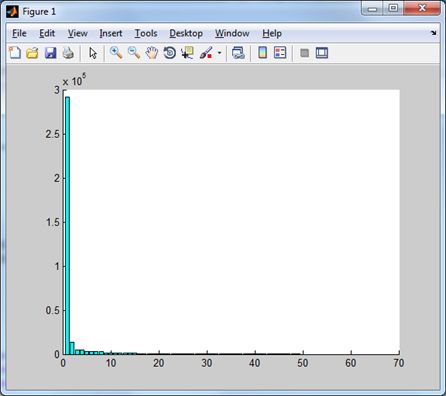Синус-перетворення дає наступний розподіл.І без низькочастотного домену.
Нарешті, перетворення Хартлі ілюструють діаграми
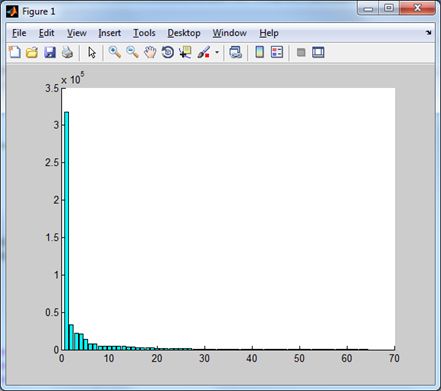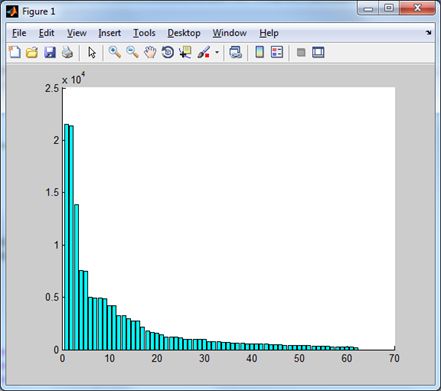Норми доменів перетворення Хартлі.Ці ж домени без низькочастотного.

Щоб порівняти ефективність кодування ДКП та ДПХ (синус перетворення зразу відкинемо як неефективне, цей факт зразу витікає з аналізу гістограм енергії доменів), візьмемо Jpeg і замінимо ДКП на ДПХ.
Коротко зупинимося на методі стиску зображень JPEG. Схематично метод JPEG полягає в наступному:
  1. Кольорове зображення перетворюється з простору змішування кольорів RGB в простір YCrCb, де Y- люмінесцентна складова (освітленість), Cr- компонента теплих відтінків і Cb- компонента холодних відтінків.
  2. На другому етапі відбувається проріджування пікселів (при високих ступенях стиснення з чотирьох значень Cr і Cb беруться не всі, або два або одне значення).
  3. Групування значень Y, Cr і Cb в блоки 8×8 з подальшою фільтрацією, шляхом застосування дискретного косинус-перетворення (ДКП).
  4. Квантування отриманих коефіцієнтів, шляхом ділення кожного коефіцієнта косинус-перетворення Фур'є на спеціальне число (QC-коефіцієнт квантування), з наступним округленням до цілого. Саме на цьому етапі йде непоправна втрата інформації, за рахунок чого, власне, і реалізується істотне стиснення зображення.
  5. Далі відквантовані значення упорядковуються (згідно змійці JPEG) і стискаються методом RLE (Run-lengthEncoding) - стиснення з використанням лічильників нулів.
  6. І на останньому етапі застосовується префіксний або ентропійний метод стиску даних без втрат.
У якості критерію оцінки відновлення оригінального зображення \(I(i,j)\) із зображенням \(K(i,j), (i=0,1,...,m-1;j=0,1,...,n-1)\), використаємо відношення сигнал/шум \[ PSNR(I,K)=20 \log_{10}\frac{255}{\sqrt{MSE(I,K)}} \] де \[ MSE(I,K)=\frac{1}{n\times m}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}|I(i,j)-K(i,j)|^2.\] Для тестування використаємо зображення тестової бази TID2008 фірми Kodak, до яких застосуємо два різних набори коефіцієнтів квантування.
Результати експериментів об’єднаємо на одному графіку.
Вісь абсцис відповідає розміру файлу, вісь ординат - значення PSNR. Точки синього кольору відповідають ДКП, пурпурного - ДПХ. Видно, що вони утворюють по два кластери, що відповідають режимам стиску. Крім того, наведені дві лінійні апроксимації, що з'єднують середні значення кожного кластера. Дана ілюстрація показує істотне поліпшення якості стиснення зображення при використанні ДПХ замість ДКП.
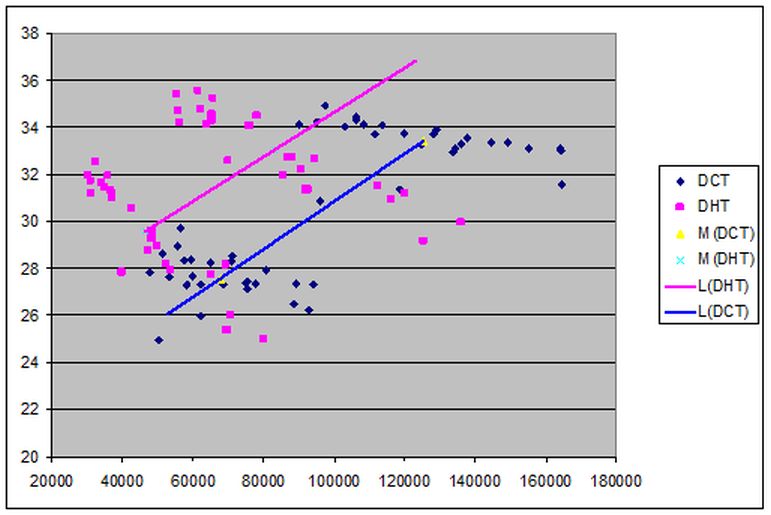
На підставі викладених результатів випливає, що використання дискретного перетворення Хартлі дозволяє отримати метод стиснення зображень, що перевищує JPEG як за ступенем стиснення, так і за якістю відновлених зображень.
Очевидно, що \[ \sum_{i=0}^{N-1}p_i\mathrm{cas } \frac{2\pi\nu i}{N}=\sqrt{2}\sum_{i=0}^{N-1}p_i\cos \left(\frac{2\pi\nu i}{N}-\frac{\pi}{4}\right) \] тобто, перетворення Хартлі представляє собою перетворення Фур’є по косинусу з фазовим зрушенням π/4 і це дає непогані результати. Таким чином виникає питання, а чи існує перетворення по косинусу з будь-яким кутом фазового зрушення.

Одновимірне дискретне тригонометричне перетворення з вільним фазовим зрушенням.

Теорема. Нехай \(\varphi\in\left(0,\frac{\pi}{2}\right)\), тоді для всіх \(\{h_m\}_{m=0}^{N-1}\) таких, що \(-\infty\lt h_m\lt \infty,m=0,1,...,N-1\) та \[ H_k=\sum_{m=0}^{N-1}h_m\cos\left(\frac{2\pi mk}{N}-\varphi\right) \] Має місце рівність \[ h_n=\frac{2}{N\sin(2\varphi)}\sum_{k=0}^{N-1}H_k\sin\left(\frac{2\pi nk}{N}+\varphi\right). \]

Доведення. Припустимо, що це насправді так. Підставимо в друге рівняння значення \(H_k\) з першої рівності, тоді отримаємо \[ \frac{2}{N\sin(2\varphi)}\sum_{k=0}^{N-1}{\left(\sum_{m=0}^{N-1}{h_m\cos\left(\frac{2\pi m k}{N}-\varphi\right)}\right)\sin\left(\frac{2\pi n k}{N}+\varphi\right)}= \] \[ \frac{2}{N\sin(2\varphi)}\sum_{m=0}^{N-1}{h_m\sum_{k=0}^{N-1}{\cos\left(\frac{2\pi m k}{N}-\varphi\right)}\sin\left(\frac{2\pi n k}{N}+\varphi\right)}= \] \[ \frac{2}{N\sin(2\varphi)}\sum_{m=0}^{N-1}{h_m\sum_{k=0}^{N-1}{\left(\sin\left(\frac{2\pi k(n+m)}{N}\right)+\sin\left(\frac{2\pi k (n-m)}{N}+2\varphi\right)\right)}}. \] Зазначимо, що (див., наприклад, [8] стор.82) \begin{equation} \label{1} \sum_{\nu=0}^{N-1}\sin(\alpha+\nu\beta)=\frac{1}{\sin\frac{\beta}{2}}\sin\left(\alpha+\frac{N-1}{2}\beta\right)\sin\frac{N\beta}{2}, \end{equation} Нехай, спочатку, \(n+m\ne N\), тоді з (\ref{1}) отримаємо, \[ \sum_{k=0}^{N-1}\sin\left(\frac{2\pi k(n+m)}{N}\right)= \frac{1}{\sin\left(\frac{2\pi (n+m)}{2N}\right)}\sin\left(\frac{2\pi(n+m)(N-1)}{2N}\right) \sin\left(\frac{2\pi(n+m)N}{2N}\right). \] З умови \(n+m\ne N\) отримуємо \[ \sin\left(\frac{2\pi (n+m)}{N}\right)\ne 0, \] а, з іншого боку, \[ \sin\left(\frac{2\pi N}{2N}\right)=\sin(\pi(n+m))=0, \] тобто, для \(n+m\ne N\) \[ \sum_{k=0}^{N-1}{\sin\left(\frac{2\pi k(n+m)}{N}\right)}=0. \] Якщо ж \(n+m= N\), тоді \[ \sum_{k=0}^{N-1}{\sin\left(\frac{2\pi k(n+m)}{N}\right)}= \sum_{k=0}^{N-1}{\sin\left(\frac{2\pi kN}{N}\right)}= \sum_{k=0}^{N-1}{\sin\left(2\pi k\right)}=0. \] Таким чином для всіх \(n,m=0,1,\ldots,N-1\) \[ \sum_{k=0}^{N-1}{\sin\left(\frac{2\pi k(n+m)}{N}\right)}=0. \] Розглянемо співвідношення \[ \sum_{k=0}^{N-1}{\sin\left(\frac{2\pi k(n-m)}{N}+2\varphi\right)}. \] Використовуючи рівняння (\ref{1}), маємо \[ \sum_{k=0}^{N-1}{\sin\left(\frac{2\pi k(n-m)}{N}+2\varphi\right)}= \frac{1}{\sin\left(\frac{2\pi (n-m)}{2N}\right)}\sin\left(\frac{2\pi (n-m)(N-1)}{2N}+2\varphi\right)\sin\left(\frac{2\pi (n-m)N}{2N}\right). \] Далі, примітимо, що так, як \(n,m=0,1,\ldots,N-1\), то \(n-m\ne N\). Нехай, \(n\ne m\) , тоді отримаємо, що \[ \sin\left(\frac{\pi (n-m)}{N}\right)\ne 0, \] але, при цьому, \[ \sin\left(\frac{2\pi (n-m)N}{2N}\right)=\sin(\pi(n-m))=0 \] для всіх \(n,m=0,1,\ldots,N-1\) і для \(n\ne m\), в тому числі. І, нарешті, нехай \(n=m\), тоді \[ \sum_{k=0}^{N-1}\sin\left(\frac{2\pi k(n-m)}{N}+2\varphi\right)=\sum_{k=0}^{N-1}\sin(0+2\varphi)=N\sin(2\varphi). \] Таким чином, отримаємо \[ \sum_{k=0}^{N-1}\left(\sin\left(\frac{2\pi k(n+m)}{N}\right)+\sin\left(\frac{2\pi k(n-m)}{N}+2\varphi\right)\right)= \left\{ \begin{array}{ll} N\sin(2\varphi), & n=m; \\ 0, & n,m=0,1,\ldots,N-1,n\ne m. \end{array} \right. \] Звідси виходить рівняння \[ \frac{1}{N\sin(2\varphi)}\sum_{m=0}^{N-1}h_m\sum_{k=0}^{N-1}\left(\sin\left(\frac{2\pi k(n+m)}{N}\right)+\sin\left(\frac{2\pi k(n-m)}{N}+2\varphi\right)\right)= \left\{ \begin{array}{ll} h_n, & n=m; \\ 0, & n,m=0,1,\ldots,N-1,n\ne m. \end{array} \right. \] Що і є завершенням доказу теореми.
Зазначимо, що, якщо \(\varphi=\frac{\pi}{4}\), то ми отримаємо дискретне перетворення Хартлі (ДПХ), тобто ДПХ є окремим випадком отриманого ДТП.
Використання можливості використання фазового зсуву для поліпшення відновлення даних дозволяє, на підставі отриманого дискретного перетворення, будувати адаптивні фільтри, підлаштовуючи фільтр не тільки для вхідних даних, але і, наприклад, для використовуваного методу квантування або природи шуму, що вносить спотворення в сигнал.

Двовимірне дискретне тригонометричне перетворення з вільним фазовим зрушенням.

Так як одною з популярних сфер використання дискретного косинус-перетворення є цифрова обробка двомірних сигналів, тобто зображень, то для використання отриманого дискретного тригонометричного перетворення в обробці зображень існує двомірне перетворення:

прямий хід \[ h_{i,j}=\frac{2}{N\sin(2\varphi)}\sum_{n=0}^{N-1}\sum_{m=0}^{N-1}p_{n,m}\cos\left(\frac{2\pi ni}{N}-\varphi\right)\cos\left(\frac{2\pi mj}{N}-\psi\right), \] та зворотний хід \[ p_{n,m}=\frac{2}{N\sin(2\psi)}\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}h_{i,j}\sin\left(\frac{2\pi ni}{N}+\psi\right)\sin\left(\frac{2\pi mj}{N}+\varphi\right). \]

Використовуючи це перетворення для блоку 8×8 пікселів, можна отримати кращий результат ніж дискретне косинус-перетворення, але для отримання такого результату необхідно вибрати відповідні фазові зрушення. Цим дискретним тригонометричним перетворенням можна замінити дискретне косинус-перетворення в стандарті JPEG без зміни логіки кодування та квантування, лише замінивши перетворення.

Визначення найкращого фазового зрушення.

Для визначення найкращого фазового зрушення, що для двомірного сигналу складається з двох параметрів \(\varphi\) та \(\psi\), запропоновано наступний підхід:
  1. Треба вирахувати значення Peak Signal to Noise Ration(PSNR) для відновленого зображення, при майже крайніх значеннях зрушення, наприклад \(\varphi_1=\pi/100, \varphi_2=\pi/8\), та \(\varphi_3=\pi/4\), значення \(\psi\) краще взяти середнє, тобто \(\pi/8\).
  2. Знайти точку максимуму параболи проведеної через точки A(PSNR1; φ1), B(PSNR2; φ2) та C(PSNR3; φ3).
  3. Координата X знайденої точки буде апроксимацією шуканого значення φ.
  4. Перейти до кроку 1 та провести цю операцію для ψ використовуючи знайдене значення φ, дану операцію можна повторювати безліч разів використовуючи по черзі φ та ψ, але практика показала, що і одного разу достатньо.
Цей метод також підходить для одновимірного сигналу. Дана операція займає багато часу, так як зображення повністю кодується та декодується мінімум 6 разів, але вона дозволяє отримати майже найкращі значення φ та ψ. Також можна розрахувати значення PSNR для усіх значень φ та ψ з певним кроком та вибрати найкращій результат, але наведений метод дозволяє значно скоротити кількість обчислень перетворення та надає більш точний результат.
Для тестування було взято тестові зображення з бази даних зображень TID2008 фірми Kodak. Для кожного зображення було визначено кращі значення зрушень, а також побудовані графіки кожного значення PSNR в залежності від фазових зрушень

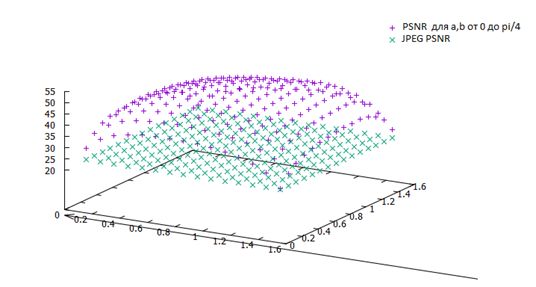Розподілення значень PSNR для різних значень φ та ψ на портретному зображенні.

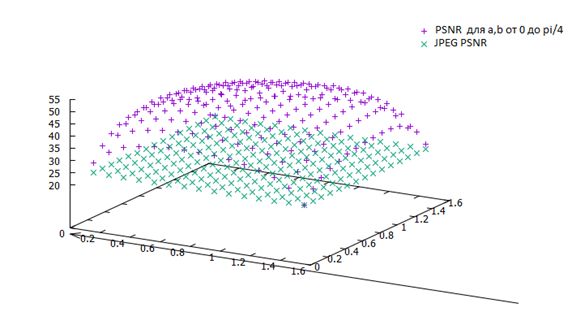Розподілення значень PSNR для різних значень φ та ψ на пейзажному зображенні.

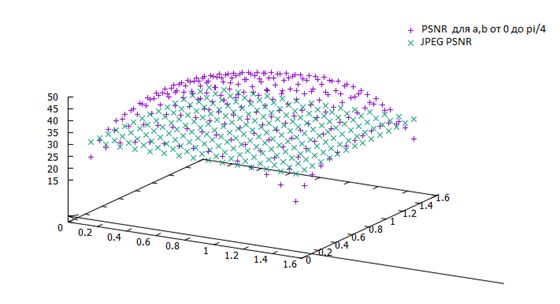Розподілення значень PSNR для різних значень φ та ψ на синтетичному зображенні.

Розглянемо наступну задачу: як вибрати базисні вектори, щоб мінімальним числом базисних векторів можна було найкращим чином наблизити дані з деякого набору.
Вирішенню цієї задачі відповідає метод головних компонент - ортогональне лінійне перетворення базису, при якому перший вектор нового базису відповідає напрямку максимальної дисперсії даних, другий вектор - наступного напрямку максимальної дисперсії і так далі.

У реальних задачах комп’ютерної графіки досить продуктивна інша евристика, яка ґрунтується на гіпотезі про наявність «сигналу» (порівняно мала розмірність, відносно велика амплітуда) і «шуму» (велика розмірність, відносно мала амплітуда). З цієї точки зору метод головних компонент працює як фільтр: сигнал міститься, в основному, в проекції на перші головні компоненти, а в інших компонентах пропорція шуму набагато вище.

Метод головних компонент.

Метод головних компонент (МГК) — один із основних способів скорочення розмірності даних із зменшенням кількості інформації, розроблений Карлом Пірсоном (Karl Pearson) у 1901 р. Використовується у багатьох областях, таких як розпізнавання образів, комп’ютерний зір, стиск даних та ін. (Більш детально що до МГК можна ознайомитися, якщо перейти за посиланням http://pzs.dstu.dp.ua/DataMining/pca/index.html). Знаходження головних компонент зводиться до обчислення власних векторів та значень коваріаційної матриці вхідних даних.
Перейдемо до розглядання метода МГК (PCA - Principal Component Analysis). Спочатку проведемо центрування даних, для чого знайдемо константу μ, яка найкращим чином описує вхідну інформацію \[ \varepsilon \left( \mu \right) = \sum\limits_{i = 1}^n {\left( {x_i - \mu } \right)^2 \to \mathop {\min }\limits_\mu } . \] Для знаходження мінімуму знайдемо похідну і прирівняємо її до нуля, після чого знайдемо значення μ, яке дає мінімум \[ \frac{d}{d\mu }\varepsilon \left( \mu \right) = - 2\sum\limits_{i = 1}^n {\left( {x_i - \mu } \right) = 0 \Rightarrow } \sum\limits_{i = 1}^n {\mu = } \sum\limits_{i = 1}^n {x_i \Rightarrow } \mu n = \sum\limits_{i = 1}^n {x_i \Rightarrow } \mu = \frac{1}{n}\sum\limits_{i = 1}^n {x_i } . \] Далі проведемо центрування даних, тобто, переозначимо вхідні значення \(x_{new} = x_{old} - \mu \), віднімаючи з кожного отримане значення μ. Ясно, що нові дані мають математичне очікування, яке дорівнює нулю \[ E\left( {X - E\left( X \right)} \right) = E\left( X \right) - E\left( X\right) = 0. \] Таким чином, ми зробили паралельний зсув в існуючий системі координат.
У подальшому будемо вважати, що наші дані центровані і ми маємо бажання знайти найбільш точне представлення даних \(D = \left\{ {x_1 ,...,x_n } \right\}\) у деякому підпросторі W з розмірністю \(k \lt n\).
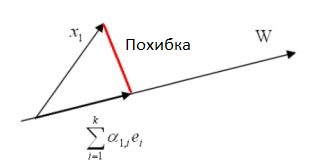
Нехай \(\left\{ {e_1 ,...,e_k } \right\}\) ортонормований базис W. Довільний вектор із W може бути записаний у вигляді лінійної комбінації векторів базису, тобто, \(x_1\) можна поставити у відповідність деякий вектор \(\sum\limits_{i = 1}^k {\alpha _{1,i} } e_i \) із W. Похибка між ними обчислюється наступним чином \[ \varepsilon _1 = \left\| {x_1 - \sum\limits_{i = 1}^k {\alpha _{1,i} } e_i } \right\|_2^2 = \left\langle {x_1 - \sum\limits_{i = 1}^k {\alpha _{1,i} } e_i ,x_1 - \sum\limits_{i = 1}^k {\alpha _{1,i} } e_i } \right\rangle . \] Ілюстрація похибки відновлення вектору.
Щоб знайти повну похибку, нам треба знайти суму величини похибок по всім \(x_j\), тому повна похибка дорівнює \begin{equation} \label{2.1} \varepsilon \underbrace {\left( {e_1 ,...,e_k ,\alpha _{1,1} ,...,\alpha_{n,k} } \right)}_{unknowns} = \sum\limits_{j = 1}^n {\varepsilon _j } = \sum\limits_{j = 1}^n {\left\| {x_j - \sum\limits_{i = 1}^k {\alpha _{j,i} } e_i } \right\|_2^2 } . \end{equation} Щоб мінімізувати похибку, треба взяти часткові похідні і урахувати обмеження на ортогональність \(\left\{ {e_1 ,...,e_k } \right\}\).
По-перше, спростимо співвідношення (\ref{2.1}) \[ \varepsilon \left( {e_1 ,...,e_k ,\alpha _{1,1} ,...,\alpha _{n,k} } \right) = \sum\limits_{j = 1}^n {\left\| {x_j - \sum\limits_{i = 1}^k {\alpha _{j,i} } e_i } \right\|_2^2 = }\] \[= \sum\limits_{j = 1}^n {\left\| {x_j } \right\|_2^2 - 2\sum\limits_{j = 1}^n {x_j^T \sum\limits_{i = 1}^k {\alpha _{j,i} } e_i + \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^k {\alpha _{j,i}^2 } = } } } \sum\limits_{j = 1}^n {\left\| {x_j } \right\|_2^2 - 2\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^k {\alpha _{j,i} x_j^T } e_i + \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^k {\alpha _{j,i}^2 } .} } } \] Тоді \[ \frac{\partial }{\partial \alpha _{m,\ell} }\varepsilon \left( {e_1 ,...,e_k,\alpha _{1,1} ,...,\alpha _{n,k} } \right) = - 2x_m^T e_\ell + 2\alpha _{m,\ell}. \] Необхідна та достатня умова екстремуму буде мати вигляд \[ - 2x_m^T e_\ell + 2\alpha _{m,\ell} = 0 \Rightarrow \alpha _{m,\ell} = x_m^T e_\ell . \] Таким чином, похибка (\ref{2.1}) буде мати вигляд \[ \varepsilon \left( {e_1 ,...,e_k } \right) = \sum\limits_{j = 1}^n {\left\| {x_j } \right\|_2^2 - 2\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^k {\left( {x_j^T e_i } \right)x_j^T } e_i + \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^k {\left( {x_j^T e_i } \right)^2} .} } } \] Проводячи спрощення, маємо \begin{equation} \label{2.2} \varepsilon \left( {e_1 ,...,e_k } \right) = \sum\limits_{j = 1}^n {\left\| {x_j } \right\|_2^2 - \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^k {\left( {x_j^T e_i } \right)^2} .} } \end{equation} Зважаючи на те, що \(\left\langle {a,b} \right\rangle = a^Tb\) і \(\left\langle {b,a} \right\rangle = \left\langle {a,b} \right\rangle \), отримуємо \[ \left( {a^Tb} \right)^2 = \left( {a^Tb} \right)\left( {a^Tb} \right) = \left( {b^Ta} \right)\left( {a^Tb} \right) = b^T\left( {aa^T} \right)b, \] тобто, \[ \varepsilon \left( {e_1 ,...,e_k } \right) = \sum\limits_{j = 1}^n {\left\| {x_j } \right\|_2^2 - \sum\limits_{i = 1}^k {e_i^T \left( {\sum\limits_{j = 1}^n {\left( {x_j x_j^T } \right)} } \right)e_i } } = \sum\limits_{j = 1}^n {\left\| {x_j } \right\|_2^2 - \sum\limits_{i = 1}^k {e_i^T Se_i } } , \] де \(S = \sum\limits_{j = 1}^n {\left( {x_j x_j^T } \right)}\) є коваріаційною матрицею.
Наступним кроком буде мінімізація \[\varepsilon \left( {e_1 ,...,e_k } \right) = \sum\limits_{j = 1}^n {\left\| {x_j } \right\|_2^2 - \sum\limits_{i = 1}^k {e_i^T Se_i } }\] при умові \(e_i^T e_i = 1\) для всіх i. Для розв’язку цієї задачі будемо використовувати метод невизначених множників Лагранжа (Lagrange), введемо множники \(\lambda _1 ,...,\lambda _k\) і, зазначаючи, що \(\sum\limits_{j =1}^n {\left\| {x_j } \right\|_2^2 } \equiv Const\), випишемо функцію мети \[ L\left( {e_1 ,...,e_k } \right) = \sum\limits_{i = 1}^k {e_i^T Se_i } - \sum\limits_{i = 1}^k {\lambda _i \left( {e_i^T e_i - 1} \right)} . \] Зазначаючи, що \(\frac{d}{dX}\left( {X^TX} \right) = \frac{d}{dX}\left\langle {X,X} \right\rangle = 2X\) і якщо A симетрична матриця, то \(\frac{d}{dX}\left( {X^TAX} \right) = 2AX\), маємо, \[ \frac{\partial }{\partial e_m }L \left( {e_1 ,...,e_k } \right) = 2Se_m - 2\lambda _m e_m = 0, \] тобто, \(Se_m = \lambda _m e_m\). Таким чином, необхідно знайти рішення рівняння \(\left( {S - \lambda I} \right)e = 0\) (де I одинична матриця), що еквівалентно тому, що \(\lambda _m \) та \(e_m\) є власні значення і власні вектори коваріаційної матриці S.
При цьому похибка має вигляд \begin{equation}\label{2.3} \varepsilon \left( {e_1 ,...,e_k } \right) = \sum\limits_{j = 1}^n {\left\| {x_j } \right\|_2^2 - \sum\limits_{i = 1}^k {\lambda _i\left\| {e_i } \right\|_2^2 } } = \sum\limits_{j = 1}^n {\left\| {x_j } \right\|_2^2 - \sum\limits_{i = 1}^k {\lambda _i} } . \end{equation} Мінімізація (\ref{2.3}) складається у виборі базису W із k власних векторів матриці S, які відповідають k найбільшим власним значенням. Більше власне значення S дає більшу варіацію у напрямі відповідного власного вектору. Цей результат можна переформулювати наступним чином – проекція X на підпростір розміру k, яка забезпечує найбільшу варіацію. Таким чином МГК може трактуватися наступним чином - беремо ортогональний базис і обертаємо його поки на одному із напрямів не отримаємо максимальну варіацію. Фіксуємо цей напрям и обертаємо інші, поки не знайдемо другий напрям і так далі.
Нехай \(\left\{ {e_1 ,...,e_n } \right\}\) всі власні вектори матриці S , відсортовані у порядку зменшення відповідного власного значення, тоді для довільного \[ x_i = \sum\limits_{j = 1}^n {\alpha _{i,j} } e_j = \underbrace {\alpha _{i,1} e_1 + ... + \alpha _{i,k} e_k }_{approximation} + \overbrace {\alpha _{i,k + 1} e_{k + 1} + ... + \alpha _{i,n} e_n }^{error} \]
коефіцієнти \(\alpha _{m,\ell} = x_m^T e_\ell\) є координатами головних компонент, і чим більше значення k, тим кращу апроксимацію отримуємо. При цьому головні компоненти стоять у порядку значення, більш важливі мають менший номер. Приведемо алгоритмізацію МГК .
Нехай \(D = \left\{ {x_1^0 ,...,x_n^0 } \right\}\) вхідні (оригінальні) дані, кожен із цих векторів \(x_i^0\) має розмір N
  1. Знайдемо середнє \(\mu = \frac{1}{n}\sum\limits_{i = 1}^n {x_i^0 }\).
  2. Віднімемо середнє із кожного вектору \(x_i= x_i^0 - \mu\).
  3. Знайдемо коваріаційну матрицю \(S = \sum\limits_{j = 1}^n {x_jx_j^T }\).
  4. Обчислимо власні вектори \(\left\{ {e_1 ,...,e_k } \right\}\), які відповідають k найбільшим власним значенням S.
  5. Нехай \(\left\{ {e_1 ,...,e_k } \right\}\) складають матрицю \(E = \left[ {e_1...e_k } \right]\).
  6. Тоді найближче до x лежить \(z^TE+\mu\).

Ітераційний алгоритм обчислення головних компонент.

Описаний метод отримання головних компонент є достатньо ресурсоємним та нестабільним, особливо у випадку, якщо власні значення матриці близькі до нуля.
Тому більш ефективним є використання ітераційного методу знаходження головних компонент. Для цієї мати розглянемо задачу (\ref{2.1}) з іншої точки зору.
Для випадку i=1 задача (\ref{2.1}) зводиться до знаходження однієї компоненти \(e_1\), яка найкращим чином відновлює всі вхідні дані \(\left\{ {x_1,...,x_n } \right\}\). \begin{equation} \label{2.4} \varepsilon \left( {e_1 ,\alpha _{1,1} ,...,\alpha _{n,1} } \right) = \sum\limits_{j = 1}^n {\left\| {x_j - \alpha _{j,1} e_1 } \right\|_2^2 } \to \min \end{equation} по всім \(e_1 \) i \(\left\{ {\alpha _{i,1} } \right\}_{i = 1}^n \) при умові \(\sum\limits_{i = 1}^n {\alpha _{i,1}^2 = 1.} \)
Якщо \(\left\{ {\tilde{\alpha }_{i,1} } \right\}_{i = 1}^n \) i \(\tilde{e}_1\) та є розв’язок цієї задачі та \(\Delta x_j = x_j - \tilde {\alpha }_{j,1}\tilde {e}_1 \) - похибка відновлення даних однією першою головною компонентою, то розв’язуючи задачу \[ \sum\limits_{j = 1}^n {\left\| {\Delta x_j - \alpha _{j,2} e_2 } \right\|_2^2 } \to \min \] по всім \(e_2\) та \(\left\{ {\alpha _{i,2} } \right\}_{i = 1}^n \) при умові \(\sum\limits_{i = 1}^n {\alpha _{i,1}^2 = 1} \), отримуємо другу головну компоненту \(\tilde {e}_2 \) і відповідний вектор \(\left\{ {\tilde {\alpha }_{i,2} } \right\}_{i = 1}^n \) i т.д. необхідна та достатня умова екстремуму співпадають. Таким чином, рішення задачі зводиться до пошуку розв’язку рівняння \[ \frac{\partial }{\partial e_1 }\varepsilon \left( {e_1 ,\alpha _{1,1} ,...,\alpha _{n,1} } \right) = - 2\sum\limits_{j = 1}^n {\left( {x_j - \alpha _{j,1} e_1 } \right)\alpha _{j,1} } = - 2\left( {\sum\limits_{j =1}^n {x_j \alpha _{j,1} } - \sum\limits_{j = 1}^n {\alpha _{j,1}^2 e_1 } } \right). \] Звідси маємо \[ \frac{\partial }{\partial e_1 }\varepsilon \left( {e_1 ,\alpha _{1,1} ,...,\alpha _{n,1} } \right) = - 2\sum\limits_{j = 1}^n {\left( {x_j - \alpha _{j,1} e_1 } \right)\alpha _{j,1} } = - 2\left( {\sum\limits_{j =1}^n {x_j \alpha _{j,1} } - \sum\limits_{j = 1}^n {\alpha _{j,1}^2 e_1 } } \right). \] враховуючи умову нормування одиницею, тобто \(\sum\limits_{i = 1}^n {\alpha _{i,1}^2 = 1}\), маємо \[ e_1 = \sum\limits_{j = 1}^n {x_j \alpha _{j,1} } . \] Наступний крок будемо робити з умови, що в задачі (\ref{2.4}) нам відома компонента \(e_1\) і треба знайти екстремум по \(\left\{ {\alpha_{i,1} } \right\}_{i = 1}^n\) \[ \frac{\partial }{\partial \alpha _{\nu ,1} }\varepsilon \left( {e_1 ,\alpha_{1,1} ,...,\alpha _{n,1} } \right) = - 2\left( {x_\nu - \alpha _{\nu ,1} e_1 } \right)e_1 = - 2\left( {\left\langle {x_\nu ,e_1 } \right\rangle - \alpha _{\nu ,1} \left\langle {e_1 ,e_1 } \right\rangle } \right) = 0, \] тобто \[ \alpha _{\nu ,1} = \frac{\left\langle {x_\nu ,e_1 } \right\rangle }{\left\langle {e_1 ,e_1 } \right\rangle }, \] де,як звичайно, \(\left\langle {x,y} \right\rangle\)- скалярний добуток векторів x та y.
Далі, вважаючи знайдені \(\left\{ {\alpha _{i,1} } \right\}_{i = 1}^n \) вже відомими, повторюємо весь процес, доки не досягнемо стабілізації похибки.
Отримані \(e_1\) будемо вважати першою головною компонентою \(\tilde {e}_1 \). Тоді \(\Delta x_j = x_j - \tilde {\alpha }_{j,1} \tilde {e}_1\) - похибка відновлення даних однією першою головною компонентою.
Застосовуючи цей алгоритм до похибки відновлення \(\Delta x_j\), знаходимо другу головну компоненту \(e_2\) разом з коефіцієнтами \(\alpha _{j,2}\), і так інше.
Наведемо алгоритмізацію цього алгоритму.
По-перше центруємо дані, віднімаючи від вхідних даних середнє значення і в подальшому вважаємо, що дані у середньому дорівнюють нулю.
  1. Нехай номер ітерації ν=1.
  2. Вибираємо стартові значення \(\left\{ {\alpha _{i,1}^\nu } \right\}_{i = 1}^n\), наприклад, нехай всі вони між собою рівні, тобто \(\alpha _{i,1}^\nu = \frac{1}{\sqrt n },i = 1,2,...,n.\).
  3. Обчислимо \(e_1^\nu = \sum\limits_{j = 1}^n {x_j \alpha _{j,1}^\nu }\).
  4. Далі знайдемо \(\beta _i = \frac{\left\langle {x_i ,e_1^\nu } \right\rangle}{\left\langle {e_1^\nu ,e_1^\nu } \right\rangle }\) і, після нормування одиницею, маємо \[ \alpha _{i,1}^{\nu + 1} = \frac{\beta _i }{\sqrt {\sum\limits_{j = 1}^n {\beta _j^2 } } }. \]
  5. Нехай ν=ν+1.
  6. Проведемо перевірку критерію зупинки, в якості якого може бути або стабілізація коефіцієнтів \(\left\{ {\alpha _{i,1}^\nu } \right\}_{i = 1}^n\), або стабілізація головної компоненти \(e_1^\nu\), або перевірка на задане фіксоване число ітерацій. Якщо умова зупинки ітераційного процесу не виконана, то переходимо до пункту 3.

Перехід від моделі RGB до оптимальної трикомпонентної моделі.

Перейдемо до використання метода головних компонент у комп’ютерній графіці. Тут важливу роль грає конвертація зображення із простору рівноправних кольорових характеристик в простір нерівноправних (див. розділ "Світло і колір"). Довільне зображення візуалізується з використанням змішування рівноправних кольорових компонент - червоної, зеленої та синьої складових - модель RGB. В якості нерівноправних кольорових компонент, як правило, використовують, відповідно, також три компоненти – значення освітленості (люмінесцентну складову), характеристику теплих тонів и характеристику холодних тонів. Використання нерівноправних кольорових компонент використовують для стиску зображень та відео-потоків,застосовуючи до кожної із нерівноправних компонент свій метод стиску.
Можна підходити до проблеми побудови нерівноправного кольорового простору з іншої точки зору, виходячи із максимальної інформативності кожної компоненти. Застосуємо метод головних компонент для отримання нерівноправної трикомпонентної моделі оптимальної с точки зору мінімізації середньоквадратичної похибки відновлення даного зображення. Таким чином, перша із отриманих кольорових компонент буде нести найбільшу інформацію щодо зображення між всіх отриманих кольорових компонент, а друга буде мати найбільшу інформацію серед тих, що осталися.
Таким чином, в нашій термінології, задача (\ref{2.1}) буде мати вигляд \[ \left\| {R - \sum\limits_{i = 1}^3 {\alpha _{r,i} } e_i } \right\|_2^2 + \left\| {G - \sum\limits_{i = 1}^3 {\alpha _{g,i} } e_i } \right\|_2^2 + \left\| {B - \sum\limits_{i = 1}^3 {\alpha _{b,i} } e_i } \right\|_2^2 \to \min , \] де мінімум береться по всім \(\alpha _{r,i} ,\alpha _{g,i} ,\alpha _{b,i} \) i \(e_i \quad i=1,2,3.\) В якості даних розглянемо тестове зображення Lena. Застосовуючи метод головних компонент, маємо \[ \left( {{\begin{array}{*{20}c} R \hfill \\ G \hfill \\ B \hfill \\ \end{array} }} \right) = \left( {\begin{array}{l} \mbox{ 0.767785 0.45439 0.4517034} \\ \mbox{ - 0.6164395 0.716085 0.3274513} \\ \mbox{ - 0.174667 - 0.5298553 0.8299064} \\ \end{array}} \right)\left( {{\begin{array}{*{20}c} {e_1 } \hfill \\ {e_2 } \hfill \\ {e_3 } \hfill \\ \end{array} }} \right). \] Тут у першому стовбці матриці стоять коефіцієнти \(\alpha _{r,1} ,\alpha_{r,2} ,\alpha _{r,3}\), у другому - \(\alpha _{g,1} ,\alpha _{g,2} ,\alpha_{g,3}\) і у третьому - \(\alpha _{b,1} ,\alpha _{b,2} ,\alpha _{b,3}\). Тоді відновлення тестового зображення по одній компоненті можна записати у вигляді \[ R_{i,j}=\mbox{0.767785 }Y_{i,j} , \\ G_{i,j}=\mbox{ 0.45439} Y_{i,j}, \\ B_{i,j}=\mbox{0.4517034} Y_{i,j}, \] де \(Y_{i,j}\) – значення першої головної компоненти \(e_1\), які відповідають пікселю з координатами (i,j).

Зображення Lena, відновлене по одній першій головній компоненті.
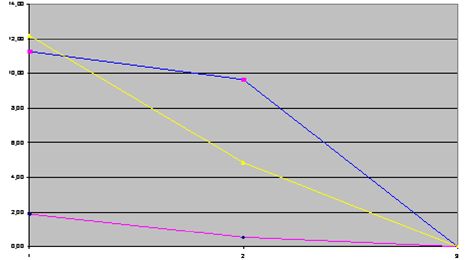
Порівняємо відновлення зображення компонентами різних просторів кольорів
Синім кольором позначена похибка відновлення зображення по одній, за двома або повна реконструкція трьома компонентами простору YUV, жовтим кольором –YСrCb, а пурпуровим – по головним компонентам.

Оптимальний метод кодування зображення.

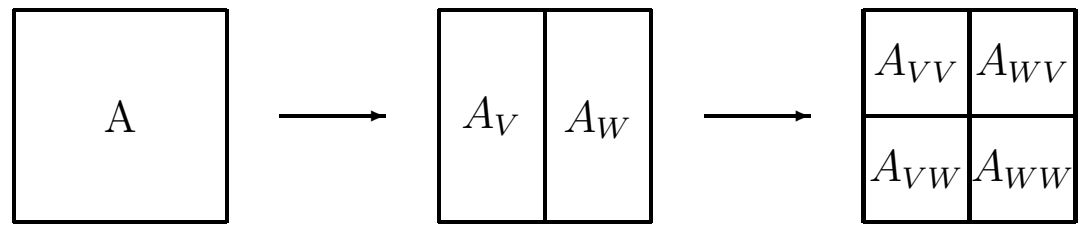
У розглянутому вище прикладі зображення було розкладене на три оптимальних (з точки зору енергії прошарків) інформаційних домени (прошарків). Узагальнимо даний підхід використовуючи для розбиття зображення на \(3\times n^2 (n\ge 1)\) інформаційних доменів з можливістю динамічного підвантаження (за аналогією з прогресивним Jpeg). Тобто, реалізувати оптимальний метод прогресивної розгортки зображення на \(3\times n^2 (n\ge 1)\) прошарків.
Суть методу складається у наступному. Розіб’ємо наше зображення розміром \(H\times W\) на квадрати \(P_{x,y}\) розміром \(n\times n (n\ge 1)\). Для простоти будемо вважати, що \(H=N\times n,W=M\times n\). Кожному пікселю \(p_{nx+i,ny+j} (i,j=0,1,...,n-1)\) даного квадрату відповідають три кольорові компоненти \(r_{nx+i,ny+j},g_{nx+i,ny+j},b_{nx+i,ny+j}\) (червона, зелена та синя складові). Тобто, загальна інформація на квадраті \(P_{x,y}\) описується даними \[ (r_{nx,ny},g_{nx,ny},b_{nx,ny}),(r_{nx+1,ny},g_{nx+1,ny},b_{nx+1,ny}),...,(r_{nx+n-1,ny+n-1},g_{nx+n-1,ny+n-1},b_{nx+n-1,ny+n-1}). \] Сформуємо домени вхідної інформації, наприклад, наступним чином \[ X_0=\{r_{0,0},r_{n,0},...,r_{nx,ny},...,r_{H-n-1,W-n-1}\}, \] \[ X_1=\{g_{0,0},g_{n,0},...,g_{nx,ny},...,g_{H-n-1,W-n-1}\}, \] \[ X_2=\{b_{0,0},b_{n,0},...,b_{nx,ny},...,b_{H-n-1,W-n-1}\}, \] \[ X_3=\{r_{1,0},r_{n+1,0},...,r_{nx+1,ny},...,r_{H-n,W-n-1}\}, \] \[ X_4=\{g_{1,0},g_{n+1,0},...,g_{nx+1,ny},...,g_{H-n,W-n-1}\}, \] \[ X_5=\{b_{1,0},b_{n+1,0},...,b_{nx+1,ny},...,b_{H-n,W-n-1}\}, \] \[\ldots\] \[ X_{3\times n^2-2}=\{r_{n-1,n-1},r_{2n-1,2n-1},...,r_{(n+1)x-1,(n+1)y-1},...,r_{H,W}\}, \] \[ X_{3\times n^2-1}=\{g_{n-1,n-1},g_{2n-1,2n-1},...,g_{(n+1)x-1,(n+1)y-1},...,g_{H,W}\}, \] \[ X_{3\times n^2}=\{b_{n-1,n-1},b_{2n-1,2n-1},...,b_{(n+1)x-1,(n+1)y-1},...,b_{H,W}\}. \] Розглянемо задачу \[ \sum_{j=0}^{3\times n^2}\left\|X_j-\sum_{i=0}^k\alpha_{j,i}Y_i\right\|^2_2\to\min, \] де мінімум береться по всім \(\left\{Y_i\right\}_{i=0}^k, \alpha_{j,i}(i=0,1,\ldots,k,j=0,1,...,3\times n^2).\)
Як видно, для розв’язку цієї задачі можна використати ітераційний метод головних компонент, алгоритм якого наведено вище.
Таким чином, нехай ми отримали всі \(\left\{Y_i\right\}_{i=0}^k, \alpha_{j,i}(i=0,1,\ldots,k,j=0,1,...,3\times n^2).\) Опишемо алгоритм прогресивного відновлення зображення.
Ясна річ, що множина \(\left\{X_j\right\}_{j=0}^{3\times n^2}\) описує всі пікселі зображення, тобто, якщо \[X^0_j=\alpha_{j,0}Y_0,\] то \(\left\{X_j^0\right\}_{j=0}^{3\times n^2}\) є першою ітерацією відновлення нашого зображення.

Зображення Lena, відновлене за одною ітерацією.
На другому кроці \( X^1_j=\alpha_{j,0}Y_0+\alpha_{j,1}Y_1 \), тобто \(X^1_j=X^0_j+\alpha_{j,1}Y_1\) і \(\left\{X_j^1\right\}_{j=0}^{3\times n^2}\) буде другою ітерацією.

Зображення Lena, відновлене за другою ітерацією.
Таким чином маємо \(X^k_j=\sum_{i=0}^k\alpha_{j,i}Y_i=X^{k-1}_j+\alpha_{j,k}Y_k\), а \(\left\{X_j^k\right\}_{j=0}^{3\times n^2}\) буде k-ю ітерацією відновлення нашого зображення.

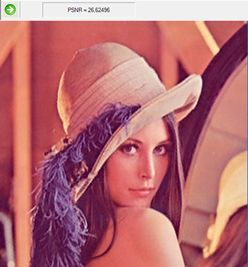Зображення Lena на десятій ітерації.
Таким чином маємо \(X^k_j=\sum_{i=0}^k\alpha_{j,i}Y_i=X^{k-1}_j+\alpha_{j,k}Y_k\), а \(\left\{X_j^k\right\}_{j=0}^{3\times n^2}\) буде k-ю ітерацією відновлення нашого зображення.

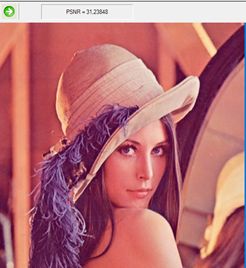Зображення Lena на 21 із 192 ітерацій.
Зазначимо, що на відміну від фільтрації на основі перетворення Фур’є, форма примітиву, по якому робиться розклад методом головних компонент, може бути будь якої форми за умовою щільної упаковки площини, очевидно, що це може бути прямокутник, шестикутник, який найбільш щільно запаковує площину, або, навіть, по така екзотична фігура, як фрактал-дракон.

Наведемо деякі приклади.

Нехай заданий будь який двовимірний паркет, що покриває всю площину. Кожен елемент паркету складається з n пікселів. Перенумеруємо всі пікселі елемента паркету довільним, але фіксованим способом. Вибираючи з кожного елемента паркету піксель з одним і тим же номером, отримаємо n компонент. Зауважимо, що результат оптимальної фільтрації не залежить від способу нумерації пікселів на елементі паркету.
Для найпростішого випадку – квадратного паркету
маємо

Зображення Lena, зібране з одного квадратного домену.

Зображення Lena, зібране із сьомих квадратних доменів.
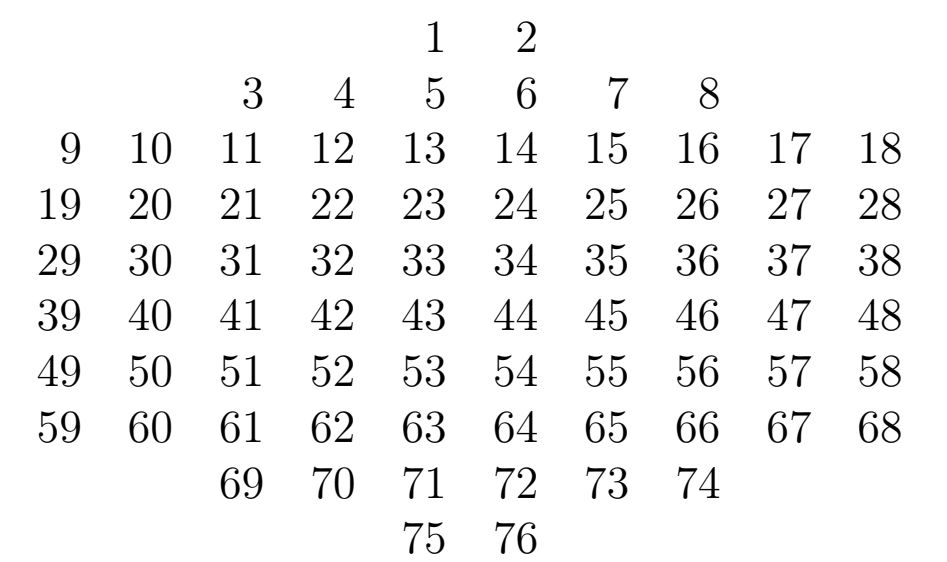
Наприклад, для паркету з елементами у вигляді шестикутних сотів з 76 пікселів можна використовувати наступну нумерацію
Застосуємо МГК до зображення Lena у градаціях сірого

Зображення Lena, зібране з одного домену з шестикутним паркетом.

Зображення Lena, зібране із сьомих доменів з шестикутним паркетом.
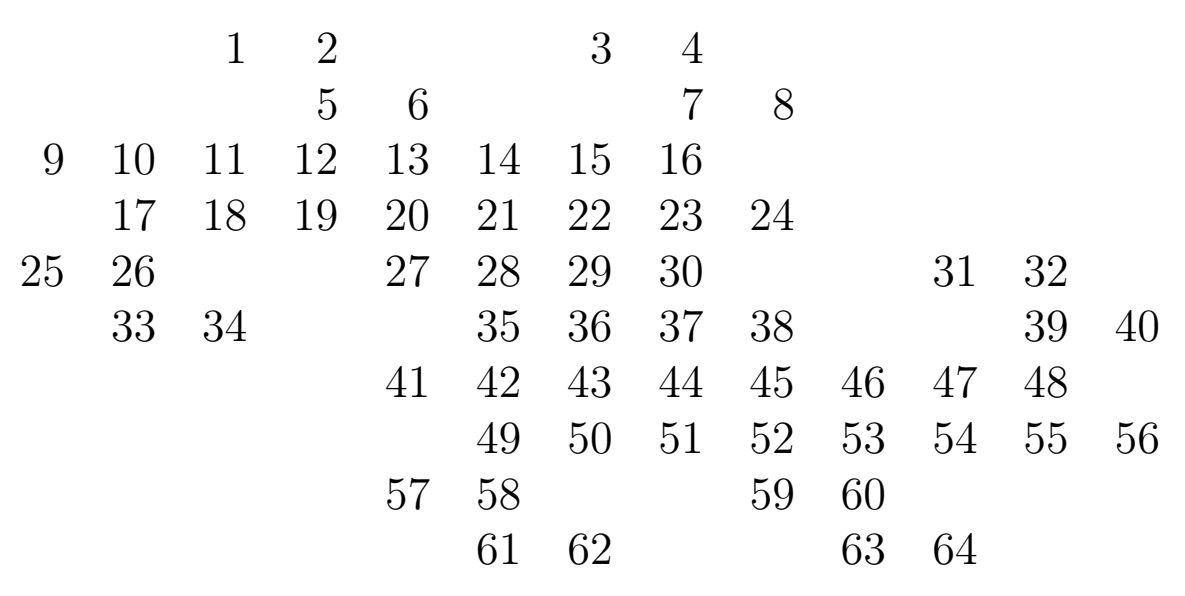
Випишемо нумерацію для паркету «Дракон» з 64 пікселів

Зображення Lena, зібране з одного домену з паркетом «Дракон».

Зображення Lena, зібране з чотирьох доменів з паркетом «Дракон».

Зображення Lena, зібране із сьоми доменів з паркетом «Дракон».
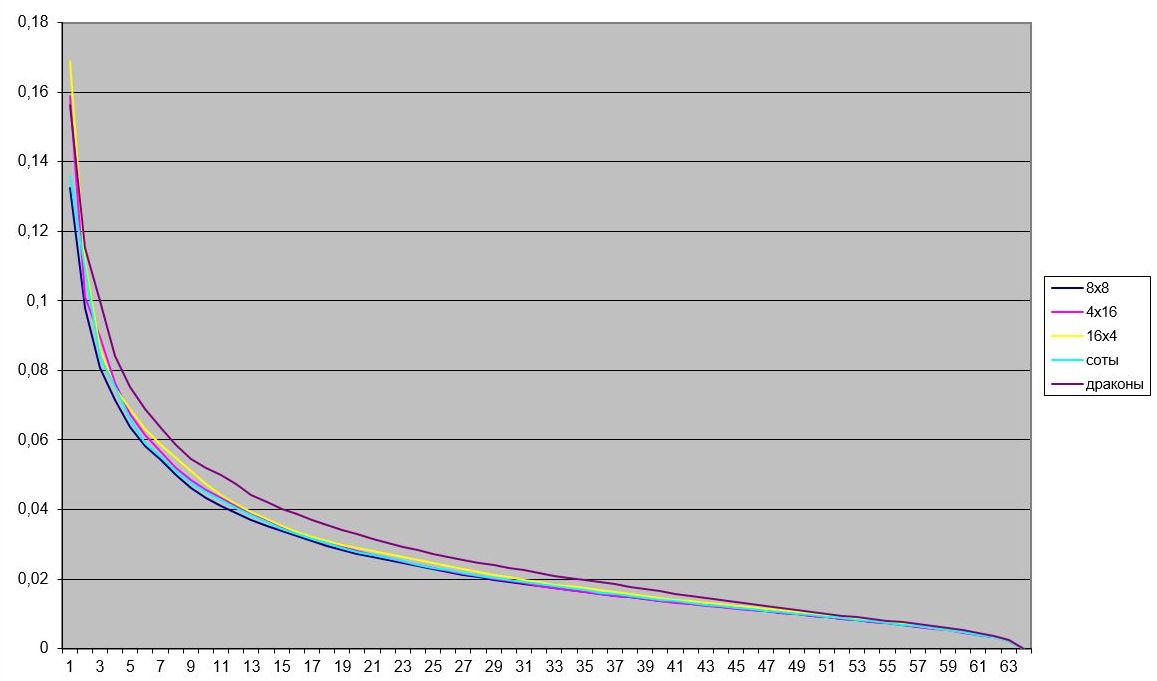
Зробимо порівняння якості фільтрації по різному паркету розміром 64 пікселя.
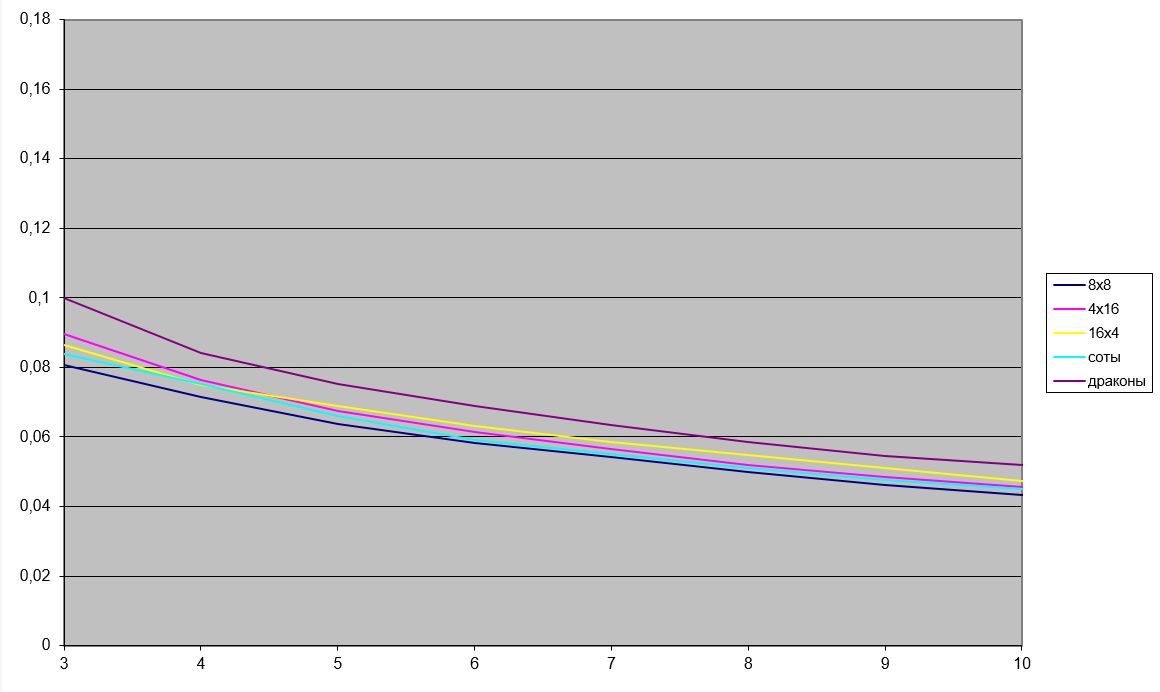
Фіолетовим кольором позначена похибка відновлення з використанням фільтрації по паркету «дракон», кольором «морської хвилі» - по шестикутним сотам, темно-синім – по квадратам 8×8, жовтим – по прямокутній решітці 16×4 и червоним – по решітці 4×16. Наведемо фрагмент цих графіків у іншому масштабі.

Вейвлети у комп’ютерній графіці

Сплески (wavelets) з'явилися на початку 1980-х років на стику теорії функцій, функціонального аналізу, обробки сигналів і зображень, квантової теорії поля. Розвиток теорії сплесків пов'язаний з іменами А. Гросмана, Ж. Морлета, Ж. Стремберга, Я. Мейєра, С. Малла, І. Добеші і багатьох ін. (Більш детально з вейвлетами можна ознайомитися, якщо перейти за посиланням http://pzs.dstu.dp.ua/DataMining/wave/index.html.)
Подібно аналізу Фур'є теорія сплесків знаходить застосування в дослідженні частотних характеристик функції f за допомогою сплеск-перетворення. При описі функцій зі скінченним носієм, сигналів, зі змінними у часі частотами за допомогою аналізу Фур'є виникають труднощі, які пояснюються властивостями тригонометричних функцій на осі \(\mathbb{R}\). Наприклад, перетворення Фур'є функції f у разі δ-функції Дірака, що має в якості носія єдину точку, вироджується в функцію \(\hat{\delta}(\omega)=1\), поширену на всю числову вісь. При обробці сигналів зі змінними частотами традиційний аналіз Фур'є не дозволяє виділити частоти, що становлять сигнал в околі довільного моменту часу. Апарат сплесків дозволяє автоматично здійснювати локалізацію як за часом, так і в частотній області.
Наведемо один алгоритм фільтрації векторного поля, тобто набору векторів однакової розмірності.
Ці результати є основоположними для всіх алгоритмів, пов'язаних з оптимальною фільтрацією фільтрами, подібними фільтрам Хаара і Уолша-Адамара однієї та багатьох змінних.
У чисельному і функціональному аналізі дискретні вейвлет-перетворення (ДВП) відносяться до вейвлет-перетворень, в яких вейвлети представлені дискретними сигналами (вибірками).
Вперше ДВП було придумано угорським математиком Альфредом Хааром. Для вхідного сигналу, представленого масивом 2n чисел, вейвлет-перетворення Хаара просто групує елементи по 2 і утворює від них суми і різниці. Угруповання сум проводиться рекурсивно для наступного рівня розкладу. У підсумку виходить 2n-1 різниця і одна загальна сума.
Це просте ДВП ілюструє загальні корисні властивості вейвлетів. По-перше, перетворення можна виконати за \(n \log_2n\) операцій. По-друге, воно не тільки розкладає сигнал на деяку подобу частотних смуг (шляхом аналізу його в різних масштабах), але і представляє тимчасову область, тобто моменти виникнення тих чи інших частот в сигналі.
Наведемо визначення і позначення, необхідні нам надалі.
Множину векторів \(X^k=\left\{x_i^k\right\}(k = 0, .., n-1, i = 0,1, .., N-1)\) однакової розмірності N будемо називати компонентами векторного поля або просто компонентами. Під фільтром \(H^\nu=\{h_i^\nu \} (\nu = 0, .., n-1)\) будемо розуміти вектор з n координатами.
Систему векторів \(H^\nu (\nu = 0, .., n-1)\) будемо називати ортонормованою, якщо \[ H^\nu\bot H^\mu \Leftrightarrow \left\lt H^\nu,H^\mu \right\gt=0 \hbox{ i } \left\lt H^\nu,H^\nu \right\gt=1. \] Тут <a, b> традиційний скалярний добуток векторів a і b.
Під фільтрацією компонентів \(X^k (k = 0, .., n-1)\) системою фільтрів \(H^k (k = 0, .., n-1)\) будемо розуміти обчислення множини (частотного домену) за правилом \begin{equation}\label{w:1} Y^\nu=\sum_{k=0}^{n-1}h_\nu^k X^k. \end{equation} У координатної формі це співвідношення буде мати вигляд \[ y_i^\nu=\sum_{k=0}^{n-1}h_\nu^k x_i^k. \] Величину \begin{equation}\label{w:2} X_m^\nu=\sum_{k=0}^{m-1}h_\nu^k Y^k \end{equation} будемо називати відновленням компоненти \(X^\nu\) по m частотним доменам. Якщо m = n, то отримуємо відновлення компоненти по повному набору частотних доменів.
Перше співвідношення називається декомпозицією, а останнє - реконструкцією даних.
У разі, якщо для даного масиву \(F = \{f_i\}\) і для n = 4 компоненти визначені правилом \[ X^0=\{x_i^0 \}=\{f_{4i} \},X^1=\{x_i^1 \}=\{f_{4i+1} \},\\ X^2=\{x_i^2 \}=\{f_{4i+2} \},X^3=\{x_i^3\}=\{f_{4i+3} \}, \] для фільтрів Уолша-Адамара \[ H^0=0.5 \{1,1,1,1\},H^1=0.5 \{1,1,-1,-1\},\\ H^2=0.5\{1,-1,1,-1\},H^3=0.5\{1,-1,-1,1\} \] процедура декомпозиції (\ref{w:1}) буде мати вигляд \[ y_i^0=0.5 (f_{4i}+f_{4i+1}+f_{4i+2}+f_{4i+3} ),\\ y_i^1=0.5(f_{4i}+f_{4i+1}-f_{4i+2}-f_{4i+3} ),\\ y_i^2=0.5 (f_{4i}-f_{4i+1}+f_{4i+2}-f_{4i+3} ),\\ y_i^3=0.5 (f_{4i}-f_{4i+1}-f_{4i+2}+f_{4i+3} ), \] а формули реконструкції (\ref{w:2}), наприклад, для m = 2 \[ f_{4i}=0.5 (y_i^0+y_i^1 ),\\ f_{4i+1}=0.5 (y_i^0+y_i^1 ),\\ f_{4i+2}= 0.5 (y_i^0-y_i^1 ),\\ f_{4i+3}=0.5(y_i^0-y_i^1 ). \] Повна реконструкція (тобто m = n) визначається співвідношеннями \[ f_{4i}=\frac{1}{2} (y_i^0+y_i^1+y_i^2+y_i^3 ),\\ f_{4i+1}=\frac{1}{2}(y_i^0+y_i^1-y_i^2-y_i^3 ),\\ f_{4i+2}=\frac{1}{2}(y_i^0-y_i^1+y_i^2-y_i^3 ),\\ f_{4i+3}=\frac{1}{2}(y_i^0-y_i^1-y_i^2+y_i^3 ). \] Таким чином, завдання використання непересічних фільтрів розбивається на дві. Перша з яких – зведення сигналу (в загальному випадку багатокомпонентного і багаторозмірного) до системи компонент однакової розмірності. Зокрема, для фільтрації зображень це 3-компонентний двовимірний сигнал, для відео - трикомпонентний тривимірний і так інше. Друге завдання полягає в отриманні системи найкращих (в тому чи іншому сенсі) фільтрів для n компонент.
Фундаментальним поняттям теорії вейвлет є поняття кратномасштабного аналізу (КМА).
Кратномасштабний аналіз в \(L^2 (\mathbb{R}^n )\) – це послідовність замкнутих підпросторів \[ \ldots \subset V^{-1}\subset V^0 \subset V^1 \subset \] для яких виконуються умови
  1. \(\overline{\bigcup_{j\in Z}V^j}=L^2 (\mathbb{R}^n );\)
  2. \(\bigcap_{j\in Z}V^j=\{0\};\)
  3. \(f\in V^j \Leftrightarrow f\left(2^{-j\circ}\right)\in V^0;\)
  4. Знайдеться така функція \(\varphi\in V^0\) (масштабуюча функція), що множина її зрушень φ(x-n) створює ортонормований базис простору \(V^0\).
Дана послідовність просторів гарантує, що для довільної інтегрованої функції f і наперед заданого числа \(\varepsilon\gt 0\) існує простір \(V^k\) і елемент \(f_k\in V^k\), що \(\|f-f_k\|\lt\varepsilon\). Зазначимо, що у евклідовому просторі найкращим наближенням функції є ортогональна проекція функції на цей простір, тому у якості \(f_k\) будемо брати ортогональну проекцію f на цей простір.
Окрім того, з властивостей КМА витікає, що для будь якого \(j\in Z\) множина функцій \(\varphi^j_k(x)=2^{j/2}\varphi(2^jx-k)\) \(k=0,\pm 1, \ldots\) створюють ортонормований базис. Множник \(2^{j/2}\) є результатом того, що заміна x на 2x зменшує норму у \(2^{1/2}\) раз.
Так як \(V^0\subset V^1\), то функція φ є лінійною комбінацією функцій \(\{\varphi^1_n\}\). Таким чином, знайдеться множина коефіцієнтів \(\{h_n \}\) така, що \begin{equation}\label{w.1} \varphi(x)=\sqrt{2}\sum_{n\in Z}h_n\varphi(2x-n), \end{equation} З рівняння Парсеваля маємо \(\sum_nh^2_n=1.\)
Функція φ(x) має назву масштабуючої (скелінг) функції, а функція \begin{equation}\label{w.2} \psi(x)=\sqrt{2}\sum_{n\in Z}(-1)^{1-n}h_{1-n}\varphi(2x-n), \end{equation} називається вейвлетом або сплеском.
Зважаючи, що \(V^{-1} \subset V^0\), можна записати \(V^{-1} \oplus W^{-1}=V^0.\) В якості сплеска, який визначає базиси зрушення у просторах \(W^j\) возьмемо функцію ψ і покладемо \[ \psi_n^j (x)=2^{j/2} \psi (2^j x-n). \] В такому разі \[ \sum_{n\in Z}c_n^{-1}\varphi_n^{-1}(x)+ \sum_{n\in Z}d_n^{-1}\psi_n^{-1}(x)= \sum_{n\in Z}c_n^{0}\varphi_n^{0}(x). \] Звідси, застосовуючи операцію скалярного добутку, отримуємо \[ c^{-1}_k=\sum_{n\in Z}c_n^0\left<\varphi^0_n(x),\varphi^{-1}_k(x)\right>= \sum_{n\in Z}c_n^0\left<\varphi^0_n(x), \sum_{m\in Z}h_{m-2k}\varphi^{-1}_m(x)\right>= \sum_{n\in Z}c_n^0{h_{n-2k}}. \] і \[ d^{-1}_k= \sum_{n\in Z}c_n^0{g_{n-2k}}. \] де \(g_n=(-1)^{1-n} h_{1-n}\).
Ясно, що в загальному випадку \(V^j \oplus W^j=V^{j+1}\) та \[\sum_{n\in Z}c_n^{j}\varphi_n^{j}(x)+ \sum_{n\in Z}d_n^{j}\psi_n^{j}(x)= \sum_{n\in Z}c_n^{j+1}\varphi_n^{j+1}(x)\] і загальні формули декомпозиції \[ c^{j}_k= \sum_{n\in Z}c_n^{j+1}{h_{n-2k}}, \] і \[ d^{j}_k= \sum_{n\in Z}c_n^{j+1}{g_{n-2k}}. \] Узагальнюючи вище сказане, маємо розклад \(V^0\) в ортогональну суму \[ V^0=W^{-1}\oplus W^{-2}\oplus \ldots W^{-k}\oplus V^{-k} \] і формула реконструкції на кожному кроці буде мати вигляд \[ c^{j+1}_k= \sum_{n\in Z}c_n^{j}h_{k-2n}+\sum_{n\in Z}d_n^{j}g_{k-2n}.\] Наведений алгоритм називається каскадним.

Ортогональні вейвлети.

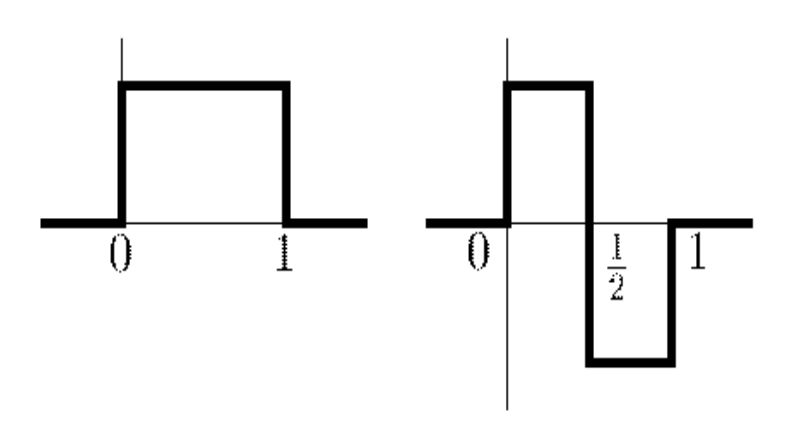
Нехай \(\varphi\) є ортогональною функцією на решітці з кроком 2, тобто \[ \left<\varphi,\varphi(\cdot-2k)\right>=\delta_{0,k} \] Або, що теж саме, \[ \sum_ih_ih_{i-2k}=\delta_{0,k}.\] Відомий факт, що якщо ортогональна функція має компактний носій, то цей носій парний. Для найпростішого випадку він дорівнює двом \[ h_0=\frac{1}{\sqrt{2}},h_1=\frac{1}{\sqrt{2}}. \] Відповідна базова функція називається функцією Хаара
Знайдемо тензорний добуток різних варіантів цих функцій \(\varphi(x)\varphi(y),\varphi(x)\psi(y),\psi(x)\varphi(y)\) та \(\psi(x)\psi(y)\), в результаті отримаємо четвірку фільтрів (фільтрів Хаара) \[ H^{++}=\frac{1}{2}\left( \begin{array}{cc} 1 & 1\\ 1 & 1 \\ \end{array} \right), H^{\pm}=\frac{1}{2}\left( \begin{array}{rr} 1 & 1\\ -1 & -1 \\ \end{array} \right), H^{+-}=\frac{1}{2}\left( \begin{array}{cc} 1 & -1\\ 1 & -1 \\ \end{array} \right), H^{--}=\frac{1}{2}\left( \begin{array}{rr} 1 & -1\\ -1 & 1 \\ \end{array} \right). \] Результатом фільтрації четвірки пікселів \(\left\{p_{n,m} \right\}_{n=2i,m=2j}^{2i+1,2j+1}\) буде \[ c_{i,j}^{++}=\frac{1}{2} (p_{2i,2j}+p_{2i+1,2j}+p_{2i,2j+1}+p_{i+1,2j+1} ),\\ c_{i,j}^{\pm}=\frac{1}{2} (p_{2i,2j}+p_{2i+1,2j}-p_{2i,2j+1}-p_{i+1,2j+1} ),\\ c_{i,j}^{+-}=\frac{1}{2} (p_{2i,2j}-p_{2i+1,2j}+p_{2i,2j+1}-p_{i+1,2j+1} ),\\ c_{i,j}^{--}=\frac{1}{2} (p_{2i,2j}-p_{2i+1,2j}-p_{2i,2j+1}+p_{i+1,2j+1} ). \] Отримані множини називаються частотними доменами, \(C^{++}=\left\{c_{i,j}^{++} \right\}\) - низько-частотний домен, \(C^{\pm}=\left\{c_{i,j}^{\pm} \right\}\) та \(C^{+-}=\left\{c_{i,j}^{+-} \right\}\) середньо-частотні домени та \(C^{--}=\left\{c_{i,j}^{--} \right\}\)–високо-частотний домен.
З них найбільш інформативним є низько-частотний домен, а найменш – високо-частотний.
Застосуємо дане перетворення (проведення декомпозиції) до тестового зображення Lena і упорядкуємо наступним чином \[ \left[ \begin{array}{ll} C^{++} & C^{+-}\\ C^{\pm} & C^{--} \\ \end{array} \right]. \] Після нормалізації результат фільтрації буде виглядати наступним чином
Зважаючи на той факт, що фільтри Хаара створюють повну систему, можна виписати реконструкцію даних \[ p_{2i,2j}=\frac{1}{2}(c_{i,j}^{++}+c_{i,j}^\pm+c_{i,j}^{+ -}+c_{i,j}^{--}),\\ p_{2i,2j+1}=\frac{1}{2}(c_{i,j}^{++}-c_{i,j}^\pm+c_{i,j}^{+ -}-c_{i,j}^{--}),\\ p_{2i+1,2j}=\frac{1}{2}(c_{i,j}^{++}+c_{i,j}^\pm-c_{i,j}^{+ -}-c_{i,j}^{--}),\\ p_{2i+1,2j+1}=\frac{1}{2}(c_{i,j}^{++}-c_{i,j}^\pm-c_{i,j}^{+ -}+c_{i,j}^{--}). \] Послідовне застосування декомпозиції до низько-частотного домену називається каскадною схемою
А застосування декомпозиції до усієї множини доменів – схемою повного пакету
Наприклад, схему повного пакету для двох кроків можна проілюструвати наступним чином
Для трьох кроків
Якість фільтрації зображення відзначається, поперед всього, тим, наскільки більш інформативний низько-частотний домен, порівнюючи його з середньо та високо-частотними доменами.
Серед усіх ортогональних вейвлетів базис Хаара має найгірші показники.
Можна порівняти розклад константи методом ДКП (дискретне косинус-перетворення) та за Хааром
Для отримання вейвлетів більш складної конструкції умови ортогональності не досить. Інгрід Добеші запропонувала додати умови дорівнювання нулю моментів до відповідного порядку \[ \int x^k\psi(x)=0, k=0,1,\ldots,n-1. \] Що еквівалентно умові \[ \sum_i i^k(-1)^{i}h_{i}=0, k=0,1,\ldots,n-1. \] У разі, коли довжина носія дорівнює 4, умови ортогональності будуть мати вигляд \[ \begin{array}{l} h_0^2+h_1^2+h_2^2+h_3^2=1, \\ h_0h_2+h_1h_3=0. \end{array} \] Додаємо дві умови дорівнювання моментів нулю \[ \begin{array}{l} h_0-h_1+h_2-h_3=0, \\ -h_1+2h_2-3h_3=0. \end{array} \] Розв’язуючи отриману систему рівнянь, отримаємо коефіцієнти ортогонального фільтру Добеші порядку 4: \[ h_0=\frac{1+\sqrt{3}}{4\sqrt{2}}, h_1=\frac{3+\sqrt{3}}{4\sqrt{2}}, h_2=\frac{3-\sqrt{3}}{4\sqrt{2}}, h_3=\frac{1-\sqrt{3}}{4\sqrt{2}}.\] У матричному вигляді процес декомпозиції можна записати так \[ \left[ \begin{array}{c} c^{-1}_{0}\\c^{-1}_{1}\\c^{-1}_{2}\\c^{-1}_{3}\\ d^{-1}_{0}\\d^{-1}_{1}\\d^{-1}_{2}\\d^{-1}_{3} \end{array} \right] = \left[ \begin{array}{cccccccc} h_0&h_1&h_2&h_3\\ &&h_0&h_1&h_2&h_3\\ &&&&h_0&h_1&h_2&h_3\\ h_2&h_3&&&&&h_0&h_1\\ h_3&-h_2&h_1&-h_0\\ &&h_3&-h_2&h_1&-h_0\\ &&&&h_3&-h_2&h_1&-h_0\\ h_1&-h_0&&&&&h_3&-h_2 \end{array} \right] \left[ \begin{array}{c} c^{0}_{0}\\c^{0}_{1}\\c^{0}_{2}\\c^{0}_{3}\\ c^{0}_{4}\\c^{0}_{5}\\c^{0}_{6}\\c^{0}_{7} \end{array} \right].\] А реконструкція буде виглядати наступним чином \[ \left[ \begin{array}{c} c^{0}_{0}\\c^{0}_{1}\\c^{0}_{2}\\c^{0}_{3}\\ c^{0}_{4}\\c^{0}_{5}\\c^{0}_{6}\\c^{0}_{7} \end{array} \right] = \left[ \begin{array}{cccccccc} h_0&&&h_2&h_3&&&h_1\\ h_1&&&h_3&-h_2&&&-h_0\\ h_2&h_0&&&h_1&h_3&&\\ h_3&h_1&&&-h_0&-h_2&&\\ &h_2&h_0&&&h_1&h_3&\\ &h_3&h_1&&&-h_0&-h_2&\\ &&h_2&h_0&&&h_1&h_3\\ &&h_3&h_1&&&-h_0&-h_2 \end{array} \right] \left[ \begin{array}{c} c^{-1}_{0}\\c^{-1}_{1}\\c^{-1}_{2}\\c^{-1}_{3}\\ d^{-1}_{0}\\d^{-1}_{1}\\d^{-1}_{2}\\d^{-1}_{3} \end{array} \right] .\] Для n=6 відповідний фільтр має вигляд \[ h_0=\frac{1}{16\sqrt{2}}\left(1+\sqrt{10}+\sqrt{5+2\sqrt{10}}\right), \] \[ h_1=\frac{1}{16\sqrt{2}}\left(5+\sqrt{10}+3\sqrt{5+2\sqrt{10}}\right), \] \[ h_2=\frac{1}{16\sqrt{2}}\left(10-2\sqrt{10}+2\sqrt{5+2\sqrt{10}}\right), \] \[ h_3=\frac{1}{16\sqrt{2}}\left(10-2\sqrt{10}-\sqrt{5+2\sqrt{10}}\right), \] \[ h_4=\frac{1}{16\sqrt{2}}\left(5+\sqrt{10}-3\sqrt{5+2\sqrt{10}}\right), \] \[ h_5=\frac{1}{16\sqrt{2}}\left(1+\sqrt{10}-\sqrt{5+2\sqrt{10}}\right), \] Використання вейвлет Добеші до фільтрації зображення зводиться до послідовного застосування фільтрів спочатку до кожного рядка зображення, тим самим проводячі розподіл на низько та високочастотний домени, а потім до кожного отриманого домену вже по стовбцям. Така послідовність обробки називається схемою Малла (Mallat).
Ортогональні фільтри Добеші порядку 4 використовуються у методі стиску DJVU.
Але найрозповсюдженими вейвлет фільтрами є біортогональні, які використовуються у широкому спектрі разних задач, так чи інакше пов’язаних з частотним аналізом сигналів, що стосуються нашої теми, то треба зазначити, що метод JPEG2000 заснований на біортогональних вейвлетах.
Біортогональне перетворення є зворотним, але не обов’язково ортогональним, що дає можливість отримати додаткові переваги, як то, зробити вейвлет-фільтри симетричними, на відміну від ортогональних, які зробити симетричними неможливо.
Пара масштабуючих функцій \[ \varphi^{(0)}(x)=\sqrt{2}\sum_{n\in Z}h^{(0)}_n\varphi^{(0)}(2x-n), \] \[ \varphi^{(1)}(x)=\sqrt{2}\sum_{n\in Z}h^{(1)}_n\varphi^{(1)}(2x-n), \] разом з відповідною парою вейвлетів \[ \psi^{(0)}(x)=\sqrt{2}\sum_{n\in Z}g^{(0)}_n\varphi^{(0)}(2x-n), \] \[ \psi^{(1)}(x)=\sqrt{2}\sum_{n\in Z}g^{(1)}_n\varphi^{(1)}(2x-n), \] де \(g_n^{(m)}=(-1)^{1-n} h_{1-n}^{(m)},m=0,1,\) називаються біортогональними, якщо \[ \left\lt \varphi^{(m)}\varphi^{(m)}(\circ -2k)\right\gt=\delta_{0,k},(m,n=0,1;n\ne m;k=0,\pm 1,…), \] тоді має місце реконструкція сигналу \[ c^{j+1}_k=\sum_{n\in Z}c^j_nh^{(1)}_{k-2n}+\sum_{n\in Z}d^j_ng^{(0)}_{k-2n} \] де формули декомпозиції такі \[ c^j_k=\sum_{n\in Z}c^{j+1}_nh^{(0)}_{k-2n}, d^j_k=\sum_{n\in Z}c^{j+1}_ng^{(1)}_{k-2n}. \] Як у ортогональному випадку простішими є фільтри Хаара, так у біортогональному, найпростіший варіант дають фільтри 1-3, які мають наступний вигляд \[ h_0^{(0)}=1, h_0^{(1)}=1, h_{\pm 1}^{(1)}=\frac{1}{2}. \] У такому разі декомпозиція сигналу виглядає наступним чином \[ с_k^j=с_{2k}^{j+1}, d_k^j=-\frac{1}{2}c_{2k}^{j+1}+с_{2k+1}^{j+1}-\frac{1}{2} с_{2k+2}^{j+1}, \] а реконструкція \[ с_{2k}^{j+1}=с_k^j, с_{2k+1}^{j+1}=d_k^j+\frac{1}{2} с_k^j+\frac{1}{2} с_{k+1}^j. \] Наведемо розрахунок класичної біортогональної пари 3-5 Коена-Добеші- Фово.
Нехай n=1 і поставимо умову точності на константі, тоді \[ h_0^{(0)}=\frac{1}{\sqrt{2}}, h_{\pm 1}^{(0)}=\frac{1}{2\sqrt{2}}, \] а для n=2 \[ h_0^{(1)}+2h_{\pm 2}^{(1)}=\frac{1}{\sqrt{2}}, h_{\pm 1}^{(1)}=\frac{1}{2\sqrt{2}}, \] і умова біортогональності має вигляд \[ \frac{1}{8}+\frac{\sqrt{2}}{2}h^{(1)}_{\pm 2}=0, \frac{3}{4}-\sqrt{2}h^{(1)}_{\pm 2}=1. \] Звідси зразу отримуємо біортогональну пару \[ h_0^{(0)}=\frac{\sqrt{2}}{2}, h^{(0)}_{\pm 1}=\frac{\sqrt{2}}{4},\\ h_0^{(1)}=\frac{3\sqrt{2}}{4}, h^{(1)}_{\pm 1}=\frac{\sqrt{2}}{4}, h^{(1)}_{\pm 2}=-\frac{\sqrt{2}}{8}. \]

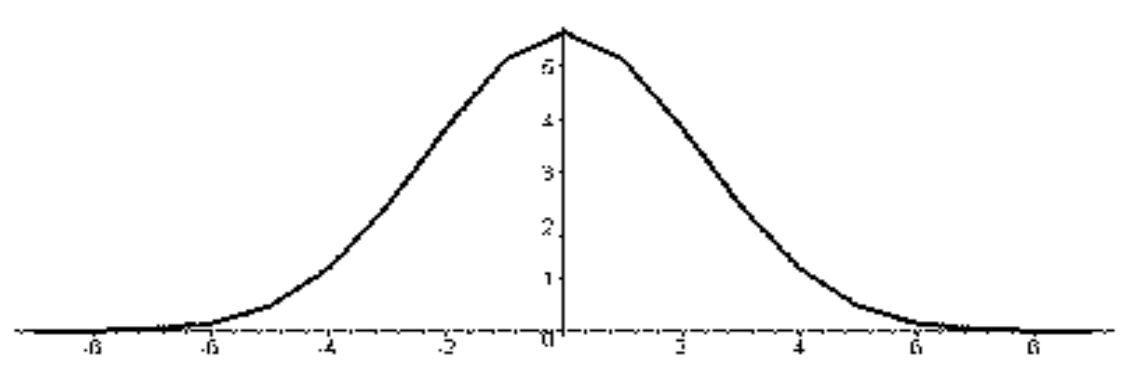
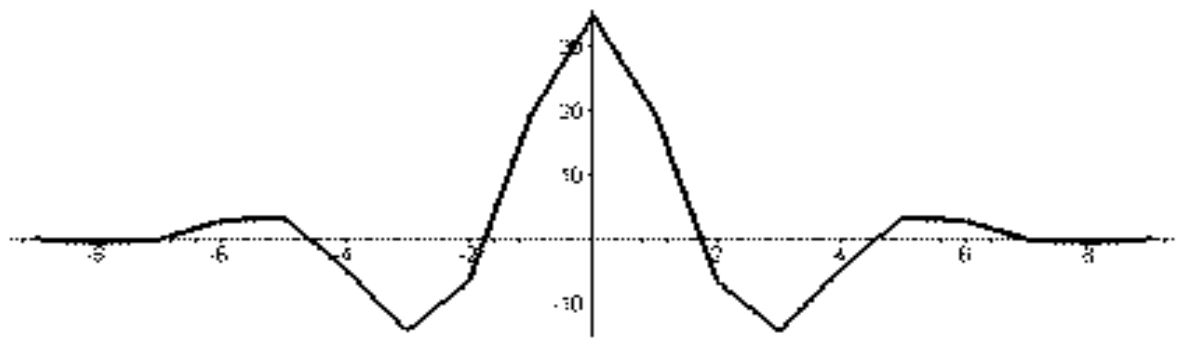Базисні функції біортогональної пари 3-5.

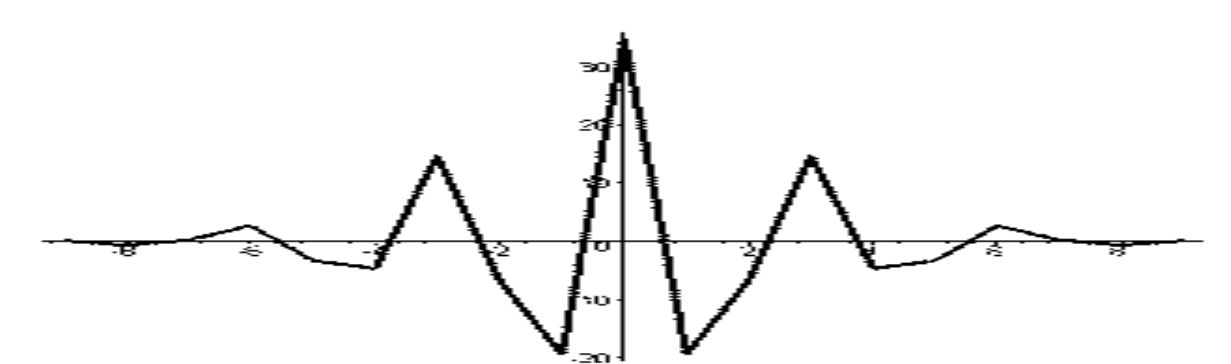
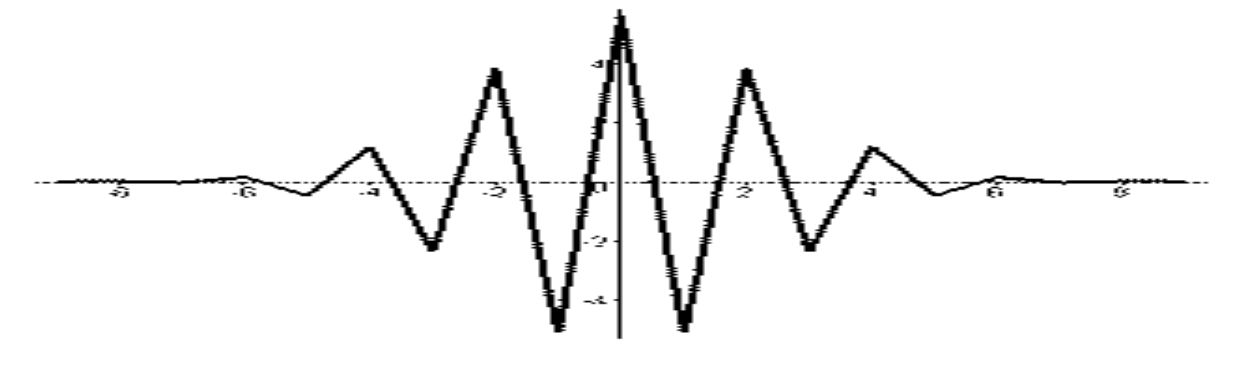Вейвлет- функції біортогональної пари 3-5.
Прямий ход вейвлет-перетворення масиву \(F=\{f_i\}\) у точці \(2i\) виглядає наступним чином \[ \hat{f}_{2i}=\frac{\sqrt{2}}{4}(f_{2i-1}+2f_{2i}+f_{2i+1}),\\ \hat{f}_{2i+1}=-\frac{\sqrt{2}}{8}(f_{2i-1}+2f_{2i}-6f_{2i+1}+2f_{2i+2}+f_{2i+3}), \] а зворотний \[ f_{2i+1}=\frac{\sqrt{2}}{4}(\hat{f}_{2i}+2\hat{f}_{2i+1}+\hat{f}_{2i+2}),\\ f_{2i}=-\frac{\sqrt{2}}{8}(\hat{f}_{2i-2}+2\hat{f}_{2i-1}-6\hat{f}_{2i}+2\hat{f}_{2i+1}+\hat{f}_{2i+2}). \] Наведемо найпопулярніші біортогональні фільтри 5-7 \[ h_0^{(0)}=\frac{3\sqrt{2}}{2}, h^{(0)}_{\pm 1}=\frac{\sqrt{2}}{4},h^{(0)}_{\pm 2}=-\frac{\sqrt{2}}{20},\\ h_0^{(1)}=\frac{17\sqrt{2}}{28}, h^{(1)}_{\pm 1}=\frac{73\sqrt{2}}{280}, h^{(1)}_{\pm 2}=-\frac{3\sqrt{2}}{56}, h^{(1)}_{\pm 3}=-\frac{3\sqrt{2}}{280}. \] Зазначимо, що у разі відомої природи шуму, вейвлет- аналіз є ефективним інструментом його видалення. В цьому разі домени частот, які відповідають шуму, можна просто обернути в ноль, в наслідок чого зображення буде трохи згладжене, але без відповідних завад, для розв’язку цієї задачі зовсім не обов’язково робити розклад у повний пакет.

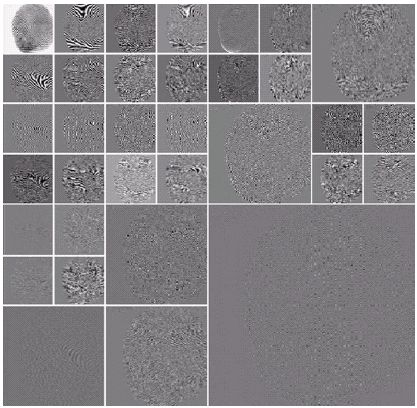Зображення відбитку пальця з відповідними частотами.

Цілочисельне вейвлет-перетворення.

Існує цілий ряд задач, коли частотне перетворення сигналу (у нашому випадку, зображення) не повинне вносити помилку округлення. І це є принциповим. У такому разі, все, що було викладене раніше, не підходить.
Використання дискретного тригонометричного перетворення Фур'є, так само, як і ортогонального (або біортогонального) вейвлет перетворення, призводить до появи помилок округлення. Тому для цілочисельного частотного аналізу зображення було запропоновано використовувати цілочисельне вейвлет-перетворення. Традиційно для цієї мети використовується сепарабельном схема або схема Малла. Зокрема, в стандарті JPEG2000 застосовується наступна конструкція.
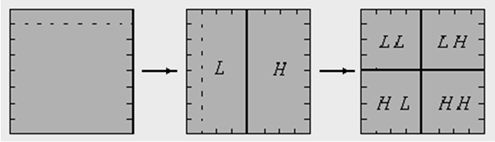
Нехай \(c^0_i\) вхідні дані, тоді прямий хід виглядає наступним чином \[ c_{2n}^{1}=c^{0}_{2n}-\left[\frac{c^{0}_{2n-1}+c^{0}_{2n+1}+2}{4}\right], c_{2n+1}^{1}=c^{0}_{2n+1}+\left[\frac{c^{1}_{2n}+c^{1}_{2n+2}}{2}\right], \] а зворотний – \[ c_{2n+1}^{0}=c^{1}_{2n+1}-\left[\frac{c^{1}_{2n}+c^{1}_{2n+2}}{2}\right], c_{2n}^{0}=c^{1}_{2n}+\left[\frac{c^{0}_{2n-1}+c^{0}_{2n+1}+2}{4}\right]. \] Множина коефіцієнтів з парними індексами утворює низькочастотний домен (L), а з непарними - високочастотний (H). Послідовне застосування того ж алгоритму дозволяє розділити вихідні дані на чотири частотних домену. З яких домен LL найбільш чутливий до помилки, а домен HH найменш чутливий.
Як правило, частотні перетворення використовуються не для компонентів рівноправного простору кольорів (R,G,B), а для нерівноправних, таких як YCrCb, YIQ та інше.
Сам процес перетворення кольорових компонентів з рівноправних (тип даних byte) до нерівноправних (тип даних double або float), вже вносить помилку округлення. У разі, коли точність перетворення є принциповою, треба зробити це у цілих числах. Таке перетворення можна провести наступним чином

Y = [(R + 2 G + B) / 4]; U = (R - G); V = (B - G);

і зворотний хід

G = (Y - [(U + V) / 4]); R = U + G; B = V + G;

де [.] ціла частина числа.
Отримані цілочисельні колірні компоненти YUV не настільки ефективні, як YCrCb або YIQ, зате позбавлені такої проблеми, як помилки округлення.
Зауважимо, що сепарабельна схема з самого початку орієнтована на одновимірні дані, тому використання двовимірної вейвлет-схеми для обробки зображень є кращим. Для фільтрації даних \(p_{i,j}\) була запропонована несепарабельна (що непредставимо у вигляді тензорного добутку одновимірних) вейвлет-схема з тією ж складністю, тобто з рівним числом арифметичних операцій.
На першому кроці проводиться децимація даних з парними індексами \[ s^0_{i,j}=p_{2i,2j}. \] На другому кроці по децимованим значенням будуємо лінійні відновлення в точках з одним непарних індексом і обчислюємо відповідні частотні коефіцієнти \[ s^1_{i,j}=p_{2i+1,2j}-\left[\frac{p_{2i,2j}+p_{2i+2,2j}}{2}\right], s^2_{i,j}=p_{2i,2j+1}-\left[\frac{p_{2i,2j}+p_{2i,2j+2}}{2}\right], \] і, нарешті, на третьому кроці отримуємо частотні коефіцієнти з непарними індексами \[ s^3_{i,j}=p_{2i,2j+1}-\left[\frac{s^0_{i,j}+s^0_{i,j+1}+s^0_{i+1,j}+s^0_{i+1,j+1}}{4}\right]-\left[\frac{s^1_{i,j}+s^1_{i,j+1}+s^2_{i,j}+s^2_{i+1,j}}{4}\right]. \] За аналогією зі схемою Малла можна записати \[ HH=\left\{s^3_{i,j}\right\}, HL=\left\{s^2_{i,j}\right\}, LH=\left\{s^1_{i,j}\right\}, LL=\left\{s^0_{i,j}\right\}. \]

Корисна література.

  1. Бабенко В.Ф. Быстрый алгоритм биортогонального дискретного всплеск-преобразования / В.Ф.Бабенко, А.А.Лигун, А.А.Шумейко // Математичне моделювання .— 2007 .— №1(16) .— C.18-21.
  2. Бабенко В.Ф. Об одном методе построения несепарабельных всплесков / В.Ф.Бабенко, А.А.Лигун, А.А.Шумейко // Математичне моделювання .— 2007 .— №2(17) .— C.35-40.
  3. Брейсуэлл Р. Преобразование Хартли.М.:Мир, 1990.- 175 с.
  4. Быстрые алгоритмы в цифровой обработке изображений / Т.С.Хуанг и др.— М.: Радио и связь, 1984 .— 224 с.
  5. Гонсалес Р. Цифровая обработка изображений / Р. Гонсалес, Р. Вудс . – М.: Техносфера, 2005 .– 1070 с.
  6. Гонсалес Р. Цифровая обработка изображений в среде MATLAB/ Р. Гонсалес, Р. Вудс, С. Эддингс . – М.: Техносфера, 2006 .– 616 с.
  7. Гришенцев А.Ю. Методы и модели цифровой обработки изображений / А.Ю.Гришенцев, А.Г.Коробейников .— СПб: Изд. Политех.ун-та, 2014 .— 190 с.
  8. Двайт Г.Б. Таблицы интегралов и другие математические формулы. / Г.Б.Двайт .— М.: Наука, 1966 .— 228 с.
  9. Добеши И. Десять лекций по вейвлетам, Ижевск, НИЦ "Регулярная и хаотическая динамика",2001.– 464 c.
  10. Залманзон Л.А. Преобразования Фурье, Уолша, Хаара и их применение в управлении, связи и других областях. / Л.А.Залманзон .— М.: Наука, 1989 .— 496 с.
  11. Лигун А.О. Комп’ютерна графіка (обробка та стиск зображень):навч.посіб./ А.О.Лигун, О.О.Шумейко.-Д.:Біла К.О., 2010.- 114 с.
  12. Малла С. Вэйвлеты в обработке сигналов / С.Малла .— М.: Мир, 2005 .— 671 с.
  13. Методы компьютерной обработки изображений/ Под ред. В.А.Сойфера.- М.:Физматлит, 2003.-784 с.
  14. Новейшие методы обработки изображений / Под ред. А.А.Потапова.- М.:Физматлит, 2008.-496 с.
  15. Новиков И.Я., Протасов В.Ю., Скопина М.А. Теория всплесков.- М., Физматлит, 2005. – 612 с.
  16. Павлидис Т. Алгоритмы машинной графики и обработки изображений / Т. Павлидис . – М.: Радио и связь, 1986 .– 400 с.
  17. Петухов А.П. Введение в теорию базисов всплесков. – СПб, Изд. СПбГТУ, 1999 – 132 c.
  18. Фурман Я.А. Цифровые методы обработки и распознавания бинарных изображений / Я.А.Фурман, А.Н.Юрьев, В.В.Яшин .— Красноярск: Изд. Краснояр. ун-та, 1992 .— 248 с.
  19. Чуи K. Введение в вейвлеты. – М.: Мир, 2001.
  20. Шумейко А. Быстрое дискретное тригонометрическое преобразование со свободным фазовым сдвигом / А.Шумейко, В.Смородский // Системні технології .— 2017 .— №4(111) .— C.46-55.
  21. Шумейко А.А. Интеллектуальный анализ данных (Введение в Data Mining) / А.А.Шумейко, С.Л.Сотник .— Днепропетровск: Белая Е.А., 2012 .— 212 с.
  22. Шумейко А.А. Применение несепарабельной вейвлет-схемы для стеганографической защиты данных / А.А.Шумейко, А.И.Пасько// Вісник східноукраїнського національного університету імені Володимира Даля.— 2008.— №8(126) .— C.50-55.
  23. Ярославский Л.П. Введение в цифровую обработку изображений. — М.: Сов. радио, 1979. — 312 с.
  24. Hartley,R."A more symmetrical Fourier analysis applied to transmission problems," Proc. IRE 30, 144–150 (1942).
  25. Mallat S.A. Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 11, No. 7, July 1989, p. 674-693.
  26. Shumeiko А. Discrete trigonometric transform and its usage in digital image processing / А.Shumeiko, V.Smorodskyi // Econtechmod. An International Quarterly Journal .— 2017 .— №4(6) .— C.21-26.

Питання-відповідь.

Задати питання: