В настоящее время задачи мониторинга природной среды, исследование природных ресурсов, наблюдение за военной деятельностью государств и контроль
выполнения договоров по сокращению вооружений во многом осуществляются с использованием дистанционного зондирования земной поверхности космическими
техническими средствами.
Из всех видов дистанционного зондирования в настоящее время фотографирование обеспечивает возможность получения максимальной степени разрешения на
местности. Фотоснимки характеризуются разными масштабами, различной степенью обзорности, высокой разрешающей способностью, черно-белым, цветным и
псевдоцветным изображением в нескольких диапазонах спектра.

Фрагмент многозональной съемки.
Кроме обычной фотосъемки из космоса осуществляется многозональная съемка. Она производится с помощью системы камер, каждая из которых имеет специальный светофильтр, рассчитанный на получение изображения в определенном диапазоне спектра на стандартную фотопленку или светочувствительную матрицу. Преимущества многозональной съемки заключается в следующем:
- Большое количество спектральных диапазонов обеспечивает выбор наиболее оптимальных условий фотографирования определенных природных и искусственных объектов.
- Изображение получается только в определенных зонах спектра, характеризующихся наибольшей контрастностью.
- Возможностью получения одного объекта одновременно в инфракрасном, видимом и ультрафиолетовом диапазонах спектра.
- Возможность обработки снимков как в различных диапазонах, так и их комбинаций, в том числе в виде синтезированных псевдоцветных изображений.
Для получения синтезированных псевдоцветных изображений используются методы сокращения размерности сигнала, одним из которых
является колоризация синтезированного изображения с учетом естественного разбиения сигнала на инфракрасный, видимый и ультрафиолетовый диапазоны, а также связь между ними. В основе предлагаемой технологии лежит модифицированный метод главных компонент.

Псевдоцветное многозональное изображение.
Пусть \(X_i (i=1,\ldots ,N)\) многозональный сигнал, причем значения \(X_{i} (i=1,\ldots ,N_1)\) соответствуют инфракрасному диапазону,
\(X_{i} (i=N_{1},\ldots ,N_{2})\) - видимому и \(X_{i} (i=N_{2},\ldots ,N)\) ультрафиолетовому.
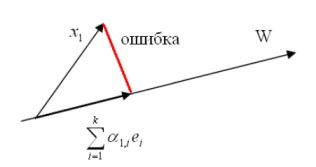
Метод главных компонент (МГК) позволяет выделить часть всего сигнала, наиболее характерно отражающего поведение всего сигнала в целом, что реализуется путем решения экстремальной задачи
\[
\min\left\{\left.\sum_{k=0}^{n-1}\left\|X^k-\sum_{\mu=0}^{m-1}\alpha^\mu_kY^\mu\right\|_2 \right|
Y^\mu,\alpha^\mu_k: \sum_{k=0}^{n-1}\left(\alpha^\mu_k\right)^2 =1 \right\}.
\]
Для решения этой задачи используем итерационный алгоритм.
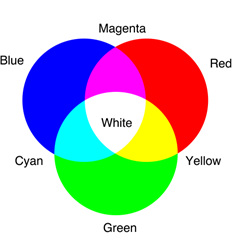
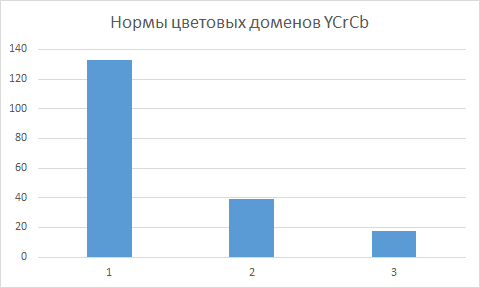
Традиционно для колоризации синтезированного изображения используется пространство цветов YCrCb, где Y - величина освещенности,
Cr - составляющая теплых тонов и Cb - составляющая холодных тонов. При этом в качестве Y берется первая главная компонента,
в качестве Cr - вторая и вместо Cb используется третья главная компонента.
Этот подход кажется достаточно надуманным и не всегда соответствующим реальному восприятию.
Наши дальнейшие рассуждения посвящены построению естественной колоризации синтезированного изображения.
Пусть векторы \(\alpha^{i }(i=1,\ldots ,N_{1})\), соответствующие главной компоненте \(Y^R\) кадров \(X_{i} (i=1,\ldots ,N_{1})\), векторы
\(\alpha^{i }(i= N_{1},\ldots ,N_{2})\), соответствующие главной компоненте \(Y^G\) кадров \(X_{i} (i= N_{1},\ldots ,N_{2})\) и
\(\alpha^{i }(i= N_{2},\ldots ,N)\) векторы, соответствующие \(Y^B\) кадров \(X_{i} (i= N_{2},\ldots ,N).\)
На следующем шаге найдем векторы \(\alpha^R,\alpha^G,\alpha^B\), доставляющие решение задачи
\begin{equation}
\label{eq_multi2}
\sum\limits_{k = 1}^N{\left({X_k - \alpha_k^R Y^R - \alpha_k^G Y^G -
\alpha_k^B Y^B} \right)^2 \to \mathop{\min }\limits_{\alpha_k^R ,\alpha
_k^G ,\alpha_k^B } }.
\end{equation}
Эта задача сводится к системе из \(3N\) линейных уравнений с \(3N\) неизвестными
Решая ее, получаем векторы \[\tilde{\alpha }^R = \left({\tilde{\alpha
}_1^R ,\tilde{\alpha }_2^R ,...,\tilde{\alpha }_N^R } \right),\tilde
{\alpha }^G = \left({\tilde{\alpha }_1^G ,\tilde{\alpha }_2^G ,...,\tilde
{\alpha }_N^G } \right)$ и $\tilde{\alpha }^B = \left({\tilde{\alpha
}_1^B ,\tilde{\alpha }_2^B ,...,\tilde{\alpha }_N^B } \right).\] Используя
найденные векторы, проведем последовательное уточнение главных компонент. Вначале рассмотрим задачу
\[
\sum\limits_{k = 1}^N{\left({X_k - \tilde{\alpha }_k^R Y^R - \tilde
{\alpha }_k^G Y^G - \tilde{\alpha }_k^B Y^B} \right)^2 \to \mathop{\min
}\limits_{Y^R} } ,
\]
решением которой будет
\[
\tilde{Y}^R = \frac{\sum\limits_{k = 1}^N{\tilde{\alpha }_k^R \left({X_k
- \tilde{\alpha }_k^G Y^G - \tilde{\alpha }_k^B Y^B} \right)}
}{\sum\limits_{k = 1}^N{\left({\tilde{\alpha }_k^R } \right)^2} }.
\]
Следующим шагом будет уточнение \(Y^{G}\), для чего рассмотрим следующую
экстремальную задачу
\[
\sum\limits_{k = 1}^N{\left({X_k - \tilde{\alpha }_k^R \tilde{Y}^R -
\tilde{\alpha }_k^G Y^G - \tilde{\alpha }_k^B Y^B} \right)^2 \to \mathop
{\min }\limits_{Y^G} } ,
\]
решением которой будет
\[
\tilde{Y}^G = \frac{\sum\limits_{k = 1}^N{\tilde{\alpha }_k^G \left({X_k
- \tilde{\alpha }_k^R \tilde{Y}^R - \tilde{\alpha }_k^B Y^B} \right)}
}{\sum\limits_{k = 1}^N{\left({\tilde{\alpha }_k^G } \right)^2} }
\]
и, наконец, уточним последнюю компоненту
\[
\tilde{Y}^B = \frac{\sum\limits_{k = 1}^N{\tilde{\alpha }_k^B \left({X_k
- \tilde{\alpha }_k^R \tilde{Y}^R - \tilde{\alpha }_k^G \tilde{Y}^G}
\right)} }{\sum\limits_{k = 1}^N{\left({\tilde{\alpha }_k^B } \right)^2}
}.
\]
Далее найдем нормированные \(\alpha ^R,\alpha ^G,\alpha ^B\) векторы
\[
\alpha_i^R = \frac{\tilde{\alpha }_i^R }{\sum\limits_{k = 1}^N{\left(
{\tilde{\alpha }_k^R } \right)^2} },
\quad
\alpha_i^G = \frac{\tilde{\alpha }_i^G }{\sum\limits_{k = 1}^N{\left(
{\tilde{\alpha }_k^G } \right)^2} },
\quad
\alpha_i^B = \frac{\tilde{\alpha }_i^B }{\sum\limits_{k = 1}^N{\left(
{\tilde{\alpha }_k^B } \right)^2} }
\]
и полагаем \(Y^R = \tilde{Y}^R,Y^G = \tilde{Y}^G,Y^B = \tilde{Y}^B.\)
Следующим этапом переходим к задаче (\ref{eq_multi2}), повторяя этот процесс итерационно, пока компоненты \(Y^R,Y^G,Y^B\) не стабилизируются.
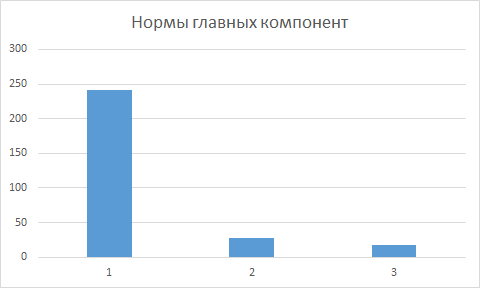
Результатом выполнения алгоритма будут три главные компоненты \(Y^R,Y^G,Y^B\), а также три вектора \(\alpha^R,\alpha^G,\alpha^B\).
Для получения колоризованного синтезированного изображения, возьмем первую главную компоненту в качестве носителя красного цвета, вторую - зеленого
и третью - синего цвета. Эта последовательность цветов определена тем, что первые \(N_{1}\) были получены в инфракрасном спектре,
а последние \(N-N_{2}\) в ультрафиолетовом.
Заметим, что по полученным компонентам легко восстановить (с некоторой точностью) все изображения исходного многоканального сигнала:
\[X_k \approx \tilde{X}_k = \alpha_k^R Y^R + \alpha_k^G Y^G + \alpha
_k^B Y^B (k=1,2,\ldots ,N).\]
Естественным является проблема улучшения качества восстановления многозонального изображения.
Примером решения этой проблемы может служить нелинейная конструкция восстановления многозонального изображения
\[
\sum\limits_{k = 1}^N{\left({X_k - \alpha_k^R Y^R - \alpha_k^G Y^G -
\alpha_k^B Y^B - \beta_k^R \left({Y^R} \right)^2 - \beta_k^G \left(
{Y^G} \right)^2 - \beta_k^B \left({Y^B} \right)^2} \right)^2 \to \mathop
{\min }\limits}
\]
На следующей диаграмме приведены значения ошибки восстановления по каждому кадру многозонального изображения.
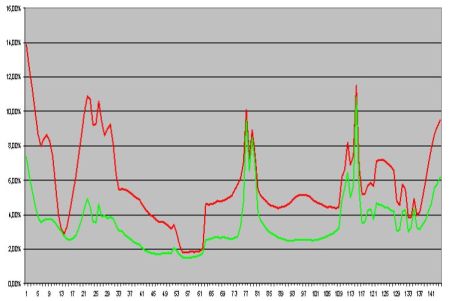
Графики ошибок покадрового восстановления многозонального изображения
линейным (красная кривая) и квадратичным методом (зеленая кривая).
Использование квадратичной функции для восстановления сигнала
усложняется тем фактом, что нужно анализировать на какой ветви параболы
лежит искомое решение. Для решения этой проблемы используем метод улучшения восстановления,
использующий линейную комбинацию главных компонент и компонент, получаемых
применением оператора дифференцирования (дискретного аналога). Для этого
найдем свертку каждой найденной главной компоненты с разностным фильтром
\[
D = \left\{{d_{i,j} } \right\}_{i,j = - 1}^1 = \left(
{{\begin{array}{*{20}r}
0 \hfill & 1 \hfill & 0 \hfill \\
1 \hfill &{ - 4} \hfill & 1 \hfill \\
0 \hfill & 1 \hfill & 0 \hfill \\
\end{array} }} \right),
\]
то есть, если \(T^\chi = \left\{{t_{i,j}^\chi } \right\},\chi \in \left\{
{R,G,B} \right\}\), то
\[
DT^\chi = \left\{{dt_{i,j}^\chi } \right\} = \left\{{\sum\limits_{\nu ,\mu
= - 1}^1{d_{\nu ,\mu } t_{i + \nu ,j + \mu }^\chi } } \right\}.
\]
Восстановление кадров многозонального изображения будем искать в виде решения оптимизационной задачи
\begin{equation}
\label{eq_multi3}
\sum\limits_{k = 1}^N{\left({X_k - \alpha_k^R Y^R - \alpha_k^G Y^G -
\alpha_k^B Y^B - \beta_k^R DY^R - \beta_k^G DY^G - \beta_k^B DY^B}
\right)^2 \to \mathop{\min }\limits_{\beta_k^R ,\beta_k^G ,\beta_k^B } }.
\end{equation}
Понятно, что не все кадры многозонального изображения восстанавливаются с одним и тем же качеством - в случае наличия на кадрах оригинального
сигнала уникальных отклонений, например, теплового шума в кадрах инфракрасного диапазона, ошибка восстановления будет большей.
Этот метод обработки многозонального сигнала дает возможность обрабатывать не все пикселы исходного сигнала, а избирательно,
что позволяет фильтровать помехи, порождаемые, например, тепловым шумом.
Этот факт позволяет получать более точные спектральные характеристики сигнала.
На следующих рисунках приведены спектрограммы точки многозонального изображения по оригинальным (желтым цветом) и данным, восстановленным по трем
компонентам \(Y^R,Y^G, Y^B\)(синим цветом). Во втором случае взята точка с
импульсным тепловым шумом, что существенно искажает спектрограмму. Поэтому целесообразно проводить предварительную обработку кадров.
Приведем схему предварительной обработки. После получения восстановленных
кадров \(\tilde{X}_k= \left\{{\tilde{x}_i } \right\}_{i = 1}^M \)
\((k=1,2,\ldots ,N)\), находим среднеквадратичную и интегральную ошибки восстановления оригинальных
кадров \(X_k= \left\{{x_i } \right\}_{i = 1}^M \)
\[
\varepsilon_k^1 = \frac{1}{M}\sum\limits_{i = 1}^M{\left|{x_i - \tilde
{x}_i } \right|} ,
\quad
\varepsilon_k^2 = \sqrt{\frac{1}{M}\sum\limits_{i = 1}^M{\left|{x_i -
\tilde{x}_i } \right|^2} } .
\]
Если для кадра величина \(\varepsilon_k^2/\varepsilon_k^1\) больше заданного порога, то этот кадр содержит пикселы с большими значениями шума.
Эти пикселы изымаются из изображения и подлежат специальному анализу.
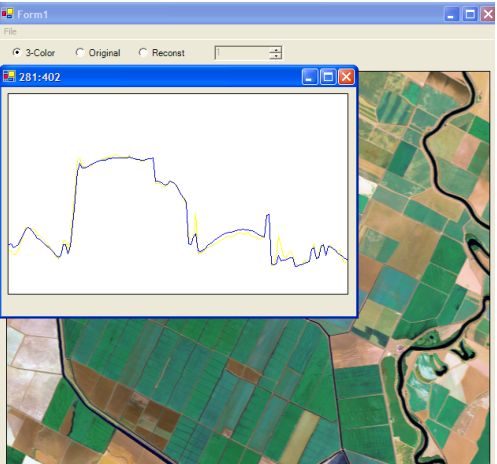
Спектрограммы оригинального многозонального изображения и
постановленного по псевдоцветному синтезированному изображению в точке.
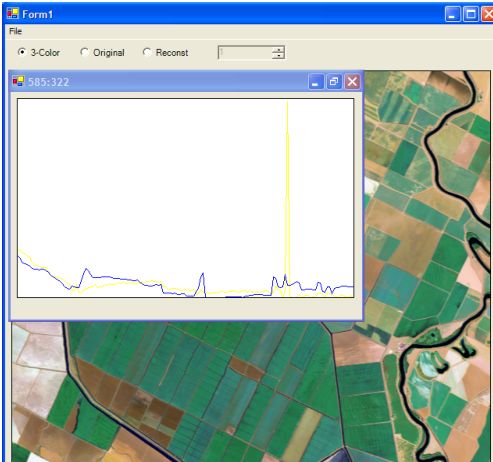
Спектрограммы оригинального многозонального изображения и постановленного по псевдоцветному синтезированному изображению в точке с импульсным тепловым шумом.
Месторасположения вынутых точек заполняются средними значениями точек окрестности, получаемыми, например, в результате решения стационарной задачи теплопроводности.
К исправленному таким образом многозональному изображению применим весь алгоритм, описанный выше, что позволит получить более корректное восстановление спектрограмм.
Заметим, этот метод восстановления многозонального изображения не является единственным, можно использовать различные комбинации полученных главных компонент.
Использование модификаций метода главных компонент позволяет повысить качество восстанавливаемых кадров многозонального изображения по синтезированному изображению с возможностью фильтрации спектрограмм от импульсного шума.