Масштабування зображень

Через дискретність відображення сигналів (образів), вся графічна інформація розглядається як дискретна. Цей факт приводить до певних незручностей при масштабуванні зображень. При зменшенні масштабу (накат на образ, збільшення геометричного розміру зображення, підвищення глибини перенесення кольорів і ін.) кількість інформації, що відображається, збільшується, а при збільшенні масштабу (зменшенні геометричного розміру зображення, зниженні глибини перенесення кольорів і ін.) її кількість зменшується. Процес збільшення точок, які відображуються, називається інтерполяцією, зменшення- децимацією (проріджування)( від латинського decimating - знищення кожного десятого полоненого воїна переможеної римлянами армії).

Методи інтерполяції і децимації одновимірних даних

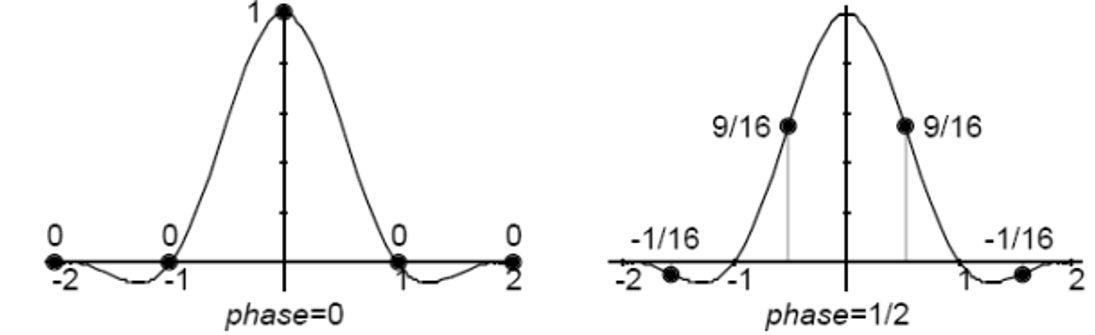
При реалізації алгоритмів інтерполяції і децимації можливо, що нове значення лежить в точці, в якій раніше було старе значення, в цьому випадку говорять, що фазове зрушення перетворення дорівнює нулю. Якщо координати нової точки лежать у середині між старими, то фазове зрушення дорівнює 1/2, 1/2 і так інше.
Найпростішим алгоритмом масштабування є метод найближчого сусіда. Ідея даного алгоритму дуже проста – при зміні масштабу зображення розраховуємо координати нових пікселів (вузли нової решітки). Для кожного нового вузла знаходимо найближчий вузол старої решітки і колір пікселя, який відповідає знайденому вузлу оригінальної решітки присвоюємо розрахованому пікселю.

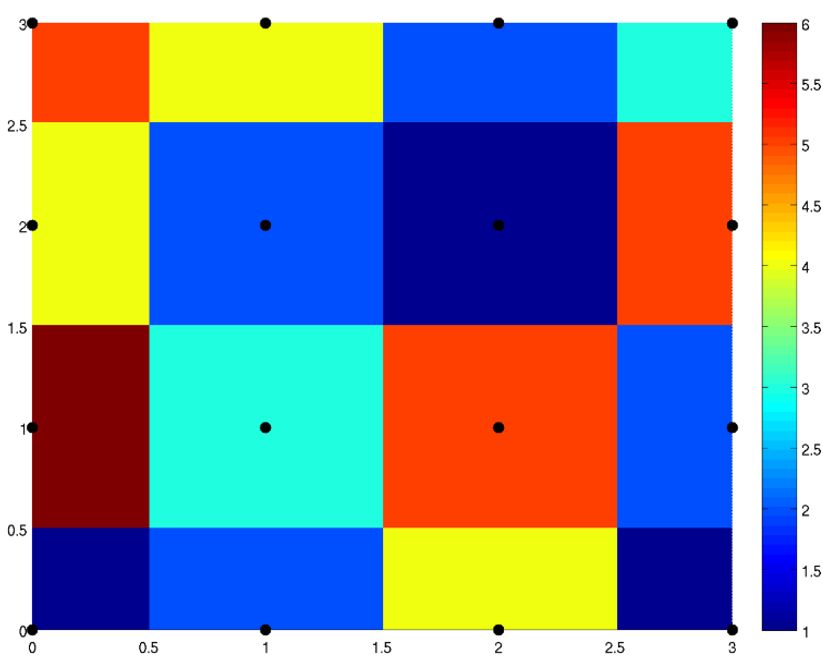Результат інтерполяції фрагменту зображення заданого
на решітці [0,3]×[0,3] методом найближчого сусіда.

Очевидно, що результат такого масштабування буде дуже фрагментованим, тому сфера використання даного алгоритму обмежується тими задачами, коли критичним є не якість отриманого результату, а швидкість роботи алгоритму, наприклад, для масштабування відео-потоку на мобільних засобах.
У разі отримання більш пристойних результатів, треба замінити дискретну множину, яку представляє собою растрове зображення, неперервною поверхнею, і вже при масштабуванні зображення, знімати нові дані з поверхні. Таким чином, задача масштабування так чи інакше зводиться до побудови векторного образу растрового зображення.
Розглянемо декілька підходів, які використовуються для вирішення такого роду задач.
Найчастіше для побудови фільтрів використовуються різні інтерполяційні формули, як правило на основі інтерполяційних многочленів. Ми розглянемо найпростіший випадок алгебраїчної інтерполяції - лінійної. Фільтр для децимації даних в два рази може бути реалізований таким чином:

децимація в три рази:

децимація в чотири рази:

Ясно, що для цього випадку, інтерполяція нових значень виходить зняттям цих значень з інтерполяційної ламаної.
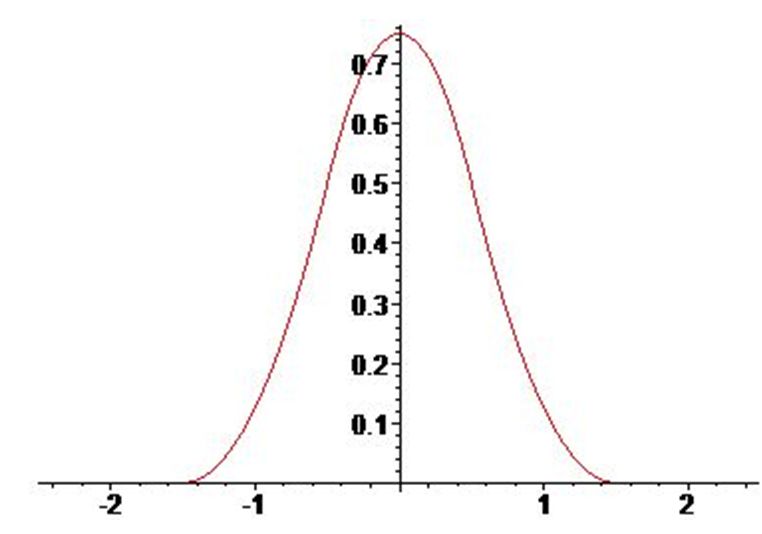
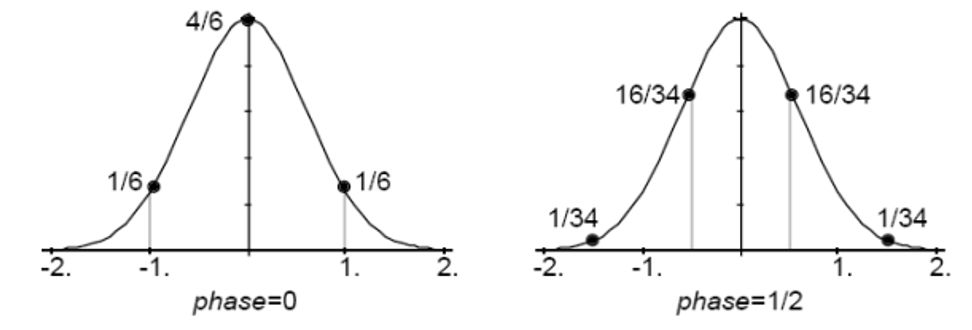
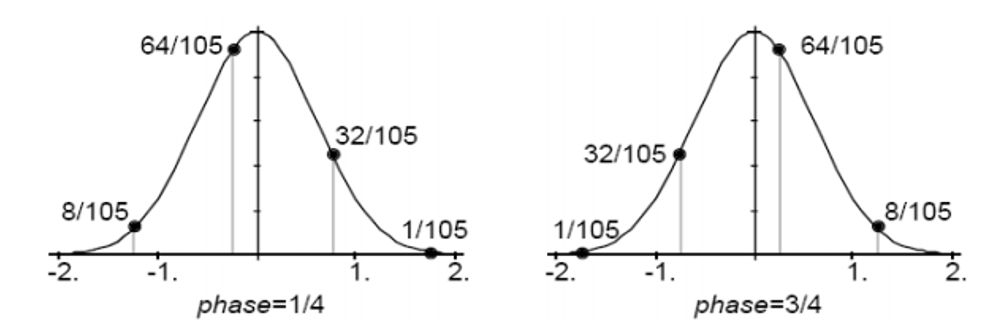
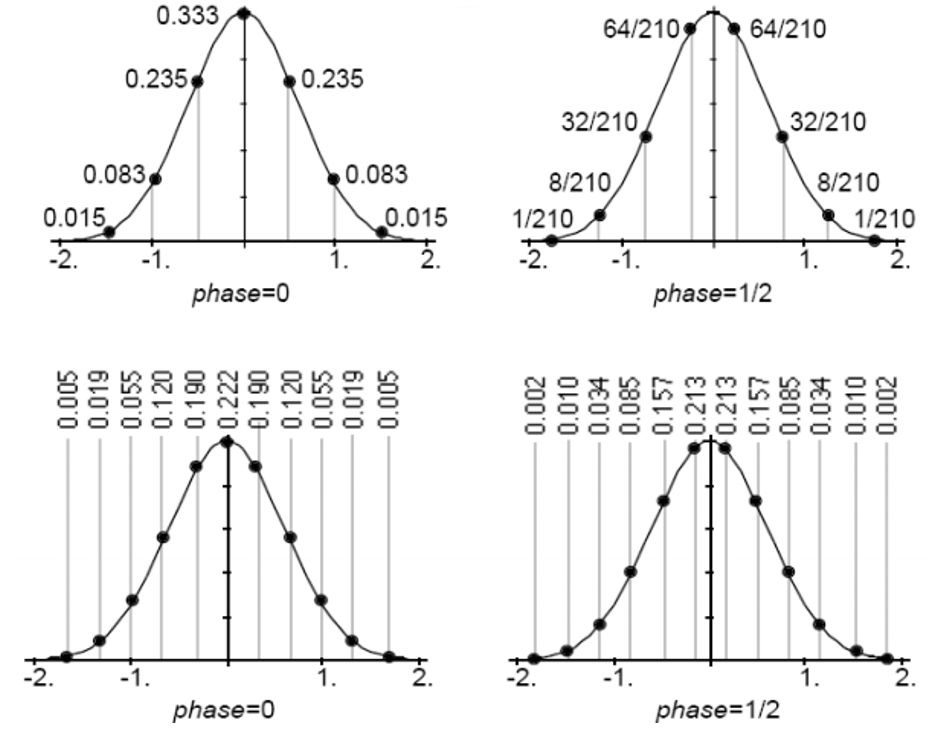
Однією з найчастіше використовуваних функцій для подібного роду задач є функція Гауса \( y=e^{-a^2 x^2 }. \) У якості прикладу, розгляне функцію \(y=2^{-\frac{1}{2} x^2 }.\)
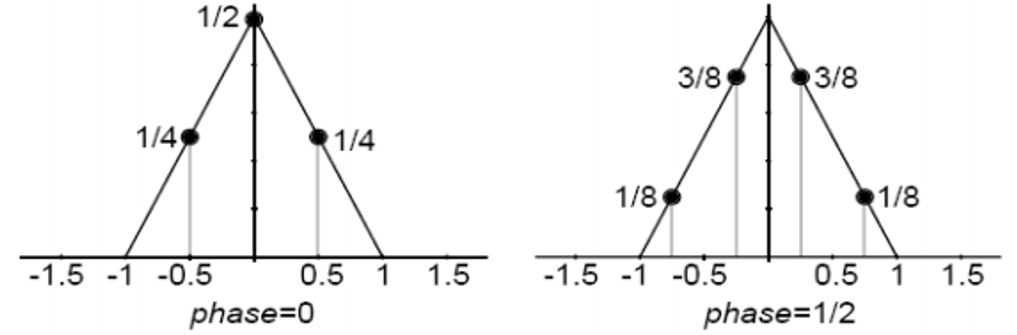
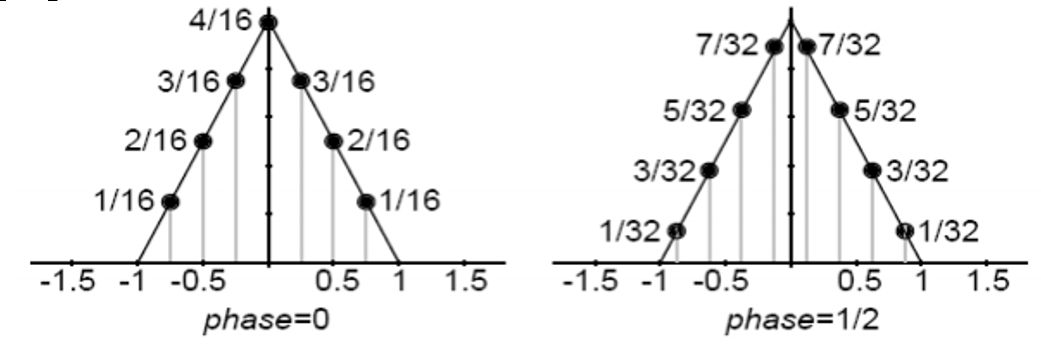
Для інтерполяції в два рази, слід використовувати наступну маску

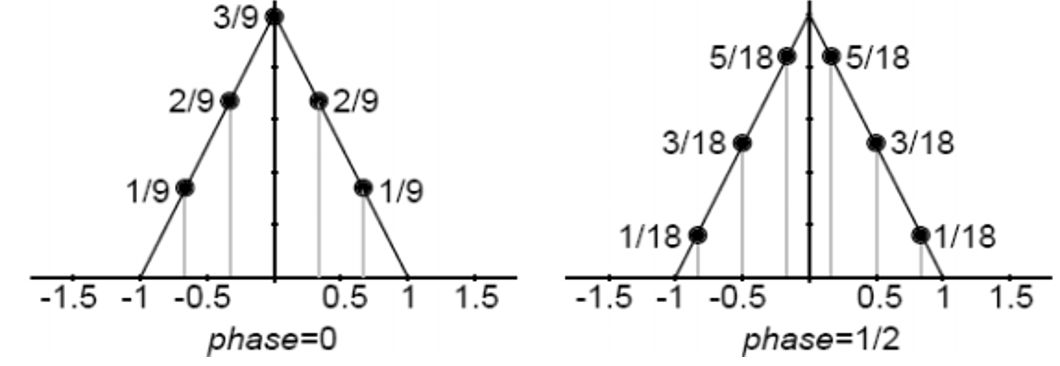
Інтерполяція в три рази виходить таким чином

Як приклад приведемо маску децимації в два і три рази:

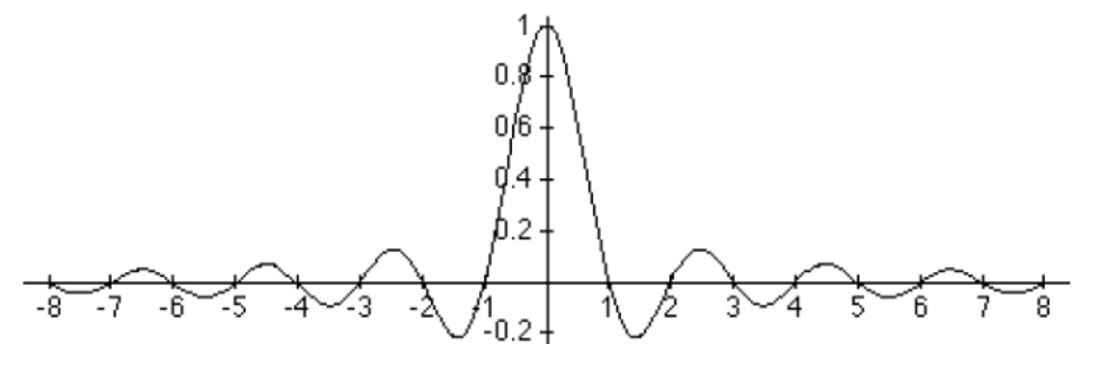
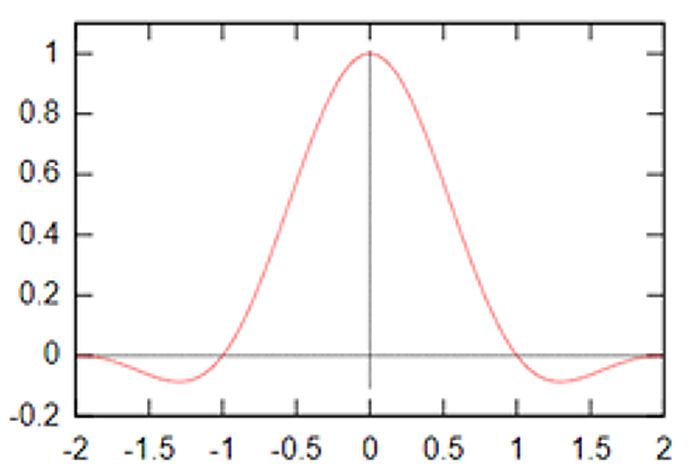
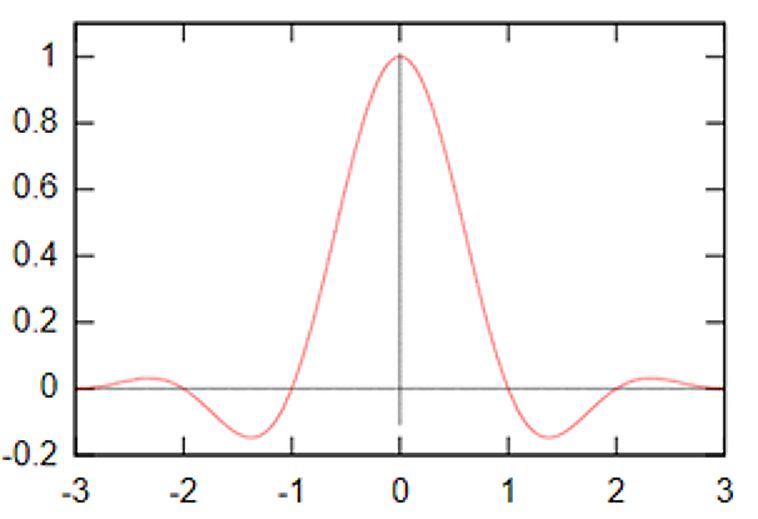
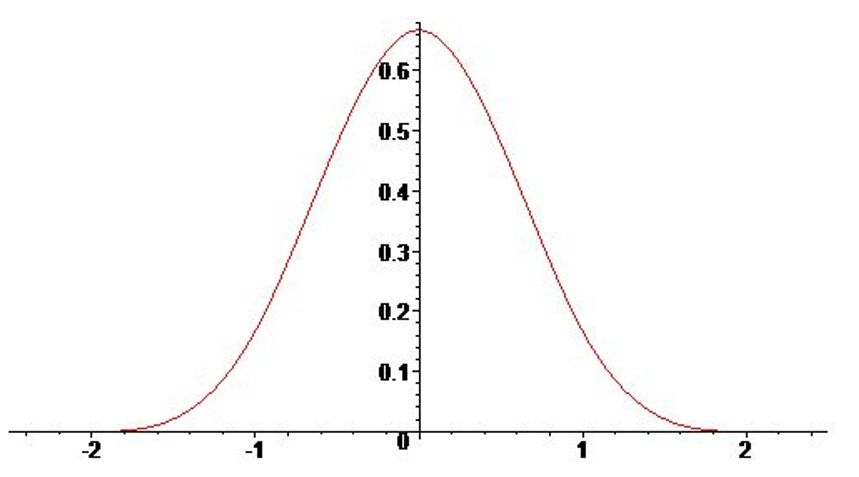
Широко вживаною функцією для побудови низькочастотного фільтру є функція sinc(x) (від лат. sinus cardinalis — кардинальний синус) \[ \mathrm{sinc}(x)=\left\{ \begin{array}{ll} \frac{\sin(\pi x)}{\pi x}, & \hbox{ }x\ne 0, \\ 1, & \hbox{ }x=0. \end{array} \right. \]

Внаслідок того, що значення цієї функції хоча і швидко затухають, але її носій не обмежений, тому для побудови фільтрів на основі цієї функції беруть добуток її на деяку віконну функцію. Результатом будуть, наприклад, наступні функції \[ \mathrm{Lanczos2}(x)=\left\{ \begin{array}{ll} \frac{\sin(\pi x)}{\pi x} \frac{\sin(\pi\frac{x}{2})}{\pi \frac{x}{2}}, & \hbox{ }|x|\lt 2, \\ 0, & \hbox{ }|x|\ge 2. \end{array} \right. \] Яка названа на честь угорського вченого Корнелія Ланцоша (Lánczos Kornél).

або \[ \mathrm{Lanczos2}(x)=\left\{ \begin{array}{ll} \frac{\sin(\pi x)}{\pi x} \frac{\sin(\pi\frac{x}{3})}{\pi \frac{x}{3}}, & \hbox{ }|x|\lt 3, \\ 0, & \hbox{ }|x|\ge 3. \end{array} \right. \]

Наведемо фільтри інтерполяції у два рази, одержані на основі функції Lanczos2

Застосування фільтра Ланцоша дозволяє добитися високої чіткості зображення, але при обробці можлива поява небажаних артефактів типу ореолів навколо контрастних переходів яскравості. Виникнення ореолів обумовлено тим, що ядро Ланцоша приймає від’ємні значення при деяких значеннях аргументу. Тому оброблений сигнал може приймати навіть від’ємні значення при додатних значеннях вибірок.
Популярним інструментом масштабування є використання моделювання поверхні зображення тензорним добутком сплайнів, як правило, це білінійні і бікубічні сплайни.
Для розглядання цього методу, нам необхідні деякі означення.
Базовий сплайн, або B-сплайн, є сплайном з мінімальним носієм для фіксованого ступеня сплайну та порядку гладкості. Їхня безумовна користь полягає в тому, що будь-який сплайн заданого ступеня і гладкості можна записати у вигляді лінійної комбінації відповідних базисних сплайнів. Тобто, їх можна використовувати як "цеглинки", за допомогою яких можна побудувати сплайн із заданими властивостями. Власне чим і пояснюється його визначення – базисний сплайн.
Надалі розглянемо В-сплайни мінімального дефекту порядку r. Найбільш популярними є В-сплайни порядку від 0 до 3, проте у нашому випадку більшу увагу треба приділити сплайнам 1-го та 3-го порядків (лінійний та кубічний відповідно).
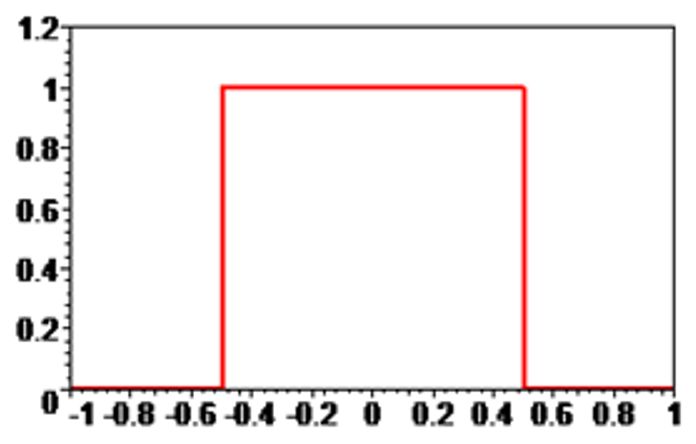
В-сплайн нульового порядку \(B_0(t)\) має наступний вигляд \[ \mathrm{B_0}(x)=\left\{ \begin{array}{ll} 1, & \hbox{ }|t|\lt \frac{1}{2}, \\ 0, & \hbox{ }|t|\ge \frac{1}{2}. \end{array} \right. \]

Типовим представником сплайнів нульового порядку, визначених на усій координатній осі по одиничній решітці, є В-сплайн нульового порядку, його зрушення та лінійні комбінації: \[ s_0 (t)=\sum_{i=-\infty}^\infty c_iB_0\left(t-\frac{2i+1}{2}\right). \] У загальному вигляді, функцію \(B_r(t)\) введемо за допомогою рекурентних співвідношень: \[ B_r(t)=\int_{t-\frac{1}{2}}^{t+\frac{1}{2}}B_{r-1}(x)dx, r=1,2,... 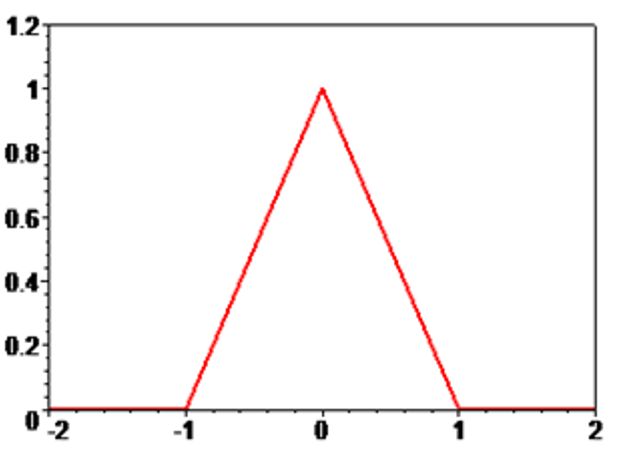\] B-сплайн першого порядку \[ \mathrm{B_1}(x)=\left\{ \begin{array}{ll} t+1, & \hbox{ }t\in [-1,0], \\ 1-t, & \hbox{ }t\in [0,1], \\ 0, & \hbox{ }|t|\ge 1. \end{array} \right. \]

Типовим представником сплайну 1-го порядку є B-сплайн 1-го порядку, його зрушення та лінійні комбінації: \[ s_1 (t)=\sum_{i=-\infty}^\infty c_iB_1\left(t-i\right). \] B-сплайн другого порядку \[ \mathrm{B_2}(x)=\left\{ \begin{array}{ll} 0.125(3-2t)^2, & \hbox{ }t\in [1/2,3/2], \\ 0.75-0.25(2t)^2, & \hbox{ }t\in [-1/2,1/2], \\ 0.125(3+2t)^2, & \hbox{ }t\in [-3/2,-1/2], \\ 0, & \hbox{ }|t|\ge 3/2. \end{array} \right. \]

Типовим представником сплайну 2-го порядку є \[ s_2 (t)=\sum_{i=-\infty}^\infty c_iB_2\left(t-i-\frac{1}{2}\right). \] Нарешті, випишемо кубічний В-сплайн \[ \mathrm{B_3}(x)=\left\{ \begin{array}{ll} (4-2t)^3, & \hbox{ }t\in [1,2], \\ 3(2t)^3-12(2t)^2+32, & \hbox{ }t\in [0,1], \\ -3(2t)^3-12(2t)^2+32, & \hbox{ }t\in [-1,0], \\ (4+2t)^3, & \hbox{ }t\in [-2,-1], \\ 0, & \hbox{ }|t|\ge 2. \end{array} \right. \]

Типовим представником кубічного сплайну буде \[ s_3 (t)=\sum_{i=-\infty}^\infty c_iB_3\left(t-i\right). \] Нехай маємо одиничну решітку з вузлами \(\mathbf{i}=(i,j)\), де \(\mathbf{i}\in Z^2\) і позначимо через \begin{equation}\label{s1} s_{r,s}(\mathbf{P},\mathbf{u})=\sum_{\mathbf{i}\in Z^2}\mathbf{P}_\mathbf{i}N_{r,s}(\mathbf{u}-\mathbf{i}) \end{equation} де \(\mathbf{u}=(u,v)\in R^2\) і \[ N_{r,s} (\mathbf{u}-\mathbf{i})≡B_r (u-i)B_s (u-i) \] нормалізований тензорний добуток В-сплайнів порядку r та s з вузлами \(\mathbf{i}=(i,j)\).
У разі r=s=1 такий сплайн називають білінійним, якщо r=s=3, то бікубічним.

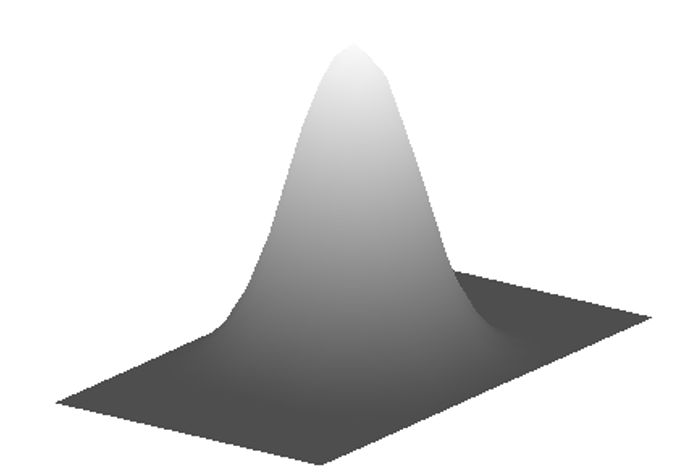Бікубічний сплайн \(s_{3,3} (\mathbf{P},\mathbf{u}).\)

Якщо \(\mathbf{P_i}\) значення кольору у пікселі \(\mathbf{i}=(i,j)\), то сплайн (\ref{s1}) можна використати у якості аналітичного опису зображення і використовувати для вирішення задачі масштабування.

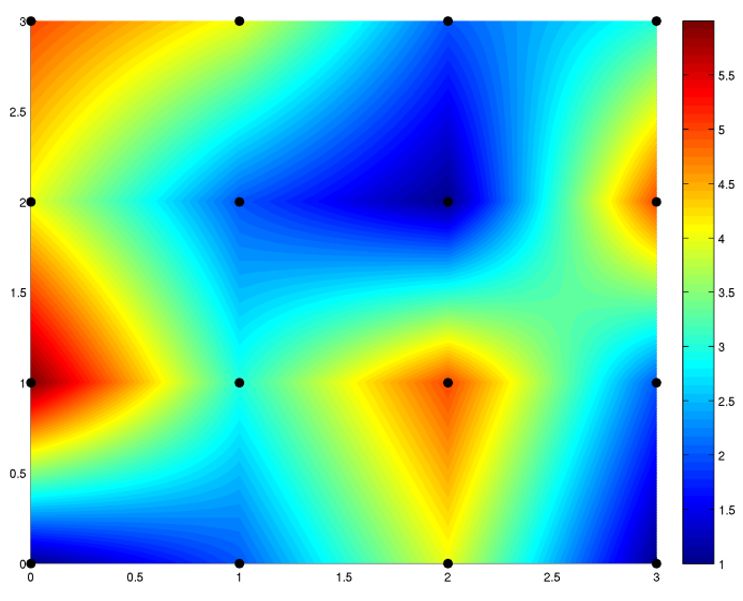Результат білінійної інтерполяції фрагменту зображення заданого на решітці [0,3]×[0,3]

Розглянемо нормалізований тензорний добуток кубічних В-сплайнів з вузлами \(\mathbf{i}=(i,j)\).
Для \(\mathbf{u}\in [i,j]×[(i+1),(j+1)]\) маємо \begin{equation}\label{2} s_{3,3}(\mathbf{P},\mathbf{u})= \left[ \begin{array}{cccc} 1 & u-i & (u-i)^2 & (u-i)^3 \\ \end{array} \right] \mathbb{M}_{3,3}\mathbb{P}_{3,3}\mathbb{M}_{3,3}^T \left[ \begin{array}{cccc} 1 \\v-j \\(v-j)^2 \\(v-j)^3 \\ \end{array} \right] \end{equation} де \(\mathbb{M}_{3,3}\) матриця розміру 4×4 \[ \mathbb{M}_{3,3}=\frac{1}{6} \left[ \begin{array}{rrrr} 1 & 4 & 1 & 0 \\ -3 & 0 & 3 & 0 \\ 3 & -6 & 3 & 0 \\ -1 & 3 & -3 & 1 \\ \end{array} \right] \] та \[ \mathbb{P}_{3,3}= \left[ \begin{array}{rrrr} \textbf{P}_{i-1,j-1} & \textbf{P}_{i,j-1} & \textbf{P}_{i+1,j-1} & \textbf{P}_{i+2,j-1} \\ \textbf{P}_{i-1,j} & \textbf{P}_{i,j} & \textbf{P}_{i+1,j} & \textbf{P}_{i+2,j} \\ \textbf{P}_{i-1,j+1} & \textbf{P}_{i,j+1} & \textbf{P}_{i+1,j+1} & \textbf{P}_{i+2,j+1} \\ \textbf{P}_{i-1,j+2} & \textbf{P}_{i,j+2} & \textbf{P}_{i+1,j+2} & \textbf{P}_{i+2,j+2} \\ \end{array} \right]. \] Таким чином, підставляючи у (\ref{s2}) значення \(\mathbf{u}\), які відповідають новій решітці, отримуємо рішення задачі масштабування зображення бікубічними сплайнами.

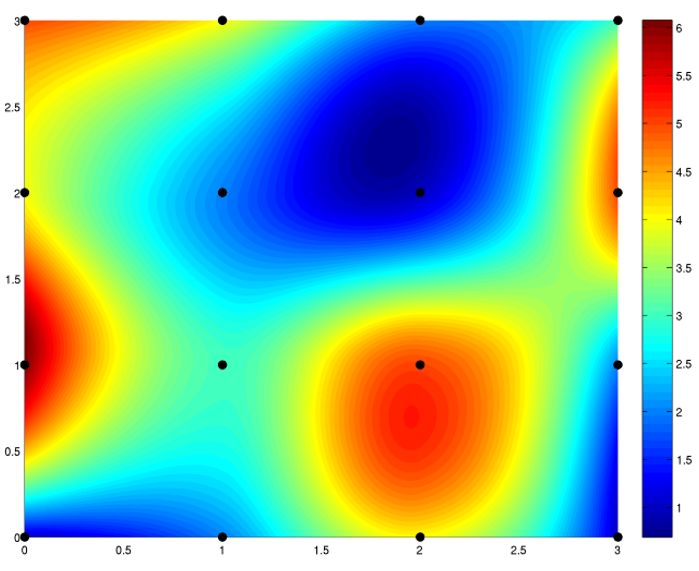Результат бікубічної інтерполяції фрагменту зображення, заданого на решітці [0,3]×[0,3]

Порівняємо обробку вхідного зображення (зміна геометричного розміру зображення) за допомогою двох алгоритмів: білінійної та бікубічної інтерполяцій.
Для порівняння візьмемо кілька зображень з TID2008 (Tampered Image Database- 2008). Ця база призначена для тестування метрик візуальної якості зображення, що має на увазі наявність еталону. TID2008 є доступною для використання у наукових цілях та вільного завантаження.

Перше тестове зображення з TID2008

Друге тестове зображення з TID2008

Третє тестове зображення з TID2008

Для порівняння результатів роботи описаних методів будемо використовувати такі показники, як час обробки зображення та PSNR.
Абревіатура PSNR (pealsignal-to-noiseratio) означає пікове співвідношення сигналу до шуму і є інженерним терміном, що визначає співвідношення між максимумом можливого значення сигналу та потужністю шуму, що спотворює значення сигналу.
Зазвичай, значення PSNR знаходиться у межах від 20 до 40 dB. У разі співпадання зображень, значення MSE стає нульовим, що дає для PSNR значення нескінченності. У такому випадку прийнято вважати, що PSNR = 100.

Для монохромних зображень I та K розміру H×W, одне з яких вважається зашумленими наближенням іншого, обчислюється наступним чином: \[ PSNR=20\times \rm{lg} \frac{\max \{I\}}{\sqrt{MSE}}, \] де \[ MSE=\frac{1}{H\times W}\sum_{i=1}^W\sum_{j=1}^H|I_{i,j}-K_{i,j}|^2. \] У разі порівняння повнокольорових зображень, використовуємо суму MSE по кожній кольоровій компоненті і поділемо на 3.

Отримані результати відображають показники часу обробки та PSNR для оброблених зображень до розмірів починаючи з 20% оригінального розміру, закінчуючи 200%.

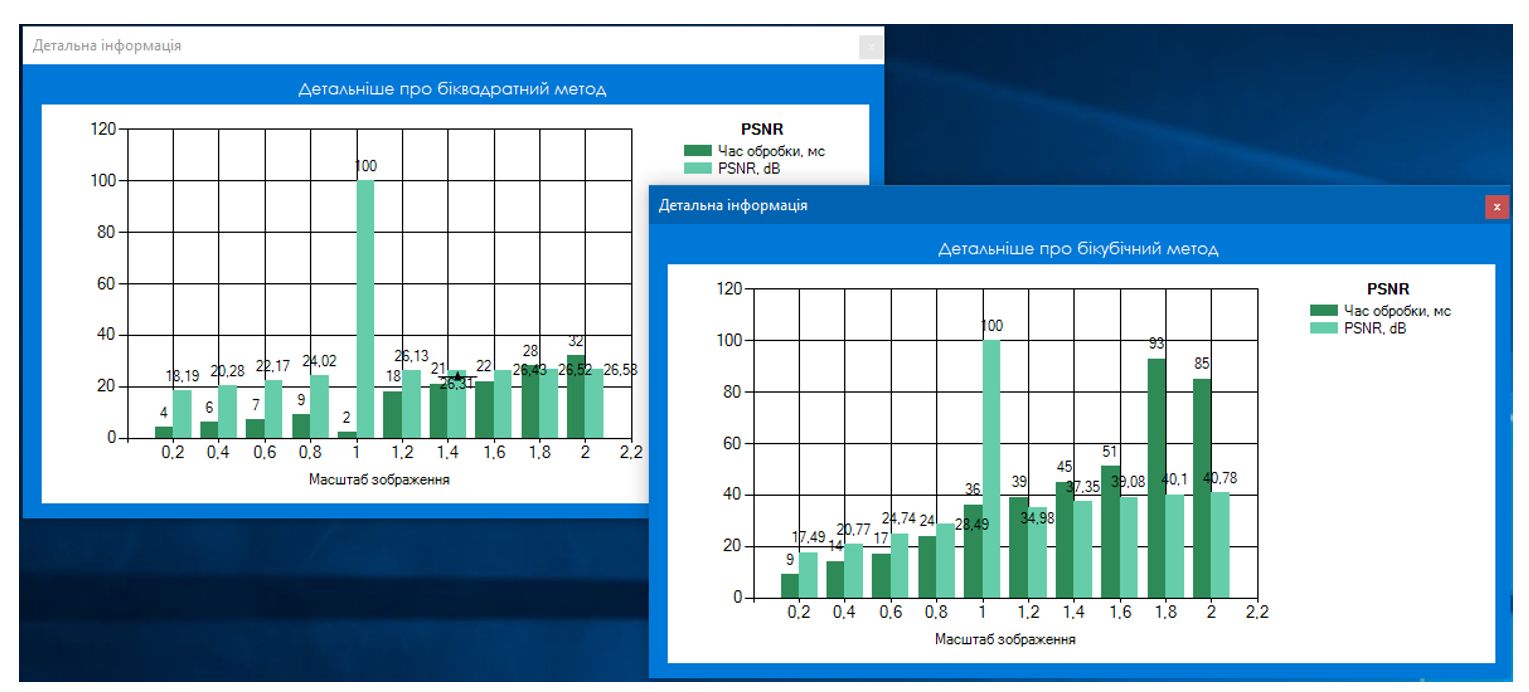Результат обробки першого зображення

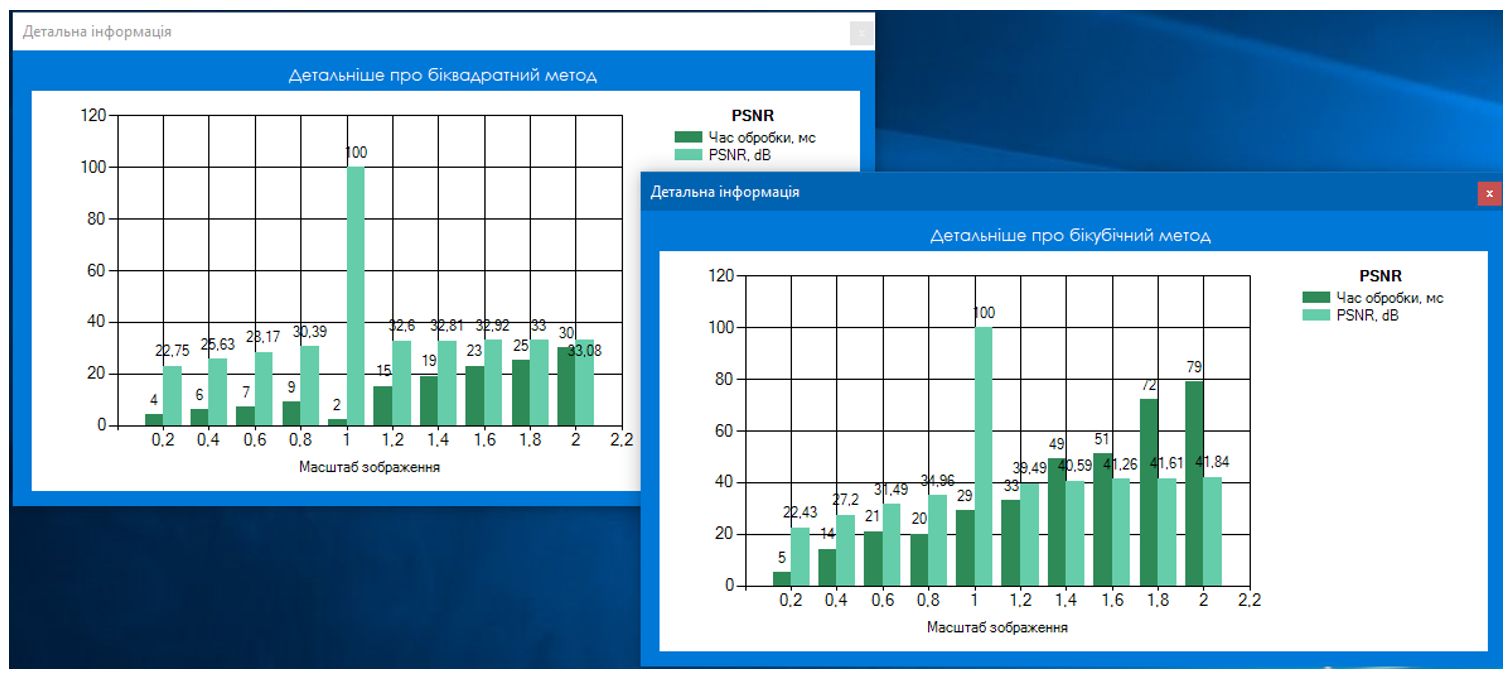Результат обробки другого зображення

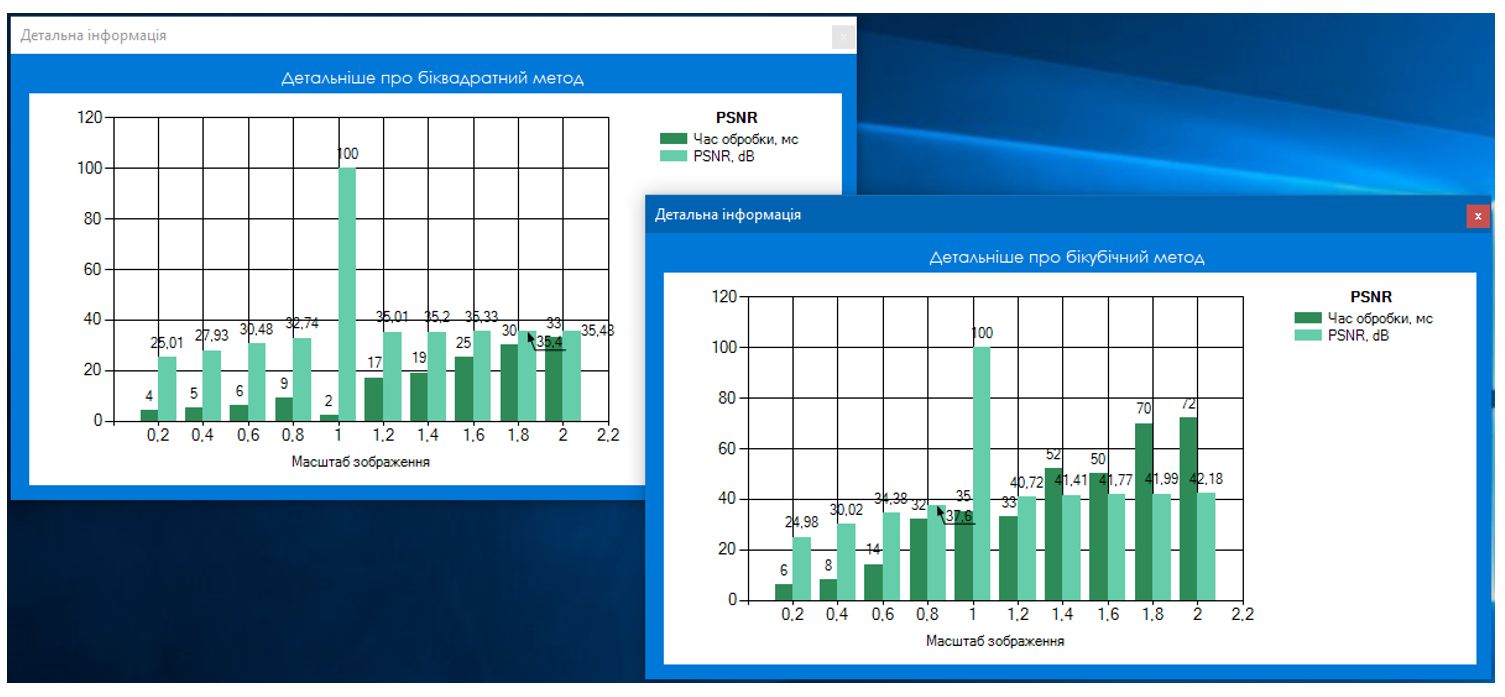Результат обробки третього зображення

Проаналізувавши отримані результати можна зробити висновок, що при бікубічній інтерполяції показник PSNR зазвичай вищий, ніж при білінійній. Чим більша схожість між порівнюваними зображеннями, тим менше величина MSE, а отже показник PSNR більший. На основі цього можна зробити висновок про те, що зображення отримане при бікубічній інтерполяції є більш якісним і близьким до оригіналу, проте також видно, що витрати часу на обробку зображення є більшими у порівнянні з білінійною інтерполяцією.
Але, треба зазначити, що апроксимативні характеристики наведених тензорний добутків як білінійного, так і бікубічного, мають один і той же порядок, хоча у другому випадку можна отримати більш якісні результати.
Наведемо на прикладі біквадратних сплайнів один з підходів, який дозволяє це зробити.
Чому біквадратні, а не бікубічні. З точки зору теорії аппроксимацій, чим вище порядок сплайну, тим краще якість наближення диференційованої функції, але зображення представляє собою функцію, яка не просто не має похідної, але і не є неперервною. Таким чином підвищення порядку сплайну не гарантує якість опису первісних даних. Так для нашої задачі використання біквадратних сплайнів більш ефективне, ніж бікубічних.
Розглянемо опис поверхні тензорним добутком квадратних В-сплайнів на квадратній решітці \(\mathbf{i}=(i,j)\), де \(\mathbf{i}\in Z^2\) \[ \textbf{s}_{2,2}(\textbf{P},\textbf{u})=\sum_{\textbf{i}\in Z^2}\textbf{P}_{\textbf{i}} N_{2,2}(\textbf{u}-\textbf{i}), \] де \(\mathbf{u}=(u,v)\in R^2\) і \[N_{2,2}(\textbf{u}-\textbf{i} h)\equiv B_2(u-i)B_2(v-j)\] нормалізований тензорний добуток В-сплайнів порядку 2 з вузлами \(\mathbf{i}=(i,j)\) по решітці з кроком 1.
Для \(\mathbf{u}\in [i,j]×[i+1,j+1]\) маємо \[ \textbf{S}_{2,2}(\textbf{P},\textbf{u})=\sum_{\textbf{i}\in Z^2}\textbf{P}_{\textbf{i}} N_{2,2}(\textbf{u}-\textbf{i})= \textbf{P}_{i,j}\frac{1+2(u-i)-2\left(u-i\right)^2}{2}\cdot \frac{1+2(v-j)-2\left(v-j\right)^2}{2}+ \] \[ +\textbf{P}_{i-1,j}\frac{\left(1-(u-i)\right)^2}{2}\cdot \frac{1+2(v-j)-2\left(v-j\right)^2}{2} +\textbf{P}_{i+1,j}\frac{\left(u-i\right)^2}{2}\,\, \frac{1+2(v-j)-2\left(v-j\right)^2}{2}+ \] \[ +\textbf{P}_{i,j-1}\frac{1+2(u-i)-2\left(u-i\right)^2}{2}\cdot \frac{\left(1-(v-j)\right)^2}{2}+ \] \[ +\textbf{P}_{i-1,j-1}\frac{\left(1-(u-i)\right)^2}{2}\cdot \frac{\left(1-(v-j)\right)^2}{2} +\textbf{P}_{i+1,j-1}\frac{\left(u-i\right)^2}{2}\cdot \frac{\left(1-(v-j)\right)^2}{2}+ \] \[ +\textbf{P}_{i,j+1}\frac{1+2(u-i)-2\left(u-i\right)^2}{2}\cdot \frac{\left(v-j\right)^2}{2}+ \textbf{P}_{i-1,j+1}\frac{\left(1-(u-i)\right)^2}{2}\cdot \frac{\left(v-j\right)^2}{2} +\textbf{P}_{i+1,j+1}\frac{\left(u-i\right)^2}{2}\cdot \frac{\left(v-j\right)^2}{2}. \] В матричній формі дане співвідношення буде мати наступний вигляд \[ \textbf{S}_{2,2}(\textbf{P},\textbf{u}) \: = \: \left[ \begin{array}{ccc} 1 & u-i & \left(u-i\right)^2 \end{array} \right] \mathbb{M}_{2,2}\mathbb{P}_{2,2}\mathbb{M}^T_{2,2} \left[ \begin{array}{c} 1 \\v-j \\\left(v-j\right)^2 \end{array} \right] \] де \( \mathbb{M}_{2,2}\) матриця розміру \(3 \times 3\) \[ \mathbb{M}_{2,2} \: = \: \frac{1}{2} \left[ \begin{array}{rrr} 1 & 1 & 0 \\ -2 & 2 & 0 \\ 1 & -2 & 1 \end{array} \right] \] та \[ \mathbb{P}_{2,2} \: = \: \left[ \begin{array}{lll} \textbf{P}_{i-1,j-1} & \textbf{P}_{i,j-1} & \textbf{P}_{i+1,j-1} \\ \textbf{P}_{i-1,j} & \textbf{P}_{i,j} & \textbf{P}_{i+1,j} \\ \textbf{P}_{i-1,j+1} & \textbf{P}_{i,j+1} & \textbf{P}_{i+1,j+1} \end{array} \right] \] Звідси отримуємо значення в точці \(\left(\left(i+\frac{1}{2}\right),\left(j+\frac{1}{2}\right)\right)\): \begin{equation}\label{tenz0} \textbf{S}_{2,2}\left(\textbf{P},\left(i+\frac{1}{2}\right),\left(j+\frac{1}{2}\right)\right)={\frac {9}{16}}\,\textbf{P}_{{i,j}}+{\frac {3}{32}} \left( \,\textbf{P}_{{i,j+1}} +\textbf{P}_{{i,j-1}}+\textbf{P}_{{i+1,j}}+\textbf{P}_{{i-1,j}} \right)+{\frac {1}{64} }\left(\,\textbf{P}_{{i-1,j+1}}+ \textbf{P}_{{i-1,j-1}}+\textbf{P}_{{i+1,j+1}}+\textbf{P}_{{i+1,j1}}\right) =\textbf{P}_{{i,j}}-\frac{1}{64}\Delta\textbf{P}_{{i,j}}, \end{equation} де \[ \Delta\textbf{P}_{{i,j}}=28\textbf{P}_{{i,j}}-6\left( \,\textbf{P}_{{i,j+1}} +\textbf{P}_{{i,j-1}}+\textbf{P}_{{i+1,j}}+\textbf{P}_{{i-1,j}} \right) -\left( \,\textbf{P}_{{i+1,j+1}} +\textbf{P}_{{i+1,j-1}}+\textbf{P}_{{i-1,j-1}}+\textbf{P}_{{i-1,j+1}} \right). \] Нехай поверхня \(\textbf{f}\) задана точками \[f_{\textbf{i} +1/2}=f\left(\left(i+\frac{1}{2}\right)h,\left(j+\frac{1}{2}\right)h\right), (i,j=0,\pm1,\pm2,\ldots)\] i \begin{equation}\label{tenz1} \textbf{P}_{\textbf{i}} (\textbf{f})=f_{\textbf{i} +1/2}-\sum_{\nu=1}^{\infty} \left(-\frac{1}{64}\right)^\nu \Delta^{\nu}f_{\textbf{i} +1/2}, \end{equation} де \(\Delta^{\nu}f_{\textbf{i} +1/2}=\Delta\left(\Delta^{\nu-1}f_{\textbf{i} +1/2}\right)\).
Тоді з (\ref{tenz0}) отримуємо \[ \textbf{S}_{2,2}\left(\textbf{P(f)},\left(i+\frac{1}{2}\right)h,\left(j+\frac{1}{2}\right)h\right) = f_{\textbf{i} +1/2}-\sum_{\nu=1}^{\infty} \left(-\frac{1}{64}\right)^\nu \Delta^{\nu}f_{\textbf{i} +1/2}-\frac{1}{64}\Delta\left(f_{\textbf{i} +1/2}-\sum_{\nu=1}^{\infty} \left(-\frac{1}{64}\right)^\nu \Delta^{\nu}f_{\textbf{i} +1/2}\right) \] \[ = f_{\textbf{i} +1/2}-\sum_{\nu=1}^{\infty} \left(-\frac{1}{64}\right)^\nu \Delta^{\nu}f_{\textbf{i} +1/2}-\frac{1}{64}\Delta f_{\textbf{i} +1/2}+\sum_{\nu=2}^{\infty} \left(-\frac{1}{64}\right)^\nu \Delta^{\nu}f_{\textbf{i} +1/2}= f_{\textbf{i} +1/2}-\sum_{\nu=1}^{\infty} \left(-\frac{1}{64}\right)^\nu \Delta^{\nu}f_{\textbf{i} +1/2}+\sum_{\nu=1}^{\infty} \left(-\frac{1}{64}\right)^\nu \Delta^{\nu}f_{\textbf{i} +1/2}= f_{\textbf{i} +1/2}. \] Таким чином, якщо коефіцієнти сплайну \(\textbf{P}_{\textbf{i}}\) визначаються рівностями (\ref{tenz1}), то для всіх \(\textbf{i}\) виконуються співвідношення \[\textbf{S}_{2,2}\left(\textbf{P(f)},\left(i+\frac{1}{2}\right)h,\left(j+\frac{1}{2}\right)h\right) = f_{\textbf{i} +1/2},\] тобто, при визначенні коефіцієнтів рівностями (\ref{tenz1}) сплайн \(\textbf{S}_{2,2}(\textbf{f},\textbf{u})\) інтерполює функцію \(\textbf{f}\) у рівновіддалених точках \(\left(\textbf{i} +\frac{1}{2}\right) h\).
Нехай \begin{equation}\label{tenz2} \textbf{P}^1_{\textbf{i}} =\textbf{P}^1_{\textbf{i}} (\textbf{f})=f_{\textbf{i} +1/2}+\frac{1}{64}\Delta f_{\textbf{i} +1/2}= \end{equation} \[ ={\frac {23}{16}}\,f_{{i+1/2,j+1/2}}-{\frac {3}{32}}\left(f_{{i+1/2,j+3/2}}+f_{{i+1/2,j-1/2}}+f_{{i+3/2,j+1/2}}+f_{{i-1/2, j+1/2}}\right) -{\frac {1}{64}}\left(f_{{i-1/2,j+3/2}}+f_{{i-1/2,j-1/2}}+f_{{i+3/2,j-1/2}}+f_{{i+3/2,j+3/2}}\right), \] відповідний сплайн позначемо через \begin{equation}\label{tenz3} \textbf{S}_{2,2}(\textbf{P}^1,\textbf{u})=\sum_{\textbf{i}\in Z^2}\textbf{P}^1_{\textbf{i}} N_{2,2}(\textbf{u}-\textbf{i} h). \end{equation} Тоді \[ \textbf{S}_{2,2}\left(\textbf{P}^1,\left(i+\frac{1}{2}\right)h,\left(j+\frac{1}{2}\right)h\right) = f_{\textbf{i} +1/2}+\frac{1}{4096}\Delta^2f_{\textbf{i} +1/2}. \] Якщо функція \(f(\textbf{u})\) має всі неперервні похідні до четвертого порядку включно, то існує точка \({\textbf{u}}_0\in [ih,jh]\times [(i+1)h,(j+1)h]\) така, що \[ \textbf{S}_{2,2}\left(\textbf{P}^1,\left(i+\frac{1}{2}\right)h,\left(j+\frac{1}{2}\right)h\right) = f_{\textbf{i} +1/2}+\frac{3}{8}h^4 \left(\left.\frac{\partial^4 f }{\partial u^4 }\right|_{\textbf{u}_0}+2\left.\frac{\partial^4 f }{\partial u^2 \partial v^2}\right|_{\textbf{u}_0}+\left.\frac{\partial^4 f }{\partial v^4 }\right|_{\textbf{u}_0}\right). \] Тобто, отриманий сплайн асимптотично співпадає з інтерполяційним з точністю до \(O(h^4)\).
Якщо використати дану конструкцію до задачі масштабування зображень, то отримаємо досить непогані результати.
Для проведення експериментів використовувалася колекція TID2008, яка створена Eastman Kodak і використовується для тестування і перевірки якості різних методів обробки зображень, до якої було додано зображення Lenna (останнє в наведеній колекції), яке є, по суті, стандартом для такого роду завдань .

Тестова колекція

Наведені результати отримані при послідовному збільшенні тестового зображення в два рази, після чого воно приводилося до вихідного розміру тим же способом, яким збільшувалася. Вийшло зображення порівнювався з оригіналом.
Природно порівняти отриманий результат з іншими методами зміни геометричних розмірів (Image Resampling).

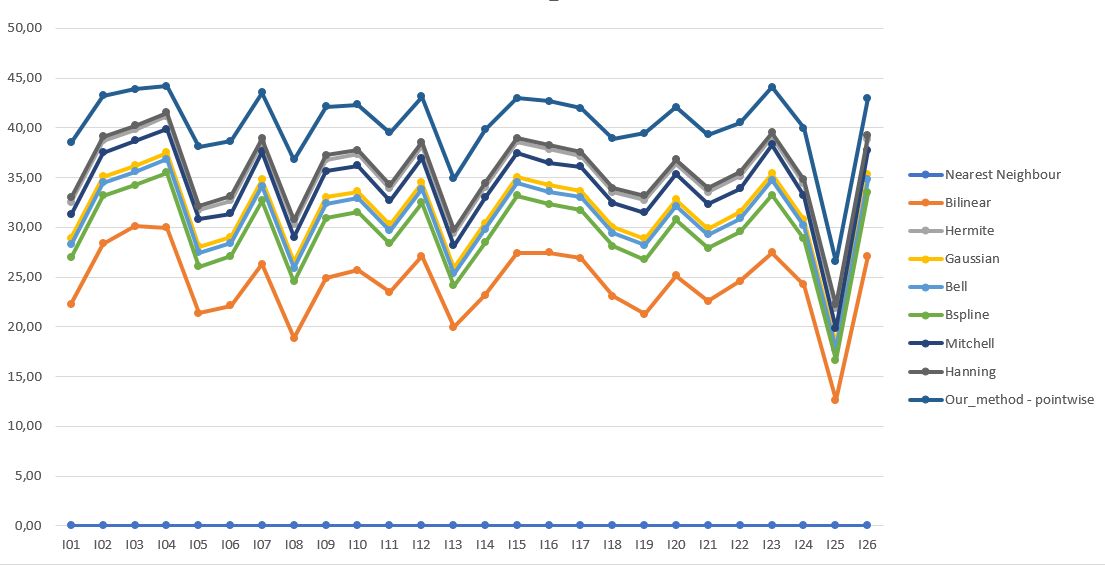Порівняння якості алгоритмів масштабування зображень.

Таким чином, нами отримано метод локальних майже інтерполяційних сплайнів двох змінних. Якщо первісних даних досить багато, то використання інтерполяційного сплайну, побудованого на розрідженій сітці, призводить до втрати інформації. Щоб уникнути таких втрат, рекомендується використовувати математичні інструменти, які об'єднують, агрегують дані. Такі інструменти включають в себе сплайни, які зберігають середнє значення функції, що апроксимується, тобто якщо апроксимуюча поверхня визначена на прямокутній решітці \((ih, jH) \), де \((i, j) \in Z ^ 2 \), то кажуть, що сплайн \(s \) зберігає середнє значення функції \(f \) на множинах \([ih, (i + 1) h] × [j H, (j + 1) H] \), якщо \[ \frac{1}{h\cdot H}\int_{v=ih}^{(i+1)h}\int_{u=jH}^{(j+1)H}f(u,v)dudv= \frac{1}{h\cdot H}\int_{v=ih}^{(i+1)h}\int_{u=jH}^{(j+1)H}s(u,v)dudv. \] Для будь-якого біквадратного сплайну, отримуємо \[ \frac{1}{hH}\int_{u=ih}^{(i+1)h}\int_{v=jH}^{(j+1)H}\textbf{S}_{2,2}(\textbf{P},\textbf{u})d\textbf{u}= \frac{1}{9}\,\textbf{P}_{{i-1,j}}+\frac{1}{36}\,\textbf{P}_{{i-1,j-1}}+\frac{4}{9}\,\textbf{P}_{{i,j}}+\frac{1}{9}\,\textbf{P}_{{i,j-1}}+\frac{1}{9}\, \textbf{P}_{{i,j+1}}+\frac{1}{9}\,\textbf{P}_{{i+1,j}}+\frac{1}{36}\,\textbf{P}_{{i-1,j+1}}+\frac{1}{36}\,\textbf{P}_{{i+1,j-1}}+\frac{1}{36}\,\textbf{P}_{{i+1,j+1}}= \] \[ \textbf{P}_{{i,j}}+ \frac{1}{9}\, \left(\textbf{P}_{{i-1,j}}+ \textbf{P}_{{i,j-1}}+ \textbf{P}_{{i,j+1}}+ \textbf{P}_{{i+1,j}}- 4\,\textbf{P}_{{i,j}} \right)+ \frac{1}{36}\,\left( \textbf{P}_{{i-1,j-1}}+ \textbf{P}_{{i-1,j+1}}+ \textbf{P}_{{i+1,j-1}}+ \textbf{P}_{{i+1,j+1}}- 4\,\textbf{P}_{{i,j}} \right)=\textbf{P}_{{i,j}}+\frac{1}{36}\,\tilde{\Delta}^2\textbf{P}_{{i,j}}, \] де \[ \tilde{\Delta}^2\textbf{P}_{{i,j}}= 4\left(\textbf{P}_{{i-1,j}}+ \textbf{P}_{{i,j-1}}+ \textbf{P}_{{i,j+1}}+ \textbf{P}_{{i+1,j}}- 4\,\textbf{P}_{{i,j}} \right)+ \\ \left( \textbf{P}_{{i-1,j-1}}+ \textbf{P}_{{i-1,j+1}}+ \textbf{P}_{{i+1,j-1}}+ \textbf{P}_{{i+1,j+1}}- 4\,\textbf{P}_{{i,j}} \right). \] Для інтегрованої функції \(f (u, v) \) покладемо \[ \textbf{P}^*_{\textbf{i}}=\textbf{P}^*_{i,j}=\frac{1}{hH}\int_{u=ih}^{(i+1)h}\int_{v=jH}^{(j+1)H}f(u,v)dudv. \] Тоді, після простих, але громіздких перетворень, отримуємо \[ \tilde{\Delta}^2\textbf{P}^*_{{i,j}}=6\,h^2\,\left.\frac{\partial^2 f(x,y)}{\partial x^2}\right|_{x=(i+1/2)h,y=(j+1/2)H}+ 6\,H^2\,\left.\frac{\partial^2 f(x,y)}{\partial y^2}\right|_{x=(i+1/2)h,y=(j+1/2)H}+\] \[ \frac{3}{4}\left( h^4\,\left.\frac{\partial^4 f(x,y)}{\partial x^4}\right|_{x=(i+1/2)h,y=(j+1/2)H}+ 2\,h^2H^2\,\left.\frac{\partial^4 f(x,y)}{\partial x^2\partial y^2}\right|_{x=(i+1/2)h,y=(j+1/2)H}+ H^4\,\left.\frac{\partial^4 f(x,y)}{\partial y^4}\right|_{x=(i+1/2)h,y=(j+1/2)H}\right)+O\left(\left(\max\{h,H\}\right)^5\right). \] Розглянемо сплайн (двовимірний сплайн Шенберга) \( \textbf{S}_{2,2}(\textbf{P}^*,\textbf{u}). \)
Розглянемо сплайн \begin{equation}\label{s2} \textbf{S}^*_{2,2}\left(\textbf{P}^*_{\textbf{i}}-\frac{1}{36}\,\tilde{\Delta}^2\textbf{P}^*_{\textbf{i}},\textbf{u}\right)= \sum_{\textbf{i}\in Z^2}\left(\textbf{P}^*_{\textbf{i}}-\frac{1}{36}\,\tilde{\Delta}^2\textbf{P}^*_{\textbf{i}}\right)N_{2,2}(\textbf{u}-\textbf{i h} ). \end{equation} Тоді \[ \frac{1}{hH}\int_{u=ih}^{(i+1)h}\int_{v=jH}^{(j+1)H}\textbf{S}^*_{2,2}\left(\textbf{P}^*_{\textbf{i}}-\frac{1}{36}\,\tilde{\Delta}^2\textbf{P}^*_{\textbf{i}},\textbf{u}\right)d\textbf{u}= \textbf{P}^*_{\textbf{i}}-\frac{1}{36}\,\tilde{\Delta}^2\textbf{P}^*_{\textbf{i}}+ \frac{1}{36}\,\tilde{\Delta}^2\left( \textbf{P}^*_{\textbf{i}}-\frac{1}{36}\,\tilde{\Delta}^2\textbf{P}^*_{\textbf{i}} \right)= \textbf{P}^*_{\textbf{i}}-\frac{1}{1296}\,\tilde{\Delta}^2\left(\tilde{\Delta}^2\textbf{P}^*_{\textbf{i}}\right)= \textbf{P}^*_{\textbf{i}}-\frac{1}{1296}\,\tilde{\Delta}^4\left(\textbf{P}^*_{\textbf{i}}\right). \] При цьому, \[ \tilde{\Delta}^4\textbf{P}^*_{{i,j}}= 36\left( h^4\,\left.\frac{\partial^4 f(x,y)}{\partial x^4}\right|_{x=(i+1/2)h,y=(j+1/2)H}+ 2\,h^2H^2\,\left.\frac{\partial^4 f(x,y)}{\partial x^2\partial y^2}\right|_{x=(i+1/2)h,y=(j+1/2)H}+ H^4\,\left.\frac{\partial^4 f(x,y)}{\partial y^4}\right|_{x=(i+1/2)h,y=(j+1/2)H}\right)+O\left(\left(\max\{h,H\}\right)^5\right). \] Таким чином, з точністю до \(O\left(\left(\max\{h,H\}\right)^4\right)\) сплайн (\ref{s2}) є інтерполяційним у середньому.
Проблема. Побудова біквадратних сплайна на множині \(\textbf {u} \in [ih, jH] \times [(i + 1) h, (j + 1) H] \) передбачає наявність інформації про функцію, що апроксимується, на всіх сусідніх прямокутниках. На межі області визначення такої інформації немає, тому потрібно якимось чином її отримати. Цим і займемося.
Розглянемо квадратичний поліном \begin{equation}\label{p2} Q(u,v)=a_{0,0}+a_{1,0}u+a_{0,1}v+a_{2,0}u^2+2a_{1,1}uv+a_{0,2}v^2 \end{equation} і розглянемо задачу \begin{equation}\label{mnk} \varepsilon=\sum_{\nu=-1}^1\sum_{\mu=-1}^1\left(\textbf{P}^*_{i+\nu,j+\mu}-\frac{1}{hH}\int_{u=(i+\nu) h}^{(i+\nu+1)h}\int_{v=(j+\mu) H}^{(j+\mu+1)H}Q(u,v)dudv\right)^2\to \min. \end{equation} де, як і раніше, \[ \textbf{P}^*_{\textbf{i}}=\textbf{P}^*_{i,j}=\frac{1}{hH}\int_{u=ih}^{(i+1)h}\int_{v=jH}^{(j+1)H}f(u,v)dudv \] Вирішуючи систему рівнянь \[ \frac{\partial \varepsilon}{\partial a_{\nu,\mu}}=0, (\nu,\mu=0,1,2, \nu+\mu\le 2), \] маємо \[ a_{0,0} = \frac{1}{144}\left(25\,\textbf{P}^*_{i-1,j-1}+40\,\textbf{P}^*_{i-1,j}-17\,\textbf{P}^*_{i-1,j+1}+40\,\textbf{P}^*_{i,j-1}+64\,\textbf{P}^*_{i,j}+16\,\textbf{P}^*_{i,j+1}-17\,\textbf{P}^*_{i+1,j-1}+16\,\textbf{P}^*_{i+1,j}-23\,\textbf{P}^*_{i+1,j+1}\right),\\ a_{1,0} = -\frac{1}{24\,h}(11\,\textbf{P}^*_{i-1,j-1}+5\,\textbf{P}^*_{i-1,j+1}-3\,\textbf{P}^*_{i+1,j-1}+3\,\textbf{P}^*_{i+1,j+1}-8\,\textbf{P}^*_{i,j-1}+8\,\textbf{P}^*_{i-1,j}-8\,\textbf{P}^*_{i,j}-8\,\textbf{P}^*_{i,j+1}),\\ a_{0,1} = -\frac{1}{24\,H}(8\,\textbf{P}^*_{i,j-1}+11\,\textbf{P}^*_{i-1,j-1}-8\,\textbf{P}^*_{i-1,j}-3\,\textbf{P}^*_{i-1,j+1}-8\,\textbf{P}^*_{i+1,j}-8\,\textbf{P}^*_{i,j}+5\,\textbf{P}^*_{i+1,j-1}+3\,\textbf{P}^*_{i+1,j+1}),\\ a_{2,0} = \frac{1}{6\,h^2}(-2\,\textbf{P}^*_{i,j-1}+\textbf{P}^*_{i-1,j-1}+\textbf{P}^*_{i-1,j}+\textbf{P}^*_{i-1,j+1}+\textbf{P}^*_{i+1,j}-2\,\textbf{P}^*_{i,j}-2\,\textbf{P}^*_{i,j+1}+\textbf{P}^*_{i+1,j-1}+\textbf{P}^*_{i+1,j+1}),\\ a_{1,1} = \frac{1}{8\,hH}(\textbf{P}^*_{i-1,j-1}-\textbf{P}^*_{i-1,j+1}-\textbf{P}^*_{i+1,j-1}+\textbf{P}^*_{i+1,j+1}), \\ a_{0,2} = \frac{1}{6\,H^2}(\textbf{P}^*_{i,j-1}+\textbf{P}^*_{i-1,j-1}-2\,\textbf{P}^*_{i-1,j}+\textbf{P}^*_{i-1,j+1}-2\,\textbf{P}^*_{i+1,j}-2\,\textbf{P}^*_{i,j}+\textbf{P}^*_{i,j+1}+\textbf{P}^*_{i+1,j-1}+\textbf{P}^*_{i+1,j+1}). \\ \] Тепер обчислимо середні значення полінома (\ref{p2}) з отриманими коефіцієнтами, на комірках, які прилягають до \([(i+\nu)h,(j+\mu)H]\times [(i+\nu+1)h,(j+\mu+1)H], \nu,\mu=-1,0,1\) \[ \tilde{\textbf{P}}_{i+\nu,j+\mu}=\frac{1}{hH}\int_{u=(i+\nu)h}^{(i+\nu+1)h}\int_{v=(j+\mu)H}^{(j+\mu+1)H}Q(u,v)dudv \] У результаті, отримуємо \[ \tilde{\textbf{P}}_{i-2, j-2}=\frac{1}{9}\left( 26 \textbf{P}^*_{i-1, j-1} - \textbf{P}^*_{i-1, j} + 2 \textbf{P}^*_{i-1, j+1} - \textbf{P}^*_{i, j-1} - 19 \textbf{P}^*_{i, j} - 7 \textbf{P}^*_{i, j+1} + 2 \textbf{P}^*_{i+1, j-1} - 7 \textbf{P}^*_{i+1, j} + 14 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i-2, j-1}=\frac{1}{18}\left( 31 \textbf{P}^*_{i-1, j-1} + 16 \textbf{P}^*_{i-1, j} + 14 \textbf{P}^*_{i-1, j+1} - 14 \textbf{P}^*_{i, j-1} - 20 \textbf{P}^*_{i, j} - 20 \textbf{P}^*_{i, j+1} + \textbf{P}^*_{i+1, j-1} + 4 \textbf{P}^*_{i+1, j} + 13 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i-2, j}=\frac{1}{9}\left( 8 \textbf{P}^*_{i-1, j-1} + 11 \textbf{P}^*_{i-1, j} + 8 \textbf{P}^*_{i-1, j+1} - 10 \textbf{P}^*_{i, j-1} - 7 \textbf{P}^*_{i, j} - 10 \textbf{P}^*_{i, j+1} + 2 \textbf{P}^*_{i+1, j-1} + 5 \textbf{P}^*_{i+1, j} + 2 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i-2, j+1}=\frac{1}{18}\left( 14 \textbf{P}^*_{i-1, j-1} + 16 \textbf{P}^*_{i-1, j} + 31 \textbf{P}^*_{i-1, j+1} - 20 \textbf{P}^*_{i, j-1} - 20 \textbf{P}^*_{i, j} - 14 \textbf{P}^*_{i, j+1} + 13 \textbf{P}^*_{i+1, j-1} + 4 \textbf{P}^*_{i+1, j} + \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i-2, j+2}=\frac{1}{9}\left( 2 \textbf{P}^*_{i-1, j-1} - \textbf{P}^*_{i-1, j} + 26 \textbf{P}^*_{i-1, j+1} - 7 \textbf{P}^*_{i, j-1} - 19 \textbf{P}^*_{i, j} - \textbf{P}^*_{i, j+1} + 14 \textbf{P}^*_{i+1, j-1} - 7 \textbf{P}^*_{i+1, j} + 2 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i-1, j-2}=\frac{1}{18}\left( 31 \textbf{P}^*_{i-1, j-1} - 14 \textbf{P}^*_{i-1, j} + \textbf{P}^*_{i-1, j+1} + 16 \textbf{P}^*_{i, j-1} - 20 \textbf{P}^*_{i, j} + 4 \textbf{P}^*_{i, j+1} + 7 \textbf{P}^*_{i+1, j-1} - 20 \textbf{P}^*_{i+1, j} + 13 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i -1, j+2}=\frac{1}{18}\left( \textbf{P}^*_{i-1, j-1} - 14 \textbf{P}^*_{i-1, j} + 31 \textbf{P}^*_{i-1, j+1} + 4 \textbf{P}^*_{i, j-1} - 20 \textbf{P}^*_{i, j} + 16 \textbf{P}^*_{i, j+1} + 13 \textbf{P}^*_{i+1, j-1} - 20 \textbf{P}^*_{i+1, j} + 14 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i, j-2}=\frac{1}{9}\left( 8 \textbf{P}^*_{i-1, j-1} - 10 \textbf{P}^*_{i-1, j} + 2 \textbf{P}^*_{i-1, j+1} + 11 \textbf{P}^*_{i, j-1} - 7 \textbf{P}^*_{i, j} + 5 \textbf{P}^*_{i, j+1} + 8 \textbf{P}^*_{i+1, j-1} - 10 \textbf{P}^*_{i+1, j} + 2 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i, j+2}=\frac{1}{9}\left( 2 \textbf{P}^*_{i-1, j-1} - 10 \textbf{P}^*_{i-1, j} + 8 \textbf{P}^*_{i-1, j+1} + 5 \textbf{P}^*_{i, j-1} - 7 \textbf{P}^*_{i, j} + 11 \textbf{P}^*_{i, j+1} + 2 \textbf{P}^*_{i+1, j-1} - 10 \textbf{P}^*_{i+1, j} + 8 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i+1, j-2}=\frac{1}{18}\left( 7 \textbf{P}^*_{i-1, j-1} - 20 \textbf{P}^*_{i-1, j} +13 \textbf{P}^*_{i-1, j+1} + 16\textbf{P}^*_{i, j-1} - 20 \textbf{P}^*_{i, j} + 4 \textbf{P}^*_{i, j+1} + 31 \textbf{P}^*_{i+1, j-1} - 14 \textbf{P}^*_{i+1, j} + \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i+1, j+2}=\frac{1}{18}\left( 13\textbf{P}^*_{i-1, j-1} - 20 \textbf{P}^*_{i-1, j} + 7 \textbf{P}^*_{i-1, j+1} + 4 \textbf{P}^*_{i, j-1} - 20 \textbf{P}^*_{i, j} + 16 \textbf{P}^*_{i, j+1} + \textbf{P}^*_{i+1, j-1} - 14 \textbf{P}^*_{i+1, j} + 31 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i+2, j-2}=\frac{1}{9}\left( 2 \textbf{P}^*_{i-1, j-1} - 7 \textbf{P}^*_{i-1, j} + 14 \textbf{P}^*_{i-1, j+1} - \textbf{P}^*_{i, j-1} - 19 \textbf{P}^*_{i, j} - 7 \textbf{P}^*_{i, j+1} + 26 \textbf{P}^*_{i+1, j-1} - \textbf{P}^*_{i+1, j} + 2 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i+2, j-1}=\frac{1}{18}\left( \textbf{P}^*_{i-1, j-1} + 4 \textbf{P}^*_{i-1, j} + 13 \textbf{P}^*_{i-1, j+1} - 14 \textbf{P}^*_{i, j-1} - 20 \textbf{P}^*_{i, j} - 20 \textbf{P}^*_{i, j+1} + 31 \textbf{P}^*_{i+1, j-1} + 16 \textbf{P}^*_{i+1, j} + 7 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i+2, j}=\frac{1}{9}\left( 2 \textbf{P}^*_{i-1, j-1} + 5 \textbf{P}^*_{i-1, j} + 2 \textbf{P}^*_{i-1, j+1} - 10 \textbf{P}^*_{i, j-1} - 7 \textbf{P}^*_{i, j} - 10 \textbf{P}^*_{i, j+1} + 8 \textbf{P}^*_{i+1, j-1} + 11 \textbf{P}^*_{i+1, j} + 8 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i+2, j+1}=\frac{1}{18}\left( 13\,\textbf{P}^*_{i-1, j-1} + 4\, \textbf{P}^*_{i-1, j} + \textbf{P}^*_{i-1, j+1} - 20\, \textbf{P}^*_{i, j-1} - 20\, \textbf{P}^*_{i, j} - 14\, \textbf{P}^*_{i, j+1} + 14\, \textbf{P}^*_{i+1, j-1} + 16\, \textbf{P}^*_{i+1, j} + 31 \textbf{P}^*_{i+1, j+1}\right),\\ \tilde{\textbf{P}}_{i+ 2, j+2}=\frac{1}{9}\left( 14 \textbf{P}^*_{i-1, j-1} - 7 \textbf{P}^*_{i-1, j} + 2 \textbf{P}^*_{i-1, j+1} - 7 \textbf{P}^*_{i, j-1} - 19 \textbf{P}^*_{i, j} - \textbf{P}^*_{i, j+1} + 2 \textbf{P}^*_{i+1, j-1} - \textbf{P}^*_{i+1, j} + 26 \textbf{P}^*_{i+1, j+1}\right). \] Використовуючи отримані значення в якості відсутніх біля межі, отримуємо можливість побудувати біквадратний сплайн за даними \(\left \{\textbf {P} ^ * _ {i, j} \right \} _ {i = 0, j = 0} ^ {n, m} \), так для знаходження відсутніх даних уздовж лівого краю досить використовувати значення \[ \tilde{\textbf{P}}_{-1, j}=\frac{1}{9}\left( 8 \textbf{P}^*_{0, j-1} + 11 \textbf{P}^*_{0, j} + 8 \textbf{P}^*_{0, j+1} - 10 \textbf{P}^*_{1, j-1} - 7 \textbf{P}^*_{1, j} - 10 \textbf{P}^*_{1, j+1} + 2 \textbf{P}^*_{2, j-1} + 5 \textbf{P}^*_{2, j} + 2 \textbf{P}^*_{2, j+1}\right), \] уздовж правого краю \[ \tilde{\textbf{P}}_{n+1, j}=\frac{1}{9}\left( 2 \textbf{P}^*_{n-2, j-1} + 5 \textbf{P}^*_{n-2, j} + 2 \textbf{P}^*_{n-2, j+1} - 10 \textbf{P}^*_{n-1, j-1} - 7 \textbf{P}^*_{n-1, j} - 10 \textbf{P}^*_{n-1, j+1} + 8 \textbf{P}^*_{n, j-1} + 11 \textbf{P}^*_{n, j} + 8 \textbf{P}^*_{n, j+1}\right), \] знизу \[ \tilde{\textbf{P}}_{i, -1}=\frac{1}{9}\left( 8 \textbf{P}^*_{i-1, 0} - 10 \textbf{P}^*_{i-1, 1} + 2 \textbf{P}^*_{i-1, 2} + 11 \textbf{P}^*_{i, 0} - 7 \textbf{P}^*_{i, 1} + 5 \textbf{P}^*_{i, 2} + 8 \textbf{P}^*_{i+1, 0} - 10 \textbf{P}^*_{i+1, 1} + 2 \textbf{P}^*_{i+1, 2}\right), \] зверху \[ \tilde{\textbf{P}}_{i, m+1}=\frac{1}{9}\left( 2 \textbf{P}^*_{i-1, m-2} - 10 \textbf{P}^*_{i-1, m-1} + 8 \textbf{P}^*_{i-1, m} + 5 \textbf{P}^*_{i, m-2} - 7 \textbf{P}^*_{i, m-1} + 11 \textbf{P}^*_{i, m} + 2 \textbf{P}^*_{i+1, m-2} - 10 \textbf{P}^*_{i+1, m-1} + 8 \textbf{P}^*_{i+1, m}\right), \] і по кутам \[ \tilde{\textbf{P}}_{n+1, m+1}=\frac{1}{9}\left( 14 \textbf{P}^*_{n-2, m-2} - 7 \textbf{P}^*_{n-2, m-1} + 2 \textbf{P}^*_{n-2, m} - 7 \textbf{P}^*_{n-1, m-2} - 19 \textbf{P}^*_{n-1, m-1} - \textbf{P}^*_{n-1, m} + 2 \textbf{P}^*_{n, m-2} - \textbf{P}^*_{n, m-1} + 26 \textbf{P}^*_{n, m}\right), \] \[ \tilde{\textbf{P}}_{-1, -1}=\frac{1}{9}\left( 26 \textbf{P}^*_{0, 0} - \textbf{P}^*_{0, 1} + 2 \textbf{P}^*_{0, 2} - \textbf{P}^*_{1, 0} - 19 \textbf{P}^*_{1, 1} - 7 \textbf{P}^*_{1, 2} + 2 \textbf{P}^*_{2, 0} - 7 \textbf{P}^*_{2, 1} + 14 \textbf{P}^*_{2, 2}\right), \] \[ \tilde{\textbf{P}}_{-1, m+1}=\frac{1}{9}\left( 2 \textbf{P}^*_{0, m-2} - \textbf{P}^*_{0, m-1} + 26 \textbf{P}^*_{0, m} - 7 \textbf{P}^*_{1, m-2} - 19 \textbf{P}^*_{1, m-1} - \textbf{P}^*_{1, m} + 14 \textbf{P}^*_{2, m-2} - 7 \textbf{P}^*_{2, m-1} + 2 \textbf{P}^*_{2, m}\right), \] \[ \tilde{\textbf{P}}_{n+1, -1}=\frac{1}{9}\left( 2 \textbf{P}^*_{n-2, 0} - 7 \textbf{P}^*_{n-2, 1} + 14 \textbf{P}^*_{n-2, 2} - \textbf{P}^*_{n-1, 0} - 19 \textbf{P}^*_{n-1, 1} - 7 \textbf{P}^*_{n-1, 2} + 26 \textbf{P}^*_{n, 0} - \textbf{P}^*_{n, 1} + 2 \textbf{P}^*_{n, 2}\right). \] Порівняємо результат застосування біквадратних сплайнів, які зберігають середні значення, до задачі масштабування зображень, з іншими існуючими методами.

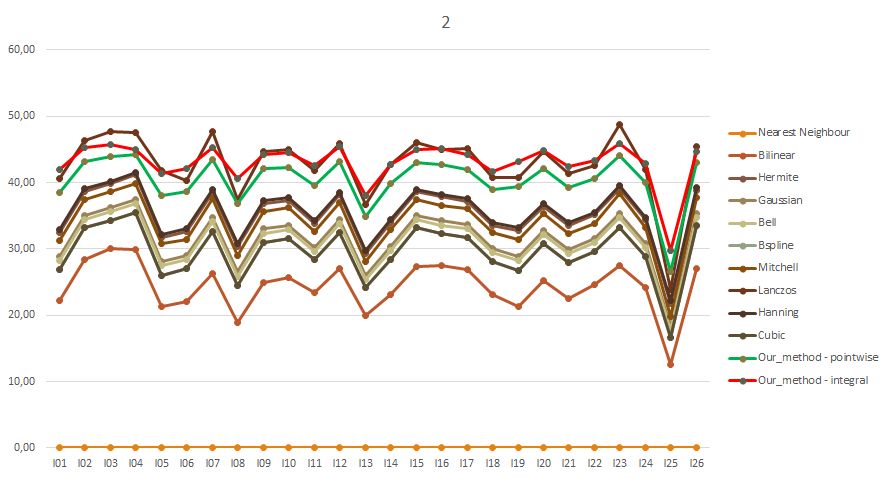Порівняння якості алгоритмів масштабування зображень.

Метод бінарного масштабування для двовимірних даних.

В зв'язку з великим обсягом обчислень при візуалізації відео-файлів, як правило, фільми зберігаються у форматі cif, тобто з розміром кадру 320x240px, а при відтворенні відео, зображення розтягується. Таким чином, стає актуальною розробка методів геометричного зменшення зображення з метою наступного збільшення його так, щоб зменшити похибку відновлення.
Розглянемо одну конструкцію збільшення розміру, яка є оптимальною для заданого методу відновлення на фіксованій множині фільтрів. На першому кроці розглянемо відновлення функцій, неперервно диференційованих (до шостого порядку включно) на всій дійсній площині. Також будемо вважати, що задана деяка фіксована функція \(\varphi(x,y)\) така, що \(\varphi *Const(x,y)=Const\), центральні моменти якої \[ m_{\nu,\mu}=\int\int_{\mathbb{R}^2}{x^\nu y^\mu\varphi(x,y)dxdy}=\int\int_{\mathbb{D}}{x^\nu y^\mu\varphi(x,y)dxdy} \] задовольняють умовам \[ m_{\nu,\mu}=m_{\mu,\nu}, m_{2\nu+1,\mu}=m_{\nu,2\mu+1}=0, \] а також, для відновлення константи необхідне виконання умови \(m_{0,0}=1\).
Будемо вважати, що інформація про функцію \(f\) задається множиною функціоналів \[ c_{2i,2j}=\int\int_{\mathbb{R}^2}{f(x+2ih,y+2jh)\varphi(x,y)dxdy}, \] де \(h\)- крок решітки та \(i,j\in Z\).
Для відновлення функції \(f\) у вузлах решітки \((ih,jh)\)побудуємо наступний алгоритм (типу метода Рунге-Кутта). На першому кроці побудуємо реконструкцію функції \(f\) у вузлах \((2ih,2jh)\) \[ \widehat{f}_{2i,2j}=\alpha_0c_{2i,2j}+\frac{\alpha_1}{4}\left(c_{2i-2,2j}+c_{2i+2,2j}+c_{2i,2j-2}+c_{2i,2j+2}\right)+ \] \[+\frac{\alpha_2}{4}\left(c_{2i-2,2j-2}+c_{2i+2,2j-2}+c_{2i-2,2j-2}+c_{2i+2,2j+2}\right)+ \frac{\alpha_3}{4}\left(c_{2i-4,2j}+c_{2i+4,2j}+c_{2i,2j-4}+c_{2i,2j+4}\right). \] На наступному кроці обчислимо реконструкцію функції \(f\) у вузлах \(((2i+1)h,(2j+1)h)\) з використанням отриманих значень \(\widehat{f}_{2i,2j}\) за правилом \[ \widehat{f}_{2i+1,2j+1}=\frac{\beta_0}{4}\left(c_{2i,2j}+c_{2i+2,2j}+c_{2i,2j+2}+c_{2i+1,2j+2}\right)+ \frac{\beta_1}{4}\left(\widehat{f}_{2i,2j}+\widehat{f}_{2i+2,2j}+\widehat{f}_{2i,2j+2}+\widehat{f}_{2i+1,2j+2}\right). \] Нарешті, з урахуванням всіх отриманих значень, знайдемо \[ \widehat{f}_{2i+1,2j}=\frac{\gamma_0}{2}\left(c_{2i,2j}+c_{2i+2,2j}\right)+ \frac{\gamma_1}{2}\left(\widehat{f}_{2i,2j}+\widehat{f}_{2i+2,2j}\right)+ \frac{\gamma_2}{2}\left(\widehat{f}_{2i+1,2j-1}+\widehat{f}_{2i+1,2j+1}\right). \] Аналогічно обчислимо значення \(\widehat{f}_{2i,2j+1}\).
Відповідний метод позначимо через \(F(C,f,\varphi)\).

Теорема 1. Для того, щоб метод \(F(C,f,\varphi)\)був такий, що \begin{equation}\label{error} f_{i,j}-F(C,f,\varphi,ih,jh)=f_{i,j}-\widehat{f}_{i,j}=O(h^6), \end{equation} необхідно і достатньо, щоб центральні моменти функції \(\varphi\) задовольняли умовам \begin{equation}\label{m} m_{0,4}=-5m_{0,2}, m_{2,2}=-m_{0,2}, \end{equation} і при цьому значення коефіцієнтів будуть визначатися наступним чином \[ \alpha_0=1 + \frac{5}{8} m_{0, 2} - \frac{1}{16} m_{2, 2} + \frac{5}{16} m_{0, 2}^2 - \frac{1}{32} m_{0, 4}, \] \[ \alpha_{1} = -\frac{2}{3} m_{0, 2} + \frac{1}{8} m_{2, 2} - \frac{1}{2} m_{0, 2}^2 + \frac{1}{24} m_{0, 4}, \] \[ \alpha_{2} = -\frac{1}{16} m_{2, 2} + \frac{1}{8} m_{0, 2}^2, \] \[ \alpha_{3} = -\frac{1}{96} m_{0, 4} + \frac{1}{24} m_{0, 2} + \frac{1}{16} m_{0, 2}^2, \] \[ \beta_{0} = - \frac{1}{m_{0, 2}}, \beta_{1} =1 + \frac{1}{m_{0, 2}}, \] \[ \gamma_{0} = -\frac{1}{2m_{0, 2}}, \gamma_{1} =\frac{1}{2} + \frac{1}{2m_{0, 2}}, \gamma_{2} = \frac{1}{2}. \]

Дійсно, використовуючи формулу Тейлора в околі точки \((2ih,2jh)\), одержуємо \[ c_{2i,2j}=\int\int_{R^2}{f(x+2ih,y+2jh)\varphi(x,y)dxdy}= \] \[ =f_{2i,2j}m_{0,0}+\left.\frac{h^2}{2}\frac{\partial^2 f}{\partial x^2}\right|_{(2i,2j)}m_{2,0} +\left.\frac{h^2}{2}\frac{\partial^2 f}{\partial y^2 }\right|_{(2i,2j)}m_{0,2} + \left.\frac{h^4}{24}\frac{\partial^4 f}{\partial^4x}\right|_{(2i,2j)}m_{4,0}+\left.\frac{h^4}{4}\frac{\partial^4 f}{\partial x^2\partial y^2}\right|_{(2i,2j)}m_{2,2}+\left.\frac{h^4}{24}\frac{\partial^4 f}{\partial y^2}\right|_{(2i,2j)}m_{0,4}+ O(h^6). \] Використовуючи формулу реконструкції в точці \((2ih,2jh)\), отримуємо \[ \hat{f}_{2i,2j}=\left( \alpha_{{0}}+\alpha_{{1}} +\alpha_{{2}} +\alpha_{{3}}\right) f_{{2i,2j}}+ \frac{h^2}{4}\left( 2\,\alpha_{{0}}m_{{0,2}}+\alpha_{{1}} \left( 4+2\,m_{{0,2}}\right) +\alpha_{{2}} \left( 8+2\,m_{{0,2}}\right)+\right.\] \[ +\left.\alpha_{{3}} \left( 16+2\,m_{{0,2}}\right) \right)\left(\left.\frac{\partial^2 f}{\partial x^2}\right|_{(2i,2j)}+\left.\frac{\partial^2 f}{\partial y^2}\right|_{(2i,2j)}\right) +\frac{h^4}{4}\left( 2\,\alpha_{{0}}m_{{2,2}}+\alpha_{{1}} \left( 4m_{0,2}+\,m_{{2,2}}\right) +\alpha_{{2}} \left( 16+8\,m_{{0,2}}+m_{{2,2}}\right)+\right.\] \[ +\left.\alpha_{{3}} \left( 16\,m_{{0,2}}+m_{{2,2}}\right) \right)\left.\frac{\partial^4 f}{\partial^2 x\partial^2 y}\right|_{(2i,2j)}+ \frac{h^4}{24}\left( \,\alpha_{{0}}m_{{0,4}}+\alpha_{{1}} \left( 8+12\,m_{{0, 2}}+\,m_{{0,4}}\right) +\alpha_{{2}} \left( 16+24\,m_{{0, 2}}+\,m_{{0,4}}\right)+\right.\] \[ +\left.\alpha_{{3}} \left( 128+48\,m_{{0, 2}}+\,m_{{0,4}}\right)\right) \left(\left.\frac{\partial^4 f}{\partial x^4}\right|_{(2i,2j)}+\left.\frac{\partial^4 f}{\partial y^4}\right|_{(2i,2j)}\right)+ O(h^6). \] Таким чином, для того, щоб умова (\ref{error}) виконувалась, треба розв'язати систему рівнянь \[ \left\{% \begin{array}{ll} \alpha_{{0}}+\alpha_{{1}} +\alpha_{{2}}+\alpha_{{3}}=1,\\ 2\,\alpha_{{0}}m_{{0,2}}+\alpha_{{1}} \left( 4+2\,m_{{0,2}}\right) +\alpha_{{2}} \left( 8+2\,m_{{0,2}}\right) +\alpha_{{3}} \left( 16+2\,m_{{0,2}}\right)=0,\\ 2\,\alpha_{{0}}m_{{2,2}}+\alpha_{{1}} \left( 4m_{0,2}+\,m_{{2,2}}\right) +\alpha_{{2}} \left( 16+8\,m_{{0,2}}+m_{{2,2}}\right)+\alpha_{{3}} \left( 16\,m_{{0,2}}+m_{{2,2}}\right)=0,\\ \,\alpha_{{0}}m_{{0,4}}+\alpha_{{1}} \left( 8+12\,m_{{0, 2}}+\,m_{{0,4}}\right) +\alpha_{{2}} \left( 16+24\,m_{{0, 2}}+\,m_{{0,4}}\right)+\\+\alpha_{{3}} \left( 128+48\,m_{{0, 2}}+\,m_{{0,4}}\right)=0.\\ \end{array}% \right. \] Розв'язуючи дану систему, отримаємо коефіцієнти \(\alpha_0, \alpha_1, \alpha_2, \alpha_3\), наведені в теоремі.
Аналогічним чином, якщо прирівняємо до нуля множники перших похідних різниці \(f_{2i+1,2j+1}- \hat{f}_{2i+1,2j+1}\), то отримаємо систему рівнянь, розв'язком якої будуть значення \[ \beta_0=-\frac{1}{m_{0,2}},\beta_1=\frac{1+m_{0,2}}{m_{0,2}}. \] При цьому похибка відновлення в точці \(((2i+1)h,(2j+1)h)\) буде дорівнювати \begin{equation}\label{s21} f_{2i+1,2j+1}-\hat{f}_{2i+1,2j+1}=\frac{h^4}{24}\left(5+\frac{m_{0,4}}{m_{0,2}}\right) \left(\left.\frac{\partial^4 f}{\partial x^4}\right|_{(2i+1,2j+1)}+ \left.\frac{\partial^4 f}{\partial y^4}\right|_{(2i+1,2j+1)}\right)+ \frac{h^4}{4}\left(1+\frac{m_{2,2}}{m_{0,2}}\right)\left.\frac{\partial^4 f}{\partial x^2\partial y^2}\right|_{(2i,2j)}+ O(h^6). \end{equation} Нарешті, мінімізуючи похибку реконструкції функції в точці \(((2i+1)h,2jh)\), отримаємо \[ \gamma_0=-\frac{1}{2\,m_{0,2}},\gamma_1=\frac{1+m_{0,2}}{2\,m_{0,2}},\gamma_2=\frac{1}{2}, \] і, в такому разі, маємо \begin{equation}\label{s3} f_{2i+1,2j}-\hat{f}_{2i+1,2j}=\frac{h^4}{24}\left(5+\frac{m_{0,4}}{m_{0,2}}\right) \left(\left.\frac{\partial^4 f}{\partial x^4}\right|_{(2i+1,2j)}+ \left.\frac{\partial^4 f}{\partial y^4}\right|_{(2i+1,2j)}\right)+ \frac{h^4}{4}\left(1+\frac{m_{2,2}}{m_{0,2}}\right)\left.\frac{\partial^4 f}{\partial x^2\partial y^2}\right|_{(2i+1,2j)}+ O(h^6). \end{equation} Таким чином, вибір моментів згідно (\ref{m}), забезпечує виконання умови (\ref{error}).
У дискретному випадку, коли значення \(\varphi(x,y)\) на кожному елементарному квадраті решітки є константою, складність \(\varphi\) визначимо наступним чином \[ \begin{array}{ccccc} 0 & 0 & 0 & 0 & 0 \\ 0 & a_{-1,1} & a_{0,1} & a_{1,1} & 0 \\ 0 & a_{-1,0} & a_{0,0} & a_{1,0} & 0 \\ 0 & a_{-1,-1} & a_{0,-1} & a_{1,-1} & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array} \] Така функція, що задовольняє умовам теореми, існує і єдина, при цьому ненульові значення декомпозиційного фільтру визначаються матрицею \[ \left[ \begin {array}{rrr} -{\frac {31}{9360}}&-{\frac {19}{720}}&-{\frac {31}{9360}}\\ -{\frac {19}{720}}&{\frac {1309}{1170}}&-{\frac {19}{720}}\\ -{\frac {31}{9360}}&-{\frac {19}{720}}&-{\frac {31}{9360}} \end {array} \right]. \]

В цьому випадку центральні моменти функції \(\varphi\) будуть такі \[ m_{0,0}=1, m_{0,2}=\frac{9}{520}, m_{2,2}=-\frac{9}{520}, m_{0,4}=-\frac{9}{104} \] і \[ \alpha_{0}=\frac{877997}{865280},\alpha_1=-\frac{9441}{540800},\alpha_2=\frac{2421}{2163200},\alpha_3=\frac{7101}{4326400}, \] \[ \beta_0=-\frac{520}{9},\beta_1=\frac{520}{9}, \] \[ \gamma=-\frac{260}{9},\gamma_1=\frac{529}{18},\gamma_2=\frac{1}{2}. \] Виникає питання, чи можливо при тій же асимптотичній точності спростити формули відновлення за рахунок скорочення числа доданків в них? Це можливо, але при цьому носій декомпозиційного фільтру \(\varphi\) необхідно збільшити. Позначимо через \(G(C,f,\varphi)\) метод відновлення, який визначається правилом реконструкції \[ \widehat{f}_{2i,2j}=\alpha_0c_{2i,2j}+\frac{\alpha_1}{4}\left(c_{2i-2,2j}+c_{2i+2,2j}+c_{2i,2j-2}+c_{2i,2j+2}\right)+ \frac{\alpha_2}{4}\left(c_{2i-2,2j-2}+c_{2i+2,2j-2}+c_{2i-2,2j-2}+c_{2i+2,2j+2}\right),\] а відновлення решти значень проводиться по тим же формулам, що й раніше.

Теорема 2. Для того, щоб метод \(G(C,f,\varphi)\) був такий, що \[ f_{i,j}-G(C,f,\varphi,ih,jh)=f_{i,j}-\widehat{f}_{i,j}=O(h^6), \] необхідно і достатньо, щоб центральні моменти функції \(\varphi\) були рівні \[ m_{0,0}=1,m_{0,2}=-\frac{3}{2},m_{2,2}=\frac{3}{2},m_{0,4}=\frac{15}{2}, \] і, при цьому, коефіцієнти формул реконструкції визначаються наступним чином \[ \alpha_0=\frac{7}{16},\alpha_1=\frac{3}{32},\alpha_2=\frac{3}{64}, \] \[ \beta_0=-\frac{1}{6},\beta_1=\frac{1}{12}, \gamma_0=-\frac{1}{6},\gamma_1=\frac{1}{12},\gamma_2=\frac{1}{4}. \]

Без доведення цієї теоремі зазначимо, що у дискретному випадку функція \(\varphi\) існує і єдина. Значення цієї функції визначаються матрицею \[ \left[ \begin {array}{rrrrr} 0&0&{\frac {263}{640}}&0&0\\ 0&{\frac {253}{576}}&-{\frac {1193}{360}}&{\frac { 253}{576}}&0\\ {\frac {263}{640}}&-{\frac {1193}{360} }&{\frac {15631}{1440}}&-{\frac {1193}{360}}&{\frac {263}{640}} \\0&{\frac {253}{576}}&-{\frac {1193}{360}}&{\frac { 253}{576}}&0\\0&0&{\frac {263}{640}}&0&0\end {array} \right] \] а графік цієї функції має наступний вигляд:

Серед двох наведених методів, для практичного використання прийнятнішим є перший, через той факт, що другий декомпозиційний фільтр \(\varphi\) надмірно контрастуючий.