Интерполяционные в среднем методы subdivision
Определения и постановка задачи.
Пусть задана последовательность \({\bf f}\) и оператор \(\mathbb{P}\)- отображающий множество последовательностей \({\bf f}\) в пару
последовательностей \({\bf f}^+ = \left\{ f_i^+ \right\}\) и \({\bf f}^- = \left\{ f_i^- \right\}\). Определим новую
последовательность \({\bf f}_1 = {\bf f}_1(\mathbb{P}) = \left\{ \hat{f}_{1,i}\right\}_{i \in \mathbb{Z}}\), где \(\hat{f}_{1,2i} = \hat{f}_i^+\),
\(\hat{f}_{1,2i-1} = \hat{f}_i^-, \,\,\,\, (i \in \mathbb{Z})\)
Полагая \({\bf f}_k = {\bf f}_k(\mathbb{P}) = {\bf f}_1({\bf f}_{k-1})\), получаем метод бинарного расслоения данных (интерполяционного в
среднем subdivision).
Рассмотрим одно из возможных правил \(\mathbb{P}\) построения subdivision. Для каждого фиксированного \(i \in \mathbb{Z}\) построим
полином второго порядка \(P_{2,i}=a_ix^2+b_ix+c_i\) однозначно определяющийся следующими условиями: \begin{equation}\label{s.118}
\left\{
\begin{array}{l}
\frac{1}{h} \int_{x{i-1}-\frac{h}{2}}^{x{i-1}+\frac{h}{2}} P_{2,i}(x) dx = \hat{f}_{i-1}; \\
\frac{1}{h} \int_{x{i}-\frac{h}{2}}^{x{i}+\frac{h}{2}} P_{2,i}(x) dx = \hat{f}_i; \\
\frac{1}{h} \int_{x{i+1}-\frac{h}{2}}^{x{i+1}+\frac{h}{2}} P_{2,i}(x) dx = \hat{f}_{i+1}.
\end{array}
\right.
\end{equation}
Положим теперь \begin{equation}\label{s.119}
\hat{f}_{i,0}^+ = \hat{f}_i^+ = \frac{2}{h} \int_{x_i}^{x_{i+\frac 12}} P_{2,i}(x) dx;
\end{equation} \begin{equation}\label{s.120}
\hat{f}_{i,0}^- = \hat{f}_i^- = \frac{2}{h} \int_{x_{i-\frac 12}}^{x_i} P_{2,i}(x) dx.
\end{equation}
Решая систему (\ref{s.118}), находим коэффициенты \(a_i, b_i, c_i\), подставляя которые в (\ref{s.119}), (\ref{s.120})
приходим к формулам пополнения:
\begin{equation}\label{s.121}
\hat{f}_{i,0}^+ = \hat{f}_{i,0} + \frac{1}{8} \left( \hat{f}_{i+1,0}-\hat{f}_{i-1,0} \right); \\
\end{equation} \begin{equation}\label{s.122}
\hat{f}_{i,0}^- = \hat{f}_{i,0} - \frac{1}{8} \left( \hat{f}_{i+1,0}-\hat{f}_{i-1,0} \right).
\end{equation}
Теперь положим
\[
x_{2i,1} = x_{i,0} + \frac{h}{4} ,\,\,\,\,\,\, \hat{f}_{2i,1} = \hat{f}_{i,0}^+;
\]
\[
x_{2i-1,1} = x_{i,0} - \frac{h}{4} ,\,\,\,\,\,\, \hat{f}_{2i-1,1} = \hat{f}_{i,0}^-.
\,\,\,\,\,\,\,\,\, (i \in \mathbb{Z})
\]
Таким образом мы получим средние значения \(\hat{f}_{i,1} (i \in \mathbb{Z})\) на новом разбиении \(\left\{ x_{i,1} \right\}_{i
\in \mathbb{Z}}\).
Полученный набор будем использовать в качестве исходного и повторяем процедуру пополнения данных, что приводит к
рекуррентным формулам:
\begin{equation}\label{s.123}
\begin{array}{c}
x_{2i,k} = x_{i,k-1} + \frac{h}{2^{k+1}} ,\,\,\,\,\,\,
\hat{f}_{2i,k} = \hat{f}_{i,k-1} + \frac{1}{8} \left( \hat{f}_{i+1,k-1}-\hat{f}_{i-1,k-1} \right); \\
x_{2i-1,k} = x_{i,k-1} - \frac{h}{2^{k+1}} ,\,\,\,\,\,\,
\hat{f}_{2i-1,k} = \hat{f}_{i,k-1} - \frac{1}{8} \left( \hat{f}_{i+1,k-1}-\hat{f}_{i-1,k-1} \right).
\end{array}
\end{equation}
Впервые этот метод subdivision был предложен D.Donoho. Схематически интерполяционный в среднем
метод subdivision можно проиллюстрировать следующей схемой
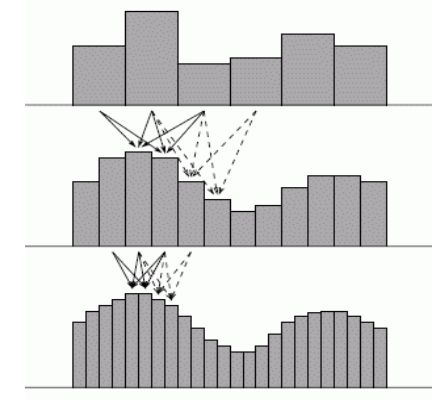
Замечание 1.
Пусть последовательность \({\bf f}\) такова, что
\[
\hat{f}_{\nu} =
\frac{1}{h} \int_{x_{\nu}-\frac{h}{2}}^{x_{\nu}+\frac{h}{2}} P_2(x)\,dx,
\]
где \(P_2(x) = ax^2+bx+c\) для \({\nu=i-2, \ldots, i+2}\),
тогда из метода построения следует, что для \({\nu=i-1,i,i+1}\)
\[
\hat{f}_{\nu}^+ = \frac{2}{h}\int_{x_{\nu}}^{x_{\nu}+\frac{h}{2}} P_2(x)\,dx
\]
и
\[
\hat{f}_{\nu}^- = \frac{2}{h}\int_{x_{\nu}-\frac{h}{2}}^{x_{\nu}} P_2(x)\,dx
\]
Отсюда следует, что для любого \(i \in \mathbb{Z}\), такого, что \(\left[ x_{i-\frac h2}, x_{i+\frac h2} \right] \in
\left[ - \frac 12, \frac 12\right]\)
\[
\hat{f}_{i,k} =
\frac{2^k}{h}\int_{x{i,k}-\frac{h}{2^{k+1}}}^{x{i,k}-\frac{h}{2^{k+1}}} P(x)\,dx.
\]
Замечание 2.
Отметим, что из замечания 1 следует, что если \(h=1\) и
\(\frac{1}{h} \int_{x_{\nu}-\frac{h}{2}}^{x_{\nu}+\frac{h}{2}} P_2(x)\,dx,\)
где \(P_2(x)=ax^2+bx+c\), то
\(\psi(P,x) = P(x)\), для \(x \in \left[ -\frac 12, \frac 12 \right]\).
Рассмотрим другой подход, приводящий к этой же задаче бинарного пополнения. Пусть \({\bf f}\) - функция, интерполируемая
на \(\mathbb{R}\) и \(\hat{f}_{i,0}\) ее средние значения на промежутках \((x_{i-\frac 12,k},x_{i+\frac 12,k}]\), т.е.
\[
\hat{f}_{i,0}=\hat{f}_i=\frac{1}{h}\int_{x_{i-\frac 12,0}}^{x_{i+\frac 12,0}} {\bf f} dx.
\]
Восстановление \(\hat{f}_{i,0}^-\) и \(\hat{f}_{i,0}^+\) будем искать в виде линейной комбинации
\begin{equation}\label{s.126}
\hat{f}_{i,0}^- =
\alpha_i^- \hat{f}_{i{-}1,0} + \beta_i^- \hat{f}_{i,0} + \gamma_i^- \hat{f}_{i{+}1,0}
\end{equation} и \begin{equation}\label{s.127} \hat{f}_{i,0}^+ = \alpha_i^+ \hat{f}_{i{-}1,0} + \beta_i^+ \hat{f}_{i,0} + \gamma_i^+ \hat{f}_{i{+}1,0}. \end{equation}
где коэффициенты \(\alpha_i^\pm\), \(\beta_i^\pm\) и \(\gamma_i^\pm\) выберем из условия наивысшей алгебраической точности.
То есть так, чтобы соотношения (\ref{s.126}) и (\ref{s.127}) обращались в тождество для функций \(f(x)=1,x,x^2\). Это
приводит к следующим двум системам трех уравнений с тремя неизвестными
\[
\left\{
\begin{array}{lc}
\alpha_i^-+\beta_i^-+\gamma_i^-=1;\\
\alpha_i^-(i+2h)+\beta_i^-i+\gamma_i^-(i-2h)=i+\frac{1}{2}h;\\
\alpha_i^-(i^2+4ih+\frac{13}{3}h^2)+\beta_i^-(i^2+\frac{1}{3}h^2)+\gamma_i^-(i^2-4ih+\frac{13}{3}h^2)=i^2+ih+\frac{1}{3}h^2
\end{array}
\right.
\]
и
\[
\left\{
\begin{array}{lc}
\alpha_i^++\beta_i^++\gamma_i^+=1;\\
\alpha_i^+(i-2h)+\beta_i^+i+\gamma_i^+(i+2h)=i+\frac{1}{2}h;\\
\alpha_i^+(i^2-4ih+\frac{13}{3}h^2)+\beta_i^+(i^2+\frac{1}{3}h^2)+\gamma_i^+(i^2+4ih+\frac{13}{3}h^2)=i^2+ih+\frac{1}{3}h^2.
\end{array}
\right.
\]
Решением этой системы будут числа
\begin{equation}\label{s.128}
\alpha^- = \frac{1}{8}, \,\,\,\,\,\, \beta^- = 1 \,\,\,\,\,\, \gamma^-=-\frac{1}{8}.
\end{equation} и \begin{equation}\label{s.129}
\alpha^+ = -\frac{1}{8}, \,\,\,\,\,\, \beta^+ = 1. \,\,\,\,\,\, \gamma^+=\frac{1}{8}.
\end{equation}
Таким образом, этот метод приводит к формулам subdivision (\ref{s.123}).
Рассмотрим еще один подход к задаче пополнения данных. Будем считать, что \(f^{(\nu)}\in C(\mathbb{R})\) \(\nu=0,\ldots,3\) и
\[
\hat{f}_i=\frac{1}{h}\int_{x_{i-\frac 12}}^{x_{i+\frac 12}}f(x)dx.
\]
Снова пополнение будем искать в виде линейной комбинации, но коэффициенты \(\alpha_i^\pm, \beta_i^\pm, \gamma_i^\pm\)
выберем из следующего условия: главный член асимптотики разности левой и правой частей должен иметь как можно более
высокий порядок точности. Используя разложение в ряд Тейлора в окрестности точки \(x_{i-\frac 12}\) сразу получаем
\[
\hat{f}_{i-1,0} = f_{i,0} + \left( i-\frac{1}{2} \right)hf'_{i,0}+\left(\frac{1}{6} -
\frac{1}{2}i+\frac{1}{2}i^2 \right)h^2f''_{i,0} + O(h^3);
\]
\[
\hat{f}_{i,0} = f_{i,0} + \left( i+\frac{1}{2} \right)hf'_{i,0}+\left( \frac{1}{6} +
\frac{1}{2}i+\frac{1}{2}i^2 \right)h^2f''_{i,0} + O(h^3);
\]
\[
\hat{f}_{i+1,0} = f_{i,0} + \left( i+\frac{3}{2} \right)hf'_{i,0}+\left( \frac{7}{6} +
\frac{3}{2}i+\frac{1}{2}i^2 \right)h^2f''_{i,0} + O(h^3)
\]
и
\[
\hat{f}_{i,0}^- = f_{i,0} + \left( i+\frac{1}{4} \right)hf'_{i,0}+\left( \frac{1}{24} +
\frac{1}{4}i+\frac{1}{2}i^2 \right)h^2f''_{i,0} + O(h^3);
\]
\[
\hat{f}_{i,0}^+ = f_{i,0} + \left( i+\frac{3}{4} \right)hf'_{i,0}+\left(\frac{7}{24} +
\frac{3}{4}i+\frac{1}{2}i^2 \right)h^2f''_{i,0} + O(h^3).
\]
Выполнение условия, что главный член асимптотики разности левой и правой частей (\ref{s.126}) должен иметь как можно
более высокий порядок точности, эквивалентно тому, что что коэффициенты при \(h^\nu\) \((\nu=0,1,2)\) должны обратиться в
ноль. Это условие приводит к системе алгебраических уравнений
\begin{equation}\label{s.130}
\left\{
\begin{array}{l}
\alpha^+ + \beta^+ + \gamma^+ = 1; \\[6pt]
\left( i{+}\frac{3}{2} \right)\alpha^+ +
\left( i{+}\frac{1}{2} \right)\beta^+ +
\left( i{-}\frac{1}{2} \right)\gamma^+ =
\left( i{+}\frac{1}{4} \right); \\[8pt]
\left( \frac{7}{6}{+}\frac{3}{2}i{+}\frac{1}{2}i^2 \right)\alpha^+ +
\left( \frac{1}{6}{+}\frac{1}{2}i{+}\frac{1}{2}i^2 \right)\beta^+ +
\left( \frac{1}{6}{-}\frac{1}{2}i{+}\frac{1}{2}i^2 \right)\gamma^+ =
\left( \frac{1}{24}{+}\frac{1}{4}i{+}\frac{1}{2}i^2 \right) ,
\end{array}
\right.
\end{equation} решениями которой будут числа (\ref{s.129}). Проведя аналогичные вычисления для \(\alpha_i^-, \beta_i^-, \gamma_i^-\)
получим числа (\ref{s.128}). Таким образом мы снова пришли к формулам пополнения (\ref{s.123}).
Положим
\[
\tilde{f}_{i+1/2,k}=\frac{9}{16}\left(\hat{f}_{i,k}+\hat{f}_{i+1,k}\right) -\frac{1}{16}\left(\hat{f}_{i+2,k}+\hat{f}_{i-1,k}\right)=
\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}-\frac{1}{8}\Delta^2 \left(\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}\right).
\]
Каждой последовательности \({\bf f}_k\) поставим в соответствие кусочно-линейную функцию \begin{equation}\label{s.131}
\psi_{k,h}({\bf f},x)=\sum_{i\in\mathbb{Z}}\left(\tilde{f}_{i+1/2,k}- \frac{1}{6}\Delta^2\tilde{f}_{i+1/2,k}\right)B\left(\frac{1}{h}
\left(x-\left(i+\frac{1}{2}\right)h\right)\right), \end{equation} где \(B(x)\)- B-сплайн первого порядка, то есть
\[
B(x)= \left\{
\begin{array}{lc}
x-1,&x\in [-1,0],\\ 1-x,&x\in [0,1],\\ 0&,x\notin [-1,1].
\end{array}
\right.
\]
Отметим несколько свойств функции \(\psi_{k,h}(x)\), которые будут нам необходимы в дальнейшем. Проводя непосредственные
вычисления, получаем
\[
\frac{2^k}{h}\int_{x_{i,k}}^{x_{i+1,k}}\psi_{k,h}({\bf f},x)dx=
\tilde{f}_{i+1/2,k}-\frac{1}{48}\Delta^2(\tilde{f}_{i+1/2,k}+\tilde{f}_{i-1/2,k}),
\]
то есть \(\psi_{k,h}({\bf f},x)\) асимптотически совпадает с ломаной интерполирующей средние значения \(\tilde{f}_{i+1/2,k}\).
Положим
\[
\Delta \psi_{k,h}({\bf f},x)=\psi_{k,h}({\bf f},x+x_{i,k})-\psi_{k,h}({\bf f},x)
\]
и
\[
\Delta^k \psi_{k,h}({\bf f},x)=\Delta\left(\Delta^{k-1}\psi_{k,h}({\bf f},x)\right)\,\,\,\,k\ge 2
\]
и
\[
\Delta \hat{f}_{i,k}=\hat{f}_{i+1,k}-\hat{f}_{i,k},
\]
\[
\Delta^k \hat{f}_{i,k}=\Delta\left(\Delta^{k-1}\hat{f}_{i,k}\right)\,\,\,\,k\ge 2.
\]
Лемма 1.
Для любой последовательности \({\bf f}\in\ell_{\infty}(\mathbb{R})\) и произвольного \(k\in\mathbb{N}\) имеет место неравенство
\begin{equation}\label{s.133} \|\Delta^2 {\bf f}_{k+1}\|_{\ell_{\infty}(\mathbb{R})}\le \frac{1}{2}\|\Delta^2
{\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}. \end{equation}
Доказательство. Вначале рассмотрим величину
\[
\Delta^2 \hat{f}_{2i,k+1} = \Delta^2 \hat{f}_{i,k}^+= \hat{f}_{i+1,k}^{-} -2\hat{f}_{i,k}^+\hat{f}_{i,k}^-=\]
\[
=\hat{f}_{i+1,k}-\frac{1}{8}\left(\hat{f}_{i+2,k}-\hat{f}_{i,k}\right)- 2\hat{f}_{i,k}-2\frac{1}{8}\left(\hat{f}_{i+1,k}-\hat{f}_{i-1,k}\right)
+\hat{f}_{i,k}-\frac{1}{8}\left(\hat{f}_{i+1,k}-\hat{f}_{i-1,k}\right)=
\]
\[
=\frac{1}{8}\left(3\Delta^2\hat{f}_{i,k}-\Delta^2\hat{f}_{i+1,k}\right)\le \frac{1}{2}\|\Delta^2
{\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}.
\]
Проводя аналогичные построения убеждаемся в том, что
\[
\Delta^2 \hat{f}_{2i+1,k+1}\le \frac{1}{2}\|\Delta^2 {\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}.
\]
Лемма 2.
Для любой последовательности \({\bf f}\in\ell_{\infty}(\mathbb{R})\) и произвольного \(k\in\mathbb{N}\) имеет место неравенство
\begin{equation}\label{s.135} \|\psi_{k+1,h}({\bf f})-\psi_{k,h}({\bf f})\|_{\infty(\mathbb{R})}\le \frac{23}{48}\|\Delta^2
{\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}. \end{equation}
Доказательство. Так как функции \(\psi_{k+1,h}({\bf f},x)\) и \(\psi_{k,h}({\bf f},x)\) линейные, то разница между ними
достигает экстремума в узлах \(x_{i,k}\) или \(x_{i+1/2,k}\). Таким образом прежде всего необходимо вычислить значения
\(\psi_{k+1,h}({\bf f},x_{i,k})\), \(\psi_{k,h}({\bf f},x_{i,k})\) и \(\psi_{k+1,h}({\bf f},x_{i+1/2,k})\),
\(\psi_{k,h}({\bf f},x_{i+1/2,k})\).
Несложно убедиться в справедливости следующих соотношений. \begin{equation}\label{s.136}
\psi_{k,h}({\bf f},x_{i+1/2,k})=\tilde{f}_{i+1/2,k}-\frac{1}{6}\Delta^2\tilde{f}_{i+1/2,k}= \end{equation}
\[
=\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}-\frac{1}{8}\Delta^2 \left(\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}\right)-
\frac{1}{6}\Delta^2 \left(\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}\right)+ \frac{1}{48}\Delta^4
\left(\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}\right)=
\]
\[
=\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}- \frac{7}{24}\Delta^2 \left(\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}\right)+
\frac{1}{48}\Delta^4 \left(\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}\right).
\]
Кроме того, \begin{equation}\label{s.137} \psi_{k,h}\left({\bf f},x_{i,k}\right)=\frac{\tilde{f}_{i+1/2,k}+\tilde{f}_{i-1/2,k}}{2}-
\frac{1}{6}\Delta^2\left(\frac{\tilde{f}_{i+1/2,k}+\tilde{f}_{i-1/2,k}}{2}\right)= \end{equation}
\[
=\frac{\hat{f}_{i+1,k}+2\hat{f}_{i,k}+\hat{f}_{i-1,k}}{4}- \frac{7}{24}\Delta^2
\left(\frac{\hat{f}_{i+1,k}+2\hat{f}_{i,k}+\hat{f}_{i-1,k}}{4}\right)+\frac{1}{48}\Delta^4
\left(\frac{\hat{f}_{i+1,k}+2\hat{f}_{i,k}+\hat{f}_{i-1,k}}{4}\right).
\]
Из метода расслоения, проводя простые, но громоздкие преобразования, получаем
\[
\psi_{k+1,h}({\bf f},x_{i+1/2,k})=
\frac{\hat{f}_{i,k}+\hat{f}_{i+1,k}}{2}- \frac{5}{64}\left(\Delta^2\hat{f}_{i+1,k}+\Delta^2\hat{f}_{i,k}\right)\] и, кроме того,
\[
\psi_{k+1,h}({\bf f},x_{i,k})=
\hat{f}_{i,k}+ \frac{1}{128}\left(\Delta^2\hat{f}_{i+1,k}-6\Delta^2\hat{f}_{i,k}+ \Delta^2\hat{f}_{i-1,k}\right).
\]
Отсюда сразу получаем
\[
\left|\psi_{k,h}({\bf f},x_{i+1/2,k})-\psi_{k+1,h}({\bf f},x_{i+1/2,k})\right|=
\left|\frac{1}{64}\left(\Delta^2\hat{f}_{i+1,k}+\Delta^2\hat{f}_{i,k}\right)\right| \le \frac{1}{32}\|\Delta^2
{\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}.
\]
Далее,
\[
\left|\psi_{k,h}({\bf f},x_{i,k})-\psi_{k+1,h}({\bf f},x_{i,k})\right|=\]
\[
= \frac{1}{384}\left|\Delta^2\left(-31\hat{f}_{i+1,k}+58\hat{f}_{i,k}-31\hat{f}_{i-1,k} \right)\right|+
\frac{1}{96}\left|\Delta^4\left(\hat{f}_{i+1,k}+2\hat{f}_{i,k}+\hat{f}_{i-1,k} \right)\right|\le\frac{23}{48}\|\Delta^2
{\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}.\]
Лемма 3.
Для любой последовательности \({\bf f}{\in}\ell_\infty(\mathbb{R})\), и \(k,m{\in}\mathbb{N}\)
имеет место неравенство
\begin{equation}\label{s.140}
\left\| \psi_{k,h}({\bf f}) - \psi_{k+m,h}({\bf f}) \right\|_{C(\mathbb{R})}
\le\frac{23}{48}\|\Delta^2 {\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}\le
\frac{23}{48}\left(\frac{1}{2}\right)^k \|\Delta^2 {\bf f}_{0}\|_{\ell_{\infty}(\mathbb{R})}. \end{equation}
Доказательство.
\[
\left\| \psi_{k,h}({\bf f}) - \psi_{k+m,h}({\bf f}) \right\|_{C(\mathbb{R})} \le
\sum_{i=k}^{m-1} \left| \psi_{i+1,h}({\bf f}) - \psi_{i,h}({\bf f}) \right|.
\]
Из леммы 2 следует
\[
\left\| \psi_{k,h}({\bf f}) - \psi_{k+m,h}({\bf f}) \right\|_{C(\mathbb{R})} \le
\frac{1}{16}
\sum_{i=k}^{m-1}\|\Delta^2 {\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}
\le \frac{23}{48}\left(
\|\Delta^2 {\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}+ \|\Delta^2 {\bf f}_{k+1}\|_{\ell_{\infty}(\mathbb{R})}+\ldots\right).
\]
Применяя лемму 1 получаем
\[
\left\| \psi_{k,h}({\bf f}) - \psi_{k+m,h}({\bf f}) \right\|_{C(\mathbb{R})} \le
\frac{23}{48}\left( \|\Delta^2 {\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}+ \frac{1}{2}\|\Delta^2
{\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}+\ldots\right)=
\]
\[
= \frac{23}{48}\|\Delta^2 {\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}\left( 1+\frac{1}{2}+\frac{1}{2^2}+\ldots\right)=
\frac{23}{48}\|\Delta^2 {\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}\le \frac{23}{48}\left(\frac{1}{2}\right)^k \|\Delta^2
{\bf f}_{0}\|_{\ell_{\infty}(\mathbb{R})}.
\]
Лемма доказана.
Из леммы 3 следует, что последовательность \(\{\psi_{k,h}({\bf f},x)\}_{k=0}^{\infty}\) сходится в себе. Нетрудно
видеть, что она ограничена. Отсюда следует, что поточечный предел \(\psi_{k,h}({\bf f},x)\) при \(k\to\infty\) существует.
Обозначим этот предел через \(\psi_{h}({\bf f},x)\).
Так как для любого \(k\in\mathbb{N}\) оператор \(\psi_{k,h}({\bf f})\) есть линейный оператор, отображающий пространство
\(\ell_{\infty}\) в пространство ограниченных на всей плоскости кусочно-линейных функций, то \(\psi_h\) есть линейный
оператор, отображающий пространство \(\ell_{\infty}\) в пространство \(C(\mathbb{R})\).
Переходя к пределу по \(m\to\infty\) в (\ref{s.140}), немедленно получаем следующее утверждение.
Теорема 1
Для любого фиксированного \(k{\in}\mathbb{N}\) и любой последовательности \({\bf f}\in \ell_{\infty}\) верно неравенство
\[
\left\| \psi_{h}({\bf f}) - \psi_{k,h}({\bf f}) \right\|_{C(\mathbb{R})}
\le
\frac{23}{48}\|\Delta^2 {\bf f}_{k}\|_{\ell_{\infty}(\mathbb{R})}\le \frac{23}{48}\left(\frac{1}{2}\right)^k \|\Delta^2
{\bf f}_{0}\|_{\ell_{\infty}(\mathbb{R})}.
\]
Из метода построения ясно, что функция \(\psi_{k,h}({\bf f},x)\) непрерывная и кусочно-дифференцируемая. Следующее
утверждение состоит в том, что предельная функция \(\psi_{h}({\bf f},x)\) обладает лучшими дифференциальными свойствами -
она непрерывно-дифференцируема.
Теорема 2.
Пусть \({\bf f}\) произвольная последовательность из \(\ell_{\infty}\), тогда \(\psi_{h}({\bf f})\in C^1(\mathbb{R})\).
Доказательство. Если, как обычно
\[
\omega(g,t)=\sup_{|\tau|\le t}\|g(\cdot+\tau)-g(\cdot)\|_{C(\mathbb{R})}
\]
равномерный модуль непрерывности функции \(g\in C(\mathbb{R})\) в точке \(t\), то
\[
\omega\left(\psi_{h}({\bf f}),\frac{h}{2^k}\right)= \sup_{|\tau|\le \frac{h}{2^k}}
\left\|\psi_{h}({\bf f},\cdot+\tau)-\psi_{h}({\bf f},\cdot)\right\|_{C(\mathbb{R})}=
\]
\[
= \sup_{|\tau|\le \frac{h}{2^k}}\max_{i\in\mathbb{Z}}\max\left\{
\left|\psi_{h}({\bf f},x_{i,k}+\tau)-\psi_{h}({\bf f},x_{i,k})\right|,
\left|\psi_{h}({\bf f},x_{i+1,k})-\psi_{h}({\bf f},x_{i+1,k}-\tau)\right| \right\}.
\]
Отсюда и из предыдущего, сразу получаем требуемое утверждение.
Базисная функция и ее свойства.
Далее нам понадобится одна функция специального вида, которая в дальнейшем будет играть роль базисной функции.
Пусть \(h=1\) и последовательность \( {\it\bf f}^* = \{\hat{f}^*_{0,i}\}_{i\in\mathbb{Z}}\), где \(\hat{f}^*_{0,i}=\delta_{0,i}\) и
\(\delta_{\nu,\mu}\) - символ Кронекера.
Положим \begin{equation}\label{s.143.1}
\Psi_k(x)=\psi_k({\bf f^*},x)
\,\,\,\,\,\,\,\,\,\, {\rm и}\,\,\,\,\,\,\,\,\,\,
\Psi(x)=\psi({\bf f^*},x).
\end{equation}
Ясно, то
\[
\psi_{k,h}({\bf f^*},x)= \Psi_k\left(\frac{x}{h}\right)
\]
и если \({\bf f^*_i}\) сдвиг последовательности \({\bf f^*}\), то
\[
\psi_{k,h}({\bf f^*_i},x)= \Psi_k\left(\frac{x}{h}-i\right).
\]
Отсюда и из линейности оператора \(\psi_{k,h}\) следует
\begin{equation}\label{s.143}
\psi_{k,h}({\bf f},x)=
\psi_{k,h}\left(\sum_{i\in\mathbb{Z}}\hat{f}_{i,0}{\bf f^*_i},x \right)=
\sum_{i\in\mathbb{Z}}\hat{f}_{i,0} \psi_{k,h}\left({\bf f^*_i},x \right)=
\sum_{i\in\mathbb{Z}}\hat{f}_{i,0}
\Psi_k\left(\frac{x}{h}-i\right),
\end{equation} следовательно, для любой последовательности \({\bf f}\in\ell_\infty\), любого \(x\in\mathbb{R}\) и \(h>0\) имеют место равенства
\begin{equation}\label{s.144}
\psi_{k,h}({\bf f},x)=\sum_{i\in\mathbb{Z}}\hat{f}_{i,0}
\Psi_k\left( \frac{x}{h}-i\right).
\end{equation}
Из построения функции \(\Psi_k(x)\), вытекает, что она имеет конечный носитель
\(\left[-\frac{1}{2}-\sum_{\nu=0}^{k-1}\left(\frac{1}{2}\right)^\nu,\frac{1}{2}+\sum_{\nu=0}^{k-1}\left(\frac{1}{2}\right)^\nu\right]\),
а функция \(\Psi(x)\) имеет конечный носитель \(\left[-\frac{5}{2},\frac{5}{2}\right]\). Исходя из этого следует, что для
\(x\in \left[x_{i-\frac 12},x_{i+\frac 12}\right]\), \(i\in\mathbb{Z}\) в равенствах (\ref{s.143}) и (\ref{s.144}) лишь пять слагаемых отличны от нуля.
Таким образом для \(x\in \left[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}\right]\) выполняются равенства
\begin{equation}\label{s.145} \psi_{k,h}({\bf f},x)=\sum_{\nu=i-2}^{i+2}\hat{f}_\nu
\Psi_k\left(\frac{x}{h}-\nu\right). \end{equation}
и
\begin{equation}\label{s.146} \psi_h({\bf f},x)=\sum_{\nu=i-2}^{i+2}\hat{f}_\nu
\Psi\left(\frac{x}{h}-\nu\right). \end{equation}
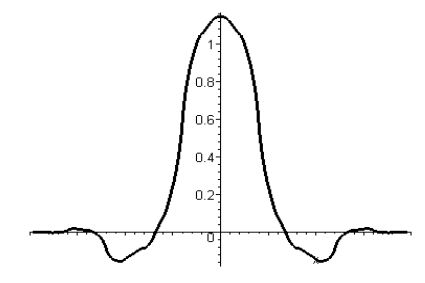
В случае, когда задана функция \(f\in C(\mathbb{R})\) и значения \(\widetilde{f}_{i,0}\) определены равенствами
\[
\widetilde{f}_{i,0}=\frac{2^k}{h}
\int_{(i-1/2)h2^{-k}}^{(i+1/2)h2^{-k}}
f(x)\,dx,
\]
и множество этих значений обозначим через \({\bf f^k }\) (\({\bf f }={\bf f^0 }={\bf f}\)). Кроме того, вместо
\(\psi_{k,h}({\bf f},x)\) будем писать \(\psi_{k,h}(f,x)\).
Из метода построения оператора \(\psi_h\) следует, что \begin{equation}\label{s.147} \psi_{h2^{-k}}
\left(\psi_{h2^{-m}}({\bf f},\cdot),x\right)= \psi_{h2^{-k}} \left({\bf f},x\right), \end{equation} \begin{equation}\label{s.148} \psi_{h2^{-k}}
\left({\bf\hat{f}^k},x\right)= \psi_{h} \left({\bf f},x\right) \end{equation} и \begin{equation}\label{s.149} \psi_{h2^{-k}}
\left({\bf{f}^\nu},x\right)= \psi_{h2^{-k}} \left({\bf f},x\right). \end{equation}
Аппроксимативные свойства интерполяионного в среднем метода subdivision
Приведем некоторые свойства метода восстановления \(\psi_k\).
Теорема 3.
Для всех \(x \in [-\frac 12,\frac 12]\) имеет место масштабирующее равенство
\begin{equation}\label{s.151}
\Psi(x) = \Psi(2x+1) + \Psi(2x-1)
+ \frac{1}{8}\left( \Psi(2x+3) + \Psi(2x-3) \right)-
\frac{1}{8}\left( \Psi(2x+5) + \Psi(2x-5) \right).
\end{equation}
Пусть \(f \in C(\mathbb{R})\) и \(\|\psi\|_{C(\mathbb{R})\to C(\mathbb{R})}\) - норма оператора \(\psi\), то есть
\[
\|\psi_h\|_{C(\mathbb{R})\to C(\mathbb{R})}=
\sup_{\|f\|_{C(\mathbb{R})}\le 1}\|\psi(f)\|_{C(\mathbb{R})}
\]
Положим
\[
N(x)=\sum_{i \in \mathbb{Z}} \left| \Psi\left(\frac{x}{h}-i\right) \right|
\]
Теорема 4.
Для любого \(h>0\) справедливо равенство
\begin{equation}\label{s.153}
\|\psi_h\| = \|\psi_h\|_{C(\mathbb{R})\to C(\mathbb{R})} = \|N\|_{C(\mathbb{R})}.
\end{equation}
Непосредственные расчеты показали, что
\begin{equation}\label{s.154}
\| \psi_h \| = \| N(x) \|_{C[-\frac{1}{2},\frac{1}{2}]} \approx 1.33333
\end{equation}
Положим для \(x \in \left[-\frac{1}{2},\frac{1}{2}\right]\)
\[
K(x)=x^3 - \sum_{i=-2}^{2} \int_{\frac{2i-1}{2}}^{\frac{2i+1}{2}} t^3 dt \, \Psi(x-i)
\]
Теорема 5.
Пусть функция \(f\) такова, что \(f^\nu \in C(\mathbb{R})\), \(\nu{=}0,1,...,4\), тогда
для \(x \in \left[(i-\frac{1}{2})h,(i+\frac{1}{2})h\right]\)
равномерно по \(i \in \mathbb{Z}\) выполняется соотношение
\begin{equation}\label{s.156}
f(x)-\psi_h(f,x)=\frac{h^3}{3!}f_i^{(3)}K\left(\frac{x}{h}-i\right)+O(h^4).
\end{equation}
Послойная передача данных по их средним значениям
Передача информации о функции по ее средним значениям широко используется в практических приложениях. Прежде всего это
связано с тем, что любые измерения снимают не точные, а усредненные значения. Результаты теоремы 5
говорят, что использование предложенного метода расслоения даст погрешность восстановления порядка \(h^3\) и при этом
(согласно утверждению 4) ошибка измерения вырастет не более чем в 4/3 раза.
С другой стороны, в силу локальности рассмотренного метода расслоения, можно его использовать по шагово - вначале
определить значения \(h\) и те значения аргумента, при которых метод расслоения дает требуемую точность восстановления
\(\varepsilon\). Далее рассматривать лишь те участки функции, которые восстанавливаются с точностью \(\varepsilon\) при
значении \(h/2\) и т.д., пока не найдется последний участок, для восстановления которого требуется шаг \(h2^{-m}\).
Покажем, что использование этого алгоритма дает тот же результат, что и применение метода с шагом \(h2^{-m}\) ко всей
функции целиком.
Действительно, пусть \(\varepsilon>0\) заданная погрешность восстановления и \( {\bf f^k}-{\bf \hat{f}^k}= {\bf
\delta^k}, \) где \({\bf \delta^k}=\delta^{k,0}+\delta^{k,1}\) и
\[
\delta^{k,0}= \left\{
\begin{array}{lc}
\delta_{i,k},&|\delta_{i,k}|>\varepsilon\\
0,&|\delta_{i,k}|\le\varepsilon\end{array}\right.,
\delta^{k,1}= \left\{
\begin{array}{lc}
\delta_{i,k},&|\delta_{i,k}|\le\varepsilon\\
0,&|\delta_{i,k}|>\varepsilon\end{array}\right.
\]
Положим
\[
\sigma_k(x)=f(x)-\psi_h(f,x)-\sum_{\nu=1}^k\psi_{h2^{-\nu}}({\bf \delta^\nu},x).
\]
Отсюда получаем
\[
\sigma_k(x)=f(x)-\psi_h(f,x)-\sum_{\nu=1}^k\psi_{h2^{-\nu}} ({\bf f^\nu}-{\bf \hat{f}^\nu},x)=
\]
\[
=f(x)-\psi_h({\bf f^0},x)-\psi_{h2^{-1}} ({\bf f^1},x)+\psi_{h2^{-1}}({\bf \hat{f}^1},x)
-\psi_{h2^{-2}}({\bf f^2},x)+\psi_{h2^{-2}}({\bf \hat{f}^2},x)+\ldots +\psi_{h2^{-k}}({\bf \hat{f}^k},x)=
\]
\[
=f(x)-\psi_h({\bf f^0},x)-\psi_{h2^{-1}}({\bf f^1},x)+ \psi_{h}({\bf \hat{f}^0},x)
-\psi_{h2^{-2}}({\bf f^2},x)+\psi_{h2^{-2}}({\bf \hat{f}^2},x)+\ldots +\psi_{h2^{-k}}({\bf \hat{f}^k},x)=
f(x)- \psi_{h2^{-k}}({\bf {f}},x).
\]
С другой стороны,
\[
\sigma_k(x)=f(x)-\psi_h(f,x)-\sum_{\nu=1}^k\psi_{h2^{-\nu}} (\delta^{k,0}+\delta^{k,1},x)=
f(x)-\psi_h(f,x)-\sum_{\nu=1}^k\psi_{h2^{-\nu}} (\delta^{k,0})-\sum_{\nu=1}^k\psi_{h2^{-\nu}}(\delta^{k,1},x).
\]
Следовательно, отсюда имеем
\[
f(x)-\psi_h(f,x)-\sum_{\nu=1}^k\psi_{h2^{-\nu}} (\delta^{k,0})=f(x)- \psi_{h2^{-k}}({\bf {f}},x)+
\sum_{\nu=1}^k\psi_{h2^{-\nu}}(\delta^{k,1},x).
\]
Отсюда и из теоремы 4 сразу получаем
\[
\left|f(x)-\psi_h(f,x)-\sum_{\nu=1}^k\psi_{h2^{-\nu}} (\delta^{k,0})\right|\le \left|f(x)- \psi_{h2^{-k}}({\bf
{f}},x)\right|+ k\| N \|_{C[-\frac{1}{2},\frac{1}{2}]}\varepsilon.
\]
Таким образом имеем
\[
\left|f(x)-\psi_h(f,x)-\sum_{\nu=1}^k\psi_{h2^{-\nu}} (\delta^{k,0})\right|\le \left|f(x)- \psi_{h2^{-k}}({\bf
{f}},x)\right|+\frac{4}{3} k\varepsilon.
\]
Интерполяционный в среднем subdivision поверхностей
Определения и постановка задачи.
Через \(\ell^2_{\infty}\) обозначим линейное пространство всех ограниченных двумерных массивов
\[
\widetilde{F} = \{\widetilde{f}_{i,j,0}\}_{(i,j)\in\mathbb{Z}^2} =
\{\widetilde{f}_{i,j}\}_{(i,j)\in\mathbb{Z}^2}
\]
с нормой
\[
\|\widetilde{F}\|_{\ell_{\infty}^2} = \sup_{(i,j)\in\mathbb{Z}^2} |\widetilde{f}_{i,j}|.
\]
Введем некоторые обозначения необходимые нам в дальнейшем. Пусть \(\mathbb{E}\) измеримое множество из \(\mathbb{R}^2\), через
\(L_\infty(\mathbb{E})\) обозначим линейное пространство всех непрерывных ограниченных на \(\mathbb{E}\) функций \(f(x,y)\) с нормой
\begin{equation}\label{s.157}
\|f\|_{L_\infty(\mathbb{E})}=vraisup\left\{|f(x,y)||(x,y)\in\mathbb{E}\right\}, \end{equation}
\(L_p(\mathbb{E})\) \((p\in [1,\infty))\) -
пространство всех измеримых суммируемых на \(\mathbb{E}\) в \(p\)-й степени функций с нормой \begin{equation}\label{s.158}
\|f\|_{p(\mathbb{E})}=\left(\int_{\mathbb{E}}|f(x,y)|^pdxdy\right)^{1/p} \end{equation} и \(C(\mathbb{E})\) обозначим линейное пространство всех
непрерывных ограниченных на \(\mathbb{E}\) функций \(f(x,y)\) с нормой
\[
\|f\|_{C(\mathbb{E})}=\max_{(x,y)\in\mathbb{E}}|f(x,y)|.
\]
Пусть \({\Delta}^0\) есть разбиение плоскости на квадраты \({\Delta}_{i,j}^0\) (\(i,j\in\mathbb{Z}\)) с шагом \(h\) и вершинами в
точках \(\{M_{i,j}\}_{i,j\in\mathbb{Z}}=\{(x_{i,0},y_{j,0})\}_{i,j\in\mathbb{Z}} =\{(ih,jh)\}_{i,j\in\mathbb{Z}}\). Каждому значению
двумерного массива \(\widetilde{F}^0= \{\widetilde{f}_{i,j,0}\}_{i,j\in \mathbb{Z}}\) поставим в соответствие элемент
\({\Delta}^0_{i,j}\) из разбиения \({\Delta}^0\).
Зададим на множестве ограниченных массивов \(\widetilde{F}^0\) линейный функционал \(B(\widetilde{F}^0)=\sum
a_{i,j}\widetilde{f}_{i,j,0}\) и положим
\[B^{++}(\widetilde{F}^0)=B(\{\widetilde{f}_{i,j,0}\}_{i,j\in \mathbb{Z}}),\]
\[B^{ - }(\widetilde{F}^0)=B(\{\widetilde{f}_{-i,-j,0}\}_{i,j\in \mathbb{Z}}),\]
\[B^{-+}(\widetilde{F}^0)=B(\{\widetilde{f}_{-i,j,0}\}_{i,j\in \mathbb{Z}}),\]
\[B^{+-}(\widetilde{F}^0)=B(\{\widetilde{f}_{i,-j,0}\}_{i,j\in \mathbb{Z}}).\]
Определим точки \(M_{i-1/2,j,0},M_{i,j-1/2,0},M_{i-1/2,j-1/2,0}\) равенствами \begin{equation}\label{s.159}
M_{i-1/2,j,0}=\frac{1}{2}(M_{i,j}+M_{i-1,j}), \end{equation} \begin{equation}\label{s.160} M_{i,j-1/2,0}=\frac{1}{2}(M_{i,j}+M_{i,j-1}), \end{equation}
\begin{equation}\label{s.161} M_{i-1/2,j-1/2,0}=\frac{1}{4}(M_{i,j-1}+M_{i-1,j}+M_{i,j}+M_{i-1,j-1}). \end{equation}
Через \(\widetilde{F}^0_{\nu,\mu}=\{\widetilde{f}_{i+\nu,j+\mu,0}\}_{i,j\in \mathbb{Z}}\) обозначим сдвиг массива \(\widetilde{F}^0\).
Определим новую решетку \(\Delta^{k+1}\) и новый массив \(\widetilde{F}^{k+1}=\{\widetilde{f}_{i,j,k+1}\}_{i,j\in \mathbb{Z}}\)
равенствами
\begin{equation}\label{s.162}
\begin{array}{llll}
M_{2i,2j,k} & = M_{i,j,{k-1}},& \widetilde{f}_{2i,2j,k} & = B^{++}(\widetilde{F}^{k-1}_{i,j}),\\
M_{2i-1,2j,k} & = M_{i-1/2,j,{k-1}},& \widetilde{f}_{2i-1,2j,k} & = B^{-+}(\widetilde{F}^{k-1}_{i,j}),\\
M_{2i,2j-1,k} & = M_{i,j-1/2,{k-1}},& \widetilde{f}_{2i,2j-1,k} & = B^{+-}(\widetilde{F}^{k-1}_{i,j}),\\
M_{2i-1,2j-1,k} & = M_{i-1/2,j-1/2,{k-1}},& \widetilde{f}_{2i-1,2j-1,k} & = B^{ - }(\widetilde{F}^{k-1}_{i,j}).\\
\end{array}
\end{equation}
Для фиксированных \((i,j)\in\mathbb{Z}^2\) соединим точки \(M_{i-1,j,k},\) \(M_{i,j,k},\) \(M_{i,j-1,k},\) \(M_{i-1,j-1,k}\) с центром
\(M_{i-1/2,j-1/2,k}\) соответствующего квадрата. Таким образом получим триангуляцию плоскости на равнобедренные
прямоугольные треугольники. Непрерывную на всей плоскости функцию двух переменных назовем k-полигоном, если она на
каждом из этих треугольников совпадает с некоторой плоскостью.
Через \(\psi_{k,h}(B,\widetilde{F},x,y)\) обозначим k-полигон интерполирующий в узлах \(M_{i,j,k}, i,j\in\mathbb{Z}\), \(k\in\mathbb{N}\)
значения \(\frac{1}{4}(\widetilde{f}_{i,j,k}+\widetilde{f}_{i-1,j,k}+\widetilde{f}_{i,j-1,k}+ \widetilde{f}_{i-1,j-1,k}),\) а в точках
\(M_{i-1/2,j-1/2,k}\) принимающий значения \(\widetilde{f}_{i,j,k}.\)
Если поточечный предел последовательности \(\psi_{k,h}(B,\widetilde{F},x,y)\) при \(k\to\infty\) существует, то будем
обозначать его через \(\psi_{h}(B,\widetilde{F},x,y)\). В дальнейшем мы будем рассматривать только те операторы \(B\), при
которых функция \(\psi_{h}(B,\widetilde{F},x,y)\) существует и единственна.
В случае, когда задана функция \(f\in C(\mathbb{R}^2)\) и значения \(\widetilde{f}_{i,j,0}\) определены равенствами
\[
\widetilde{f}_{i,j,0}=\frac{1}{h^2}
\int_{(i-1)h}^{ih}
\int_{(j-1)h}^{jh} f(x,y)\,dx\,dy,
\]
вместо \(\psi_{k,h}(B,\widetilde{F},x,y)\) будем писать \(\psi_{k,h}(B,f,x,y)\).
Из построения оператора \(\psi_{k,h}(B,\widetilde{F})\) следует, что для любых \(k,\nu=0,1,2,\ldots\) имеют место равенства
\begin{equation}\label{s.163} \psi_{k,h2^{-\nu}}(B,\widetilde{F}^\nu,x,y)= \psi_{k,h2^{-\nu}}(B,\psi_{\nu,h}(\widetilde{F}),x,y)=
\psi_{k+\nu,h}(B,\widetilde{F},x,y). \end{equation}
Переходя к пределу при \(k\to\infty\), получаем \begin{equation}\label{s.164}
\psi_{h2^{-\nu}}(B,\widetilde{F}^\nu,x,y)=\psi_{h}(B,\widetilde{F},x,y). \end{equation} Из построения функции \(\psi_{h}(B,\widetilde{F},x,y)\)
ясно, что \begin{equation}\label{s.165} \psi_{h}(B,\widetilde{F},x,y)= \psi_{h/2^k}(\psi_{h}(B,\widetilde{F}),x,y). \end{equation} Кроме того
\begin{equation}\label{s.166} \psi_{h}(B,\widetilde{F}_{\nu,\mu},x,y)= \psi_{h}(B,\widetilde{F},x-\nu h,y-\mu h) \end{equation} и \begin{equation}\label{s.167}
\psi_{h}\left(B,\widetilde{F},x,y\right)= \psi_{H}\left(B,\widetilde{F},\frac{H}{h}x, \frac{H}{h}y\right). \end{equation}
Приведем один из методов построения функционала \(B\).
Набор из \(n\) пар индексов \((i,j)\in\mathbb{Z}^2\), содержащих \((0,0)\) назовем апертурой порядка \(n\) и будем обозначать \(A^n\).
Объединение квадратов со сторонами параллельными координатным осям и равными единице с левым нижним углом \((i,j)\)
(\((i,j)\in A^n\)) назовем геометрической апертурой и обозначим \({\cal A}^n\).
Каждый набор \({\cal B}\) чисел \(a_{i,j}\) (\((i,j)\in A^n\)) определяет функционал \begin{equation}\label{s.168} B(A^n,{\cal
B},\widetilde{F}^0)=\sum_{(i,j)\in A^n} a_{i,j}\widetilde{f}_{i,j,0}. \end{equation}
Приведем одну из возможных конструкций выбора коэффициентов \(a_{i,j}\).
Зафиксируем набор тестовых функций \(L^m=\{\ell^0,\ldots,\ell^m\}\) и коэффициенты \(a_{i,j}\) будем искать из условия
выполнения равенства
\begin{equation}\label{s.169} B(A^n,{\cal B},\widetilde{\ell}^k)= \frac{4}{h^2} \int_{h/2 }^{h}
\int_{h/2}^h \ell^k(x,y)\,dx\,dy\,\,\,\,(k=0,\ldots,m).
\end{equation}
Если эта система совместна, то решая ее, получаем конкретный функционал расслоения \(B(A^n(L^m),\widetilde{F}^0)\).
Апертуру \(A^n(L^m)\) в этом случае будем называть апертурой точной на множестве \(L^m=\{\ell^0,\ldots,\ell^m\}\). Если
равенство (\ref{s.169}) выполняется для всех маномов \(x^\nu y^\mu\) таких, что \(\nu+\mu\le m+1\), то множество всех таких
пар (\(\nu,\mu\)) обозначим через \({\cal P}({\cal A}^n,{\cal B})\). Множество всех пар (\(\nu,\mu\)) таких, что
\(\nu+\mu=m+1\), для которых равенство (\ref{s.169}) не выполняется, обозначим через \({\widetilde{\cal P}}({\cal
A}^n,{\cal B})\).
Базисная функция
Пусть \(h=1\) и \( \widetilde{F}^* = \{\widetilde{f}^*_{0,i,j}\}_{(i,j)\in\mathbb{Z}^2}\), где
\[
\widetilde{f}^*_{0,i,j}= \left\{\begin{array}{cc}
1 & ,\nu{=}\mu{=}0; \\
0 & ,\nu,\mu\ne 0
\end{array}
\right.
\]
Положим
\[
\Psi_k({\cal A}^n,{\cal B},x,y)=\psi_{k,1}({\cal A}^n,{\cal B},\widetilde{F}^*,x,y)
\]
и
\[
\Psi({\cal A}^n,{\cal B},x,y)=\psi_1({\cal A}^n,{\cal B},\widetilde{F}^*,x,y).
\]
Ясно, что
\[
\psi_{k,h}({\cal A}^n,{\cal B},\widetilde{F}^*,x,y)= \Psi_k\left({\cal A}^n,{\cal B},\frac{x}{h},\frac{y}{h}\right)
\]
и если \(\widetilde{F}^*_{i,j}\) сдвиг массива \(\widetilde{F}^*\), то
\[
\psi_{k,h}({\cal A}^n,{\cal B},\widetilde{F}^*_{i,j},x,y)= \Psi_k\left({\cal A}^n,{\cal
B},\frac{x}{h}-i,\frac{y}{h}-j\right).
\]
Отсюда и из линейности оператора \(\psi_{k,h}({\cal A}^n,{\cal B})\) следует
\[ \psi_{k,h}({\cal A}^n,{\cal B},\widetilde{F},x,y)=
\psi_{k,h}\left({\cal A}^n,{\cal B},\sum_{(i,j)\in\mathbb{Z}^2}\widetilde{f}_{i,j,0}
\widetilde{F}^*_{i,j},x,y \right)=\] \begin{equation}\label{s.170} = \sum_{(i,j)\in\mathbb{Z}^2}\widetilde{f}_{i,j,0} \psi_{k,h}\left({\cal
A}^n,{\cal B},\widetilde{F}^*_{i,j},x,y \right)=
\sum_{(i,j)\in\mathbb{Z}^2}\widetilde{f}_{i,j,0}
\Psi_k\left({\cal A}^n,{\cal B},\frac{x}{h}-i,\frac{y}{h}-j \right).
\end{equation} Таким образом, если \(\psi_h({\cal A}^n,{\cal B},\widetilde{F},x,y)\) существует, то для любого массива
\(\widetilde{F}\in\ell_\infty^2\) и любого \((x,y)\in\mathbb{R}^2\) и \(h>0\) имеет место соотношение \begin{equation}\label{s.171}
\psi_h({\cal A}^n,{\cal B},\widetilde{F},x,y)=\sum_{(i,j)\in\mathbb{Z}^2}\widetilde{f}_{i,j,0}
\Psi\left({\cal A}^n,{\cal B}, \frac{x}{h}-i,\frac{y}{h}-j \right).
\end{equation}
Объединение всех сдвигов вдоль координатных осей на целые числа апертуры \({\cal A}^n\) и ее отображений относительно
координатных осей и точки \((0,0)\) таких, что все они содержат точку \((0,0)\) обозначим \({\cal G}^n\). Радиус множества
\({\cal G}^n\) обозначим \(R({\cal A}^n)\).
Носитель функции \(\Psi\left({\cal A}^n,{\cal B}\right)\) есть \({\cal G}^n\), таким образом равенства (\ref{s.170}) и
(\ref{s.171}) можно переписать в виде \begin{equation}\label{s.172}
\psi_{k,h}({\cal A}^n,{\cal B},\widetilde{F},x,y)=\sum_{(i,j)\in {\cal G}}\widetilde{f}_{i,j,0}
\Psi_k\left({\cal A}^n,{\cal B}, \frac{x}{h}-i,\frac{y}{h}-j \right),
\end{equation} и \begin{equation}\label{s.173}
\psi_h({\cal A}^n,{\cal B},\widetilde{F},x,y)=\sum_{(i,j)\in {\cal G}}\widetilde{f}_{i,j,0}
\Psi\left({\cal A}^n,{\cal B}, \frac{x}{h}-i,\frac{y}{h}-j \right).
\end{equation}
Многие свойства метода восстановления \(\psi_h({\cal A}^n,{\cal B},\widetilde{F})\) (или \(\psi_{k,h}({\cal A}^n,{\cal
B},\widetilde{F})\)) следуют из свойств базисных функций \(\Psi({\cal A}^n,{\cal B},x,y)\) (или \(\Psi_k({\cal A}^n,{\cal
B},x,y)\)) и равенств (\ref{s.172}) и (\ref{s.173}).
Из (\ref{s.163}) следует, что
\[\psi_{h}({\cal A}^n,{\cal B},\widetilde{F}^0,x,y)=\psi_{h/2}({\cal A}^n,{\cal B},\widetilde{F}^1,x,y),\]
в частности,
\[\psi_{1}({\cal A}^n,{\cal B},\widetilde{F}^{*,0},x,y)=\psi_{1/2}({\cal A}^n,{\cal B},\widetilde{F}^{*,1},x,y).\]
Поэтому \begin{equation}\label{s.174}
\Psi({\cal A}^n,{\cal B},x,y) =
\sum_{(\mu,\nu)\in \mathbb{Z}^2}
\widetilde{f}^{*,1}_{\nu,\mu} \Psi\left( {\cal A}^n,{\cal B},2x-\nu, 2y-\mu \right).
\end{equation} Если \((\nu,\mu)\) таковы, что \(0\le \nu,\mu\le 4\), то равенство (\ref{s.174}) можно записать в виде
\[
\Psi({\cal A}^n,{\cal B},x,y) =
\sum_{\mu,\nu=-4}^3
\alpha_{\nu,\mu} \Psi\left( {\cal A}^n,{\cal B},2x-\nu, 2y-\mu \right),
\]
где \begin{equation}\label{s.175} (\alpha_{i,j})_{i,j=-4}^3=\left(
\begin{array}{llllllll}
a_{2,2} &a_{-1,2} &a_{1,2} &a_{0,2}& a_{0,2} &a_{1,2} &a_{-1,2} &a_{2,2}\cr
a_{2,-1}&a_{-1,-1}&a_{1,-1}&a_{0,-1}& a_{0,-1}&a_{1,-1}&a_{-1,-1}&a_{2,-1}\cr
a_{2,1 }&a_{-1,1}&a_{1,1}&a_{0,1}& a_{0,1 }&a_{1,1}&a_{-1,1}&a_{2,1}\cr
a_{2,0 }&a_{-1,0}&a_{1,0}&a_{0,0}& a_{0,0 }&a_{1,0}&a_{-1,0}&a_{2,0}\cr
a_{2,0 }&a_{-1,0}&a_{1,0}&a_{0,0}& a_{0,0 }&a_{1,0}&a_{-1,0}&a_{2,0}\cr
a_{2,1 }&a_{-1,1}&a_{1,1}&a_{0,1}& a_{0,1 }&a_{1,1}&a_{-1,1}&a_{2,1}\cr
a_{2,-1}&a_{-1,-1}&a_{1,-1}&a_{0,-1}& a_{0,-1}&a_{1,-1}&a_{-1,-1}&a_{2,-1}\cr
a_{2,2} &a_{-1,2} &a_{1,2} &a_{0,2}& a_{0,2} &a_{1,2} &a_{-1,2} &a_{2,2}
\end{array}
\right). \end{equation}
О норме оператора \(\psi_{k,h}({\cal A}^n,{\cal B},f)\).
Пусть \({\cal L}\) есть линейный оператор отображающий пространство \(X\) в пространство \(Y\). Как обычно, нормой оператора
\({\cal L}\) будем называть величину \begin{equation}\label{s.176} \|{\cal L}\|_{X\to Y}=\sup_{\|F\|_X\le 1}\|{\cal L}(F)\|_{Y}.\end{equation}
Положим для \(k \in \mathbb{N}\)
\[
N_k({\cal A}^n,{\cal B},x,y)=\sum_{(i,j) \in \mathbb{Z}^2} \left| \Psi_k\left({\cal A}^n,{\cal B},x-i, y-j\right) \right|.
\]
Теорема 6.
Справедливо равенство
\begin{equation}\label{s.178}
\|\psi_{k,h}({\cal A}^n,{\cal B})\|_{\ell^2_{\infty}\to C(\mathbb{R}^2)} =
\|\psi_{k,h}({\cal A}^n,{\cal B})\|_{L_{\infty}(\mathbb{R}^2)\to C(\mathbb{R}^2)} =
\end{equation}
\[=
\|\psi_{k,h}({\cal A}^n,{\cal B})\|_{C(\mathbb{R}^2)\to C(\mathbb{R}^2)} =
\|N_k({\cal A}^n,{\cal B})\|_{C([0,1]\times [0,1])}.
\]
Доказательство. Из (\ref{s.173}) и (\ref{s.174}) вытекает, что
\[
\|\psi_{k,h}({\cal A}^n,{\cal B})\|_{\ell^2_{\infty}\to C(\mathbb{R}^2)} =
\sup_{\|F\|_{\ell^2_{\infty}}\le 1} \left\|
\sum_{(\mu,\nu)\in\mathbb{Z}^2}
\widetilde{f}_{\nu,\mu} \Psi_k\left({\cal A}^n,{\cal B},\frac{x}{h}-\nu, \frac{y}{h}-\mu\right)
\right\|_{C(\mathbb{R}^2)}\le
\]
\[
\le \sup_{\|F\|_{\ell^2_{\infty}}\le 1}
\sum_{(\mu,\nu)\in\mathbb{Z}^2}\left\|
\widetilde{f}_{\nu,\mu} \Psi_k\left({\cal A}^n,{\cal B},\frac{x}{h}-\nu, \frac{y}{h}-\mu\right)
\right\|_{C(\mathbb{R}^2)}\le
\]
\[
\le \sup_{(x,y) \in \mathbb{R}^2}
\sum_{(\mu,\nu)\in\mathbb{Z}^2}
\left| \Psi_k\left({\cal A}^n,{\cal B},\frac{x}{h}-\nu, \frac{y}{h}-\mu\right) \right| =
\| N_k({\cal A}^n,{\cal B}) \|_{C([0,1]\times [0,1])}.
\]
Функция \(N_k({\cal A}^n,{\cal B},x,y)\) есть 1-периодическая непрерывная функция по каждой переменной, поэтому
существует точка \((\hat{x},\hat{y})\in [0,1]\times [0,1]\) такая, что
\[
N_k({\cal A}^n,{\cal B},\hat{x},\hat{y})=
\max_{(x,y)\in \mathbb{R}^2} N_k({\cal A}^n,{\cal B},x,y).
\]
Через \(F_0\) обозначим двумерный массив со значениями
\[
{\rm sign} \Psi_k({\cal A}^n,{\cal B},\hat{x}-i, \hat{y}-j)
\]
на квадратах
\( \left(ih,(i+1)h\right) \times \left(jh,(j+1)h\right)\).
Тогда
\[
\|\psi_{k,h}({\cal A}^n,{\cal B})\|_{\ell^2_{\infty}\to C(\mathbb{R}^2)}\ge
\frac{\|\psi_{k,h}({\cal A}^n,{\cal B},F_0)\|_{C(\mathbb{R}^2)}} {\|F_0\|_{\ell^2(\infty)}}= \|\psi_{k,h}({\cal A}^n,{\cal
B},F_0)\|_{C(\mathbb{R}^2)}\ge\]
\[\ge
|\psi_{k,h}({\cal A}^n,{\cal B},F_0,\hat{x}h,\hat{y}h)|\ge
\sum_{(\mu,\nu)\in\mathbb{Z}^2}
{\rm sign} \Psi_k({\cal A}^n,{\cal B},\hat{x}-\nu, \hat{y}-\mu)
\Psi_k({\cal A}^n,{\cal B},\hat{x}-\nu, \hat{y}-\mu)=\]
\[
=\|N_k({\cal A}^n,{\cal B})\|_{C([0,1]\times [0,1])}.
\]
Первое утверждение доказано, теперь докажем второе утверждение.
Пусть \(f \in L_\infty(\mathbb{R}^2)\) и
\[
\widetilde{f}_{\nu,\mu} =
\frac{1}{h^2}
\int_{\mu h }^{(\mu+1)h}
\int_{\nu h}^{(\nu+1) h}
f(t,\tau)\,dt\,d\tau
\,\,\,\,\,\, (\nu,\mu \in \mathbb{Z}).
\]
Аналогично предыдущему получаем
\[
\|\psi_{k,h}({\cal A}^n,{\cal B})\|_{L_\infty(\mathbb{R}^2)\to C(\mathbb{R}^2)} =
\sup_{\|f\|_{L_{\infty}(\mathbb{R}^2)}\le 1} \left\|
\sum_{(\mu,\nu)\in\mathbb{Z}^2}
\widetilde{f}_{\nu,\mu} \Psi_k\left({\cal A}^n,{\cal B},\frac{x}{h}-\nu, \frac{y}{h}-\mu\right)
\right\|_{C(\mathbb{R}^2)}\le
\]
\[
\le \sup_{(\mu,\nu)\in\mathbb{Z}^2} |\widetilde{f}_{\nu,\mu}| \sup_{(x,y) \in \mathbb{R}^2}\sum_{(\mu,\nu)\in\mathbb{Z}^2}
\left| \Psi_k\left({\cal A}^n,{\cal B},\frac{x}{h}-\nu, \frac{y}{h}-\mu\right) \right| =
\sup_{(\mu,\nu)\in\mathbb{Z}^2} |\widetilde{f}_{\nu,\mu}| \| N_k({\cal A}^n,{\cal B}) \|_{C([0,1]\times [0,1])}.
\]
Отсюда и из очевидного неравенства
\[
\sup_{(\mu,\nu)\in\mathbb{Z}^2} |\widetilde{f}_{\nu,\mu}|\le \|f\|_{L_\infty(\mathbb{R}^2)}
\]
получаем \begin{equation}\label{s.179} \|\psi_{k,h}({\cal A}^n,{\cal B},f)\|_{C(\mathbb{R}^2)}\le \|f\|_{L_\infty(\mathbb{R}^2)}\| N_k({\cal
A}^n,{\cal B}) \|_{C([0,1]\times [0,1])} \end{equation} и \begin{equation}\label{s.180} \|\psi_{k,h}({\cal A}^n,{\cal B})\|_{C(\mathbb{R}^2)\to
C(\mathbb{R}^2)}\le \|\psi_{k,h}({\cal A}^n,{\cal B})\|_{L_\infty(\mathbb{R}^2)\to C(\mathbb{R}^2)} \le \| N_k({\cal A}^n,{\cal B})
\|_{C([0,1]\times [0,1])}. \end{equation}
Функция \(N_k(x,y)\) есть 1-периодическая непрерывная функция по каждой переменной, поэтому существует точка
\((\hat{x},\hat{y})\) такая, что
\[
N_k({\cal A}^n,{\cal B},\hat{x},\hat{y})=\max_{(x,y)\in \mathbb{R}^2} N_k({\cal A}^n,{\cal B},x,y).
\]
Через \(f^*(x,y)\) обозначим функцию из \(L_\infty(\mathbb{R}^2)\), принимающую значения
\[
{\rm sign} \Psi_k\left({\cal A}^n,{\cal B},\hat{x}-i, \hat{y}-j\right)
\]
на квадратах \( ((ih,(i+1)h)) \times ((jh,(j+1)h))\)
и
\[
f^*(ih,y)=\frac{1}{2}(f^*(ih+0,y)+f^*(ih-0,y)) \,\,\,\,(y\ne jh),
\]
\[
f^*(x,jh)=\frac{1}{2}(f^*(x,jh+0)+f^*(x,jh-0)) \,\,\,\,(x\ne ih),
\]
\[
f^*(ih,jh)=\frac{1}{4}(f^*(ih+0,jh+0)+f^*(ih+0,jh-0))+f^*(ih-0,jh+0)+f^*(ih-0,jh-0)).
\]
Тогда
\[
\widetilde{f}^*_{\nu,\mu}=
{\rm sign} \Psi_k\left({\cal A}^n,{\cal B},\hat{x}-i, \hat{y}-j\right)
\]
и аналогично предыдущему получаем \begin{equation}\label{s.181} \|\psi_{k,h}({\cal A}^n,{\cal B},f^*)\|_{C(\mathbb{R}^2)}\ge \| N_k({\cal
A}^n,{\cal B}) \|_{C([0,1]\times [0,1])}. \end{equation} Положим
\[
f_\delta(x,y)=\frac{1}{4\delta^2}\int_{x-\delta}^{x+\delta} \int_{y-\delta}^{y+\delta}f(u,v)du\,dv.
\]
Ясно, что для любой функции \(f\in L_\infty(\mathbb{R}^2)\) и произвольного \(0\lt\delta\lt h/2\) будет \(f_\delta\in C(\mathbb{R}^2)\) и
\[
\|f_\delta\|_{C(\mathbb{R}^2)}=\|f\|_{L_{\infty}(\mathbb{R}^2)}.
\]
Кроме того, для любого \(\varepsilon>0\) найдется такое \(\delta>0\), что
\[
\|\psi_{k,h}({\cal A}^n,{\cal B},f^*_\delta)\|_{C(\mathbb{R}^2)}\le \|\psi_{k,h}({\cal A}^n,{\cal
B},f^*)\|_{C(\mathbb{R}^2)}-\varepsilon.
\]
Отсюда
\[
\|\psi_{k,h}({\cal A}^n,{\cal B})\|_{C(\mathbb{R}^2)\to C(\mathbb{R}^2)}\ge
\frac{\|\psi_{k,h}({\cal A}^n,{\cal B},f^*_\delta)\|_{C(\mathbb{R}^2)}} {\|f^*_\delta\|_{C(\mathbb{R}^2)}}\ge \| N_k({\cal
A}^n,{\cal B}) \|_{C([0,1]\times [0,1])}- \varepsilon.
\]
Учитывая произвольность \(\varepsilon\), из полученного неравенства и из (\ref{s.181}) сразу получаем доказательство
требуемого утверждения.
Следствие 1.
\[
\|\psi_{h}({\cal A}^n,{\cal B})\|_{\ell^2_{\infty}\to C(\mathbb{R}^2)} =
\|\psi_{h}({\cal A}^n,{\cal B})\|_{L_{\infty}(\mathbb{R}^2)\to C(\mathbb{R}^2)} =
\|\psi_{h}({\cal A}^n,{\cal B})\|_{C(\mathbb{R}^2)\to C(\mathbb{R}^2)} =
\|N({\cal A}^n,{\cal B})\|_{C([0,1]\times [0,1])}.
\]
О погрешности приближения.
Пусть \(L^m\) множество маномов \(x^\nu y^\mu\) для \((\nu,\mu)\in {\cal P}({\cal A}^n,{\cal B})\), где \(\nu+\mu\le m+1\) и
\(A^n=A^n(L^m)\).
Для
\((x,y) \in \left[ 0, 1 \right]{\times}\left[0, 1 \right]\)
положим \begin{equation}\label{s.183}
K_{\nu,\mu}({\cal A}^n,{\cal B},x,y) = x^\nu y^\mu -
\sum_{(i,j)\in\mathbb{Z}^2}
\left(
\int_{i}^{(i+1)}
\int_{j}^{(j+1)}
t^\nu p^\mu \, dt \, dp
\right) \Psi({\cal A}^n,{\cal B}, x - i, y - j ).
\end{equation}
Теорема 7.
Пусть функция \(f\) такова, что
\begin{equation}\label{s.185}
\frac{\partial f^{\nu+\mu}}{\partial x^\nu\partial y^\mu}
\in C(\mathbb{R}^2)
\,\,\,\,\,\nu,\mu=0,1,\ldots,m+1,\,\,\,\,\nu+\mu \le m+1,
\end{equation}
и величина \(\|\psi_h({\cal A}^n)\|\) конечна,
тогда для \((x,y)\in (ih,(i+1)h)\times (jh,(j+1)h)\)
равномерно по \(i,j\in\mathbb{Z}\) выполняется соотношение
\begin{equation}\label{s.186}
|f(x,y) - \psi_h({\cal A}^n,{\cal B},f,x,y)|=\end{equation}
\[
=\frac{h^{m+1}}{(m+1)!}
\Biggl|
\sum_{(\nu,\mu)\in{\cal P}({\cal A}^n,{\cal B})
}
C_{m+1}^{\nu}
\frac{\partial f^{m+1}}{\partial x^\nu \partial y^\mu}\Biggm|_{(ih,jh)}
K_{\nu,\mu}\left({\cal A}^n,{\cal B},\frac{x}{h},\frac{y}{h}\right)
\Biggr|+
\]
\[
{+}\beta(x,y)\left(1+\|N({\cal A}^n,{\cal B})\|_{C([0,1]\times [0,1]
)}\right)
\frac{h^{m+1}}{(m+1)!}\omega(f^{(m+1)},h(R({\cal A}^n)+1)),
\]
где \(|\beta(x,y)|\le 1\) и
\[\omega(f^{(m+1)},\delta)=\max_{
\stackrel{\scriptstyle \nu+\mu=m+1}{\scriptstyle \nu,\mu \ge 0}}
\sup_{|M'-M''|\lt \delta}
\left|f^{(\nu+\mu)}_{x^\nu y^\mu}(M')-f^{(\nu+\mu)}_{x^\nu y^\mu}(M'')\right|.
\]
Доказательство. Ввиду инвариантности относительно сдвига вдоль координатных осей на шаг кратный \(h\), без потери
общности можно считать \(i=j=0\).
Из (\ref{s.185}) следует, что для \((x,y)\in [0,h]\times [0,h]\) формулу Тейлора можно записать в виде \begin{equation}\label{s.187}
f(x,y)= \sum_{r=0}^{m+1}
\frac{1}{r!}
\sum_{
\stackrel{\scriptstyle \nu+\mu=r}{\scriptstyle \nu,\mu \ge 0}
}
C_{r}^{\nu}
\frac{\partial f^{r}}{\partial x^\nu \partial y^\mu}\Biggm|_{(0,0)}
x^\nu y^\mu
{+}\alpha(x,y)\varepsilon_h(f),
\end{equation} где
\[
\varepsilon_h(f)=\frac{h^{m+1}}{(m+1)!}\omega(f^{(m+1)},h(R({\cal A}^n)+1)).
\]
Тогда из линейности оператора \(\psi_h({\cal A}^n,{\cal B},f)\) следует, что
\[
\psi_h({\cal A}^n,{\cal B},f,x,y)=\]
\[=
\psi_h\left({\cal A}^n,{\cal B}, \sum_{r=0}^{m+1}
\frac{1}{r!}
\sum_{
\stackrel{\scriptstyle \nu+\mu=r}{\scriptstyle \nu,\mu \ge 0}
}
C_{r}^{\nu}
\frac{\partial f^{r}}{\partial x^\nu \partial y^\mu}\Biggm|_{(0,0)}
(\cdot)^\nu(\cdot\cdot)^\mu
{+}\alpha\varepsilon_h(f),x,y\right)=
\]
\[
= \sum_{r=0}^{m+1}
\frac{1}{r!}
\sum_{
\stackrel{\scriptstyle \nu+\mu=r}{\scriptstyle \nu,\mu \ge 0}
}
C_{r}^{\nu}
\frac{\partial f^{r}}{\partial x^\nu \partial y^\mu}\Biggm|_{(0,0)}
\psi_h({\cal A}^n,{\cal B},(\cdot)^\nu(\cdot\cdot)^\mu,x,y)
{+}\]
\[+ \psi_h({\cal A}^n,{\cal B},\alpha\varepsilon_h(f),x,y)=
\]
\[
= \sum_{(\nu,\mu)\in \widetilde{{\cal P}}({\cal A}^n,{\cal B})}
\frac{1}{(\nu+\mu)!}
C_{\nu+\mu}^{\nu}
\frac{\partial f^{\nu+\mu}}{\partial x^\nu \partial y^\mu}\Biggm|_{(0,0)}
\psi_h({\cal A}^n,{\cal B},(\cdot)^\nu(\cdot\cdot)^\mu,x,y)
{+}\]
\[
+\sum_{(\nu,\mu)\in {{\cal P}}({\cal A}^n,{\cal B})}
\frac{1}{(\nu+\mu)!}
C_{\nu+\mu}^{\nu}
\frac{\partial f^{\nu+\mu}}{\partial x^\nu \partial y^\mu}\Biggm|_{(0,0)}
\psi_h({\cal A}^n,{\cal B},(\cdot)^\nu(\cdot\cdot)^\mu,x,y)
{+}\]
\[+ \psi_h({\cal A}^n,{\cal B},\alpha\varepsilon_h(f),x,y).
\]
Если равенство (\ref{s.169}) выполняется на маномах \(x^\nu y^\mu\), то
\[
\psi_h({\cal A}^n,{\cal B},(\cdot)^\nu(\cdot\cdot)^\mu,x,y)=x^\nu y^\mu.
\]
Таким образом получаем
\[
\psi_h({\cal A}^n,{\cal B},f,x,y)= \sum_{(\nu,\mu)\in \widetilde{{\cal P}}({\cal A}^n,{\cal B})}
\frac{1}{(\nu+\mu)!}
C_{\nu+\mu}^{\nu}
\frac{\partial f^{\nu+\mu}}{\partial x^\nu \partial y^\mu}\Biggm|_{(0,0)}
x^\nu y^\mu {+}\]
\[
+\sum_{(\nu,\mu)\in {{\cal P}}({\cal A}^n,{\cal B})}
\frac{1}{(\nu+\mu)!}
C_{\nu+\mu}^{\nu}
\frac{\partial f^{\nu+\mu}}{\partial x^\nu \partial y^\mu}\Biggm|_{(0,0)}
\psi_h({\cal A}^n,{\cal B},(\cdot)^\nu(\cdot\cdot)^\mu,x,y)
{+}\]
\[+ \psi_h({\cal A}^n,{\cal B},\alpha\varepsilon_h(f),x,y).
\]
Следовательно
\[
f(x,y)-\psi_h({\cal A}^n,{\cal B},f,x,y)=
\]
\[
=\sum_{(\nu,\mu)\in {{\cal P}}({\cal A}^n,{\cal B})}
\frac{1}{(\nu+\mu)!}
C_{\nu+\mu}^{\nu}
\frac{\partial f^{\nu+\mu}}{\partial x^\nu \partial y^\mu}\Biggm|_{(0,0)}
(x^\nu y^\mu- \]
\[-
\psi_h({\cal A}^n,{\cal B},(\cdot)^\nu(\cdot\cdot)^\mu,x,y)) + \alpha(x,y)\varepsilon_h(f)-\psi_h({\cal A}^n,{\cal
B},\alpha\varepsilon_h(f),x,y)=
\]
\[
=\sum_{(\nu,\mu)\in {{\cal P}}({\cal A}^n,{\cal B})}
\frac{1}{(\nu+\mu)!}
C_{\nu+\mu}^{\nu}
\frac{\partial f^{\nu+\mu}}{\partial x^\nu \partial y^\mu}\Biggm|_{(0,0)}
(x^\nu y^\mu- \]
\[-\left.
\frac{1}{h^2} \sum_{(i,j)\in\mathbb{Z}^2}
\left(
\int_{ih}^{(i+1)h}
\int_{jh}^{(j+1)h}
t^\nu \tau^\mu \, dt \, d\tau
\right) \Psi\left({\cal A}^n,{\cal B}, \frac{x}{h} - i,
\frac{y}{h} - j \right)\right)+\]
\[
+ \alpha(x,y)\varepsilon_h(f)-\psi_h({\cal A}^n,{\cal B},\alpha\varepsilon_h(f),x,y).
\]
Так как
\[
\int_{ih}^{(i+1)h}
\int_{jh}^{(j+1)h}
t^\nu \tau^\mu \, dt \, d\tau=
h^{\nu+\mu+2}\int_{i}^{i+1}
\int_{j}^{j+1}x^\nu y^\mu \, dx \, dy,
\]
то
\[
x^\nu y^\mu- \frac{1}{h^2} \sum_{(i,j)\in\mathbb{Z}^2}
\left(
\int_{ih}^{(i+1)h}
\int_{jh}^{(j+1)h}
t^\nu \tau^\mu \, dt \, d\tau
\right) \Psi\left({\cal A}^n,{\cal B}, \frac{x}{h} - i,
\frac{y}{h} - j \right)=\]
\[=
h^{\nu+\mu}\left( \left(\frac{x}{h}\right)^\nu \left(\frac{y}{h}\right)^\mu-
\sum_{(i,j)\in\mathbb{Z}^2}
\left(
\int_{i}^{i+1}
\int_{j}^{j+1}
t^\nu \tau^\mu \, dt \, d\tau
\right) \Psi\left({\cal A}^n,{\cal B}, \frac{x}{h} - i,
\frac{y}{h} - j \right)
\right).
\]
Используя этот факт в (\ref{s.183}), получаем
\[
|f(x,y) - \psi_h({\cal A}^n,{\cal B},f,x,y)|=\]
\[
=\frac{h^{m+1}}{(m+1)!}
\Biggl|
\sum_{(\nu,\mu)\in{\cal P}({\cal A}^n,{\cal B})
}
C_{m+1}^{\nu}
\frac{\partial f^{m+1}}{\partial x^\nu \partial y^\mu}\Biggm|_{(ih,jh)}
K_{\nu,\mu}\left({\cal A}^n,{\cal B},\frac{x}{h},\frac{y}{h}\right)
\Biggr|+
\]
\[
+ \alpha(x,y)\varepsilon_h(f)- \psi_h({\cal A}^n,{\cal B},\alpha\varepsilon_h(f),x,y).
\]
Кроме того, если \((x,y)\in [0,h]\times [0,h]\), то
\[
\psi_h({\cal A}^n,{\cal B},\alpha\varepsilon_h(f),x,y)= \varepsilon_h(f) \sum_{(i,j)\in {\cal G}}\widetilde{\alpha}_{i,j}
\Psi\left({\cal A}^n,{\cal B}, \frac{x}{h}-i,\frac{y}{h}-j \right)\le
\]
\[
\le \varepsilon_h(f)\sup_{(x,y)\in {\cal G}}\left( |\widetilde{\alpha}(x,y)| \left|\sum_{(i,j)\in {\cal G}} \Psi\left({\cal
A}^n,{\cal B}, \frac{x}{h}-i,\frac{y}{h}-j \right)\right| \right).
\]
Отсюда и из следствия 1 вытекает, что
\[
\psi_h({\cal A}^n,{\cal B},\alpha\varepsilon_h(f),x,y)\le
\varepsilon_h(f)\sup_{(x,y)\in {\cal G}}
|\widetilde{\alpha}(x,y)| \|N\left({\cal A}^n,{\cal B}\right)\|_{C([0,1]\times [0,1])}\le
\]
\[\le
\varepsilon_h(f)
\|N\left({\cal A}^n,{\cal B}\right)\|_{C([0,1]\times [0,1])},
\]
следовательно,
\[
\alpha(x,y)\varepsilon_h(f)- \psi_h({\cal A}^n,{\cal B},\alpha\varepsilon_h(f),x,y)\le\]
\[\le
\left(1+\|N({\cal A}^n,{\cal B})\|_{C([0,1]\times [0,1])}\right)
\frac{h^{m+1}}{(m+1)!}\omega(f^{(m+1)},h(R({\cal A}^n)+1)).
\]
Тогда найдется \(\beta(x,y)\) \((|\beta(x,y)|\le 1)\) такое, что
\[
\alpha(x,y)\varepsilon_h(f)- \psi_h({\cal A}^n,{\cal B},\alpha\varepsilon_h(f),x,y)=\]
\[=\beta(x,y)
\left(1+\|N({\cal A}^n,{\cal B})\|_{C([0,1]\times [0,1])}\right)
\frac{h^{m+1}}{(m+1)!}\omega(f^{(m+1)},h(R({\cal A}^n)+1)),
\]
что и завершает доказательство.
Алгоритм послойного кодирования и передачи информации.
Тот факт, что оператор восстановления \(\psi_{h}({\cal A}^n,{\cal B},f,x,y)\) можно записать в виде (\ref{s.173}) (вместе
со свойствами функции \(\Psi({\cal A}^n,{\cal B},x,y)\)) позволяет построить метод послойного кодирования и передачи
информации.
Для фиксированного \(\varepsilon>0\) положим
\[
z^+_\varepsilon= \left\{
\begin{array}{cc}
z, & |z|\ge \varepsilon, \\
0, & |z|\lt \varepsilon,
\end{array}
\right.
\]
и
\begin{equation}\label{s.188}
z^-_\varepsilon=z-z^+_\varepsilon. \end{equation}
Назовем \(\mathfrak{G}_{1,h}({\cal A}^n,{\cal B},f,x,y)=\psi_{h}({\cal A}^n,{\cal B},f,x,y)\) восстановлением функции \(f(x,y)\) по
первому слою информации. Пусть \( f(x,y)-\mathfrak{G}_{1,h}({\cal A}^n,{\cal B},f,x,y) \) погрешность восстановления по первому
слою.
Для \(k>1\) восстановление на \(k-\)м слое информации определим рекуррентными соотношениями \begin{equation}\label{s.189}
\mathfrak{G}_{k,h}({\cal A}^n,{\cal B},f,x,y)=\mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f,x,y)+ \end{equation}
\[+
g_{h/2^{k-1}}\left({\cal A}^n,{\cal B},\left(f-\mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f)\right)^+_\varepsilon,x,y\right).
\]
Ясно, что
\[
f(x,y)-\mathfrak{G}_{k,h}({\cal A}^n,{\cal B},f,x,y)=f(x,y)- \mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f,x,y)+
\]
\[+
\psi_{h/2^{k-1}}\left({\cal A}^n,{\cal B},\left(f- \mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f)\right)- \left(f-
\mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f)\right)^-_\varepsilon,x,y\right).
\]
Из линейности метода \(\psi_{h/2^{m}}({\cal A}^n,{\cal B})\) следует, что
\[
f(x,y)-\mathfrak{G}_{k,h}({\cal A}^n,{\cal B},f,x,y)=f(x,y)- \mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f,x,y)+\]
\[+\psi_{h/2^{k-1}}\left({\cal A}^n,{\cal B},\left(f-
\mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f)\right),x,y\right)-\]
\[-
\psi_{h/2^{k-1}}\left({\cal A}^n,{\cal B},\left(f- \mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f)\right)^-_\varepsilon,x,y\right)=
\]
\[
=f(x,y)- \mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f,x,y)+\psi_{h/2^{k-1}}({\cal A}^n,{\cal B},f,x,y)-\]
\[-
\psi_{h/2^{k-1}}\left({\cal A}^n,{\cal B},\mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f),x,y\right)-
\]
\[-
\psi_{h/2^{k-1}}\left({\cal A}^n,{\cal B},\left(f- \mathfrak{G}_{k-1,h}({\cal A}^n,{\cal B},f)\right)^-_\varepsilon,x,y\right).
\]
Отсюда, из (\ref{s.189}), свойства (\ref{s.164}) и соотношений для нормы опрератора восстановления, сразу получаем
\[
f(x,y)-\mathfrak{G}_{k,h}({\cal A}^n,{\cal B},f,x,y)=
f(x,y)-\psi_{h/2^{k-1}}({\cal A}^n,{\cal B},f,x,y)+
\theta_k\varepsilon \|N({\cal A}^n,{\cal B})\|_{C(\mathbb{R}^2)},
\]
где \(\theta_k=\theta_k(f,h)\in [-1,1]\) и \(N(x)\) поточечная норма.
Таким образом, с учетом \(k-\)го слоя информации метод \(\mathfrak{G}_{k,h}({\cal A}^n,{\cal B},f)\) восстанавливает искомую
функцию с точностью до \(\theta_k\varepsilon \|N({\cal A}^n,{\cal B})\|_{C(\mathbb{R}^2)}\) так же, как и первоначальный метод
с шагом \(h/2^{k-1}\). При этом в реальных задачах количество ненулевых единиц информации, которое требуется для этого,
гораздо меньше, чем информации отличной от нуля, необходимой для метода \(\psi_{h/2^{k-1}}({\cal A}^n,{\cal B},f)\).
Примеры интерполяционного в среднем метода subdivision
Рассмотрим один способ построения функционала \(B\). Пусть \(P(\widetilde{F}^0,x,y)\) полином второго порядка
имеющий средние значения
\(\hat{f}_{0,-1,0}\), \(\hat{f}_{-1,0,0}\), \(\hat{f}_{0,0,0}\), \(\hat{f}_{1,0,0}\), \(\hat{f}_{0,1,0}\), \(\hat{f}_{1,1,0}\) на соответствующих им
квадратах (см. рисунок).

Положим \begin{equation}\label{p2s1} B(\widetilde{F}^0)=\hat{f}_{0,0,0}^{++} =
\frac{4}{h^2}
\int_{0}^{\frac h2 }
\int_{0}^{\frac h2} P(\widetilde{F}^0,x,y)\,dx\,dy=
\end{equation}
\[
= -\frac{1}{8}\hat{f}_{0,-1,0}
-\frac{1}{8}\hat{f}_{-1,0,0}
+\frac{17}{16}\hat{f}_{0,0,0}
+\frac{1}{16}\hat{f}_{1,0,0}
+\frac{1}{16}\hat{f}_{0,1,0}
+\frac{1}{16}\hat{f}_{1,1,0}.
\]
Таким образом формулы расслоения (\ref{s.162}) вид
\[
x_{2i,k} = x_{i,k-1} + \frac{h}{2^{k+1}}, \,\,\,\,
y_{2j,k} = y_{j,k-1} + \frac{h}{2^{k+1}}, \]
\[
\hat{f}_{2i,2j,k} =
-\frac{1}{8}\hat{f}_{i,j-1,k-1}
-\frac{1}{8}\hat{f}_{i-1,j,k-1}
+\frac{17}{16}\hat{f}_{i,j,k-1} +
\frac{1}{16}\hat{f}_{i+1,j,k-1}
+\frac{1}{16}\hat{f}_{i,j+1,k-1}
+\frac{1}{16}\hat{f}_{i+1,j+1,k-1},\]
\[
x_{2i-1,k} = x_{i,k-1} -\frac{h}{2^{k+1}},\,\,\,\,
y_{2j,k} = y_{j,k-1} + \frac{h}{2^{k+1}},
\]
\begin{equation}\label{pop}
\hat{f}_{2i-1,2j,k} =
-\frac{1}{8}\hat{f}_{i,j-1,k-1}
-\frac{1}{8}\hat{f}_{i+1,j,k-1}
+\frac{17}{16}\hat{f}_{i,j,k-1} +\end{equation}
\[
+\frac{1}{16}\hat{f}_{i-1,j,k-1}
+\frac{1}{16}\hat{f}_{i,j+1,k-1}
+\frac{1}{16}\hat{f}_{i-1,j+1,k-1},
\]
\[
x_{2i,k} = x_{i,k-1} + \frac{h}{2^{k+1}},\,\,\,\,
y_{2j-1,k} = y_{j,k-1} - \frac{h}{2^{k+1}}, \]
\[
\hat{f}_{2i,2j-1,k} =
-\frac{1}{8}\hat{f}_{i,j+1,k-1}
-\frac{1}{8}\hat{f}_{i-1,j,k-1}
+\frac{17}{16}\hat{f}_{i,j,k-1} +\]
\[
+\frac{1}{16}\hat{f}_{i+1,j,k-1}
+\frac{1}{16}\hat{f}_{i,j-1,k-1}
+\frac{1}{16}\hat{f}_{i+1,j-1,k-1},\]
\[
x_{2i-1,k} = x_{i,k-1} -\frac{h}{2^{k+1}}, \,\,\,\,
y_{2j-1,k} = y_{j,k-1} -\frac{h}{2^{k+1}}, \]
\[
\hat{f}_{2i-1,2j-1,k} =
-\frac{1}{8}\hat{f}_{i,j+1,k-1}
-\frac{1}{8}\hat{f}_{i+1,j,k-1}
+\frac{17}{16}\hat{f}_{i,j,k-1} +\]
\[
+\frac{1}{16}\hat{f}_{i-1,j,k-1}
+\frac{1}{16}\hat{f}_{i,j-1,k-1}
+\frac{1}{16}\hat{f}_{i-1,j-1,k-1}.\]
Функционал (\ref{p2s1}) можно определить исходя из других соображений. Пусть функция \(f(x,y)\) интегрируемая на
\(\mathbb{R}^2\) такова, что \(\frac{\partial^{\nu}f}{\partial x^n \partial y^m} \in C(\mathbb{R}^2)\) , \(\,\,\nu=0,\ldots,2, \,\,\,
n,m \ge 0, \,\,\, n+m \le 2\) и \(\hat{f}_{i,j}\) - ее среднее значение на квадратах \((x,y) \in (x_{i-1/2}, x_{i+1/2})
\times (y_{j-1/2}, \, y_{j+1/2})\). Функционал \(B\) будем искать в виде \begin{equation}\label{fhsuperpp}
\alpha_{0} \hat{f}_{1,1,0} +
\alpha_{1}\frac{\hat{f}_{0,1,0}+\hat{f}_{1,0,0}}{2} +
\alpha_{2} \hat{f}_{0,0,0} +
\alpha_{3}\frac{\hat{f}_{0,-1,0}+\hat{f}_{-1,0,0}}{2},
\end{equation} где коэффициенты \(\alpha_{i}\) выбираются так, чтобы разность между \(\hat{f}_{0,0,0}^{++}\) и выражением
(\ref{fhsuperpp}) имела как можно более высокий порядок точности. Используя формулу Тейлора нетрудно видеть, что это
условие сводится к системе линейных уравнений с решением \begin{equation}\label{foefs++}
\alpha_{0} = \frac{1}{16}; \,\,\,\,
\alpha_{1} = \frac{1}{8}; \,\,\,\,
\alpha_{2} = \frac{17}{16}; \,\,\,\,
\alpha_{3} = -\frac{1}{4}.
\end{equation} Таким образом мы придем к функционалу (\ref{p2s1}).
Рассмотрим еще один подход к построению функционала (\ref{p2s1}). Снова расслоение \(\hat{f}_{i,j,0}\) будем искать в виде
линейной комбинации (\ref{fhsuperpp}), но коэффициенты \(\alpha_{r}\,\,(r = 0, \ldots, 3)\) выберем из условия наивысшей
алгебраической точности. То есть так, чтобы соотношение (\ref{fhsuperpp}) обращалось в равенство для функций \(f(x,y) =
x^ny^m\,\,(n,m \ge 0, \,\,\, n+m \le 2)\). Это приводит к системе
\begin{equation}\label{sys3}
\left\{
\begin{array}{r}
\alpha_{0} + \alpha_{1} + \alpha_{2} + \alpha_{3} = 1; \\[6pt]
4\alpha_{0} + 2\alpha_{1} - 2\alpha_{3} = 1; \\[6pt]
13\alpha_{0} + 7\alpha_{1} + \alpha_{2} + 7\alpha_{3} = 1; \\[6pt]
\alpha_{0} = \frac{1}{16}. \\[6pt]
\end{array}
\right.
\end{equation}
Решением системы есть числа (\ref{foefs++}).
Ниже приведены графики базисной функции и поточечной нормы.
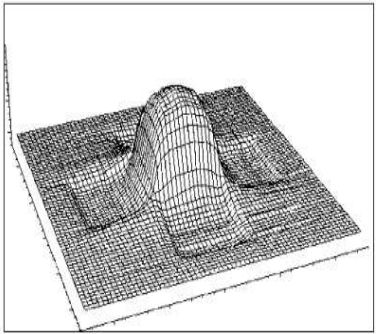
График базисной функции.
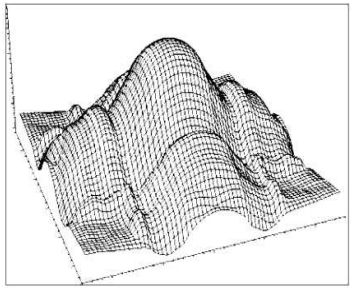
График поточечной нормы.
Приведем еще один пример соответствующий апертуре \(A\):
Выбирая в качестве тестовых функций маномы \(x^\nu y^\mu\) (\(0\le\nu,\mu\le 3\) и пары \(\nu=4,\mu=1\) и \(\mu=4,\nu=1\)),
приходим к функционалу (\ref{s.169}), где \begin{equation}\label{s.190} {\cal B}= \{a_{i,j}\}_{i,j=-1}^2 =\frac{1}{512} \left(\begin
{array}{cccc}
0 & -21& 0 & -3\\
0 & 102& 34 & 0\\
-50 & 409& 102 & -21\\
10 & -50& 0 & 0
\end{array}
\right). \end{equation}
Ниже приведены графики базисной функции и поточечной нормы.
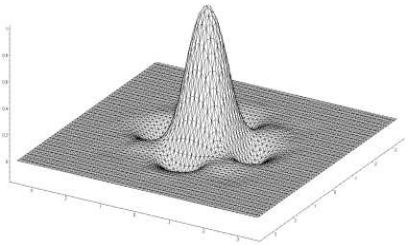
График функции \(\Psi_4(A,{\cal B},x,y)\).
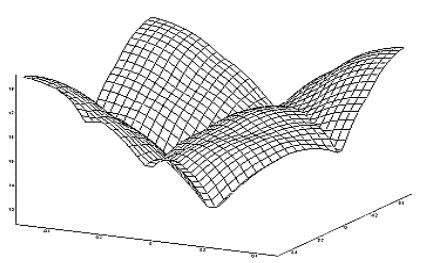
График функции \(N_6(A_1,{\cal B},x,y)\).
Для этого примера приведем соответствующие оценки.
В дальнейшем вместо \(\psi_{k,h}(A,{\cal B},\widetilde{F},x,y),\) \(\Psi_k\left(A,{\cal B},x,y\right)\) и т.д. будем писать
\(\psi_{k,h}(\widetilde{F},x,y),\) \(\Psi_k\left(x,y\right)\) и т.д.
Пусть
\[
\Delta^2_xz(x,y)=z(x+2^{-k}h,y)-2z(x,y)+z(x-2^{-k}h,y),
\]
\[
\Delta^2_yz(x,y)=z(x,y+2^{-k}h)-2z(x,y)+z(x,y-2^{-k}h),
\]
\[
\Delta^2_{-}z(x,y)=z(x,y)+z(x+2^{-k}h,y+2^{-k}h)-z(x+2^{-k}h,y)- z(x,y+2^{-k}h),
\]
\[
\Delta^2_{+}z(x,y)=z(x+2^{-k}h,y)+z(x,y+2^{-k}h)+z(x-2^{-k}h,y)+z(x,y-2^{-k}h) -4z(x,y),
\]
и
\[
\|\sigma^2 z\|_{C(\mathbb{R}^2)}= \max\{\|\Delta^2_xz\|_{C(\mathbb{R}^2)},\|\Delta^2_yz\|_{C(\mathbb{R}^2)},
\|\Delta^2_{-}z\|_{C(\mathbb{R}^2)}, \|\Delta^2_{+}z\|_{C(\mathbb{R}^2)}\},
\]
\[
\|\sigma^2\widetilde{F}\|_{\ell_{\infty}^2}=\max_{i,j\in\mathbb{Z}}\max\{|\hat{f}_{i+1,j,0}-2\hat{f}_{i,j,0} + \hat{f}_{i-1,j,0}|,
|\hat{f}_{i,j+1,0}-2\hat{f}_{i,j,0}+\hat{f}_{i,j-1,0}|,\]
\[
|\hat{f}_{i,j,0}+\hat{f}_{i+1,j+1,0}-\hat{f}_{i,j+1,0}-\hat{f}_{i+1,j,0}|,
|\hat{f}_{i-1,j,0}+\hat{f}_{i,j+1,0}+\hat{f}_{i+1,j,0}+\hat{f}_{i,j-1,0}-4\hat{f}_{i,j,0}|\}.
\]
Лемма 4.
Для любого массива \(\widetilde{F}{\in}{\ell^2_{\infty}}\) и \(k{\in}\mathbb{N}\) выполняется неравенство \begin{equation}\label{s.192}
\| \sigma^2\psi_{k+1,h}(\widetilde{F}) \|_{L_{\infty}(\mathbb{R}^2)} \le
\frac{61}{128}\| \sigma^2\psi_{k,h}(\widetilde{F}) \|_{L_{\infty}(\mathbb{R}^2)}\le
\left(\frac{61}{128}\right)^{k+1}\| \sigma^2 \widetilde{F} \|_{\ell_{\infty}^2}.
\end{equation}
Доказательство. Представим индексы \(i\) и \(j\) в виде \(i=2\nu+\xi\) и \(j=2\mu+\eta\), где \(\nu,\mu\in\mathbb{Z}\) и
\(\xi,\eta=0,1\), тогда для
\[(x,y) \in
\left( \left(i-\frac{1}{2}\right)\frac{h}{2^k}, \left(i+\frac{1}{2}\right)\frac{h}{2^k} \right)
\times \left(\left(j-\frac{1}{2}\right)\frac{h}{2^k}, \left(j+\frac{1}{2}\right)\frac{h}{2^k} \right)\] имеет место
равенство
\[
\Delta_{x}^2 \psi_{k+1,h}(\widetilde{F}, x_{2\nu+\xi, k+1},y_{2\mu+\eta, k+1})= \psi_{k+1,h}(\widetilde{F}, x_{2\nu+\xi-1,
k+1},y_{2\mu+\eta, k+1})-
\]
\begin{equation}\label{s.193} -2\psi_{k+1,h}(\widetilde{F}, x_{2\nu+\xi, k+1},y_{2\mu+\eta, k+1})+ \psi_{k+1,h}(\widetilde{F},
x_{2\nu+\xi+1, k+1},y_{2\mu+\eta, k+1})= \end{equation}
\[
=\sum_{n=-3}^{2}\sum_{m=-2}^{2}a^{\xi,\eta}_{n,m} \psi_{k,h}(\widetilde{F}, x_{\nu+n, k},y_{\mu+m, k}),
\]
где \(A_{\xi,\eta}=\| a^{\xi,\eta}_{n,m}\|_{n=-3,m=-2}^{2,2}\) и, например,
\[
A_{1,0}= {\frac{1}{2048}}\,\left [\begin {array}{cccccc}
0&0&0&0&0&0\\
0&13&-84&142&-84&13\\
0&-29&404&-750&404&-29\\
0&-29&404&-750&404&-29\\
0&13&-84&142&-84&13
\end {array}\right ].
\]
Таким образом, для \(\xi=1,\eta=0\) имеет место соотношение
\[
\Delta_x^2 \psi_{k+1,h}(\widetilde{F}, x_{2\nu+1},y_{2\mu})= \sum_{n=-3}^{2}\sum_{m=-2}^{2}a^{1,0}_{n,m}
\psi_{k,h}(\widetilde{F}, x_{\nu+n, k},y_{\mu+m, k})=
\]
\[
= \frac{1}{2048} \left(
13\Delta_x^2\left({
\psi_{k,h}(\widetilde{F}, x_{\nu-1, k},y_{\mu+1, k})+
\psi_{k,h}(\widetilde{F}, x_{\nu+1, k},y_{\mu+1, k})+}
\right.
\right.
\]
\[
\left.{+\psi_{k,h}(\widetilde{F}, x_{\nu-1, k},y_{\mu-2, k})+
\psi_{k,h}(\widetilde{F}, x_{\nu+1, k},y_{\mu-2, k})}\right)-
\]
\[
-29\Delta_x^2\left({\psi_{k,h}(\widetilde{F}, x_{\nu-1, k},y_{\mu, k})+
\psi_{k,h}(\widetilde{F}, x_{\nu+1, k},y_{\mu, k})+}\right.
\]
\[
\left.{+\psi_{k,h}(\widetilde{F}, x_{\nu-1, k},y_{\mu-1, k})+
\psi_{k,h}(\widetilde{F}, x_{\nu+1, k},y_{\mu-1, k})}\right)-
\]
\[
-58\Delta_x^2\left({
\psi_{k,h}(\widetilde{F}, x_{\nu, k},y_{\mu+1, k})+
\psi_{k,h}(\widetilde{F}, x_{\nu, k},y_{\mu-2, k})}\right)+
\]
\[
\left.{+346\Delta_x^2\left({
\psi_{k,h}(\widetilde{F}, x_{\nu, k},y_{\mu, k})+
\psi_{k,h}(\widetilde{F}, x_{\nu, k},y_{\mu-1, k})}\right.}\right).
\]
Следовательно, для \(\xi=1,\eta=0\) имеет место соотношение \begin{equation}\label{s.194} \sup_{\nu,\mu\in\mathbb{Z}} |\Delta_{x}^2
\psi_{k+1,h}(\widetilde{F}, x_{2\nu+\xi, k+1},y_{2\mu+\eta, k+1})| \le\frac{61}{128}\| \sigma^2\psi_{k,h}(\widetilde{F})
\|_{L_\infty(\mathbb{R}^2)}. \end{equation}
Рассматривая остальные случаи убеждаемся, что соотношение (\ref{s.194}) справедливо для всех \(\xi,\eta=0,1\), то есть
\[
\|\Delta_x^2 \psi_{k+1,h}(\widetilde{F})\|_{L_\infty(\mathbb{R}^2)}\le \frac{61}{128}\| \sigma^2\psi_{k,h}(\widetilde{F})
\|_{L_\infty(\mathbb{R}^2)}.
\]
Аналогично получаем
\[
\|\Delta_{-}^2 \psi_{k+1,h}(\widetilde{F})\|_{L_\infty(\mathbb{R}^2)}\le \frac{401}{1024}\| \sigma^2\psi_{k,h}(\widetilde{F})
\|_{L_\infty(\mathbb{R}^2)},
\]
\[
\|\Delta_y^2 \psi_{k+1,h}(\widetilde{F})\|_{L_\infty(\mathbb{R}^2)}\le \frac{61}{128}\| \sigma^2\psi_{k,h}(\widetilde{F})
\|_{L_\infty(\mathbb{R}^2)},
\]
\[
\|\Delta_+^2 \psi_{k+1,h}(\widetilde{F})\|_{L_\infty(\mathbb{R}^2)}\le \frac{113}{256}\| \sigma^2\psi_{k,h}(\widetilde{F})
\|_{L_\infty(\mathbb{R}^2)}.
\]
Таким образом,
\[
\|\sigma^2 \psi_{k+1,h}(\widetilde{F})\|_{L_\infty(\mathbb{R}^2)}\le \frac{61}{128}\| \sigma^2\psi_{k,h}(\widetilde{F})
\|_{L_\infty(\mathbb{R}^2)}
\]
и
\[
\| \sigma^2\psi_{k+1,h}(\widetilde{F}) \|_{L_{\infty}(\mathbb{R}^2)} \le
\left(\frac{61}{128}\right)^{k+1}
\| \sigma^2\psi_{0,h}(\widetilde{F}) \|_{L_{\infty}(\mathbb{R}^2)},
\]
что вместе с равенством \begin{equation}\label{s.195} \left\| \sigma^2\psi_{0,h}(\widetilde{F}) \right\|_{L_\infty(\mathbb{R}^2)}= \left\|
\sigma^2 \widetilde{F} \right\|_{\ell_\infty^2} \end{equation} завершает доказательство (\ref{s.192}).
Лемма 5.
Для любого массива \(\widetilde{F}{\in}{\ell^2_{\infty}}\), и любого фиксированного
\(k{\in}\mathbb{N}\) имеет место неравенство
\begin{equation}\label{s.197}
\| \psi_{k+1,h}(\widetilde{F})-\psi_{k,h}(\widetilde{F}) \|_{L_\infty(\mathbb{R}^2)} \le
\frac{159}{512} \| \sigma^2\psi_{k,h}(\widetilde{F}) \|_{L_\infty(\mathbb{R}^2)}.
\end{equation}
Доказательство. Функция \(\psi_{k+1,h}(\widetilde{F},x,y)\) является полигоном по разбиению \(\Delta^{k+1}\), а
\(\psi_{k,h}(\widetilde{F},x,y)\) есть полигон по разбиению \(\Delta^{k}\), поэтому экстремум величины \(
\psi_{k+1,h}(\widetilde{F},x,y)-\psi_{k,h}(\widetilde{F},x,y)\) может достигаться только в точках \(M_{2i,2j,k},\)
\(M_{2i+1/2,2j+1/2,k},\) \(M_{2i+1,2j+1,k},\) \(M_{2i+1,2j,k},\) \(M_{2i,2j+1,k}\). Таким образом
\[
\psi_{k+1,h}(\widetilde{F},x_{2i,k+1},y_{2j+1,k+1})- \psi_{k,h}(\widetilde{F},x_{i,k},y_{j+1/2,k})=
\sum_{n=1}^4\sum_{m=1}^{5}\beta_{n,m} \psi_{k,h}(\widetilde{F}, x_{\nu+n-5/2, k},y_{\mu+7/2-m, k}),
\]
где
\[
(\beta_{n,m})_{n=1,m=1}^{4\,\,\,5}= {\frac{1}{2048}}\,\left [\begin {array}{cccc} 3&21&21&3
\\ {}-10&170&170&-10\\ {}142&-510&-510&
142\\ {}-10&170&170&-10\\ {}3&21&21&3
\end {array}\right ],
\]
и
\[
|\psi_{k+1,h}(\widetilde{F},x_{2i,k+1},y_{2j+1,k+1})- \psi_{k,h}(\widetilde{F},x_{i,k},y_{j+1/2,k})|\le\frac{159}{512} \|
\sigma^2\psi_{k,h}(\widetilde{F}) \|_{L_\infty(\mathbb{R}^2)}.
\]
Аналогично
\[
|\psi_{k+1,h}(\widetilde{F},x_{2i+1,k+1},y_{2j+1,k+1})- \psi_{k,h}(\widetilde{F},x_{i+1/2,k},y_{j+1/2,k})|\le\frac{29}{128} \|
\sigma^2\psi_{k,h}(\widetilde{F}) \|_{L_\infty(\mathbb{R}^2)},
\]
\[
|\psi_{k+1,h}(\widetilde{F},x_{2i,k+1},y_{2j,k+1})- \psi_{k,h}(\widetilde{F},x_{i,k},y_{j,k})|\le\frac{71}{256} \|
\sigma^2\psi_{k,h}(\widetilde{F}) \|_{L_\infty(\mathbb{R}^2)},
\]
\[
|\psi_{k+1,h}(\widetilde{F},x_{2i+1/2,k+1},y_{2j+1/2,k+1})- \psi_{k,h}(\widetilde{F},x_{i+1/4,k},y_{j+1/4,k})|\le
\frac{137}{512} \| \sigma^2\psi_{k,h}(\widetilde{F}) \|_{L_\infty(\mathbb{R}^2)}.
\]
Следовательно, полигон \(\psi_{k+1,h}(\widetilde{F},x,y)\) уклоняется от полигона \(\psi_{k,h}(\widetilde{F},x,y)\) на треугольнике
с вершинами в точках \(M_{2i,2j,k+1}\), \(M_{2i+1,2j+1,k+1}\), \(M_{2i,2j+1,k+1}\) не более чем на величину
\[
\frac{159}{512}\| \sigma^2\psi_{k,h}(\widetilde{F}) \|_{L_\infty(\mathbb{R}^2)}.
\]
Лемма 6.
Для любого массива \(\widetilde{F}\in \ell^2_{\infty}\), и \(k{\in}\mathbb{N}\)
имеет место неравенство
\begin{equation}\label{s.199}
\left\| \psi_{k+m,h}(\widetilde{F}) - \psi_{k,h}(\widetilde{F}) \right\|_{L_\infty(\mathbb{R}^2)}
\le \frac{159}{268}\left(\frac{61}{128}\right)^k \left\| \sigma^2 \widetilde{F} \right\|_{\ell_\infty^2}. \end{equation}
Доказательство. Из очевидного неравенства
\[
\left\| \psi_{k+m,h}(\widetilde{F}) - \psi_{k,h}(\widetilde{F}) \right\|_{L_\infty(\mathbb{R}^2)}
\le
\sum_{i=0}^{m-1} \left\| \psi_{k+i+1,h}(\widetilde{F}) -
\psi_{k+i,h}(\widetilde{F})\right\|_{\ell_\infty^2}
\]
и леммы 5 вытекает
\[
\left\| \psi_{k+m,h}(\widetilde{F}) - \psi_{k,h}(\widetilde{F}) \right\|_{L_\infty(\mathbb{R}^2)}
\le
\frac{159}{512} \sum_{i=0}^{m-1} \| \sigma^2\psi_{k+i,h}(\widetilde{F}) \|_{L_\infty(\mathbb{R}^2)}.
\]
Применяя лемму 4, отсюда получаем
\[
\left\| \psi_{k+m,h}(\widetilde{F}) - \psi_{k,h}(\widetilde{F}) \right\|_{L_\infty(\mathbb{R}^2)}
\le
\]
\[
\le \frac{159}{512}
\| \sigma^2\psi_{k,h}(\widetilde{F}) \|
\left(
1 + \frac{61}{128} + \left(\frac{61}{128}\right)^2 +
\left(\frac{61}{128}\right)^3 + \ldots
\right)\le
\frac{159}{268}\left(\frac{61}{128}\right)^k \left\| \sigma^2\psi_{0,h}(\widetilde{F}) \right\|_{L_\infty(\mathbb{R}^2)}.
\]
Отсюда сразу следует утверждение леммы.
Из последней леммы следует, что последовательность \(\{\psi_{k,h}(\widetilde{F},x,y)\}_{k=0}^{\infty}\) сходится в себе.
Нетрудно видеть, что она ограничена (более того, далее мы покажем, что норма оператора \(\psi_{k,h}(\widetilde{F},x,y)\)
ограничена в совокупности и невелика). Отсюда следует, что поточечный предел \(\psi_{k,h}(\widetilde{F},x,y)\) при
\(k\to\infty\) существует. Обозначим этот предел через \(\psi_{h}(\widetilde{F},x,y)\).
Так как для любого \(k\in\mathbb{N}\) оператор \(\psi_{k,h}(f)\) есть линейный оператор, отображающий пространство
\(\ell_{\infty}^2\) в пространство полигонов определенных на квадратных областях \(\big( x_{i,k}-h/2^{k},x_{i,k}+h/2^{k}
\big) \times
\big( y_{j,k}-h/2^{k},y_{j,k}+h/2^{k} \big)\),
то \(\psi_h\) есть линейный оператор, отображающий пространство \(\ell_{\infty}^2\) в пространство \(C(\mathbb{R}^2)\).
Используя предельный переход, сразу получаем
Теорема 8.
Для любого фиксированного \(k{\in}\mathbb{N}\) и любого массива \(\widetilde{F}\in \ell^2_{\infty}\) верно неравенство
\[
\left\| \psi_{h}(\widetilde{F}) - \psi_{k,h}(\widetilde{F}) \right\|_{L_\infty(\mathbb{R}^2)}
\le \frac{159}{268}\left(\frac{61}{128}\right)^k \left\| \sigma^2 \widetilde{F} \right\|_{\ell_\infty^2}.
\]
Следствие 2.
Пусть \(p\in [1,\infty)\), числа \(k\in\mathbb{N}\) и \(\Re\in\mathbb{R}^2\). Для любого массива \(\widetilde{F}\in\ell_\infty^2\) имеют место
неравенства
\begin{equation}\label{s.201} \left|\|\psi_h(\widetilde{F})\|_{p(\Re)}-\|\psi_{k,h}(\widetilde{F})\|_{p(\Re)}\right|\le
(mes\Re)^p \frac{159}{268}\left(\frac{61}{128}\right)^k \left\| \sigma^2 \widetilde{F} \right\|_{\ell_\infty^2},
\end{equation}
и \begin{equation}\label{s.202} \|\psi_{k,h}(\widetilde{F})\|_{L_\infty(\Re)}\le \|\psi_{h}(\widetilde{F})\|_{L_\infty(\Re)}\le
\|\psi_{k,h}(\widetilde{F})\|_{L_\infty(\Re)} +\frac{159}{268}\left(\frac{61}{128}\right)^k \left\| \sigma^2 \widetilde{F}
\right\|_{\ell_\infty^2}.
\end{equation}
Действительно, из теоремы 8, из неравенств верных для любых \(p\in [1,\infty)\) и \(g,c\in L_p (\Re)\)
\[
\|g\|_{L_p(\Re)}-\|c\|_{L_p(\Re)}\le\|g-c\|_{L_p(\Re)} \le\|g\|_{L_p(\Re)}+\|c\|_{L_p(\Re)}
\]
и очевидного неравенства
\[
\|g\|_{L_p(\Re)}\le (mes \Re)^p\|g\|_{L_\infty(\Re)},
\]
сразу получаем для \(p\in [1,\infty)\) соотношение (\ref{s.201}).
Оценка снизу в (\ref{s.202}) вытекает из того факта, что норма функции \(\psi_{k,h}(\widetilde{F},x,y)\) в \(L_\infty(\Re)\) не
превышает нормы функции \(\psi_h(\widetilde{F},x,y)\).
В частности при \(k=8\) следует
\[
1.84695\lt\|N\|_{C([0,1]\times [0,1])}\lt 1.84697.
\]
Вычисляя числа \(\hat{f}^{*,1}_{\nu,\mu}\), получаем свойство масштабируемости
\begin{equation}\label{s.203} \Psi(x,y)
=\sum_{\nu=-4}^{3}\sum_{\mu=-4}^{3} \alpha_{\nu,\mu}\Psi(2x{-}\nu,2y{-}\mu), \end{equation} где
\[
(\alpha_{\nu,\mu})_{\nu,\mu=-4}^{3} =
{\frac{1}{512}}\,\left [\begin {array}{cccccccc}
-3&0&0&-21&-21&0&0&- 3\\
0&10&0&-50&-50&0&10&0\\
0&0&34& 102&102&34&0&0\\
-21&-50&102&409&409&102&-50&-21\\
-21&-50&102&409&409&102&-50&-21\\
0&0&34&102&102&34&0&0\\
0&10&0&-50&-50&0&10&0\\
-3&0&0&-21&-21&0&0&-3\end {array} \right ].
\]







