Fuzzy

Fuzzy decision

Введение, или что такое нечеткое мышление?

Проблема ИИ (искусственного интеллекта) преследует человечество испокон веков, от Галатеи, созданной Пигмалионом, до «Скайнета», побежденного Шварцнеггером-Терминатором. Как же отличить этот коварный ИИ от нормального человека? Ответ на этот вопрос пытался дать еще в 1950 году Алан Тьюринг в своей статье «Вычислительные машины и разум». Предложенное решение известно, как тест Тьюринга. Но 6 июня 2014 года виртуальный мальчик «Евгений Густман из Одессы» смог убедить беседовавших с ним людей в том, что выдаваемые компьютером ответы принадлежат человеку, а не машине. Почему же этот этап был преодолен через такой долгий срок? И почему же это случилось?
В отличие от компьютерной программы, человек (эксперт), при решении проблемы, обычно полагается на здравый смысл, используя неопределенные и двусмысленные термины. Например, эксперт может сказать: «хотя я немного подустал, но все же могу выполнить эту работу за некоторое время». При этом другие эксперты не испытывают затруднений с пониманием и толкованием этого заявления. А каково IT-специалисту с предоставлением компьютеру того же уровня понимания. Как можно представить в компьютере экспертные знания, которые используют неопределенные и двусмысленные термины? Можно ли вообще это сделать?
Инструментом для достижения этой целя является нечеткая логика. Нечеткая логика использует теорию нечетких множеств, то есть, множеств, которые калибруют неопределенность. Нечеткая логика основана на идее, что все понятия допускают градацию. Кипяток очень горячий, чай недостаточно крепкий, борщ немного недосолен, кондиционер недостаточно хорошо охлаждает. Такая градиентная шкала часто позволяет отличить элементы, принадлежащие некоторому классу от элементов, которые ему не принадлежат.
Классическая четкая логика использует резкие различия. Это как нарисовать линию, разделяющую два множества. Например, согласно шкале Бофорта, если ветер имеет скорость 10.7 м/сек, то он свежий, а если 10.8, то уже сильный.
Нечеткая логика отражает то, как люди думают, пытается моделировать наше чувство слов, наше принятие решений и наш здравый смысл. В результате, это приводит к построению новых, если можно так сказать, более человеческих интеллектуальных систем.
Нечеткая или многозначная логика была введена в 1930-х годах польским логиком и философом Яном Лукасевичем. Классическая логика работает только с двумя значениями 1 (истина) и 0 (ложь), Лукасевичем была введена логика, которая расширила диапазон значений истинности до всех действительных чисел в интервале между 0 и 1. Этот подход привел к неточным методам рассуждений, которые назывались «Теория возможностей».
В 1965 году Лотфи Заде, профессор и заведующий кафедрой электротехники Калифорнийского университета в Беркли опубликовал свой знаменитый труд «Нечеткие множества». Фактически, Заде вновь открыл размытость, осмыслил и исследовал это явление, переведя теорию возможностей в формальную систему математической логики и, что еще важнее, он ввел новую концепцию для применения понятий естественного языка. Эта новая логика для представления и манипулирование нечеткими терминами называется нечеткой логикой.
В отличие от двузначной классической логики, нечеткая логика многозначна. Она имеет дело со степенями соответствия и степенями правды. Нечеткая логика использует континуум логических значений между 0 (полностью ложным) и 1 (полностью верно). Вместо просто черного и белого, использует спектр цветов, принимая то, что понятия могут быть отчасти верным и частично ложным одновременно. На следующем рисунке проиллюстрирован диапазон значений четкой и нечеткой логики.

Понятия и определения.

Нечеткие множества

Концепция множества (набора) фундаментальна для математики. Пусть \(X\) - классическое (четкое) множество, а x – некоторый элемент. Тогда элемент \(x\) принадлежит \(X (x\in X)\) или не принадлежит \(X (x\notin X)\), таким образом, классическая теория множеств накладывает резкую границу и дает каждому элементу множества значение 1 и всем элементам, которые не находятся в пределах установленного множества, значение равное 0. Теория четких множеств определяется логикой, которая использует одно из двух значений: true или false. Основная идея теории нечетких множеств состоит в том, что элемент принадлежит нечеткому множеству с определенной степенью принадлежности. Таким образом, предложение не является ни истинным, ни ложным, но может быть отчасти истинным (или отчасти ложным) в какой-то степени. Эта степень обычно принимается как действительное число в интервале [0,1].
Так, четкий вопрос: «Сильный ли сегодня ветер?» , имеет четкий ответ - так как по шкале Бофорта сильный ветер начинается со скорости 10.8 м./сек., то если скорость ветра больше 10.8 м./сек., то ветер сильный.

Четкое множество, описывающее сильный ветер

А на вопрос: «Насколько сегодня сильный ветер?» ответ может быть только в нечетких терминах. Нечеткое множество способно обеспечить плавный переход через границу между понятиями сильный и несильный ветер.

Нечеткое множество, описывающее сильный ветер

При этом можно рассмотреть такие понятия, как «не очень сильный ветер», «совсем слабый ветер», «так себе ветерок» и др.
Нечеткое множество можно просто определить, как множество с нечеткими границами.
Пусть \(X\) - универсум, а его элементы обозначаются как \(x\). В классической теории множеств, четкое множество \(A\) из \(X\) определяется функцией \(f_A(х)\) (так называемая характеристическая функция \(A\)): \(f_A(x):X\to \{0,1\}\), где \[ f_A(x)=\left\{ \begin{array}{lll} 1, & \hbox{если} &x\in A, \\ 0, & \hbox{если} &x\notin A. \end{array} \right. \] В результате получаем отображение \(X\) в набор из двух элементов. Для любого элемента \(x\) из универсума \(X\), характеристическая функция \(f_A(x)\) равна 1, если \(x\) - элемент множества A, и равна 0, если \(x\) не является элементом \(A\).
Для нечеткого случая нечеткое множество \(A\) универсума \(X\) определяется функцией \(\mu_A(x)\) , которая называется функцией принадлежности множества \(A\) \(\mu_A(x):X\to [0,1]\), где

\(\mu_A(x)=1\), если \(x\) полностью из \(А\),
\(\mu_A(x)=0\) , если \(x\) не лежит в \(А\),
\(0 \lt \mu_A(x)\lt 1\), если \(x\) частично лежит в \(А\).

Этот набор допускает континуум возможных вариантов. Для любого элемента \(х\) универсума \(X\), функция принадлежности \(\mu_A(x)\) равна степени, в которой \(x\) является элементом множества \(A\). Эта степень (значение от 0 до 1) представляет степень членства, также называемое значением принадлежности, элемента \(x\) к множеству \(A\).
Чтобы формализовать непрерывное нечеткое множество (без этого невозможна его программная реализация), нам нужно выразить его в функциональном виде и затем сопоставить элементы множества с их степенью принадлежности. Типичным является треугольное, трапециевидное представлением, а также различные сигмоиды и пр. На практике большинство приложений используют линейные функции (треугольная и трапециевидная формы).

Иллюстрация четких и нечетких множеств и их функций принадлежности.

Отталкиваясь от оценивания силы ветра по шкале Бофорта, можем описать четкие множества, описывающие слабый, средний и сильный ветер.

Четкий набор классификации силы ветра.

Аналогичное нечеткое множество можно представить в виде

Нечеткий набор классификации силы ветра.

Заметим, что при этом ветер со скоростью 13.8 м./сек. принадлежит множеству «среднего ветра» со степенью 0.37 и является «сильным ветром» со степенью принадлежности 0.47. Таким образом, ветер со скоростью 13.8 м./сек. Имеет частичное членство в нескольких множествах.
Теперь, пусть универсум X представляет собой четкий набор, содержащий семь элементов \[ X=\{x_1; x_2; x_3; x_4; x_5; x_6; x_7\}, \] кроме того, пусть A – четкое подмножество X и состоит только из трех элементов: \(A =\{x_2; x_3; x_6\}\). В этом случае подмножество \(A\) можно описать следующим образом \[ A =\{(x_1, 0),(x_2, 1),(x_3,1),(x_4, 0),(x_5, 0) ,(x_6, 1) ,(x_7, 0)\}, \] то есть в виде набора пар \(\{(x_i,\mu_A(x_i))\}\) где \(\mu_A(x_i)\) - функция принадлежности элемента \(x_i\) подмножеству \(A\).
Если \(X\) является опорным множеством и \(A\) является подмножеством \(X\), то \(A\) называется нечетким подмножеством \(X\), тогда и только тогда, если \[ A=\{(x,\mu_A(x))\},x\in X,\mu_A(x):X\to [0,1]. \] В частном случае, если \(X\to \{0,1\}\), то нечеткое подмножество \(A\) становится четким.
Нечеткое подмножество \(А\) конечного опорного множества \(X\) может быть представлено в виде \[ A=\{(x_1,\mu_A(x_1))\},\{(x_2,\mu_A(x_2))\},...,\{(x_n,\mu_A(x_n))\}. \] Часто представляют подмножество \(A\) в виде \[ A=\{\mu_A(x_1)/x_1\},\{\mu_A(x_2)/x_2\},...,\{\mu_A(x_n)/x_n\}. \] Здесь разделительный символ “/” используется для связывания значения членства с его координатой по горизонтальной оси (абсциссой).
В качестве примера можно записать следующие вектора соответствия

Сильный ветер=(0/5.5; 0/10.8;0.47/13.8;1/17.2)

Средний ветер=(0/3.4;1/8.0;0.37/13.8;0/17.2) и т.д.

Лингвистические переменные и лингвистические усиления (Linguistic variables and hedges).

В основе теории нечетких множеств лежит идея лингвистических переменных. Лингвистическая переменная - нечеткая переменная. Например, утверждение «высокий рейтинг» означает, что лингвистическая переменная «рейтинг» имеет повышенную лингвистическую ценность. В нечетких экспертных системах, лингвистические переменные используются для построения нечетких правил. Например,

ЕСЛИ ветер сильный ТОГДА следует закрыть окно

ЕСЛИ наступил вечер ТОГДА следует зажечь свет

Диапазон возможных значений лингвистической переменной может быть самым разнообразным, так скорость ветра может иметь диапазон от 0 до более чем 32.7 м./сек., включая такие подмножества как штиль, тихий ветер, слабый ветер, крепкий ветер, шторм, ураган и пр.
Кроме того, существует концепция лингвистического усиления, это термины, которые изменяют форму нечетких множеств. Они включают наречия, такие как очень, несколько, довольно, более или менее, слегка и пр.
Лингвистические усиления используются как

Универсальные модификаторы, такие как очень, довольно или крайне.
Истинные значения, такие как вполне истинное или в основном ложное.
Вероятности, например, вероятные или не очень вероятные.
Квантификаторы, такие как большинство, несколько или немного.
Возможности, такие как почти невозможные или вполне возможные.

Лингвистические усиления позволяют эффективно создавать новые подмножества. Из множества «спелых помидоров» получаем подмножество «не очень спелых помидоров», «не совсем спелых помидоров», «очень спелых помидоров», «более-менее спелых помидоров» и пр. При этом набор «более-менее спелых помидоров» шире, чем просто набор «спелые помидоры», то есть тем самым, используя лингвистические усиления, можно как расширять, так и сужать исходное множество.
Так, применений лингвистического усиления позволяет на множестве «сильного ветра» выделить подмножество «очень сильного ветра». В этом случае ветер со скоростью 13.8 м./сек. со степенью принадлежности 0.47 является «сильным ветром» и со степенью 0.22 «очень сильным», что довольно разумно.

Пример лингвистического усиления.

Перейдем к математической формализации лингвистического усиления, и прежде всего рассмотрим конструкции, часто используемые в практических приложениях.

«Очень» - операция концентрации, которая сужает множество вниз и, таким образом, уменьшает степень принадлежности нечетких элементов. Операция “очень” может быть задана как квадрат функции принадлежности \[ \mu_A^{очень}(x)=\left(\mu_A(x)\right)^2, \] например, если степень принадлежности у помидора к множеству «спелых» равно 0.8, то для «очень спелых» степень принадлежности равно 0.64.
«Чрезвычайно» служит той же цели, но делает это в большей степени, что может быть выполнено путем возведения \(\mu_A(x)\) в третью степень: \[ \mu_A^{чрезвычайно}(x)=\left(\mu_A(x)\right)^3. \] Для предыдущего примера помидор будет «чрезвычайно спелым» со степенью принадлежности 0.512.
«Очень очень» просто расширение концентрации. \[ \mu_A^{очень-очень}(x)=\left(\mu_A^{очень}(x)\right)^2=\left(\mu_A(x)\right)^4. \]
«Более или менее» - операция расширения, в результате расширяется набор и, следовательно, увеличивает степень принадлежности нечетких элементов. Эта операция может представлена в виде: \[ \mu_A^{более-менее}(x)=\sqrt{\mu_A(x)}. \] Таким образом наш помидор со степенью 0.89 «более-менее спелый».

«Действительно» (в самом деле, впрямь, где-то так, возможно), операция интенсификации усиливает смысл целого предложение. Это можно сделать, увеличив степень членства выше 0,5 и уменьшая их ниже 0,5, что может быть записано в виде

\(\mu_A^{действительно}(x)=2\left(\mu_A(x)\right)^2\), если \(0\le \mu_A(x)\le 0.5\)
или
\(\mu_A^{действительно}(x)=1-2\left(1-\mu_A(x)\right)^2\), если \(0.5 \lt \mu_A(x)\le 1\).

Следовательно, если степень принадлежности у помидора к множеству «спелых» равно 0.8, то он будет «действительно спелым» со степенью принадлежности 0.92.
Если же степень принадлежности у помидора к множеству «спелых» равно 0.2, то он будет «действительно спелым» со степенью принадлежности 0.08.

Лингвистическое усиление	Математическая конструкция	Графическая иллюстрация
Очень	\(\left(\mu_A(x)\right)^2\)
Чрезвычайно	\(\left(\mu_A(x)\right)^3\)
Очень-очень	\(\left(\mu_A(x)\right)^4\)
Более-менее	\(\sqrt{\mu_A(x)}\)
Где-то так	\(2\left(\mu_A(x)\right)^2\), если \(0\le \mu_A(x)\le 0.5\) или \(1-2\left(1-\mu_A(x)\right)^2\), если \(0.5 \lt \mu_A(x)\le 1\)

Представление лингвистического усиления (hedges) в нечеткой логике.

Операции над нечеткими множествами.

В данном разделе мы ограничимся только теми операциями, которые нам будут необходимы в дальнейшем, это - дополнение, включение (доминирование) , пересечение и объединение.

Исходной множество А.

Дополнение множества противоположно этому множеству. Например, если мы имеем набор «спелых помидоров», его дополнением является набор «НЕ спелых помидоров».
Если \(A\) - нечеткое множество с функцией принадлежности \(\mu_A(x)\), функция принадлежности его дополнения \(\neg A\) равна \(\mu_{\neg A}(x)=1-\mu_A(x)\).

Дополнение множества А.

Например, если у нас есть нечеткое множество «слабого ветра», мы можем легко получить нечеткое множество «НЕ слабого ветра»

Слабый ветер = (1/0.3; 1 / 1.5; 0.71 /4.0; 0.24 /5.0; 0 /5.5; 0 /8.0; 0 /10.8; 0 /17.2; 0 /32.7)

НЕ слабый ветер =(0/0.3; 0/1.5; 0.29 /4.0; 0.76 /5.0; 1 /5.5; 1 /8.0; 1 /10.8; 1 /17.2; 1 /32.7)

Включение (доминирование). Подобно матрешке, один набор может содержать другие наборы. Например, множество «сильный ветер» содержит «очень сильный ветер». Поэтому «очень сильный ветер» - это подмножество «сильного ветра». В четком случае все элементы подмножества полностью принадлежат большему и их значения принадлежности равны 1. В нечетких множествах, каждый элемент может принадлежать меньше подмножеству, чем к большему множеству. Элементы нечеткого подмножества имеют меньшее членство в нем, чем в большем наборе.

Сильный ветер =(0/10.8; 0. 47 / 13.8; 1/ 17.2; 1 / 32.7)

Очень сильный ветер =(0/10.8; 0. 22 / 13.8; 1/ 17.2; 1 / 32.7)

Включение множества А в множество В.

Пересечение. В классической теории множеств пересечение двух множеств содержит элементы, одновременно принадлежащие обеим множествам. Для нечетких множеств элемент может частично принадлежать к обоим множествам с различным членством. Таким образом, нечеткое пересечение - нижнее членство в обоих наборах каждого элемента.
Нечеткая операция для создания пересечения двух нечетких множеств \(A\) и \(B\) на универсуме \(X\) может быть получена следующим образом \[ \mu_{A\cap B}(x)=\min\{\mu_A,\mu_B\}=\mu_A\cap \mu_B (x\in X). \] Рассмотрим, например, нечеткие множества «среднего ветра» и «сильного ветра».

Средний ветер =(0/ 3.4; 0.46/ 5.5; 1/ 8.0; 0.7/10.8; 0. 37/ 13.8; 0/ 17.2; 0 /32.7)

Сильный ветер =(0/ 3.4; 0/ 5.5; 0/ 8.0; 0/10.8; 0. 47 / 13.8; 1/ 17.2; 1 / 32.7)

Пересечение этих двух множеств -

«средний ветер» ∩ «сильный ветер» =(0/ 3.4; 0/ 5.5; 0/ 8.0; 0/10.8; 0. 37 / 13.8; 0/ 17.2; 0 / 32.7)
или
«средний ветер» ∩ «сильный ветер» =(0/10.8; 0. 37 / 13.8; 0/ 17.2).

Пересечение множеств А и В.

Объединение. В четком случае объединение двух множеств состоит из элементов, которые попадают в любое из множеств. Для нечетких множеств объединение является обратным к пересечению. То есть объединение является наибольшим значением членства элемента в любом наборе.
Нечеткая операция для образования объединения двух нечетких множеств \(A\) и \(B\) на универсуме \(X\) может быть задана как: \[ \mu_{A\cup B}(x)=\max\{\mu_A,\mu_B\}=\mu_A\cup \mu_B (x\in X). \] Рассмотрим снова нечеткие множества «среднего ветра» и «сильного ветра».

Средний ветер =(0/ 3.4; 0.46/ 5.5; 1/ 8.0; 0.7/10.8; 0. 37/ 13.8; 0/ 17.2; 0 /32.7)

Сильный ветер =(0/ 3.4; 0/ 5.5; 0/ 8.0; 0/10.8; 0. 47 / 13.8; 1/ 17.2; 1 / 32.7)

Тогда

«средний ветер» ∪ «сильный ветер» =(0/ 3.4; 0.46/ 5.5; 1/ 8.0; 0.7/10.8; 0. 47 / 13.8; 1/ 17.2; 1 / 32.7)

Объединение множеств А и В.

Коммутативность

A∪ B =B∪ A, A∩ B =B∩ A.

Пример:

«средний ветер» ИЛИ «сильный ветер» = «сильный ветер» ИЛИ «средний ветер»

«средний ветер» И «сильный ветер» = «сильный ветер» И «средний ветер».

Ассоциативность

A∪ (B∪ C)= (A∪ B)∪ C), A∩ (B∩ C)= (A∩ B)∩ C).

Пример:

«сильный ветер» ИЛИ («слабый ветер» ИЛИ «средний ветер») = («сильный ветер» ИЛИ «слабый ветер») ИЛИ «средний ветер»

«сильный ветер» И («слабый ветер» И «средний ветер») = («сильный ветер» И «слабый ветер») И «средний ветер»

Дистрибутивность

A∪ (B∩ C)= (A∪ B)∩(A∪ C), A∩ (B∪ C)= (A∩ B)∪(A∩ C).

Пример:

«сильный ветер» ИЛИ («слабый ветер» И «средний ветер»)) = («сильный ветер» ИЛИ «слабый ветер») И («сильный ветер» ИЛИ «средний ветер»))

«сильный ветер» И («слабый ветер» ИЛИ «средний ветер»)) = («сильный ветер» И «слабый ветер») ИЛИ («сильный ветер» И «средний ветер»))

Ну и заметим, что

A∪ A= A и A∩ A= A.

Пример:

«средний ветер» ИЛИ «средний ветер» =«средний ветер»

«средний ветер» И «средний ветер» = «средний ветер»

Тождественность

A∪ ∅ =A, A∩ ∅ =∅, A∪ X =X, A∩ X =A.

Пример:

«сильный ветер» ИЛИ неопределенность = «сильный ветер»

«сильный ветер» И «неизвестный ветер» = «сильный ветер»

«сильный ветер» И неопределенность = неопределенность

«сильный ветер» ИЛИ «неизвестный ветер» = «неизвестный ветер»

где неопределенность - пустой (нулевой) набор, множество, имеющее всю степень членства 0, а неизвестный - это набор, имеющий все степени членства равным 1.
Инволюция \[ \neg (\neg A)=A. \] Пример:

НЕ (НЕ «сильный ветер» ) = «сильный ветер»

Транзитивность.

Если (A⊂ B)∩ (B⊂ C) тогда A⊂ C.

Каждое множество содержит подмножества его подмножеств.
Пример:

ЕСЛИ («чрезвычайно сильный ветер» ⊂ «очень сильный ветер» ) И («очень сильный ветер» ⊂ «сильный ветер» ) ТОГДА («чрезвычайно сильный ветер» ⊂ «сильный ветер» ).

Законы Де Моргана \[ \neg (A\cap B)=\neg A\cup \neg B, \neg (A\cup B)=\neg A\cap \neg B. \] Пример:

НЕ («сильный ветер» И «слабый ветер») = НЕ «сильный ветер» ИЛИ НЕ «слабый ветер»

НЕ («сильный ветер» ИЛИ «слабый ветер») = НЕ «сильный ветер» И НЕ «слабый ветер».

Используя операции нечеткого множества, их свойства и лингвистические усиления, мы можем легко получить множество нечетких множеств из существующих. Например, если у нас есть нечеткое множество A из «сильного ветра» и нечеткого набора B «слабого ветра»), мы можем получить нечеткое множество C «не очень сильного ветра» и «не очень слабого ветра» или даже установить D не очень сильного и не очень слабого ветра из следующих операций: \[ \mu_C(x)=\left(1-\left(\mu_A(c)\right)^2\right)\cap \left(1-\left(\mu_B(c)\right)^2\right), \] \[ \mu_D(x)=\left(1-\left(\mu_A(c)\right)^4\right)\cap \left(1-\left(\mu_B(c)\right)^4\right) \] и т.д.

Правила нечеткого вывода

В 1973 году Лотфи Заде опубликовал свою вторую самую влиятельную статью (3. Zadeh L. Outline of a new approach to the analysis of complex systems and decision processes / L.Zadeh // IEEE Transactions on Systems, Man, and Cybernetics.— 1973 .— №3(1) .— C.28–44. ). В этом документе излагается новый подход к анализу сложных систем, в котором Заде предложил описать процедуру человеческого вывода в нечетких правилах.
Нечеткое правило может быть определено как условное выражение в форме:

ЕСЛИ \(x\) равно \(A\) ТОГДА \(y\) равно \(B\),

где \(x\) и \(y\) - лингвистические переменные, \(A\) и \(B\) - лингвистические величины, определенные нечеткими множествами на универсумах \(X\) и \(Y\) соответственно.
В общем случае рассуждение ЕСЛИ-ТОГДА включает две отдельные части: оценка правила (ЕСЛИ часть правила) и применение результата к последующему (ТОГДА часть правила). Классическое правило ЕСЛИ-ТОГДА использует двоичную логику, то есть, если первая часть верна, верна и вторая и наоборот. В нечетких системах, все правила в какой-то степени срабатывают, другими словами, они срабатывают частично.
В случае верности с некоторой степенью условия ЕСЛИ, получаем, что с той же степенью это будет верно и для условия ТОГДА.
Рассмотрим, например, два нечетких множества: «скорость ветра» и «облачность»:

Монотонный выбор значений облачности (в баллах).

А как быть, если правило нечеткого вывода имеет несколько частей?
Например:

ЕСЛИ погода морозная И лежит снег ТОГДА будет лыжная прогулка.

ЕСЛИ погода хорошая ИЛИ приятная компания ТОГДА пикник удался.

Результатом каждого правила является нечеткое множество, но обычно нам нужно получить единственное число. Другими словами, мы хотим получить точное решение, а не нечеткое. Чтобы получить одно четкое решение для выходной переменной, нечеткая экспертная система вначале агрегирует все выходные нечеткие множества в одно выходное нечеткое множество, а затем собирает полученный нечеткий набор в одно число.
Наиболее часто используемым методом нечеткого вывода является так называемый метод Мамдани.
В 1975 году профессор Лондонского университета Эбрахим Мамдани построил одну из первых нечетких систем для управления комбинацией паровых двигателей и котлов (Mamdani E.H. An experiment in linguistic synthesis with a fuzzy logic controller / E.H.Mamdani, S.Assilian // International Journal of Man–Machine Studies .— 1975 .— №7(1) .— C.1–13.).
Процесс нечеткого вывода в стиле Мамдани выполняется в четыре этапа: фаззификация входных переменных, оценка правил, агрегация правил вывода и, наконец, дефаззификация , то есть, приведение к четкости.

Алгоритмы нечеткого вывода.

Пусть \(x, y\) – входные переменные, имеющие четкие значения \(x_0, y_0\) и \(z\) – выходная переменная.
Заданы функции принадлежности \(\mu_{A_1}, \mu_{A_2}, \mu_{B_1}, \mu_{B_2}, \mu_{C_1}, \mu_{C_2}\) и правила:

Если \(x\) есть \(A_1\) и \(y\) есть \(B_1\), ТО \(z\) есть \(C_1\),

Если \(x\) есть \(A_2\) и \(y\) есть \(B_2\), ТО \(z\) есть \(C_2\).

Алгоритм Mamdani. В системах типа Mamdani база знаний строится из нечетких высказываний вида «z есть α» с помощью связок «И», «ЕСЛИ-ТО». Этапы нечеткого вывода реализуются следующим образом:

Фаззификация: находятся степени истинности для предпосылок каждого правила: \(\mu_{A_1}(x_0), \mu_{A_2}(x_0), \mu_{B_1)(x_0}, \mu_{B_2}(x_0)\).
Вывод: находятся уровни отсечения для предпосылок каждого из правил с использованием операции минимум: \[ \alpha_1=\min\{\mu_{A_1}(x_0),\mu_{B_1}(y_0)\}, \alpha_2=\min\{\mu_{A_2}(x_0),\mu_{B_2}(y_0)\}. \] Затем находятся усеченные функции принадлежности: \[ \mu_{C_1'}(z)=\min\{\alpha_1,\mu_{C_1}(x_0)\}, \mu_{C_2'}(z)=\min\{\alpha_2,\mu_{C_2}(x_0)\}. \]
Композиция: с использованием операции максимум производится объединение найденных усеченных функций, что приводит к получению итогового нечеткого подмножества для переменной выхода с функцией принадлежности: \[ \mu_\Sigma=\mu_C(z)=\max\{\mu_{C_1'},\mu_{C_2'}\}=\max\left\{\min\{\alpha_1,\mu_{C_1}(z)\},\min\{\alpha_2,\mu_{C_2}(z)\}\right\}. \]
Приведение к четкости для получения \(z_0\) производится с использованием центра тяжести. \[ z_0=\frac{\int_{Min}^{Max}z\cdot \mu_\Sigma(z)dz}{\int_{Min}^{Max}\mu_\Sigma(z)dz}, \] где \(Min\) и \(Max\) — границы универсума нечетких переменных.

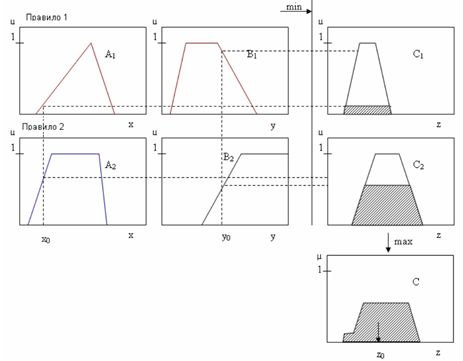
Алгоритм Mamdani.

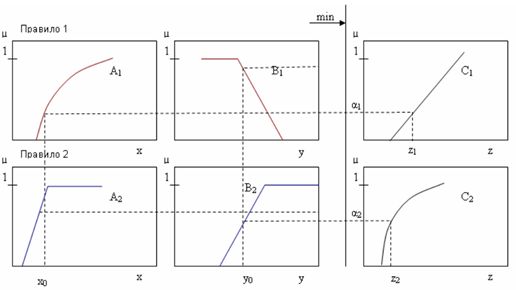
Алгоритм Tsukamoto. Исходные данные и база знаний такие же, как и в алгоритме Mamdani, но предполагается, что функции \(\mu_{С_1}(z), \mu_{С_2}(z)\) являются монотонными.
Этапы нечеткого вывода:

Фаззификация: находятся степени истинности для предпосылок каждого правила: \(\mu_{A_1}(x_0), \mu_{A_2}(x_0), \mu_{B_1}(y_0), \mu_{B_2}(y_0)\).
Вывод: Находятся уровни отсечения для предпосылок каждого из правил с использованием операции минимум: \[ \alpha_1=\min\{\mu_{A_1}(x_0),\mu_{B_1}(y_0)\}, \alpha_2=\min\{\mu_{A_2}(x_0),\mu_{B_2}(y_0)\}. \]
Затем находятся четкие значения z1 и z2 из уравнений \(\alpha_1=\mu_{C_1}(z), \alpha_2=\mu_{C_2}(z)\).
Определяется четкое значение переменной вывода, как взвешенное среднее \(z_1\) и \(z_2\) \[ z_0=\frac{\alpha_1z_1+\alpha_2z_2}{\alpha_1+\alpha_2}. \]

В общем случае четкое значение \(z_0\) определяется с использованием центра тяжести.

Алгоритм Tsukamoto.

Алгоритм Sugeno. В алгоритме Sugeno база знаний строится из правил в следующей форме:

Если \(x\) есть \(A_1\) и \(y\) есть \(B_1\), ТО \(z_1=a_1x+b_1y\),

Если \(x\) есть \(A_2\) и \(y\) есть \(B_2\), ТО \(z_2=a_2x+b_2y\).

Этапы нечеткого вывода:

Фаззификация: находятся степени истинности для предпосылок каждого правила: \(\mu_{A_1}(x_0), \mu_{A_2}(x_0), \mu_{B_1}(y_0), \mu_{B_2}(y_0)\).
Вывод: Находятся уровни отсечения для предпосылок каждого из правил с использованием операции минимум: \(\alpha_1=\min\{\mu_{A_1}(x_0),\mu_{B_1}(y_0)\}\), \(\alpha_2=\min\{\mu_{A_2}(x_0),\mu_{B_2}(y_0)\}\).
Находятся индивидуальные выходы правил: \(z^*_1=a_1x+b_1y\), \(z^*_2=a_2x+b_2y\).
Определяется четкое значение переменной вывода: \[ z_0=\frac{\alpha_1z^*_1+\alpha_2z^*_2}{\alpha_1+\alpha_2}. \]

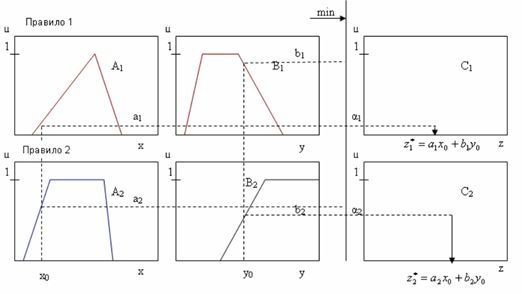
Алгоритм Sugeno.

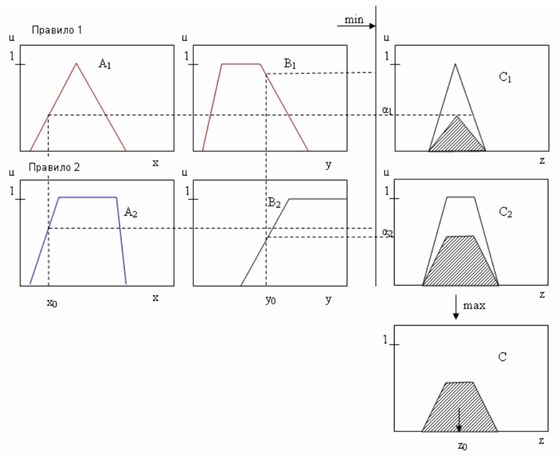
Алгоритм Larsen. Вид базы знаний совпадает с видом базы знаний для алгоритма Mamdani.

Нечеткость: находятся степени истинности для предпосылок каждого правила: \(\mu_{A_1}(x_0), \mu_{A_2}(x_0), \mu_{B_1}(y_0), \mu_{B_2}(y_0)\).
Вывод: находятся уровни отсечения для предпосылок каждого из правил с использованием операции минимум: \(\alpha_1=\min\{\mu_{A_1}(x_0),\mu_{B_1}(y_0)\}\), \(\alpha_2=\min\{\mu_{A_2}(x_0),\mu_{B_2}(y_0)\}\).
В алгоритме Larsen нечеткое подмножество переменной вывода для каждого правила находится с использованием оператора умножения по формуле: \(\mu_{C_1'}(z)=\alpha_1\cdot \mu_{C_1}(z), \mu_{C_2'}(z)=\alpha_2\cdot \mu_{C_2}(z).\)
Композиция: с использованием операции максимум производится объединение найденных частных нечетких подмножеств. Находится итоговое нечеткое подмножество для переменной выхода с функцией принадлежности: \[ \mu_\Sigma(z)=\mu_C(z)=\max\{\mu_{C_1'}(z),\mu_{C_2'}(z)\}=\max\{\alpha_1\cdot \mu_{C_1}(z),\alpha_2\cdot \mu_{C_2}(z)\}. \]
Приведение к четкости также производится методом центра тяжести.

Алгоритм Larsen.

Пример использования нечетких рассуждений.

Требуется оценить уровень риска, связанного с проектом разработки программного обеспечения. Заметим, что данные можно изменить и посмотреть как изменится результат. Будем считать, что есть возможность варьирования только двумя параметрами - объемом финансирования проекта и размером штатного расписания (пример отсюда и отсюда ).

Шаг 1

На первом этапе преобразуем четкий ввод в нечеткий. Поскольку у нас есть два входящих параметра, у будет, соответственно, и два четких значения. Первое значение - это размер штатного расписания проекта. Второе значение - объем финансирования проекта.
Предположим, что имеем следующие ресурсы - проект_финансирование = 35% и проект_штат= 60%. Мы можем получить нечеткие значения для этих четких значений, используя функции принадлежности соответствующих множеств. Наборы, определенные для проект_финансирование, являются недостаточными, критичными и адекватными. Множества, определенные для проект_штат, являются малыми и большими.
Таким образом, мы имеем следующие нечеткие значения для проект_финансирование:

\(\mu_{финансирование = недостаточно}\)(35) = 0,5;

\(\mu_{финансирование = критично}\) (35) = 0,2;

\(\mu_{финансирование = адекватно} \) (35) = 0,0.

Имеем следующее визуальное представление этой процедуры:

Нечеткое представление финансирования проекта.

Ниже приведены нечеткие значения для проект_штат.

\(\mu_{штат= малый}\) (60) = 0,1

\(\mu_{штат= большой}\) (60) = 0,7.

Ниже приведено визуальное представление этой процедуры:

Нечеткое представление штата сотрудников проекта.

Правила

Теперь, когда есть нечеткие значения, можно использовать нечеткие правила для получения конечного нечеткого значения. Правила заключаются в следующем:

Если финансирование проекта является достаточным и штат небольшим, тогда риск низкий.
Если финансирование является критичным или штат является большим, то риск является нормальным.
Если финансирование недостаточно, то риск высокий.

Правило 1 - Если финансирование является адекватным и штат мал, тогда риск низкий
\[ \mu_{A\cup B}(x)=\max\{\mu_A(x),\mu_B(x)\}, \]

\(\mu_{риск = низкий} = \max [\mu_{финансирование = адекватный}\) (35), \(\mu_{штат= малый}\) (60)\(] = \max[\) 0.0,0.1] = 0.1

Правило 2 - Если финансирование является критичным или штат- большим, то риск нормальный.
Конъюнкции в нечетких правилах вычисляются следующим образом \[ \mu_{A\cap B}(x)=\min\{\mu_A(x),\mu_B(x)\} \]

\(\mu_{риск = нормальный} = \min[\mu_{финансирование = критичное}\) (35), \(\mu_{штат= большой}\) (60)\(] = \min \){0.2, 0.7} = 0.2.

Правило 3 - Если финансирование недостаточно, тогда риск высокий

\(\mu_{риск = высокий}\) = 0.5.

Результаты оценки правила
Результат оценки правил показан ниже: \(\mu_{риск = низкий}\) (z) = 0.1

Оценка малости риска проекта.

\(\mu_{риск = нормально}\) (z) =0.2

Оценка нормального риска проекта.

\(\mu_{риск = высокий}\) (z) = 0.5

Оценка высокого риска проекта.

Мы выполняем объединение на всех масштабируемых функциях для получения конечного результата. Результат снова отображается зеленым цветом.

Оценка общего риска проекта.

Дефаззификация

Дефаззификация может быть выполнена несколькими различными способами. Наиболее популярным методом является метод центроида.
Метод центроида.
Этот метод состоит в вычислении центра тяжести для области под кривой. \[ C_0=\frac{\sum_{x=a}^b\mu_A(x)x}{\sum_{x=a}^b\mu_A(x)}. \] Тогда риски этого проекта в процентах равны

\[ COG=\frac{0*0.10+10*0.10+20*0.10+30*0.10+40*0.20+50*0.20+60*0.20+70*0.20+80*0.50+90*0.50+100*0.50} {0.10+0.10+0.10+0.10+0.20+0.20+0.20+0.20+0.50+0.50+0.50}=68.81% \]

Биссектриса.
Находится вертикальная линия, которая делит область на два субрегиона равной площади. Это иногда, но не всегда, совпадает с центроидной линией.
Среднее значение.
Предполагается, что плато при максимальном значении конечной функции принимает среднее значение.
Наименьшее значение максимального.
Предполагается, что плато при максимальном значении конечной функции принимает наименьшее из значений, которое оно охватывает.
Наибольшее значение максимального.
Предполагается, что плато при максимальном значении конечной функции принимает наибольшее из значений, которое оно охватывает.

Ранжирование.

Заметим, что достаточно часто требуется упорядочить имеющийся набор нечетких множеств, то есть ранжировать их. К примеру, для имеющего набора проектов требуется приписать каждому из них рейтинг . Как и в предыдущих случаях будем использовать оценку в виде трапецевидного нечёткого числа и треугольного, как частный случай.
Итак, после того, как каждый проект получил общую оценку в виде трапецевидного нечёткого числа, можно упорядочить проекты в соответствии с приписанным им рейтингом.

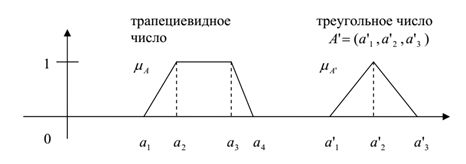
Трапецевидные и треугольные нечёткие числа.

Для сравнения нечётких чисел имеется несколько различных методов:

Метод Чью-Парка. Фиксируется параметр w. Каждому трапецевидному числу \(A=(a_1,a_2,a_3,a_4)\) ставится в соответствие (чёткое) число \[ cp(A)=\frac{1}{4}(a_1+a_2+a_3+a_4)+\frac{w}{2}(a_2+a_3). \] Упорядочение производится по возрастанию величин cp(A).
Метод Чанга. Трапецевидные числа \(A=(a_1,a_2,a_3,a_4)\) упорядочиваются по возрастанию величин \[ ch(A)=\frac{1}{4}(a_3^2+a_3a_4+a_4^2-a_1^2-a_1a_2-a_2^2). \]
Метод Кауфмана-Гупты. Вычисляются три следующие величины: \[ kg_1(A)=\frac{1}{6}(a_1+2a_2+2a_3+a_4), kg_2(A)=\frac{1}{6}(a_3+a_4), kg_3(A)=\frac{1}{6}(a_4-a_1). \] Полагаем, что \(A \ge B\), если \(kg_1(A)>kg_1(B)\) или \(kg_1(A)=kg_1(B)\) и \(kg_2(A)>kg_2(B)\), или \(kg_1(A)=kg_1(B)\), \(kg_2(A)=kg_2(B)\) и \(kg_3(A)>kg_3(B)\).
Метод Джейна. Метод задаёт порядок в наборе нечётких чисел \(A_1,A_2,...,A_n\). Пусть возможные значения чисел из данного набора лежат на промежутке от \(b_1\) до \(b_2\). Тогда нечёткое число \(B = (b_1,b_2,\infty,\infty)\) можно рассматривать как нечёткое множество «больших чисел». Для каждого \(A_i\) рассматривается степень, в которой число \(A_i\) является «большим»: \[ Pos(A_i\in B)=\max_x\min\{\mu_{A_i}(x),\mu_B(x)\}. \] Набор упорядочивается по возрастанию величин \(Pos(A_i \in B)\).
Метод Дюбуа-Прада. Как и в предыдущем методе, рассматривается набор нечётких чисел \(A_1,A_2,...,A_n\). Каждому числу \(A_i\) отвечает его степень доминирования над остальными числами: \[ PD(A_i)=Pos\left(A_i\ge \max_{j\ne i}A_j\right)=\min_{j\ne i}\max_{x,y}\min\{\mu_{A_i}(x),\mu_{A_j}(x)\}. \] Числа упорядочиваются по возрастанию величин \(PD(A_i)\).

Рассмотренные методы сравнения в общем случае могут давать разные результаты.
Пример ранжирования проектов.
Пусть имеется три проекта, оцененные числами \(A_1 = (3,5,5,9) , A_2 = (3,7,7,8) , A_3 = (1,6,6,10).\) По методу Чью-Парка с параметром \(w = 1\) имеем:

cp(A₁) = 10.5 < cp(A₃) = 11.75 < cp(A₂ ) = 13.25 .

Наилучшим является второй проект, далее следуют третий и первый проекты. Метод Чанга приводит к следующему результату

ch(A₂ ) = 15 < ch(A₁) = 17 < ch(_A) = 25.5 ,

то есть второй проект оказывается наихудшим.
По методу Кауфмана-Гупты получаем:

kg₁(A₁) = 5.33 < kg₁(A₃) = 5.83 < kg₁(A₂) = 6.5 ,

что совпадает с результатом метода Чью-Парка.
В методе Джейна определим множество больших чисел как \(B = (0,10,\infty,\infty)\). Тогда \[ Pos(A_1 \in B) = 6.43 \lt Pos(A_3 \in B) = 7.14 \lt Pos(A_2 \in B) = 7.27. \] Порядок совпадает с порядком Чью-Парка.
Применение метода Дюбуа-Прада даёт следующие неравенства: \[ PD(A_1) = 0.75 \lt PD(A_3) = 0.875 \lt PD(A_2 ) = 1. \] Это приводит к следующему ранжируемому списку: « проект 1 < проект 3 < проект 2».

Выбор альтернатив с использованием правил нечеткого вывода

Рассмотрим метод многокритериального выбора альтернатив на основе композиционного правила агрегирования описаний альтернатив с информацией о предпочтениях в виде нечетких суждений .
Пусть \(U\)- множество элементов, \(А\)-его нечеткое подмножество, степень принадлежности элементов которого есть число из единичного интервала [0,1]. Подмножества \(А\) являются значениями лингвистической переменной \(Х\).
Пусть множество решений характеризуется набором критериев \(X_1,X_2,...,X_p\), то есть лингвистических переменных на базовых множествах \(U_1,U_2,...,U_p\) соответственно. Набор из нескольких критериев с соответствующими значениями характеризуют представления об удовлетворительности (приемлемости) решения. Переменная \(S\) «Удовлетворительность» также является лингвистической. Пример высказывания:

d₁: «Если X₁ = НИЗКАЯ и X₂=ХОРОШЕЕ, то S=ВЫСОКАЯ»

В общем случае высказывание имеет вид

d_i: «Если X₁=A_1,i и X₂=A_2,i и ... X_p=A_p,i, то S=B_i».

Обозначим пересечение \(X_i=A_{1,i}\cap X_2=A_{2,i}\cap\ldots X_p=A_{p,i}\) через \(X=A_i\). Операции пересечения нечетких множеств соответствует нахождение минимума их функций принадлежности \[ \mu_{A_i}(v)=\min_{v\in V}\left\{\mu_{A_{i,1}}(u_1),\mu_{A_{i,2}}(u_2),...,\mu_{A_{i,p}}(u_p)\right\} \] где \(V=U_1\times U_2\times ...\times U_p \), \(v=(u_1,u_2,..., u_p)\), \(\mu_{A_{i,j}}(u_j)\) - значение принадлежности элемента \(u_j\) нечеткому множеству \(A_{i,j}\) . Тогда высказывание примет вид

d_i: «Если X=A_i, то S=B_i»

Обозначим базовое множество (U или V) через W. Тогда Aⁱ - нечеткое подмножество W, в то время как Bⁱ-нечеткое подмножество единичного интервала I.
Импликация («если…, то…») нечетких множеств выражается следующим образом \[ \mu_H(w,i)=\min_{w\in W}\{1,(1-\mu_A(w)+\mu_B(i))\}, \] где H- нечеткое подмножество на \(W\times I,w\in W, i\in I\). Аналогичным образом высказывания \(d_1,d_2,...,d_q\) преобразуются в множества \(H_1,H_2,...,H_q\). Их объединением является множество D: \[ D=H_1\cup H_2\cup ... \cup H_q \] и для каждого \((w,i)\in W\times I\) \[ \mu_D(w,i)=\min_{w\in W}\{\mu_{H_i},(w,i)\},i=1,2,...,q. \] Рассмотрим выбор альтернатив, каждая из которых описывается нечетким подмножеством C из W. Удовлетворительность альтернативы определяется на основе композиционного правила вывода \(G=C\circ D\), где G- нечеткое подмножество интервала I. Тогда \[ \mu_G(i)=\max_{w\in W}\left\{\min\{\mu_C(w),\mu_D(w,i)\}\right\}. \] Сопоставление альтернатив происходит на основе точечных оценок. Для нечеткого множества \(A\subset I\) определим \(\alpha\)-уровневое множество \(\alpha\in [0,1]\) \[ A_{\alpha}=\left\{x|\mu_A(x)\ge \alpha,x\in I\right\}. \] Для каждого \(A_{\alpha}\) можно вычислить среднее число элементов \(M(A_{\alpha})\):

Для множества из n элементов \(M(A_{\alpha})=\frac{1}{n}\sum\{x_i|x_i\in A_\alpha\}\).
Для \(A_{\alpha}=\{a\le x\le b\}\) \(M(A_{\alpha})=\frac{a+b}{2}. \)
Для \(0\le a_1\le b_1\le a_2\le b_2\le ...\le a_n\le b_n\le 1\), \(A_\alpha=\bigcup_{i=1}^n\{a_i\le x\le b_i\}\) \[ M(A_\alpha)=\frac{\sum_{i=1}^n\frac{a_i+b_i}{2}(b_i-a_i)}{\sum_{i=1}^n(b_i-a_i)}. \]

Тогда точечное значение для множества \(A\) \[ F(A)=\frac{1}{\alpha_{\max}} \int_0^{\alpha_\max}M(A_\alpha)d\alpha, \] где \(\alpha_\max\)- значение, при котором А имеет максимум.
При выборе альтернатив, для каждой из них определяется удовлетворительность и вычисляется соответствующая точечная оценка, Лучшей считается альтернатива с наибольшим ее значением.

Пример выбора альтернатив на основе нечеткого вывода.

Задача – из списка кандидатов нужно выбрать наиболее подходящего (пример отсюда).
Имеем следующий результат обсуждения претендентов

d₁: «Если кандидат – опытный исследователь, имеет некоторый производственный стаж и опыт преподавания в вузе, то он удовлетворяющий (отвечающий требованиям)»

d₂: «Если он к d₁ может преподавать теорию информационных систем, то он более чем удовлетворяющий»

d₃: «Если он к d₂ может найти заказчика наукоемкой продукции, то он безупречный»

d₄: : «Если он имеет все оговоренное в d₃, кроме способности преподавать теорию информационных систем, то он очень удовлетворяющий»

d₅: «Если кандидат – очень опытный исследователь, имеет способность найти заказчика и хороший преподаватель, но без производственного стажа, то он удовлетворяющий»

d₆: «Если не имеет квалификации исследователя или способность к преподаванию, он неудовлетворяющий»

Анализ информационный фрагментов дает пять критериев используемых в принятии решения

Х1-исследовательские способности
Х2- производственный стаж
Х3-опыт преподавания
Х4-опыт преподавания теории информационных систем
Х5-способность найти заказчика

Будем измерять эти переменные на базовом множестве U кандидатов.

d₁: «Если Х₁=ОБРАЗОВАННЫЙ и Х₂=НЕКОТОРЫЙ ОПЫТ и Х₃=ХОРОШИЙ, то Y=УДОВЛЕТВОРЯЮЩИЙ»

d₂: «Если Х₁=ОБРАЗОВАННЫЙ и Х₂=НЕКОТОРЫЙ ОПЫТ и Х₃=ХОРОШИЙ и Х₄-СПОСОБНЫЙ, то Y=БОЛЕЕ ЧЕМ УДОВЛЕТВОРЯЮЩИЙ»

d₃: «Если Х₁=ОБРАЗОВАННЫЙ и Х₂=НЕКОТОРЫЙ ОПЫТ и Х₃=ХОРОШИЙ и Х₄-СПОСОБНЫЙ и Х₅-СПОСОБНЫЙ, то Y=БЕЗУПРЕЧНЫЙ»

d₄: «Если Х₁=ОБРАЗОВАННЫЙ и Х₂=НЕКОТОРЫЙ ОПЫТ и Х₃=ХОРОШИЙ и Х₅-СПОСОБНЫЙ, то Y=ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ»

d₅: «Если Х₁=ОЧЕНЬ ОБРАЗОВАННЫЙ и Х₂=НЕ ИМЕЕТ ОПЫТА и Х₃=ХОРОШИЙ и Х₅-СПОСОБНЫЙ, то Y=УДОВЛЕТВОРЯЮЩИЙ»

d₆: «Если Х₁=НЕ ОБРАЗОВАННЫЙ и Х₃=НЕ СПОСОБНЫЙ К ПРЕПОДАВАНИЮ, то Y=НЕ УДОВЛЕТВОРЯЮЩИЙ»

Переменная Y задана на множестве \(J=\{0;0.1;0.2;...,1\}\).

УДОВЛЕТВОРЯЮЩИЙ определено как \(\mu_S(x)=x,x\in J\)
БОЛЕЕ ЧЕМ УДОВЛЕТВОРЯЮЩИЙ – как \(\mu_{MS}(x)=\sqrt{x^3},x\in J\)
БЕЗУПРЕЧНЫЙ – как \[ \mu_p(x)= \left\{ \begin{array}{ll} 1, & \hbox{ если }& x=1 \\ 0, & \hbox{ если }& x\ne 1. \end{array} \right. \]
ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ – как \(\mu_{VS}(x)=x^2,x\in J\)
НЕ УДОВЛЕТВОРЯЮЩИЙ – как \(\mu_{US}(x)=1-x2,x\in J\).

Выбор проводится из пяти кандидатов \(U=\{u_1,u_2,u_3,u_4,u_5\}\). Имеем следующие оценки каждого кандидата

A=ОБРАЗОВАННЫЙ ИССЛЕДОВАТЕЛЬ={0.8/u₁,0.6/u₂,0.5/u₃,0.1/u₄,0.3/u₅}}

B=НЕКОТОРЫЙ ПРОИЗВОДСТВЕННЫЙ ОПЫТ= {0.5/u₁,1/u₂,0/u₃,0.5/u₄,1/u₅}}

С=ХОРОШАЯ СПОСОБНОСТЬ ПРЕПОДАВАНИЯ= {0.6/u₁,0.9/u₂,1/u₃,0.7/u₄,1/u₅}}

D=СПОСОБНОСТЬ ПРЕПОДАВАНИЯ ТЕОРИИ ИНФОРМАЦИОННЫХ СИСТЕМ= {1/u₁,0.3/u₂,1/u₃,0/u₄,0/u₅}}

E=СПОСОБНОСТЬ ПОЛУЧИТЬ ВНЕШНЕЕ ФИНАНСИРОВАНИЕ={0/u₁,0.5/u₂,1/u₃,0.8/u₄,0.1/u₅}}

После этого фрагменты знаний примут вид

d₁: Если Х=А и В и С, то Y=S

d₂: Если Х=А и В и С и D, то Y=MS

d₃: Если Х=А и В и С и D и E, то Y=P

d₄: Если Х=А и В и С и E, то Y=VS

d₅: Если Х=очень А и не В и С и E, то Y=S

d₆: Если Х= не А или не С, то Y=US

Тогда, учитывая, что операция пересечения нечетких множеств соответствует нахождение минимума их функций принадлежности, а объединению – их максимуму, получаем \[ d_1:\mu_{M_1}(u)=\min\{\mu_A(u),\mu_B(u),\mu_C(u)\} M_1=\{0.5/u_1,0.6/u_2,0/u_3,0.1/u_4,0.3/u_5\}, \] \[ d_2:\mu_{M_2}(u)=\min\{\mu_A(u),\mu_B(u),\mu_C(u),\mu_D(u)\} M_2=\{0.5/u_1,0.3/u_2,0/u_3,0/u_4,0/u_5\}, \] \[ d_3:\mu_{M_3}(u)=\min\{\mu_A(u),\mu_B(u),\mu_C(u),\mu_D(u),\mu_E(u)\} M_3=\{0/u_1,0.3/u_2,0/u_3,0/u_4,0/u_5\}, \] \[ d_4:\mu_{M_4}(u)=\min\{\mu_A(u),\mu_B(u),\mu_C(u),\mu_E(u)\} M_4=\{0/u_1,0.5/u_2,0/u_3,0.1/u_4,0.1/u_5\}, \] \[ d_5:\mu_{M_5}(u)=\min\{\mu_{A^2}(u),1-\mu_B(u),\mu_C(u),\mu_E(u)\} M_5=\{0/u_1,0/u_2,0/u_3,0.1/u_4,0/u_5\}, \] \[ d_6:\mu_{M_6}(u)=\max\{1-\mu_A(u),1-\mu_C(u)\} M_6=\{0.4/u_1,0.4/u_2,0.5/u_3,0.9/u_4,0.7/u_5\}. \] Таким образом,

d₁: Если Х=M₁, то Y=S,

d₂: Если Х=M₂, то Y=MS,

d₃: Если Х=M₃, то Y=P,

d₄: Если Х=M₄, то Y=VS,

d₅: Если Х=M₅, то Y=S,

d₆: Если Х=M₆, то Y=US.

Используя правило преобразования импликации «Если Х=М, то Y=Q» в выражении \(\mu_D(u,i)=\min\{1,1-\mu_M(u)+\mu_Q(u)\}\), для каждой пары \((u,i)\in U\times J\) получаем следующие нечеткие подмножества из \(U\times J\)

D₁=

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
u₁	0.5	0.6	0.7	0.8	0.9	1	1	1	1	1	1
u₂	0.4	0.5	0.6	0.7	0.8	0.9	1	1	1	1	1
u₃	1	1	1	1	1	1	1	1	1	1	1
u₄	0.9	1	1	1	1	1	1	1	1	1	1
u₅	0.7	0.8	0.9	1	1	1	1	1	1	1	1

D₂=

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
u₁	0.5	0.53	0.59	0.66	0.75	0.85	0.96	1	1	1	1
u₂	0.7	0.73	0.79	0.86	0.95	1	1	1	1	1	1
u₃	1	1	1	1	1	1	1	1	1	1	1
u₄	1	1	1	1	1	1	1	1	1	1	1
u₅	1	1	1	1	1	1	1	1	1	1	1

D₃=

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
u₁	1	1	1	1	1	1	1	1	1	1	1
u₂	0.7	0.7	0.7	0.7	0.7	0.7	0.7	0.7	0.7	0.7	1
u₃	1	1	1	1	1	1	1	1	1	1	1
u₄	1	1	1	1	1	1	1	1	1	1	1
u₅	1	1	1	1	1	1	1	1	1	1	1

D₄=

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
u₁	1	1	1	1	1	1	1	1	1	1	1
u₂	0.5	0.51	0.54	0.59	0.66	0.75	0.86	0.99	1	1	1
u₃	1	1	1	1	1	1	1	1	1	1	1
u₄	0.9	0.91	0.94	0.99	1	1	1	1	1	1	1
u₅	0.9	0.91	0.94	0.99	1	1	1	1	1	1	1

D₅=

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
u₁	1	1	1	1	1	1	1	1	1	1	1
u₂	1	1	1	1	1	1	1	1	1	1	1
u₃	0.75	0.85	0.95	1	1	1	1	1	1	1	1
u₄	0.99	1	1	1	1	1	1	1	1	1	1
u₅	1	1	1	1	1	1	1	1	1	1	1

D₆=

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
u₁	1	1	1	1	1	1	1	0.9	0.8	0.7	0.6
u₂	1	1	1	1	1	1	1	0.9	0.8	0.7	0.6
u₃	1	1	1	1	1	1	0.9	0.8	0.7	0.6	0.5
u₄	1	1	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.1
u₅	1	1	1	1	0.9	0.8	0.7	0.6	0.5	0.4	0.3

В результате получаем общее функциональное решение \(D=D_1\cap D_2\cap D_3\cap D_4\cap D_5\cap D_6\), то есть \(\mu_D(u,i)=\min_{j=1,...,6}\{\mu_{D_i}(u,i)\}\)

	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
u₁	0.5	0.53	0.59	0.66	0.75	0.85	0.96	0.9	0.8	0.7	0.6
u₂	0.4	0.5	0.54	0.59	0.66	0.7	0.7	0.7	0.7	0.7	0.6
u₃	0.75	0.85	0.95	1	1	1	0.9	0.8	0.7	0.6	0.5
u₄	0.9	0.91	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.1
u₅	0.7	0.8	0.9	0.99	0.9	0.8	0.7	0.6	0.5	0.4	0.3

Для вычисления удовлетворительности каждой из альтернатив применим правило композиционного вывода в нечеткой среде: \(E_k= G_k\circ D\), где \(E_k\)-степень удовлетворения альтернативы \(k\), \(G_k\)-изображение альтернативы \(k\) в виде нечеткого подмножества U, D- функциональное решение. Тогда \[ \mu_{E_k}(i)=\max_{u\in U}\{min\{\mu_{G_k}(u),\mu_{D_k}(u,i)\}\}. \] Кроме того, в этом случае \(\mu_{G_k}(u)=0,u\ne u_k; \mu_{G_k}(u)=1,u=u_k\). Отсюда \(\mu_{E_k}(i)=\mu_D(u_k,i)\). Другими словами, \(E_k\) есть \(k\)-я строка матрицы \(D\).
Теперь применим процедуру для сравнения нечетких множеств \(E_1,E_2,E_3,E_4,E_5\) в единичном интервале для получения наилучшего решения.
Для первой альтернативы

E_1={0.5/0;0.53/0.1;0.59/0.2;0.66/0.3;0.75/0.4;0.85/0.5;0.96/0.6;0.9/0.7;0.8/0.8;0.7/0.9;0.6/1}

Вычисляем уровневые множества \(E_{j\alpha}\). Их мощность \(M(E_{j\alpha})\) равна \[ M(E_{j\alpha})=\frac{1}{n}\sum_{i=1}^nx_i, \] где

0≤α ≤ 0.5, dα = 0.5, E_1,α={0;0.1;0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9;1}; M(E_1,α)=0.5;

0.5≤α ≤ 0.53, dα = 0.03, E_1,α={0.1;0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9;1}; M(E_1,α)=0.55;

0.53≤α ≤ 0.59, dα = 0.06, E_1,α={0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9;1}; M(E_1,α)=0.6;

0.59≤α ≤ 0.6, dα = 0.01, E_1,α={0.3;0.4;0.5;0.6;0.7;0.8;0.9;1}; M(E_1,α)=0.65;

0.6≤α ≤ 0.66, dα = 0.06, E_1,α={0.3;0.4;0.5;0.6;0.7;0.8;0.9}; M(E_1,α)=0.6;

0.66≤α ≤ 0.7, dα = 0.04, E_1,α={0.4;0.5;0.6;0.7;0.8;0.9}; M(E_1,α)=0.65;

0.7≤α ≤ 0.75, dα = 0.05, E_1,α={0.4;0.5;0.6;0.7;0.8}; M(E_1,α)=0.6;

0.75≤α ≤ 0.8, dα = 0.05, E_1,α={0.5;0.6;0.7;0.8}; M(E_1,α)=0.65;

0.8≤α ≤ 0.85, dα = 0.05, E_1,α={0.5;0.6;0.7}; M(E_1,α)=0.6;

0.85≤α ≤ 0.9, dα = 0.05, E_1,α={0.6;0.7}; M(E_1,α)=0.65;

0.9≤α ≤ 0.96, dα = 0.06, E_1,α={0.6}; M(E_1,α)=0.6.

Найдем точечную оценку E₁: \[ F(E_1)=\frac{1}{\alpha_{\max}}\int_0^{\alpha_{\max}}M(E_{1,\alpha})d\alpha=\frac{1}{0.96}\int_0^{0.96}M(E_{1,\alpha})d\alpha= \] \[ =1/0.96(0.5*0.5+0.55*0.03+0.6*0.06+0.65*0.01+0.6*0.06+0.65*0.04+0.6*0.05+0.6*0.05+0.65*0.05+0.65*0.05 +0.6*0.06)=0.554. \] Для второй альтернативы

E_2={0.4/0;0.5/0.1;0.54/0.2;0.59/0.3;0.66/0.4;0.7/0.5;0.7/0.6;0.7/0.7;0.7/0.8;0.7/0.9;0.6/1}

Вычисляем уровневые множества

0≤α ≤ 0.4, dα = 0.4, E_2,α={0;0.1;0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9;1}; M(E_2,α)=0.5;

0.4≤α ≤ 0.5, dα = 0.1, E_2,α={0.1;0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9;1}; M(E_2,α)=0.55;

0.5≤α ≤ 0.54, dα = 0.04, E_2,α={0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9;1}; M(E_2,α)=0.6;

0.54≤α ≤ 0.59, dα = 0.05, E_2,α={0.3;0.4;0.5;0.6;0.7;0.8;0.9;1}; M(E_2,α)=0.65;

0.59≤α ≤ 0.6, dα = 0.01, E_2,α={0.4;0.5;0.6;0.7;0.8;0.9;1}; M(E_2,α)=0.7;

0.6≤α ≤ 0.66, dα = 0.06, E_2,α={0.4;0.5;0.6;0.7;0.8;0.9}; M(E_2,α)=0.65;

0.66≤α ≤ 0.7, dα = 0.04, E_2,α={0.5;0.6;0.7;0.8;0.9}; M(E_2,α)=0.75;

Точечная оценка E₂:

F(E₂)=1/0.7(0.5*0.4+0.55*0.1+0.6*0.04+0.65*0.05+0.7*0.01+0.65*0.06+0.75*0.04)=0.554.

Для третьей альтернативы

E₃={1/0;0.1/0.1;1/0.2;1/0.3;1/0.4;1/0.5;0.9/0.6;0.8/0.7;0.7/0.8;0.6/0.9;0.5/1}

F(E₃)= 1/1(0.5*0.5+0.45*0.1+0.4*0.1+0.35*0.1+0.3*0.1+0.25*0.1)=0.448.

Для четвертой

E₄={0.9/0;0.91/0.1;0.9/0.2;0.8/0.3;0.7/0.4;0.6/0.5;0.5/0.6;0.4/0.7;0.3/0.8;0.2/0.9;0.1/1}

F(E₄)= 1/0.91(0.5+0.45+0.4+0.35+0.3+0.25+0.2+0.15+0.1*0.1+0.1*0.01)=0.298.

И, наконец, для пятой,

E₅={0.7/0;0.8/0.1;0.9/0.2;0.99/0.3;0.9/0.4;0.8/0.5;0.7/0.6;0.6/0.7;0.5/0.8;0.4/0.9;0.3/1}

F(E₅)=1/0.99(0.5*0.3+(0.45+0.4+0.35*0.3*3)*0.1+0.3*0.09)=0.391.

Таким образом точечная оценка удовлетворительности для альтернативы u₁ равна 0.554, для u₂ равна 0.554, u₃ - 0.425, u₄ - 0.298 и u₅ - 0.391. В качестве наилучшей альтернативы выбираем ту, чья оценка выше.

Ранжирование альтернатив на основе эвристического подхода.

Рассмотрим проблему упорядочивания альтернативы на основе композиции нечетких критериальных оценок и эвристических соображений в виде лингвистических оценок полезности.
Модель процесса принятия решения включает: оценки альтернатив, представления лица, принимающего решения, описание процесса принятия решения.
Каждую альтернативу можно описать с помощью критериев качества \( D_i,i=1,2,...,n\). Область определения представляется как декартово произведение n множеств \( D_i, D=D_1\times D_2\times D_3\times ...\times D_n\). Точка задается соответствующим набором из n значений \((d_1,d_2,...,d_n)\in D\), где \(d_)i\in D_i\) и обозначается \(d^{(n)}\).
Если значения критериев неточно определены (то есть подразумеваются нечеткими), то альтернатива \(А\) есть нечеткое подпространство \(D\) и представляется как декартово произведение нечетких множеств на \(D_i\): \(A=F(D_1)\times F(D_2)\times ...\times F(D_n)\), где \(F(D_i)\)-нечеткое подмножество \(D_i\).
Функция принадлежности \(\mu_A(d_i)\) находится в соответствии с обычным определением нечеткой композиции \(\\mu_A(d^{(n)})=\min_{i=1,...,n}\mu_A(d_i)), где \(\mu_A(d_i)\) - функция принадлежности оценки альтернативы по критерию \(D_i\).
Множество всех возможных альтернатив обозначается через \(\textbf{A}\) и является множеством нечетких подмножеств.
Элементы u универсального множества U выбираются в соответствии с некоторыми простыми правилами, например,

U={ВЫСОКАЯ, ДОСТАТОЧНО ВЫСОКАЯ, СРЕДНЯЯ, ДОСТАТОЧНО НИЗКАЯ, НИЗКАЯ}

Словарь может быть расширен введением модификаторов, таких как

ОЧЕНЬ, ВПОЛНЕ, БОЛЕЕ-МЕНЕЕ.

Полезность может быть интерпретирована как лингвистическая переменная, значения которой есть термы нечеткого множества, определенного на интервале [0,1]. Знание о полезности задается нечетким отношением Ф из \(D=\{d_i^{(n)}\}\) в \(U=\{u\}\) , являющимся нечетким множеством на декартовом произведении \(D\times U\). Ф характеризуется с помощью функции \(\mu_{\Phi}(d^{(n)},u)\), посредством которой каждой паре присваивается значение из интервала [0,1]. Отношение Ф обычно представляется в виде таблицы, дающей полезность различных точек из D.
Знание о полезности как нечетком отношении Ф дает возможность характеризовать альтернативу \(A\in\textbf{A}\) нечетким подмножеством \(V\in U\), где \(V=\textbf{A}\circ \Phi\) с помощью соотношения \(\mu_V(u)=\max\left\{\min\{\mu_\Phi(d^{(n)},u),\mu_A(u)\}\right\}\).
В соответствии с определением множества V каждая альтернатива \(\textbf{A}\) имеет более одного значения полезности, которые характеризуются разными степенями принадлежности. Ранжируя альтернативы, необходимо установить их упорядочивание, используя оценки ЛУЧШЕ, РАВНОЗНАЧНО, ХУЖЕ, а также выяснить насколько одно нечеткое множество лучше другого.
Иногда полезность с наибольшей степенью принадлежности может быть принята в качестве характерного представителя для сравнения альтернатив. Путем ранжирования альтернатив устанавливается полезность в виде предложения, составленного из элементов U. Оно выражает V лингвистически. Кроме того, V может быть выражено графически, что позволяет визуально сравнить альтернативы.

Пример использования эвристического подхода.

Пусть деканат имеет возможность дать премию студентам (пример отсюда). В выборе кандидата на премию принимают участие две заинтересованные стороны: деканат и актив группы, которые высказывают свои предпочтения относительно кандидата. Их высказывания определяют совокупность критериев эффективности и цели, в частности,

Успеваемость студента D₁={отличная, хорошая, удовлетворительная}.}
Общественная активность студента D₂={очень высокая, высокая, приемлемая, низкая}.
Дисциплина (посещаемость занятий) студента D₃={хорошая, приемлемая, низкая }.
Материальное положение студента D₄={хорошее, приемлемое, плохое }.

Универсальное множество для полезности задается следующим образом:

U={ВЫСОКАЯ, ДОСТАТОЧНО ВЫСОКАЯ, СРЕДНЯЯ, ДОСТАТОЧНО НИЗКАЯ, НИЗКАЯ}

Здесь же можно использовать модификаторы «и», «или», «очень». На основе опроса представителей деканата и актива группы определены лингвистические величины полезности. Базовая переменная полезности изменяется в интервале [0,1].
Эвристики деканата:

Успеваемость отличная предпочтительней хорошей.
Активность может быть приемлемой, если успеваемость отличная, но должна быть очень высокой, если успеваемость хорошая.
Дисциплина должна быть хорошей.
Материальное положение не учитывается.

Эвристики актива группы:

Успеваемость не должна быть удовлетворительной.
Полезность высокая при приемлемой активности, отличной успеваемости и плохом материальном положении; полезность достаточно высокая при очень высокой или просто высокой активности, хорошей успеваемости, хорошем материальном положении.
Оценка дисциплины не учитывается.
При хорошем материальном положении кандидат рассматривается только при условии отличной успеваемости и очень высокой активности.

Идеальный кандидат с точки зрения деканата: Отличная успеваемость, очень высокая активность, хорошая дисциплина.
Идеальный кандидат с точки зрения актива группы: Отличная успеваемость, очень высокая активность, плохое материальное положение.
Конструирование отношений полезности. Пространство эффективности \(D=D_1\times D_2\times D_3\times D_4\) содержит \(3\times 4\times 3\times 3=108\) n-наборов. Отбрасывая на основании рассмотренных эвристик несущественные для обеих групп критериальные оценки эффективности, получаем сокращенные наборы критериев

D₁

D₂={очень высокая, высокая, удовлетворительная},
D₃={хорошая},
D₄=={хорошее, плохое }.

Таким образом, число n-наборов, покрывающих область полезности, уменьшается до \(2\times 3\times 1\times 2=12\) точек (n-наборов). После этого группы договариваются об оценках полезности n-наборов.
Отношения полезности Ф для оценки альтернатив.

Успеваемость	Активность	Дисциплина	Материальное положение	Полезность для деканата	Полезность для группы
ОТЛИЧНАЯ	ОЧЕНЬ ВЫСОКАЯ	ХОРОШАЯ	ПЛОХОЕ	ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ	ОЧЕНЬ-ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ
ОТЛИЧНАЯ	ОЧЕНЬ ВЫСОКАЯ	ХОРОШАЯ	ХОРОШЕЕ	ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ	ОЧЕНЬ-ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ
ХОРОШАЯ	ОЧЕНЬ ВЫСОКАЯ	ХОРОШАЯ	ПЛОХОЕ	ВЫСОКАЯ	ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ
ХОРОШАЯ	ОЧЕНЬ ВЫСОКАЯ	ХОРОШАЯ	ХОРОШЕЕ	ВЫСОКАЯ	ВЫСОКАЯ
ОТЛИЧНАЯ	ВЫСОКАЯ	ХОРОШАЯ	ПЛОХОЕ	ОЧЕНЬ ВЫСОКАЯ	ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ
ОТЛИЧНАЯ	ВЫСОКАЯ	ХОРОШАЯ	ХОРОШЕЕ	ОЧЕНЬ ВЫСОКАЯ	ВЫСОКАЯ
ХОРОШАЯ	ВЫСОКАЯ	ХОРОШАЯ	ПЛОХОЕ	ВЫСОКАЯ	ОЧЕНЬ ВЫСОКАЯ
ХОРОШАЯ	ВЫСОКАЯ	ХОРОШАЯ	ХОРОШЕЕ	ВЫСОКАЯ	ДОСТАТОЧНО ВЫСОКАЯ
ОТЛИЧНАЯ	УДОВЛЕТВОРИ- ТЕЛЬНАЯ	ХОРОШАЯ	ПЛОХОЕ	ДОСТАТОЧНО ВЫСОКАЯ	ДОСТАТОЧНО ВЫСОКАЯ
ОТЛИЧНАЯ	УДОВЛЕТВОРИ- ТЕЛЬНАЯ	ХОРОШАЯ	ХОРОШЕЕ	ДОСТАТОЧНО ВЫСОКАЯ	СРЕДНЕЕ
ХОРОШАЯ	УДОВЛЕТВОРИ- ТЕЛЬНАЯ	ХОРОШАЯ	ПЛОХОЕ	СРЕДНЯЯ	ДОСТАТОЧНО ВЫСОКАЯ
ХОРОШАЯ	УДОВЛЕТВОРИ- ТЕЛЬНАЯ	ХОРОШАЯ	ХОРОШЕЕ	СРЕДНЯЯ	СРЕДНЯЯ

Пусть имеется три кандидата на премию, которых можно охарактеризовать следующим образом:

Студент с хорошей успеваемостью, очень высокой активностью, хорошей дисциплиной и плохим материальным положением
A₁={ХОРОШАЯ, ОЧЕНЬ ВЫСОКАЯ, ХОРОШАЯ, ПЛОХОЕ}.
Для второго студента активность оценивается скорее как высокая, чем удовлетворительная. Это может быть выражено нечетким множеством
F(D₂)={0.6/ВЫСОКАЯ; 0.4/УДОВЛЕТВОРИТЕЛЬНАЯ}.
Величины остальных критериев являются четкими. Альтернатива описывается следующим образом:
A₂ ={0.6/(ОТЛИЧНАЯ,ВЫСОКАЯ,ХОРОШАЯ, ПЛОХОЕ);0.4/(ОТЛИЧНАЯ,УДОВЛЕТВОРИТЕЛЬНАЯ, ХОРОШАЯ, ПЛОХОЕ}.
Оценки третьего кандидата могут быть записаны следующим образом
F(D₁) ={0.6/ОТЛИЧНАЯ;0.3/ХОРОШАЯ};

F(D₂) ={0.2/ВЫСОКАЯ;0.8/УДОВЛЕТВОРИТЕЛЬНАЯ};

F(D₂) ={1/ХОРОШАЯ}.

F(D₂) ={0.6/ХОРОШЕЕ;0.4/ПЛОХОЕ}.

Третья альтернатива задается как прямое произведение множеств, при этом берется минимум по функциям принадлежности, то есть

A₃ ={min{0.6, 0.2, 1, 0.6}/(ОТЛИЧНАЯ, ВЫСОКАЯ,ХОРОШАЯ, ХОРОШЕЕ);
min{0.6, 0.8, 1, 0.6}/(ОТЛИЧНАЯ, УДОВЛЕТВОРИТЕЛЬНАЯ, ХОРОШАЯ, ХОРОШЕЕ);
min{0.6, 0.2, 1, 0.4}/(ОТЛИЧНАЯ, ВЫСОКАЯ, ХОРОШАЯ, ПЛОХОЕ);
min{0.6, 0.8, 1, 0.4}/(ОТЛИЧНАЯ, УДОВЛЕТВОРИТЕЛЬНАЯ, ХОРОШАЯ, ПЛОХОЕ);
min{0.3, 0.2, 1, 0.6}/ (ХОРОШАЯ,ВЫСОКАЯ, ХОРОШАЯ, ХОРОШЕЕ);
min{0.3, 0.8, 1, 0.6}/(ХОРОШАЯ, УДОВЛЕТВОРИТЕЛЬНАЯ, ХОРОШАЯ, ХОРОШЕЕ);
min{0.3, 0.2, 1, 0.4}/(ХОРОШАЯ,ВЫСОКАЯ, ХОРОШАЯ, ПЛОХОЕ);
min{0.3, 0.8, 1, 0.4}/(ХОРОШАЯ, УДОВЛЕТВОРИТЕЛЬНАЯ, ХОРОШАЯ, ПЛОХОЕ)}.

Таким образом, имеем

A₃ ={0.2/(ОТЛИЧНАЯ, ВЫСОКАЯ,ХОРОШАЯ, ХОРОШЕЕ);
0.6/(ОТЛИЧНАЯ, УДОВЛЕТВОРИТЕЛЬНАЯ, ХОРОШАЯ, ХОРОШЕЕ);
0.2/(ОТЛИЧНАЯ, ВЫСОКАЯ, ХОРОШАЯ, ПЛОХОЕ);
0.4/(ОТЛИЧНАЯ, УДОВЛЕТВОРИТЕЛЬНАЯ, ХОРОШАЯ, ПЛОХОЕ);
0.2/ (ХОРОШАЯ,ВЫСОКАЯ, ХОРОШАЯ, ХОРОШЕЕ);
0.3/(ХОРОШАЯ, УДОВЛЕТВОРИТЕЛЬНАЯ, ХОРОШАЯ, ХОРОШЕЕ);
0.2/(ХОРОШАЯ,ВЫСОКАЯ, ХОРОШАЯ, ПЛОХОЕ);
0.3/(ХОРОШАЯ, УДОВЛЕТВОРИТЕЛЬНАЯ, ХОРОШАЯ, ПЛОХОЕ)}

Вычисление полезности альтернатив. На основании описания альтернатив и таблиц оценок полезности наборов значений для каждой из групп находим величины полезности \(\V(A_i)):
Значения полезности в виде нечетких множеств

Альтернатива	Деканат	Группа
A₁	{ВЫСОКАЯ}	{ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ}
A₂	{0.6/ОЧЕНЬ ВЫСОКАЯ; 0.4/ДОСТАТОЧНО ВЫСОКАЯ}	{0.6/ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ; 0.4/ДОСТАТОЧНО ВЫСОКАЯ}
A₃	{0.2/ОЧЕНЬ ВЫСОКАЯ; 0.6/ДОСТАТОЧНО ВЫСОКАЯ; 0.2/ОЧЕНЬ ВЫСОКАЯ; 0.4/ДОСТАТОЧНО ВЫСОКАЯ; 0.2/ ВЫСОКАЯ; 0.3/СРЕДНЯЯ; 0.2/ВЫСОКАЯ; 0.3/СРЕДНЯЯ}	{0.2/ВЫСОКАЯ; 0.6/СРЕДНЯЯ; 0.2/ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ; 0.4/ДОСТАТОЧНО ВЫСОКАЯ; 0.2/ОЧЕНЬ ВЫСОКАЯ; 0.3/СРЕДНЯЯ; 0.2/ДОСТАТОЧНО ВЫСОКАЯ; 0.3/ДОСТАТОЧНО ВЫСОКАЯ}

Упорядочивание альтернатив. Полезности альтернатив представлены как нечеткие множества V. Следующий шаг состоит в ранжировании нечетких множеств и тем самым в установлении лучшей альтернативы. Каждый терм полезности может быть представлен как нечеткое множество на базовой переменной \(U^*=[0,1]\). Элемент нечеткого множества V можно представить как нечеткое подмножество \(U^*\) вместо \(U\), то есть если

ВЫСОКАЯ={1/1;0.7/0.9;0.3/0.8}, то 0.5/ВЫСОКАЯ={0.5/1;0.5/0.9;0.3/0.8}.

При этом применяется «правило минимума», которое сохраняет коммутативность, то есть порядок выполнения вычислений несущественен. Это означает, что если V вычислено на U, а потом переведено на \(U^*\), то такое же значение будет получено, если вычислять V сразу на \(U^*\).
После перевода с U на \(U^*\) элементы \(V\) могут быть скомбинированы с помощью «правила максимума». Полученные результаты выражают каждую альтернативу лингвистически

Альтернатива	Деканат	Группа
A₁	ВЫСОКАЯ	ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ
A₁	ОЧЕНЬ ВЫСОКАЯ или ДОСТАТОЧНО ВЫСОКАЯ	ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ или ДОСТАТОЧНО ВЫСОКАЯ
A₁	ДОСТАТОЧНО ВЫСОКАЯ	СРЕДНЯЯ или ДОСТАТОЧНО ВЫСОКАЯ, но НЕ ОЧЕНЬ-ОЧЕНЬ ВЫСОКАЯ

Нечеткие множества V (полезность альтернатив) полезно визуально сравнить для групп, принимающих решение. На основании полученных функций можно сделать вывод, что наилучшей является альтернатива

A₁ ={ХОРОШАЯ успеваемость, ОЧЕНЬ ВЫСОКАЯ активность, ХОРОШАЯ дисциплина, ПЛОХОЕ материальное положение}.

Этот результат получен из соотношения \(\mu_{A\cap B}(u)=\min\{\mu_A(u),\mu_B(u)\), где А-деканат, В-актив группы, u- полезность рассматриваемой альтернативы.

Функции принадлежности лингвистических полезностей (низкая, достаточно низкая, средняя, достаточно высокая, высокая)

Оценки полезности для деканата Оценки полезности для актива группы

Выбор альтернатив с использованием нечеткой логики

Выбрать наиболее подходящего адвоката.

Критерий:

Если адвокат имеет некоторый адвокатский стаж и опыт ведения дел в суде, к тому же может выявить юридические риски и применить к целевому спору актуальную практику Верховного суда, то он слабо удовлетворяющий.
Если он к тому же имеет успешные процессы по специализации целевого спора, то он удовлетворяющий.
Если он имеет все оговоренное в предыдущем, и не имеет удовлетворенных жалоб клиентов в Квалификационной комиссии адвокатуры, то он очень удовлетворяющий.
Если адвокат имеет все оговоренное в предыдущем и, кроме того, имеет публикации, преподает, имеет звание "заслуженный юрист" или ученую степень, то он безупречный.
Если адвокат имеет все оговоренное в предыдущем, но без опыта преподавания и публикаций, и имеет высокий уровень доверия, то он безупречный.
Если адвокат – начинающий юрист, имеет малый адвокатский стаж и опыт ведения дел в суде или имеет меньше успешно завершенных дел, чем неуспешных или низкую степень доверия, то он мало удовлетворяющий (мало отвечающий требованиям).

Данные

Оценка претендента по 10-балльной шкале.

Задачи для самостоятельной работы.

Задача 1.

Рассмотрим задачу управления движением электропоезда HRCS2 «Hyundai Rotem».
Электропоезд HRCS2 «Hyundai Rotem» имеет следующие характеристики:

Максимальная эксплуатационная скорость — 160 км/ч;
Ускорение при скорости от 0 до 60 км/ч составляет 0,7 м/с²;
Максимальное замедление скорости - 1,0 м/с²;
Тормозной путь при скорости 160 км/ч — 1300 м.

Управление движением поезда определяется, прежде всего, контролем его ускорения.

Будем считать, что ускорение определяется в зависимости от расстояния до следующей станции и текущей скорости поезда и имеют следующие нечеткие представления:

Нечеткое представление скорости движения поезда.

Нечеткое представление расстояния до ближайшей станции.

Нечеткое представление ускорения движения поезда.

Правила управления движением:

ЕСЛИ расстояние малое И скорость малая ТО ускорение очень слабое,
ЕСЛИ расстояние малое И скорость средняя ТО торможение слабое,
ЕСЛИ расстояние малое И скорость большая ТО торможение сильное,
ЕСЛИ расстояние среднее И скорость малая ТО ускорение слабое,
ЕСЛИ расстояние среднее И скорость средняя ТО ускорение очень слабое,
ЕСЛИ расстояние среднее И скорость большая ТО торможение слабое,
ЕСЛИ расстояние большое И скорость малая ТО ускорение большое,
ЕСЛИ расстояние большое И скорость средняя ТО ускорение слабое,
ЕСЛИ расстояние большое И скорость большая ТО ускорение очень слабое.

Определить режим управления движением поезда.

Задача 2.

Пусть известна информация об восприятии температурного режима

t^o	18	25	30
μ_A(t)	0.1	0.5	1
	Прохладно	Комфортно	Жарко

и влажности

h^o	20	50	70	90
μ_B(h)	0.2	0.6	0.7	1
	Сухо	Комфортно	Влажновато	Сыро

Fuzzy decision

Введение, или что такое нечеткое мышление?

Понятия и определения.

Нечеткие множества

Лингвистические переменные и лингвистические усиления (Linguistic variables and hedges).

Операции над нечеткими множествами.

Правила нечеткого вывода

Алгоритмы нечеткого вывода.

Пример использования нечетких рассуждений.

Шаг 1

Правила

Дефаззификация

Ранжирование.

Выбор альтернатив с использованием правил нечеткого вывода

Пример выбора альтернатив на основе нечеткого вывода.

Ранжирование альтернатив на основе эвристического подхода.

Пример использования эвристического подхода.

Выбор альтернатив с использованием нечеткой логики

Выбрать наиболее подходящего адвоката.

Критерий:

Данные

Задачи для самостоятельной работы.

Задача 1.

Задача 2.

Полезная литература. Книги.

Полезная литература. Статьи.

Вопрос-ответ.


Оценки полезности для деканата	Оценки полезности для актива группы