Методи стиску зображень

Мультімедійні дані, що зберігаються на різних носіях і передаються по каналах зв'язку, як правило, мають значну надмірність. Використання алгоритмів стиску інформації дозволяє зменшити розмір файлів і, відповідно, підвищити швидкість обміну по каналах зв'язку і в стільки ж разів економити об'єм дискового простору. На сьогоднішній день існує безліч підходів до стиску інформації і алгоритмів, які їх реалізують. Перш за все, це статистичні і словарні методи. Розглянемо декілька з них.

Метод Хаффмана

Метод стиску Хаффмана (Huffman, 1952) - це загальна схема стиску інформації, для дискретних даних різної природи [1]. Ідея методу полягає в заміні даних ефективнішими кодами, і складається з привласнення бінарного коду кожній унікальній величині. Коротші коди використовуються для тих величин, що зустрічаються частіше. Ці привласнення зберігаються в таблиці перекодування, яка завантажується в декодуючу програму перед самими кодами.
Наприклад, в серії abccddeeeeeeecbbf є шість унікальних величин. Частоти їх запису дорівнюють

a:1, b:3, c:3, d:2, e:7 ,f:1.

Щоб отримати мінімальний код, будемо використовувати бінарне дерево

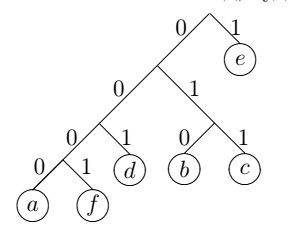
Основний алгоритм об'єднує разом всі елементи, що з'являються як найрідше, потім пара розглядається як один елемент і їх частоти об'єднуються. Це повторюється до тих пір, поки всі елементи не об'єднаються в пари.
Для даного прикладу найрідше використовуються значення a і f, які складають першу пару - a привласнюється 0-а гілка, а f - відповідно 1 - а. Це значить, що в кодах цих символів молодшими бітами будуть відповідно 0 і 1. Старші біти отримуємо по мірі побудови дерева. Наступна частота - 2. Тому одержана пара об'єднується з символом, який має частоту 2, тобто з d. Початковій парі привласнюється 0 гілка нового дерева, а елементу d гілка 1. Таким чином, на новому етапі елемент a має код 00, а елемент f код 01. Продовжуючи побудову дерева, одержуємо, що чим частіше зустрічається елемент, тим коротше його код.
Таблиця кодів для даного випадку виглядатиме наступним чином:

Хоча даний приклад і ілюструє метод Хаффмана, код, одержуваний в результаті використання такого алгоритму, не є найкоротшим.
Спорідненим методом для кодування Хаффмана є кодування Шеннона-Фано (Shannon-Fano method), яке здійснюється наступним чином:

Ділимо множину символів на дві підмножини так, щоб сума вірогідності появи символів однієї підмножини була приблизно рівна сумі вірогідності появи символів іншого. Для лівої підмножини кожному символу приписуємо "0", для правого - "1".
Повторюємо попередній крок до тих пір, поки всі підмножини не будуть складатися з одного елементу.

Розглянемо цей підхід на нашому прикладі. Розташуємо елементи алфавіту відповідно до їх частотних характеристик

e:7, b:3, c:3, d:2, a:1, f:1.

Розіб'ємо одержану таблицю на дві частини так, щоб суми частот в кожній з цих частин були приблизно рівні, і елементам, які стоять в першій таблиці привласнимо значення 1, а в другій - 0.

Далі, з кожною з одержаних таблиць проведемо таке ж перетворення, і так до тих пір, поки не одержимо набір таблиць, що складаються з одного елементу:

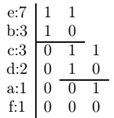
Відповідне бінарне дерево виглядає таким чином:

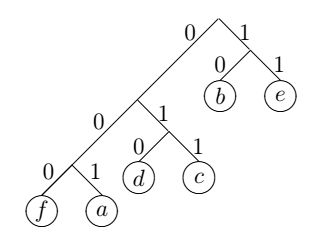
Код Шеннона-Фано [2] не завжди є оптимальним, кращих результатів дозволяє добитися власне метод Хаффмана. При його використанні кожен етап кодування полягає у відсіканні двох символів, що найбільш часто зустрічаються (що повністю співпадає з приведеним раніше прикладом). Алгоритм створення коду Хаффмана кодує знизу-вгору, а Шеннона-Фано -зверху-вниз.
Схема Хаффмана досягає ступеня стиску 1:8 і потребує точної статистики опису частот використання того або іншого елементу. Без точної статистики кінцевий файл не стає набагато меншим за початковий, тому для забезпечення ефективного ступеня стиску ця схема часто реалізується в два проходи. За перший прохід створюється статистична модель, за другий - кодуються дані. У результаті компресія і декомпресія по Хаффману - порівняльно повільні процеси. Крім того, оскільки біти стискаються без урахування границь байта, єдиний спосіб, за допомогою якого дешифратор може дізнатися про завершення кода - досягти кінця гілки, інакше (тобто за наявності збою) дешифратор починає з середини, і, решта даних стає безглуздою.
Приведемо ще одне зауваження: алгоритм Хаффмана не годиться для адаптивних моделей. На це є наступні причини:

По-перше, кожного разу при зміні моделі необхідно змінювати і весь набір кодів. Хоча ефективні алгоритми роблять це за рахунок невеликих додаткових витрат, їм все одно потрібне місце для розміщення дерева кодів. Якщо його використовувати в адаптованому кодуванні, то, для різної вірогідності розподілу і відповідної множини кодів, будуть потрібні свої класи умов для прогнозу символу. Оскільки моделі можуть бути досить громіздкі, то зберігання всіх дерев кодів стає надмірно дорогим. Добре наближення до кодування Хаффмана може бути досягнуте застосуванням різновиду дерев, що розширяються. При цьому, представлення дерева достатньо компактне, щоб зробити можливим його застосування в моделях, що мають декілька сотень класів умов.

По-друге, метод Хаффмана неприйнятний в адаптивному кодуванні, оскільки виражає значення -log p цілим числом бітів. Це особливо недоречно коли один символ має високу вірогідність (що і є частим випадком в складних адаптованих моделях). Як найменший код, який може бути отриманий методом Хаффмана, має 1 біт у довжину, хоча часто бажано використовувати менший. Наприклад, "o" в контексті "to be or not to be" можна закодувати в 0.014 біти. Код Хаффмана перевищує необхідний вихід в 71 разів, роблячи точний прогноз даремним.

Цю проблему можна подолати блокуванням символів, які зустрічаються досить рідко. Проте, це вносить свої проблеми, пов'язані з розширенням алфавіту (який тепер є множиною всіх можливих блоків).

Словарні методи стиску LZ.

Найпоширеніші на сьогоднішній день методи стиску засновані на словарних алгоритмах.
Існують дві гілки словарних алгоритмів. Перша бере початок від алгоритму LZ77 [3] і ґрунтується на заміні рядка символів в потоці на посилання на такий же рядок, що раніше зустрівся, з довжиною замінюваного рядка. Друга походить від алгоритму LZ78 [4]. У алгоритмах цієї гілки по ходу роботи заповнюється словник. Якщо у вхідному потоці зустрівся рядок, вже присутній в словнику, він замінюється на відповідний номер елемента словника. В даний час LZ77-подібні алгоритми практично не використовуються самостійно - створена безліч вдалих комбінованих алгоритмів, де вихідний потік LZ77-подібного алгоритму стискається контекстно-вільним алгоритмом вірогідності. Як правило, це (у порядку спадання швидкодії і підвищення ступеня стиску) алгоритми Шеннона-Фоно, Хаффмана, арифметичного стиску. Саме ці комбіновані алгоритми успішно використовуються в більшості сучасних універсальних архіваторів (7-Zip, ARJ, PKZIP, LHA, RAR та ін.). Сімейство LZ78 складається з алгоритму LZW і його незначних модифікацій. LZC - чисто практична реалізація LZW-алгоритму, вживана в програмі COMPRESS, яка використовується в операційній системі UNIX і в графічному форматі GIF.
Своєю появою словарні (префіксні) методи зобов'язані двом дослідникам з Ізраїлю: Якобу Зіву і Абраму Лемпелу (Jacob Ziv & Abraham Lempel). У 1977 році вони оприлюднили роботу [3]. Її поява ознаменувала початок нової ери в стиску інформації. Практично всі сучасні комп'ютерні програми-архіватори використовують ту, або іншу, модифікацію алгоритму LZ.
Основна ідея алгоритму LZ полягає у тому, що друге і подальші входження деякого рядка символів у вхідних даних замінюються посиланням на її першу появу в даних.
LZ77 використовує вже переглянуту частину даних в якості словника. Щоб отримати стиск, він намагається замінити черговий фрагмент даних на покажчик у змісті словника. Як модель даних LZ77 використовує "ковзаюче" по рядку даних вікно, розділене на дві нерівні частини. Перша, велика за розміром, включає вже переглянуту частину вхідних даних. Друга, набагато менша, є буфером, що містить ще не закодовані символи вхідного потоку. Звичайно розмір вікна складає декілька кілобайт. Буфер набагато менший, зазвичай не більше ніж сто байтів. Алгоритм намагається знайти у словнику фрагмент, співпадаючий зі змістом буфера.
Алгоритм LZ77 видає коди, що складаються з трьох елементів:

Зсув у словнику щодо його початку підрядка, співпадаючого з вмістом буфера;
Довжина підрядка;
Перший символ в буфері, наступний за підрядком.

Алгоритми групи LZ мають істотний недолік. Оскільки вони використовують в якості словника тільки невеликий фрагмент вхідних даних, то немає можливості кодувати підрядки, що повторюються, відстань між якими в повідомленні більше, ніж розмір словника. Крім того, алгоритми обмежують розмір підрядка, який можна закодувати.
Чисто механічний підхід до поліпшення характеристик кодеру LZ за рахунок збільшення розмірів словника і буфера звичайно дає результати, зворотні бажаним. Припустімо, що ми збільшимо розмір словника до 64 К і розмір буфера до 1 К. Це приведе до того, що для кодування зсуву в словнику, знадобиться 16 бітів замість 12, а для кодування довжини збігу буде потрібно 10 бітів замість 4. Таким чином кожна фраза буде закодована в 27 бітів замість 17, що, по-перше, приведе до значного зниження ступеня стиску на коротких рядках даних, а по-друге, зробить неможливим кодувати підрядки, що повторюються та завдовжки менші 4 байтів.
Оскільки перераховані проблеми не могли не турбувати творців алгоритму Якоба Зіва і Абрама Лемпела, в 1978 році вони в роботі [4] запропонували нову версію свого алгоритму, яка далі називатиметься LZ78. LZ78 йде від ідеї ковзаючого по тексту вікна. На відміну від LZ77, в LZ78 словником є потенційно нескінченний список вже проглянутих рядків, а не підрядків, як в LZ77. У LZ78 і кодер, і декодер починають роботу з "майже порожнього" словника, що містить тільки один закодований рядок - НУЛЬ-рядок. Коли кодер прочитує черговий символ даних, символ додається до поточного рядка. Доти, доки поточний рядок відповідає якій-небудь фразі із словника, процес продовжується. Але, рано чи пізно, поточний рядок перестає відповідати якій-небудь фразі словника. У цей момент, коли поточний рядок є "останнім збігом" із словником, плюс тільки що прочитаний символ даних, кодер LZ78 видає код, що складається з індексу збігу і наступного за ним символу, що порушив збіг рядків. Окрім того, нова фраза, що складається з індексу збігу і наступного за ним символу, додається в словник. Наступного разу, коли ця фраза з'явиться в повідомленні, вона може бути використана для побудови довшої фрази, що підвищує ступінь стиску інформації.
У 1984 році Terry А. Welch опублікував роботу [5], в якій приведена модифікація алгоритму LZ78, яка одержала назву LZW (Lempel-Ziv-Welch).
Алгоритм роботи кодеру LZW можна описати таким чином:

	Провести ініціалізацію словника односимвольними фразами, відповідними символам вхідного алфавіту (звично це 256 ASCII символів); 
	Прочитати перший символ даних в поточну фразу PHRASE;
	LABEL: Прочитати черговий символ  SYMBOL; 
	IF КІНЕЦЬ  ДАНИХ - Видати код PHRASE;
	EXIT;
	END IF;
	IF фраза PHRASE+SYMBOL вже є в словнику, Замінити PHRASE на код фрази PHRASE+SYMBOL;
	GOTO LABEL;
	ELSE Видати код PHRASE;
	Додати  PHRASE+SYMBOL в словник;
	GOTO LABEL;
	END IF;

Алгоритм декодування LZW може бути описаний таким чином:

	CODE = Прочитати перший код даних; 
	Попередній CODE = CODE;
	Видати символ SYMBOL, у якого CODE(SYMBOL) = CODE;
	LABEL: Наступний код: CODE = Прочитати черговий код даних; 
	Вхідний CODE = CODE; 
	IF КІНЕЦЬ ДАНИХ EXIT;
	END IF;
	Наступний символ:
	Якщо CODE = CODE(PHRASE+SYMBOL) Видати SYMBOL;
	CODE = CODE(PHRASE);
	GOTO LABEL;
	ELSE IF CODE = CODE(SYMBOL) Видати SYMBOL;
	Додати в словник (Попередній CODE, SYMBOL);
	Попередній CODE = Вхідний CODE;
	GOTO LABEL;
	END IF;

При декодуванні може виникнути виняткова ситуація, коли кодер намагається закодувати, наприклад, рядок ABABA, де фраза AB вже присутня в словнику. Кодер виділить AB, видає код(AB) і додає ABA в словник. Потім він виділить ABA і відправить тільки що створений код (ABA). Декодер при отриманні коду (ABA) ще не додав цей код в словник, тому що поки ще не знає символ-розширення попередньої фрази. Проте, коли декодер зустрічає невідомий йому код, він може визначити, який символ видавати першим. Це символ-розширення попередньої фрази, який буде останнім символом поточної фрази, який був останнім символом попередньої фрази, що був останнім розкодованим символом. Для обробки цієї ситуації зручно скористатися стеком. Традиційно функцію поміщення в стек позначимо PUSH, а витягання зі стеку - POP.
Модифікований алгоритм декодування виглядає таким чином:

	CODE = Прочитати перший код рядка даних;
	Попередній CODE = CODE;
	Видати символ SYMBOL, у якого CODE(SYMBOL)= CODE;
	Останній SYMBOL = SYMBOL
	Наступний код: CODE = Прочитати черговий код повідомлення;
	Вхідний CODE = CODE;
	IF КІНЕЦЬ ПОВІДОМЛЕННЯ EXIT;
	END IF;
	IF Невідомий(CODE)

Тоді обробка виняткової ситуації

	Видати(Останній SYMBOL)  
    CODE = Попередній CODE
    Вхідний CODE = CODE (Попередній CODE, Останній SYMBOL)
	END IF;
	LABEL: Наступний символ: 
    Якщо CODE = CODE(PHRASE+SYMBOL)  PUSH(SYMBOL);
    CODE = CODE(PHRASE);
	Повторити Наступний SYMBOL;
	ELSE якщо CODE = CODE(SYMBOL) Видати SYMBOL;
	Останній SYMBOL = SYMBOL;
	IF стек не порожній POP;
	END IF;
	Додати в словник (Попередній CODE, SYMBOL);
	Попередній CODE = Вхідний CODE;
	GOTO LABEL;
	END IF;

Очевидно, що декодер LZW використовує той же словник, що і кодер, будуючи його за аналогічними правилами при відновленні стиснутих даних. Кожен прочитуваний код розбивається за допомогою словника на попередню фразу w і символ К. Потім рекурсія продовжується для попередньої фрази w до тих пір, поки вона не виявиться кодом одного символу, що і завершує декомпресію цього коду. Оновлення словника відбувається для кожного декодованого коду, окрім першого. Після завершення декодування коду його останній символ, сполучений з попередньою фразою, додається в словник. Нова фраза одержує те ж значення коду (позицію в словнику), що привласнив їй кодер. Так, крок за кроком, декодер відновлює той словник, який побудував кодер.

Розглянемо приклад для трисимвольної абетки: A,B,C. Потік символів виглядає як ABACABABABA.

Кодування.

Спочатку проведемо ініціалізацію ланцюжків: 0=A, 1=B, 2=C.
Перший символ є А, який входить в таблицю ланцюжків, отже PHRASE стає рівним А. Далі ми беремо AB, яка не входить в таблицю, отже ми виводимо код 0 (для PHRASE), і додаємо AB в таблицю ланцюжків з кодом 3. PHRASE стає рівним B. Далі ми беремо PHRASE+A = BA, яка не входить в таблицю ланцюжків, отже виводимо код 1, і додаємо BA в таблицю ланцюжків з кодом 4. PHRASE стає рівним А. Далі ми беремо АС, яка не входить в таблицю ланцюжків. Виводимо код 0, і додаємо АС в таблицю ланцюжків з кодом 5. Тепер PHRASE рівно C. Далі ми беремо PHRASE+A = CA, яка не входить в таблицю. Виводимо 2 для C, і додаємо CA до таблиці під кодом 6. Тепер PHRASE=A. Далі ми беремо AB, яка входить в таблицю ланцюжків, отже PHRASE стає рівним AB, і ми шукаємо ABA, якої немає в таблиці ланцюжків, тому ми виводимо код для AB, який дорівнює 3, і додаємо ABA в таблицю ланцюжків під кодом 7. Далі, PHRASE рівно А, ланцюжок AB вже закодований, тому PHRASE+=B, наступний ланцюжок -- ABA також закодована, отже, як PHRASE вже беремо ABA і одержуємо PHRASE+B=ABAB, яке в таблиці кодів ще не зустрічалося, тому додаємо ABAB з кодом 8, а в кодову послідовність записуємо код ABA=7. На наступному кроці PHRASE рівно BА. Ми не можемо більш узяти символів, тому ми виводимо код 4 для BА і закінчуємо процедуру кодування. Отже, потік кодів рівний 0,1,0,2,3,7,4.

Попередній код (префікс)	Наявний символ	Наявна послідовність	Додається у словник	Кодова послідовність
	A	A
A	B	AB	3	0
B	A	BA	4	1
A	C	AC	5	0
C	A	CA	6	2
A	B	AB
AB	A	ABA	7	3
A	B	AB
AB	A	ABA
ABA	B	ABAB	8	7
B	A	BA
BA		BA		4

Декодування.

Процес декодування практично повністю повторює процедуру кодування.
Також, як і при кодуванні, спочатку ініціалізуємо таблицю ланцюжків: 0=A, 1=B, 2=C.
Тепер перейдемо до процедури декодування початкової послідовності 0,1,0,2,3,7,4.
Перший код 0 відповідає символу А, другий код 1 відповідає символу B. Обидва коди входять в таблицю. Далі ми беремо ланцюжок 01, відповідно AB, яка не входить в таблицю, отже ми додаємо AB в таблицю ланцюжків з кодом 3. PHRASE стає рівним 1=B. Далі ми беремо PHRASE+0 = BA, яка не входить в таблицю ланцюжків, отже виводимо символ А, і додаємо BA в таблицю ланцюжків з кодом 4. PHRASE стає рівним 2=A. Далі ми беремо АС, яка не входить в таблицю ланцюжків. Виводимо символ C, і додаємо АС в таблицю ланцюжків з кодом 5. Тепер PHRASE рівне 3=C. Далі ми беремо PHRASE+0 = CA, яка не входить в таблицю. Виводимо 2 C, і додаємо CA до таблиці під кодом 6. Наступний код 7.

Важливо!! Оскільки коду 7 в словнику немає, то конструюємо фрагмент для нього з поточного фрагмента+перший символ поточного фрагмента, в результаті отримаємо ABA і додаємо в таблицю ланцюжків під кодом 7.

На наступному кроці PHRASE дорівнює BА. Ми не можемо більш узяти символів, тому ми виводимо код 4 для BА і закінчуємо декодування.
Таким чином початковий потік даних є ABACABABABA.

Вхідні дані	Вихідні дані	Додається в словник
0	A
1	B	AB(3)
0	A	BA(4)
2	C	AC(5)
3	AB	CA(6)
7	ABA	ABA(7)
4	BA

Як вже згадувалося, Тері Велч працював над створенням програми compress разом з групою програмістів Unix. При реалізації compress він дещо удосконалив початковий алгоритм LZ78. Найцікавіше удосконалення - адаптивне скидання (обнуління) лічильника (adaptive reset). Замість того, щоб очищати словник після досягнення певного об'єму пам'яті для його зберігання (варіант, розглянутий до цього), програма compress продовжує використовувати словник до тих пір, поки залишається високим рівень стиску. Цей підхід базується на двох спостереженнях, що стосуються процесу стиску LZW. Одне з них полягає у тому, що на перших кроках розмір стиску сильно залежить від розміру словника. Адаптивне скидання намагається експлуатувати великий словник якомога довше. Інше спостереження полягає у тому, що багато файлів (особливо архіви TAR (архіви системи UNIX), що містять різні види файлів усередині архіву) містять області з різними типами даних. В процесі роботи алгоритму LZW формується словник, спеціально пристосований для певного типу даних. При значній зміні типу даних словник вже не даватиме високого ступеня стиску. Контролюючи ефективність стиску, програма compress може скидати словник у момент падіння продуктивності.
При стиску даних (надходженні на вхід програми чергової порції) програма на основі LZW намагається знайти в словнику фрагмент максимальної довжини, співпадаючий з даними, замінює знайдену в словнику порцію даних кодом фрагмента і доповнює словник новим фрагментом. При заповненні всього словника (розмір словника обмежений за визначенням) програма очищає словник і починає процес заповнення словника знову. Реалізації цього методу розрізняються конструкцією словника, алгоритмами його заповнення і очищення при переповненні. Звичайно, при ініціалізації словник заповнюється початковими (елементарними) фрагментами - всіма можливими значеннями байта від 0 до 255. Це гарантує, що під час попадання на вхід чергової порції даних буде знайдений в словнику хоча б однобайтовий фрагмент. Алгоритм LZW резервує спеціальний код, який вставляється в упаковані дані, відзначаючи момент скидання словника. Значення цього коду звичайно приймають рівним 256. Таким чином при початку кодування мінімальна довжина коду складає 9 біт. Максимальна довжина коду залежить від об'єму словника - кількості різних фрагментів, які туди можна помістити. Якщо об'єм словника вимірювати в байтах (символах), то очевидно, що максимальна кількість фрагментів рівна числу символів, а, отже, максимальна довжина коду дорівнює $\log_2 W$ (W - об'єм словника в байтах).

Арифметичний стиск.

Арифметичний стиск, як і алгоритм Хаффмана використовує більш короткі коди для елементів, що часто з'являються, і довші для тих, що рідко з'являються, хоча подібно алгоритму LZW стискає послідовності величин, а не самі величини. Арифметичний стиск достатньо близько лежить біля теоретичної межі стиску. Арифметичний стиск включає відображення кожної відмінної послідовності величин в діапазон цифр між 0 і 1. Потім ця область представляється як двійковий дріб змінної точності, при цьому менш загальні послідовності вимагають вищої точності (більше біт).
Розглянемо приклад. Нехай маємо набір величин з частотою їх появи

a:100, b:300, c:300, d:200, e:900, f:100.

Таким чином вірогідність появи кожної з цих величин з точністю до четвертого знаку

P(a) =0.0526, P(b) =0.1579, P(c) =0.1579,
P(d) =0.1052, P(e) =0.4737, P(f) =0.0526.

Серія елементів ab матиме вірогідність P(a)×P(b), проте якщо поставити кожній серії у відповідність її вірогідність, це не забезпечить її унікальність, в даному випадку таку ж вірогідність мають пари bf.
Представимо величину b сегментом рядка від 0.0526 до 0.2105. Довжина цього сегменту є вірогідність P(b) появи елементу b. Величина c має ту ж вірогідність, але розташована в іншому діапазоні: від 0.2105 до 0.3684. Тепер можна однозначно представити елемент числом, що вказує на сегмент цього елементу. Так число 0.25 указує на елемент c. Для представлення послідовностей з двох елементів можна розділити кожний з цих сегментів. Наприклад, послідовність ba (з вірогідністю 0.0526) буде представлена першими 5.26% цієї області, величина bb (з вірогідністю 0.1579) наступними 15.79% і так далі. Тоді елемент ba можна представити будь-яким числом в діапазоні від 0.0526 до 0.0554. Таким чином, ми одержуємо схему однозначного кодування будь-якої послідовності величин. При цьому потрібна велика точність (більше біт) для маловірогідних величин. Такі послідовності представляють невеликий сегмент і навпаки, потрібно менше біт для послідовностей з високою вірогідністю. Чим більше сегмент, тим більша ймовірність знайти дріб низької точності, наприклад, 1/2, 1/4 або 1/8 для ідентифікації елементів цього сегменту.
Так само як і алгоритм Хаффмана, арифметичне кодування ефективне для тих послідовностей елементів, що часто повторюються. Ефективність алгоритму арифметичного стиску може досягати 1:100.
Найважливішими властивостями арифметичного кодування є наступні:

Здатність кодування символу вірогідності p кількістю бітів досить близькою до $\log_2 p$;
Вірогідність символів може бути на кожному кроці різною;
Дуже незначні обсяги пам'яті незалежно від кількості класів умов в моделі;
Велика швидкість роботи.

У арифметичному кодуванні символ може відповідати дробовій кількості вихідних бітів. На практиці результат повинен, звичайно, бути цілим числом бітів, що можливо, якщо декілька послідовних високо вірогідних символів кодувати разом, поки у вихідний потік не можна буде додати 1 біт. Кожен закодований символ вимагає тільки одного цілочисельного множення і декількох додавань, для чого звичайно використовується тільки три 16-бітових внутрішніх регістра. Тому, арифметичне кодування ідеально підходить для адаптивних моделей, і його відкриття породило безліч модифікацій, що набагато перевершує ті, що застосовуються разом з кодуванням Хаффмана.
Складність арифметичного кодування полягає у тому, що воно працює з накопичуваною вірогідністю розподілу, яка вимагає внесення для символів деякої впорядкованості. Відповідна символу накопичувана вірогідність є сумою вірогідності всіх символів, передуючих йому.

Скалярне квантування

Розглядаючи задачі стиску зображень, не можемо не розглянути алгоритми квантування. Як правило, під квантуванням розуміють заміну неперервних даних системою індексів. В разі, коли дані описуються лише своїми значеннями, використовується скалярне квантування. Якщо під час квантування береться до уваги не тільки значення тих чи інших інформаційних характеристик, але і їхнє геометричне положення, то використовується векторне квантування.
Розглянемо деякі питання скалярного квантування.

Основні визначення

Хай $\pmb{f}=\left\{f_i\right\}_{i=0}^N$ масив вхідних даних. Надалі вважатимемо, що $\pmb{\varphi}=\left\{\varphi_i\right\}_{i=0}^N$ набір коефіцієнтів початкових даних, розгорнутих в одновимірний масив. При цьому будемо виходити з того факту, що в розкладанні використовувалися ортогональні або близькі до ортогональних фільтри. В якості таких фільтрів можуть використовуватися фільтри на основі сплесків, наведених раніше, або перетворення Фур'є.
Для будь-якого масиву $\tilde{\pmb{\varphi}}=\left\{\tilde{\varphi}_i\right\}_{i=0}^N$ через $\tilde{\pmb{f}}=\left\{\tilde{f}_i\right\}_{i=0}^N$ позначимо результат застосування зворотного перетворення до $\tilde{\pmb{\varphi}}$.
Через ортогональності фільтру має місце рівність Парсеваля \[ \sum_{i=0}^Nf_i^2=\sum_{i=0}^N\varphi_i^2, \sum_{i=0}^N\tilde{f}_i^2=\sum_{i=0}^N\tilde{\varphi}_i^2 \] і, через лінійність процесу фільтрації і рівності Парсеваля маємо \begin{equation}\label{1} \sum_{i=0}^N\left(f_i-\tilde{f}\right)^2=\sum_{i=0}^N\left(\varphi_i-\tilde{\varphi}_i\right)^2. \end{equation} У подальшому будемо вважати \[ A^-=\min_i\varphi_i, A^+=\max_i\varphi_i, \] і нехай, крім того, $B=B_{n+m+1}$ розбиття відрізка $[A^-,A^+]$ на $n+m+1$ проміжків точками \[ A^-=b_{-m-1/2}\lt b_{-m+1/2}\lt...\lt b_{-1/2}\lt 0\lt b_{1/2}\lt ...\lt b_{n+1/2}=A^+. \] Для кожного індексу $i=0,1,2,…,N$ знайдеться індекс $k=k(i) (k=-m,…, n)$ такий, що \[b_{k-1/2}\lt \varphi_i\le b_{k+1/2},\] якщо $k=1,…,n,$ або \[b_{k-1/2}\le \varphi_i\lt b_{k+1/2},\] якщо $k=-1,…, -m,$ або \[b_{-1/2}\le \varphi_i\le b_{1/2},\] якщо $k=0.$
Легко бачити, що для будь-яких $\{a_i\}_{i=1}^M$ задача \[ \sum_{i=1}^M(a_i-c)^2\to\min \] має єдиний розв'язок \[ c=\frac{1}{M}\sum_{i=1}^Ma_i. \] Таким чином якщо для фіксованого $k=-m,…,n$ всі значення $\varphi_i$, що знаходяться в одному з інтервалів, замінені на одне і те ж число $c_k$, то найменша похибка в середньоквадратичній метриці буде при $c_k=b_k$, де \[ b_k=\frac{s_k}{n_k},k=-m,...,n,\\ s_k=\sum\left\{\varphi_i|i:k(i)=k\right\}, n_k=\sum\left\{1|i:k(i)=k\right\}. \] Тому послідовність $g_i=b_{(i)}(i=0,1,2,...,N)$ буде як найкращою (у значенні середньоквадратичного наближення) зі всіх послідовностей постійних на кожному з проміжків.
Для фіксованих чисел $b_k (k=-m,...,n)$ (таблиця квантування) для кожної послідовності $g_i(i=0,1,2,...,N)$ однозначно ставиться у відповідність послідовність $\psi_i=k(i)$.
Іноді замість цієї послідовності зручніше використовувати наступну послідовність \[ \theta_i=\left\{ \begin{array}{ll} 2k(i)-1, & \hbox{ }k(i)\gt 0, \\ -2k(i), & \hbox{ } k(i)\lt 0,\\ 0, & \hbox{ }k(i)=0. \end{array} \right. \] Таким чином, при фіксованому векторі B кожне значення $\varphi_i$ округлено до значення $g_i$ (значення $\psi_i$ або $\theta_i$ називатимемо кодом масиву $\pmb{\varphi}$ ). Надалі цю процедуру називатимемо квантуванням послідовності $\pmb{\varphi}$ по вектору B.
З (\ref{1}) витікає, що похибка RMSE (Root Mean Square Error) виникла в результаті квантування \[ RMSE(B,\pmb{f})=\|\pmb{f}-\tilde{\pmb{f}}\|_{\ell^2}, \] де $\tilde{\pmb{f}}$ результат застосування зворотного ортогонального (чи біортогонального) перетворення до масиву $\pmb{g}$, дорівнює \[ RMSE(B,\pmb{f})=\|\pmb{f}-\tilde{\pmb{f}}\|_{\ell^2}=\|\pmb{f}-\pmb{g}\|_{\ell^2}=\sqrt{\frac{1}{N+1}\sum_{i=0}^N(\varphi_i-g_i)^2}. \] Основною характеристикою якості відновлення є величина \[ p=PSNR(B,\pmb{f})=20\log_{10}\frac{\min\limits_i|\varphi_i|}{RMSE(B,\pmb{f})}, \] PSNR (Peak Signal-to-Noise Ratio) - відношення сигнал/шум (у dB).
Процес квантування можна переписати в іншій термінології.
Покладемо \[ \Phi^+_{k+1/2}=\left\{\varphi_i:\varphi_i\le b_{k+1/2}\right\}, \Phi^-_{k+1/2}=\left\{\varphi_i:\varphi_i\ge b_{k+1/2}\right\}. \] Крім того, нехай для $k=0,1,2,…,n$ \[ \Delta\Phi_k=\Phi^+_{k+1/2}\setminus \Phi^+_{k-1/2}, \] а для $k=-m,…, -1$ \[ \Delta\Phi_k=\Phi^-_{k-1/2}\setminus \Phi^-_{k+1/2}, \] \[ \Delta\Phi_0=\Phi^+_{1/2}\bigcap \Phi^+_{-1/2}. \] Тут A\B є теоретико-множинна різниця множин A і B.
Далі нехай $n_k$ число елементів множини $\Delta \Phi_k$. Покладемо \[ b_k=\frac{1}{n_k}\sum\left\{\varphi_i|i:\varphi_i\in \Delta\Phi_k\right\} \] тоді RMSE можна переписати у вигляді \[ RMSE(B,\pmb{f})=\sqrt{\frac{1}{N+1}\sum_{i=-m}^n\sum\left\{(\varphi_i-b_k)^2|i:\varphi_i\in \Delta\Phi_k\right\}}. \] Цей процес легко алгоритмізувати, наприклад, для $k=1,…,n$ псевдокод виглядатиме таким чином

i=0;
 for k=1 to n do
   begin
     s[k]=0; n[k]=0;
     if (fi[i]>b1[k])&(fi[i]<=b1[k+1]) then
        begin
         s[k]=s[k]+fi[i];
         n[k]=n[k]+1;
         psi[i]=k;
         i=i+1;
        else
         b[k]=s[k]/n[k];
     end if;
   end do.

Далі вважатимемо, що задані метод лінійного кодування послідовностей, що повторюються (RLE) і метод ентропійного кодування A. В якості ентропійного кодування може бути взятий метод Хаффмана, LZW, арифметичного кодування та ін.
Нехай $V_0(\pmb{\varphi})$ розмір (у байтах) початкового масиву $\{\varphi_i\}$, і $V_1(\pmb{\varphi})$ розмір вихідного масиву, тобто розмір вихідних даних одержаних після застосування RLE і ентропійного кодування до послідовності $\theta_i$ або $\Psi_i$.
Величину \[ c(B)=c(B,\pmb{\varphi},RLE,A)=\frac{V_0(\pmb{\varphi})}{V_1(\pmb{\varphi})} \] назвемо ступенем стиску даних (compression ratio або CR).
Таким чином, для фіксованого масиву $\pmb{f}$ (а отже, і масиву $\pmb{\varphi}$ ) кожен вектор B однозначно визначає точку на площині з координатами $(p(B,\pmb{\varphi}),c(B, \pmb{\varphi})$, де $p(B,\pmb{\varphi})$- характеристика якості файлу після стиску. Ця точка характеризує якість квантування - чим вона вища, тим квантуватель краще. Точне формулювання цього факту ми наведемо нижче.
Під правилом квантування $\aleph$ будемо розумітимемо процедуру побудови набору векторів {B}.
Умовно розділятимемо цю процедуру на дві частини

вибір нульового інтервалу квантування $[b_{-1/2},b_{1/2}]$,
по вибраному нульовому інтервалу квантування побудова решти інтервалів $[b_{k-1/2},b_{k+1/2}], |k|\gt 0$.

Процедура квантування полягає в наступному. Виберемо деяке число $\delta>0$ і вважаймо $b_{1/2}=-b_{-1/2}=\delta$.
Кількість інтервалів квантування n і m виберемо таким чином \[ n=\left[\left(A^+-b_{1/2}\right)\delta\right], m=\left[\left(b_{-1/2}-A^-\right)\delta\right], \] де [•] ціла частина числа, і обчислимо межі інтервалів квантування \[ b_{k+1/2}=b_{1/2}+\frac{k}{n}(A^+-b_{1/2}), k=1,...,n,\\ b_{k-1/2}=b_{-1/2}-\frac{k}{m}(A^--b_{-1/2}), k=-1,...,-m. \] А також таблицю квантування $b_k=\frac{1}{n_k}\sum\{\varphi_i|i\in I_k\},$ де $I_k=\{i:b_{k-1/2}\le \varphi_i\lt b_{k+1/2}\}$ і $n_k$ число елементів множини $I_k$. Ця процедура дає набір B і називається рівномірним квантуванням. Міняючи $\delta$, одержуємо набір векторів B квантування, тобто одержуємо метод квантування.
Надалі вважатимемо, що фільтри, RLE і $\pmb{\varphi}$ фіксовані. Метод квантування (вектор $\hat{B}=\hat{B}(p)$ називатимемо якнайкращим на класі W для заданої якості $p_0$, якщо $p(\hat{B},p_0)\ge p_0$ і для будь-якого іншого вектору B∈ W такого, що $p(B,p_0)\ge p_0$ справедлива нерівність $p(\hat{B},p_0)\ge p(B,p_0).$

Вибір нульового інтервалу квантування.

Розглянемо декілька підходів до вирішення першої задачі - побудові нульового інтервалу квантування $[b_{-1/2},b_{1/2}]$.
Позначимо через $\{\phi_i\}_{i=0}^N$ незростаючу перестановку послідовності $\{\varphi_i\}_{i=0}^N$ , а через $\{\phi^+_i\}_{i=0}^N$ позначимо незростаючу перестановку множини $\{|\varphi_i|\}_{i=0}^N$ . При заданій якості $p_0$ (PSNR) вважатимемо, що нульовий інтервал квантування дає, наприклад, 80% (це значення параметра підібране статистично) всієї похибки. В цьому випадку число $n_0$ виберемо з умови \[ 0.80\left(\phi^+_010^{-p_0/20}\right)^2\le \frac{1}{N-n_0}\sum_{i=0}^{N-n_0}\le 0.81\left(\phi^+_010^{-p_0/20}\right)^2 \] Розглянемо інший підхід до розв'язку цієї задачі.
Нехай $i_{-1}$ і $i_1$ є розв’язок екстремальної задачі \[ \left\{ \begin{array}{l} \sum_{i=i_{-1}}^{i_1}\phi_i\to\min\\ i_1-i_{-1}=n_0. \end{array} \right. \] Тоді вважаємо $b_{1/2}=\phi_{i_1}$ і $b_{-1/2}=\phi_{i_{-1}}$. Для дослідження якнайкращих методів квантування зручно використовувати саме цей підхід. Змінюючи $n_0$ і підбираючи $b_{\pm 1/2}$ можна одержати якнайкращий метод квантування в деякому діапазоні зміни p.
Нульовий інтервал квантування можна також визначити виходячи з вирішення наступної екстремальної задачі.
Нехай числа $\delta_{-1},\delta_1\gt 0, \delta_{-1}+\delta_1=\delta$. Через $I_0$ позначимо множину, що складається з $n_0$ індексів таких, що $-\delta_{-1}\le \varphi_i\le\delta_1$ , тобто $I_0=\{i:-\delta_{-1}\le\varphi_i\le\delta_1\}$ і покладемо \[ \varepsilon(\delta_{-1},\delta_1)=\sum_{i\in I_0}\left(\varphi_i-\frac{1}{n_0}\sum_{i\in I_0}\varphi_i\right)^2. \] Для будь-якого фіксованого ε>0 через $n_0$ позначимо розв'язок екстремальної задачі $n_0\to \max$ при умові $\varepsilon(\delta_{-1},\delta_1)\lt \varepsilon$. Кожний з розглянутих підходів має свої плюси і мінуси. Зокрема, перший підхід використовує незростаючу перестановку модулів коефіцієнтів, другий, перестановку самих коефіцієнтів, для третього підходу перестановка не потрібна, проте обчислювальна складність цього алгоритму не менша. Крім того, в цьому випадку потрібно достатньо точно запам'ятовувати величину $\frac{1}{n_0}\sum_{i\in I_0}\varphi_i$ до якої квантуються значення в цьому інтервалі.
Перейдемо до розгляду другої задачі. При її вирішенні будемо вважати, що числа $b_{-1/2}$ і $b_{1/2}$ вже вибрані.

Вибір інтервалів квантування.

Раніше було розглянуте рівномірне квантування. Опишемо ще декілька методів квантування.
Нехай задані межі інтервалу $[b_{-1/2},b_{1/2}]=[\varphi_{i_{-1}},\varphi_{i_1}]$. Обчислимо $i_2=\left[\frac{i_1}{2}\right]$, де $[\cdot]$ ціла частина числа. Нехай α деякий параметр, на практиці його доцільно брати $\alpha\in[1/2,2/3]$.
Якщо \[ \frac{1}{i^\alpha_2}\sum_{i=0}^{i_2}\left(\varphi_i-\frac{1}{i_2}\sum_{k=0}^{i_2}\varphi_k\right)^2\gt \frac{1}{(i_1-i_2)^\alpha}\sum_{i=i_2}^{i_1}\left(\varphi_i-\frac{1}{i_1-i_2}\sum_{k=i_2}^{i_1}\varphi_k\right)^2, \] то покладемо $i_3=\left[\frac{i_2}{2}\right]$, інакше $i_3=i_2+\left[\frac{i_1-i_2}{2}\right]$, тобто проміжок з найбільшим значенням RMSE розбиваємо на дві рівні частини.
Далі цей процес продовжуємо аналогічним чином: вибираємо проміжок з найбільшим значенням RMSE і розбиваємо його на дві рівні частини. Цей процес продовжуємо або задане число раз, або, використовуючи деякий критерій, наприклад, поки не одержимо необхідну величину похибки квантування.
Цей метод квантування можна модернізувати, вибираючи на кожному кроці $i_k$ так, щоб сума значень RMSE на даному проміжку була мінімальною.
Далі розглянемо один метод квантування, який спирається на наступну лему.

Лема 1. Нехай $\phi(x)$ неперервна незростаюча функція, що задана на проміжку x∈ [0,T]. Задача \[ F(B)=\sum_{k=-m}^n\left(\int_{x_{k-1/2}}^{x_{k+1/2}}\left(\phi(x)-\frac{1}{x_{k+1/2}-x_{k-1/2}}\int_{x_{k-1/2}}^{x_{k+1/2}}\phi(z)dz\right)^2dx\right)\to\min \] за умовою \begin{equation}\label{2} 0=x_{1/2}\lt...\lt x_{n+1/2}=T \end{equation} має єдиний розв'язок $\hat{x}_{k+1/2}$ , який визначається співвідношенням \[ \phi(\hat{x}_{k+1/2})=\frac{1}{2}\left(\frac{1}{x_{k+1/2}-x_{k-1/2}}\int_{x_{k-1/2}}^{x_{k+1/2}}\phi(z)dz+ \frac{1}{x_{k+3/2}-x_{k+1/2}}\int_{x_{k+1/2}}^{x_{k+3/2}}\phi(z)dz\right), k=1,...,n-1. \]

Для вирішення цієї екстремальної задачі використовуємо традиційні методи математичного аналізу.
Дійсно, для $k=1,…,n-1$ \[ \frac{\partial F}{\partial x_{k+1/2}} =\int _{x_{{k-1/2}}}^{x_{{k+1/2}}}\!2\,\left (\phi(z)-{\frac {\int _{x_ {{k-1/2}}}^{x_{{k+1/2}}}\!\phi(z){dz}}{x_{{k+1/2}}-x_{{k-1/2}}}} \right )\left ({\frac {\int _{x_{{k-1/2}}}^{x_{{k+1/2}}}\!\phi(z){dz}} {\left (x_{{k+1/2}}-x_{{k-1/2}}\right )^{2}}}-{\frac {\phi(x_{{k+1/2}} )}{x_{{k+1/2}}-x_{{k-1/2}}}}\right ){dz}+ \left (\phi(x_{{k+1/2}})-{ \frac {\int _{x_{{k-1/2}}}^{x_{{k+1/2}}}\!\phi(z){dz}}{x_{{k+1/2}}-x_{{k-1/2}}}}\right )^{2}+ \] \[+ \int _{x_{{k+1/2}}}^{x_{{k+ 3/2}}}\!2\,\left (\phi(z)-{\frac {\int _{x_{{k+1/2}}}^{x_{{k+3/2}}}\! \phi(z){dz}}{x_{{k+3/2}}-x_{{k+1/2}}}}\right )\left (-{\frac {\int _{x _{{k+1/2}}}^{x_{{k+3/2}}}\!\phi(z){dz}}{\left (x_{{k+3/2}}-x_{{k+1/2}} \right )^{2}}}+{\frac {\phi(x_{{k+1/2}})}{x_{{k+3/2}}-x_{{k+1/2}}}} \right ){dz}- \left (\phi(x_{{k+1/2}})-{\frac {\int _{x_{{k+1/2}}}^{x_{ {k+3/2}}}\!\phi(z){dz}}{x_{{k+3/2}}-x_{{k+1/2}}}} \right )^{2}= \] \[ =\left( \frac{1}{x_{{k+3/2}}-x_{{k+1/2}}} {\int _{x_{{k+1/2}}}^{x_{ {k+3/2}}}\!\phi(z){dz}}+ \frac{1}{x_{{k+1/2}}-x_{{k-1/2}}} {\int _{x_{{k-1/2}}}^{x_{ {k+1/2}}}\!\phi(z){dz}}\right)\times \] \[ \times\left(2\phi(x_{{k+1/2}}) - \frac{1}{x_{{k+3/2}}-x_{{k+1/2}}} {\int _{x_{{k+1/2}}}^{x_{ {k+3/2}}}\!\phi(z){dz}}-\frac{1}{x_{{k+1/2}}-x_{{k-1/2}}} {\int _{x_{{k-1/2}}}^{x_{ {k+1/2}}}\!\phi(z){dz}}\right). \] Звідси прирівнюючи похідну нулю, відразу одержуємо \[ b_{k+1/2}=\phi(x_{k+1/2})=\frac{1}{2}\left( \frac{1}{x_{k+1/2}-x_{k-1/2}}\int_{x_{k-1/2}}^{x_{k+1/2}}\phi(x)dx+ \frac{1}{x_{k+3/2}-x_{k+1/2}}\int_{x_{k+1/2}}^{x_{k+3/2}}\phi(x)dx \right). \] Наведений доказ не є строгим - необхідно показати, що при цьому досягається мінімум, і що одержана умова є не тільки необхідною, але і достатньою. Для цього потрібно детально розглянути випадок "злиплих" вузлів (коли деякі з нерівностей (\ref{2}) обертаються в рівність). Строгий доказ цього факту є громіздким і ми його наводити не будемо.
У дещо іншому вигляді цей результат приведений в роботах Ллойда і Макса (див. [6-7]).
Переписуючи затвердження леми в термінах приведених вище, приходимо до висновку, що при фіксованих $b_{1/2}$, $b_{-1/2}$ і числах $n$ і $m$ вектор $B$ буде оптимальним по RMSE, тоді і тільки тоді, коли виконується рівність \[ b_{k+1}=2b_{k+1/2}-b_k,\,\,\,\,\,\,(k=-m,\ldots,n,\,\,k\ne 0)\] або, що те ж, \begin{equation}\label{3} b_{k+1}=b_{k+1/2}+(b_{k+1/2}-b_k), \,\,\,\,\textrm{якщо}\,\,\,\,\, k=1,\ldots,n, \end{equation} і \begin{equation}\label{4} b_{k-1}=b_{k-1/2}+(b_{k-1/2}-b_k), \,\,\,\,\textrm{якщо}\,\,\,\,\,k=-m,\ldots, -1. \end{equation} Рівність (\ref{3}), (\ref{4}) можна використовувати як у разі, коли задане число інтервалів квантування (тобто задані числа $n,m$) так і вибирати $b_k$ згідно рекурентних співвідношень (\ref{3}), (\ref{4}), так і при заданих межах нульового інтервалу квантування $b_{-1/2}$, $b_{1/2}$ і значеннях $b_{-1}$, $b_{1}$. В цьому випадку легко знайти решту інтервалів $[b_{k-1/2},b_{k+1/2}]$, покласти $[b_{n-1/2},b_{n+1/2}]=[b_{n-1/2},A^+]$ і $[b_{m-1/2},b_{m+1/2}]=[A^-,b_{m+1/2}]$.
При цьому однозначно визначаються безперервні зліва функції $n(\delta)$ і $m(\delta)$. Для лівих меж в точках розривів цих функцій рівності (\ref{3}), (\ref{4}) виконуються для всіх інтервалів $[b_{k-1/2},b_{k+1/2}]$ ($k=-m,\ldots,n,\,\,k\ne 0$).
Модифікуємо цей алгоритм, розглянувши замість співвідношень (\ref{3}), (\ref{4}) рівності \begin{equation}\label{5} b_{k+1}=b_{k+1/2}+\lambda_{k+1}(b_{k+1/2}-b_k), \,\,\,\,\textrm{якщо}\,\,\,\,\, k=1,\ldots,n, \end{equation} \begin{equation}\label{6} b_{k-1}=b_{k-1/2}+\lambda_{k-1}(b_{k-1/2}-b_k), \,\,\,\,\textrm{якщо}\,\,\,\,\,k=-m,\ldots, -1, \end{equation} де числа $\lambda_{k}$ вибираються із статистики або інших міркувань, про що буде сказано нижче.
Ясно, що при $\lambda_{k}=1$ рівності (\ref{5}) та (\ref{6}) переходять в рівність (\ref{3}) та (\ref{4}).
Нехай, як і раніше, $\{\phi_i\}_{i=0}^N$ спадаюча перестановка скінченної послідовності $\{\varphi_i\}_{i=0}^N$, а також задані межі нульового інтервалу $b_{1/2}=\phi_{i_1}$, $b_{-1/2}=\phi_{i_{-1}}$ і $b_0=0$.
Зафіксуємо числа $\lambda_k$. Наприклад, $\lambda_{1}=\lambda_{-1}=1/2$ і $\lambda_{k}=1$ для $|k|>1$.
Нехай, спочатку, $k>0$.
З (\ref{6}), при $k=1$ ( при цьому визначено $\lambda_1$), знаходимо $b_{1}$. Цьому числу відповідає індекс $i_{1}$ такий, що $b_1=\varphi_{i_1}$. Для $i=i_{1}-1$ виконується умова \[ \sum_{\nu=i}^{i_{1}-1}(\phi_\nu-b_{1})\le 0. \] Послідовно зменшуючи індекс $i$ на одиницю, однозначно знайдемо такий індекс $i_{2}$, що або \[ \sum_{i=i_{2}}^{i_{1}-1}(\phi_i-b_{1})\le 0 \,\,\,\,\textrm{і}\,\,\,\,\, \sum_{i=i_{2}-1}^{i_{1}-1}(\phi_i-b_{1})> 0, \] або досягається значення $i=0$. У першому випадку покладемо $b_{3/2}=\varphi_{i_{2}}$ і $b_{2}=b_{3/2}+\lambda_2(b_{3/2}-b_1)$, у другому покладемо $n=2$ і обчислимо \[b_{n}=\frac{1}{i_{n}}\sum_{i=0}^{i_{n}-1}\phi_i, b_{n+1/2}=A^+. \] Нехай вже обчислені $b_{1/2},b_{1},\ldots,b_{k}$, тоді однозначно знайдеться такий індекс $i_{k+1}$, що або \[ \sum_{i=i_{k+1}}^{i_{k}-1}(\phi_i-b_{k})\le 0 \,\,\,\,\textrm{і}\,\,\,\,\, \sum_{i=i_{k+1}-1}^{i_{k}-1}(\phi_i-b_{k})> 0, \] або досягається значення $i=0$.
У першому випадку покладемо $b_{k+1/2}=\varphi_{i_{k+1}}$ і $b_{k+1}=b_{k+1/2}+\lambda_{k+1}(b_{k+1/2}-b_{k})$, у другому покладемо $n=k+1$ і обчислимо \[b_{n}=\frac{1}{i_{n}}\sum_{i=0}^{i_{n}-1}\phi_i,\,\,\,\,\,\,\, b_{n+1/2}=A^+. \] Обчислення закінчуються, коли буде досягнуто значення $i=0$.
Псевдокод цієї процедури виглядає наступним чином

j=i[1];s=0; k=1; m=0;
 while j>0 do
   begin
     s=s+(fi[j]-b[k]);
     m=m+1;
     if s*(s+(fi[j-1]-b[k]))<=0
       then j=j-1
       else
        begin
          k=k+1;
          i[k]=j;
          b[k]=fi[j]+lambda[k]*(fi[j]-b[k-1]);
          s=0;
          m=0;
        end;
   end if;
   n=k;
   b[n]=s/m;
  end do.

По аналогії з попередніми викладками, для $k\lt 0$ одержуємо індекс $i_{k-1}$ з умов \[ \sum_{i=i_{k}+1}^{i_{k-1}}(\phi_i-b_{k})\ge 0 \,\,\,\,\textrm{і}\,\,\,\,\, \sum_{i=i_{k}+1}^{i_{k-1}+1}(\phi_i-b_{k})\lt 0 \] поки $i_{k-1}+1\lt N$, інакше \[ b_{k}=\frac{1}{N-i_{k}-1}\sum_{i=i_k+1}^N\phi_i,\,\,\,\,\,\,\, b_{k-1/2}=A^-. \] Псевдокод виглядає аналогічно.
Після того, як будуть визначені всі інтервали квантування $[b_{k-1/2},b_{k+1/2}]$ потрібно перерахувати всі $b_k$, вважаючи \[ b_k=\frac{1}{i_{k}-i_{k+1}-1}\sum_{i=i_{k+1}}^{i_k-1}\varphi_i. \] Таким чином, якщо числа $\lambda_k$ фіксовані, і вибирати $b_{1/2}$ і $b_{-1/2}$, наприклад, по числу $n_0$ елементів, квантованих в нульовому інтервалі, то однозначно одержуємо набір інтервалів квантування $[b_{k-1/2},b_{k+1/2}]$, тобто вектор $B$.

Алгоритм оптимального квантування

Як вже зазначалося раніше, у багатьох задачах цифрової обробки сигналів (і зображень в тому числі) неперервний динамічний діапазон значень ділиться на ряд дискретних рівнів. Ця процедура називається квантуванням. Квантуватель перетворює неперервну змінну $x (t)$ у дискретну змінну $\hat{x}_k$, яка приймає скінченне число значень, і є елементам кодової таблиці квантування. Ці значення називаються рівнями квантування. Значення змінної $x (t)$, що відповідають одному рівню квантування $\hat{x}_k$ описуються індексом k .
Нехай $x (t)$ змінна з областю значень $X $, і $\{X_k\}_{k=0}^{N-1}$ набір множин таких, що \[ X_k\bigcap X_\nu=\varnothing, (k\ne\nu),\bigcup_{k=0}^{N-1}X_k=X. \] Кожному значенню $x (t) \in X_k$ поставимо у відповідність (квантовочне) число $\mu(k)$, яке є унікальним для кожного $X_k$ (наприклад, $\mu(k) = k$ ). Цю процедуру будемо називати квантуванням змінної $x (t)$ на N рівнів.
Заміна квантовочного числа μ(k) значенням, що описує елементи класу $X_k$ називається деквантуванням. Цим значенням може бути медіана, середнє арифметичне елементів класу $X_k$ або будь-яке інше значення, яке описує елементи цього класу.
Перепишемо в іншому вигляді результат Ллойда і Макса, наведений раніше.
Нехай набір $\{x_i\}_{i=0}^n$ такий, що \[\min_{i=0,...,n}x_i=0, \max_{i=0,...,n}x_i=M\gt 0.\] Через $\{\eta_k\}_{k=0}^N$ позначимо набір такий, що \[ 0=\eta_0\lt\eta_1\lt...\lt\eta_{N-1}\lt\eta_N=M, \] і \[ X_{k+1/2}=\{x_i:\eta_k\le x_i\le \eta_{k+1}\}. \] Через \[ m_{k+1/2}=m(M_{k+1/2})=\frac{\sum\left\{x_i|i:x_i\in X_{k+1/2}\right\}}{\sum\left\{1|i:x_i\in X_{k+1/2}\right\}} \] позначимо математичне очікування всіх елементів $x_i$ з множини (класу) $X_{k + 1/2}$.
Доведено, що існує єдиний набір$\{\eta_k\}_{k=0}^N$ такий, що \[ \hat{m}_{k+1/2}=\frac{1}{2}(\eta_k+\eta_{k+1}) \] причому для будь-яких класів $\{X_{k+1/2}\}_{k=0}^N$ і будь-яких чисел $\{m_{k+1/2}\}_{k=0}^N$ має місце нерівність \[ \sum_{k=0}^{N-1}\sum\left\{\left(x_i-\hat{m}_{k+1/2}\right)^2|i:x_i\in\hat{X}_{k+1/2}\right\}\le \sum_{k=0}^{N-1}\sum\left\{\left(x_i-{m}_{k+1/2}\right)^2|i:x_i\in {X}_{k+1/2}\right\} \] Більш того, якщо ${X}_{k+1/2}\ne \hat{X}_{k+1/2}$ або ${m}_{k+1/2}\ne \hat{m}_{k+1/2}$ , то нерівність строга.
Наведемо ітераційний алгоритм вирішення цієї задачі.
Для будь-якого набору $\{\eta^0_k\}_{k=0}^N$ такого, що $0=\eta^0_0\lt\eta_1^0\lt...\lt\eta_{N-1}^0\lt\eta_N^0=M,$ покладемо v = 0 і $ X^\nu_{k+1/2}=\{x_i:\eta_k^\nu\le x_i\le \eta_{k+1}^\nu\}$ і \[ m^\nu_{k+1/2}=m(M_{k+1/2})=\frac{\sum\left\{x_i|i:x_i\in X_{k+1/2}^\nu\right\}}{\sum\left\{1|i:x_i\in X_{k+1/2}^\nu\right\}} \] Знайдемо, $\eta^{\nu+1}_k=\frac{1}{2}(m^\nu_{k-1/2}+m^\nu_{k+1/2})$ і v:=v+1.
Далі ітераційно повторюємо цей процес.
Якщо \[ \Delta^\nu=\sum_{k=0}^{N-1}\sum\left\{(x_i-m^\nu_{k+1/2})^2|i:x_i\in X_{k+1/2}^\nu\right\} \] то доведено, що $\Delta^{\nu+1}\lt\Delta^\nu$.
Послідовно використовуючи описану процедуру, отримуємо ітераційний процес, який досить швидко збігається.
Якщо в якості вхідних даних $\{\eta^0_k\}_{k=0}^N$ взяти $\left\{\frac{M}{N}k\right\}_{k=0}^N$ і $m^0_{k+1/2}=\frac{M}{N}\left(k+\frac{1}{2}\right)$, тоді не потрібно зберігати кодову таблицю, але тоді і похибка більше.
У разі якщо для рівномірного наближення замість медіани взяти математичні очікування, тоді похибка буде істотно менше, але при цьому значення цих математичних очікувань потрібно зберігати в кодовій таблиці.
Квантування з найменшою середньоквадратичною помилкою називається квантуванням Ллойда-Макса [8]. Не дивлячись на очевидні переваги, квантування Ллойда-Макса практично не використовується. На це існують вагомі причини. Насамперед, алгоритм Ллойда-Макса досить нестійкий при квантуванні дискретних даних, які використовуються в практичних задачах. По-друге, те, що добре для середньоквадратичної метрики не завжди добре для візуального сприйняття. Мається на увазі той факт, що при оптимальному квантуванні (в сенсі мінімізації середньоквадратичної помилки) інтервали квантування розташовуються таким чином, щоб на кожному проміжку середньоквадратична помилка була однакова. Таким чином, чим більше на проміжку згруповано заквантованих чисел, тим цей проміжок буде вужче. А так як великих (по модулю) чисел істотно більше, то помилка квантування кожного окремого великого числа істотно більше помилки квантування малого числа. Внесок великого коефіцієнта в формування сигналу більше, ніж внесок малого, то як наслідок, відновлюваний сигнал, до якого застосовувалося квантування Ллойда-Макса, створює істотні артефакти. Все це обмежує використання оптимального квантування і призводить до того факту, що найбільш поширеним квантуванням є рівномірний. При цьому квантовочними числами є або значення математичного очікування коефіцієнтів, що потрапили в один інтервал квантування, або значення медіани - середини проміжку квантування. У першому випадку потрібно зберігати кодову таблицю, яка містить квантовочні числа, а в другому, тільки значення максимального коефіцієнта і число інтервалів квантування.
Наведемо ілюстрацію використання оптимального квантування на шістнадцять інтервалів з десятьма ітераціями для коефіцієнтів, отриманих в результаті фільтрації тестового зображення frymire.bmp

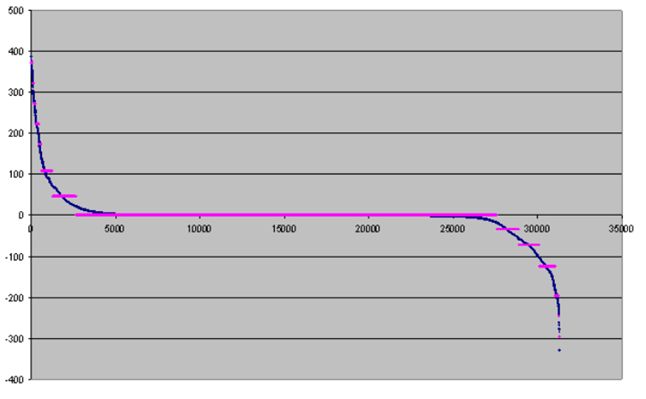
Наведемо значення помилки квантування в залежності від числа ітерацій

Число ітерацій	1	2	3	4	5	32	100
Похибка квантування	6578.5	6443.6	6311.3	6136.1	6014.2	4551.5	4550.4

Зауважимо, що незалежно від числа ітерацій, швидкість декодування одна і та ж. Як видно з наведеного графіка, ширина інтервалу квантування великих чисел істотно відрізняється від ширини інтервалу квантування маленьких чисел. Щоб уникнути артефактів, породжених цим ефектом, нами запропонована наступна модифікація. Спочатку опишемо цю модифікацію для додатних значень квантування. Для заданого числа 2N інтервалів квантування, використовуючи описаний ітераційний процес, одержуємо оптимальний розподіл інтервалів квантування, вибираємо N отриманих інтервалів квантування, відповідних малим значенням квантованим числам і залишаємо їх без зміни. Решту чисел квантуємо рівномірно на N інтервалів.
Якщо ж дані зі знаком, то ця модифікація буде такою: спочатку, для заданого числа 4N інтервалів квантування, використовуючи описаний ітераційний процес, одержуємо оптимальний розподіл інтервалів квантування, вибираємо 2N отриманих інтервалів квантування, відповідних малим значенням квантуємих чисел і залишаємо їх без зміни.
Решта великі за модулем числа квантуємо рівномірно на N інтервалів, відповідно додатні і на N інтервалів від’ємні.
В цьому випадку окремо зберігаються кодові таблиці для малих і великих чисел.
Ілюстрація цього методу квантування приведена на наступному малюнку.

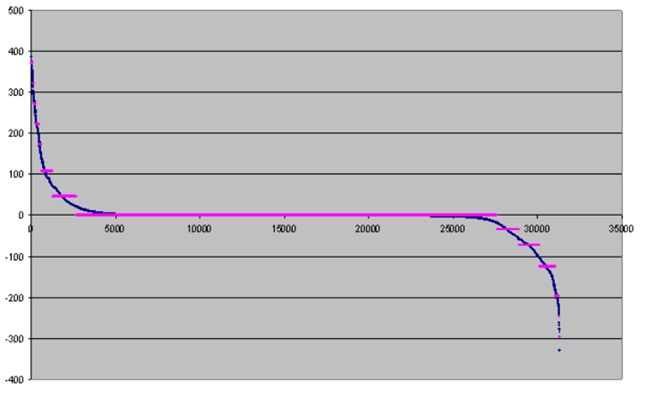
Ясно, що можна реалізувати модифікації алгоритму, для будь-якого наперед заданого числа оптимального і рівномірного квантування. Відзначимо той факт, що отриманий алгоритм оптимального квантування можна використовувати для вирішення інших, супутніх задач - очищення зображенні або для збіднення палітри кольорів. У цьому випадку, на початку проводимо оптимальне квантування колірних компонент, далі вводимо напівінтервали, в яких значення кольорів розподіляємо по ймовірності їх зустрічі. Як результат отримуємо зображення зі збідненою палітрою і без різких границь.

Кодування повторів (Run-Length Encoding)

Кодування повторів або метод групового стиску є одним із старіших і найпростіших алгоритмів. На сучасному етапі він використовується в основному для стиску графічних файлів [9]. Одним з перших поширених форматів, організованих за допомогою цього типу компресії, є формат PCX. "Класичний" варіант цього методу передбачає заміну послідовності символів, що повторюються, на рядок, що містить сам цей символ, і число (лічильник), яке показує, скільки разів цей символ повторюється. Наприклад, рядок 'AAAAAA CCCCCEEEFFFFFF' буде записано у вигляді: '6A5C3E6F'. При цьому можна перші чотири біти відвести під лічильник, другі під значення. Таким чином весь рядок буде записаний в чотирьох байтах.
Існує велика кількість різних модифікацій RLE. Всі вони так чи інакше пов'язані з структурою даних, які підлягають стиску. Перш за все структура методу групового стиску істотно залежить від використовуваного словника і вибору значень, до яких застосовується RLE. Як правило, використовування RLE в класичному значенні не тільки не зменшить загальний об'єм даних, але може навіть його збільшити. Тому, для ефективного використання методу групового стиску, треба використати ознаку повторів. Як правило, для ознаки повторів використовується прапорець, в якості якого може бути старший біт. Наприклад, якщо словник складається не більше, ніж з 128 символів, то в байті, що визначає символ, сім біт відведені під його значення. Старший біт (прапорець) вказує на наявність чи відсутність повторів. Якщо значення цього біта дорівнює нулю, то повторів немає, якщо одиниці, то наступний байт містить число повторів. В тому разі, якщо ланцюжки символів, що повторюються, істотно довше ніж 256, то старший біт лічильника можна також зарезервувати. Якщо старший біт лічильника дорівнює нулю, то решта семи біт містить значення цього лічильника, якщо одиниці, то під лічильник відводиться не тільки сім біт, що залишилися, але і наступний байт.
При стиску послідовностей елементів, що повторюються, доцільно використовувати ті закономірності, які є у послідовності даних. При використовуванні закономірностей зміни даних можна використовувати різні прийоми для того, щоб перегрупувати дані найвигіднішим для нас чином.
Наприклад, при використанні сплесків і застосування квантування до частотних доменів, відквантовані коефіцієнти не тільки утворюють повторні ланцюжки, але і їх структура така, що довжини цих ланцюжків мають загальну тенденцію до збільшення або зменшення, тобто дані згруповані таким чином, що їх значення по модулю "майже" спадають, тобто даних, які порушують закон спадання на багато менше.
Описаний алгоритм використовує той факт, що якщо з послідовності даних викинути нулі, то з однієї сторони, значення, що залишилися, утворюватимуть "майже" спадаючу послідовність (то є їх розрядність спадатиме), а з другого боку, кількість "пачок" нулів, тобто кількість згрупованих в однозв'язну множину нулів в первинній послідовності, буде такою що їх розрядність буде зростати (але не монотонно).
Приведемо докладний опис алгоритму на прикладі.

Дані	2	3	-5	0	11	31	0	0	-3	-9	0	0	0	0	1	-1	1	0	1
Прапорець	1	1	0		1	0			1	0					1	1	0		1
Знак	1	1	0		1	1			0	0					1	0	1		1
Числа	2	3	5		11	31			3	9					1	1	1		1
Нулі				1			2				4							1

Перший рядок таблиці містить вхідні дані.
Другий рядок - послідовність прапорців. Значення прапорця дорівнює одиниці відповідає тому, що за даним числом йде число відмінне від нуля, якщо ж значення прапорця дорівнює нулю, це значить, що за даним числом йде послідовність нулів (може бути ця послідовність складається тільки з одного нуля).
Третій рядок містить прапорці знаків відмінних від нуля. Кожному числу послідовності відмінному від нуля ставиться у відповідність прапорець із значенням рівним 1, якщо це число позитивне і 0, якщо воно негативне.
У четвертому рядку стоять модулі значущих (тобто відмінних від нуля) значень послідовності даних.
Останній рядок містить довжини послідовностей нулів, що повторюються.

Тестове зображення frymire

Методи зберігання графічних даних

Проглядаючи зміст жорсткого диска типового ПК, майже напевно знайдете багато файлів з розширеннями BMP, ICO, PNG, GIF, TIF, PCX і JPEG. Всі ці файли містять растрові графічні зображення. Розширення в імені файлу говорить про те, в якому форматі зберігається інформація. Наприклад, розширення BMP позначає BMP-файл, підтримуваний в системах Windows і OS/2 (BMP - скорочення від bitmap, тобто бітовий, растровий); TIF - скорочення від TIFF або Tagged Image File Format. Це тільки два представники великого сімейства форматів, які використовуються на персональних комп'ютерах. Кожний з цих форматів по різному зберігає графічну інформацію, і кожний з них розроблявся під конкретні цілі. Формат GIF (Graphics Interchange File - файл графічного обміну), наприклад, був придуманий для того, щоб умістити якомога більше інформації в обмеженому обсязі з метою зменшити час отримання файлів для користувачів мережі CompuServe. Формат PCX спочатку був придуманий для зберігання чорно-білих графічних файлів, які створювалися ранньою версією програми розфарбовування PC Paintbrush для комп'ютерів IBM PC.
Що містить растровий графічний файл?
Такий файл звичайно містить інформацію двох видів: графічну і не графічну. У графічних даних указуються кольори пікселів, неграфічні дані містять іншу інформацію, необхідну для відновлення зображення, наприклад його висоту і ширину. Якщо зображення містить 1 мільйон пікселів, то графічній програмі потрібно знати її розміри: чи малювати їй зображення 500 на 2000 або 1000 на 1000 пікселів? Неграфічна частина файлу може також включати іншу інформацію, таку як номер версії або інформацію про авторські права. Все залежить від формату і від того хто (або який програмний пакет) створив цей файл. У растрових файлах використовується звичайно один з двох методів зберігання даних про пікселі. У повнокольорових зображеннях піксел може приймати будь-яке з більш, ніж 16 мільйонів значень, тому і колір піксела зберігається звичайно як 24-розрядне значення - по 8 бітів на червоний, зелений і синій компоненти кольору. Якщо зображення містить 1 мільйон пікселів, то розмір файлу буде рівний 3 мільйонам байтів плюс довжина неграфічних даних. Якщо ж зображення обмежено 256 або менш кольорами, то колірна інформація звичайно кодується з використовуванням фіксованої палітри. Замість того, щоб зберігати значення кольору піксела, інформація про піксел вказує на рядок в палітрі, а вона, у свою чергу, містить значення, яке відповідає даному кольору.
Розглянемо докладніше один з форматів -- BMP, який широко використовується в системах Windows.

Формат BMP

Перші 14 байтів BMP-файлу складають його заголовок.
Заголовок файлу містить три значення: букви BM (сігнатура), які говорять про те, що графічний файл має BMP формат, число, що означає розмір файлу і число, яке вказує на те, де знаходяться растрові дані. Останнє число дорівнює кількості байтів від початку файлу. Ще два поля в заголовку файлу зарезервовані для майбутніх потреб і звичайно містять нулі.
Необхідні неграфічні дані заховані в інформаційному заголовку. Поля в інформаційному заголовку, в числі інших, містять його розмір (40 байтів в BMP-файлах для Windows), висоту і ширину зображення в пікселах, і кількість бітів на піксел.
Таблиця кольорів (палітра) містить 256 полів по 4 байти. Перший байт в кожному полі відповідає за синю компоненту кольору, другий за зелену і третій - за червону. Четвертий байт не використовується і встановлюється в 0. Якщо перші три значення в таблиці кольорів дорівнюють 0, 192 і 192, то це значить, що нульовий номер відповідає жовтому кольору середньої інтенсивності (суміш зеленого і червоного). У палітрі визначені всі кольори, що використовуються в зображенні.
Решта частини файлу містить значення пікселів. Якщо зображення складається з 1 мільйона пікселів, а кожен піксел вимагає 8 бітів - одного байта колірної інформації, тоді, ця частина файлу займає 1 мільйон байтів. Послідовність байтів відповідає порядку пікселів в зображенні: зліва направо, починаючи з нижнього рядка зображення. Значення кожного байта є номер кольору в таблиці кольорів.
Відображення на екран малюнка, що зберігається в BMP-файлі, починається з читання заголовка файлу і інформаційного заголовка. Програма, таким чином, отримує розміри зображення і кількість кольорів. Потім програма читає таблицю кольорів. Якщо комп'ютер виводить не більше 256 кольорів, то програма заповнює колірну палітру значеннями з таблиці кольорів. Таким чином, забезпечується правильна передача кольорів малюнка. Якщо використовуємо повнокольорову картинку - 24 або 32 біти на піксел, то колірну палітру заповнювати не потрібно. В цьому випадку на кожен піксел відводиться три (або чотири) байти значення, що містять синій, зелений і червоний кольори (для 32 бітного зображення ще один байт відводиться для альфа-компоненти, тобто ступеня прозорості даного піксела). Зауважимо, що кожен рядок доповнюється нулями до межі в 4 байта.
І, нарешті, прочитуються растрові дані. Як тільки рядок із значеннями пікселів прочитаний з файлу, він передається у відео-буфер для отримання зображення на екрані. У таких графічних середовищах як Windows, програма пересилає значення кольорів не безпосередньо у відео-буфер, а в Windows, і вже Windows заносить їх у відео-буфер. Зауважимо, що малюнок на екрані заповнюється не зверху вниз, а навпаки.

Опис формату bmp - файлу (24, 32 bits per pixel).

FILE HEADER   (Заголовок файлу)
BM signature (2 bytes) =BM
File size (4 bytes) Reserved (2 bytes) =0
Reserved (2 bytes)=0
Location of bitmap data (4 bytes)

INFORMATION HEADER  (Заголовок Bitmap)
Size of information header (4 bytes) =40
(Розмір заголовка)
Image width (4 bytes)
(Ширина зображення в пікселах)
Image height (4 bytes)
(Висота зображення в пікселах)
Number of color planes (2 bytes) =1
(Число площин кольорів)
Number of bits per pixel (2 bytes)
(Число бітів на піксел)
Compression method used (4 bytes)
(Тип стиску)
Number of bytes of bitmap data (4 bytes)
(Розмір стислого зображення або 0)
Horizontal screen resolution (4 bytes)
(Горизонтальне розрішення  в пікс/метр)
Vertical screen resolution (4 bytes)
(Вертикальне розрішення в пікс/метр)
Number of colors used in the image (4 bytes) =0
(Кількість кольорів)
Number of important colors (4 bytes)
(Кількість важливих кольорів)

"TABLE"  (Таблиця кольорів)

Палітра (таблиця кольорів) містить опис 256 відтінків кольорів по 4 байти на кожен.

"BITMAP DATA."

Дані описують колір пікселів що йдуть зліва направо і знизу до верху. Якщо зображення має глибину кольору 24 біти на піксел, то кожні три байти відповідають одному пікселу, визначаючи колірну гамму в послідовності BGR. Якщо глибина кольору 32 біти на піксел, то на кожну крапку відводиться ще один байт, що містить значення $\alpha$- компоненти (прозорість).
Кожен рядок доповнюється нулями до кінця параграфа.

Конструкція формату JPEG

У середині восьмидесятих років для вирішення задачі стиску повнокольорових зображень був розроблений формат JPEG (Joint Photographic Experts Group). Схема роботи методів стиску, що лежать в основі JPEG полягає в наступному. Після переводу повнокольорового зображення з колірного простору RGB (red, green, blue) в колірний простір YСrCb (Y- люмінесцентна складова, Cr- хроматичний червоний, тобто теплі тони, і Cb- хроматичний синій- холодні тони), зображення розбивається на квадрати розміру $8\times 8$ пікселів. До кожного з цих квадратів застосовується дискретне косинус- перетворення Фур'є. Для цієї мети створюється матриця D дискретного косинус-перетворення Фур'є, значення якої обчислюються за правилом \[ D_{i,j}=\frac{1}{n^2}, \] при $i=0$ чи $j=0$, та \[ D_{i,j}=\frac{4}{n^2}\cos\frac{\pi(2i+1)}{2n}\cos\frac{\pi(2j+1)}{2n}, \] для $i,j>0.$ Тут $i,j=0,1,...,7$ і $n=8$.
Таким чином одержуємо матрицю $D$.
Результатом застосування до матриці F первинних даних дискретного косинус~- перетворення Фур'є, буде матриця \[DF=D\times F\times D^T.\] Для заданого коефіцієнта стиску q обчислимо таблицю квантування Q за правилом \[Q_{i,j}=1+(1+i+j)q, i,j=0,1,...,7.\] Процедура квантування полягає в обчисленні чисел \[DFQ_{i,j}=\textrm{Round}\left(\frac{DF_{i,j}}{Q_{i,j}}\right),\] де $Round(\cdot)$ є функція приведення до цілого.
Одержана матриця відквантованих коефіцієнтів містить велику кількість коефіцієнтів рівних нулю. Для послідовного ефективного використовування методу групового кодування, одержані дані упорядковуються відповідно до номерів матриці Z-зігзагу Jpeg \[ \left(% \begin{array}{rrrrrrrr} 1& 2& 6& 7& 15& 16& 28& 29 \\ 3& 5& 8& 14& 17& 27& 30& 43 \\ 4& 9& 13& 18& 26& 31& 42& 44 \\ 10& 12& 19& 25& 32& 41& 45& 54 \\ 11& 20& 24& 33& 40& 46& 53& 55 \\ 21& 23& 34& 39& 47& 52& 56& 61 \\ 22& 35& 38& 48& 51& 57& 60& 62 \\ 36& 37& 49& 50& 58& 59& 63& 64 \\ \end{array}% \right) \] Унаслідок того факту, що людське око більш сприйнятливе до зміни яскравості (компоненти Y), ніж до зміни кольорів, при подальшій обробці колірних компонентів використовується децимація в пропорції 4:2:2 (береться тільки кожне четверте значення Cr і Cb) або 4:1:1 (береться тільки кожне восьме значення Cr і Cb). При реалізації зворотного ходу, значення, яких бракує, знаходять використовуючи інтерполяційні формули.
До одержаних послідовностей застосовується 7-бітне RLE кодування повторів (Run-Length Encoding). Подальша обробка полягає в застосуванні LZW з кодом змінної довжини і стиску без втрат за допомогою коду Хаффмана.
Завдяки великій колекції варіантів кодування (таблиці квантування, z-обхід, різні методи групування коефіцієнтів Фур'є для різних колірних компонентів) цей формат достатньо ефективний. Проте для високих ступенів стиску (більше 25 разів) стиснуте зображення візуально розпадається на квадратні ділянки постійності інтенсивності, що заважає нормальному сприй\-няттю образу. Крім того, з причини фіксованості таблиць квантування, одержати зображення із заданим ступенем стиску у форматі JPEG не завжди можливо.
Ці і інші супутні причини привели до необхідності розробки принципово нових методів стиску повнокольорових зображень.
Серед методів стиску, конкуруючих за право створення наступника JPEG, перш за все, розглядалися методи, засновані на фрактальному і на сплесковому (wavelets, або вейвлети) стиску даних.
Фрактальні методи засновані на виділенні і групуванні фрагментів зображення зі схожою структурою. Основною складністю фрактальних методів є вибір геометричного примітиву, на якому порівнюється структура даних і можливість його обертання. Для реалізації фрактальних методів потрібні не тільки великі обчислювальні витрати, але, і найголовніше, вони вимагають досить великого часу.
Сплескові методи стиску є продовженням і розвитком класичного аналізу Фур'є. У основі wavelet-методів стиску лежить частотний аналіз характеристик зображення. При цьому, для низьких частот використовується акуратніша обробка, а для високих - грубіша.
Сплескові методи стиску показують вищі показники, як за якістю стиску, так і за часом роботи. Цей факт зумовив використовування саме сплескових методів для розробки наступника JPEG.
Численні дослідження в цьому напрямі вилилися, врешті-решт, в ухвалення нового стандарту - JPEG2000.

Особливості формату JPEG2000

Розробка JPEG2000 почалася в 1996 році. Якраз з цього часу стала ясною істотна перевага алгоритмів стиску на основі вейвлетів перед ДКП, використаним в JPEG. Проте, тільки ради збільшення ступеня стиску не варто було б витрачати величезні кошти. При створенні нового стандарту, разом з досягненням більшої ефективності стиску ставилися ще і наступні цілі:

Стійкість алгоритму до помилок каналу зв'язку при передачі стислого зображення. Тут видно націленість нового стандарту на мобільні застосування, на передачу зображень по радіоканалу.
Уніфікована архітектура декодера. У JPEG реалізовано 44 різних режимів декодування, залежно від його застосування. Синтаксис JPEG2000 такий, що в незалежності від вживаного способу кодування використовується один і той же декодер.
Масштабованість. Залежно від потреби, це може бути масштабованість за розміром, дозволом. частотному змісту, кількості кольорів.
Обробка окремих областей на зображенні (Region Of Interest). Наприклад, користувача може цікавити не все зображення вулиці, а лише фото окремої машини, він виділяє його (мишею), і декодер з високою якістю відновлює цей фрагмент. (Все неможливо "підняти" з високою якістю через обмеження на об'єм передаваної інформації).
Стиск зображень великих розмірів.
Можливість обробки стислого зображення без декомпресії.

Локальна, масштабована структура вейвлет-функцій дозволила вирішити вище перелічені задачі. Робочою групою були розглянуті сотні пропозицій дослідників і відібрані найперспективніші. Основні блоки, що входять в структурну схему алгоритму стиску JPEG2000.

Попередня обробка. Зображення, як правило, є набором ненегативних цілих чисел. На етапі попередньої обробки з нього віднімають середнє. Крім того, якщо зображення великого розміру, то воно може бути розбито на частини. Тоді кожна частина стискається окремо, а для запобігання появі помітних ліній на стику відновлених частин застосовуються спеціальні заходи.
Вейвлет-перетворення. У JPEG2000 як фільтр використовується тензорний добуток одновимірних фільтрів. У першій частині стандарту визначені два вейвлет-фільтри - фільтр Добеши (9, 7) для стиску з втратами і теж біортогональний фільтр з цілочисельними коефіцієнтами (5, 3) для стиску без втрат. У другій частині стандарту дозволяється застосування будь-яких фільтрів, а також не тільки октавополосне розбиття, але і довільне (вейвлет-пакети і т.д.) В стандарті визначено, що вейвлет-~перетворення здійснюється не шляхом згортки з імпульсними характеристиками фільтрів, а на основі алгоритму, відомого як ліфтінгова схема.
Квантування. У першій частині стандарту визначено рівномірне квантування, у якого нульовий інтервал удвічі ширший за інші. У разі стиску без втрат розмір кроку квантування дорівнює 1, інакше він вибирається залежно від необхідного ступеня стиску.
Ентропійне кодування. Застосовується адаптивний арифметичний кодер (а в JPEG був кодер Хаффмана). Зважаючи на патентні обмеження використовується не QM-кодер розробки IBM, а трохи гірший MQ-кодер, спеціально розроблений для JPEG2000.
Кодування ведеться не всього зображення в цілому і навіть не окремих субсмуг, а дрібніших об'єктів - кодованих блоків (КБ). Розмір кодованого блоку може бути не більше 4096 пікселів, висота не менше 4 пікселів. Таке розбиття хоча і знижує декілька коефіцієнт стиску, але підвищує стійкість стислого потоку до похибок каналу зв'язку: похибка зіпсує лише невеликий блок. Кодування блоків ведеться в три етапи, бітовими площинами.
Потік стиснутих даних упаковується в пакети.

Ліфтінгові схеми фільтрації, реалізовані у форматі JPEG2000.

У форматі JPEG2000 реалізовано два режима стиску зображень -- без втрат і з втратами. Для стиску зображень без втрат використовується цілочисельне перетворення, яке має наступний вигляд -- Декомпозиція (прямий хід) \[ c^1_{2n}=c^0_{2n}-\left[\frac{c^0_{2n-1}+c^0_{2n+1}+2}{4}\right], \] \[ c^1_{2n+1}=c^0_{2n+1}+\left[\frac{c^1_{2n}+c^1_{2n+2}}{2}\right]. \] Реконструкція (зворотний хід) \[ c^0_{2n+1}=c^1_{2n+1}-\left[\frac{c^1_{2n}+c^1_{2n+2}}{2}\right], \] \[ c^0_{2n}=c^1_{2n}-\left[\frac{c^0_{2n-1}+c^0_{2n+1}+2}{4}\right], \] Для високих ступенів стиску JPEG2000 використовує біортогональну пару 7-9. В цьому випадку ліфтінгова схема для декомпозиції виглядає наступним чином \[ \left\{ \begin{array}{ll} c^1_{2n}\leftarrow kc^0_{2n},& \textrm{перший \,\,\,крок}, \\ c^1_{2n+1}\leftarrow -k^{-1}c^0_{2n+1},& \textrm{другий \,\,\,крок}, \\ c^1_{2n}\leftarrow c^1_{2n}-\delta\left(c^1_{2n-1}+c^1_{2n+1}\right),& \textrm{третій \,\,\,крок}, \\ c^1_{2n+1}\leftarrow c^1_{2n+1}-\gamma\left(c^1_{2n}+c^1_{2n+2}\right),& \textrm{четвертий\,\,\,крок}, \\ c^1_{2n}\leftarrow c^1_{2n}-\beta\left(c^1_{2n-1}+c^1_{2n+1}\right),& \textrm{п'ятий\,\,\,крок}, \\ c^1_{2n+1}\leftarrow c^1_{2n+1}-\alpha\left(c^1_{2n}+c^1_{2n+2}\right),& \textrm{шостий\,\,\,крок}, \end{array} \right. \] де \[ \alpha=-1.586 134 342, \beta=-0.052 980 118, \gamma=0.882 911 075, \delta=0.443 506 852,\] і масштабуючий коефіцієнт $k=1.230 174 105.$
Реконструкція (відновлення) сигналу проводиться наступним чином \[ \left\{ \begin{array}{ll} c^0_{2n+1}\leftarrow c^1_{2n+1}+\alpha\left(c^1_{2n}+c^1_{2n+2}\right),& \textrm{перший\,\,\,крок}\\ c^0_{2n}\leftarrow c^1_{2n}+\beta\left(c^0_{2n-1}+c^0_{2n+1}\right),& \textrm{другий\,\,\,крок}, \\ c^0_{2n+1}\leftarrow c^0_{2n+1}+\gamma \left(c^0_{2n}+c^0_{2n+2}\right),& \textrm{третій\,\,\,крок}, \\ c^0_{2n}\leftarrow c^0_{2n}+\delta\left(c^0_{2n-1}+c^0_{2n+1}\right),& \textrm{четвертий\,\,\,крок}, \\ c^0_{2n+1}\leftarrow -k^{-1}c^0_{2n+1},& \textrm{п'ятий \,\,\,крок}, \\ c^0_{2n}\leftarrow kc^0_{2n},& \textrm{ шостий\,\,\,крок}. \end{array} \right. \]

Методи кодування відеоінформації

Телевізійний кадр стандарту PAL містить 576 активних рядків (всього їх 625, але частина з них - службові). Згідно стандарту ITU-R ВТ.601 міжнародного телекомунікаційного співтовариства (ITU - International Telecommunications Union) кожен рядок містить 720 незалежних відліків. Таким чином, телевізійний кадр є матрицею з 720$\times$576 точок, а гранично досяжний дозвіл обмежений 700 лініями. У відцифрованому телевізійному сигналі кожен кадр є піксельним зображенням, де точка (піксель) утворена відліком в горизонтальному рядку. Таких зображень повинно проходити 25 за секунду (якщо строго - 50 напівкадрів полів, що складаються з парних і непарних рядків відповідно). Тоді інформаційний об'єм однієї хвилини цифрового відеосигналу з дозволом, відповідним мовному, і при глибині кольору 24 біти (True Color) складе 720$\times$576 точок $\times$ 24 біта кольорів $\times$ 25 кадрів/с $\times$ 60 с = 1866 Мб. Тобто без малого 2 гігабайти. При цьому швидкість цифрового відеопотоку буде дорівнювати 250 Мбіт/с. Навіть якщо поступитися якістю, і розглядати удвічі гірший розподіл по обох вісях (360$\times$288), що приблизно відповідає якості VHS-запису, об'єм хвилини відеопрограми займе 467 Мб, а відповідна швидкість цифрового потоку складе більше 60 Мбіт/с. Треба врахувати, що кожен фільм має і звуковий супровід. Виходить, що такий сигнал є дуже громіздким для прямого використовування, навіть в сучасних комунікаціях, або на сучасних носіях.
Керуючись подібними орієнтирами, в рамках міжнародної організації по стандартизації (ISO), був створений комітет розробки міжнародних стандартів кодування і стиску відео- і аудіоінформації. Офіційне найменування цій групі було дане просто жахливе - ISO/IECJTC1 SC29 WG11. Згодом вона стала відома як "Експертна група по кінематографії" (Moving Picture Expert Group), а абревіатура MPEG, утворена від англійського варіанту назви цієї групи, давно вже використовується як позначення розроблених нею норм і стандартів. У основу правил стиску відеоданих була закладена ідея пошуку і усунення надмірної інформації, що не впливає на кінцеве сприйняття якості зображення. В першу чергу, був врахований 'людський чинник' -- психофізіологічна модель сприйняття людиною відеозображень (HVS - Human Visual Sense); зокрема, той факт, що градації яскравості сприймаються зоровим апаратом людини значно тонше, ніж градації кольору. Це означає, що колірну інформацію можна зберігати "грубо", в порівнянні з яскравістю, при цьому в суб'єктивному сприйнятті якість зображення не погіршає. Тобто першочерговим напрямом в побудові алгоритмів всіх стандартів MPEG стає відшукання і усунення інформації, надмірної з погляду суб'єктивного сприйняття.
Працювала експертна група вельми плідно: за десятиліття розроблене ціле сімейство стандартів; більш того, майже всі вони живуть і успішно працюють. Кращим свідоцтвом тому служить той факт, що абревіатури MPEG і МР стали повсякденними на побутовому рівні. Розглянемо найважливіші етапи становлення MPEG.

MPEG1. Перший стандарт з'явився в 1992 р. і був розрахований на передачу відео по низькошвидкісних мережах, або для запису на компакт-диски (Video-CD). Максимально можлива швидкість цифрового потоку була спочатку обмежена порогом в 150 кб/с (одношвидкісний CD-ROM або стандартний аудіопрогравач компакт-дисків). Щоб укластися в задані рамки, довелося поступитися якістю. У MPEG1 роздільна здатність зображення понижена, в порівнянні з розгорткою телебачення, в 2 рази по обох осях: 288 активних рядків в ТБ-кадрі і 360 відліків в активній частині ТБ-рядка. У принципі, ця якість близька по рівню до аналогового VHS-відеозапису. Але не можна забувати про JPEG-компресію. Зменшення числа відліків означає тим самим збільшення блоків і макроблоків усередині кожного кадру. Тобто зниження якості автоматично робить внутрішньокадрову компресію грубішою, і, як наслідок, помітнішою споживачу. Однотонні поверхні виявляються як би складені з квадратів, що розсипаються; особливо настирливо квадрати "вилазять" на динамічних сценах.

Відомі випадки, коли при випуску версій фільмів на Video-CD доводилося урізати у декілька разів багато сцен з великою кількістю руху: гонитва, бійки, вибухи і т.п. З цих причин, а також унаслідок прогресу цифрових технологій стандарт MPEG1 не встиг набути широкого розповсюдження.

MPEG2. Час йшов, і прогрес у області цифрових технологій дозволив істотно удосконалити процес компресії відеоданих. Так з'явився новий стандарт MPEG2, робота над яким, власне, почалася відразу після виходу MPEG1 і завершилася в 1995 році. "Другий" MPEG не приніс революційних змін, це добротна доробка старого стандарту під нові можливості техніки і нові вимоги замовників - найбільших компаній mass-media. MPEG2 призначався для обробки відеозображення з телевізійною якістю, при пропускній спроможності каналів передачі даних від 3 до 15 Мбіт/с. Зараз стандарт MPEG2 асоціюється у переважної більшості користувачів з DVD-дисками. Але в 1992 року, коли стартували роботи над цим стандартом, ще не існувало широкодоступних носіїв, на які можна було б записати відеоінформацію, стиснуту по алгоритмах MPEG2. Найголовніше, комп'ютерна техніка того часу не могла забезпечити і потрібну смугу пропускання. Зате супутникове телебачення з новітнім на ті часи устаткуванням вже тоді було готове надати канал передачі з необхідними характеристиками. У жовтні 1995 року через телевізійний супутник "Pan Am Sat" було реалізовано перше 20-канальне цифрове ТБ-віщання, що використало стандарт MPEG2. Супутник здійснював трансляцію на території Скандинавії, країн Бенілюксу, Близького Сходу і Північної Африки.

З появою у середині 90-х роках цифрового багатоцільового диска DVD (Digital Versatile Disk, Digital Video Disk), що надає в простій - односторонній і одношаровій версії ємкість у 4,7 Гб (майже в 8 разів більше CD), він стає практично безальтернативним масовим носієм для розповсюдження якісної продукції, стиснутої за стандартом MPEG2. Це зумовило масове виробництво бюджетних DVD-програвачів і, звичайно, появу недорогих апаратних кодерів/декодерів. На стандарті MPEG2 зараз побудовані всі системи цифрового супутникового телебачення. На ньому ж ґрунтуються ефірні системи цифрового телемовлення DVB, які одержують все більш широке розповсюдження у ряді країн Західної Європи і в США. У професійній студійній апаратурі для реалізації цифрового нелінійного монтажу використовується версія EDITABLE MPEG, в якій всі кадри ключові, а швидкість потоку у форматі 4:2:2 досягає 50 Мбіт/с.
Революційних змін в новому стандарті немає, але удосконалення торкнулося практично всіх етапів "пакування" даних, більш того, з'явилися операції, що раніше не застосовувалися. Наприклад, після розбиття відеопотоку на кадри і групи кадрів, кодер аналізує зміст чергового кадру на предмет надмірних даних. Складається список оригінальних ділянок і таблиця ділянок, що повторюються. Оригінали зберігаються, копії видаляються, а таблиця ділянок, що повторюються, використовується при декодуванні стислого відеопотоку. Значне підвищення ступені стиску було досягнуте завдяки застосуванню у внутрішньокадровому стисненні нелінійного перетворювача Фурье замість лінійного. Оптимізації піддався алгоритм прогнозу руху, а також введені декілька нових алгоритмів компресії відеоданих. Вони в сукупності дозволяють кодувати різні шари кадру залежно від їх важливості з різною інтенсивністю цифрового потоку.
Стандарт MPEG2 надає можливість в процесі кодування задавати точність частотних коефіцієнтів матриці квантування, що безпосередньо впливає на якість і розмір одержуваного в результаті стиску зображення. Точність квантування може варіюватися в діапазоні 8-11 біт на одне значення елементу. Для порівняння: у MPEG1 передбачалося тільки одне фіксоване значення - 8 біт на елемент. Тобто, в рамках стандарту MPEG2 є можливість гнучкої настройки якості зображення залежно від пропускної спроможності мережі або місткості носія (от чому на перших DVD можна було бачити різне за якістю зображення). В той же час, користувачі таких апаратів, як DVD- або HD-рекордери, які використовують MPEG2-компресію, знають, як можна самим задавати рівень якості запису (HQ, SP, LP і т.п.), міняючи таким чином обсяг записаного матеріалу. Ця гнучкість, зокрема, і зробила MPEG2 основою для прийому/передачі цифрового телебачення в різних цифрових мережах.
В результаті для фільмів, створених в стандартах PAL і SECAM, підтримується розподільна якість 720 $\times$ 576 при 25 кадрах в секунду при умові високій якості. Власне, MPEG-фільм не можна віднести до якої-небудь системи кольорового телебачення, оскільки кадри в MPEG є просто зображеннями і не мають прямого відношення до початкової для фільму системи телебачення, може йти мова лише про відповідність розміру і частоти проходження кадрів. У частині аудіо в MPEG2, в порівнянні з MPEG1, додана підтримка багатоканального звуку(Dolby Digital 5.1, DTS і т.п.) {\bf MPEG3}. Перш за все, не слід змішувати з широковідомим форматом компресії звуку МР3. Стандарт MPEG3 спочатку розроблявся для використовування в системах телебачення високої чіткості (High Definition Television, HDTV) із швидкістю потоку даних 20-40 Мбіт/с. Але, ще в процесі розробки, стало ясно, що параметри, які вимагаються для передачі HDTV, цілком забезпечуються використанням стандарту MPEG2 при збільшеній швидкості цифрового потоку. Іншими словами, гострої потреби в існуванні окремого стандарту для HDTV немає. Таким чином, MPEG3, ще не народився, як став складовою частиною стандарту MPEG2 і окремо тепер навіть не згадується.

MPEG4. У новому стандарті MPEG4, що з'явився наприкінці 1999 року, запропоновано ширший погляд на медіа-реальність. Стандарт задає принципи роботи з контентом (цифровим представленням медіа-даних) для трьох областей: власне інтерактивне мультимедіа (включаючи продукти, які поширювані на оптичних дисках і через Інтернет), графічних додатків (синтетичного контента) і цифрового телебачення (DTV). Фактично даний стандарт задає правила організації середовища, причому середовища об'єктно орієнтованого. Він має справу не просто з потоками і масивами медіа-даних, а з медіа-об'єктами (ключове поняття стандарту). Крім роботи з аудіо- і відеоданими, стандарт дозволяє працювати з природними і синтезованими комп'ютером 2D- і 3D-об'єктами, проводити прив'язку їх взаємного розташування і синхронізацію один щодо одного, а також організує їх інтерактивну взаємодію з користувачем. Зображення розділяється на складові елементи - медіа-обьекти, описується структура цих об'єктів і їх взаємозв'язок, щоб потім зібрати їх в єдину відеозвукову сцену.

Такий спосіб представлення даних дозволяє змінити результуючу сцену, забезпечити високий рівень інтерактивності для кінцевого користувача, надаючи йому цілий ряд можливостей. Наприклад, переміщати об'єкти в будь-яке місце сцени, трансформувати об'єкти, змінювати їх форму і геометричні розміри, збирати з окремих об'єктів складний об'єкт і проводити над ним операції, міняти текстуру і колір об'єкту, маніпулювати їм (примусити, наприклад, стіл пересуватися в просторі), міняти точку спостереження за всією сценою і тому подібне.
У боротьбі з конкурентами на ринку потокового відео (зокрема, згадаємо компанію Apple з її QuickTime) в корпорації Microsoft зайнялися розробкою кодера, що дозволяє компресувати відеопотік відповідно до стандарту MPEG4. На одному з етапів відладки нового продукту бета-версія цього кодера стала надбанням хакерської громадськості. Отже, двоє хакерів, відомих під прізвиськами MaxMorice і Gej, презентували новий формат стиску відеофайлів, названий ними DivX ;-). Насправді це лише зламана версія Microsoft MPEG-4 Video Codeс (Low-Motion кодек версія 4.1.00.4920 M\$ MPEG4v3, та High-Motion кодек - 4.1.4917 M\$ MPEGv3). Як затверджують автори, вони прибрали деякі недоліки і трошки його поліпшили. Далі - більше: через приблизно півроку тепер уже цілком легальна фірма DivXNetworks Inc. переробила цей продукт і зняла з нього клеймо "Веселого Роджера". Microsoft ще на "піратській" стадії цієї історії з "політичних" мотивів (в той час з судовими позивами до Microsoft звернулися кілька досить відомих софтверних корпорацій і Білу Гейтсу було не до DivX ;-)) згорнула розробки в даному напрямі.
Особливу увагу надамо тій області стандарту MPEG4, яка нас найбільш цікавить - стиску відеоматеріалів. Алгоритм компресії відео, у принципі, працює за тією ж схемою, що і в попередніх стандартах, але є декілька радикальних нововведень.

Основна ідея всієї схеми MPEG - це передбачати рух від кадру до кадру, а потім застосовувати дискретне косинус перетворення (ДКП), щоб перерозподілити надмірність в просторі.

При обробці відеопослідовності кожне зображення може бути представлене у вигляді суперпозиції об'єктних відеоплощин (video object plane - VOP). Максимальна кількість таких площин - 256. Кожна площина також є зображенням у форматі YUV 4:2:0. Вона містить певну частину початкового (повного) зображення і, як правило, формально пов'язана з якоюсь візуально помітною його частиною. Площини кодуються незалежно. При декодуванні зображення "збирається" з окремих декодованих площин з використанням інформації, що зберігається окремо, на форму (shape) об'єктів, що містяться в тій або іншій площині (інформація про форму утворюють так звані альфа-площини (alpha planes)). В окремому випадку ми маємо всього одну площину, яка містить все початкове зображення. Внаслідок відсутності ефективних методів розподілу зображення на окремі об'єкти, саме цей випадок найчастіше зустрічається.

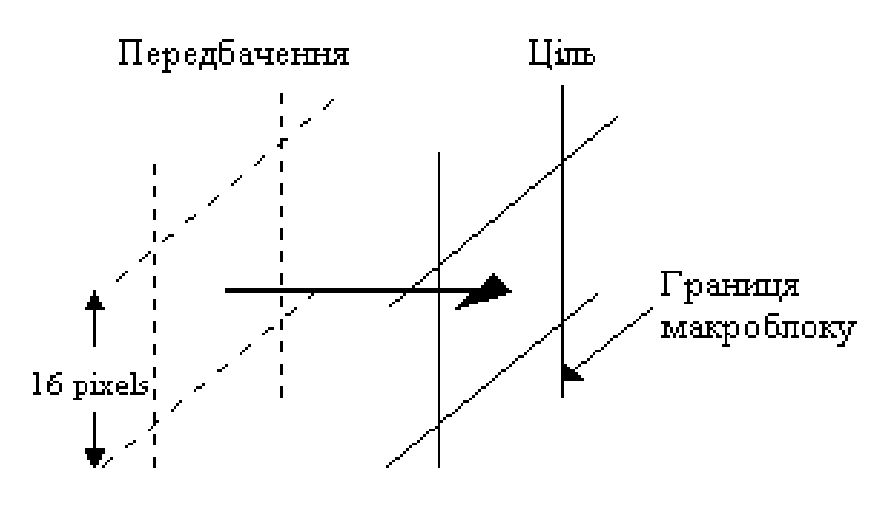
При обробці відеоплощини (фрейми) розділяються на чотири типи: I-площина, Р-площина, В-площина і S-площина. І-площини кодуються без використання будь-якої інформації про інші площини. I-площину можна декодувати, не декодуючи ніякі інші площини, що дозволяє забезпечити швидкий доступ до довільних частин закодованого відеопотоку. Кожна I-площина розбивається на макроблоки розміру 16$\times$16 (тут і далі указується розмір для компоненти Y, відповідний розмір для компонентів U і V - 8$\times$8). Такі макроблоки називаються intra-макроблоками. Intra-макроблок, у свою чергу, розбивається на 4 intra-блоки розміру 8$\times$8, кожен з яких бере участь в подальшому блоковому кодуванні/декодуванні (все сказане відноситься тільки до компоненти Y, для компонентів U і V використовується блок 8$\times$8, який відповідає макроблоку компоненти Y). Р-площини кодуються з використанням інформації про попередні I- і P-площини. Р-площина також розбивається на макроблоки 16$\times$16 і блоки 8$\times$8, проте, крім intra-макроблоків і intra-блоків, тут присутні inter-макроблоки і inter-блоки. Перед кодуванням над inter-макроблоками/блоками здійснюється процедура компенсації руху (motion compensation): у попередніх площинах шукається макроблок/блок (він може знаходитися на довільній позиції, не обов'язково кратній 16 або 8), який максимально відповідає поточному inter-макроблоку/блоку (так званий прогноз (prediction)), після чого знаходиться поточечна різниця. Різницевий макроблок/блок (помилка прогнозу (prediction error)), що був отриманий в результаті цієї операції, надалі використовується при кодуванні. Важливо відзначити, що площини, на основі яких здійснюється процедура компенсації руху (опорні площини (reference planes)), повинні співпадати з площинами, які відновлюються в процесі декодування (при обчисленні помилки прогнозу у жодному випадку не повинна використовуватися інформація, доступна тільки на етапі кодування). Результатом дії описаної процедури крім блоків, що містять помилку прогнозу, є поле двокомпонентних векторів руху (motion vectors).

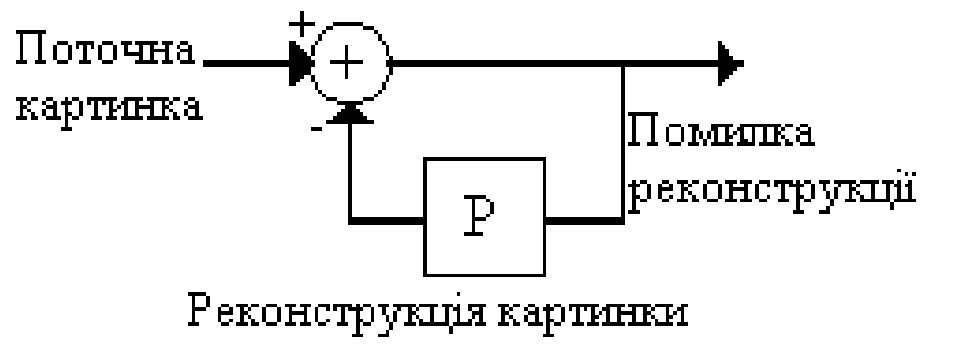
Пошук схожих блоків проводиться тільки для компоненти Y, вектори для компонентів U і V знаходяться шляхом ділення навпіл векторів для першої компоненти. Згідно стандарту, вектори руху мають в загальному випадку нецілу довжину, кратну 1/2 або 1/4. Для отримання нецілих векторів, опорні площини збільшуються (масштабуються), відповідно, в 2 і в 4 рази по кожному з вимірювань (для збільшення використовується білінійна інтерполяція). Крім збільшення, стандарт визначає застосування так званого педдінга (padding). Процедура полягає в розширенні площини з усіх боків на величину, рівну 16 точкам для компоненти Y і 8 - для компонентів U і V (і те і інше в цілих одиницях). Новим точкам привласнюються кольори найближчих до них граничних точок початкової площини. Педдінг (в даному випадку, можливо, має сенс використовувати термін доповнення/розширення) сприяє підвищенню ефективності компенсації руху поблизу меж відеоплощин. Компенсація руху може здійснюватися як макроблоками, так і блоками, тому для кожного макроблоку можуть бути знайдені або 1, або 4 вектори руху.

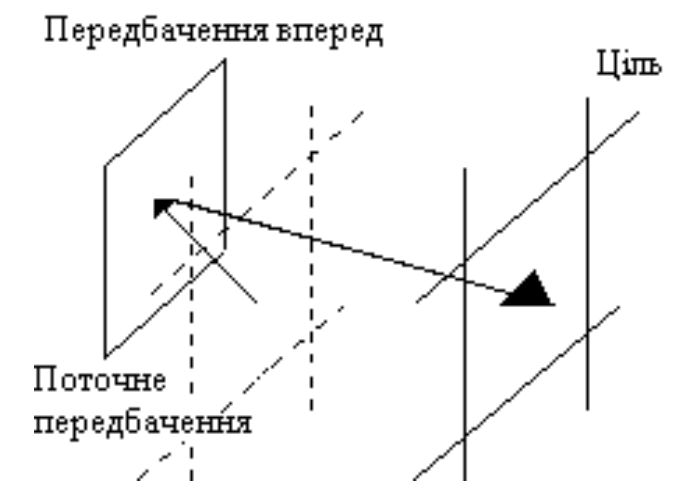
Вибір здійснюється на основі порівняння обсягів, які буде займати закодований макроблок в тому і в іншому випадку, з урахуванням внеску коду вектора руху. Як було відмічено, Р-площини можуть містити як inter-, так і intra-макроблоки. Завдяки компенсації руху, inter-макроблоки, як правило, кодуються з більшою ефективністю в порівнянні з intra-макроблоками, проте використання intra-макроблоків не пов'язане із зберіганням додаткової інформації про вектори руху, що знову ж таки може виявитися вигіднішим. Дилема вирішується так само, як і у попередньому випадку: тип використовуваного макроблоку вибирається виходячи з обсягу його сумарного коду. Стандарт передбачає особливий тип компенсації - компенсація з перекриттям (overlapped motion compensation). Компенсація з перекриттям використовується тільки для блоків компоненти Y. При використанні цього методу різниця береться не між поточним блоком і деяким схожим блоком, який належнить попереднім площинам, а між поточним блоком і зваженою суперпозицією трьох схожих блоків. Відповідно вибираються наступні вектори: вектор для даного блоку і два вектори для блоків, сусідніх до даного блоку в макроблоці, який обробляється. В-площина є розширенням поняття Р-площини. Відмінність В-площини від Р-площини полягає в тому, що при кодуванні В-площини для компенсації руху можуть використовуватися як попередні, так і подальші I- і P- площини (із зрозумілих причин, самі В-площини для цього використовуватися не можуть). Відповідно вводяться поняття прямого і зворотного прогнозу (forward and backward prediction). Кожен макроблок в B-площині може бути передбачений макроблоком на попередній площині, макроблоком на подальшій площині і суперпозицією цих макроблоків.

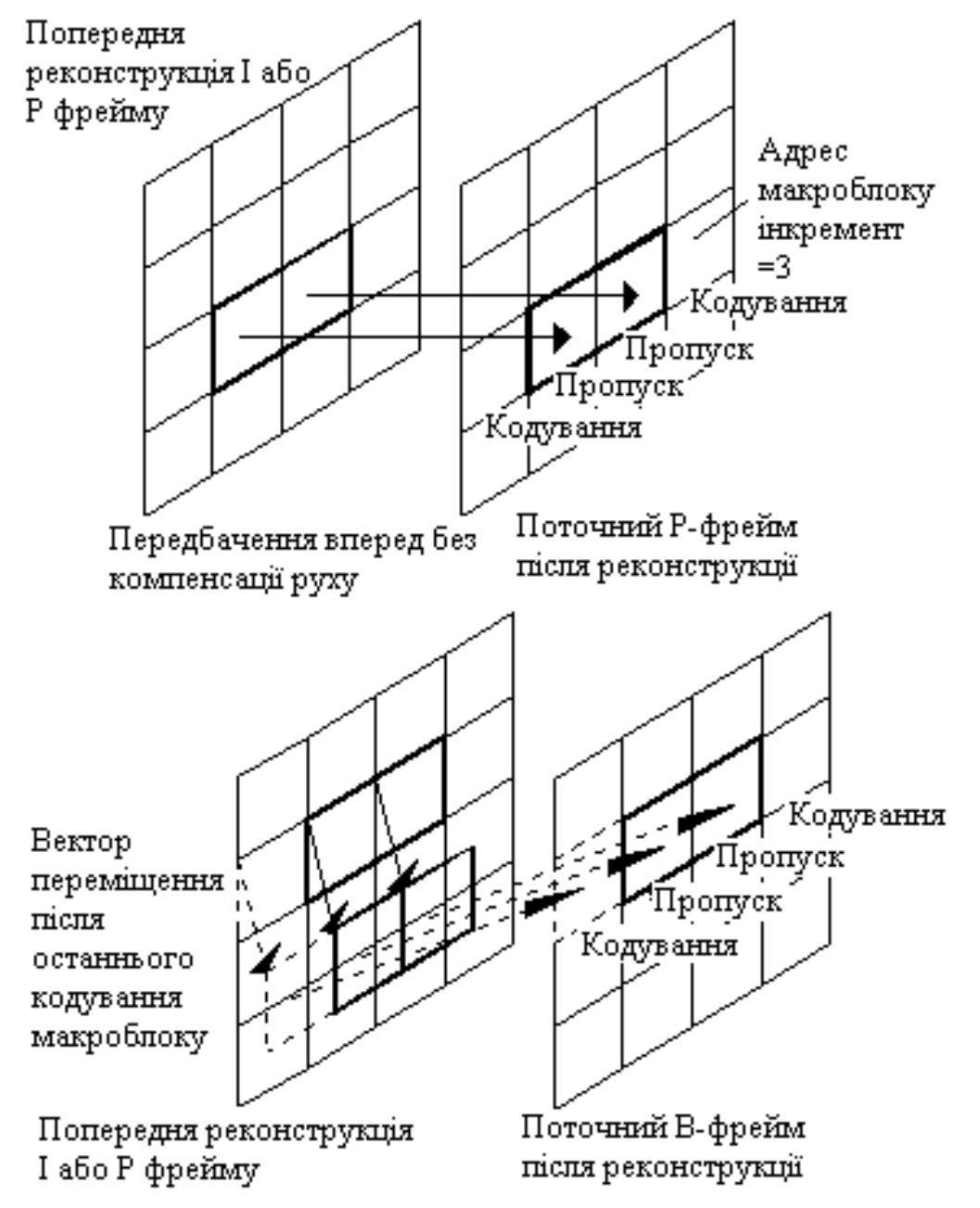
Використання двонаправленого прогнозу (bidirectional prediciton) дозволяє помітно підвищити ефективність прогнозу, а отже, і ефективність кодування.

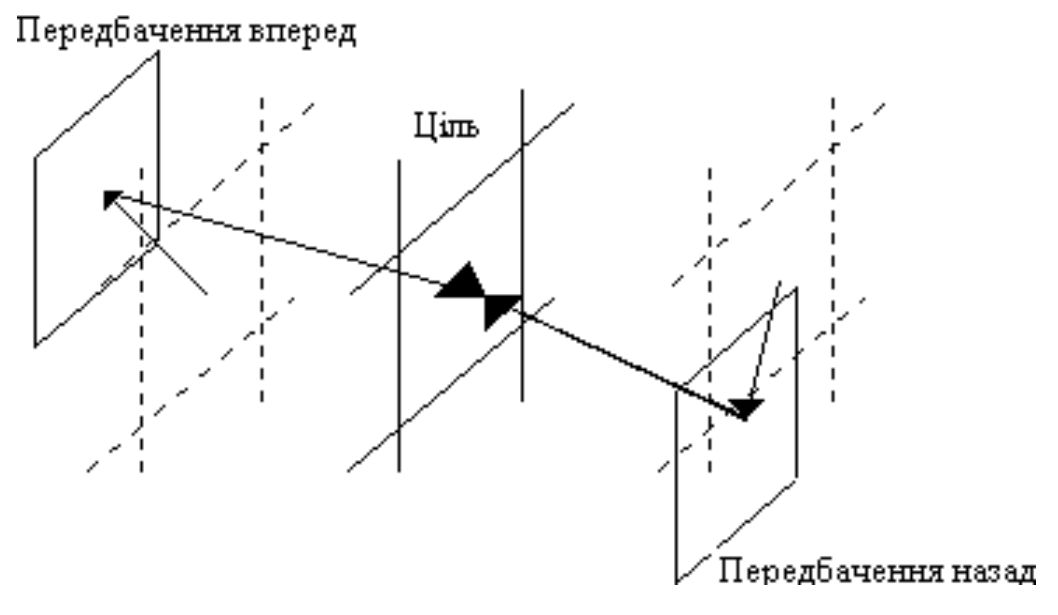
Останній тип закодованої відеоплощини - S-площина. Вона має безпосереднє відношення до спрайтів (sprite). Спрайтом в стандарті MPEG4 називається частина зображення, видима впродовж певного інтервалу у відеопослідовності. В ролі спрайту найчастіше виступає фон (задній план). При декодуванні з використанням спрайту фрейми частково відновлюються з окремих областей спрайту шляхом відображення цих областей на ту або іншу область декодованого фрейма з використанням перспективного перетворення (крім відображення, застосовуються також і інші спеціальні процедури). Спрайт зазвичай зберігається і кодується окремо, при цьому спосіб його кодування ідентичний способу кодування І-площин. Окремим випадком використання спрайту є S(GMC) - площини. В ролі спрайту тут виступає одна з попередніх I- або Р-площин. Цей метод майже нічим не відрізняється від методу обробки Р-площин, за тим виключенням, що процедурі компенсації руху передує процедура глобальної (вживаної до всієї площини) компенсації руху з використанням перспективного перетворення. Технологія GMC (global motion compensation), найчастіше застосовується для нівеляції руху і зміни оптичних параметрів камери. Площини різних типів, які ідуть поряд, розподіляються на відособлено кодовані групи. На початку групи повинна знаходитися I-площина, оскільки тільки вона може бути декодована першою. Далі розташовані площини інших типів. В- площини зазвичай чергуються з P- або S(GMC) - площинами (хоча це і не обов'язково, наприклад, нерідко одна P- або S(GMC) - площин чередується з двома і найчастіше йдуть підряд В- площини). Розподіл площин на групи полегшує процес доступу до інформації, а також забезпечує велику перешкодостійкість. Останнє обумовлюється тим, що у разі помилки пошкодженим виявляється не весь закодований потік, а тільки окрема його частина.
Послідовність розкодованих кадрів зазвичай виглядає наступним чином

I B B P B B P B B P B B I B B P B B P B ...

Зауважимо, що від I до наступного I фрейму лежить 12 кадрів. Це зумовлено вимогою довільного доступу, згідно якому початкова точка повинна повторюватися кожні 0.4 секунди. Співвідношення P і B засноване на досвіді. Щоб декодер міг працювати, необхідно, щоб перший P-фрейм в потоці зустрівся з першим B-фреймом, тому стислий потік виглядає наступним чином: 0 $\times\times$ 3 1 2 6 4 5 ..., де числа - це номери кадрів, а $\times\times$ може бути нічим, якщо це початок послідовності, або B-фрейми -2 і -1, якщо це фрагмент з середини потоку. Спочатку необхідно розкодувати I-фрейм, потім P, потім, маючи їх обидва в пам'яті, розкодувати B. Під час декодування P показується I-фрейм, B показуються відразу, а розкодований P показується під час декодування наступного. Прогноз макроблоків формується на основі відповідних 16$\times$16 блоків точок (16$\times$8 в MPEG-2) на попередніх відновлених кадрах. Ніяких обмежень на положення макроблоку в попередньому зображенні, окрім її меж, не існує.
Як тільки кадр розкодований, він стає не набором блоків, а звичним плоским цифровим піксельним зображенням.

В MPEG розміри зображення, що відображається, і частота кадрів може відрізнятися від закодованого в потоці. Наприклад, перед кодуванням деяка підмножина кадрів в початковій послідовності може бути викинута, а потім кожен кадр фільтрується і обробляється. При відновленні кадру для створення початкового розміру і частоти кадрів використовується інтерполяція. Фактично, три фундаментальні фази (початкові дані, закодовані дані і розкодовані для візуалізації) можуть відрізнятися в параметрах. Синтаксис MPEG описує кодовану частоту і частоту відновлених кадрів через заголовки, таким чином, початкова частота кадрів і розмір відомий тільки кодеру. Саме тому в заголовки MPEG-2 введені елементи, що описують розмір екрану для показу відео-послідовності. В I-фреймі, якщо не використовуються режими масштабування, макроблоки повинні бути закодовані як внутрішні - без посилань на попередні або подальші кадри. Проте, макроблоки в P-фреймі можуть бути як внутрішніми, так і мати посилання на попередні кадри. Макроблоки в B-фреймі можуть бути як внутрішніми, так і можуть посилатися на попередній кадр, подальший, або на обидва. У заголовку кожного макроблоку є елемент, що визначає його тип.

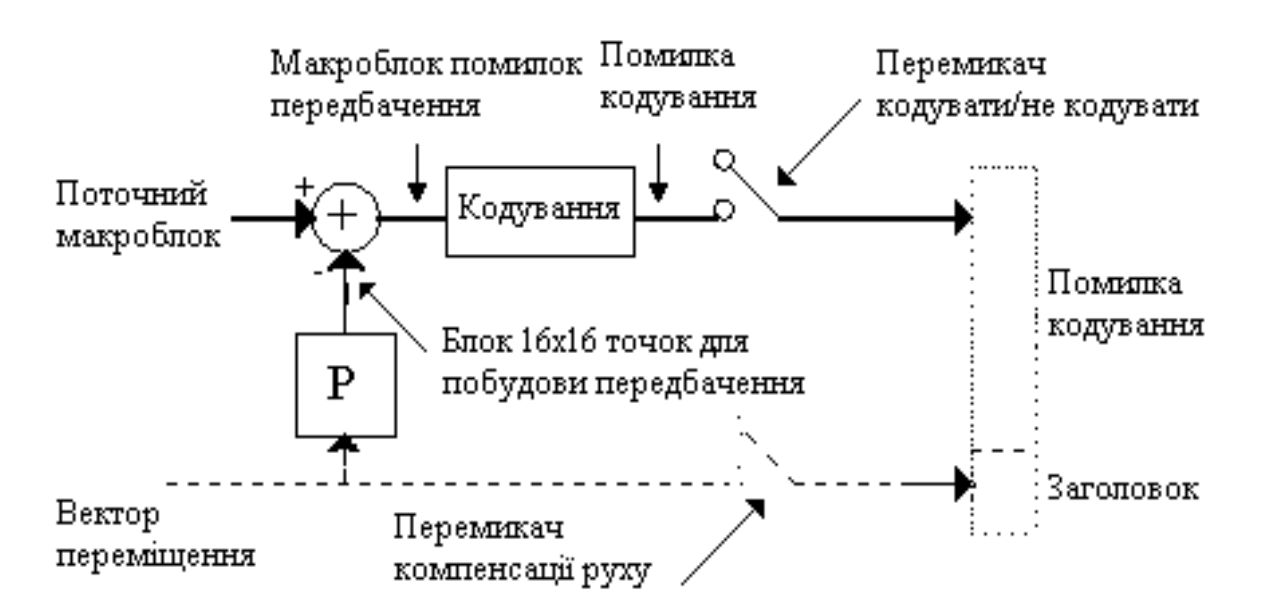
Послідовність кадрів може мати будь-яку структуру розміщення I, P і B фреймів. На практиці прийнято мати фіксовану послідовність (на зразок I B B P B B P B B P B B P B B), проте, сучасні кодери можуть оптимізувати вибір тип кадру залежно від контексту і глобальних характеристик відео-послідовності. Кожен тип кадру має свої плюси залежно від особливостей зображення (активність руху, тимчасові ефекти маскування та подібне). Наприклад, якщо послідовність зображень мало міняється від кадру до кадру, є сенс кодувати більше B-фреймів, ніж P. Оскільки B-фрейми не використовуються в подальшому процесі декодування, вони можуть бути стиснуті сильніше, без впливу на якість відео-послідовності в цілому. Вимоги конкретного застосування також впливають на вибір типу кадрів: ключові кадри, перемикання каналів, індексація програм, відновлення від помилок і т.п.
Розглянемо коротко процедури кодування intra/inter-блоков і векторів руху. Intra- та inter-блоки кодуються практично одним і тим же методом за невеликими виключеннями: спочатку проводиться блокове дискретне косинусне перетворення (discrete cosine transform - DCT), потім отримані в результаті перетворення коефіцієнти (DCT-коефіцієнти) квантуються, після чого квантовані коефіцієнти кодуються з використанням заздалегідь фіксованої системи кодів змінної довжини. Основна відмінність методу кодування intra-блоків від методу кодування inter-блоків полягає в тому, що в intra-блоках по-особливому обробляється старший коефіцієнт перетворення, що описує середній по блоку рівень сигналу (DC-коефіцієнт): кодується не сам коефіцієнт, а різниця між ним і DC-коефіцієнтом деякого сусіднього блоку.
Схема кодування решти всіх коефіцієнтів виглядає насупним чином. Здійснюється обхід блоку в зигзагоподібному порядку - від старшого коефіцієнта, що знаходиться в лівому верхньому кутку блоку, до молодшого, що знаходиться в правому нижньому кутку (передбачено три варіанти зигзагоподібного обходу). В процесі обходу послідовно кодуються групи коефіцієнтів наступного типу: послідовність нульових коефіцієнтів і перший наступний за ними ненульовий коефіцієнт. Групи нумеруються, причому один номер резервується для специфічного випадку - ситуації, коли всі коефіцієнти є нульовими. Груповим номерам зіставляються коди змінної цілої довжини. Довжина вибирається виходячи з наступного критерію: номерам груп, що зустрічаються частіше, ставляться у відповідність коротші коди. Система кодів є префіксною: коди, що належать системі, не є початком інших кодів з цієї системи.
Спосіб кодування блоків коефіцієнтів, отриманих в результаті застосування дискретного косинусного перетворення, обумовлений наступною особливістю: при обробці реальних зображень, як правило, DCT-коефіцієнти убувають по абсолютній величині при русі по блоку зліва направо і зверху вниз. Відповідно, під час зигзагоподібного обходу коефіцієнти убувають по абсолютній величині, причому, будучи квантованими, дуже багато з них (особливо коефіцієнти, що виявляються при обході останніми) мають нульове значення. Крім приведеного способу кодування, існує декілька модифікованих способів, при яких з коефіцієнтів верхнього рядка і лівого стовпця блоку заздалегідь віднімаються коефіцієнти, що стоять на тих же позиціях в сусідніх блоках.
Стандартом передбачається дві схеми квантування коефіцієнтів, що отримуються в результаті дискретного косинусного перетворення. Одна з них повторює схему, яка використовується в стандарті H.263, і полягає в діленні всіх коефіцієнтів, окрім DC-коефіцієнта в intra-блоках, на одне і те ж число - подвоєний параметр квантування. При цьому у разі inter-блоків перед квантуванням з абсолютного значення коефіцієнта віднімається значення, рівне половині параметра квантування. DC-коефіцієнт в intra-блоці завжди ділиться на 8. В альтернативній схемі ретельніше враховуються особливості візуального сприйняття інформації. Для DC-коефіцієнта використовується нерівномірне квантування, при якому дільник залежить не тільки від параметра квантування, але і від типу колірної компоненти. Решта всіх коефіцієнтів кодується в два етапи. Спочатку кожен з них ділиться на відповідне йому число із стандартної для даного типу блоку (intra або inter) матриці квантування (розмір матриці співпадає з розміром блоку - 8$\times$8). Матриця влаштована так, щоб при русі зліва направо і зверху вниз дільники збільшувалися. (Річ у тому, що зір сильніше сприймає зміни, що описуються низькими частотами гармонійного спектру, тому високими частотами часто можна безболісно нехтувати.) На другому етапі частково квантовані коефіцієнти повторно діляться на число, рівне подвоєному параметру квантування. Вектори руху кодуються покоординатно.
Як і у випадку з DCT-коефіцієнтами, при генерації коду використовуються системи префіксних кодів змінної довжини. Кодується не сама координата вектора, а різниця між нею і однією із відповідних координат вектора деякого сусіднього блоку (у виборі беруть участь координати векторів трьох сусідніх блоків - вибирається середня з трьох координат). Різним значенням різниці координат ставляться у відповідність різні коди змінної довжини, при цьому маленьким по абсолютному значенню різницям відповідають коротші коди. Описані методи кодування коефіцієнтів і векторів руху задіються не завжди, виникають ситуації, коли дані процедури взагалі не потрібні. Однією з таких ситуацій є випадок рівності нулю всіх DCT-коефіцієнтів блоку. Про це сигналізує спеціальний прапорець. Крім цього прапорця, існує також і інший прапорець, наявність якого дозволяє спростити процедуру кодування. Він сигналізує про те, чи кодується даний inter-макроблок взагалі. Якщо прапорець має одиничне значення, ніяка додаткова інформація, що описує коефіцієнти і вектора руху не передається, а в якості вектора руху беруться нульові вектори, також нульовою вважається помилка прогнозу. У стандарті використовуються два методи пост-обробки відеопослідовності: деблокінг (deblocking) і дерингінг (deringing). Перший застосовується для зменшення блокового ефекту - особливого типу помилки відновлення закодованого зображення, обумовленого поблочним кодуванням з високим рівнем втрат, другий є технікою адаптивного згладжування сигналу, що дозволяє усувати окремі високочастотні спотворення.
Серед іншого, стандарт MPEG4 описує формат представлення деяких вельми специфічних візуальних об'єктів, таких, як нерухоме зображення (still image), анімація обличчя (face animation) і сітчастий об'єкт (mesh object). Нерухоме зображення кодується із застосуванням вейвлет-перетворення. Здійснюється стандартна двомірна частотна декомпозиція, при цьому використовується біортогональний базис (9,3), або якийсь специфічний базис, параметри якого заздалегідь відомі чи передаються разом з кодом.
Коефіцієнти, отримані в результаті вейвлет-перетворення, квантуються із використанням рівномірного скалярного квантування, а потім кодуються по стандартній схемі, в якій застосовуються так звані нуль-дерева (zero-tree). Код генерується на основі високоефективного арифметичного кодування.
У стандарті описується достатньо оригінальна технологія, призначена для опису міміки людського обличчя. Обличчя відновлюється на основі його параметричної моделі (анімація обличчя). Уніфікований опис дозволяє представляти особу в достатньо економній формі, у порівнянні із звичайними методами кодування, які описані вище.
Найбільш вірогідна область застосування такого рішення - кодування відеоконференцій. Спеціальне представлення об'єктів на площині у вигляді трикутної сітчастої структури з накладеною на неї текстурою носить назву mesh-технологія. Опис топології сітки здійснюється шляхом кодування координат вершин трикутників, а також векторів руху, що визначають зміну положення цих вершин в часі. Паралельно із трансформацією топології сітки проводиться трансформація текстури, що накладається. Сітчасте представлення об'єктів ефективно в тих випадках, коли ці об'єкти задаються у векторній формі.

Стандарт H.264

При розробці стандарту вперше були об'єднані зусилля фахівців Міжнародного Телекомунікаційного Союзу (International Telecommunication Union - ITU) в особі їх сектора (ITU-T) стандартизації, Міжнародної Організації з Стандартизації (International Organization for Standardization - ISO) і Міжнародній Комісії з Електротехніки (International Electrotechnical Commission - IEC). До цього об'єднання перша організація займалася розробкою телекомунікаційних стандартів, тоді як останні дві -стандартами загального плану. Раніше ними були запропоновані стандарти кодування відеоінформації Н.261, H.263 (ITU-T); JPEG, JPEG2000, MPEG (ISO/IEC).
На відміну від стандарту MPEG4, технології, що описуються в стандарті H.264, призначені для обробки звичайних відеопослідовностей, заздалегідь не розділених на відеоплощині. Природно, це не є обмеженням, оскільки всі методи кодування можуть бути з тим же успіхом застосовані і до випадку багатоплощинного кодування. Описувані в новому стандарті методи, в цілому, не сильно відрізняються від методів, передбачених стандартом MPEG4. Проте новий стандарт включає декілька достатньо перспективних рішень які заслуговують найпильнішої уваги. Як базові одиниці кодування в даному випадку виступають блоки розміру $4\times 4$, $8\times 8$, $8\times 4$ і $4\times 8$. При цьому розмір макроблоку залишається тим же - $16\times 16$, що дає можливість здійснювати компенсацію руху з великою кількістю різних варіантів розбиття макроблоку на блоки.
Розбиття здійснюється в два етапи. Спочатку макроблок $16\times 16$ розбивається на одну, або декілька, прямокутних областей, кожна з яких має свій, відмінний від інших вектор руху (можливі наступні варіанти розбиття: $16\times 16$, $16\times 8+16\times 8$, $8\times 16+8\times 16$ і $8\times 8+8\times 8+8\times 8+8\times 8$). На другому етапі кожен підблок розміру $8\times 8$, у свою чергу, розбивається на області одним з перелічених способів: $8\times 8$,$8\times 4$ + $8\times 4$,$4\times 8$+ $4\times 8$ і $4\times 4$+ $4\times 4$+ $4\times 4$+ $4\times 4$. Для блоків $4\times 4$ застосовується вельми специфічне перетворення, відмінне від дискретного косинусного перетворення.
Дане перетворення володіє ефективністю схожою з дискретним косинусним перетворенням, але з меншою обчислювальною складністю (використовуються тільки операції складання і зрушення). Вельми оригінальною ідеєю в даному випадку є повторне кодування старших коефіцієнтів перетворення. Кодування кожного блоку є повторним застосування 24 процедур кодування блоків (16 для компоненти Y і по 4 для компонентів U і V). Отримані 16 старших коефіцієнтів перетворення для компоненти Y і, відповідно, по 4 старших коефіцієнта для компонентів U і V піддаються повторному перетворенню. Для блоку старших коефіцієнтів компоненти Y використовується дещо відмінне від попереднього перетворення $4\times 4$, а для блоку старших коефіцієнтів компонентів U і V спеціальне перетворення $2\times 2$. Для блоків $8\times 8$, $8\times 4$ і $4\times 8$ також передбачені свої перетворення, які, проте, не є обов'язковими.
Замість кодування на основі перетворення може застосовуватися екстраполяція. При використанні такого рішення значення яскравості/кольору усередині блоку отримуються шляхом наближення, в якому враховуються значення яскравості/кольору граничних точок сусідніх блоків. Компенсація руху зазнала досить істотних змін в порівнянні із стандартом MPEG4. Слід зазначити дві його особливості- це велика точність представлення векторів руху і інший спосіб збільшення масштабу опірних фреймів, які використовуються для отримання прогнозу. Допускається точність,яка дорівнює або 1/4, або 1/8 (у MPEG4 максимальна точність складає 1/4).
Для масштабування опірних фреймів застосовується досить складна багатоточкова інтерполяція. У сукупності дані рішення дозволяють отримати вагомий приріст в ефективності. Великий інтерес викликає метод кодування квантованих коефіцієнтів перетворення. Для intra-макроблоків/блоків застосовується так званий intra-прогноз. Із значень коефіцієнтів intra-макроблоків/блоків віднімаються числа, що отримуються із множини значень коефіцієнтів сусідніх макроблоків/блоків з використанням однієї із схем прогнозу (для макроблоків передбачено 4 схеми, а для блоків - 9 схем). При кодуванні отриманих різниць для випадку intra-блоків і помилок прогнозу для випадку inter-блоків задіюється метод, практично ідентичний методу, який описано в стандарті MPEG4.
Дієвим прийомом збільшення ефективності представлення відеоінформації є використання для генерації коду арифметичного кодування замість префіксного. Особливістю пропонованої реалізації арифметичного кодування є те, що кодування приймає на вхід тільки бінарні символи. З одного боку, це дещо ускладнює застосування даного способу генерації коду (доводиться використовувати бінарну декомпозицію для багатосимвольних алфавітів), з іншого боку, подібний підхід робить можливими достатньо швидкі реалізації і полегшує процес побудови ймовірнісних моделей.
Стандарт H.264 спочатку був орієнтований на застосування в комунікаційних системах, тому особлива увага тут приділена підвищенню перешкодостійкості і забезпеченню високого ступеня гнучкості інформаційного уявлення, необхідного для забезпечення зручності передачі закодованої відеоінформації в мережах різної природи. Передбачені особливі алгоритми розподілу закодованого потоку на блоки, що забезпечує необхідні характеристики інформаційного уявлення для кожного конкретного випадку.

Стандарт дійсно є помітним кроком вперед у порівнянні з поточною версією стандарту MPEG4. Формат кодування дозволяє добиватися ефективності представлення інформації, що перевершує ефективність, яка отримується в рамках стандарту MPEG4, більш ніж на 30%. Природно, обчислювальна складність пропонованих методів дещо вище ніж у MPEG4.