Бустинг

Boosting

Введение

Бустинг (повышение, поднятие) - это класс методов машинного обучения, основанный на идее, что комбинация простых классификаторов (полученных слабым учеником) может работать лучше, чем любой из простых классификаторов. Слабый ученик (WL) - это алгоритм обучения, способный производить классификаторы с вероятностью ошибки строго (но незначительно) меньше случайного угадывания (0.5, в двоичном случае). С другой стороны, сильный ученик (SL) способен (учитывая достаточное количество обучающих данных) давать классификаторы с произвольно малой вероятностью ошибки.
Ансамбль (или комитет) классификаторов - это классификатор, построенный на некой комбинации слабых учеников. Стратегия повышения и ансамбли классификаторов, состоит в том, чтобы обучить много слабых классификаторов и каким-то образом объединить их, вместо того, чтобы пытаться получить один сильный классификатор.
Пусть \(H_m: \mathfrak{X} \to \{−1, + 1\}\) \(m\)-й слабый двоичный классификатор (для \(m = 1, ..., M\)), и \(x \in \mathfrak{X}\) некоторый входной шаблон для классификации. Существует много способов объединить \(\{H_m\}_{m=1}^M\) в единый прогноз класса. Например, предполагая, что классификаторы ошибаются независимо друг от друга, комбинация большинства голосов должна давать более низкую вероятность ошибки, чем любой из отдельных классификаторов. Если взять взвешенную линейную комбинацию выходов слабых классификаторов, то функция прогнозирования ансамбля \(H: \mathfrak{X} \to \{−1, + 1\}\) задается следующим образом \begin{equation}\label{1} H(x)=\textrm{sign} \left(\sum_{m=1}^M\alpha_m H_m(x)\right), \end{equation} где \(\alpha_1,...,\alpha_M\) - набор весов (использование простого большинства голосов получается, если все веса равны между собой).
По сути, бустинг (повышение) состоит в многократном использовании слабых алгоритмов обучения на разно взвешенных версиях обучающих данных. Вес каждого метода на каждом раунде алгоритма зависит от точности предыдущих классификаторов, что позволяет алгоритму сосредоточить свои внимание на те примеры, которые все еще неправильно классифицированы.

Интерес к бустингу порожден алгоритмом AdaBoost (адаптивное повышение), предложенным в работах Фрейнда и Шапире (Freund,Schapire).
Данный раздел написан по мотивам книги "Ensemble Machine Learning".

Вспомогательная информация.

Bootstrapping и Bagging.

Слово bootstrap (самовытягивание) происходит от выражения: «To pull oneself over a fence by one’s bootstraps» (дословно — «перебраться через ограду, потянув за ремешки на ботинках». В вольном переводе -"сделать из дерьма конфетку (получить из ничего - что-то)."
Это статистический метод общего назначения на основе выборок нескольких (непересекающихся) обучающих наборов, полученных случайным образом, из одного базового набора данных. В наборе данных с N выборками, каждый экземпляр выбран с вероятностью 1 / N, следовательно, после N розыгрышей (с большим N), вероятность того, что данный экземпляр не был выбран \[ \left(1-\frac{1}{N}\right)^N\approx \exp(-1)\approx 0.368. \] Это означает, что каждый образец содержится примерно в 63,2% случаев наборов.

Классически, bootstrap используется для получения некоторой статистики T (P) о (скажем, бесконечно большой) совокупности P из N выборок из: \(Z = \{z_1, ..., z_N\}\). Идея чтобы получить B множеств \(Z^*_b\subseteq Z\), для \( b = 1, ..., B\), каждая из которых содержит N случайных выборок из Z, из которого получены оценки B (P). Эти оценки затем усредняются в окончательную оценку; также возможно получить оценки дисперсии или доверительные интервалы.

Алгоритм Bootstrap

Ввод. Исходные данные: выборка размером N: \(Z = \{z_1, z_2, ..., z_N\}\) (потенциально бесконечной) совокупности P. B - номер бутстрап выборки.
Вывод: Оценка T (P) статистики P.

for b=1 do
- Выбрать (с заменой) N наборов из Z, получив b-й бутстрап \(Z^*_b\).
- Вычислить для каждой выборки \(Z^*_b\) статистику \(\hat{T}(Z^*_b).\)
end for
Вычислить начальную оценку \(\hat{T} (P)\) как среднее значение \(\hat{T}(Z^*_1),\hat{T}(Z^*_2),...,\hat{T}(Z^*_B)\).
Вычислить точность оценки, используя, например, дисперсию \(\hat{T}(Z^*_1),\hat{T}(Z^*_2),...,\hat{T}(Z^*_B).\)

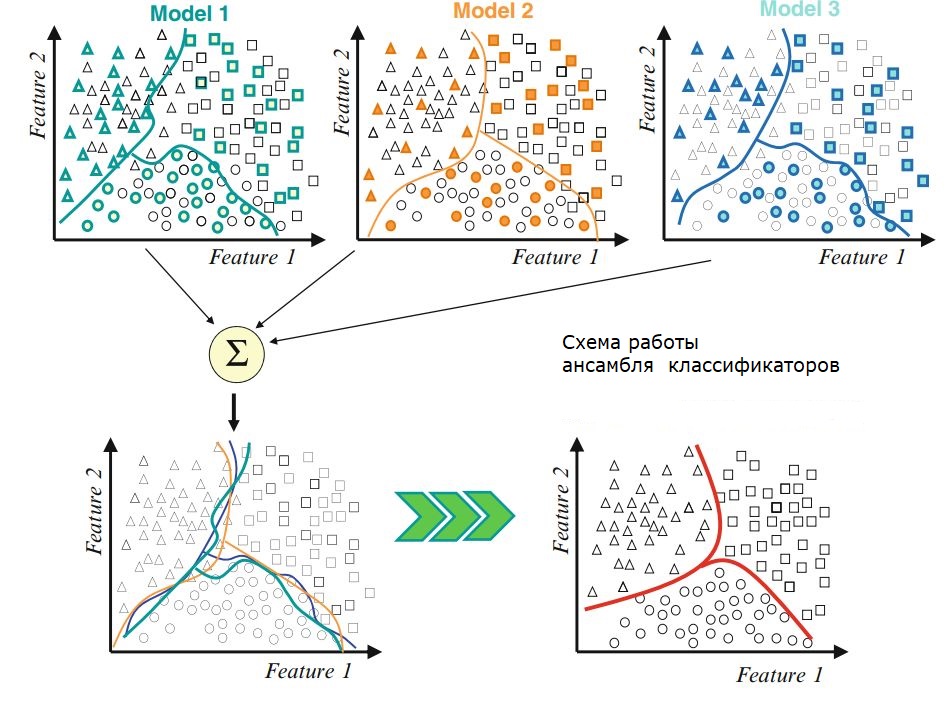
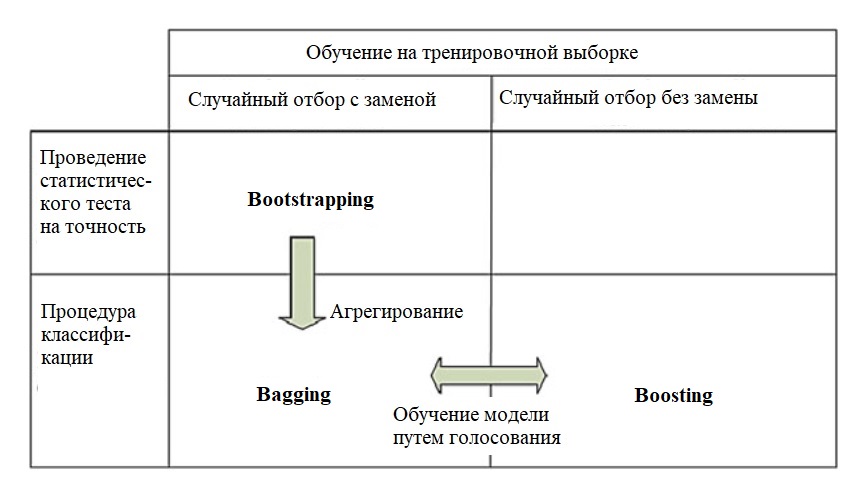
Bagging (агрегация бутстрэп) - это метод, который использует усреднение выборки для уменьшения дисперсии и / или повышения точности некоторых алгоритмов (может использоваться в классификации и регрессии).
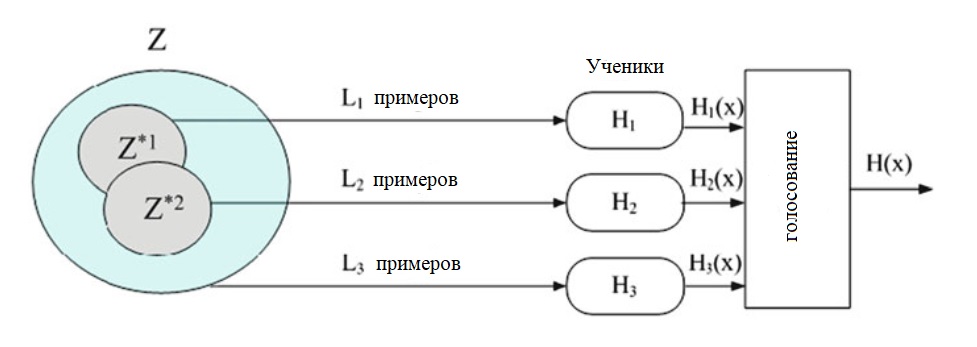
Рассмотрим набор данных размера N: \(Z = \{z_1, z_1, ..., z_N\}\), где \(z_i = (x_i, y_i)\), и \(y_i\) - метка класса в задаче классификации или действительное число, в задаче регрессии. Цель bagging в получении набора В предикторов (каждый из bootstrap выборки \(Z^*_b\subseteq Z\), для \( b = 1, ..., B\)) а затем создать окончательный предиктор путем объединения (путем усреднения, в регрессии или большинство голосов, в классификации).
По сравнению с полным обучающим набором, у агрегации есть два основных преимущества:

повышает стабильность и точность классификатора;
уменьшает дисперсию классификатора.

Использование агрегации улучшает результаты классификации всякий раз, когда базовые классификаторы нестабильны, и это является основной причиной, по которой этот подход хорошо работает для классификации.

Процедура Bagging для задачи бинарной классификации.

Ввод. Исходные данные: выборка размером N: \(Z = \{z_1, z_2, ..., z_N\}\), где \(z_i = (x_i, y_i)\), \(x_i\in \mathfrak{X}\) и \(y_i\in \{-1,+1\}\), B - номер бутстрап выборки.
Вывод: Полученный классификатор \(H:\mathfrak{X}\to \{-1,+1\}\).

for b=1 do
- Выбрать (с заменой) N наборов из Z, получив b-й бутстрап \(Z^*_b\).
- Вычислить для каждой выборки \(Z^*_b\) обучить классификатор \(H_b\).
end for
Найти окончательный классификатор большинством голосов из \(H_1,...,H_B\), то есть \(H(x)=\textrm{sign} \left(\sum_{b=1}^BH_b(x)\right).\)

Окончательное решение о классификации производится на выходе большинством голосов слабых учеников.

Сильные и слабые ученики

Слабое и сильное обучение являются фундаментальными понятиями в основе усиления алгоритмов, поэтому кратко рассмотрим их формальные определения.
Рассмотрим правило классификации \(f: \mathfrak{X}\to \{−1, + 1\}\), такое, что \(f \in F\), где \(F\) - некоторый класс функций из \(\mathfrak{X} \to \{-1, + 1\}\). Рассмотрим также набор пар \(\{(x_i, y_i), i = 1, ..., N\}\), такой что \(y_i = f (x_i)\) и \(x_i\) являются выборками некоторого распределения \(P\).
Сильный ученик, учитывая достаточное число данных, способен реализовать произвольно хороший классификатор с высокой вероятностью, то есть для каждого \(P, f \in F,\) ε ≥0 и δ ≤ 1/2, он выводит с вероятностью не менее 1 −δ классификатор \(h:\mathfrak{X} \to \{−1, + 1\}\), удовлетворяющий условию \(\mathbb{P}_P [h (x) \ne f (x)] ≤ ε\) с полиномивльной сложностью по времени.
Слабый ученик определяется так же, как сильный, но с более слабыми условиями по ε и δ. Для конкретной пары (а не для всех) \(\varepsilon_0 \ge 0\) и \(\delta_0 \le 1/2\), слабый ученик реализует, с вероятностью не меньше чем 1 −δ, классификатор \(h: \mathfrak{X} \to \{-1, + 1\}\), удовлетворяющий условию \(\mathbb{P}_P [h (x) \ne f (x)] \le \varepsilon_0\).
В основе идеи бустинга лежит доказанный Шапире факт, что сильного ученика возможно получить путем объединения слабых учеников.

В качестве иллюстрации приведем простой пример бустинга линейной регрессии для множества \((x_i,y_i) i=1,...,N\).

Инициализация весов \(\omega^{(1)}_i=1/N,i\in\{1,...,N\}\) и \(m=1.\)
while \(m\le M\) do
- Используя веса \(\omega_i^{(1)}\), методом наименьших квадратов построим линейную регрессию и найдем приближенные значения \(\tilde{y}_i^{(m)}=a^{(m)}+b^{(m)}x_i\).
- Для каждого \(i = 1, ..., N\) обновим вес \(\nu^{(m)}_i=(y_i-\tilde{y}_i^{(m)})\).
- Перенормируем веса, для чего вычислим \(S_m=\sum_{j=1}^N\nu^{(m)}_j\) и для \(i = 1, ..., N, \omega^{(m+1)}_i=\frac{\nu^{(m)}_i}{S_m} \)
- Увеличим счетчик итераций: \(m:= m + 1\).
end while
В результате получаем прогноз \[ Y_i=\frac{\sum_{m=1}^M\omega_i^{(m)}(x_i)\tilde{y}^{(m)}_i}{\sum_{m=1}^M\omega_i^{(m)}}. \]

Алгоритмы бустинга

Вначале приведем классический алгоритм Шапире.

Процедура Boosting для задачи классификации.

Ввод. Исходные данные: выборка размером N: \(Z = \{z_1, z_2, ..., z_N\}\), где \(z_i = (x_i, y_i)\), \(x_i\in \mathfrak{X}\) и \(y_i\in \{-1,+1\}\).
Вывод: Классификатор \(H:\mathfrak{X}\to \{-1,+1\}\).

Произвольно выбрать без замены \(L_1 \lt N\) выборок из \(Z\) и получить \(Z^*_1\).
Используя слабого ученика для \(Z^*_1\), получим классификатор \(H_1\).
Выберем \(L_2 \lt N\) выборок из \(Z\), для половины выборок, неправильно классифицированных по \(H_1\), чтобы получить \(Z^*_2\).
Используя слабого ученика из \(Z^*_2\), получим классификатор \(H_2\).
Выберем все образцы из \(Z\), на которых \(H_1\) и \(H_2\) не совпадают, получая \(Z^*_3\).
Используя слабого ученика на \(Z^*_3\), получим классификатор \(H_3\).
И, наконец, получим окончательный классификатор большинством голосов: \(H(x)=\textrm{sign} \left(\sum_{b=1}^3H_b(x)\right).\)

Как видно из алгоритма Шапире, обучающий набор случайным образом делится без замены на три множества, \(Z^*_1,Z^*_2,Z^*_3\). Если при определении принадлежности элемента, первые два классификатора (\(H_1\) и \(H_2\)) согласны с меткой класса, то это окончательное решение. Множество примеров, по которым они не согласны, определяет разбиение \(Z^*_3\), 3 который используется для изучения \(H_3\). Шапире показал, что этот метод обучения позволяет построить сильный классификатор. В дальнейшем, опираясь на идеи Шапире Фрейнд предложил новый алгоритм, который значительно эффективней первоначального.

Связь между бустингом, бэггингом и бутстрепом

Алгоритм AdaBoost

После того, как каждый из авторов (Фрейнд и Шапире) предложил свою идею усиления ансамблей алгоритмов классификации (бустинг), в 1996 году появилась их совместная работа, посвященная адапивному алгоритму бустинга - AdaBoost. Ключевая идея AdaBoost состоит в использовании взвешенных версий тех же данных вместо их случайных подвыборок. Один и тот же обучающий (тренировочный) набор многократно используется, то есть этот набор может быть очень большим, как требовалось более ранними методами повышения.

Алгоритм AdaBoost для бинарной классификации

Ввод. Исходные данные: выборка размером N: \(Z = \{z_1, z_2, ..., z_N\}\), где \(z_i = (x_i, y_i)\), \(x_i\in \mathfrak{X}\) и \(y_i\in \{-1,+1\}\), М - максимальное количество классификаторов.
Вывод: Классификатор \(H:\mathfrak{X}\to \{-1,+1\}\).

Инициализация весов \(\omega^{(1)}_i=1/N,i\in\{1,...,N\}\) и \(m=1.\)
while \(m\le M\) do
- Применяя слабый классификатор к множеству \(Z\) и используя веса \(\omega^{(m)}_i\), получем классификатор \(H_m:\mathfrak{X}\to \{-1,+1\}\).
- Вычислим взвешенную ошибку данного классификатора \(\varepsilon_m =\sum_{i=1}^N\omega^{(m)}_ih(-y_iH_m(x_i))\).
- Найдем вес слабого классификатора \(\alpha_m=\frac{1}{2}\log\frac{1-\varepsilon_m}{\varepsilon_m}\).
- Для каждого \(i = 1, ..., N\) обновим вес \(\nu^{(m)}_i=\omega^{(m)}_i\exp\left(-\alpha_my_iH_m(x_i)\right)\).
- Перенормируем веса, для чего вычислим \(S_m=\sum_{j=1}^N\nu^{(m)}_j\) и для \(i = 1, ..., N, \omega^{(m+1)}_i=\frac{\nu^{(m)}_i}{S_m} \)
- Увеличим счетчик итераций: \(m:= m + 1\).
end while
Результирующий классификатор: \(H(x)=\mathrm{sign}\left(\sum_{j=1}^M\alpha_jH_j(x)\right)\).

Функция \(h: R \to \{0, 1\}\), назывется ступенькой Хевисайда и определяется следующим образом \[ h(x)=\left\{ \begin{array}{ll} 1, & \hbox{ если }x\ge 0 \\ 0, & \hbox{ если }x\lt 0. \end{array} \right. \] Следовательно, так как и \(y_i,\) и \(H_m(x_i)\) принимают значения из {−1, + 1}, имеем \(h (−y_i H_m (x_i)) = 1\), если \(y_i\ne H_m(x_i)\) и \(h (−y_i H_m (x_i)) = 0\) в случае \(y_i= H_m(x_i)\), соответственно, \(\varepsilon_m\) представляет собой взвешенную ошибку \(m\)-го классификатора.
По сути, AdaBoost является жадным алгоритмом, который создает «сильный классификатор», путем оптимизации весов и добавления одного слабого классификатора за раз.

Простая иллюстрация работы AdaBoost.

Иллюстрация шагов алгоритма AdaBoost

Шаг 1. На первом шаге присвоили равные веса каждой точке данных и применили линейный классификатор, с целью разделения их на множества точек с "плюсами" и, соответственно, с "минусами". Первый классфикатор (D1) сгенерировал вертикальную линию с левой стороны, разделяя точки данных. Как видим, эта вертикальная линия неправильно предсказала три значения "+" (плюс).

В таком случае назначим более высокие веса этим трем точкам "+" (плюс) и применим другой классификатор. На приведенной иллюстрации это соотносится с размером соответствующей точки, то есть, размер трех неправильно предсказанных точек "+" (плюс) больше по сравнению с остальными точками данных.
Шаг 2. Второй классификатор (D2) попытается предсказать эти точки правильно. Теперь вертикальная линия (D2) с правой стороны поля правильно классифицировала три то этого неправильно классифицированных точки "+" (плюс).

Но опять же, это вызвало ошибки полученной классификации. На этот раз это три точки "-" (минус). Опять же, назначим более высокий вес на эти три "-" (минус) и применим еще один классификатор.
Шаг 3. Третий классификатор (D3) применяется для правильного прогнозирования этих ошибочно классифицированных наблюдений. На этот раз горизонтальная линия генерируется для классификации "+" (плюс) и "-" (минус) на основе более высокого веса неправильно классифицированных наблюдений.

Шаг 4. Теперь, когда процесс разделения классов прошел успешно, остается объединить методы D1, D2 и D3, чтобы сформировать сильный прогноз, имеющий более сложное правило по сравнению с каждым индивидуальным слабым классификатором (учеником).

Почему это работает?

AdaBoost можно рассматривать как жадную оптимизацию. Определим \[ \mathcal{H}(x)=\sum_{j=1}^M\alpha_jH_j(x) \] и перепишем классификатор как \(H(x)=\mathrm{sign}\left(\mathcal{H}(x)\right)\). Затем можно просмотреть AdaBoost как оптимизацию экспоненциальной ошибки: \[ \varepsilon_{\exp}(x,y)=\exp(-y\mathcal{H}(x)) \] так что целевая функция обучения, учитывая тренировочные данные \(\left\{(x_i,y_i)\right\}_{i=1}^N\), равна \[ \varepsilon(x,y)=\sum_{i=1}^N\exp\left(-y_i\sum_{j=1}^M\alpha_jH_j(x)\right) \] которая должна быть минимизирована по отношению к весам α и параметрам слабых классификаторов.
Процесс оптимизации является жадным и последовательным: мы добавляем один слабый классификатор за раз, выбирая α оптимальным по отношению к \(\varepsilon\) , а затем не меняем его снова.
Для того, чтобы свести к минимуму общее количество ошибок классификации, рассмотрим функцию штрафов, которая называется функцией 0-1 потерь: \[ \varepsilon_{0-1}(x,y)= \left\{ \begin{array}{ll} 0, & \hbox{ если }y\mathcal{H}(x)\lt 0 \\ 1, & \hbox{ иначе. } \end{array} \right. \] Заметим, что \(y\mathcal{H}(x)\gt 0\) совпадает с тем, что \(y\) и \(\mathcal{H}(x)\) имеют один и тот же знак. Функция \(\varepsilon_{0-1}\) говорит, что мы платим штраф в 1, если неправильно классифицируем элемент и штраф в ноль, если классифицируем его правильно.
Тогда \(\varepsilon_{\exp} (x,y)\ge \varepsilon_{0-1}(x,y)\). Следовательно, если экспоненциальная ошибка стремится к нулю, то потеря 0-1 будет равна нулю, и все точки правильно классифицированы.
Рассмотрим слабый классификатор \(H_m\), то есть классификатор, используемый на шаге m. Выделим из целевой функции вклад этого классификатора: \[ \varepsilon_m=\sum_{i=1}^N\exp\left(-y_i\sum_{j=1}^{m-1}\alpha_jH_j(x)-y_i\alpha_mH_m(x)\right)= \sum_{i=1}^N\exp\left(-y_i\sum_{j=1}^{m-1}\alpha_jH_j(x)\right)\exp\left(-y_i\alpha_mH_m(x)\right). \] Поскольку мы сохраняем постоянные первые \(m – 1\) членов, можем заменить их одной константой \[ \omega^{(m)}_i=\sum_{i=1}^N\exp\left(-y_i\sum_{j=1}^{m-1}\alpha_jH_j(x)\right). \] Заметим, что это те же весовые коэффициенты, вычисленные рекурсией AdaBoost, то есть \[ \omega^{(m)}_i\varpropto \omega^{(m)}_i\exp\left(-y_i\alpha_{m-1}H_{m-1}(x_i).\right) \] (Существует постоянная пропорциональности, которая может быть игнорирована). Следовательно, мы имеем \[ \varepsilon_m=\sum_{i=1}^N\omega^{(m)}_i\exp\left(-y_i\alpha_{m}H_{m}(x_i).\right) \] Мы можем разбить это на два слагаемых, один для данных, правильно классифицированных по \(H_m\), и один для тех неправильно классифицирован: \[ \varepsilon_m=\sum\left\{\left.\omega^{(m)}_i\exp (-\alpha_m)\right|i:H_m(x_i)=y_i\right\}+ \sum\left\{\left.\omega^{(m)}_i\exp (\alpha_m)\right|i:H_m(x_i)\ne y_i\right\}. \] Перегруппируя, получаем \[ \varepsilon_m=\left(\exp(\alpha_m)-\exp(-\alpha_m)\right)\sum_i\omega^{(m)}_i\mathrm{sign}(|H_m(x_i)-y_i|)+\exp(-\alpha_m)\sum_i\omega^{(m)}_i. \] Оптимизация полученного соотношения по отношению к \(H_m\) эквивалентна оптимизации \[ \sum_i\omega^{(m)}_i\mathrm{sign}(|H_m(x_i)-y_i|), \] что и делает AdaBoost. Оптимальное значение для \(\alpha_m\) можно получить, решая \[ \frac{d\varepsilon_m}{d\alpha_m}= \alpha_m\left(\exp(\alpha_m)+\exp(-\alpha_m)\right)\sum_i\omega^{(m)}_i\mathrm{sign}(|H_m(x_i)-y_i|)-\alpha_m\exp(-\alpha_m)\sum_i\omega^{(m)}_i =0. \] Разделив обе части на \(\alpha_n\left(\sum_i\omega^{(m)}_i\right)^{-1}\), имеем цепочку соотношений \[ 0=\varepsilon_m\exp(\alpha_m)+\varepsilon_m\exp(-\alpha_m)-\exp(-\alpha_m), \] \[ \varepsilon_m\exp(\alpha_m)=(1-\varepsilon_m)\exp(-\alpha_m), \] \[ \ln \varepsilon_m+\alpha_m=-\alpha_m+\ln(1-\varepsilon_m), \] \[ \alpha_m=\frac{1}{2}\ln\frac{1-\varepsilon_m}{\varepsilon_m}. \] Проблемы. Экспоненциальная потеря не очень хорошая функция потерь. Например, если непосредственно оптимизируем в классификаторе экспоненциальную потерю по всем переменным (например, градиентным спуском), мы часто получаем ужасную производительность.
Можно было бы ожидать, что, когда AdaBoost достигнет нулевой ошибки, то для переобучения можно добавлять любые новые слабые классификаторы. На практике часто происходит обратное: продолжение добавления слабых классификаторов фактически увеличивает размер поля классификации.

Варианты AdaBoost

Появление алгоритма AdaBoost стимулировало значительное количество исследований по этому типу обучения. Рассмотрим некоторые результаты, полученные в этом направлении.
Real AdaBoost - алгоритм, в котором используются классификаторы, работающие со значениями из действительной оси (устанавливающие значения порога). Это реальное значение может рассматриваться как вероятность или степень уверенности, что данный входной шаблон принадлежит классу, учитывая текущее распределение веса.

Real AdaBoost

Инициализация весов \(\omega^{(1)}_i=1/N,i\in\{1,...,N\}\) и \(m=1.\)
while \(m\le M\) do
- Используя веса \(\omega_i^{(1)}\), найдем оценку вероятности принадлежности к классу \(p_m(x)=P_\omega(y=1|x)\).
- Установим \(H_m=\frac{1}{2}\log\left(p_m(x)/(1-p_m(x))\right)\in \mathbb{R}\).
- Для каждого \(i = 1, ..., N\) обновим вес \(\nu^{(m)}_i=\omega^{(m)}_i\exp\left(-y_iH_m(x_i)\right)\).
- Перенормируем веса, для чего вычислим \(S_m=\sum_{j=1}^N\nu^{(m)}_j\) и для \(i = 1, ..., N, \omega^{(m+1)}_i=\frac{\nu^{(m)}_i}{S_m} \)
- Увеличим счетчик итераций: \(m:= m + 1\).
end while
Результирующий классификатор: \(H(x)=\mathrm{sign}\left(\sum_{j=1}^MH_j(x)\right)\).

Logit Boost

Инициализация \(\omega^{(1)}_i=1/N, p(x_i)=\frac{1}{2}, i\in\{1,...,N\}\), \(H(x)=0\) и \(m=1.\)
for \(m=1 \) to \(M\) and while \(H_m\ne 0\) do
- Вычислим \(z_i=\frac{y^*_i-p(x_i)}{p(x_i)(1-p(x_i))}\) и веса \(\omega_i=p(x_i)(1-p(x_i))\), где \(y^*_i=\frac{y_i+1}{2}\in[0,1]\).
- Используя метод наименьших квадратов, построим регрессионную модель (например, линейную регрессию) \(H_m(x)\), приближая множество \(x_i\) значениями \(z_i\) с весами \(\omega^{(m)}_i.\)
- Положим \(H(x)=H(x)+\frac{1}{2}H_m\) и \(p(x)=\frac{\exp(H(x))}{\exp(H(x))+\exp(-H(x))}\).
end for
Результирующий классификатор: \(H(x)=\mathrm{sign}\left(\sum_{j=1}^MH_j(x)\right)\).

Существует много разных алгоритмов бустинга, среди которых, алгоритм Gentle AdaBoost, который является улучшением Real AdaBoost за счет использования шагов Ньютона, обеспечивая тем самым более надежный и стабильный ансамбль, Modest AdaBoost который дает меньшую по сравнению с Real AdaBoost и Gentle AdaBoost, и многие другие.
В заключение приведем примеры алгоритмов бустинга для случая многих классов.

AdaBoost.MH

Ввод. Исходные данные: выборка \(Z = \{z_{i,j}\}\) размером N из \(N\times k\) пар, где \(z_{i,j} = ((x_i,j), y_i)\), \((x_i,j)\in \mathfrak{X}\) и \(y_{i,j}\in \{-1,+1\}\) признак соответствия классу \(j\) при наблюдении \(i\), где \(i=1,...,N\) и \(j=1,...,k\).

Последовательно применяя Real AdaBoost к проекциям исходным данных, получаем функцию \[ H:\mathfrak{X}\times (1,...,k)\to \mathbb{R}, H(x,j)=\sum_mH_m(x,j). \]
Вывод: Классификатор \( \textrm{arg} \max_j H(x,j)\).

Logit Boost (k классов)

Инициализация \(\omega^{(1)}_{i,j}=1/N, p_j(x_i)=\frac{1}{k}, H_j(x)=0, i\in\{1,...,N\}, j\in\{1,...,k\}\) и \(m=1.\)
for \(m=1 \) to \(M\) do
for \(j=1 \) to \(k\) do
- Вычислим \(z_{i,j}=\frac{y^*_{i,j}-p_j(x_i)}{p_j(x_i)(1-p_j(x_i))}\) и веса \(\omega_{i,j}=p_j(x_i)(1-p_j(x_i))\), где \(y^*_{i,j}=\frac{y_{i,j}+1}{2}\in[0,1]\).
- Используя метод наименьших квадратов, построим регрессионную модель (например, линейную регрессию) \(H_{m,j}(x)\), приближая множество \(x_i\) значениями \(z_{i,j}\) с весами \(\omega^{(m)}_{i,j}.\)
- Обновим классификаторы \[ H_{m,j}(x)\leftarrow \frac{k-1}{k}\left(H_{m,j}(x)-\frac{1}{k}\sum_{\nu=1}^kH_{m,\nu}(x)\right), \] \[ H_{j}(x)\leftarrow H_j(x)+H_{m,j}. \]
- Положим \(p_j(x)=\frac{\exp(H_j(x))}{\exp(H_j(x))+\exp(-H_j(x))}\).
end for
Результирующий классификатор: \( \textrm{arg} \max_j H_j(x)\).

Градиентный бустинг

Вначале рассмотрим общую задачу обучения с учителем.
По имеющейся выборке \(\{(x_i,y_i)\}_{i=1}^n\) нужно восстановить зависимость \(y=f(x)\). Решение \(\hat{f}\) будем искать из условия минимизации средней ошибки \[ \varepsilon(f)=\frac{1}{n}\sum_{i=1}^nL(y_i,f(x_i)), \] где \(L(\cdot)\) - функция потерь (например, среднеквадратическая ошибка), тогда \[ \hat{f}=\textrm{arg}\min_{f\in \mathcal{F}}\varepsilon(f), \] здесь \(\mathcal{F}\) некий класс функций, называемый классом модели, что может быть линейными методами, методами локальной регрессии ( k-ближайших соседей, ядерная регрессия и др.), сплайны и пр.
Среди методов решения оптимизационных задач, одними из наиболее популярных являются градиентный спуск и метод Ньютона. Рассмотрим как эти методы можно адаптировать для задачи бустинга.
Рассмотрим ансамбль моделей \[ f(x)=\sum_{m=0}^Mf_m(x), \] которые могут быть представлены как модели адаптивных базисных функций \[ f(x)=\theta_0+\sum_{m=1}^M\theta_m\phi_m(x), \] где \(f_0(x)=\theta_0\), \(f_m(x)=\theta_m\phi_m(x), m=1,...,M\) и \(\phi_m-\) последовательное добавление базисных функций для улучшения соответствия текущей модели. В используемых терминах это множество слабых классификаторов (учеников).
Остается только применить подходящий алгоритм для минимизации ошибки. Вначале для этой цели используем градиентный спуск, то есть, найдем градиент ошибки и используя итерационные оценки \(\theta_m\) будем двигаться вдоль него (заметим, что так как нашей целью является не увеличение, а уменьшение ошибки, то градиент будем брать со знаком минус "-").

Gradient boosting.

Ввод. Исходные данные: \(\mathcal{D}\).
Функция потерь: \(L\).
Число итераций:\(M\).
Характеристика скорости обучения:\(\eta\).

Инициализация \[\hat{f}^{(0)}(x)=\hat{f}_0=\theta_0=\textrm{arg}\min_\theta\sum_{i=1}^nL(y_i,\theta).\]
for \(m=1 \) to \(M\) do
Вычислим \[ \hat{g}_m(x_i)=\left[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}\right]_{f(x)=\hat{f}^{(m-1)}(x)}, \] \[ \hat{\phi}_m=\textrm{arg}\min_{\phi\in\Phi,\beta}\sum_{i=1}^n\left[(-\hat{g}_m(x_i))-\beta\phi(x_i)\right]^2, \] \[ \hat{\rho}_m=\textrm{arg}\min_{\rho}\sum_{i=1}^nL\left(y_i,\hat{f}^{(m-1)}(x_i)+\rho\hat{\phi}_m(x_i)\right), \] \[ \hat{f}_m(x)=\eta\hat{\rho}_m\hat{\phi}_m(x), \] \[ \hat{f}^{(m)}(x)=\hat{f}^{(m-1)}(x)+\hat{f}_{m}(x). \]
end for
Результирующий классификатор: \( \hat{f}(x)=\hat{f}^{(M)}(x)=\sum_{m=0}^M\hat{f}_m(x)\).

Здесь \(\hat{g}_m(x_i)-\) отрицательный градиент,
\(\hat{\phi}_m\) слабый классификатор,
\(\hat{\rho}_m-\) длина шага градиентного спуска.

Newton boosting.

Инициализация \[\hat{f}^{(0)}(x)=\hat{f}_0=\theta_0=\textrm{arg}\min_\theta\sum_{i=1}^nL(y_i,\theta).\]
for \(m=1 \) to \(M\) do
Вычислим \[ \hat{g}_m(x_i)=\left[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}\right]_{f(x)=\hat{f}^{(m-1)}(x)}, \] \[ \hat{h}(x_i)=\left[\frac{\partial^2 L(y_i,f(x_i))}{\partial f(x_i)^2}\right]_{f(x)=\hat{f}^{(m-1)}(x)}, \] \[ \hat{\phi}_m=\textrm{arg}\min_{\phi\in\Phi}\sum_{i=1}^n\frac{1}{2}\hat{h}_m(x_i)\left[\left(-\frac{\hat{g}_m(x_i)}{\hat{h}_m(x_i)}\right)-\phi(x_i)\right]^2, \] \[ \hat{f}_m(x)=\eta\hat{\phi}_m(x), \] \[ \hat{f}^{(m)}(x)=\hat{f}^{(m-1)}(x)+\hat{f}_{m}(x). \] Здесь \(\hat{h}_m\) эмпирический гессиан.
end for
Результирующий классификатор: \( \hat{f}(x)=\hat{f}^{(M)}(x)=\sum_{m=0}^M\hat{f}_m(x)\).

Здесь \(\hat{g}_m(x_i)-\) отрицательный градиент,

Характеристика обучения \(\eta\) имеет тенденцию изменять скорость сходимости.

Boosted Trees.

Одним из наиболее популярных сфер использования бустинга является его применение для построения деревьев. Вот, например, простая иллюстрация этого подхода.