Scale Invariant Feature Transform - SIFT.

Розділ є вільним перекладом статті Rey-Otero, Ives and Mauricio Delbracio. Anatomy of the SIFT Method./ IPOL Journal.— 4 (2013) .— P.370-396.

Метою перетворення просторово-інваріантних ознак SIFT є отримання набору дескрипторів з зображення таких, що  витягнуті дескриптори інваріантні до зсуву, повороту і масштабування зображення (зміни масштабу).  Дескриптори SIFT також виявилися стійкими до широкого сімейства перетворень зображення, таких як невеликі зміни точки огляду, шум, розмиття, зміна контрасту,  деформація сцени, залишаючись при цьому досить стійкими для зіставлення.  

Алгоритм SIFT складається з двох послідовних і незалежних операцій: виявлення точок інтересу (тобто ключових точок) і витяг дескриптора, пов'язаного з кожною з них.
Оскільки ці дескриптори стійкі, їх можна використовувати для вирішення широкого класу задач, таких як, зіставлення пар зображень, розпізнавання об'єктів, стабілізація відео і багато інших.
Ідея алгоритму. SIFT виявляє серію ключових точок з багаторівневого представлення зображення. Це багатомасштабне уявлення складається із сімейства все більш розмитих зображень. Кожна ключова точка являє собою блокову структуру з центром (x, y) і характеристикою масштабу σ. Далі SIFT обчислює домінуючу орієнтацію θ над регіоном, оточуючим кожну з цих ключових точок. Для кожної ключової точки четвірка величин (x, y, σ, θ) визначає центр, розмір і орієнтацію нормалізованої латки, в якій обчислюється дескриптор SIFT. В результаті нормалізації дескриптори ключових точок SIFT не залежать від зсуву, повороту і зміни масштабу. Дескриптор кодує розподіл просторового градієнта навколо ключової точки 128-вимірним вектором.
В подальшому цей вектор ознак зазвичай використовується для зіставлення ключових точок, витягнутих з різних зображень.
Алгоритмічний ланцюжок. Щоб досягти масштабної інваріантності, SIFT побудований на Гаусівському масштабному просторі, тобто, маємо зображення в декількох масштабах, що імітує сімейство всеяких зменшень зображення за допомогою все більш розмитих версій вхідного зображення. Для цієї мети використовується згортка вхідних даних з функцією Гауса, що діє як апроксимація оптичного розмиття. Таким чином, Гаусів масштабний простір можна інтерпретувати як сімейство зображень, кожне з яких відповідає різному коефіцієнту масштабування.
Щоб досягти незалежності від зсуву, повороту при масштабної інваріантності, витягнуті ключові точки повинні бути пов'язані зі структурами, які однозначно розташовані, як в масштабі, так і безпосередньо на площині зображення. При цьому алгоритм виключає кути і краї зображення, оскільки вони не можуть бути точно локалізовані як в масштабі, так і в просторі.
Виявлення і визначення місця розташування ключових точок полягає в обчисленні тривимірних екстремумів диференціального оператора, застосованого до масштабуючого простору. Диференціальний оператор, який використовується в алгоритмі SIFT, являє собою різницю Гаусіанів (DoG - difference of Gaussians).
Виділення тривимірних безперервних екстремумів складається з двох етапів:
по-перше, уявлення DoG сканується на наявність тривимірних дискретних екстремумів. Це дає перше грубе розташування екстремумів, яке потім уточнюється з використанням локальної квадратичної моделі. Оскільки існує багато явищ, які можуть привести до появи нестабільних ключових точок, SIFT включає в себе каскад тестів для відкидання менш надійних точок. Залишаються тільки ті, які точно розташовані і досить контрастні.
Для цього розглядаються два різних кроки відкидання: відхилення 3d-екстремумів з малим значенням DoG і відхилення ключових точок, що лежать на ребрах.
SIFT-інваріантність до обертання виходить шляхом присвоєння кожній ключовій точці еталонної орієнтації. Ця характеристика обчислюється з орієнтації градієнта по околиці ключової точки. Нарешті, просторовий розподіл градієнта всередині орієнтованої латки кодується для створення дескриптора ключової точки SIFT. Це завершує алгоритмічний ланцюжок, який визначає алгоритм SIFT.

Тепер докладніше.

Гаусовий масштабний простір

Гаусове масштабне представлення - сімейство все більш розмитих зображень. Це розмивання імітує втрату деталізації, що виникає при фотографуванні.  Отже, SIFT може бути інтерпретований як симуляція набору знімків даної сцени, зроблених з різних відстаней.  

 Введемо визначення, необхідні у подальшому.  

Розмиття за Гаусом.

Розглянемо безперервний графічний образ u ( x ), визначений для кожного x = (x, y) ∈ R 2 . Гаусове згладжування визначається як згортка \[ G_ \sigma u (\mathbf {x}) = \int {G_ \sigma (\mathbf {x} ') u (\mathbf {x} - \mathbf{x}') d \mathbf{x} ',} \] де \[ G_ \sigma (\mathbf {x}) = \frac {1} {2 \pi \sigma ^ 2} e ^ {- \frac {| \mathbf{x} | ^ 2} {2 \sigma ^ 2}} \] - ядро ​​Гауса, параметризоване його стандартним відхиленням σ ∈ R + .
Гаусів оператор згладжування задовольняє напівгруповому співвідношенню, \begin{equation} \label {1} G _ {\sigma_2} (G _ {\sigma_1} u) (\mathbf {x}) = G_ \sqrt {\sigma_1 ^ 2 + \sigma_2 ^ 2} u (\mathbf {x}). \end{equation} Будемо називати Гаусівим масштабним простором u тривимірне (3d) відображення \begin{equation} \label {2} v: (\sigma, \mathbf{x}) \to G_ \sigma u (\mathbf {x}). \end{equation} У разі цифрових зображень Гаусіве згладжування реалізовано у вигляді дискретної згортки вибірки c усіченим Гаусівим ядром.

Опис етапу SIFT

  1. Знайти Гаусів масштабний простір
    in: u зображення
    out: v масштабуючий простір
  2. Обчислити різницю Гаусіанів (DoG)
    in: v масштабний простір
    out: w DoG
  3. Знайти ключові точки-кандидати (3d дискретні екстремуми DoG)
    in: w DoG
    out: {(x d , y d , σ d )} список дискретних екстремумів (положення і масштаб)
  4. Уточнення розташування точок-кандидатів з точністю до субпікселя
    in: w DoG і {(x d , y d , σ d )} список дискретних екстремумів
    out: {(x, y, σ)} список інтерпольованих екстремумів
  5. Фільтрувати нестабільні ключові точки через шум
    in: w DoG і {(x, y, σ)}
    out: {(x, y, σ)} список відфільтрованих ключових точок
  6. Відфільтрувати нестабільні точки по краях
    in: w DoG и {(x, y, σ)}
    out: {(x, y, σ)} список відфільтрованих ключових точок
  7. Призначити еталонну орієнтацію кожній ключовій точці
    in: (∂mv, ∂nv) градієнт масштабного простору і {(x, y, σ)} список ключових точок
    out: {(x, y, σ, θ)} список відфільтрованих ключових точок
  8. Створення дескрипторів ключових точок
    in: (∂mv, ∂nv) градієнт масштабного простору і {(x, y, σ, θ)} список ключових точок
    out: {(x, y, σ, θ, f)} остаточний список ключових точок

Цифрове згладжування за Гаусом.

Нехай g σ - одновимірне цифрове ядро, отримане урізанням функції Гауса зі стандартним відхиленням σ \begin{equation}\label{3} \mathbf{g}_\sigma(k)=Ke^{-\frac{k^2}{2\sigma^2}}, -[4\sigma]\le k\le [4\sigma],k\in Z, \end{equation} де [ · ] ціла частина, а k встановлюється так, щоб \(\sum \mathbf{g} _ \sigma (k) = 1 \). Нехай G σ позначає цифрову Гаусову згортку параметра σ і u буде цифровим зображенням розміру M × N. Його цифрове Гаусіве згладжування, що позначається G σ u , обчислюється за допомогою сепарабельної двовимірної (2d) дискретної згортки \begin{equation}\label{4} \mathbf{G}_\sigma\mathbf{u}(k,l)=\sum_{k'=-[4\sigma]}^{[4\sigma]}\mathbf{g}_\sigma(k') \sum_{l'=-[4\sigma]}^{[4\sigma]}\mathbf{g}_\sigma(l')\bar{\mathbf{u}}(k-k',l-l'), \end{equation} де \(\bar{\mathbf{u}}\) позначає розширення u до Z 2 за допомогою сімметрізаціі щодо -1/2, а саме \[ \bar{\mathbf{u}} (k, l) = \mathbf{u}(s_M (k), s_N (l)) \] с \(s_M (k) = \min (k\mod 2M, 2M - 1 - k\mod 2M)\).
Для діапазону значень σ, що розглядається в описаному алгоритмі (тобто σ ≥ 0,7), цифровий Гаусів оператор згладжування приблизно задовольняє напівгруповому співвідношенню з похибкою нижче 10 -4 . Застосування послідовно двох цифрових Гаусівих згладжувань з параметрами σ 1 і σ 2 приблизно одно застосування одного цифрового Гаусівого згладжування з параметром \(\sqrt {σ_1 ^ 2 + σ_2 ^ 2} \), \begin{equation} \label {5} \mathbf{G} _ {\sigma_2} (\mathbf {G} _ {\sigma_1} \mathbf{u}) = \mathbf{G} _ {\sqrt {σ_1 ^ 2 + σ_2 ^ 2}} \mathbf{ u}. \end{equation}

Цифровий Гаусів масштабний простір

Як було введено раніше, Гаусівий масштабний простір \(v: (\sigma, \mathbf{x}) \to G_ \sigma u (\mathbf {x}) \) є сімейством розмитих зображень, де значення елемента масштабного простору ( x , σ) співвідноситься з пікселем x у створеному зображенні з розмиванням σ.
Будемо називати цифровим масштабним простором сімейство цифрових зображень щодо дискретного набору рівнів розмиття і різних частот дискретизації, всі вони отримані із вхідного зображення u in з рівнем розмиття σ in . Це сімейство розбите на підмножини зображень із загальною частотою дискретизації. Так як в оригіналі SIFT частота вибірки ітеративно зменшується в два рази, ці підмножини називаються октавами.
Нехай n oct - загальна кількість октав у цифровому масштабному просторі, o ∈ {1, ..., n oct } множина октав і δ o їх міжпіксельна відстань. Будемо вважати, що вхідне зображення u in з міжпіксельною відстанню δ in = 1. Таким чином, міжпіксельна відстань δ = 0,5 відповідає 2-кратному підвищенню частоти дискретизації цього зображення, в той час як підвибірка 2 × призводить до міжпіксельної відстані δ = 2. Нехай n spo дорівнює кількості шкал на октаву (значення за замовчуванням n spo = 3). Кожна октава o містить зображення \(\mathbf {v} ^ o_s \) для s = 1 ,. .., n spo , кожне з яких з різним рівнем розмиття \(σ_s ^ o \). 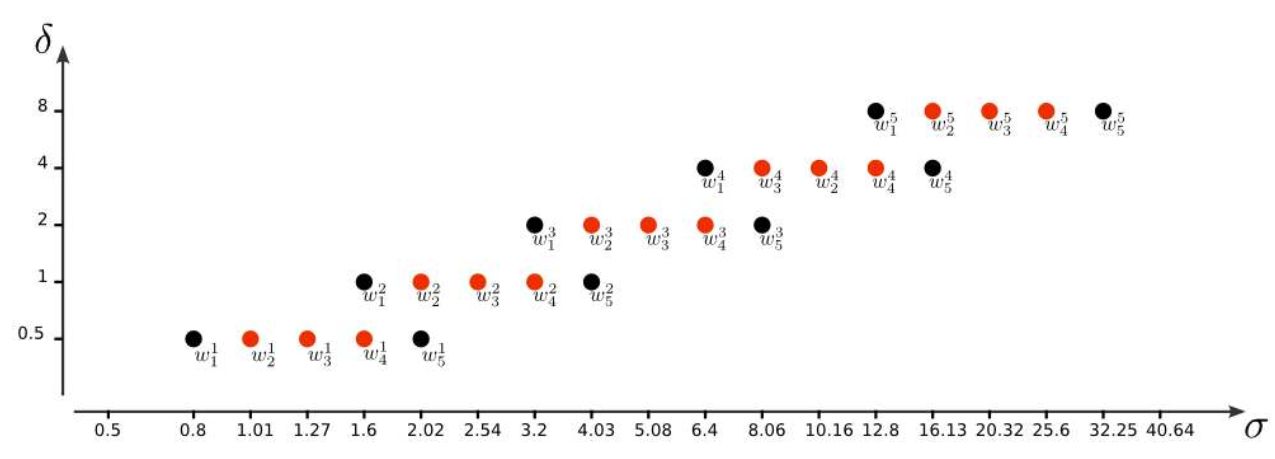В якості одиниці вимірювання рівня розмиття використовується відстань між вибірками вхідного зображення uin (то есть δin = 1). Дана конфігурація показана на рисунку


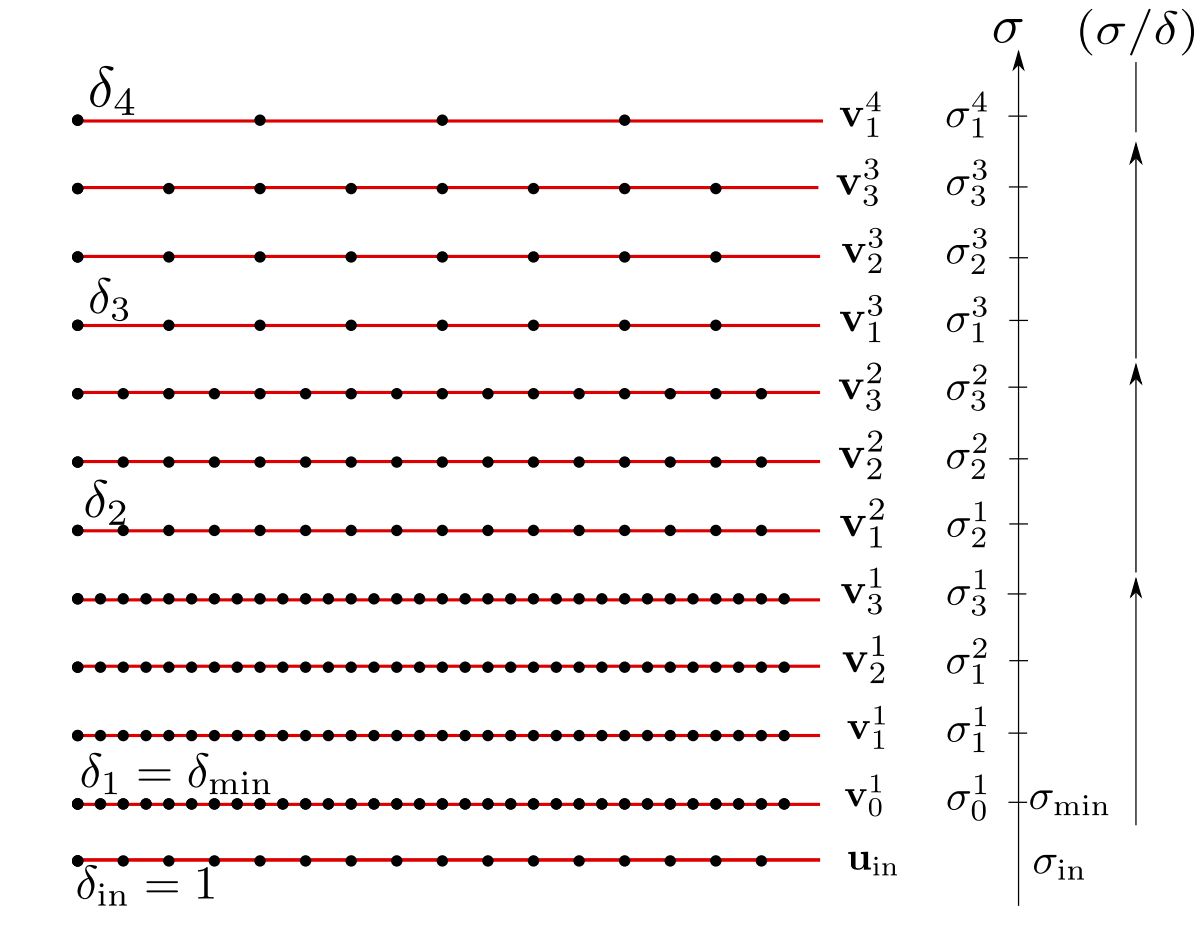Для сітки вибірки цифрового масштабного простору v .
Рівень розмиття розглядається щодо сітки вибірки вхідного зображення.
Параметри встановлюються автоматично, а саме σ min = 0,8, n spo = 3, n oct = 8, σ in = 0,5.

Цифровий масштабний простір також включає три додаткових зображення на октаву, \(\mathbf {v} _ {0} ^ o, \mathbf{v} _ {n_ {spo} +1} ^ o, \mathbf{v} _ {n_ {spo} +2} ^ o \). Обгрунтування цього стане ясним пізніше.
Побудова цифрового масштабного простору починається з обчислення початкового зображення, позначеного \(\mathbf {v} ^ 1_0 \). Це зображення буде мати рівень розмиття \(σ_0 ^ 1 = σ_ \min \), який є мінімальним рівнем розмиття з міжпіксельною відстанню δ 0 = δ min :\begin{equation}\label{6} \mathbf{v}^1_0=\mathbf{G}_{\frac{1}{\delta_\min}\sqrt{\sigma^2_\min-\sigma^2_{in}}}\mathbf{I}_{\delta_\min}\mathbf{u}_{in}. \end{equation} де Iδmin - цифровий білінійний інтерполятор з коефіцієнтом 1/δ min (Алгоритм 1), а G σ - цифрова Гаусіва згортка. Всі цифрові масштабні простори отримано з цього зображення.   Значення за замовчуванням δ min = 0.5 має на увазі початкову 2-кратну інтерполяцію. Рівень розмиття для зображення щодо сітки вибірки   вхідного зображення за замовчуванням встановлений значенням σ min = 0,8.  
Друге і наступні масштабно-просторові зображення s = 1,. .., n spo + 2 в кожній октаві o обчислюються рекурсивно відповідно до \[ \mathbf{v}^o_s=\mathbf{G}_{\rho_{[(s-1)\to s]}}\mathbf{v}^o_{s-1}, \] де \[ ρ _{[(s − 1) → s] }=\frac{σ_\min}{δ_\min}\sqrt{2^{2s/n_{spo}}-2^{2(s-1)/n_{spo}}} . \] Для першого зображення (тобто s = 0) октави o = 2, ..., n o розраховуються як \[ \mathbf{v} ^ o_0 = \mathbf{S} _2 \mathbf{v} ^ {o-1} _ {n_ {spo}}, \] де S 2 - оператор підвибірки з коефіцієнтом 2, ( S 2 u) (m, n) = u (2m, 2n). Ця процедура створює сімейство зображень \((\mathbf {v} _s ^ o), o = 1, ..., n_ {oct} \) і s = 0,. .., n spo + 2, з міжпіксельною відстанню \[ δ_o = δ_ \min 2 ^ {o - 1} \] і уровенем розмиття \[ σ^o_s =\frac{δ_o}{δ_\min} σ_\min 2^{s/n_{spo}}. \] Отже, змодельовані розмиття слідують геометричній прогресії. Таким чином, цифровий масштабний простір визначається п'ятьма параметрами:


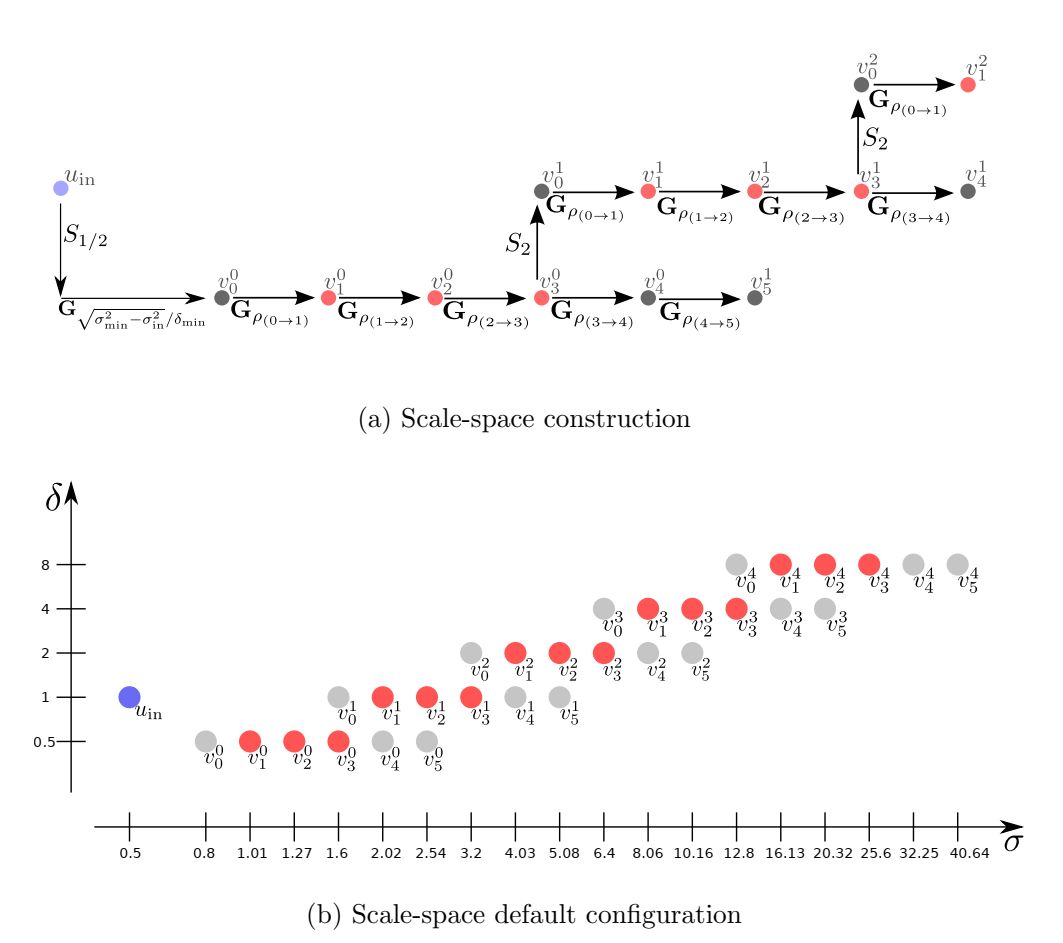Діаграма зображає цифрову масштабно-просторову архітектуру з точки зору частоти дискретизації і рівнів розмиття.
 Кiожна точка символізує масштабне зображення \(\mathbf {v} ^ o_s \), що має міжпіксельну відстань δ o і розмиття рівня \(\mathbf {\sigma} ^ o_s \).

Конфігурація проводиться зі значень параметрів за замовчуванням: σ min = 0,8, δ min = 0,5, n spo = 3 і σ in = 0,5. Кількість октав обмежена кількістю можливих підвибірок. На малюнку показаний приклад цифрового масштабного простору зображення, створеного із заданою конфігурацією.


Параметри масштабного простору встановлені на
n spo = 3, σ min = 0,8 і передбачуваний рівень розмиття вхідного зображення σ in = 0,5.

Визначення ключової точки

Точне виявлення характерних особливостей зображення є складним завданням. Ключові особливості в SIFT визначаються як екстремуми нормованого Лапласіана масштабного простору σ 2 Δv. Лапласіан екстремуму однозначно характеризується своїми масштабно-просторовими координатами (σ, x ), де x відноситься до просторового положення його центру, а σ відноситься до його розміру (масштабу). Коваріація екстремуму (σ, x ) забезпечує інваріантність до зрушення і масштаба асоційованого з ним дескриптора.
Замість обчислення Лапласіану масштабного простору зображення, SIFT використовує різницю Гаусіанів - оператор (DoG). Нехай v Гаусів масштабний простір і k> 1. Різниця Гаусіанів (DoG) відносно k визначається виразом w : (σ, x ) → v (kσ, x ) - v (σ, x ).
Оператор DoG використовує зв'язок між Гаусівським ядром і рівнянням теплопровідності для наближеного обчислення нормованого Лапласіану σ 2 Δv. Насправді, з набору отриманих латок, які йдуть з геометричною прогресією зі знаменником k, рівняння теплопровідності апроксимується наступним чином \[ σ∆v = \frac{∂v}{∂σ} ≈\frac{v (κσ, \mathbf{x}) - v (σ, \mathbf{x})}{κσ - σ}=\frac{w (σ, \mathbf{x})}{(κ - 1) σ}. \] Звідси маємо, \(w (σ, \mathbf{x}) ≈ (κ - 1) σ^2∆v (σ, \mathbf{x})\).
Точки SIFT на зображенні визначаються як тривимірні екстремуми різниці Гаусіанів (DoG). Оскільки ми маємо справу з цифровими зображеннями, безперервні тривимірні екстремуми DoG не можуть бути безпосередньо обчислені. Таким чином, спочатку виявляються дискретні екстремуми цифрового DoG, а потім їх положення уточнюються. Виявлені точки у кінцевому підсумку перевіряються, щоб відкинути можливі нестабільні і помилкові виявлення через шум. Виявлення ключових точок SIFT включає в себе наступні етапи:
  1. обчислити цифровий DoG;
  2. перевірити цифровий DoG на наявність дискретних 3d екстремумів;
  3. уточнити положення і масштаб цих кандидатів за допомогою квадратичної інтерполяції;
  4. відкинути нестабільних кандидатів, таких як неконтрастні або ті, що лежать по краях.
Детально розглянемо кожен з цих кроків.

Масштабно-просторовий аналіз: різниця Гаусіанів

Цифровий DoG w побудований з цифрового масштабного простору v . Для кожної октави o = 1, ..., n oct і для кожного зображення \(\mathbf {w} ^ o_s \) з s = 0, ..., n spo + 1 \[ \mathbf{w}^o_s(m, n) = \mathbf{v}^o_{s+1}(m, n) - \mathbf{v}^o_s (m, n) \] с m = 0,..., Мо - 1, n = 0,... , No - 1. До зображення \(\mathbf {w} ^ o_s \) застосуємо рівень розмиття \(σ_s ^ o \).

Алгоритм 1: Обчислення цифрового Гаусівого масштабного простору
In: u in , введення цифрового зображення розміром M × N пікселів.
Out: (\(\mathbf {v} ^ o_s \)), цифровий масштабний простір, o = 1 ,. .., n oct і s = 0, ..., n spo + 2.
\(\mathbf {v} ^ o_s \) - цифрове зображення розміром M o × N o , рівнем розмиття \(σ_s ^ o \) і відстанню між пікселями \(Δ ^ o = δ_ \min2 ^ {o - ​​1} \), де \(M_o = \left [\frac {δ_ \min} {δ_o} M \right], N_o = \left [\frac {δ_ \min} {δ_o} N \right] \). Отриманий результат \(\mathbf {v} ^ o_s \) позначається через \(\mathbf {v} ^ o_s \) (m, n).
параметри:

// Обчислюємо першу октаву
// Обчислюємо початкове зображення \(\mathbf {v} ^ 1_0 \)
//1.Інтерполяція даного зображення (Білінійна інтерполяція , Алгоритм 2)
u′ ← білінійна інтерполяція (uin, δmin)
// 2. Размиття інтерпольованого зображення (размиття за Гаусом) \[ \mathbf{v}^1_0 =\mathbf{G}_{\frac{1}{\delta_\min}\sqrt{\sigma^2_\min-\sigma^2_{in}}}\mathbf{u}' \] // Обчислюємо зображення у першій октаві
for s = 1... , nspo + 2 do \[ \mathbf{v}^1_s =\mathbf{G}_{ρ [(s − 1) → s] }\mathbf{v}^1_{s-1} \] // Обчислюємо наступні октави
for о = 2,..., noct do
// Знайдемо перше зображення в октаві за допомогою підвибірки
for m = 0,... , Mo - 1 and n = 0,..., No -1 do \[ \mathbf{v}^o_0(m,n) \leftarrow \mathbf{v}^{o-1}_{n_{spo}}(2m,2n) \] // Знаходимо інші зображення в октаві o
for s = 1,...,nspo + 2 do \[ \mathbf{v}^o_s=\mathbf{G}_{ρ [(s − 1) → s]}\mathbf{v}^o_{s-1}. \] Алгоритм 2: білінійна інтерполяція зображення
In: u, цифрове зображення розміром M × N пікселів. Пікселі зображення позначимо як u (m, n).
Вивід:u′, цифрове зображення, M ′ × N ′ пікселів, де \(M ′ = \left[\frac{M}{δ′} \right]\) і \(N ′ = \left[\frac{N}{δ′} \right].\)
Параметр: δ ′ <1, міжпіксельна відстань вихідного зображення.
for m ′ = 0,... , M ′ - 1 and n ′ = 0,. .. , N ′ - 1 do
x ← δ′m ′ y ← δ′n ′
u ′ (m ′, n ′) ← (x - ⌊x⌋) (y - ⌊y⌋) \(\bar{\mathbf{u}}\) (⌊x⌋ + 1, ⌊y⌋ + 1) + (1 + ⌊x⌋ - x) ( y - ⌊y⌋) \(\bar{\mathbf{u}}\) (⌊x⌋, ⌊y⌋ + 1) + (x - ⌊x⌋) (1 + ⌊y⌋ - y) \(\bar{\mathbf{u}}\) (⌊x⌋ + 1, ⌊y⌋) + (1 + ⌊x⌋ - x) (1 + ⌊y⌋ - y) \(\bar{\mathbf{u}}\)(⌊x⌋, ⌊y⌋)
\(\bar{\mathbf{u}}\) позначує розширення u до Z2 за допомогою симетризації відносно −0.5: \(\bar{\mathbf{u}}\)(k, l) = \({\mathbf{u}}\) (sM (k), sN (l)) з sN (k) = min (k mod 2M, 2M - 1 - k mod 2M).
тут ⌊ · ⌋ дробова частина.


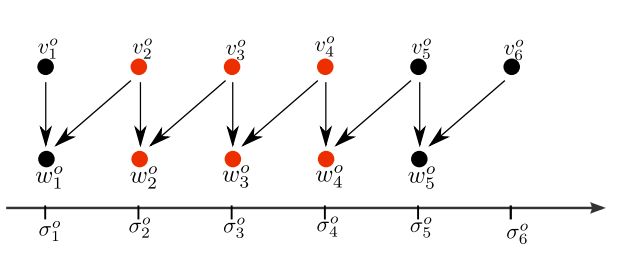Різниця операторів Гауса обчислюється шляхом віднімання пар суміжних масштабних зображень.
Процедура не центрована: різниці між зображеннями в масштабах κσ і σ приписується рівень розмиття σ.


Масштабний простір DoG. Різниця Гаусіанів діє як наближення нормованого Лапласіану σ 2 Δ.
Різниця \(\mathbf {w} ^ o_ {s} = \mathbf{v} ^ o_ {s + 1} - \mathbf{v} ^ o_ {s} \) щодо рівня розмиття \(σ_s ^ o \).
Кожна октава містить n spo зображень плюс два допоміжних зображення (чорного кольору).

 

Витяг ключових точок

Безперервні тривимірні екстремуми цифрового DoG розраховуються в два послідовні кроки.
3d дискретні екстремуми спочатку витягуються з (\(\mathbf {w} ^ o_ {s} \)) з точністю до пікселя, потім їх розташування уточнюється інтерполяцією цифрового DoG з використанням квадратичної моделі. Надалі значення \(\mathbf{v} ^ o_ {s} (m, n) \) і \(\mathbf{w} ^ o_ {s} (m, n) \) позначені, відповідно, \(\mathbf{v} ^ o_ {s, m, n} \) і \(\mathbf{w} ^ o_ {s, m, n} \).
Виявлення DoG 3D дискретних екстремумів. Кожен елемент \(\mathbf {w} ^ o_ {s, m, n} \) шкали DoG, з s = 1 ,. ,,, N spo , o = 1 ,. ,, N oct , m = 1 ,. ,,, М про - 2, n = 1 ,. ,, N o -2 (Виключаючи зображення границі і допоміжні зображення) порівнюється зі своїми сусідами для виявлення 3d дискретних максимумів і мінімумів (кількість сусідів 26 = 3 × 3 × 3 - 1). Алгоритм підсумовує витягнуті 3d екстремуми з цифрового DoG. Ці порівняння можливі завдяки допоміжним зображень \(\mathbf {w} ^ o_ {0} \), \(\mathbf {w} ^ o_ {n_ {spo} +1} \) для кожної октави o. Цей процес чутливий до шуму, виробляє нестабільні виявлення і інформація, яку він реалізує щодо місця розташування та масштабу, може бути помилковою, оскільки процес обмежений сіткою вибірки. Щоб виправити ці недоліки, за цим попереднім етапом слідує інтерполяція, уточнююча локалізацію екстремумів і каскад фільтрів, що відкидають ненадійні виявлення.
Уточнення ключової позиції. Розташування дискретних екстремумів обмежено сіткою вибірки (визначається октавою o). Це груба локалізація. SIFT уточнює положення і масштаб кожної потенційної ключової точки, використовуючи модель локальної інтерполяції.
Позначимо через \(ω_ {s, m, n} ^ o (α) \) квадратичну функцію в точці вибірки (s, m, n) в октаві o: \[ ω^o_{s, m, n} (α) = \mathbf{w}^o_{s,m, n}+ α^T \bar{g}^o_{s, m, n} + \frac{1}{2}α^T\bar{H}_{s, m, n}^o α, \] де \( α = (α_1, α_2, α_3)^T ∈ [−1/2, 1/2]^3,\bar{g}_{s, m, n}^o\) і \(\bar{H}_{s, m, n}^o\) позначають відповідно 3d-градієнт і Гессіан в точці (s, m, n) і октаві o. Для розрахунку застосуємо схему скінченних різниць: \[ \bar{g}_{s, m, n}^o = \left( \begin{array}{c} \frac{1}{2}\left(\mathbf{w}^o_{s+1,m, n}-\mathbf{w}^o_{s-1,m, n}\right) \\ \frac{1}{2}\left(\mathbf{w}^o_{s,m+1, n}-\mathbf{w}^o_{s,m-1, n}\right) \\ \frac{1}{2}\left(\mathbf{w}^o_{s,m, n+1}-\mathbf{w}^o_{s,m, n-1}\right) \\ \end{array} \right), \bar{H}_{s, m, n}^o = \left( \begin{array}{ccc} h_{1,1} & h_{1,2} & h_{1,3} \\ h_{1,2} & h_{2,2} & h_{2,3} \\ h_{1,3} & h_{2,3} & h_{3,3} \\ \end{array} \right) \] где \[ h_{1,1} = \mathbf{w}^o_{s+1,m, n} + \mathbf{w}^o_{s-1,m, n}- 2\mathbf{w}^o_{s,m, n}, h_{1,2} = \frac{1}{4}\left(\mathbf{w}^o_{s+1,m+1, n}-\mathbf{w}^o_{s+1,m-1, n}-\mathbf{w}^o_{s-1,m+1, n}+\mathbf{w}^o_{s-1,m-1, n}\right),\\ h_{2,2} = \mathbf{w}^o_{s,m+1, n} + \mathbf{w}^o_{s,m-1, n}- 2\mathbf{w}^o_{s,m, n}, h_{1,3} = \frac{1}{4}\left(\mathbf{w}^o_{s+1,m, n+1}-\mathbf{w}^o_{s+1,m, n-1}-\mathbf{w}^o_{s-1,m, n+1}+\mathbf{w}^o_{s-1,m, n-1}\right),\\ h_{3,3} = \mathbf{w}^o_{s,m, n+1} + \mathbf{w}^o_{s,m, n-1}- 2\mathbf{w}^o_{s,m, n}, h_{2,3} = \frac{1}{4}\left(\mathbf{w}^o_{s,m+1, n+1}-\mathbf{w}^o_{s,m+1, n-1}-\mathbf{w}^o_{s,m-1, n+1}+\mathbf{w}^o_{s,m-1, n-1}\right).\\ \]


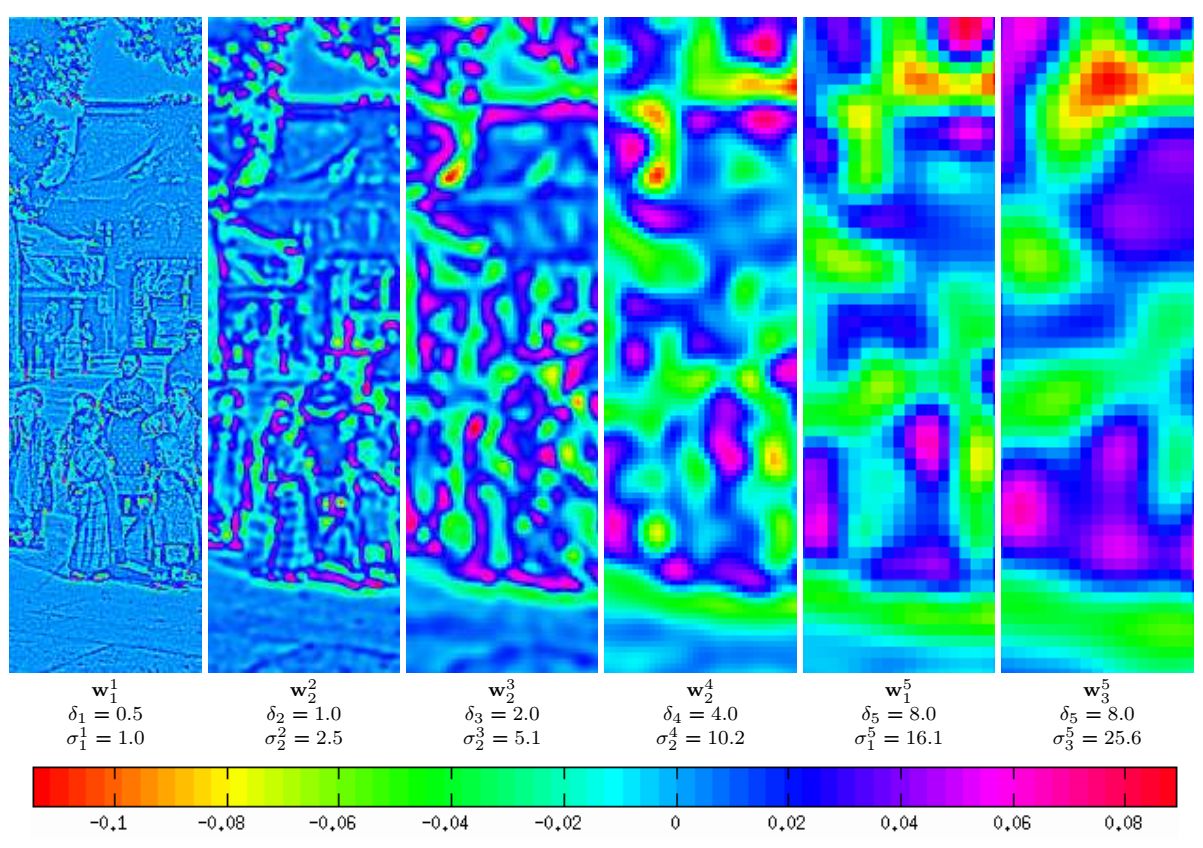Фрагменти підмножини зображень, витягнутих з масштабного простору DoG зображення.
Оператор DoG є наближенням нормованого оператора Лапласа σ 2 Δv.
Масштабний простір DoG з параметрами за замовчуванням: n spo = 3, σ min = 0,8, σ in = 0,5.

Ця квадратична функція є наближенням розкладання Тейлора другого порядку неперервної функції (де її похідні апроксимуються скінченно-різницевими схемами). Далі проводиться уточнення положення дискретного екстремуму (s e , m e , n e ) в октаві наступним чином.
  1. Ініціалізувати (s, m, n) дискретними координатами екстремуму (s e , m e , n e ).
  2. Обчислити безперервні екстремуми \(ω_ {s, m, n} ^ o \), вирішивши рівняння \(∇ω_ {s, m, n} ^ o (α) = 0 \) (Алгоритм 7). Це \[ α^∗ = - \left(\bar{H}_{s, m, n}^o\right)^{ −1} \bar{g}_{s, m, n }^o. \]
  3. Якщо \( \max (| α_1^* |, | α_2^*|, | α_3^*|) ≤ 0,5 \) (Тобто екстремум квадратичної функції лежить всередині області) екстремум прийнятий. Відповідні координати ключових точок \[ (σ, x, y) = \left(\frac{δ_{o_e}}{δ_\min} σ_\min 2^{(α_1^* + s)/n_{spo}}, δ_{o_e} (α_2^* + m), δ_{o_e} (α_3^* + n)\right). \]
  4. Якщо \(α^*\) виходить за межі області, інтерполяція відхиляється. Оновити (s, m, n) до найближчого дискретного значення \((s, m, n) + α ^ * \) і повторити з (2).
Цей процес повторюється до п'яти разів або до підтвердження інтерполяції. Якщо після п'яти ітерацій результат все ще не підтверджений, ключова точка-кандидат відкидається. На практиці область дії визначається як \(\max (| α_1 ^ * |, | α_2 ^ * |, | α_3 ^ * |) \lt 0.6 \), щоб уникнути можливої чисельної нестійкості через те, що кусково-інтерполяційна модель не є безперервною.
Відповідно до моделі локальної інтерполяції значення інтерпольованого екстремуму DoG \[ ω: = ω^o_{s, m, n} (α^*) = \mathbf{w}^o_{s,m, n} + (α^*)^T \bar{g}_{s, m, n }^o + \frac{1}{2} (α^*)^T \bar{H}_{s, m, n }^o α^* =\mathbf{w}^o_{s,m, n} +\frac{1}{2}(α^*)^T \bar{g}_{s, m, n }^o. \] Це значення буде використовуватися для видалення неконтрастних ключових точок.

Фільтрація нестабільних ключових точок

Відмова від низької контрастності екстремумів

Шум на зображенні зазвичай викликає кілька помилкових екстремумів DoG. Такі екстремуми нестійкі і не пов'язані з будь-якою конкретною структурою у зображенні. SIFT намагається усунути ці помилкові виявлення відкидаючи ключові точки-кандидати зі значенням DoG ω нижче порогу C DoG (Алгоритм 8),

if | ω | < CDoG then відкине кандидата на ключову точку.

Оскільки функція DoG апроксимує (κ - 1) σ 2 Δv, де κ є функцією числа шкал на октаву n spo , значення порогу C DoG має залежати від n spo (значення за замовчуванням C DoG = 0,015 для n spo = 3). Граничне значення становить \(\tilde{C}_{DoG} = \frac{2^{1/n_{spo}}−1}{2^{1/3}-1} C_{DoG}\), с CDoG відносно nspo = 3. Це гарантує, що застосований поріг не залежить від вибірки конфігурації. Для уточнення екстремумів і щоб уникнути непотрібних обчислень, застосовується менший консервативний поріг в 80% від C DoG (Алгоритм 5)

if \(| \mathbf{w} ^ o_ {s, m, n} | \lt 0.8 × C_ {DoG} \) then відкинути дискретний 3-й екстремум .

Відкидання ключових точок-кандидатів по краях

Ключові точки-кандидати, що лежать на краях, досить важко точно локалізувати. Це є прямим наслідком того факту, що ребро інваріантне щодо зрушень уздовж його головної осі. Такі виявлення не допомагають визначити коваріантні ключові точки і повинні бути відкинуті. 2D Гессіан DoG дає характеристику цих небажаних ключових кандидатів. Краї мають велику головну кривизну, ортогональну до краю і маленьку по краю.  У термінах власних значень матриці Гессе наявність ребра це велике співвідношення між найбільшим власним значенням λ max і найменшим λ min .
Матриця Гессе від DoG обчислюється на найближчій вибірці сітки з використанням кінцево-різницевої схеми: \[ H^o_{s, m, n} = \left( \begin{array}{cc} h_{1,1} & h_{1,2} \\ h_{1,2} & h_{2,2} \\ \end{array} \right) \] де \[ h_{1,1} = \mathbf{w}^o_{s,m+1, n} + \mathbf{w}^o_{s,m-1, n}- 2\mathbf{w}^o_{s,m, n}, h_{2,2} = \mathbf{w}^o_{s,m, n+1} + \mathbf{w}^o_{s,m, n-1}- 2\mathbf{w}^o_{s,m, n},\\ h_{1,2} = h_{2,1} = \frac{1}{4}\left(\mathbf{w}^o_{s,m+1, n+1}-\mathbf{w}^o_{s,m+1, n-1}-\mathbf{w}^o_{s,m-1, n+1}+\mathbf{w}^o_{s,m-1, n-1}\right). \] Алгоритм SIFT відкидає кандидатів в ключові точки, відношення власних значень r: = λ max / λ min яких перевищує певний поріг C edge (значення за замовчуванням C edge = 10).
Оскільки релевантним є тільки це відношення, обчислення власних значень можна уникнути. Співвідношення визначника матриці Гессе і його сліду пов'язані \[ edgeness (H_ {s, m, n} ^ o) = \frac {tr (H_ {s, m, n} ^ o) ^ 2} {det (H_ {s, m, n} ^ o)} = \frac {(λ_ \max + λ_ \min) ^ 2} {λ_ \max λ_ \min} = \frac {(r + 1) ^ 2} {r}. \] Таким чином, фільтрація кандидатів ключових точок на ребрах полягає в наступній перевірці:

if \(edgeness (H_ {s, m, n} ^ o)> \frac {(C_ {edge} + 1) ^ 2} {C_ {edge}} \) then відкидати кандидата на ключову точку.

Зауважимо, що \(H_ {s, m, n} ^ o \) - нижня права 2 × 2 підматріця \(\bar {H} _ {s, m, n} ^ o \), попередньо обчислена для інтерполяції ключових точок. Цьому питанню присвячено алгоритм 9.

Алгоритм 3: Обчислення різниці масштабного простору Гауса (DoG)

In: \((\mathbf {v} ^ o_ {s}) \), цифровий Гаусовий масштабний простір, o = 1,... , noct і s = 0,... , nspo + 2.
Out: \((\mathbf{w}^o_{s})\), цифровий DoG, o = 1,. .. , noct і s = 0,..., nspo + 1.
for о = 1 , ... , noct and s = 0,... , nspo + 1 do
for m = 0,... , Mo - 1 and n = 0,.. . , No -1 do
\(\mathbf{w}^o_{s}(m,n)=\mathbf{v}^o_{s+1}(m,n)-\mathbf{v}^o_{s}(m,n).\)

Алгоритм 4: Визначення 3d дискретних екстремумів для шкали DoG
In: \((\mathbf{w}^o_{s})\), цифровий DoG, o = 1,. .. , noct і s = 0,. .. , nspo + 1.
Елементи цифрового зображення \(\mathbf{w}^o_{s}\) позначені \(\mathbf{w}^o_{s,m,n}\).
Out: LA = {(o, s, m, n)}, список дискретних 3d екстремумів DoG.
for о = 1 , ... , noct do
for s = 0,..., nspo, m = 0,... , Mo - 1 and n = 0,.. . , No -1 do
if \(\mathbf{w}^o_{s}\) більше або менше, ніж всі її 33 - 1 = 26 сусіди, then
додати дискретний екстремум (o, s, m, n) у LA

Алгоритм 5: відкидання низько контрастних ключових точок-кандидатів (консервативний тест)
In: - \((\mathbf{w}^o_{s})\), цифровий DoG, o = 1,. .. , noct і s = 0,. .. , nspo + 1.
- LA = {(o, s, m, n)}, список дискретних 3d екстремумів DoG.
Out: LA ’= {(o, s, m, n)}, відфільтрований список дискретних 3d екстремумів DoG.
Параметр: порог CDoG.
for each DoG дискретного 3d екстремуму (o, s, m, n) у LA do
if \(|\mathbf{w}^o_{s}| ≥ 0,8 × C_{DoG} \) then
Додати дискретний екстремум (o, s, m, n) до LA ’

Алгоритм 6: інтерполяція ключових точок
In: - LA’= {(o, s, m, n)}, список дискретних 3d екстремумів DoG.
- \((\mathbf{w}^o_{s})\), цифрова шкала DoG, o = 1,. .. , noct і s = 0,. .. , nspo + 1.
Out: LB = {(o, s, m, n, x, y, σ, ω)}, список можливих ключових точок.
for each DoG дискретного 3d екстремуму (oe , se , me , ne ) у LA do
(s, m, n) ← (se , me , ne ) //ініціалізація розташування інтерполяції
repeat
// Обчислюємо розташування екстремумів і значення локальної квадратичної функції (Алгоритм 7)
(Α * , ω) ← квадратична інтерполяція (o e , s, m, n)
// Обчислюємо відповідні абсолютні координати \[ (σ, x, y) = \left(\frac{δ_{o_e}}{δ_\min} σ_\min 2^{(α_1^* + s)/n_{spo}}, δ_{o_e} (α_2^* + m), δ_{o_e} (α_3^* + n)\right). \] // Оновлюємо позицію інтерполяції \[ (s, m, n) ← ([s + α_1^∗], [m + α_2^∗], [n + α_3^∗]) \] until \(\max (| α_1^*|, | α_2^*|, | α_3^*|) \lt 0.6\) або після 5 невдалих спроб.
if \(\max (| α_1^*|, | α_2^*|, | α_3^*|) \lt 0.6,\) then
Додати кандидата на ключову точку (oe, s, m, n, σ, x, y, ω) до LB
тут [·] позначуємо функцію округлення.

Алгоритм 7: квадратична інтерполяція на дискретній множині DoG
In: - \((\mathbf{w}^o_{s})\), цифрова шкала DoG, o = 1,. .. , noct і s = 0,. .. , nspo + 1.
- (o, s, m, n), координати дискретного 3d екстремуму DoG.
Вихідні дані: - α* зміщення від центру інтерпольованого 3d-екстремума.
- ω, значення інтерпольованого 3d екстремума.
Обчислити \(\bar{g}_{s, m, n }^o\) і \(\bar{H}_{s, m, n }^o\) // 3D-градієнт DoG і Гессіан
Обчислити \(α^∗ = - \left(\bar{H}_{s, m, n }^o\right)^{ −1} \bar{g}_{s, m, n }^o\)
Обчислити \(ω = \mathbf{w}^o_{s,m,n} - \frac{1}{2} (\bar{g}_{s, m, n }^o)^T \left(\bar{H}_{s, m, n }^o\right)^{ −1} \bar{g}_{s, m, n }^o\)

Алгоритм 8: відкидання низько контрастних кандидатів на ключові точки
In: LB = {(o, s, m, n, σ, x, y, ω)} список можливих ключових точок.
Out: LB’= {(o, s, m, n, σ, x, y, ω)} скорочений список ключових точок-кандидатів.
Параметр: порог CDoG.
for each ключової точки кандидата (σ, x, y, ω) у LB do
if | ω | ≥ CDoG then
Додати кандидатну ключову точку (σ, x, y, ω) до LB ’.

Алгоритм 9: відкидання ключових точок-кандидатів на ребрах
In: - \((\mathbf{w}^o_{s})\), DoG масштабного простору.
- LB ’= {(o, s, m, n, σ, x, y, ω)}, список можливих ключових точок.
Out: LC = {(o, s, m, n, σ, x, y, ω)}, список ключових точок SIFT.
Параметр: Cedge, поріг відношення між власними значеннями матриці Гессе.
for each кандидата на ключову точку (o, s, m, n, σ, x, y, ω) в LB ’ do
Обчислити \(H_{s, m, n }^o\) // 2d Гессіан
Обчислити \(\frac{tr (H_{s, m, n }^o)^2}{det(H_{s, m, n }^o)}\) // для визначення краю і ребер
if \(\frac{tr (H_{s, m, n }^o)^2}{det(H_{s, m, n }^o)}\lt \frac{(C_{edge}+1)^2}{C_{edge}}\) then
Додайте кандидата на ключову точку (o, s, m, n, σ, x, y, ω) в L C .

Опис ключовий точки

Дескриптори, інваріантні до обертання, діляться на дві категорії. З одного боку, ті, які засновані на властивостях зображення, і вже інваріантні до обертання, а з іншого боку, дескриптори, засновані на нормалізації відносно встановленої орієнтації. Дескриптор SIFT заснований на нормалізації.
SIFT обчислює локальний домінантний кут градієнта, який використовується як орієнтир. Потім локальний розподіл градієнта нормується по відношенню до цього опорного напрямку.
Дескриптор SIFT побудований на основі нормалізованої градієнтної орієнтації зображення у формі квантованих гістограм. Далі опишемо, як визначається і обчислюється еталонна орієнтація, специфічна для кожної ключової точки.


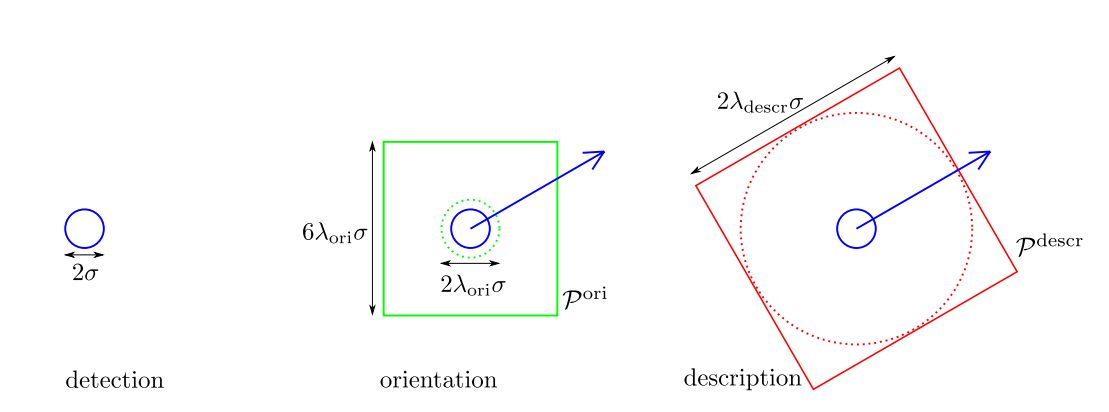
Опис ключової точки, виявленої при масштабі, відповідному σ (радіус синього кола), включає в себе аналіз розподілу градієнта зображення навколо ключової точки в двох радіальних Гаусових околицях з різними розмірами. Перший етап локального аналізу спрямований на те, щоб співвіднести ключову точку (синя стрілка). Він виконується над Гаусовим вікном стандартного відхилення λ ori σ ( радіус зеленого кола). Ширина відповідної латки 𝒫 ori (зелений квадрат) становить 6λ ori σ. На малюнку показаний випадок для значення за замовчуванням λ ori = 1,5. Другий етап аналізу спрямований на створення дескриптора. Виконується над Гаусовим вікном стандартного відхилення λ descr σ (радіус червоного кола) всередині квадратного вікна 𝒫 descr (червоний квадрат) приблизною ширини 2λ descr σ. На малюнку зображено настройки за замовчуванням: λ descr = 6, з Гаусовим вікном стандартного відхилення 6σ і латкою 𝒫 descr шириною 12σ.

Орієнтація ключових точок

В якості еталонної орієнтації використовується орієнтація домінуючого градієнта над околицею ключової точки.
 Обчислення цієї еталонної орієнтації включає в себе три етапи:

A. накопичення локального розподілу кута градієнта в нормалізованому вікні гістограми орієнтації;

B. згладжування гістограми орієнтації;

C. витягування однієї або декількох опорних орієнтацій зі згладженої гістограми.

А. Орієнтація гістограми накопичення. Для заданої ключової точки (x, y, σ) аналізована латка витягується з зображення масштабного простору \(\Mathbf {v} ^ o_ {s} \), масштаб якого \(σ_s ^ o \) є найближчим до σ. Цей нормалізована латка, що позначається 𝒫 ori , являє собою набір пікселів (M, n) з \(\mathbf {v} ^ o_ {s} \), що задовольняють умові \[ \max (| δ_om - x |, | δ_on - y |) ≤ 3λ_{ori}σ. \] Ключові точки, від яких відстань до границь зображення менше 3λoriσ, відкидаються, так як клаптик 𝒫ori не повністю лежить зображенні. Гістограма орієнтації h, з якої визначається домінуюча орієнтація, лежить у діапазоні [0, 2π]. Він складається із nbins бінів з центрами θk = 2πk/nbins. Кожен піксель (m, n) з 𝒫ori буде вносити свою долю у гістограму з загальною вагою \(c^{ori}_{m,n}\), яка є добутком норми градієнту та Гаусової ваги стандартного відхилення λoriσ (значення за умовчанням λori = 1,5), що зменшує внесок віддалених пікселів. \[ c^{ori}_{m,n}=e^{-\frac{\|(m\delta_o,n\delta_o)-(x,y)\|^2}{2(\lambda_{ori}\sigma)^2}}\|(\partial_m\mathbf{v}^o_{s,m,n},\partial_n\mathbf{v}^o_{s,m,n})\| \] Цей внесок присвоюється найближчого біну, а саме біну \[ b^{ori}_{m,n}=\left[\frac{n_{bins}}{2\pi}\left(\mathrm{arctan}2(\partial_m\mathbf{v}^o_{s,m,n},\partial_n\mathbf{v}^o_{s,m,n})\right)\right]. \] де [·] позначає функцію округлення, а \(\mathrm{arctan} 2 \) - зворотна до тангенсу тригонометрическая функція з двома аргументами і областю визначення [0, 2π].
Арктангенс з двома аргументами, на відміну від функції з одним аргументом, визначає відповідний квадрант обчисленого кута завдяки додатковій інформації про знаки вхідних даних: \(\mathrm{arctan} 2 (x, y) = \mathrm{arctg} \left (\frac {x} {y} \right) + \frac {\pi} {2} \mathrm{ sign} (y) (1 - \mathrm{sign} (x)) \).
Компоненти градієнта масштабного зображення \(\mathbf {v} ^ o_ {s} \) обчислюються за схемою скінченних різниць \[ ∂_m\mathbf{v}^o_{s,m,n}=\frac{1}{2}\left(\mathbf{v}^o_{s,m+1,n}-\mathbf{v}^o_{s,m-1,n}\right), ∂_n\mathbf{v}^o_{s,m,n}=\frac{1}{2}\left(\mathbf{v}^o_{s,m,n+1}-\mathbf{v}^o_{s,m,n-1}\right), \] для m = 1,..., Mo - 2 і n = 1,..., No -2.
B. Згладжування гістограми. Після накопичення, гістограма орієнтації згладжується шляхом застосування шестиразової кругової згортки за допомогою усреднюючого фільтру [1, 1, 1] / 3.
C. Витяг еталонної орієнтації. Опорні орієнтири ключових точок вибираються серед положень локальних максимумів згладженої гістограми. Точніше, еталонні орієнтації позицій локальних максимумів більше ніж t, помножені на глобальний максимум (значення за замовчуванням t = 0.8). Нехай k ∈ {1, ..., n bins } - індекс біна, такого що \(h_k> h_ {k ^ -}, h_k> h_ {k ^ +} \), де \(k ^ - = (k - 1) \mod n_ {bins} \) і \(k ^ + = (k + 1) \mod n_ {bins} \) і такого, що h k ≥ t max (h). Цей бін центрований при орієнтації \(θ_k = 2 \pi (k - 1) / n_ {bins} \). Відповідна еталонна орієнтація ключової точки θ ref обчислюється з максимальної позиції квадратичної функції, яка інтерполює значення \(h_ {k ^ -}, h_k, h_ {k ^ +} \) \[ θ_{ref} = θ_k + \frac{\pi}{n_{bins}}\left( \frac{h_{k^−}- h_{k^+}}{h_{k^-}-2h_k+h_{k^+}}\right). \] Кожна з виділених опорних орієнтацій призводить до обчислення одного локального дескриптора околиці ключовий точки. Отже, кількість дескрипторів може перевищувати кількість ключових точок. На малюнку показано, як еталонна орієнтація прив'язана до ключової точки.


Ширина нормалізованої латки 𝒫ori (нормалізованної по масштабу і повороту) дорівнює 6λoriσkey.
Величина градієнту має вагу згідно Гаусового вікна стандартного відхилення λoriσkey.
Ориєнтації градієнта накопичуються у гістограмі орієнтації h, яка потім згладжується.

Нормалізований дескриптор ключової точки

Дескриптор SIFT кодує локальний просторовий розподіл орієнтації градієнта в конкретній околиці. Дескриптори SIFT можуть бути обчислені де завгодно. Однак в оригіналі SIFT дескриптори обчислюються для всіх виявлених ключових точок в його нормалізованій околиці, що робить їх інваріантними до зрушень, поворотів і змін масштабу. Для кожної виявленої ключової точки, нормалізована околиця складається з квадратного вікна, центрована в ключовій точці і вирівняна з еталонною орієнтацією.
Дескриптор складається з набору зважених гістограм орієнтації градієнта, обчислених в різних областях нормалізованого квадратного вікна.
Нормалізована латка. Для кожної ключової точки (x key , y key , σ key , θ key ) нормалізована латка виділяється з Гаусівського масштабного зображення щодо найближчого дискретного масштабу (o, s) для масштабування σ key , а саме \(\mathbf{v} ^ o_ {s} \). Точка (m, n) з \(\mathbf{v} ^ o_ {s} \) з координатами (x m, n , y m, n ) = ( mδ o , nδ o ) щодо сітки вибірки вхідного зображення і має нормалізовані координати (\(\hat {x} _ {m, n}, \hat {y} _ {m, n} \)) щодо ключової точки (xkey, ykey, σkey, θkey) \[ \hat{x}_{m, n} = \frac{1}{σ_{key}}((mδ_o - x_{key}) \cos θ_{key} + (nδ_o - y_{key}) \sin θ_{key}),\\ \hat{y}_{m, n} = \frac{1}{σ_{key}}(-(mδ_o - x_{key}) \sin θ_{key} + (nδ_o - y_{key}) \cos θ_{key}). \] Нормализована латка, позначена 𝒫descr, це набір точок (m, n) з \(\mathbf{v}^o_{s}\) і нормалізованими координатами. \((\hat{x}_{m, n},\hat{y}_{m, n})\), задовольняє умові \[ \max (| \hat{x}_{m, n}|, | \hat{y}_{m, n}|) ≤ λ_{descr}. \] Ключові точки, відстань від яких до границі зображення менше \(\sqrt {2} λ_ {descr} σ \), відкидаються, щоб гарантувати, що латка 𝒫 descr включена в зображення. При цьому повторна вибірка зображення не виконується. Кожне значення (m, n) характеризується орієнтацією градієнта, нормованого щодо орієнтації ключової точки θ key , \[ \hat{Θ}_{m, n} = \mathrm{arctan2}( ∂_m \mathbf{v}^o_{s,m,n}, ∂_n\mathbf{v}^o_{s,m,n}) - θ_{key} \mathrm{mod} 2\pi, \] і його загальний внесок \(c ^ {descr} _ {m, n} \). Загальний внесок представляє собою добуток норми градієнта на Гаусівську вагу (зі стандартним відхиленням λ descr σ key ), що зменшує внесок віддалених пікселів, \[ c^{descr}_{m,n} = е^{-\frac{\|(mδ_o, nδ_o) - (х, у)\|^2}{2 (λ_{descr}σ)^2}}\|( ∂_m \mathbf{v}^o_{s,m,n}, ∂_n\mathbf{v}^o_{s,m,n})\| \] Масив гістограм орієнтації. Орієнтація градієнта кожного пікселя в нормалізованій латці 𝒫 descr накопичується в масив n hist × n hist гістограм орієнтації (значення за замовчуванням n hist = 4). Кожна з цих гістограм позначається hi, j для (i, j) ∈ {1,. , , , nhist} 2 і має позицію асоціоновану відносно ключової точки (xkey, ykey, σkey, θkey), яка визначається \[ \hat{x}^i =\left( i - \frac{1 + n_{hist}}{2} \right)\frac{2λ_{descr}}{n_{hist}}, \hat{y}^j =\left( j - \frac{1 + n_{hist}}{2}\right) \frac{2λ_{descr}}{n_{hist}}. \] Кожна гістограма h i, j складається з n ori бінів \(h ^ {i, j} _k \) з k ∈ {1 ,. ,,, N ori } з центрами в \(\hat {θ} ^ k = 2 \pi (k - 1) / n_ {ori} \) (Значення за замовчуванням n ori = 8). Кожна точка (m, n) в нормалізованій латці 𝒫 descr вносить внесок у найближчі гістограми (До чотирьох гістограм). Його загальний внесок \(c ^ {descr} _ {m, n} \) ділиться білінійну на найближчі гістограми в залежності від відстані до кожної з них. Так само, внесок всередині кожної гістограми згодом ділиться лінійно між двома найближчими бінами. Це призводить до наступних оновлень.
Для кожного(i, j, k) ∈ {1, . . . , nhist}2 × {1, . . . , nori} таких, що \[ |\hat{x}^i − \hat{x}_{m,n}| ≤ \frac{2λ_{descr}}{n_{hist}}, |\hat{y}^j − \hat{y}_{m,n}| ≤ \frac{2λ_{descr}}{n_{hist}} \] і \[ |\hat{θ}^k − \hat{θ}_{m,n}\mod 2\pi| ≤ \frac{2\pi}{n_{ori}} \] гістограма \(h^{i,j}_{ k}\) може бути оновлена \[ h^{i,j}_k ← h^{i,j}_k + \left(1 − \frac{n_{hist}}{2λ_{descr}}|\hat{x}^i − \hat{x}_{m,n}|\right) \left(1 − \frac{n_{hist}}{2λ_{descr}}|\hat{y}^j − \hat{y}_{m,n}|\right) \left(1 − \frac{n_{ori}}{2\pi}|θ^k − \hat{θ}_{m,n}\mod 2\pi \right)c^{descr}_{n,m}. \]


Конструкція дескриптора SIFT.
Нормалізована латка 𝒫descr поділена на набір nhist × nhist підлаток (значення за замовчуванням n hist = 4).
Кожна точка (m, n) всередині 𝒫 descr , розташована в (mδ o , nδ o ), вносить внесок у величину, яка є функцією їх
нормованих координат \((\hat {x} _ {m, n}, \hat {y} _ {m, n}) \). Кожна підлатка= \(\mathcal {P} ^ {descr} _ {(i, j)} \) центрується в \(\hat{x}_i, \hat{y}_j\).

Вектор функції SIFT. Накопичений масив гістограм кодується в векторний елемент f довжиною n hist × n hist × n ori наступним чином \[ f_{(i − 1) n_{hist}n_{ori} + (j − 1) n_{ori} + k} = h^{i, j}_k, \] де i = 1,. .. , nhist, j = 1,... , nhist і k = 1,. , , nori. Компоненти вектора ознак f насичуються до максимального значення 20% його евклідової норми, тобто \(f_k ← \min (f_k, 0.2 \| f \|) \).
Насиченість векторного компонента прагне зменшити вплив нелінійних змін освітленості областей.
Нарешті, вектор перенормується так, щоб \(\| f \| _2 = 512 \), відквантований на 8-бітові цілі числа наступним чином: fk ← min (⌊fk⌋, 255). Метою квантування є прискорення о відстаней між різними векторами ознак.


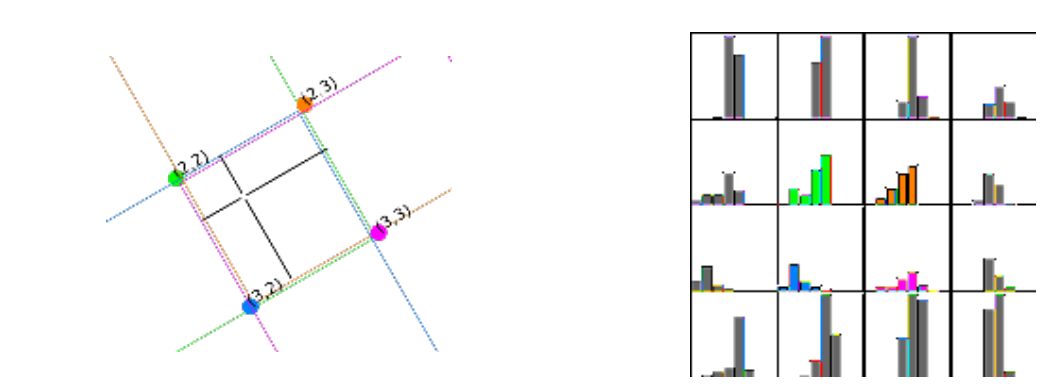Ілюстрація просторового вкладу елемента всередині латки 𝒫 descr .
Точка (m, n) вносить внесок у зважені гістограми (2, 2) (зелений), (2, 3) (помаранчевий), (3, 2) (синій) і (3, 3) (рожевий).
Внесок \(c ^ {descr} _ {m, n} \) ділиться на чотири пари елементів.

 


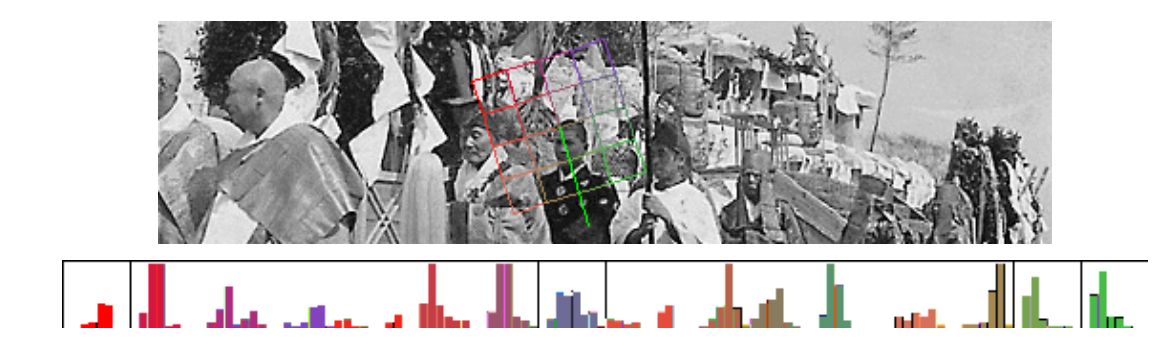Зображення зверху показує підлатки масиву n hist × n hist щодо ключової точки;
відповідні гістограми \(n_ {ori} \) бінів впорядковані в 1D-вектор \(\overrightarrow {v} \) (знизу).
Цей вектор згодом піддається обмеженню по порогу і нормалізується, так що евклідова норма дорівнює 512 для кожного дескриптора.
Розмірність вектору ознак в цьому прикладі дорівнює 128 щодо параметрів n hist = 4, n ori = 8 (значення за замовчуванням).

Алгоритм 10: Обчислення 2d градієнта на кожному зображені масштабного простору
In: - \((\mathbf{v}^o_{s})\), цифровий Гаусів масштабний простір, o = 1,. .. , noct и s = 0,. .. , nspo + 2.
Out: - (\(\partial_m \mathbf{v}^o_{s,m,n}\)), градієнт простору масштабування уздовж x, o = 1,. .. , noct и s = 0,. .. , nspo.
- (\(\partial_n \mathbf{v}^o_{s,m,n}\)), масштабно-просторовий градієнт уздовж y, o = 1,. .. , noct и s = 0,. .. , nspo.
for o = 1,. .. , noct and s = 0,. .. , nspo do
for m = 1,... , Mo - 2 and n = 1,..., No -2 do \[ ∂_m\mathbf{v}^o_{s,m,n}=\frac{1}{2}(\mathbf{v}^o_{s,m+1,n}-\mathbf{v}^o_{s,m-1,n}),\\ ∂_n\mathbf{v}^o_{s,m,n}=\frac{1}{2}(\mathbf{v}^o_{s,m,n+1}-\mathbf{v}^o_{s,m,n-1}). \]

Алгоритм 11: Обчислення еталонної орієнтації ключової точки
In: - LC = {(okey, skey, xkey, ykey, σkey, ω)}, список ключових точок.
- (\(\partial_m \mathbf{v}^o_{s,m,n}\)) градієнт масштабного простору уздовж x, o = 1,. .. , noct і s = 0,. .. , nspo
- (\(\partial_n \mathbf{v}^o_{s,m,n}\)) масштабно-просторовий градієнт уздовж y, o = 1,. .. , noct і s = 0,. .. , nspo.
Параметри: - λori. Латка 𝒫ori має ширину 6λoriσkey для ключової точки масштабу σkey.
Вікно Гауса має стандартне відхилення λoriσkey.
- nbins, кількість бінів у гістограмі орієнтації h.
- t, поріг для вторинних еталонних орієнтацій.
Out: LD = {(o, s ′, m ′, n ′, x, y, σ, ω, θ)} список орієнтованих ключових точок.
Проміжні дані: hk гістограма орієнтації, k = 1,. .. , nbins и с hk покриттям \(\left[\frac{2π(k-3/2)}{n_{bins}}; \frac{2π(k-1/2)}{n_{bins}}\right]\).
for each ключової точки (okey, skey, xkey, ykey, σkey, ω) із LC do
// Перевіряємо, чи достатньо віддалена ключова точка від границі зображення
if 3λoriσkey ≤ xkey ≤ h - 3λoriσkey and 3λoriσkey ≤ ykey ≤ w - 3λoriσkey, then // Ініціалізація гістограми орієнтації h
for 1 ≤ k ≤ nbins do hk ← 0
// Накопичуємо точки із нормалізованої латки 𝒫ori
for m = [(xkey - 3λoriσkey/δokey, ..., [(xkey + 3λoriσkey/δokey] do
for n = [(ykey- 3λoriσkey/δokey, ..., [(ykey + 3λoriσkey/δokey] do
// Обчислюємо внесок точки \[ c^{ori}_{m,n}=e^{-\frac{\|(m\delta_{o_{key}},n\delta_{o_{key}})-(x_{key},y_{key})\|^2}{2(\lambda_{ori}\sigma_{key})^2}} \|(\partial_m\mathbf{v}^{o_{key}}_{s_{key},m,n},\partial_n\mathbf{v}^{o_{key}}_{s_{key},m,n})\| \] //Знаходимо бін із відповідним індексом \[ b^{ori}_{m,n}=\left[\frac{n_{bins}}{2\pi}\left(\mathrm{arctg}2(\partial_m\mathbf{v}^{o_{key}}_{s_{key},m,n},\partial_n\mathbf{v}^{o_{key}}_{s_{key},m,n})\right)\right]. \] // Оновлюємо гістограму \[ h_{b^{ori}_{n,m}}← h_{b^{ori}_{n,m}}+c^{ori}_{n,m} \] // Сгладжування h
Застосувати для h шість разів кругову згортку з фільтром [1, 1, 1] / 3.
// Витягуємо еталонні орієнтації
for 1 ≤ k ≤ nbins do
if \(h_k> h_k^−, h_k> h_k^+\) and \(h_k ≥ t \max (h)\), then
// Обчислюємо нталонну орієнтацію θkey \[ θ_{key} = θ_k + \frac{\pi}{n_{bins}}\left(\frac{h_{k^-}-h_{k^+}}{h_{k^-}-2h_k+h_{k^+}}\right) \] тут [·] позначає функцію округлення, а arctan2 позначає арктангенс з двома аргументами

Алгоритм 12: Побудова дескриптора ключової точки
In: - L D = {(o key , s key , x key , y key , σ key , θ key )} список ключових точок.
- (\(\partial_m \mathbf{v} ^ o_ {s, m, n} \)) масштабно-просторовий градієнт уздовж x.
- (\(\partial_n \mathbf{v} ^ o_ {s, m, n} \)) градієнт масштабного простору уздовж y (див. Алгоритм 10).
Out: L E = {(o key , s key , x key , y key , σ key , θ key , f)} список ключових точок з вектором об'єктів f.
Параметри: - n hist . Дескриптор є масив n hist × n hist гістограм орієнтації.
- n ori , кількість бінів у гистограммах орієнтації.
Вектори об'єктів f мають довжину n hist × n hist × n ori
- λ descr .
Вікно Гауса має стандартне відхилення λ descr σ key .
Латка 𝒫 descr з шириною \(2λ_ {descr} \frac {n_ {hist} + 1} {n_ {hist}} \).
Проміжні дані: \(h ^ {i, j} _k \) масив орієнтованих гістограм, (i, j) ∈ {1, ..., n hist } і k ∈ {1, ..., n ori }
for each ключової точки (o key , s key , x key , y key , σ key , θ key ) з L D do
// Перевіряємо, чи достатньо віддалена ключова точка від границі зображення
if \(\sqrt{2}λ_{descr}σ_{key} ≤ x_{key} ≤ h - \sqrt{2}λ_{descr}σ_{key}\) и \(\sqrt{2}λ_{descr}σ_{key} ≤ y_{key} ≤ w - \sqrt{2}λ_{descr}σ_{key}\) then
// Ініціалізація масиву зважених гистограмм
for 1 ≤ i ≤ nhist, 1 ≤ j ≤ nhist and 1 ≤ k ≤ nori do \(h^{i,j}_k ← 0\)
// Накопичуємо дані нормалізованої латки 𝒫descr у гістограмах масиву
for \(m = \left[\left( x_{key} - \sqrt{2}λ_{descr}σ_{key}\frac{n_{hist}+1}{n_{hist}} \right)/ δ_o\right],... , \left[\left(x_{key} + \sqrt{2}λ_{descr}σ_{key}\frac{ n_{hist}+1}{ n_{hist}} \right)/ δ_o\right]\) do
for \(n = \left[\left( y_{key} - \sqrt{2}λ_{descr}σ_{key}\frac{n_{hist}+1}{n_{hist}} \right)/ δ_o\right],... , \left[\left(y_{key} + \sqrt{2}λ_{descr}σ_{key}\frac{ n_{hist}+1}{ n_{hist}} \right)/ δ_o\right]\) do
// Обчислюємо нормалізовані координати.
\(\hat{x}_{m,n} = ((mδ_{o_{key}} - x_{key}) \cos θ_{key} + (nδ_{o_{key}} - y_{key}) \sin θ_{key}/σ_{key})\)
\(\hat{y}_{m,n} = (-(mδ_{o_{key}} - x_{key}) \sin θ_{key} + (nδ_{o_{key}} - y_{key}) \cos θ_{key}/σ_{key})\)
//Перевіряємо, чи знаходиться точка (m, n) всередині нормалізованої латки 𝒫descr.
if \(\max (| \hat{x}_{m, n} |, | \hat{y}_{m, n} |) \lt λ_{descr} \frac{n_{hist}+1}{ n_{hist}}\) then
// Обчислюємо нормалізовану градієнтну орієнтацію. \[ \hat{\theta}_{m, n} = \mathrm{arctan2}\left( \partial_m \mathbf{v}^{o_{key}}_{s_{key},m,n},\partial_n \mathbf{v}^{o_{key}}_{s_{key},m,n}\right) - θ_{key} \mathrm{mod} 2π \]
// Обчислюємо сумарний внесок точки (m, n) \[ c^{descr}_{m,n} = е^{-\frac{\|(mδ_{o_{key}}, nδ_{o_{key}}) - (х_{key}, у_{key})\|^2}{2 (λ_{descr}σ_{key})^2}}\|( ∂_m \mathbf{v}^{o_{key}}_{s_{key},m,n}, ∂_n\mathbf{v}^{o_{key}}_{s_{key},m,n})\| \] // Оновлення найближчих гістограм і найближчих бінів.
for (i, j) ∈ {1,..., nhist}2 such that \(|\hat{x}^i - \hat{x}_{m, n}| ≤ \frac{2λ_{descr}}{n_{hist}}\) and \(|\hat{y}^j - \hat{y}_{m, n}| ≤ \frac{2λ_{descr}}{n_{hist}}\) do
for k ∈ {1,. .. , nori} such that \(|\hat{θ}^k - \hat{θ}_{m, n} \mathrm{mod} 2π| \lt \frac{2\pi}{n_{ori}} \) do \[ h^{i,j}_k ← h^{i,j}_k + \left(1−\frac{n_{hist}}{2λ_{descr}}| \hat{x}_{m, n} − \hat{x}^i |\right)\left(1−\frac{n_{hist}}{2λ_{descr}}| \hat{y}_{m, n} - \hat{y}^j |\right) \left( 1− \frac{n_{ori}}{2π} | \hat{θ}_{m, n} − \hat{θ}^k \mathrm{mod} 2π |\right) c^{descr}_{ m, n} \] // Побудувати вектор ознак f з масиву зважених гістограм.
for 1 ≤ i ≤ nhist, 1 ≤ j ≤ nhist and 1 ≤ k ≤ nori do
\(f_{(i-1)n_{hist}n_{ori}+(j-1)n_{ori}+k}=h^{i,j}_k\)
for 1 ≤ l ≤ nhist × nhist × nori do
fl ← min (fl, 0.2\(\|f\|\))/* нормалізація f * /
Обчислити l2-норму \(f_l ← \min \left(\left[512\frac{f_l}{\|f\|}\right], 255\right)\)/* квантувати до 8-бітних цілих чисел * /
Додати (x, y, σ, θ, f) до LE

Порівняння і виявлення

Класична задача виявлення і опису ключових точок полягає в тому, щоб знайти збіги (пари ключових точок) між зображеннями. При відсутності додаткових знань про проблему, наприклад, про форму геометричних обмежень, процедура зіставлення зазвичай складається з двох етапів:
співставлення однакових ключових точок з відповідних зображень і вибір надійних пар значень.
Нехай L A і L B будуть набором дескрипторів, пов'язаних з ключовими точками, виявленими на зображеннях u A і < b> u B . Зіставлення виконується шляхом розгляду кожного дескриптора, пов'язаного зі списком L A , і пошуку одного можливого збігу в списку L B . Перший дескриптор fa ∈ LA зв'язаний з дескриптором fb ∈ LB, який мінімізує евклідову відстань між дескрипторами, \[ f^b=\arg \min_{f\in L^B}\|f-f^a\|_2 \] Сполучення ключової точки з дескриптором f a вимагає обчислення відстаней до всіх дескрипторів з L B . Пара вважається надійною тільки в тому випадку, якщо її абсолютна відстань нижче певного порогу \(C ^ {match} _ {absolute} \). В іншому випадку це відкидається.
Щоб уникнути залежності від абсолютного значення відстані, метод SIFT використовує другого найближчого сусіда, щоб визначити надійність збігу. SIFT застосовує адаптивне порогове значення \(\| f ^ a - f ^ {b '} \| C ^ {match} _ {relative} \), де f b' - другий найближчий сусід, \[ f ^ {b '} = \arg \min_ {f \in L ^ B \setminus \{f ^ b \}} \| f-f ^ a \| _2 \] Це докладно описано в алгоритмі 13. Головний недолік використання відносного порога полягає в тому, що він пропускає ключові точки, пов'язані з структурою, що повторюється в зображенні. Дійсно, в цьому випадку відстань до найближчого і другого найближчого дескриптора буде порівнянним.  Були розроблені більш складні методи, щоб виділити надійне зіставлення зображень з повторюваними структурами.
Час виконання цього алгоритму пропорційний величині c · N A · N B , де N A і N B - це кількість ключових точок на зображеннях u A і u B відповідно, а c - це константа, пропорційна часу, який потрібен для порівняння двох ознак SIFT. Це занадто повільно для зображень середнього розміру, хоча зіставлення ключових точок легко розпаралелити. Кращим рішенням є використання більш компактних дескрипторів, які знижують ціну обчислення відстані (і, отже, зменшують значення c). Серед запропонованих рішень можемо знайти більш компактні SIFT-подібні дескриптори або виконавчі дескриптори, які використовують переваги швидкого обчислення відстані Хеммінга між двома двійковими векторами.

Алгоритм 13: Відповідність ключових точок
In: - LA = {(xa, ya, σa, θa, fa)} ключові точки і дескриптори зображення uA.
- LB = {{xb, yb, σb, θb, fb}} ключові точки і дескриптори зображення uB.
Out: M = {(xa, ya, σa, θa, fa), (xb, yb, σb, θb, fb)} список збігів з позиціями.
Параметр: \(C^{match}_{relative}\) відносний поріг
for each дескриптора fa із LA do
Знайти fb і fb′,найближчих і других найближчих сусідів fa:
for each дескриптора f із LB do
Обчислити відстань d (fa, f)
Виберіть пари, що задовольняють відносному порогу.
if \(d(f^a,f^b)\lt C^{match}_{relative}d(f^a,f^{b'})\) then
Додати пару (fa, fb) в M.


Приклад пошуку збігів на зображеннях (полігон в околицях містечка Черкаське).