Достаточно распространенным аппаратом приближения являются кусочно-полиномиальные функции или сплайны. Наиболее распространенным видом сплайнов являются ломаные или полигональные функции. Рассмотрим в качестве регрессионной модели ломаную с весовой функцией равной единице. Пусть \(\Delta _n \)фиксированное разбиение отрезка \(\left[ {t_0 ,T} \right]\)точками \(\tau _i (i = 0,1,2,...,n)\), и \(\Re \left( {\Delta _n } \right)\) множество ломаных \(P(\Delta _n ,t) =P\left( {\left\{ {a_i }\right\}_{i = 0}^n ,\Delta _n ,t} \right)\) с узлами в точках разбиения \(\Delta _n \). Тогда задача нахождения кусочно-линейной регрессионной модели с фиксированными узлами имеет вид \[ \inf \left\{ {\left. {\sum\limits_{i = 0}^N {\left( {x_i - P\left( {\Delta _n ,t_i } \right)} \right)^2} } \right|P\left( {\Delta _n } \right) \in \Re \left( {\Delta _n } \right)} \right\}. \] Нетрудно видеть, что \[ P(\Delta _n ,t) = P\left( {\left\{ {a_i } \right\}_{i = 0}^n ,\Delta _n ,t} \right) = \sum\limits_{i = 0}^n {a_i B_i \left( {\Delta _n ,t} \right),} \] где \(B_i \left( {\Delta _n ,t} \right) \quad \mbox{(i = 0,... ,n)}\)базисные функции, которые можно записать в следующем виде:

В частности, \(B_0 \left( {\Delta _n ,t} \right) = \left\{ {{\begin{array}{*{20}c} {\left( {\tau _1 - t} \right)\left( {\tau _1 - \tau _0 } \right)^{ - 1},} \hfill & {t \in \left[ {\tau _0 ,\tau _1 } \right],} \hfill \\ {0,} \hfill & {иначе,} \hfill \\ \end{array} }} \right.\)

\(B_i \left( {\Delta _n ,t} \right) = \left\{ {{\begin{array}{*{20}c} {\left( {\tau _{i - 1} - t} \right)\left( {\tau _{i - 1} - \tau _i } \right)^{ - 1},} \hfill & {t \in \left[ {\tau _{i - 1} ,\tau _i } \right],} \hfill & \hfill \\ {\left( {\tau _{i + 1} - t} \right)\left( {\tau _{i + 1} - \tau _i } \right)^{ - 1},} \hfill & {t \in \left[ {\tau _i ,\tau _{i + 1} } \right],} \hfill & {(i = 2,...,n - 1).} \hfill \\ {0,} \hfill & {иначе,} \hfill & \hfill \\ \end{array} }} \right.\)

\(B_n \left( {\Delta _n ,t} \right) = \left\{ {{\begin{array}{*{20}c} {\left( {\tau _{n - 1} - t} \right)\left( {\tau _{n - 1} - T} \right)^{ - 1},} \hfill & {t \in \left[ {\tau _{n - 1} ,T} \right],} \hfill \\ {0,} \hfill & {иначе,} \hfill \\ \end{array} }} \right.\) Выпишем функцию цели \[ S\left( {a_0 ,a_1 ,...,a_n } \right) = \sum\limits_{i = 0}^N {\left( {\sum\limits_{j = 0}^n {a_j B_j \left( {\Delta _n ,t_i } \right)} - x_i } \right)^2} , \] и найдем решение задачи \(S\left( {a_0 ,a_1 ,...,a_n } \right) \to \mathop {\min }\limits_{a_0 ,a_1 ,...,a_n } \). Необходимое и достаточное условие экстремума будет иметь вид \[ \frac{\partial }{\partial a_i }S\left( {a_0 ,a_1 ,...,a_n } \right) = 0,i = 0,1,...,n. \] Нахождение экстремума сводится к решению системы уравнений \[ \left( {{\begin{array}{*{20}c} {\left\langle {B_0 ,B_0 } \right\rangle } \hfill & {\left\langle {B_0 ,B_1 } \right\rangle } \hfill & \cdots \hfill & {\left\langle {B_0 ,B_n } \right\rangle } \hfill \\ {\left\langle {B_1 ,B_0 } \right\rangle } \hfill & {\left\langle {B_1 ,B_1 } \right\rangle } \hfill & \cdots \hfill & {\left\langle {B_1 ,B_n } \right\rangle } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\left\langle {B_n ,B_0 } \right\rangle } \hfill & {\left\langle {B_n ,B_1 } \right\rangle } \hfill & \cdots \hfill & {\left\langle {B_n ,B_n } \right\rangle } \hfill \\ \end{array} }} \right)\left( {{\begin{array}{*{20}c} {a_0 } \hfill \\ {a_1 } \hfill \\ \vdots \hfill \\ {a_n } \hfill \\ \end{array} }} \right) = \left( {{\begin{array}{*{20}c} {\left\langle {x,B_0 } \right\rangle } \hfill \\ {\left\langle {x,B_1 } \right\rangle } \hfill \\ \vdots \hfill \\ {\left\langle {x,B_n } \right\rangle } \hfill \\ \end{array} }} \right), \] где \[ \left\langle {x,B_j } \right\rangle = \sum\limits_{i = 0}^N {x_i B_j \left( {\Delta _n ,t_i } \right)} ,j = 0,1,...,n, \] а замечая, что \(\left\langle {B_i ,B_j } \right\rangle = 0,\forall i,j:\vert i - j\vert \ge 2\mbox{,}\) получаем систему уравнений с трехдиагональной матрицей \[ A = \left( {{\begin{array}{*{20}c} {\left\langle {B_0 ,B_0 } \right\rangle } \hfill & {\left\langle {B_0 ,B_1 } \right\rangle } \hfill & 0 \hfill & \cdots \hfill & 0 \hfill \\ {\left\langle {B_1 ,B_0 } \right\rangle } \hfill & {\left\langle {B_1 ,B_1 } \right\rangle } \hfill & {\left\langle {B_1 ,B_2 } \right\rangle } \hfill & \cdots \hfill & 0 \hfill \\ 0 \hfill & {\left\langle {B_2 ,B_1 } \right\rangle } \hfill & {\left\langle {B_2 ,B_2 } \right\rangle } \hfill & \cdots \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \cdots \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & \cdots \hfill & {\left\langle {B_n ,B_n } \right\rangle } \hfill \\ \end{array} }} \right). \] Применяя метод прогонки, получаем эффективный алгоритм нахождения уравнения кусочно-линейной регрессии с фиксированными узлами.

Через \(P(\Delta_n)\) обозначим оператор отображающий \(C^\rho\) в \(S_r(\Delta_n)\), \(\rho\gt r-1\). При фиксированном \(r\) последовательность \(\left\{P^*\left(\Delta_n^*\right)\right\}_{n=1}^\infty\) будем называть асимптотически наилучшей сплайн-регрессией для функции \(x(t)\), если при \(n\to \infty\) \begin{equation}\label{1} \int_0^T\left(x(t)-P^*\left(\Delta_n^*,t\right)\right)^2dt= \inf_{\Delta_n}\left\{\inf\left\{\left.\int_0^T\left(x(t)-P\left(\Delta_n,t\right)\right)^2dt\right|P\left(\Delta_n\right) \in S_r(\Delta_n)\right\}\right\}(1+o(1)). \end{equation} Пусть на отрезке \([0,T]\) в узлах разбиения \(\Delta_n\) заданы значения функции \(x_i\) \(i=0,1,...,n.\) Кубический сплайн \(s_3(x,\Delta_n)=s_3\left(\left\{x_i\right\}_{i=0}^n,\Delta_n\right)\) называется интерполяционным с граничными условиями \(s^{(i)}_3(x,\Delta_n,0)=x^{(i)}(0)\) и \(s^{(i)}_3(x,\Delta_n,T)=x^{(i)}(T)\) при \(i=0,1\), если \[ s_3(x,\Delta_n,t_i)=x_i,i=0,1,...,n. \] Если \(x_i=Ti/n\) \(i=0,1,...,n\), то вместо \(s_3\left(x,\left\{\frac{Ti}{n}\right\}_{i=0}^n,t\right)\) будем писать \(s_3\left(\left\{x_i\right\}_{i=0}^n,t\right)\).

Теорема 1. Пусть \(x\in L^3_2\) такова, что \(x''\) обращается в ноль на конечном числе отрезков или точек из \([0,T]\) и \(X(t)\) вторая первообразная \(x(t)\) такая, что \(X'(0)=0\) и \(X(0)=0\).
Выберем \(M_i\) из условий \[ \lambda_iM_{i-1}+2M_i+\mu_iM_{i+1}= \frac{6}{h_{i-1}+h_i}\left(\frac{X_{i+1}-X_i}{h_i}-\frac{X_{i}-X_{i-1}}{h_{i-1}}\right),i=1,2,...,n-1, \] где \(\mu_i=h_{i-1}\left(h_{i-1}+h_i\right)^{-1}\), \(\lambda_i=1-\mu_i\).
Тогда \[ \inf\left\{\|x-s_1(\Delta_n)\|_2\left|s_1(\Delta_n)\in S_1(\Delta_n)\right.\right\}= \left\|x-s_3''\left(\{M_i\}_{i=0}^n,\Delta_n\right)\right\|_2 \] Выберем узлы \(t^*_i\) разбиения \(\Delta^*_n\) из условия \[ \int_{0}^{t^*_i}\left(\left|s_3^{(4)}\left(\left\{x_i\right\}_{i=0}^n,t\right)\right|+\frac{1}{n^\gamma}\right)^\alpha dt=\frac{i}{n}A_n, A_n=\int_{0}^{T}\left(\left|s_3^{(4)}\left(\left\{x_i\right\}_{i=0}^n,t\right)\right|+\frac{1}{n^\gamma}\right)^\alpha dt, \] тогда при \(n\to\infty\) \[ \inf_{\Delta_n}\inf\left\{\|x-\ell(\Delta_n)\|_2\left|\ell(\Delta_n)\in S_1(\Delta_n)\right.\right\}= \left\|x-s_1\left(\{M^*_i\}_{i=0}^n,\Delta^*_n\right)\right\|_2(1+o(1))=\frac{\theta}{n^2}\|x''\|_\alpha+o\left(\frac{1}{n^2}\right), \] где \(\theta=\frac{1}{2!}\left(t^2(1-t^2)\right)^{1/2}\) и \(\alpha=2/5\).

Теорема 2. Пусть \(x\in L^3_2\) такова, что \(x''\) обращается в ноль на конечном числе отрезков или точек из \([0,T]\), и \(s_1(x,\Delta_n,t)\) интерполяционная ломаная по разбиению \(\Delta_n\). Тогда при \(n\to\infty\) \[ \inf_{\Delta_n}\|x-s_1(x,\Delta_n)\|_2=\frac{\theta}{n^2}\|x''\|_2+o\left(\frac{1}{n^2}\right). \]

Действительно, \[ \varepsilon(x,\Delta_n,t)=x-s_1(x,\Delta_n,t)=x(t)-x_{i-1}(1-\tau)-x_i\tau=(x(t)-x_{i-1})(1-\tau)+(x(t)-x_i)\tau= \] \[ =(1-\tau)\int_{t_{i-1,n}}^tx'(u)du-\tau\int_{t}^{t_{i,n}}x'(u)du =\int_{i_{i-1,n}}^{t_{i,n}}K(t,u)x'(u)du,\] где \[ K(t,u)= \left\{ \begin{array}{ll} (1-\tau), & \hbox{ }u\in [t_{i-1,n},t], \\ \tau, & \hbox{ }u\in (t,t_{i,n}] \end{array} \right. \] Интегрируя последнее соотношение по частям и учитывая, что \(K(t,u)\), как функция по \(u\), в среднем равна нулю на промежутке \([t_{i-1,n},t_{i,n}]\), получаем для \(t\in [t_{i-1,n},t_{i,n}]\) \[ x(t)-s_1(x,\Delta_n,t)-\int_{t_{i-1,n}}^{t_{i,n}}\mathbb{K}(t,u)x''(u)du, \] где \[ \mathbb{K}(t,u)= \left\{ \begin{array}{ll} (u-t_{i-1,n})(1-\tau), & \hbox{ }u\in [t_{i-1,n},t], \\ -(u-t_{i,n})\tau, & \hbox{ }u\in (t,t_{i,n}] \end{array} \right. \] Замечая, что для \(t\in [t_{i-1,n},t_{i,n}]\), функция \(\mathbb{K}(t,u)\) знакопостоянна, можем записать \[ m^-_i|\mathbb{K}(t)|\le |\varepsilon(x,\Delta_n,t)|\le m^+_i|\mathbb{K}(t)|, \] где \[ \mathbb{K}(t)=\int_{t_{i-1,n}}^{t_{i,n}}\mathbb{K}(t,u)du=\frac{1}{2!}(t-t_{i-1,n})(t_{i,n}-t) \] и \[ m^-_i=\min\left\{|x''(t)|\left|t\in [t_{i-1,n},t_{i,n}]\right.\right\}, m^+_i=\max\left\{|x''(t)|\left|t\in [t_{i-1,n},t_{i,n}]\right.\right\}. \] Сделав замену переменных \(\tau=t-t_{i-1,n}\), получим \[ \|\mathbb{K}\|_{2[t_{i-1,n},t_{i,n}]}=h^{1/\alpha}_i\theta, \] и, следовательно, \begin{equation}\label{2} m^-_ih^{1/\alpha}_i\theta\le \|\varepsilon(x,\Delta_n)\|_{2[t_{i-1,n},t_{i,n}]}\le m^+_ih^{1/\alpha}_i\theta. \end{equation} Таким образом, получаем \[ \|x(t)-s_1(x,\Delta_n)\|^2_2\ge \theta^2\sum_{i=0}^n\left|m^-_ih^{1/\alpha}_i\right|^2= \theta^2\sum_{i=0}^n\left(\int_{t_{i-1,n}}^{t_{i,n}}\left|y^-_n(t)\right|^\alpha dt\right)^{2/\alpha} \] где \(y^-_n(t)\) есть кусочно-постоянная функция, равная \(m^-_i\) для \(t\in [t_{i-1,n},t_{i,n}]\).
Далее нам понадобится следующее простое утверждение: Для любого \(n=1,2,...\) и \(\alpha\gt 1\) при условиях \begin{equation}\label{3} A_i\gt 0,\sum_{i=1}^nA_i=\mathbb{A} \end{equation} справедливо соотношение \[ \min\left\{\left.\sum_{i=1}^nA^\alpha_i\right|A_i\right\}=\mathbb{A}n^{1-\alpha}, \] причем минимум правой части достигается при \(A^*_i=\frac{\mathbb{A}}{n}.\)
Действительно, составим функцию Лагранжа \[ \mathcal{L}(\lambda,A_1,A_2,...,A_n)=\sum_{i=1}^nA^\alpha_i-\lambda\left(\sum_{i=1}^nA_i-\mathbb{A}\right) \] Для нахождения минимума функции Лагранжа, найдем производную по \(A_i\) \(i=1,2,...,n\) и приравняем ее нулю \[ \frac{\partial}{\partial A_i} \mathcal{L}(\lambda,A_1,A_2,...,A_n)=-\lambda+\alpha A_i^{\alpha-1}=0, i=1,2,...,n. \] Решением этой системы является \[ A^*_i=\left(\frac{\lambda}{\alpha}\right)^{\frac{1}{\alpha-1}}, i=1,2,...,n. \] Отсюда и из (\ref{3}) получаем \(A^*_i=\frac{\mathbb{A}}{n},\) и экстремальное значение этой задачи равно \[ \sum_{i=1}^n\left(A^*_i\right)^\alpha=\sum_{i=1}^n\frac{\mathbb{A}^\alpha}{n^\alpha}= \frac{\mathbb{A}^\alpha}{n^{\alpha-1}}. \] Отсюда и из предыдущего получаем, что для любой функции \(y\in C\) , произвольного набора \(t_i\in [0,T]\) и любого \(\beta\in (0,\infty)\) выполняется неравенство \[ \sum_{i=1}^n\left(\int_{t_{i-1}}^{t_{i}}|y(t)|\right)^{\beta+1}\ge \frac{1}{n^\beta}\left(\int_{0}^{T}|y(t)|\right)^{\beta+1} \] Следовательно, для любого разбиения \(\Delta_n\) \[ \|x-s_1(x,\Delta_n)\|_2\ge \frac{\theta}{n^2}\left(\int_{0}^{T}|y^-_n(t)|^\alpha\right)^{1/\alpha}. \] Ясно, что если при \(n\to \infty\) интеграл \(\int_0^T|y^-_n(t)|^\alpha dt\) не стремится к \(\int_0^T|x''(t)|^\alpha dt\), а значит и ошибка приближения \(\|x-s_1(x,\Delta_n)\|_2\) не стремится к нулю. Таким образом, получаем \begin{equation}\label{4} \|x-s_1(x,\Delta_n)\|_2\ge \frac{\theta}{n^2}\|x''\|_\alpha+o\left(\frac{1}{n^2}\right). \end{equation} Пусть \(z_n(t)\) произвольная последовательность функций, такая, что при \(n\to\infty\) \begin{equation}\label{5} \|z_n-x''\|_2\le \varepsilon_n, \end{equation} где \[ \varepsilon_n=\frac{1}{n^\gamma}\left(1-\frac{\mathbb{A}\|x''\|_C}{n^{2(\alpha+1)}}\right),\gamma=(3\alpha+2)^{-1}. \] Выберем узлы \(t^*_{i,n}\) разбиения \(\Delta^*_n\) из условия \[ \int_0^{t^*_{i,n}}\left(|z_n(t)|+\frac{1}{n^\gamma}\right)^\alpha dt=\frac{i}{n}A_n, \] где \(A_n=\int_0^T\left(|z_n(t)|+\frac{1}{n^\gamma}\right)^\alpha dt\).
Тогда \begin{equation}\label{6} \int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|z_n(t)|+\frac{1}{n^\gamma}\right)^\alpha dt=\frac{1}{n}A_n, i=1,2,...,n. \end{equation} Учитывая, что \(a_n\to \mathbb{A}\) при \(n\to\infty\), получаем, что при достаточно больших \(n\) будут иметь место неравенства \[ h_i\le\frac{A_n}{n^{1-\alpha\gamma}}\le \frac{2\mathbb{A}}{n^{1-\alpha\gamma}}. \] Из неравенства (\ref{2}) имеем \[ \|\varepsilon(x,\Delta^*_n)\|_{2[t^*_{i-1,n},t^*_{i,n}]}\le m^+_ih^{1/\alpha}_i\theta= \theta\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}|m^+_i|^\alpha dt\right)^{1/\alpha} \] а так как найдется точка \(\xi\in [t^*_{i-1,n},t^*_{i,n}]\) такая, что \[ m^+_i=\max\left\{|x''(t)|\left|t\in [t^*_{i-1,n},t^*_{i,n}]\right.\right\}=x''(t)+x'''(\xi)(t^*_{i,n}-t), \] то получаем \[ \|\varepsilon(x,\Delta^*_n)\|_{2[t^*_{i-1,n},t^*_{i,n}]}\le \theta\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|x''(t)|+\|x'''\|_\infty h_i\right)^\alpha dt\right)^{1/\alpha} \le \theta\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|z_n(t)|+\varepsilon_n+2 \mathbb{A}\|x'''\|_\infty n^{\alpha\gamma-1}\right)^\alpha dt\right)^{1/\alpha} =\theta\left(\int_{t^*_{i-1,n}}^{t^*_{i,n}}\left(|z_n(t)|+\frac{1}{n^\gamma}\right)^\alpha dt\right)^{1/\alpha}. \] Отсюда и из (\ref{6}) сразу получаем \[ \|\varepsilon(x,\Delta^*_n)\|_{2[t^*_{i-1,n},t^*_{i,n}]}\le \theta\left(\frac{A_n}{n}\right)^{1/\alpha}. \] Следовательно, \[ \inf_{\Delta_n}\|x-s_1(x,\Delta_n)\|_2\le \left(\sum_{i=1}^n\|\varepsilon(x,\Delta^*_n)\|_{2[t^*_{i-1,n},t^*_{i,n}]}\right)^{1/2} \le \frac{\theta}{n^2}A_n^{1/\alpha} \] и при \(n\to\infty\) \[ \inf_{\Delta_n}\|x-s_1(x,\Delta_n)\|_2\le \frac{\theta}{n^2}\|x''\|_\alpha+o\left(\frac{1}{n^2}\right), \] что вместе с (\ref{6}) и завершает доказательство теоремы 2.
Теперь вернемся к основному утверждению.
В соответствии с теоремой Холлидея (см., например, с. 155) \[ \min\left\{\left.\int_0^T\left(x''(t)-\ell''(t)\right)^2dt\right|\ell(t)\in S_3(\Delta_n)\right\}= \int_0^T\left(x''(t)-s_3''(x,\Delta_n,t)\right)^2dt, \] таким образом, \[ \min\left\{\left.\int_0^T\left(x(t)-\ell(t)\right)^2dt\right|\ell(t)\in S_1(\Delta_n)\right\}= \int_0^T\left(x(t)-s_3''(X,\Delta_n,t)\right)^2dt \] где \(X(t)\) вторая первообразная \(x(t)\) такая, что \(X'(0)=0\) и \(X(0)=0.\)
Кроме того, если для интерполяционного сплайна \(s_3(x,\Delta_n)=s_3\left(\left\{x_i\right\}_{i=0}^n,\Delta_n\right)\) положим \[ s''_3(x,\Delta_n,t_{i,n})=M_i, i=0,1,...,n, \] то для \(t\in [t_{i,n},t_{i+1,n}]\) сплайн \(s_3(x,\Delta_n)\) можно записать в виде \[ s_3(x,\Delta_n,t)=x_i(1-t)+x_{i+1}t-\frac{h_{i}^2}{6}t(1-t)\left((2-t)M_i+(1+t)M_{i+1}\right) \] где \(M_i\) находятся из условий \begin{equation}\label{7} s''_3(x,\Delta_n,t_{i,n}-0)=s''_3(x,\Delta_n,t_{i,n}+0), i=1,2,...,n-1. \end{equation} и определяются системой \[ \lambda_iM_{i-1}+2M_i+\mu_iM_{i+1}= \frac{6}{h_{i-1}+h_i}\left(\frac{x_{i+1}-x_i}{h_i}-\frac{x_{i}-x_{i-1}}{h_{i-1}}\right),i=1,2,...,n-1, \] Тогда \[ s''_3(x,\Delta_n,t)=M_i(1-t)+M_{i+1}t, \] то есть \(s''_3(x,\Delta_n)=s_1\left(\left\{M_i\right\}_{i=0}^n,\Delta_n\right)\) .
Кроме того, например, с.115 имеем \[ |x''(t)-s''_3(x,\Delta_n,t)|\le \frac{3}{8}h^2_{\max}\|x^{(4)}\|_\infty, h_{\max}=\max\{h_i|i=1,2,...,n\}, \] то есть, \(s''_3\left(\{M_i\}_{i=0}^n,\left\{\frac{Ti}{n}\right\}_{i=0}^n,t\right)\) удовлетворяет условию (\ref{5}).
Сопоставляя полученные результаты и утверждение теоремы 2, сразу получаем теорему 1.
Ясно, что этот подход позволяет получить решение задачи сплайн-регрессионной модели степени больше, чем единица. Для сплайн-регрессионной модели порядка 2 и 3, можно использовать следующее утверждение. Его доказательство достаточно сложное и выходит за рамки данного обзора.

Теорема A.
Пусть \(r=1,...,5\), \(p\in [1,\infty], \alpha=(r+1+p^{-1}-\nu)^{-1}\) и \(\nu=0,...,r\). Тогда для любой функции \(x\in L^{r+1}_\infty\) такой, что \(|x^{(r+1)}|(t)>0 (t\in [a,b])\) при \(n\to\infty\) последовательность разбиений \(\left\{\Delta^*_n\right\}_{n=1}^\infty=\left\{\left\{t^*_{i,n}\right\}_{i=0}^n\right\}_{n=1}^\infty\), определяемая из равенств \[ \int_a^{t^*_{i,n}}|z_n(t)|^\alpha dt=\frac{i}{n}\int_a^b\left|z_n(t)\right|^\alpha dt (i=0,\ldots,n), \] где \(z_n(t)\)- любая последовательность функций, такая, что \(\left|z_n-x^{(r+1)}\right|_\infty \to 0\) будет асимптотически оптимальной для интерполяционных сплайнов порядка \(r\), при этом \[ \inf_{\Delta_n}\left\|x^{\nu}-s^{(\nu)}_r(x,\Delta_n)\right\|_p= \left\|x^{\nu}-s^{(\nu)}_r(x,\Delta^*_n)\right\|_p(1+o(1))= \frac{\|D_{r+1-\nu}\|_p}{n^{r+1-\nu}}\|x^{(r+1)}\|_\alpha (1+o(1)), \] где \(D_{r+1}(t)\) есть \(r\)-й 1-периодический интеграл, в среднем равный нулю на \([0,1]\) от функции \(D_1(t)=t-0.5\).

Восстановление непрерывных данных.

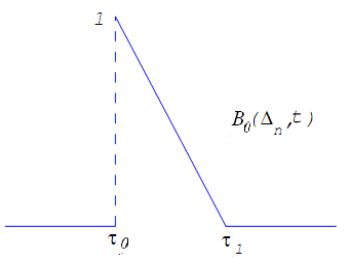
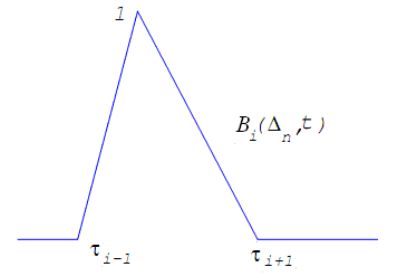
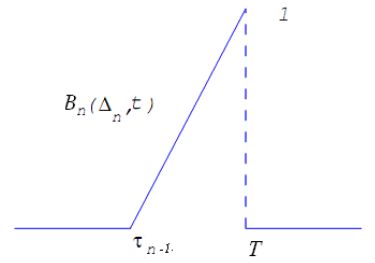
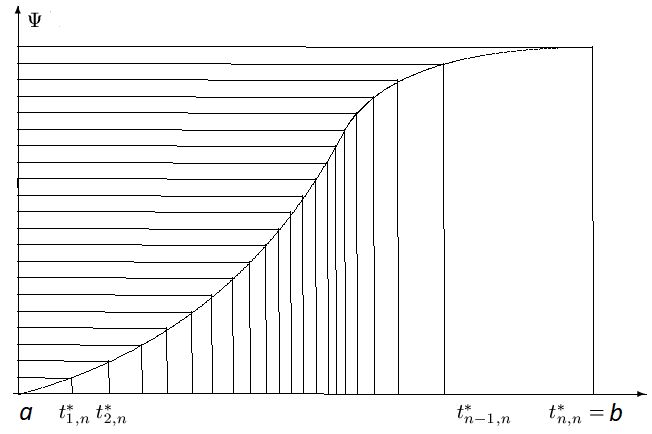
Вначале рассмотрим построение регрессионного сплайна для интегрируемой на \([a,b]\) функции \(x(t)\), то есть для фиксированного разбиения \(\Delta_n\) найдем решение задачи \[ \min\left\{\left.\int_a^b\left(x(t)-\ell(t)\right)^2dt\right|\ell(t)\in S_{2}(\Delta_n)\right\} \]
В соответствии с теоремой Холлидея (см., например, с. 155) для \(f\in C^r,\,r=1,2,...\) имеет место соотношение \[ \min\left\{\left.\int_a^b\left(f^{(r)}(t)-\ell^{(r)}(t)\right)^2dt\right|\ell(t)\in S_{2r-1}(\Delta_n)\right\}= \int_a^b\left(f^{(r)}(t)-s_{2r-1}^{(r)}(x,\Delta_n,t)\right)^2dt, \] таким образом, \begin{equation}\label{holliday} \min\left\{\left.\int_a^b\left(x(t)-\ell(t)\right)^2dt\right|\ell(t)\in S_{2}(\Delta_n)\right\}= \int_a^b\left(X(t)-s_5^{(3)}(X,\Delta_n,t)\right)^2dt \end{equation} где \(X(t)\) третья первообразная \(x(t)\) такая, что \(X''(a)=0\), \(X'(a)=0\) и \(X(a)=0.\)
Таким образом, путь к решению поставленной задачи лежит через построение интерполяционного сплайна пятой степени.
Легко убедиться в том, что интерполяционный для функции \(f(t)\) сплайн пятой степени для \(t\in [t_{i-1},t_i]\) имеет вид \begin{equation}\label{s:5} s_5(x,\Delta_n,t)=f_{{i -1}} \left( 1-\tau \right) ^{2} \left( 1+2\,\tau \right) +f_{{i }}{\tau }^{2} \left( 3-2\,\tau \right) +m_{{i -1}}\tau \left( 1-\tau \right) ^{2}h_{{i -1/2}}-m_{{i }}{\tau}^{2} \left( 1-\tau \right) h_{i -1/2}+ \end{equation} \[+{\tau}^{2} \left( 1-\tau \right) ^{2} \left( \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{{i -1}} \right) +6\,(f_{{i }}-\,f_{{i-1 }})-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) \tau+ 0.5\,M_ {{i -1}}h_{i -1/2}^{2}+3(\,f_{{i -1}}-f_{{i }})+ \left( 2\,m_ {{i -1}}+m_{{i }} \right) h_{i -1/2} \right) \] Здесь \(\tau=\frac{t-t_{i-1}}{h_{i-1/2}}\), \(h_{i-1/2}=t_i-t_{i-1}\), \(f_i=f(t_i)\), \(m_i=s'_5(t_i)\) и \(M_i=s''_5(t_i).\)
Выпишем производные данного сплайна.
Первая производная будет иметь вид \[ s'_5(x,\Delta_n,t)=-2\,f_{{i -1}} \left( 1-{\tau} \right) \left( 1+2\,{\tau} \right) h_{i -1/2}^{-1 }+2\,f_{{i -1}} \left( 1-{\tau} \right) ^{2}h_{i -1/2}^{-1}+2\,f_{{i }}\tau\, \left( 3-2\,{\tau} \right) h_{i -1/2}^{-1}- 2\,{\frac {f_{{i }}{\tau}^{2}}{h_{i -1/2}}}+\] \[+m_{{i -1}} \left( 1-{\tau} \right) ^{2}-2\,m_{{i -1}}\tau\, \left( 1-{\tau} \right) -2\,m_{{i }}\tau\, \left( 1-\tau \right)+m_{{i }}{\tau}^{2}+\] \[+2\,\tau\, \left( 1-\tau \right) ^{2} \left( \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_{{ i }}-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) \tau+ 0.5\,M_{{i -1}}h_{i -1/2}^{2}+3\,f_{{i - 1}}-3\,f_{{i }}+ \left( 2\,m_{{i -1}}+m_{{i }} \right) h_{{i -1/2} } \right) h_{i -1/2}^{-1}-\] \[-2\,{\tau}^{2} \left( 1-{\tau} \right) \left( { \left( 0.5\,h_{i -1/2}^{2 } \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }}-3 \, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) \tau}+ 0.5\,M_{{i -1}}h_{i -1/2}^{2}+3\,f_{{i -1}}-3\,x _{{i }}+ \left( 2\,m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-1}+\] \[+{\tau}^{2} \left( 1-{\tau} \right) ^{2} \left( 0.5\,h_{i -1/2}^{2} \left( M_{{ i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }}-3\, \left( m_{{ i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-1} \] Упрощая, получаем \[s'_5(x,\Delta_n,t)= \frac{1}{2\,h_{i-1/2}}\,{ \left( - 60\,f_{{i -1}}+ 60\,f_{{i }}- 30\,h_{{i -1/2}}m_{{i -1}}+ 5\,h_{i -1/2}^{2}M_{{i }}- 5\,M_{{i -1}}h_{i -1/2}^{2}- 30\,h_{{i -1/2}}m_{{i }} \right) {\tau}^{4}}+\] \[+ \frac{1}{2\,h_{i-1/2}}\,{ \left( - 8\,h_{i -1/2}^{2}M_{{i }}+ 64\,h_{i -1/2} m_{{i -1}}+ 12\,M_{{i -1}}h_{i -1/2}^{2}+ 56\,{h_{{i -1/2} }}m_{{i }}+ 120\,f_{{i -1}}- 120\,f_{{i }} \right) {\tau}^{3}}+ \] \[+\frac{1}{2\,h_{i-1/2}}\,{ \left( - 9\,M_{{i -1}}h_{i -1/2}^{2}- 24\,{h_{{i -1/2}}}m_{{i }}- 60\,f_{{i -1}}- 36\,m_{{i -1}}h_{i -1/2}+ 3\,h_{i -1/2}^{2}M_{{i }}+ 60\,f_{{i }} \right) {\tau}^{2}}+ M_{{i -1}}\,h_{i -1/2}\tau+ m_{{i -1}} \]
Вторая производная будет равна \[ s_5^{(2)}(x,\Delta_n,t)=2\,f_{{i -1}} \left( 1+2\,{\tau} \right) h_{i -1/2}^{-2}-8\,f_{{i -1}} \left( 1-{\tau} \right) h_{i -1/2}^{-2}+2\,f_{{i }} \left( 3-2\,{\tau} \right) h_{i -1/2}^{-2}-8\,{\frac {f_{{i }}\tau}{ h_{i -1/2}^{2}}}-\] \[-4\,m_{{i -1}} \left( 1-\tau \right) h_{i -1/2}^{-1}+2\,{\frac {m_{{i -1}}\tau}{h_{i -1/2}^{2}}}-2\,m_{{i }} \left( 1-{\tau}\right) h_{i -1/2}^{-1}+4\,{\frac {m_{{i }}\tau}{h_{i -1/2}^{2}}}+\] \[+2\, \left( 1-{\tau} \right) ^{2} \left( { \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{ {i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }}-3\, \left( m_{{i -1}}+m _{{i }} \right) h_{{i -1/2}} \right) \tau}+ 0.5\,M_{ {i -1}}h_{i -1/2}^{2}+3\,f_{{i -1}}-3\,f_{{i }}+ \left( 2\,m_{ {i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-2}-\] \[- 8\,\tau\, \left( 1-{\tau} \right) \left( { \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }}-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) \tau}+ 0.5\,M_{{i -1}} h_{i -1/2}^{2}+3\,f_{{i -1}}-3\,f_{{i }}+ \left( 2\,m_{{i -1}} +m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-2}+\] \[+4\,\tau \, \left( 1-{\tau} \right) ^{2} \left( 0.5\,{h _{{i -1/2}}}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}} +6\,f_{{i }}-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-2}+\] \[+2\,{\tau}^{2} \left( { \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{ {i -1}}+6\,f_{{i }}-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) \tau}+ 0.5\,M_{{i -1}}h_{i -1/2}^{2}+3\,f_{{i -1}}-3\,f_{{i }}+ \left( 2\,m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-2}-\] \[-4\,{\tau}^{2} \left( 1-{\tau} \right) \left( 0.5\,{h_{{i -1/2}}}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_ {{i }}-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-2} \] После упрощений получаем \[s_5^{(2)}(x,\Delta_n,t)= \frac{1}{h_{i-1/2}^2}\,{ \left( - 120\,f_{{i -1}}+ 10\,h_{i -1/2}^{2}M_{{i }}+ 120\,f_{{i }}- 10\,M_{{i -1}}h_{i -1/2}^{2}- 60\,h_{{ i -1/2}}m_{{i }}- 60\,h_{{i -1/2}}m_{{i -1}} \right) {\tau}^{3}}+\] \[ +\frac{1}{h_{i-1/2}^2}\,{ \left( 84\,h_{i -1/2}m_{{ i }}- 12\,h_{i -1/2}^{2}M_{{i }}+ 18\,M_{{i -1}}h_{i -1/2}^{2}+ 180\,f_{{i -1}}- 180\,f_{{i }} + 96\,h_{i -1/2}m_{{i -1}} \right) {\tau}^{2}}+\] \[ +\frac{1}{h_{i-1/2}^2}\, { \left( - 9\,M_{{i -1}}h_{i -1/2}^{2}- 24\,h_{i -1/2}m_{{i }}- 60\,f_{{i -1}}- 36\,m_{{i -1}}h_{i -1/2}+ 3\,h_{i -1/2}^{2}M_{{i }}+ 60\,f_{{i }} \right) \tau}+M_{{i -1}} \] Третья \[ s_5^{(3)}(x,\Delta_n,t)=12\,{\frac {f_{{i -1}}}{h_{i -1/2}^{3}}}-12\,{\frac {f_{{i }}}{ h_{i -1/2}^{3}}}+6\,{\frac {m_{{i -1}}}{h_{i -1/2}^{2}}}+6 \,{\frac {m_{{i }}}{h_{i -1/2}^{2}}}-\] \[- 12\, \left( 1-\tau \right) \left( { \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }} -3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) \tau}+ 0.5\,M_{{i -1}}h_{i -1/2}^{2}+3\,f_{{i -1}}-3 \,f_{{i }}+ \left( 2\,m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-3}+\] \[+6\, \left( 1-{\tau} \right) ^{2} \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{{ i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }}-3\, \left( m_{{i -1}}+m_ {{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-3}+\] \[+12\,\tau\, \left( { \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{ {i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }}-3\, \left( m_{{i -1}}+m _{{i }} \right) h_{{i -1/2}} \right) \tau}+ 0.5\,M_{ {i -1}}h_{i -1/2}^{2}+3\,f_{{i -1}}-3\,f_{{i }}+ \left( 2\,m_{ {i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-3}-\] \[- 24\,\tau\, \left( 1-{\tau} \right) \left( 0.5 \,h_{i -1/2}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }}-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-3}+6\,{\frac {{\tau}^{2} \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+ 6\,f_{{i }}-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) }{h_{i -1/2}^{3}}} \] После несложных преобразований получаем \[s_5^{(3)}(x,\Delta_n,t)= \frac{3}{h_{i-1/2}^3}\,{ \left( - 120\,f_{{i -1}}+ 10\,h_{i -1/2}^{2}M _{{i }}+ 120\,f_{{i }}- 10\,M_{{i -1}}h_{i -1/2}^{2}- 60 \,h_{{i -1/2}}m_{{i }}- 60\,h_{{i -1/2}}m_{{i -1}} \right) {\tau }^{2}}+ \] \[+ \frac{3}{h_{i-1/2}^3}\,{ \left( - 8\,{h_{{i -1/2}}}^{2}M_{{i }}+ 64\,h_{i -1/2}m_{{i -1}}+ 12\,M_{{i - 1}}h_{i -1/2}^{2}+ 56\,h_{i -1/2}m_{{i }}+ 120\,f_{{i -1}}- 120\,f_{{i }} \right) \tau}+\] \[+ \frac{3}{h_{i-1/2}^3}\, \left( {- 12\,m_{{i -1}}h_{i -1/2}- 8\,h_{i -1/2}m_{{i }}- 20\,f_{{i -1}} - 3\,M_{{i -1}}h_{i -1/2}^{2}+ 20\,f_{{i }}+h_{i -1/2}^{2}M_{{i }}}\right). \] и, наконец, четвертая производная сплайна будет иметь вид \[ s_5^{(4)}(x,\Delta_n,t)=24\, \left({ \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }} -M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }}-3\, \left( m_{{i -1 }}+m_{{i }} \right) h_{{i -1/2}} \right) \tau}+ 0.5 \,M_{{i -1}}h_{i -1/2}^{2}+3\,f_{{i -1}}-3\,f_{{i }}+ \left( 2 \,m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^ {-4}-\] \[-48\, \left( 1-{\tau} \right) \left( 0.5 \,h_{i -1/2}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_{{i }}-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) h_{i -1/2}^{-4}+48\,{\frac { \left( 0.5\,h_{i -1/2}^{2} \left( M_{{i }}-M_{{i -1}} \right) -6\,f_{{i -1}}+6\,f_{{ i }}-3\, \left( m_{{i -1}}+m_{{i }} \right) h_{{i -1/2}} \right) \tau}{h_{i -1/2}^{4}}} \] После преобразований, имеем \[s_5^{(4)}(x,\Delta_n,t)= \frac{12}{h_{i-1/2}^4}\,{ \left( - 60\,f_{{i -1}}+ 60\,f_{{i }}- 30\,h_{{i -1/2}}m_{{i }}- 5\,M_{{i -1}}h_{i -1/2}^{2}- 30\,h_{{i -1/2}}m_{{i -1}}+ 5\,h_{i -1/2}^{2}M_{{i }} \right) \tau}+\] \[+ \frac{12}{h_{i-1/2}^4}\,\left({ 3\,M_{{i -1}}h_{i -1/2}^{2}+ 16\,h_{i -1/2}m_{{i -1}}- 30\,f_{{i }}+ 30\,f_{{i -1}}+ 14\,h_{i -1/2}m_{{i }}- 2\,h_{i -1/2}^{2}M_{{i }}}\right). \] Заметим, что \[ s_5^{(3)}(x,\Delta_n,t_i-0)= 3\,{\frac {- 20\,f_{{i -1}}+ 20\,f_{{i }}- 8\,h_{{i -1/2}} m_{{i -1}}- 12\,h_{{i -1/2}}m_{{i }}+ 3\,h_{i -1/2}^{2}M_{ {i }}- 1\,M_{{i -1}}h_{i -1/2}^{2}}{h_{i -1/2}^{3}}}, \] и \[s_5^{(3)}(x,\Delta_n,t_i+0)= - 3\,{\frac { 20\,f_{{i }}- 20\,f_{{i +1}}+ 12\,h_{{i +1/2}} m_{{i }}+ 8\,h_{{i +1/2}}m_{{i +1}}+ 3\,M_{{i }}h_{i +1/2}^{2}- 1\,M_{{i +1}}h_{i +1/2}^{2}}{h_{i +1/2}^{3}}} \] Тогда условие непрерывности третьей производной сплайна в точке \(t_i\): \(s_5^{(3)}(x,\Delta_n,t_i+0)=s_5^{(3)}(x,\Delta_n,t_i-0)\) будет равно \[ 3\,{\frac {- 20\,f_{{i -1}}+ 20\,f_{{i }}- 8\,h_{{i -1/2}} m_{{i -1}}- 12\,h_{{i -1/2}}m_{{i }}+ 3\,h_{i -1/2}^{2}M_{ {i }}- 1\,M_{{i -1}}h_{i -1/2}^{2}}{h_{i -1/2}^{3}}}=- 3\,{\frac { 20\,f_{{i }}- 20\,f_{{i +1}}+ 12\,h_{{i +1/2}} m_{{i }}+ 8\,h_{{i +1/2}}m_{{i +1}}+ 3\,M_{{i }}h_{i +1/2}^{2}- 1\,M_{{i +1}}h_{i +1/2}^{2}}{h_{i +1/2}^{3}}} \] Отсюда, условие непрерывности третьей производной будет \begin{equation}\label{e:1} M_{i-1}\frac{1}{h_{i-1/2}}- 3\,M_i\left(\frac{1}{h_{i-1/2}}+\frac{1}{h_{i+1/2}}\right)+M_{i+1}\frac{1}{h_{i+1/2}} +8\,m_{i-1}\frac{1}{h_{i-1/2}^2}+12\,m_i\left(\frac{1}{h_{i-1/2}^2}-\frac{1}{h_{i+1/2}^2}\right)-8\,m_{i+1}\frac{1}{h_{i+1/2}^2}= \end{equation} \[= -20f_{i-1}\frac{1}{h_{i-1/2}^3}+20\,f_i\left(\frac{1}{h_{i-1/2}^3}+\frac{1}{h_{i+1/2}^3}\right)-20f_{i+1}\frac{1}{h_{i+1/2}^3}, (i=1,...,n-1). \] Условие непрерывности четвертой производной будет в узле \(t_i\): \(s_5^{(4)}(x,\Delta_n,t_i+0)=s_5^{(4)}(x,\Delta_n,t_i-0)\) \[ 12\,{\frac { 3\,h_{i -1/2}^{2}M_{{i }}- 30\,f_{{i -1}}+ 30\,f_{{i }}- 14\,h_{{i -1/2}}m_{{i -1}}- 16\,h_{{i -1/2}}m_{{i }}- 2\,M_{{i -1}}h_{i -1/2}^{2}}{h_{i -1/2}^{4}}}= 12\,{\frac { 3\,M_{{i }}h_{i +1/2}^{2}+ 30\,f_{{i }}- 30\,f_{{i +1}}+ 16\,h_{{i +1/2}}m_{{i }}+ 14\,h_{{i +1/2}}m_{{i +1}}- 2\,M_{{i +1}}h_{i +1/2}^{2}}{h_{i +1/2}^{4}}} \] Отсюда получаем условие непрерывности четвертой производной сплайна \begin{equation}\label{e:2} 2\,M_{i-1}\frac{1}{h_{i-1/2}^2}-3\,M_i\left(\frac{1}{h_{i-1/2}^2}-\frac{1}{h_{i+1/2}^2}\right)-2\,M_{i+1}\frac{1}{h_{i+1/2}^2} +14\,m_{i-1}\frac{1}{h_{i-1/2}^3}+16\,m_i\left(\frac{1}{h_{i-1/2}^3}+\frac{1}{h_{i+1/2}^3}\right)+14\,m_{i+1}\frac{1}{h_{i+1/2}^3}= \end{equation} \[ -30\,f_{i-1}\frac{1}{h_{i-1/2}^4}+30\,f_i\left(\frac{1}{h_{i-1/2}^4}-\frac{1}{h_{i+1/2}^4}\right)+30\,f_{i+1}\frac{1}{h_{i+1/2}^4}, (i=1,...,n-1).\] Решая систему линейных уравнений (\ref{e:1}) и (\ref{e:2}), находим значения \(M_i\) и \(m_i\) \(i=1,...,n-1\), которые позволяют получить сплайн (\ref{s:5}).

Подведем итог.

Таким образом, если \(X(t)\) третья первообразная \(x(t)\) такая, что \(X''(a)=0\), \(X'(a)=0\) и \(X(a)=0\), то для фиксированного разбиения \(\Delta_n=\left\{a=t_{0}\lt t_{1}\lt\ldots \lt t_{n-1}\lt t_{n}=b\right\} \) и множества \(\{X_i\}_{i=0}^n\), где \(X_i=X(t_i)\), параболический регрессионный сплайн ( третья производная (\ref{holliday}) интерполяционного сплайна пятой степени \(s_5(X,\Delta_n)\)) для \(t\in[t_{i-1},t_i]\) будет иметь вид \begin{equation}\label{regression} \tilde{s}_2(x,\Delta_n,t)= 30\,{\frac { \left(12\,(X_{{i }}-X_{i-1}) - 6\,h_{{i -1/2}}(m_{{i -1}}+m_{{i }})+ h_{i -1/2}^{2}(M_i-M_{i-1}) \right) {\tau}^{2}}{h_{i -1/2}^{3}}}+ \end{equation} \[+12\,{\frac { \left( - 30\,(X_{{i }}-X_{i-1})+ 16\,h_{i -1/2}m_{{i -1}}+ 14\,h_{i -1/2}m_{{i }}- 2\,h_{i -1/2}^{2}M_{{i }}+ 3\,M_{{i -1}}h_{i -1/2}^{2} \right) \tau}{h_{i -1/2}^{3}}}+\] \[+ 3\,{\frac { 20\,(X_{{i }}-X_{i-1})- 8\,m_{{i }}h_{i -1/2}- 12\,m_{{i -1}}h_{i -1/2}+h_{i -1/2}^{2}M_{{i }} - 3\,M_{{i -1}}h_{i -1/2}^{2}}{h_{i -1/2}^{3}}} \]

Восстановление дискретных данных с помощью параболической сплайн-регрессии.

Дано: \((z_i,\hat{x}_i), i=0,1,...,N,\) где \(z_i\in [a,b]\) и будем считать (аргумент всегда можно упорядочить), что \(z_{i-1}\lt z_i, i=1,...,N.\) При этом \(a=z_0,b=z_N.\) Будем считать, что \(\hat{x}_i=x(z_i)\) и нужно получить восстановлением функции \(x(t)\) с помощью параболического регрессионного сплайна.
Тогда \[ \hat{x}_i=\int_a^b{x(t)\delta(t-z_i)}dt=\hat{x}_i\int_E{\delta(t-z_i)}dt, \] где \(\delta(t)-\) дельта-функция Дирака, а \(E\subset [a,b]\) такое, что \(z_i\in E.\) Будем считать, что \(E_i=[z_{i},z_{i+1}).\) Тогда для \(t\in E_i\) \[ \int_a^t\int_a^t{x(t)\delta(t-z_j)}dt=\int_a^t\sum_{j=0}^i\int_{E_j}{x(t)\delta(t-z_j)}dt, \] и для \(t\in E_i\) \[ \mathcal{I}(t)=\int_a^t\int_a^t{x(t)\delta(t-z_j)}dt=\sum_{j=0}^i\hat{x}_j\chi(t-z_j), \] где \(\chi(t)\) - ступенька Хевисайда \[ \chi(t)=\left\{ \begin{array}{ll} 0, & t\lt 0;\\ 1, & t\ge 0. \end{array} \right. \] Это следует из того факта, что \[ \chi(t)=\int_{-\infty}^t\delta(t)dt. \] Таким образом, \(\mathcal{I}(t)\) - кусочно-постоянная функция, принимающая значение \(\sum_{j=0}^i\hat{x}_j\) для \(t\in [z_{i},z_{i+1})\), то есть, \[ \int\int{\mathcal{I}(t)}dt \] представляет собой параболический сплайн минимального дефекта \(\hat{s}_2(\{z_i\}_{i=0}^N,t)\) по разбиению \(\{z_i\}_{i=0}^N\), такой, что \begin{equation}\label{sd2} \hat{s}''_2(\{z_i\}_{i=0}^N,t)=\mathcal{I}(t). \end{equation} Для \(t\in [z_{i},z_{i+1})\) параболический сплайн по разбиению \(\{z_i\}_{i=0}^N\) можно записать в виде \begin{equation}\label{spline_data} 2\,\mu_i \left( {\theta}^{2}- 0.5\,\theta \right) -4\,s_{i+1/2} \left( {\theta}^{2}- 0.25 \right) +2\,\mu_{{i+1}} \left( {\theta}^{2}+ 0.5\,\theta \right) \end{equation} где \(\mu_i\) - значение сплайна в узле \(z_i\), а \(s_{i+1/2}\) - его значение в точке \(z_{i+1/2}=(z_{i}+z_{i+1})/2\), а параметр \(\theta\) равен \[\theta=\frac{t-z_{i+1/2}}{\hbar_{i+1/2}}, \hbar_{i+1/2}=z_{i+1}-z_{i}, i=0,1,...,N-1.\] Для \(t\in [z_{i},z_{i+1})\) первая производная этого сплайна равна \[ \frac {2\,\mu_i \left( 2\,\theta - 0.5 \right) -8\,s_{i+1/2}\theta +2\,\mu_{{ i+1}} \left( 2\,\theta + 0.5 \right) }{\hbar_{i+1/2}} \] и для \(t\to z_i+0\) \[ {\frac {- 3\,\mu_i+ 4\,s_{i+1/2}- \,\mu_{i+1}}{\hbar_{i+1/2}}} \] а для \(t\to z_{i+1}-0\) \[ {\frac { \,\mu_i- 4\,s_{i+1/2}+ 3\,\mu_{i+1}}{\hbar_{i+1/2}}}. \] Таким образом, условие непрерывности производной сплайна в точке \(z_i\) будет иметь вид \[ {\frac {- 3\,\mu_i+ 4\,s_{i+1/2}- \,\mu_{i+1}}{\hbar_{i+1/2}}}= {\frac {\mu_{{i-1}}- 4\,s_{i-1/2}+ 3\,\mu_i}{\hbar_{i-1/2}}}, i=1,...,N-1. \] или, что то же, \[ \frac {\mu_{i+1}}{\hbar_{i+1/2}}+3\,\mu_i\left(\frac {1}{\hbar_{i+1/2}}+\frac {1}{\hbar_{i-1/2}}\right)+\frac {\mu_{i-1}}{\hbar_{i-1/2}}= 4\frac {s_{i+1/2}}{\hbar_{i+1/2}}+4\frac {s_{i-1/2}}{\hbar_{i-1/2}}, i=1,...,N-1. \] Решая эту систему, получаем значения сплайна \(\mu_i\), которые обеспечивают минимальный дефект.
Остается найти \(s_{i+1/2}\) \((i=0,...,N-1)\). Это легко сделать из условия (\ref{sd2}). Для \(t\in [z_{i},z_{i+1})\) вторая производная сплайна равна \[ {\frac {4\,\mu_{{i}}-8\,s_{{i+1/2}}+4\,\mu_{{i+1}}}{\hbar_{i+1/2}^{2}}}=\sum_{j=0}^i\hat{x}_{j} \] тогда \[s_{i+1/2}=-\frac{\hbar_{i+1/2}^2}{8}\sum_{j=0}^i\hat{x}_{j}+\frac{1}{2}(\mu_i+\mu_{i+1}). \] Таким образом, при \(t\in [z_{i},z_{i+1})\) для построения сплайна \[ \hat{s}_2(\{z_i\}_{i=0}^N,t)= 2\,\mu_i \left( {\theta}^{2}- 0.5\,\theta \right) -4\,s_{i+1/2} \left( {\theta}^{2}- 0.25 \right) +2\,\mu_{{i+1}} \left( {\theta}^{2}+ 0.5\,\theta \right) \] нужно решить систему линейных уравнений \begin{equation}\label{sys} \frac {\mu_{i+1}}{\hbar_{i+1/2}}-\,\mu_i\left(\frac {1}{\hbar_{i+1/2}}+\frac {1}{\hbar_{i-1/2}}\right)+\frac {\mu_{i}}{\hbar_{i-1/2}}= \frac {\hbar_{i+1/2}}{2}\sum_{j=0}^i\hat{x}_{j}+\frac {\hbar_{i-1/2}}{2}\sum_{j=0}^{i-1}\hat{x}_{j}, i=1,...,N-1. \end{equation} \[ \mu_0=0, \mu_N=\sum_{j=0}^{N}\hat{x}_{j}. \] Подведем итог. Для построения параболической сплайновой регрессии по набору данных \((z_i,\hat{x}_i), i=0,1,...,N,\) нужно
Решить систему (\ref{sys}), найти \(\mu_i\) и получить из (\ref{spline_data}) сплайн \(\hat{s}_2(\{z_i\}_{i=0}^N,t)\).
Для заданного разбиения \(\Delta_n=\left\{a=t_{0}\lt t_{1}\lt \ldots \lt t_{n-1}\lt t_{n}=b\right\} \) отрезка \([a,b]\) найдем \(X_i=\hat{s}_2(\{z_i\}_{i=0}^N,t_i)\) и решая систему уравнений (\ref{e:1}) и (\ref{e:2}), находим значения \(M_i\) и \(m_i\) \(i=1,...,n-1\), которые позволяют получить регрессионный сплайн (\ref{regression}).

Мы рассмотрели построение параболического регрессионного сплайна для произвольного разбиения, но, как правило, при отсутствии априорной информации о структуре разбиения, используют сплайны с узлами по равномерной решетке, то есть, по разбиению \(\bar{\Delta}_n=\left\{a+ih\right\}_{i=0}^{n-1} \), где \(h=\frac{b-a}{n}\) и, соответственно, \(t_i=a+ih,\,i=0,...,n\).
Для такого случая рассмотрим использование В-сплайнов (см., например, с. 60).
Обозначим \begin{equation} B_{0,h}(t)=\cases{1\,\,\,\,\, (|t|\lt h/2),\cr\cr 0\,\,\,\,\, (|t| \ge h/2).} \end{equation}

B-сплайн \(B_{0,h}(t)\).

Функцию \(B_{r,h}(t)\) введем с помощью рекуррентных соотношений \begin{equation} B_{r,h}(t)=\frac{1}{h}\int_{t-h/2}^{t+h/2}{B_{r-1,h}(t)dt} \,\,\,\,\,\,(r=1,2,\ldots). \end{equation} Эту функцию назовем нормализованным B- сплайном по равномерному разбиению или просто В- сплайном.
Прежде всего отметим, что В- сплайн порядка \(r\) имеет в качестве носителя (замыкание множества, где он отличен от нуля) промежуток \[d_r=\left[-\frac{r+1}{2}h,\frac{r+1}{2}h\right],\] т.е. \(B_{r,h}(t)\ne 0\) внутри отрезка \(d_r\).
Другим важным свойством В-сплайнов является тот факт, что \[ \sum_{i=-\infty}^{\infty}B_{2r-1,h}(t-ih)=1 \] и \[ \sum_{i=-\infty}^{\infty}B_{2r,h}\left(t-(2i+1)\frac{h}{2}\right)=1. \] Более того, для любого набора \(c_i\) линейная комбинация В-сплайнов \(\sum_{i=-\infty}^{\infty}c_iB_{r,h}(t-ih)\) является сплайном порядка \(r\) минимального дефекта по разбиению \(\{ih\}\).
Как было показано ранее, для построения параболического регрессионного сплайна нужно построить сплайн пятой степени минимального дефекта, который интерполирует значения \(X_i=X(a+ih)\), где \(X(t)\) третья первообразная \(x(t)\) такая, что \(X''(a)=0\), \(X'(a)=0\) и \(X(a)=0.\)
Любой \(s_5(\bar{\Delta}_n,t)\in S_{5,1}(\bar{\Delta_n})\) можно записать в виде \[ s_5(\bar{\Delta}_n,t)=\sum_{i=-2}^{n+2}c_iB_{5,h}\left(t-a-ih\right), \] где \[ B_{5,1}(t)= \cases{0,&$t\lt -3$,\cr {\frac {1}{120}}\, \left( t+3 \right) ^{5},&$t\in [-3,-2]$,\cr {\frac {17}{40}}-\frac {5}{8}\,t-\frac {7}{4}\,{t}^{2}-\frac {5}{4}\,{t}^{3}-\frac {3}{8}\,{t}^{4}-\frac {1}{24}\,{t}^{5},&$t\in [-2,-1]$,\cr {\frac {11}{20}}-\frac {1}{2}\,{t}^{2}+\frac {1}{4}\,{t}^{4}+\frac {1}{12}\,{t}^{5},&$t\in [-1,0]$,\cr {\frac {11}{20}}-\frac {1}{2}\,{t}^{2}+\frac {1}{4}\,{t}^{4}-\frac {1}{12}\,{t}^{5},&$t\in [0,1]$,\cr {\frac {17}{40}}+\frac {5}{8}\,t-\frac {7}{4}\,{t}^{2}+\frac {5}{4}\,{t}^{3}-\frac {3}{8}\,{t}^{4}+\frac {1}{24}\,{t}^{5},&$t\in [1,2]$,\cr {\frac {1}{120}}\, \left( 3-t \right) ^{5},&$t\in [2,3]$,\cr 0,&$3\leq t$.\cr} \]

B-сплайн \(B_{5,h}(t)\).

При этом \[ s_5(\bar{\Delta}_n,a+ih)=\frac{11}{20}c_i+\frac{13}{60}(c_{i-1}+c_{i+1})+\frac{1}{120}(c_{i-2}+c_{i+2})=\] \[ c_i-\frac{9}{20}c_i+\frac{13}{60}(c_{i-1}+c_{i+1})+\frac{1}{120}(c_{i-2}+c_{i+2})= \] \[ c_i+\frac{1}{4}\left(c_{i-1}-2\,c_i+c_{i+1}\right)+\frac{1}{120}\left(c_{i-2}-4\,c_{i-1}+6\,c_{i}-4\,c_{i+1}+c_{i+2}\right)= \] \[ c_i+\frac{1}{4}\Delta^2c_i+\frac{1}{120}\Delta^4c_i. \] Пусть \(f_i=f(a+ih),\) где \(f(t)\) непрерывная на \([a,b]\) функция и положим \[ \bar{c}_i=f_i-\frac{1}{4}\Delta^2f_i-\frac{1}{120}\Delta^4f_i, \] тогда \[ s_5(\{\bar{c}_i\}_{i=-2}^{n+2},\bar{\Delta}_n,a+ih)=\bar{c}_i+\frac{1}{4}\Delta^2\bar{c}_i+\frac{1}{120}\Delta^4\bar{c}_i= \] \[ f_i-\frac{1}{4}\Delta^2f_i-\frac{1}{120}\Delta^4f_i+ \frac{1}{4}\Delta^2\left(f_i-\frac{1}{4}\Delta^2f_i-\frac{1}{120}\Delta^4f_i\right)+ \frac{1}{120}\Delta^4\left(f_i-\frac{1}{4}\Delta^2f_i-\frac{1}{120}\Delta^4f_i\right)= \] \[ f_i-\frac{1}{4}\Delta^2f_i-\frac{1}{120}\Delta^4f_i+ \frac{1}{4}\Delta^2f_i-\frac{1}{16}\Delta^4f_i-\frac{1}{480}\Delta^6f_i+ \frac{1}{120}\Delta^4f_i-\frac{1}{480}\Delta^6f_i-\frac{1}{14400}\Delta^8f_i= \] \begin{equation}\label{err} f_i-\frac{1}{16}\Delta^4f_i-\frac{1}{14400}\Delta^8f_i. \end{equation} Замечая, что если функция \(f(t)\) имеет не менее чем четыре непрерывных производных, то \[ \max_i|\Delta^4f_i|=O(h^4), \] получаем, что \begin{equation}\label{mi} s_5(\{\bar{c}_i\}_{i=-2}^{n+2},\bar{\Delta}_n,a+ih)=f_i+O(h^4). \end{equation} Но если, с учетом (\ref{err}), сделаем поправку \[ \bar{c}_i=f_i-\frac{1}{4}\Delta^2f_i-\frac{1}{120}\Delta^4f_i+\frac{1}{16}\Delta^4f_i= f_i-\frac{1}{4}\Delta^2f_i+\frac{13}{240}\Delta^4f_i, \] то \[ s_5(\{\bar{c}_i\}_{i=-2}^{n+2},\bar{\Delta}_n,a+ih)=\bar{c}_i+\frac{1}{4}\Delta^2\bar{c}_i+\frac{1}{120}\Delta^4\bar{c}_i= \] \begin{equation}\label{err1} f_i+\frac{11}{960}\Delta^6f_i-\frac{13}{28800}\Delta^8f_i. \end{equation} Учитывая, что (см., например) для \(f\in C^6\) \[ s_{5,1}(f,\bar{\Delta}_n,t)=f(t)+O(h^6), \] сплайн \(s_5(\{\bar{c}_i\}_{i=-2}^{n+2},\bar{\Delta}_n,t)\) будет "почти" интерполяционный.
Учитывая, что исходные данные, как правило, заданы с ошибкой, то использование "почти" интерполяционных сплайнов имеет перед интерполяционными ряд преимуществ, во-первых, для их построения не нужно решать систему уравнений (\ref{e:1}) и (\ref{e:2}). А, во вторых, "почти" интерполяционные сплайны обладают свойством сглаживания, чем уменьшают случайную ошибку.
Для решения регрессионной задачи достаточно найти третью производную В-сплайна пятой степени \[ B_{5,1}^{(3)}(t)= \cases{ 0,&$t\lt -3$,\cr \frac{1}{2}\, \left( t+3 \right) ^{2},&$t\in [-3,-2]$,\cr -\frac{15}{2}-9\,t-\frac{5}{2}\,{t}^{2},&$t\in [-2,-1],$\cr 6\,t+5\,{t}^{2},&$t\in [-1,0],$\cr 6\,t-5\,{t}^{2},&$t\in [0,1],$\cr \frac{15}{2}-9\,t+\frac{5}{2}\,{t}^{2},&$t\in [1,2],$\cr -\frac{1}{2}\, \left( t-3 \right) ^{2},&$t\in [2,3],$\cr 0,&$3\lt t$.\cr} \]

Функция \(B^{(3)}_{5,h}(t)\).

Таким образом, если \(X(t)\) третья первообразная \(x(t)\) такая, что \(X''(a)=0\), \(X'(a)=0\) и \(X(a)=0\), то для фиксированного разбиения \(\bar{\Delta}_n=\left\{a+ih\right\}_{i=0}^{n-1} \) и множества \(\{X_i\}_{i=0}^n\), где \(X_i=X(t_i)\), параболический "почти" регрессионный сплайн ( третья производная (\ref{mi}) "почти" интерполяционного сплайна пятой степени \(s_5(\{\bar{c}_i\}_{i=-2}^{n+2},\bar{\Delta}_n,t)\)) будет иметь вид \begin{equation}\label{regression1} \bar{s}_2(x,\bar{\Delta}_n,t)= \sum_{i=-2}^{n+2}\left(X_i-\frac{1}{4}\Delta^2X_i+\frac{13}{240}\Delta^4X_i\right)B^{(3)}_{5,h}\left(t-a-ih\right). \end{equation} Полученное решение не является точным, как было получено ранее, но более технологично.

Решение задачи восстановления дискретных данных через параболические В-сплайны.

Как и ранее, дано: \((z_i,\hat{x}_i), i=0,1,...,N,\) где \(z_i\in [a,b]\) и будем считать (аргумент всегда можно упорядочить), что \(z_{i-1}\lt z_i, i=1,...,N\) и \(h_{i+1/2}=z_{i+1}-z_i\). При этом \(a=z_0,b=z_N.\) Будем считать, что \(\hat{x}_i=x(z_i)\) и нужно получить восстановлением функции \(x(t)\) с помощью параболического регрессионного сплайна.
Прежде всего возьмем В-сплайн второго порядка по произвольному разбиению \[B_{2,\{h_{i-1/2},h_{i+1/2},h_{i+3/2}\}}(t)= \cases{0,&$t\lt -h_{{i-1/2}}-\frac{1}{2}\,h_{i+1/2}$,\cr {\frac { \left( t+h_{{i-1/2}}+\frac {1}{2}\,h_{i+1/2}\right) ^{2}}{h_{{i-1/2}} \left( h_{i+1/2}+h_{{i-1/2}} \right) }},&$t\in \left[-h_{{i-1/2}}- \frac{1}{2}\,h_{i+1/2},-\frac{1}{2}\,h_{i+1/2}\right]$,\cr -{\frac { \left( t+\frac {1}{2}\,h_{i+1/2} \right) ^{2}}{h_{i+1/2} \left( h_{{i+3/2}}+h_{i+1/2} \right) }} -{\frac { \left( t+ \frac {1}{2}\,h_{i+1/2} \right) ^{2}}{\left( h_{i+1/2}+h_{{i-1/2}} \right)h_{i+1/2}}}-{\frac { \left( t+\frac {1}{2}\,h_{i+1/2} \right) ^{2}- \left( t+h_{{i-1/2}}+\frac {1}{2}\,h_{i+1/2} \right) ^{2}}{\left( h_{i+1/2}+h_{{i-1/2}} \right)h_{{i-1/2}}}} ,&$t\in \left[-\frac{1}{2}\,h_{i+1/2}, \frac{1}{2}\,h_{i+1/2}\right]$,\cr {\frac { \left( t-h_{{i+3/2}}-\frac {1}{2}\,h_{i+1/2} \right) ^{2}}{h_{{i+3/2}} \left( h_{i+1/2}+h_{{i+3/2}} \right) }},&$t\in \left[\frac{1}{2}\,h_{i+1/2}, h_{i+3/2}+\frac{1}{2}\,h_{i+1/2}\right]$,\cr 0,&$h_{{i+3/2}}+\frac {1}{2}\,h_{i+1/2}\le t$.\cr} \]

Параболический В-сплайн.

Тогда, если \[ s_2(\{C_i\},t)=\sum_{i=0}^{N+1}C_iB_{2,\{h_{i-1/2},h_{i+1/2},h_{i+3/2}\}}(t), \] то \[ s_2\left(\{C_i\},z_i+\frac{h_{i+1/2}}{2}\right)= \frac {1}{4}\frac {h_{i+1/2}}{h_{i+1/2}+h_{i-1/2}}C_{i-1}+ \frac {1}{4}\frac {2\,h_{i+1/2}^2+3\,h_{i-1/2}\,h_{i+1/2}+3\,h_{i+1/2}\,h_{i+3/2}+4\,h_{i-1/2}\,h_{i+3/2}}{(h_{i+1/2}+h_{i-1/2})(h_{i+3/2}+h_{i+1/2})}C_{i} +\frac {1}{4}\frac {h_{i+1/2}}{h_{i+3/2}+h_{i+1/2}}C_{i+1}. \] Остается значения \(C_i\) выбрать таким, чтобы \(s''_2(\{C_i\}_{i=0}^{N+1},z_i+h_{i+1/2}/2)=\sum_{j=0}^i\hat{x}_j\).

Вторая производная параболического В-сплайна.

Тогда \[ s''_2(\{C_i\},t)=\sum_{i=0}^{N+1}C_iB''_{2,\{h_{i-1/2},h_{i+1/2},h_{i+3/2}\}}(t), \] замечая, что \[ B''_{2,\{h_{i-1/2},h_{i+1/2},h_{i+3/2}\}}(t)= \cases{0,&$t\lt -h_{{i-1/2}}-\frac{1}{2}\,h_{i+1/2},$\cr 2\,{\frac {1}{h_{{i-1/2}} \left( h_{i+1/2}+h_{{i-1/2}} \right) }},&$t\in \left[-h_{{i-1/2}}-\frac{1}{2}\,h_{i+1/2},-\frac{1}{2}\,h_{i+1/2}\right],$\cr -2\,{\frac {1}{h_{i+1/2} \left( h_{{i+3/2}}+h_{i+1/2} \right) }}-2\,{\frac {1}{h_{i+1/2} \left( h_{i+1/2}+h_{{i-1/2}} \right) }},&$t\in \left[-\frac{1}{2}\,h_{i+1/2},\frac{1}{2}\,h_{i+1/2}\right],$\cr 2\,{\frac {1}{h_{{i+3/2}} \left( h_{{i+3/2}}+h_{i+1/2}\right) }},&$t\in \left[\frac{1}{2}\,h_{i+1/2},h_{i+3/2}+\frac{1}{2}\,h_{i+1/2}\right],$\cr 0,&$h_{{i+3/2}}+\frac{1}{2}\,h_{i+1/2}\le t,$\cr } \] то \[ s''_2\left(\{C_i\},z_i+\frac{h_{i+1/2}}{2}\right)= 2\frac {1}{h_{i+1/2}(h_{i+1/2}+h_{i-1/2})}C_{i-1}- 2\frac {2h_{i+1/2}+h_{i-1/2}+h_{i+3/2}}{h_{i+1/2}(h_i+h_{i-1/2})(h_{i+1/2}+h_{i+3/2})}C_{i}+ 2\frac {1}{h_{i+1/2}(h_{i+3/2}+h_{i+1/2})}C_{i+1}. \] Таким образом, решая систему \[ \frac {1}{h_{i+1/2}(h_{i+1/2}+h_{i-1/2})}C_{i-1}- \frac {2h_{i+1/2}+h_{i-1/2}+h_{i+3/2}}{h_{i+1/2}(h_i+h_{i-1})(h_{i+1/2}+h_{i+3/2})}C_{i}+ \frac {1}{h_{i+1/2}(h_{i+3/2}+h_{i+1/2})}C_{i+1}=\frac{1}{2}\sum_{j=0}^i\hat{x}_j, i=0,...,N, \] получаем требуемые коэффициенты и, тем самым, первообразную \(X(t)=s_2(\{C_i\},t)\).