Obscurum per obscurius.
Обработка данных, в том числе и результатов эксперимента, является важнейшим средством получения новых знаний не только в области естественных и
технических наук, но и в экономике, социологии, политике, психологии, литературоведении и в других отраслях. Эти исследования дают критерии оценки
обоснованности и приемлемости на практике любых теорий и теоретических предположений. Обработка данных направлена, как правило, на построение
математической модели исследуемого объекта или явления, а также на получение ответа на вопрос: «Достоверны ли имеющиеся данные в пределах требуемой
точности или допусков?».
Сама же математическая модель в зависимости от целей (исследование, управление, контроль) может быть использована для разных целей: для
предметно-смыслового анализа объекта или явления, прогнозирования их состояния в разных условиях функционирования, управления ими в конкретных
ситуациях, оптимизации отдельных параметров, а также для решения каких-то других специфичных задач.
Конечной целью любой обработки данных является выдвижение гипотез о классе и структуре математической модели исследуемого явления, определение
состава и объема дополнительных измерений, выбор возможных методов последующей статистической обработки и анализ выполнения основных предпосылок,
лежащих в их основе. Для ее достижения необходимо решить некоторые частные задачи, среди которых можно выделить следующие:
- Анализ, выбраковка и восстановление аномальных (сбитых) или пропущенных измерений. Эта задача связана с тем, что исходная информация обычно неоднородна по качеству. В основной массе результатов прямых измерений, получаемых с возможно малыми погрешностями, в имеющихся данных часто имеются грубые ошибки или просчеты, вызванные разными причинами. К ним могут быть отнесены особенности информационной системы (например, при использовании рекомендующих систем), а также, сбои вычислительной техники, аномалии в работе измерительных приборов и т. д. Без глубокого анализа качества данных, устранения или, хотя бы, существенного уменьшения влияния аномальных данных на результаты последующей обработки можно сделать ложные выводы об изучаемом объекте или явлении.
- Оценка параметров и числовых характеристик наблюдаемых случайных величин или процессов. Выбор методов последующей обработки, направленной на построение и проверку адекватности математической модели исследуемому явлению, существенно зависит от закона распределения наблюдаемых величин. Получаемые при решении этой задачи выводы о природе экспериментальных данных могут быть как общими (независимость измерений, характер погрешностей и др.), так и содержать детальную информацию о статистических свойствах данных (вид закона распределения, его параметры). Решение задачи предварительной обработки не является чисто математическим, а требует также и содержательного анализа изучаемого процесса, а при возможности, схемы и методики проведения эксперимента.
- Группировка исходной информации при большом объеме обрабатываемых данных. При этом должны быть учтены особенности их законов распределения, которые выявлены на предыдущем этапе обработки.
- Объединение нескольких групп измерений, полученных, возможно, в различное время или в различных условиях, для совместной обработки.
- Выявление скрытых связей и взаимовлияния различных измеряемых факторов и результирующих переменных, последовательных измерений одних и тех же величин. Решение этой задачи позволяет отобрать те переменные, которые оказывают наиболее сильное влияние на результирующий признак. Выделенные факторы используются для дальнейшей обработки, в частности, методами регрессионного анализа. Анализ корреляционных связей делает возможным выдвижение гипотез о структуре взаимосвязи переменных и, в конечном итоге, о структуре модели объекта исследований.
В ходе предварительной обработки, кроме указанных выше задач, часто решают и другие, имеющие частный характер: отображение, преобразование и унификацию типа
наблюдений, визуализацию многомерных данных и др.
Следует отметить, что в зависимости от конечных целей исследования, сложности изучаемого явления и уровня априорной информации о нем, объем задач,
выполняемых в ходе предварительной обработки, может существенно изменяться. То же самое можно сказать и о соотношении целей и задач, которые
решаются при предварительной обработке и на последующих этапах анализа, направленных на построение модели явления.
В основе Data Mining лежат методы классификации и кластеризации, моделирования и прогнозирования, генетические и эволюционные алгоритмы, методы
«мягких вычислений» и пр. Нельзя оставлять в стороне и методы прикладной статистики, которые составляют фундамент Data Mining, прежде всего это
корреляционный и регрессионный анализ, факторный и дискриминантный анализ и многое другое.
Но для того, чтобы во всем этом разобраться, нужен хоть какой-то базис, вот этому то и посвящен данный раздел.
Базовая информация.
Кое-что необходимое из линейной алгебры.
В дальнейшем нам понадобятся базовые знания из курса линейной алгебры и теории вероятностей. Не углубляясь подробно, приведем
информацию, необходимую при изложении материала последующих разделов.
Напомним, что для матрицы \(А\) размером \(n\times m\) под транспонированием понимаем замену строк столбцами с теми же номерами, в частности, если
\[
X = \left[ {{\begin{array}{*{20}c}
{{\begin{array}{*{20}c}
{x_{1,1} } \hfill \\
{x_{2,1} } \hfill \\
{x_{3,1} } \hfill \\
{x_{4,1} } \hfill \\
\end{array} }} \hfill & {{\begin{array}{*{20}c}
{x_{1,2} } \hfill \\
{x_{2,2} } \hfill \\
{x_{3,2} } \hfill \\
{x_{4,2} } \hfill \\
\end{array} }} \hfill \\
\end{array} }} \right],
\]
то
\[
X^T = \left[ {{\begin{array}{*{20}c}
{{\begin{array}{*{20}c}
{x_{1,1} } \hfill & {x_{2,1} } \hfill & {x_{3,1} } \hfill & {x_{4,1} }
\hfill \\
\end{array} }} \hfill \\
{{\begin{array}{*{20}c}
{x_{1,2} } \hfill & {x_{2,2} } \hfill & {x_{3,2} } \hfill & {x_{4,2} }
\hfill \\
\end{array} }} \hfill \\
\end{array} }} \right].
\]
Важной характеристикой, используемой в дальнейшем, является скалярное произведение двух векторов
\[
\left\langle {X,Y} \right\rangle = X^TY = x_1 y_1 + x_2 y_2 + ... + x_n y_n
= \sum\limits_{i = 1}^n {x_i y_i } ,
\]
где
\[
X^T = \left[ {{\begin{array}{*{20}c}
{x_1 } \hfill & {x_2 } \hfill & \cdots \hfill & {x_n } \hfill \\
\end{array} }} \right]\mbox{и}
\quad
Y = \left[ {{\begin{array}{*{20}c}
{y_1 } \hfill \\
{y_2 } \hfill \\
\vdots \hfill \\
{y_n } \hfill \\
\end{array} }} \right].
\]
С другой стороны, замечая, что \(\left\langle {X,Y} \right\rangle = \left| X \right|\left| Y \right|\cos \theta \), где \(\theta \) угол между векторами X и Y, имеем
\[
\cos \theta = \frac{X^TY}{\left| X \right|\left| Y \right|}.
\]
Таким образом, скалярное произведение характеризует отклонение вектора X от вектора Y. Евклидовой метрикой или длиной вектора называется число
\[
\left| X \right| = \sqrt {\left\langle {X,X} \right\rangle } = \sqrt
{\sum\limits_{i = 1}^n {x_i^2 } } ,
\]
а евклидовым расстоянием между двумя векторами назовем число
\[
\left| {X - Y} \right| = \sqrt {\sum\limits_{i = 1}^n {\left( {x_i - y_i }
\right)^2.} }
\]
Векторы \(X_1, X_2, \ldots, X_m\) называются линейно независимыми, если равенство
\[
\alpha _1 X_1 + \alpha _2 X_2 + ... + \alpha _m X_m = 0
\]
выполняется тогда и только тогда, когда все \(\alpha _i = 0,i = 1,2,...,m.\)
Если выполнение этого условия возможно хотя бы при одном \(\alpha _i \ne 0,\) то эта система векторов является линейно зависимой.
Множество всех векторов размерности n называется векторным пространством V той же размерности.
Множество векторов \(\left\{ {U_1 ,U_2 ,...,U_m } \right\}\) называется
базисом векторного пространства \(V\), если для \(\forall v \in V\) найдется такое множество \(\left\{ {\alpha _i } \right\}_{i = 1}^m \), что
\[
v = \alpha _1 U_1 + \alpha _2 U_2 + ... + \alpha _m U_m .
\]
Базис \(\left\{ {U_1 ,U_2 ,...,U_m } \right\}\) называется ортогональным, если \(U_i \bot U_j \) для \(\forall i \ne j\) (т.е. \(\left\langle {U_i ,U_j } \right\rangle = 0)\), если же при этом \(\left| {U_i } \right| = 1,i =1,...,m\), то базис называется ортонормированным.
Если для квадратной матрицы \(А\) размером \(m\times m\) найдется ненулевой вектор \(Х\) такой, что выполняется условие \(AX = \lambda X\), то \(Х\) называется собственным вектором матрицы \(А\), а число \(\lambda \) называется собственным значением матрицы. Таким образом, линейное преобразование, реализованное матрицей \(А,\) переводит собственный вектор \(Х\) в коллинеарный, направленный в ту же сторону, если \(\lambda \gt 0\), и в обратную, если \(\lambda \lt 0\).
Отметим несколько важных свойств собственных чисел.
Если матрица \(А\) действительна и симметрична (то есть \(A^T = A)\), то все собственные значения действительны.
Если матрица не сингулярная (то есть ее ранг равен числу строк), то ее
собственные числа не нулевые.
Если матрица \(А\) положительно определена (то есть \(X^TAX > 0)\), то все ее собственные числа положительны.
Кое-что необходимое из теории вероятностей.
Пусть \(\Omega \) - множество всех возможных исходов некоторых событий, и S - алгебра событий, то есть S совокупность подмножеств множества \(\Omega \), для которого выполнены следующие условия:
S содержит невозможное и достоверное события.
Если события \(A{ }_1,A_2 ,...\)(конечное или счетное множество) принадлежит S, то S принадлежит сумма, произведение и дополнение этих событий.
Вероятностью называется функция \(P(A),\) определенная на S, принимающая
действительные значения и удовлетворяющая аксиомам:
Аксиома неотрицательности: \(\forall A \in S:P(A) \ge 0.\)
Аксиома нормированности: вероятность достоверного события равна единице: \(P(\Omega ) = 1.\)
Аксиома аддитивности: вероятность суммы несовместных событий равна сумме вероятностей этих событий: если \(A_i \cap A_j = \emptyset (i \ne j),\) то
\[
P\left( {\bigcup\limits_k {A_k } } \right) = \sum\limits_k {P(A_k )} .
\]
Приведем свойства вероятности:
\[
P\left( \emptyset \right) = 0;
\]
\[
P\left( A \right) \le 1;
\]
\[
A \subset B \Rightarrow P\left( A \right) \lt P\left( B \right);
\]
\[
P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left(
{A \cap B} \right).
\]
Вероятность того, что произойдет событие \(А\) при условии, что произошло событие \(В,\) называется условной вероятностью \(P\left( {A\left| B \right.} \right)\) и вычисляется следующим образом
\[
P(A\vert B) = \frac{P(A \cap B)}{P(B)}.
\]
В случае, если события А и В независимы, то \(P(A \cap B) = P(A)P(B)\), и для условной вероятности можно записать
\[
P(A\vert B) = \frac{P(A \cap B)}{P(B)} = \frac{P(A)P(B)}{P(B)} = P(A).
\]
Пусть
\[
A = \left( {A \cap B_1 } \right) \cup \left( {A \cap B_2 } \right) \cup
\left( {A \cap B_3 } \right) \cup ... \cup \left( {A \cap B_n } \right),
\]
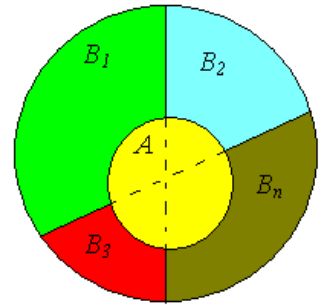
Иллюстрация формулы полной вероятности.
тогда из формулы условной вероятности получаем
\[
P(A) = P\left( {A\left| {B_1 } \right.} \right)P\left( {B_1 } \right) +
P\left( {A\left| {B_2 } \right.} \right)P\left( {B_2 } \right) + ... +
P\left( {A\left| {B_n } \right.} \right)P\left( {B_n } \right),
\]
то есть
\[
P(A) = \sum\limits_{k = 1}^n {P(A\vert B_k )P(B_k ).}
\]
Важную роль в дальнейших рассуждениях играет формула Байеса или теорема гипотез. Это утверждение позволяет переоценить вероятность гипотез \(B_i \),
принятых до опыта (события) и называемых априорными (a priori -- до опыта) по результатам уже проведенного опыта, то есть используя апостериорные (a posteriori- после опыта) вероятности. Пусть \(B_1 ,B_2 ,...,B_n \) составляющие множества S, тогда вероятность того, что событие \(A\) приведет к событию \(B_i \) будет равно
\[
P(B_i \vert A) = \frac{P(B_i \cap A)}{P(A)} = \frac{P(A\vert B_i )P(B_i
)}{\sum\limits_{k = 1}^n {P(A\vert B_k )P(B_k )} }.
\]
Случайной величиной \(Х\) называется функция, определенная на множестве событий \(\Omega \), которая каждому элементарному событию \(\omega\) ставит в соответствие число \(X\left( \omega \right).\) Случайная величина может быть дискретная и непрерывная.
Любое правило, позволяющее находить вероятности произвольных событий \(A \subseteq S\), называется законом распределения случайной величины, и при этом говорят, что случайная величина подчиняется данному закону
распределения.
Функцией распределения случайной величины \(Х\) называется функция \(F(x)\), которая для любого \(x \in R\) равна вероятности события \(\left\{ {X \le x} \right\}\)
\[
F(x) = P\{X \le x\}.
\]
Функция распределения обладает следующими свойствами
\[
0 \le F(x) \le 1,
\]
\(F(x)\) неубывающая функция, то есть, если \(x_2 \gt x_1\) , то
\(
F(x_2 ) \ge F(x_1 ),
\)
кроме того,
\(
F( - \infty ) = 0,F( + \infty ) = 1
\)
и
\(
P\{a \le X \lt b\} = F(b) - F(a).
\)
Для дискретной случайной величины \(X\) положим
\(
p\left( x \right) = P\left( {X = x} \right),
\)
тогда
\[
F(x) = P(X \le x) = \sum\limits_{a \le x} {P(X = x) = } \sum\limits_{a \le
x} {p(x).}
\]
Для непрерывной случайной величины функцию \(f(x) \ge 0\) назовем функцией плотности распределения вероятностей, если
\[
F(a) = P(X \le a) = \int\limits_{ - \infty }^a {f(x)dx} .
\]
Тогда
\[
P(a \le x \le b) = \int\limits_a^b {f(x)dx.}
\]
Заметим, что
\(
\frac{d}{dx}F(x) = f(x),
\)
кроме того,
\[
P(x = a) = \int\limits_a^a {f(x)dx = 0,} \mbox{и}
\quad P( - \infty \le x \le \infty ) = \int\limits_{ - \infty }^\infty {f(x)dx = 1.}
\]
Рассмотрим некоторые важные характеристики случайной величины. Первый момент случайной величины называется математическим ожиданием. Для дискретного случая математическое ожидание будет иметь вид
\(
\mu = E(X) = \sum\limits_x {xp(x)} ,
\)
для непрерывного случая
\(
\mu = E(X) = \int\limits_{ - \infty }^\infty {xf(x)dx.}
\)
Величина
\[
\sigma ^2 = \mbox{var}(X) = E\left( {(X - E(X))^2} \right)
\]
называется вариацией или дисперсией. Это число характеризует разброс
случайной величины, а \(\sigma \) называется среднеквадратичным отклонением случайной величины от математического ожидания.
Особую роль в теории вероятностей играет нормальный закон (закон Гаусса), что обусловлено, прежде всего, тем фактом, что он является предельным законом, к которому приближаются (при определенных условиях) другие законы распределения.
Будем говорить, что непрерывная случайная величина \(Х\) распределена по
нормальному закону \(N(\mu ,\sigma )\), если ее плотность распределения имеет вид (функция Гаусса)
\[
f(x) = \frac{1}{\sigma \sqrt {2\pi } }\exp \left( { - \frac{\left( {x - \mu
} \right)^2}{2\sigma ^2}} \right),x \in R.
\]
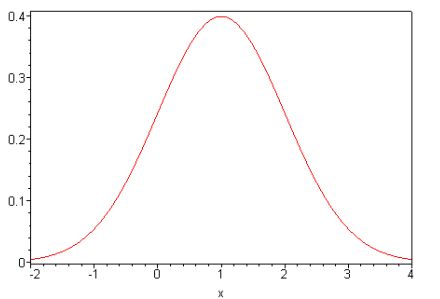
График функции плотности нормального распределения (функция Гаусса) для \(\mu = 1,\sigma = 1.\)}
Заметим, что, в соответствии с нормальным законом распределяются самые
различные величины, например, ошибки измерений, износ деталей в механизмах, вес плодов и животных, рост человека, колебания курса акций и многое другое.
Несмотря на важность одномерного случая, для нас более актуальным является рассмотрение случая многих переменных.
Упорядоченный набор \(\left( {X_1 ,X_2 ,...,X_n } \right)\) случайных величин \(X_i\) \((i = 1,2,\ldots,n),\) заданных на одном и том же множестве \(\Omega \) называется n-мерной случайной величиной. Одномерные случайные величины \(X_1 ,X_2 ,...,X_n \) называются компонентами \(n\)-мерной случайной величины. Компоненты удобно рассматривать как координаты случайного вектора \(X = (X_1,X_2 ,...,X_n)\) в пространстве n измерений.
Упорядоченная пара \(\left( {X,Y} \right)\) двух случайных величин называется двумерной случайной величиной. Полной характеристикой системы \(\left( {X,Y} \right)\) является ее закон распределения вероятностей, указывающий область возможных значений системы случайных величин и вероятности этих значений.
Функцией распределения двумерной случайной величины \(\left( {X,Y} \right)\) называется функция \(F(x,y)\), которая для любых двух действительных чисел \(x\) и \(y\) равна вероятности совместного выполнения двух событий \(\left\{ {X \le x} \right\}\) и \(\left\{ {Y \le y} \right\},\) то есть
\[
F(x,y) = P\{X\le x,Y \le y\} = P(\omega \in \Omega,
X(\omega) \le x,Y(\omega) \le y).
\]
Для дискретной случайной пары \(\left( {X,Y} \right)\) в качестве функции плотности положим
\(
p(x,y) = P(X = x,Y = y),
\)
в непрерывном случае \(f(x,y) \ge 0\) назовем функцией плотности распределения вероятностей, если
\[
F(a,b) = P(X \le a,Y \le b) = \int\limits_{ - \infty }^a {\int\limits_{ - \infty }^b {f(x,y)dx} dy} .
\]
Тогда
\[
P(a \le x \le b,c \le y \le d) = \int\limits_a^b {\int\limits_c^d {f(x,y)dx}dy}
\]
Заметим, что
\[
\frac{\partial ^2}{\partial x\partial y}F(x,y) = f(x,y).
\]
Важную роль в дальнейших исследованиях играет смешанный момент второго
порядка, называемый ковариацией
\[
\mbox{cov }\left( {\mbox{X,Y}} \right)\mbox{ = E}\left( {\left( {\mbox{X -
E(X)}} \right)\left( {\mbox{Y - E(Y)}} \right)} \right) = \mbox{E(XY) -E(X)E(Y).}
\]
В координатной форме ковариацию можно записать в виде
\[
\mbox{cov}(X,Y) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\left( {x_i - \mu
_X } \right)\left( {y_j - \mu _Y } \right)p_{i,j} } } ,
\]
где \(p_{i,j} = p(x_i ,y_j ).\)
Если для двух случайных величин X и Y при возрастании одной случайной
величины есть тенденция к возрастанию другой, то \(\mbox{cov}(X,Y) > 0\), если при возрастании одной случайной величины есть тенденция к убыванию другой, то \(\mbox{cov}(X,Y) < 0\).
Если же поведение не предсказуемо, то \(\mbox{cov}(X,Y) = 0.\) В этом случае говорят, что случайные величины некоррелируемы, но это не значит, что они независимы, правда, для независимых случайных величин \(\mbox{cov}(X,Y) = 0\).
Нормализованную ковариацию называют корреляцией
\[
- 1 \le \mbox{cor}(X,Y) = \frac{\mbox{cov}(X,Y)}{\sqrt {\mbox{var}(X)\mbox{var}(Y)} } \le 1.
\]
Пусть \(X = \left( {X_1 ,X_2 ,...,X_n } \right)\) вектор, координаты которого являются случайными величинами, тогда
\[
\mbox{cov}\left( X \right) = \mbox{cov}\left( {X_1 ,X_2 ,...,X_n } \right) = \Sigma = E\left( {\left( {X - u} \right)\left( {X - u} \right)^T} \right) =
\]
\[
= \left( {{\begin{array}{*{20}c}
{E\left( {\left( {X_1 - \mu _1 } \right)\left( {X_1 - \mu _1 } \right)}
\right)} \hfill & \cdots \hfill & {E\left( {\left( {X_n - \mu _n }
\right)\left( {X_1 - \mu _1 } \right)} \right)} \hfill \\
\vdots \hfill & \ddots \hfill & \vdots \hfill \\
{E\left( {\left( {X_1 - \mu _1 } \right)\left( {X_n - \mu _n } \right)}
\right)} \hfill & \cdots \hfill & {E\left( {\left( {X_n - \mu _n }
\right)\left( {X_n - \mu _n } \right)} \right)} \hfill \\
\end{array} }} \right).
\]
Матрица \(\Sigma \) называется ковариационной.
Для случая многих переменных непрерывная n-мерная случайная величина \(Х\) распределена по нормальному закону \(N(\mu ,\Sigma )\), если ее плотность распределения имеет вид
\[
f(x) = \frac{1}{\left( {2\pi } \right)^{n / 2}\left| \Sigma \right|^{1 / 2}}\exp \left( { - \frac{1}{2}\left( {\left( {x - \mu } \right)^T\Sigma ^{ - 1}\left( {x - \mu } \right)} \right)} \right) =
\]
\[
= \frac{1}{\left( {2\pi } \right)^{n / 2}\left| \Sigma \right|^{1 / 2}}\exp
\left( { - \frac{1}{2}\left( {\left( {x_1 - \mu _1 ,...,x_n - \mu _n }
\right)\Sigma ^{ - 1}\left( {{\begin{array}{*{20}c}
{x_1 - \mu _1 } \hfill \\
\vdots \hfill \\
{x_n - \mu _n } \hfill \\
\end{array} }} \right)} \right)} \right),
\]
здесь \(\Sigma \) ковариационная матрица, \(\vert \Sigma \vert \) - ее
определитель и \(\Sigma ^{-1}\) матрица, обратная к ковариационной.
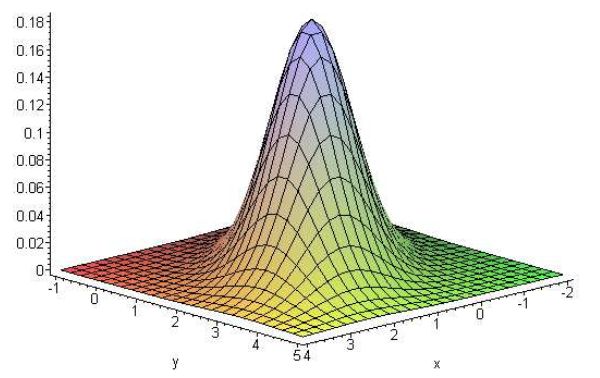
График функции плотности \(N\left( {\left( {{\begin{array}{*{20}c}
1 \hfill \\
2 \hfill \\
\end{array} }} \right),\left( {{\begin{array}{*{20}c}
1 \hfill & {0.5} \hfill \\
{0.5} \hfill & 1 \hfill \\
\end{array} }} \right)} \right)\).
Если все величины \(\left( {X_1 ,X_2 ,...,X_n } \right)\) независимы, то
функция плотности будет иметь вид
\[
f(x) = \prod\limits_{i = 1}^n {\frac{1}{\sigma _i \sqrt {2\pi } }\exp \left(
{ - \frac{\left( {x_i - \mu _i } \right)^2}{2\sigma _i^2 }} \right).}
\]
Пусть \(\Phi \) матрица, столбцы которой являются нормированными собственными векторами матрицы \(\Sigma \), тогда (в силу ортонормированности)
\[
\Phi ^{ - 1} = \Phi ^T.
\]
Если \(\Sigma \Phi = \Phi \Lambda \), то \(\Lambda \) диагональная матрица с соответствующими собственными значениями матрицы \(\Sigma \) на диагонали, тогда \(\Sigma = \Phi \Lambda \Phi ^{ - 1}\) и, следовательно, \(\Sigma ^{ - 1}= \Phi \Lambda ^{ - 1}\Phi ^{ - 1}\). Через \(\Lambda ^{ - 1 / 2}\) обозначим матрицу, такую, что \(\Lambda ^{ - 1 / 2}\Lambda ^{ - 1 / 2} = \Lambda ^{ - 1}\), тогда \(\Sigma ^{ - 1} = \left( {\Phi \Lambda ^{ - 1 / 2}} \right)\left({\Phi \Lambda ^{ - 1 / 2}} \right)^T = \Xi \Xi ^T\).
Таким образом,
\[
\left( {\left( {x - \mu } \right)^T\Sigma ^{ - 1}\left( {x - \mu } \right)}\right) = \left( {\left( {x - \mu } \right)^T\Xi \Xi ^T\left( {x - \mu }\right)} \right) =\]
\[= \left( {\Xi ^T\left( {x - \mu } \right)} \right)^T\left(
{\Xi ^T\left( {x - \mu } \right)} \right) = \left| {\Xi ^T\left( {x - \mu }\right)} \right|^2.
\]
Замечая, что матрица \(\Xi \) представляет собой матрицу преобразований
(поворотов и растяжений), получаем, что точки x, удовлетворяющие условию \(\left| {\Xi ^T\left( {x - \mu } \right)} \right|^2 \equiv const\) лежат на эллипсе.
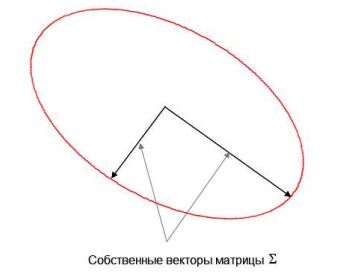
Множество точек равноудаленных от центра в смысле расстояния Махаланобиса.
Число \(\sqrt {\left( {\left( {x - \mu } \right)^T\Sigma ^{ - 1}\left( {x -\mu } \right)} \right)} \) называется расстоянием Махаланобиса (Mahalanobis) между \(x\) и \(\mu \). В частности, если все величины \(\left( {X_1 ,X_2 ,...,X_n } \right)\) независимы, то в этом случае расстояние Махаланобиса вырождается в Евклидово расстояние \(\sqrt {\left( {\left( {x - \mu } \right)^T\left( {x - \mu } \right)} \right)} \).
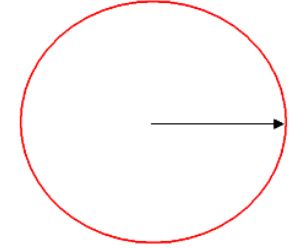
Множество точек равноудаленных от центра в смысле расстояния Евклида.
Приведем пример двумерной функции Гаусса.
Пусть \(\mu = (1,2),\Sigma = \left( {{\begin{array}{*{20}c}
1 \hfill & {0.5} \hfill \\
{0.5} \hfill & 1 \hfill \\
\end{array} }} \right)\), тогда линии уровня соответствующей функции Гаусса будут иметь вид

Изолинии функции Гаусса при \(\mu = (1,2),\Sigma = \left( {{\begin{array}{*{20}c}
1 \hfill & {0.5} \hfill \\
{0.5} \hfill & 1 \hfill \\
\end{array} }} \right)\).
Если \(\mu = (1,2), \Sigma = \left( {{\begin{array}{*{20}c}
1 \hfill & {0.} \hfill \\
0 \hfill & 1 \hfill \\
\end{array} }} \right)\), то
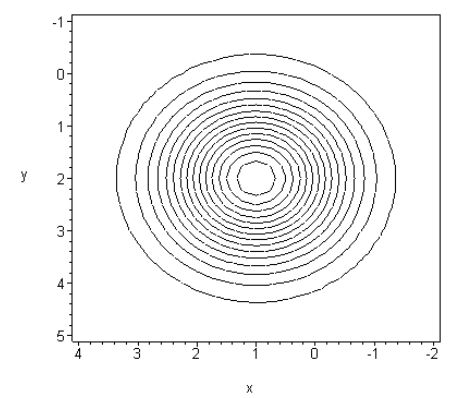
Изолинии сферической функции Гаусса при \(\mu = (1,2), \Sigma = \left( {{\begin{array}{*{20}c}
1 \hfill & {0.} \hfill \\
0 \hfill & 1 \hfill \\
\end{array} }} \right)\).
Если n-мерная случайная величина \(X\) имеет плотность \(N\left( {\mu ,\Sigma } \right)\), то величина \(AX\) имеет плотность \(N\left( {A^T\mu ,A^T\Sigma A} \right)\), таким образом для любой случайной величины \(X\) можно подобрать преобразование, переводящее в случайную величину со сферической плотностью распределения.
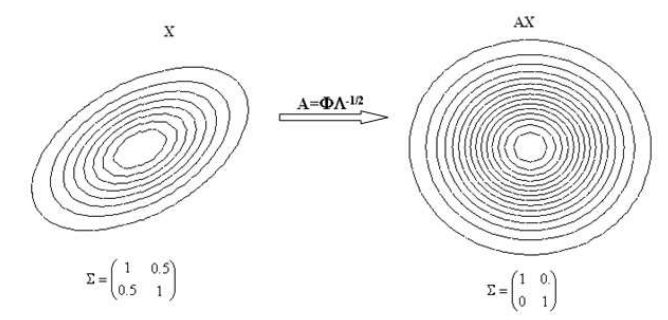
Преобразование случайной величины с плотностью распределения при \(\Sigma = \left( {{\begin{array}{*{20}c}
1 \hfill & {0.5} \hfill \\
{0.5} \hfill & 1 \hfill \\
\end{array} }} \right)\) в случайную величину со сферической функцией плотности.
При исследовании разного рода задач достаточно часто возникает необходимость нахождения решения той или иной экстремальной задачи. Эта проблема
сама по себе обширна и многогранна, но для решения проблем, возникающих в русле интересов данного обзора, по большей части, можно обойтись
достаточно простыми инструментами, которые мы и рассмотрим.
Метод Ньютона-Рафсона (одномерный случай).
Часто этот метод называют методом касательных или просто методом Ньютона.
Для того, чтобы найти численное решение алгебраического уравнения \(f(x)=0\), вначале выбирается случайное начальное значение \(x_0\)
и далее проводятся итерации:
\[
x\Leftarrow x-\frac{f(x)}{f'(x)}.
\]
Эта формула может быть получена следующим образом.
Уравнение касательной к \(f(x)\) в точке \(x=x_0\) имеет вид
\[
f'(x)=\frac{f(x_1)-f(x_0)}{x_1-x_0}.
\]
Если \(f(x_1)=0\), то есть, \(x_1\) есть нулевое значение касательной, получим
\[
x_1=x_0-\frac{f(x)}{f'(x)},
\]
приближенное значение решения, которое находится ближе к искомому решению, чем \(x_0\).
Повторяя этот процесс, получим последовательность приближенных значений \(x_2,x_3,...\) фактического решения.
Метод Ньютона-Рафсона (многомерный случай).
Этот метод может быть обобщен на многомерный случай решения \(n\) алгебраических уравнений
\[
\left\{
\begin{array}{l}
f_1(x_1,x_2,\ldots,x_n)=f_1(\mathbf{x})=0, \\
\ldots \\
f_n(x_1,x_2,\ldots,x_n)=f_n(\textbf{x} )=0.
\end{array}
\right.
\]
Формула Ньютона-Рафсона для многомерного случая будет иметь вид \(x\Leftarrow x-J^{-1}_f(x)f(x)\),
где \(J_f(x)\) -якобиан функции \(f(x)\):
\[
J_f(x)=
\left[
\begin{array}{ccc}
\frac{\partial f_1}{\partial x_1}& \cdots &\frac{\partial f_1}{\partial x_n} \\
\vdots & \ddots & \vdots \\
\frac{\partial f_n}{\partial x_1} & \cdots & \frac{\partial f_n}{\partial x_n} \\
\end{array}
\right].
\]
Для получения этого соотношения, рассмотрим ряд Тейлора
\[
f_i(x+\delta x)=f_i(x)+\sum_j\frac{\partial f_i}{\partial x_j}\delta x_j+O\left(\delta x_j^2\right) i=1,2,...,n.
\]
Проигнорируем слагаемые порядка два и выше и результат приравняем нулю (т.е. \(x+\delta x\) является нулевым значением касательной),
тогда получим
\[
\sum_j\frac{\partial f_i}{\partial x_j}\delta x_j=-f_i(x), i=1,2,...,n.
\]
Решение этой системы линейных уравнений для \(\delta x\)
\[\delta x=-J^{-1}_f(x)f(x)\]
и получаем формулу Ньютона-Рафсона: \(x\Leftarrow x+\delta x=x-J^{-1}_f(x)f(x)\).
Задача 1.
Даны точки \(A=(1,2,3,4 )\), \(B=(4,1,3,4 )\) и \(C=(-1,2,-3,1 )\). Найти расстояние от точки \(C\) до прямой \(AB\).
Задача 2.
Преобразовать нормально распределенную случайную величину с ковариационной матрицей \(\left(
\begin{array}{cc}
1 & 0.5 \\
0.25 & 0.2 \\
\end{array}
\right)
\)
в случайную величину со сферической функцией плотности.
Задача 3.
Та же задача, что и в предыдущем случае, но если
\(\Sigma=\left(
\begin{array}{ccc}
1 & 2&-0.5 \\
2 & 1& 0\\
-0.5 & 0&1 \\
\end{array}
\right)
\)
Вопрос-ответ.
Задать вопрос:







