Математичні принципи масштабно-інваріантних дескрипторів зображень.
Процес отримання масштабно-інваріантних дескрипторів можна розбити на чотири етапи:
- Виявлення характерної точки (також званою ключовою точкою).
- Локалізація характерних точок.
- Завдання орієнтації.
- Генерація дескриптора функції.
На перший погляд характеристикою зміни масштабу незалежного дескриптора може бути наявність кута. Значення кута зберігається як при повороті, так і при зміні масштабу.
Виявлення кутових точок. Детектор Харріса.
Harris Corner Detector - це оператор виявлення кутів, який зазвичай використовується в алгоритмах комп'ютерного зору для вилучення кутів і визначення характеристик зображення.
Кут - це точка, локальна околиця якої має для освітленості два домінуючих і різних напрямки.
Іншими словами, кут можна інтерпретувати як поєднання двох країв, де край - це раптова зміна яскравості зображення.
Кути є важливими елементами зображення, і їх зазвичай називають точками інтересу, що не залежать від переміщення, повороту і освітлення.
Для находженія зміни освітленості (яскравості) будемо використовувати градієнт зображення в кожній точці і візьмемо критерій у вигляді
\[
E(u,v) = \sum_{x,y} w(x,y)[I(x+u, y+v) - I(x,y)]^2
\]
де:
$w(x,y)$ є функцією вікна в точці $(x,y)$
$ I (x, y) $ є інтенсивністю (яскравістю, освітленістю) в точці $ (x, y) $
$ I (x + u, y + v) $ є інтенсивність у переміщеному вікні $ (x + u, y + v) $
Перш за все, чому кути є зручними дескрипторами, що дозволяють порівняти об'єкти, зображені з різних ракурсів і з різними масштабами.
Для рівної області ніякої зміни градієнта не спостерігається ні в одному напрямку, для ребра (краю) не спостерігається зміни градієнта уздовж ребра.
Таким чином, як рівна область, так і крайова область є поганими для зіставлення об'єктів, оскільки вони не дуже помітні (мається багато схожих фрагментів уздовж краю
у крайової області).
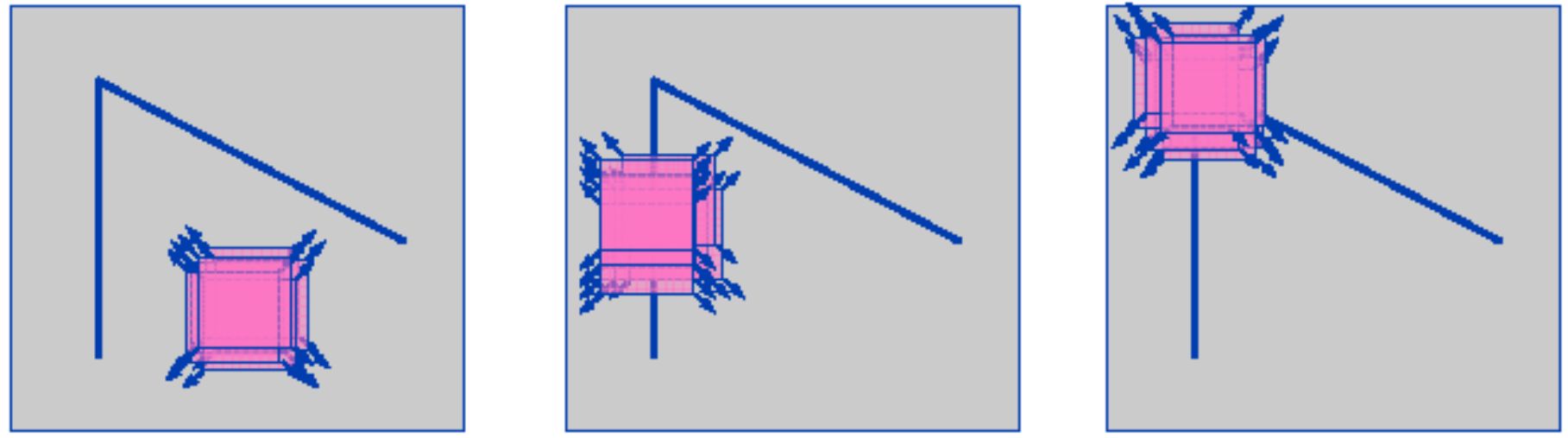
Перебуваючи у кутовий області, спостерігаємо значну зміну градієнта в усіх напрямках.
Завдяки цьому кути є хорошими дескрипторами для зіставлення об'єктів (зміщення вікна в будь-якому напрямку призводить до значної зміни величини $ E (u, v) $)
і в цілому більш стабільно при зміні точки огляду.
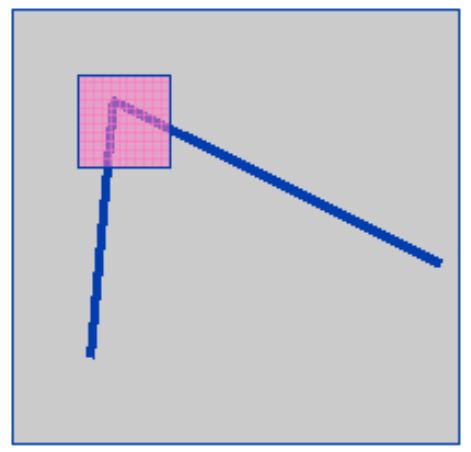
Проілюструємо цей факт, візьмемо дві невеликі ділянки однакового розміру зображення, обмежених вікном $ w (x, y) $ синім і червоним

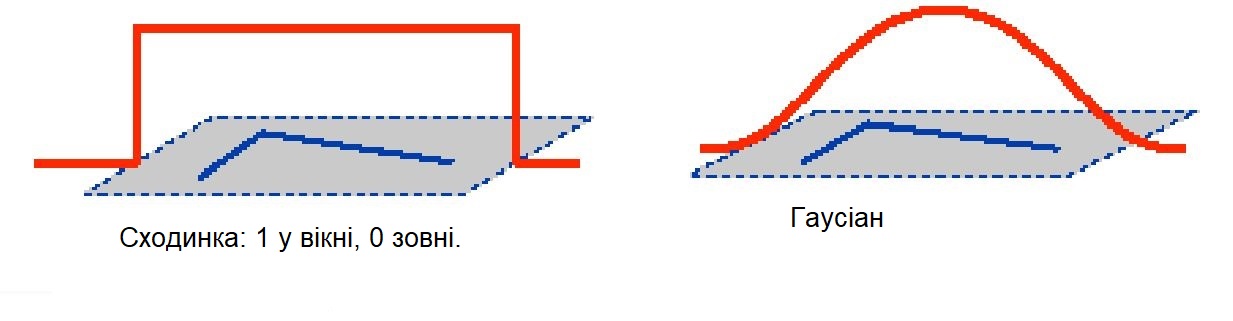
Функція вікна ступінчаста - всередині вікна дорівнює 1 і за його межами дорівнює 0, тобто значення всередині вікна стале.
Таким чином, функція вікна вибирає, які пікселі хочемо переглянути, і привласнює відносні ваги кожному пікселю
(найбільш поширеним є вікно Гаусіана, оскільки в цьому випадку встановлюється різна значимість пікселів в залежності від віддаленості від центру вікна).
Синій прямокутник переміщується на $ (u, v) $.
Обчислимо суму квадрата різниці між частинами зображення, обмеженими червоним і синім вікнами, тобто знайдемо попіксельно різницю,
зведемо її в квадрат і знайдемо суму.
Таким чином для кожного зсуву $ (u, v) -> E (u, v) $ отримуємо одне число.
Подивимося, що станеться, якщо обчислимо для різних значень $ u, v $:
Спочатку $ v = 0 $:
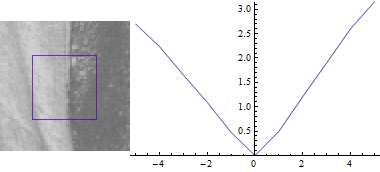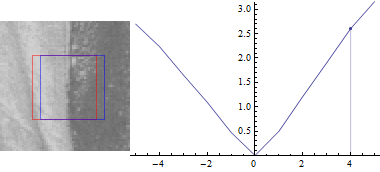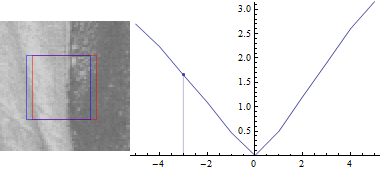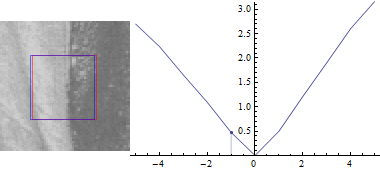
Це не дивно: різниця між частинами зображення є найменшою, коли зсув $ (u, v) $ між ними становить 0.
У міру збільшення відстані між двома вікнами, сума квадратів відмінностей також збільшується.
Тепер, нехай $ u = 0 $:
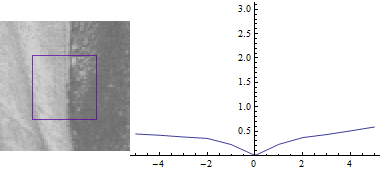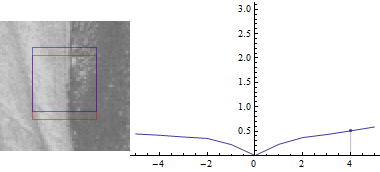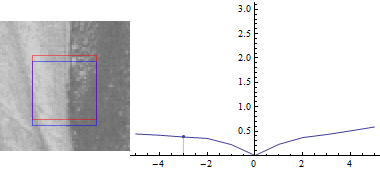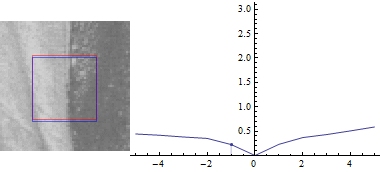
Результат виглядає схоже, але сума квадратів відмінностей між двома частинами зображення набагато менше при зміщенні синього вікна в сторону краю.
Поверхня, що описується функцією двох змінних $ E (u, v) $ виглядає наступним чином:
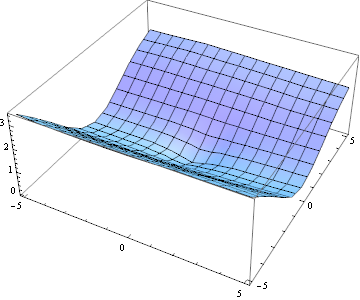
Поверхня схожа на "яр": уздовж осі яру зміна рівня поверхні невелика, і це зрозуміло - освітленість зображення має домінуючу (вертикальну)
орієнтацію.
Чи можемо зробити те ж саме для іншого зображення:
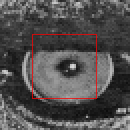
Тут $ E (u, v) $ виглядає по-іншому:
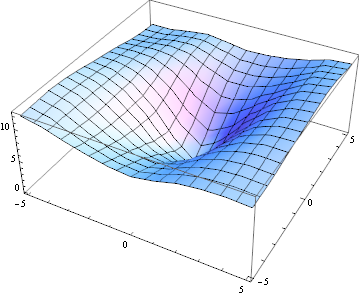
Таким чином, форма функції $ E (u, v) $ говорить про структуру зображення:
якщо $ E (u, v) $ всюди знаходиться десь біля нуля, то в зображенні немає текстури, маємо рівну поверхню
якщо $ E (u, v) $ є "каньйон-подібною", то фрагмент зображення має домінуючу орієнтацію (це може бути край або текстура)
якщо $ E (u, v) $ є "конусоподібною", то фрагмент зображення має текстуру, але не домінуючу орієнтацію.
Саме цей вид фрагмента зображення, шукає кутовий детектор.
Як правило, немає необхідності обчислювати $ E (u, v) $ для всього зображення.
Цікавим є тільки форма цієї поверхні в околиці $ (0,0) $ зрушення $ (u, v) $.
Для цієї мети досить використовувати часткову суму ряду Тейлора функції $ E (u, v) $ в околиці $ (0,0) $, що повністю описує цікаву для нас "форму".
Виявлення кута
Отже, ідея полягає в тому, щоб розглянути невелике вікно навколо кожного пікселя $ p $ на зображенні.
Далі потрібно ідентифікувати всі такі піксельні вікна, які є унікальними.
Унікальність може бути виміряна шляхом зсуву кожного вікна на невелику величину в заданому напрямку і вимірювання величини зміни освітленості в значеннях пікселів.
Більш формально, беремо суму квадрата різниці значень пікселів до і після зсуву і визначаємо вікна пікселів, де ця величина велика для зрушень у всіх 8 напрямках.
Визначимо функцію зміни $ E (u, v) $ як суму всіх квадратів різниць
\[
E(u,v)=\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2
\]
де $ u, v $ - зсув координати $ x, y $ кожного пікселя у вікні 3 x 3, а $ I $ - значення інтенсивності освітленості пікселя.
Об'єктами зображення є всі пікселі, які мають значення $ E (u, v) $, більше фіксованого порогу.
Для виявлення кута потрібно максимізувати цю функцію $ E (u, v) $.
Перш за все, випишемо часткову суму ряду Тейлора функції двох змінних
\[
f(x+u,y+v)=f(x,y)+uf_x(x,y)+vf_y(x,y)+\frac{1}{2!}\left(u^2f_{xx}(x,y)+uvf_{xy}(x,y)+v^2f_{yy}(x,y)\right)+...
\]
Проапроксимуємо нашу функцію лінійною частиною ряду Тейлора
\[
f(x+u,y+v)\approx f(x,y)+uf_x(x,y)+vf_y(x,y).
\]
Тоді
\[
\sum\left[I(x+u,y+v)-I(x,y)\right]^2\approx
\sum\left[I(x,y)+uI_x(x,y)+vI_y(x,y)-I(x,y)\right]^2=
\sum\left[u^2I^2_x+2uvI_xI_y+v^2I^2_y\right]=
\]
\[
\sum
\begin{bmatrix}
u&v
\end{bmatrix}
\begin{bmatrix}
I^2_x & I_xI_y\\
I_xI_y &I^2_y
\end{bmatrix}
\begin{bmatrix}
u\\
v
\end{bmatrix}=
\begin{bmatrix}
u&v
\end{bmatrix}\left(\sum
\begin{bmatrix}
I^2_x & I_xI_y\\
I_xI_y &I^2_y
\end{bmatrix}
\right)
\begin{bmatrix}
u\\
v
\end{bmatrix}.
\]
Нехай
\[
M=\sum w(x,y)
\begin{bmatrix}
I^2_x & I_xI_y\\
I_xI_y &I^2_y
\end{bmatrix}.
\]
Матрицю $M$ називають тензором структури.
Таким чином, для невеликих зрушень $ (u, v) $ отримуємо білінійну апроксимацію:
\[
E(u,v)\approx \begin{bmatrix}
u&v
\end{bmatrix}M
\begin{bmatrix}
u\\
v
\end{bmatrix}
\]
Власні вектори $ (e_1, e_2) $ матриці $ M $ визначають напрямки як для найбільшої, так і для найменшої зміни $ E (u, v) $,
відповідні власні значення $ \lambda_1, \lambda_2 $ дають фактичну величину цих змін.
Отримуємо наступний критерій
Якщо $ \lambda_1 \approx 0, \lambda_2 \approx 0 $, тоді точка $ (x, y) $ не має ніяких особливостей, що представляють інтерес.
Якщо $ \lambda_1 \approx 0, \lambda_2 $ має досить велике позитивне значення, то знайдений край (ребро).
Якщо $ \lambda_1, \lambda_2 $ мають великі позитивні значення, то знайдено кут.
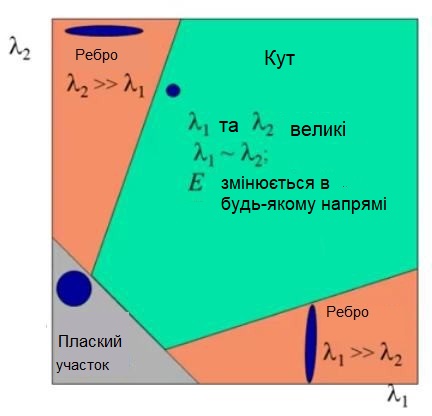
щоб уникнути розв'язання задачі на власні вектори і числа, що є обчислювально дорогим, використовується критерій:
\[
R = det(M) - k(trace(M))^{2},
\]
$k$ емпірічна константа, як правило, 0.04 ~ 0.06.
Зазначимо, що
\[
det (M)=\lambda_1\lambda_2,
\]
\[
trace (M)=\lambda_1+\lambda_2.
\]
Оцінка $ R $ розраховується для кожного вікна.
Таким чином, отримуємо
Коли величина $ | R | $ мала, що відбувається, коли $ λ_1 $ і $ λ_2 $ малі, область рівна.
Коли $ R \lt 0 $, що відбувається, коли $ λ_1 \gg λ_2 $ (або навпаки), область є ребром.
Коли $ R $ велике, що відбувається, коли $ λ_1 $ і $ λ_2 $ великі і $ λ_1 \sim λ_2 $, область є кутом.
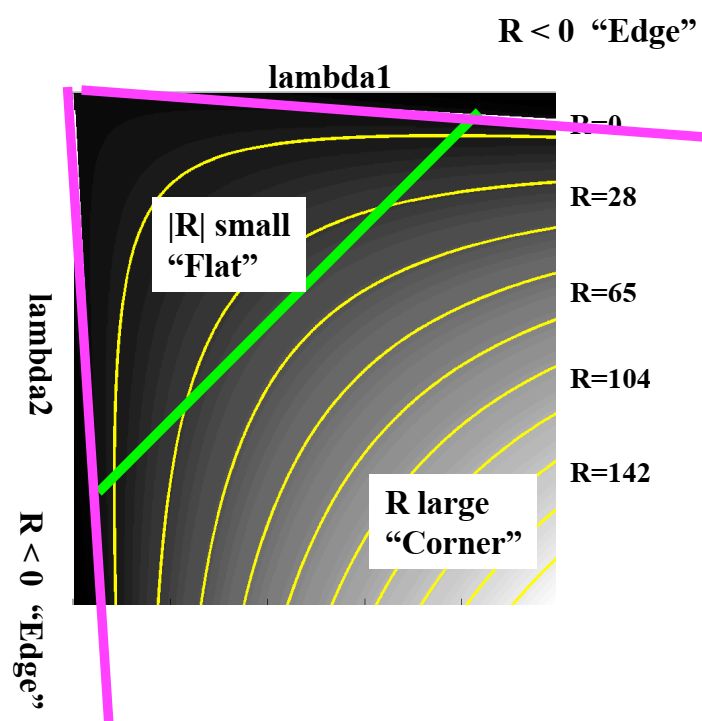
Питання в тому, чому? Чому матриця M здатна визначити кут?
Розглянемо для кожного пікселя коваріаційну матрицю $ \Sigma $ градієнта $ (I_x, I_y) $.
Нехай $ \mu_ {x} = E [I_ {x}], \mu_ {y} = E [I_ {y}] $. За визначенням коваріаційна матриця дорівнює
\[
\begin{array}{rl} \Sigma & = \begin{bmatrix} E[ (I_{x}-\mu_{x})(I_{x}-\mu_{x}) ] & E[ (I_{x}-\mu_{x})(I_{y}-\mu_{y}) ] \\E[ (I_{y}-\mu_{y})(I_{x}-\mu_{x}) ] & E[ (I_{y}-\mu_{y})(I_{y}-\mu_{y}) ] \\\end{bmatrix} \\& = \begin{bmatrix} E[ I_{x}I_{x} ] - \mu_{x}^{2} & E[ I_{x}I_{y} ] - \mu_{x}\mu_{y}\\E[ I_{y}I_{x} ] - \mu_{y}\mu_{x} & E[ I_{y}I_{y} ] - \mu_{y}^{2}\\\end{bmatrix} \\& \triangleq \begin{bmatrix} E[ I_{x}I_{x} ] & E[ I_{x}I_{y} ]\\E[ I_{y}I_{x} ] & E[ I_{y}I_{y} ]\\\end{bmatrix}\\\end{array}
\]
Останній крок будується на основі припущення, що середнє значення похідних $ I_x I_y $ є нулем, тобто $ (\mu_ {x}, \mu_ {y}) = 0 $.
З іншого боку, якщо застосуємо фільтр усереднення (при цьому даємо єдину вагу пикселам), то:
\[
\begin {array} {rl} M & = \frac {1} {f} \sum_ {x, y} \begin {bmatrix} I_ {x} ^ 2 & I_ {x} I_ {y} \\I_ { x} I_ {y} & I_ {y} ^ 2 \\\end {bmatrix} \\& = \begin {bmatrix} \widehat {I_ {x} ^ 2} & \widehat {I_ {x} I_ {y }} \\\widehat {I_ {x} I_ {y}} & \widehat {I_ {y} ^ 2} \\\end {bmatrix} \\\end {array}
\]
де $ f $ загальна кількість пікселів у вікні, і $ \widehat {f} $ середнє $ f $.
Видно, що тензор M насправді є оцінкою ковариационої матриці градієнта пікселів у вікні.
Таким чином, будь-які висновки що до коваріаційної матриці можуть бути використані для аналізу структури тензорів.
Нехай $ (e_1, \lambda_1) $ і $ (e_2, \lambda_2) $ власні вектори і власні числа матриці $ M $ і $ \lambda_1 \geq \lambda_2 $.
тоді
\[
\begin{array} {rl} E(u,v)=&[u v]M\begin{bmatrix}u\\v\end{bmatrix} \\= &[u v][e_1 e_2]\begin{bmatrix} \lambda_1 & 0 \\0 & \lambda_2 \end{bmatrix}
\begin{bmatrix}e_1^T\\e_2^T \end{bmatrix}\begin{bmatrix}u\\v \end{bmatrix}\\= &[u' v']\begin{bmatrix} \lambda_1 & 0 \\0 & \lambda_2 \end{bmatrix}
\begin{bmatrix}u'\\v' \end{bmatrix}\\= & \lambda_1 u'^2+\lambda_2 v'^2 \end{array}
\]
де $ (u ', v') $ нова координатна система по векторах $ (e_1, e_2) $.
Після очевидних перетворень отримуємо
\[
\frac{u'^2}{\frac{E(u,v)}{\lambda_1}}+\frac{v'^2}{\frac{E(u,v)}{\lambda_2}} = 1\]
тобто,
\[
\frac{u'^2}{\left(\sqrt{\frac{E(u,v)}{\lambda_1}}\right)^2}+\frac{v'^2}{\left(\sqrt{\frac{E(u,v)}{\lambda_2}}\right)^2} = \frac{u'^2}{a^2} + \frac{v'^2}{b^2} =1
\]
Тут $a=\sqrt{\frac{E(u,v)}{\lambda_1}}$ і $b=\sqrt{\frac{E(u,v)}{\lambda_2}}$, де $a \leq b$, є піввісями еліпсу.
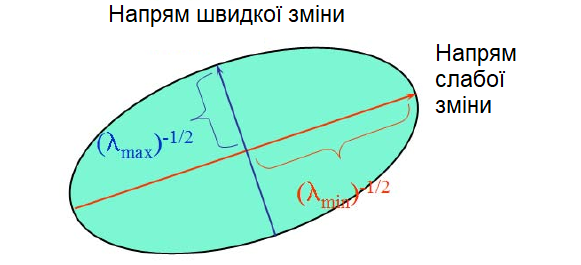
Розглянемо приклад, який показує, як похідні розподіляються для різних типів фрагментів зображень (тобто положень вікна)

Алгоритм детектора Харріса.
- Для зображення $ I $ в градаціях сірого обчислимо згортку з похідними функції Гауса ($\sigma=1$)
\[
I_x=G_\sigma^x\otimes I,I_y=G_\sigma^y\otimes I.
\]
- Для кожного пікселя $ p $ обчислимо величини
\[
I_{xx}=I_x\cdot I_x,I_{xy}=I_x\cdot I_y,I_{yy}=I_y\cdot I_y.
\]
- Для кожного пікселя $ p $ зображення в градаціях сірого розглянемо вікно 3 × 3 і навколо нього обчислимо суми
\[S_ {xx} = G _ {\sigma \ell} \otimes I_ {xx}, S_ {xy} = G _ {\sigma \ell} \otimes I_ {xy}, S_ {yy} = G _ {\sigma \ell} \otimes I_ {yy}. \]
- Для кожного пікселя визначимо матрицю
\[H (x, y) = \begin {bmatrix} S_ {xx} (x, y) & S_ {xy} (x, y) \\S_ {xy} (x, y) & S_ {yy} ( x, y) \end {bmatrix}. \]
- Для кожного пікселя $ (x, y) $ обчислимо значення дескриптора
\[
R = det (M) - k (trace (M)) ^ {2},
\]
- Знайдемо всі пікселі, освітленість яких перевищує певний поріг і є локальними максимумами в певному вікні (щоб уникнути надлишкового дублювання об'єктів)
- Для кожного знайденого пікселя обчислити дескриптор об'єкта і якщо це значення досить велике, вважаємо, що кут знайдений.
Застосуємо детектор Харріса до зображення костелу святого Миколая (м Кам'янське кінець XIX століття)
і він же, в іншому часі і масштабі
Результат застосування детектора Харріса з різним масштабом.
Детектор Харріса реагує на кути, але при зміні масштабу кут може стати ребром, як показано на наступному малюнку:
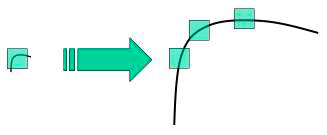
На жаль, детектор Харріса не є масштабно-інваріантним.
Масштабна інваріантність
Далі розглянемо математичні основи побудови масштабно-незалежних дескрипторів.
Одним з кращих масштабно-інваріантних дескрипторів є SIFT (Scale-invariant feature transform), идею побудови якого і розглянемо.
Отже, що таке масштаб і що означає масштабна інваріантність?
Невід'ємною властивістю об'єктів є те, що вони існують тільки як значущі об'єкти в певних масштабах.
Великий Леонард Ейлер зауважив, що будь-яка крива під великим збільшенням виглядає як відрізок прямої, але говорити про те, що будь-яка крива є ламана, нерозумно.
Так, не можна обговорювати смакові якості кулінарного блюда з точки зору взаємодії елементарних частинок, з яких воно складається.
Грубо кажучи, масштаб зображення об'єкта - це його діаметр на зображенні. Він позначається величиною σ, яка вимірюється в пікселях.
В якості ілюстрації, наведемо наступну піраміду
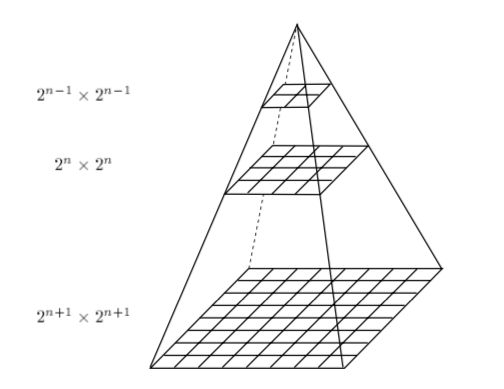
Для алгоритмічної реалізації різного масштабу одного і того ж зображення, застосуємо згортку $ L (x, y, \sigma) = G (x, y, \sigma) \otimes I (x, y) $ цього зображення $ I (x, y ) $ і функції Гаусса
\[\displaystyle G (x, y, \sigma) = \frac {1} {2 \pi \sigma ^ 2} \exp \left (- \left ({\frac {(x-x_ {o}) ^ {2}} {2 \sigma ^ {2}}} + {\frac {(y-y_ {o}) ^ {2}} {2 \sigma ^ {2}}} \right) \right) \]
з різними σ,
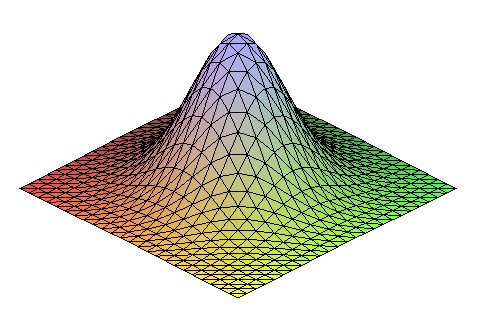
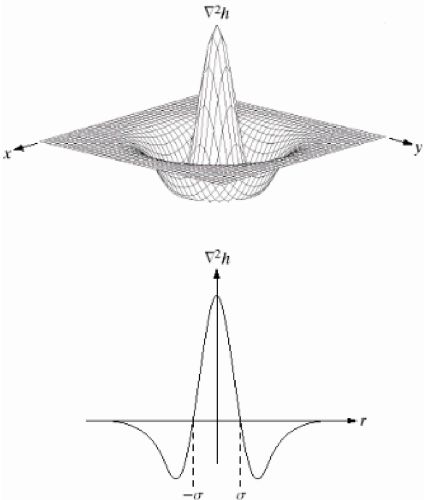
а до результату застосуємо оператор Лапласа (LoG-Laplacian of Gaussian):
\(\displaystyle \Delta = {\frac {\partial ^ {2}} {\partial x ^ {2}}} + {\frac {\partial ^ {2}} {\partial y ^ {2}}} . \)
Справедливе співвідношення
\(\displaystyle \Delta = \nabla ^ {2} = {\text {div}} \; \nabla \).
Таким чином, беремо зображення і трохи розмиваємо його (використовуючи ядро Гауса), потім від отриманого результату знаходимо суму часткових похідних другого порядку
(або «Лапласіан»). Дана процедура дозволяє знайти краї і кути на зображенні. Ці краї і кути є непоганим інструментом для знаходження ключових точок.
LoG часто використовується для виявлення плям, характерних для даного зображення.
Для знаходження Лапласіану зручно використовувати зв'язок між згорткою і оператором диференціювання:
\[
\frac {d} {dx} \left (f (x) \otimes g (x) \right) = \left (\frac {d} {dx} f (x) \right) \otimes g (x).
\]
Таким чином можна просто згорнути зображення з другими похідними гауссіана і знайти суму (або просто згорнути, використовуючи LoG).
Розглянемо одновимірний приклад, f - це лінія розгортки зображення (тобто масив пікселів з лінії зображення).
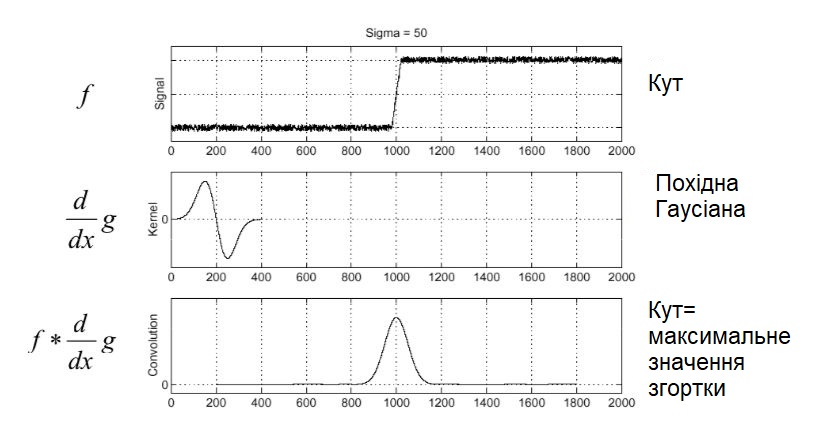
Детектор знаходження кута, який використовує згортку сигналу з похідною функції Гаусса.
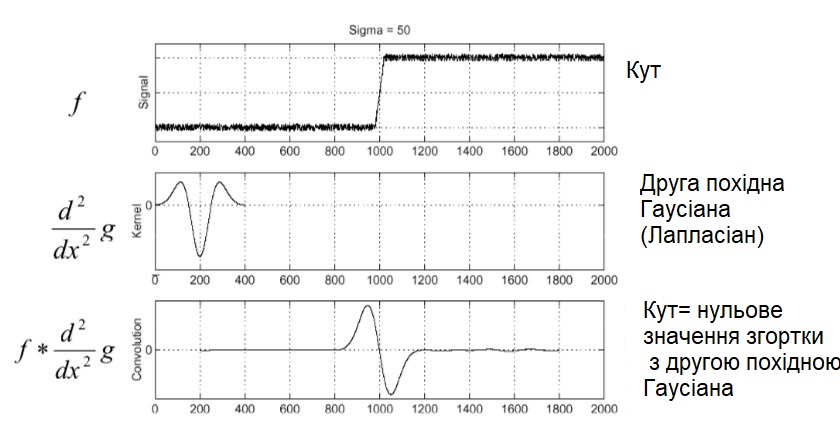
Детектор знаходження кута, який використовує згортку сигналу з другою похідною функції Гаусса (Лапласіаном).
Зауважимо, що можна використовувати LoG для виявлення плями на зображенні
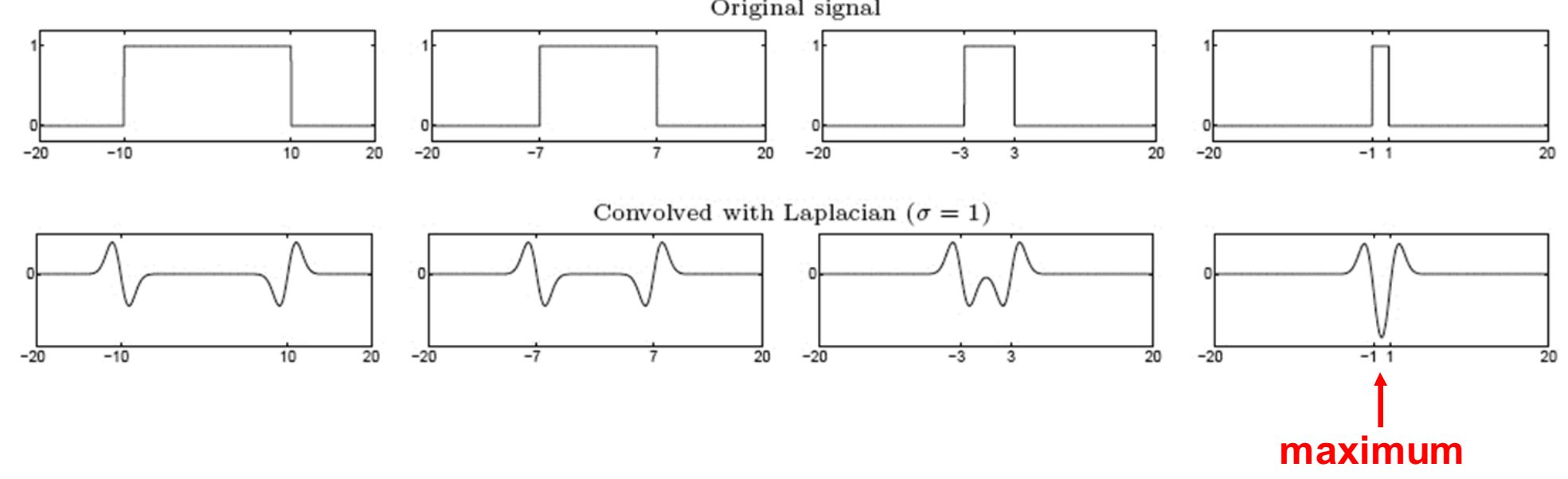
Детектор знаходження плями (згустку, краплі) - величина згортки сигналу і Лапласіна досягне максимуму в центрі плями
(За умови, що масштаб Лапласіану узгоджений з розміром плями.)
Таким чином, не потрібно знаходити перетин з абсцисою, натомість можемо знайти екстремуми (максимуми і мінімуми).
Однак LoG не є по-справжньому масштабним інваріантом: відгук Лапласа загасає зі збільшенням масштабу:
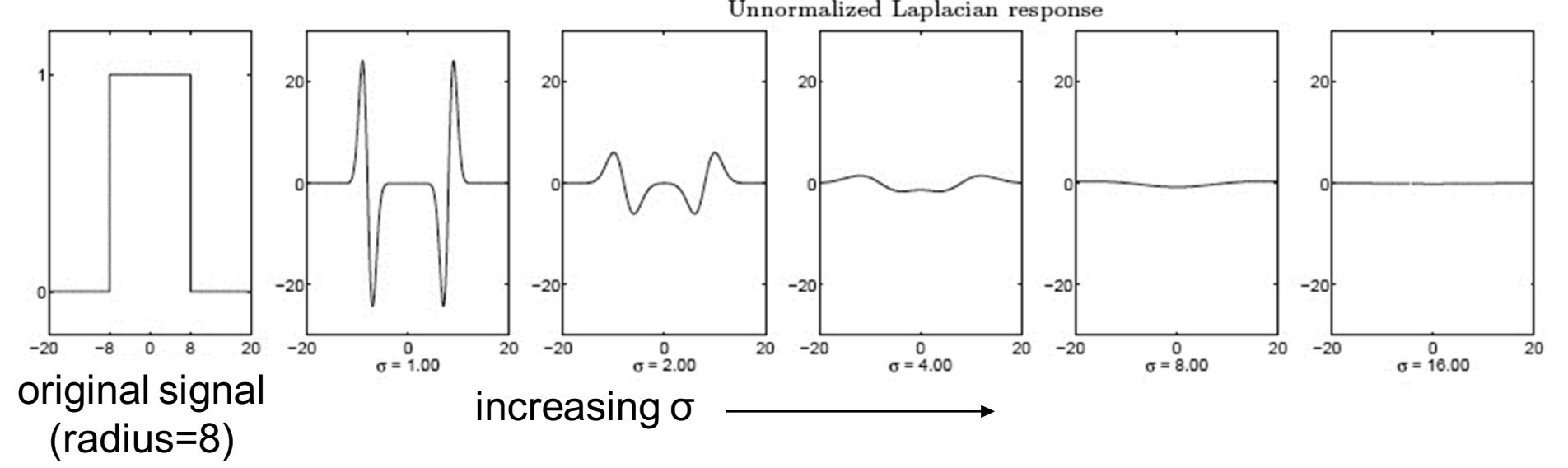
Зауважимо, що відгук похідної гаусовского фільтру на краю, зменшується зі збільшенням σ, тому, щоб зберегти відгук однаковим (масштабно-інваріантним),
необхідно помножити гаусову похідну на σ.
А так як Лапласіан є другою Гаусівською похідною, то він повинен бути помножений на $ σ ^ 2 $.
Розглянемо край зображення $ I (x) = u (x - x_0) $. Як було сказано раніше, для виявлення краю шукаємо згортку з похідною функції Гауса і потім знаходимо пікове значення.
Визначимо масштабний простір, згортаючи $ I (x) $ із сімейством перших похідних гаусівських фільтрів, де термін сімейство означає, що є множина фільтрів
з різними значеннями σ.
\[
I(x)\otimes \frac{d}{dx}G_\sigma(x)=G_\sigma(x)\otimes\frac{d}{dx}I(x)=G_\sigma(x)\otimes\delta(x-x_0)=G_\sigma(x-x_0),
\]
де $\delta$- узагальнена функція Дірака.
У місті краю (ребра) $x = x_0$ маємо
\[
\left(I\otimes \frac{d}{dx}G_\sigma\right)(x_0)=G_\sigma(0)=\frac{1}{\sqrt{2\pi}\sigma},
\]
що залежить від σ.
Якщо у нас є 2D-зображення, то по горизонталі отримуємо
\[
\sigma \frac {\partial} {\partial x} G_ \sigma (x, y)
\]
і аналогічно, по вертикалі.
Після того, як відфільтруємо ребро (край) згорткою $ I (x) = u (x - x_0) $ з першою похідною Гаусіану, у місці розташування ребра отримаємо піковий відклик.
З цього відразу маємо, що якби фільтрували ребро з другою похідною гаусіана
\[
I(x)\otimes \frac{d^2}{dx^2}G_\sigma(x)
\]
тоді в місці розташування краю відклик би дорівнював нулю.
Дійсно,
\[
u(x-x_0)\otimes \frac{d^2}{dx^2}G_\sigma(x)=\frac{d}{dx}\left(u(x-x_0)\otimes \frac{d}{dx}G_\sigma(x)\right)=\frac{d}{dx}G_\sigma(x-x_0)=
-\frac{x-x_0}{\sqrt{2\pi}\sigma^3}\exp\left(-\frac{(x-x_0)^2}{2\sigma^2}\right).
\]
Відповідь дорівнює 0, коли $ x = x_0 $, як і очікувалося.
Знайдемо піки, для чого обчислимо похідну
\[
\frac{d}{dx}\left(u(x-x_0)\otimes \frac{d^2}{dx^2}G_\sigma(x)\right)=-\left(1-\frac{(x-x_0)^2}{\sigma^2}\right)\frac{1}{\sqrt{2\pi}\sigma^3}
\exp\left(-\frac{(x-x_0)^2}{2\sigma^2}\right)
\]
і прирівняємо її до нуля.
Таким чином, піковому значенню відповідає
\[
1-\frac{(x-x_0)^2}{\sigma^2}=0,
\]
тобто $x=x_0\pm \sigma.$
А саме пікове значення дорівнює
\[
\pm \frac{1}{\sqrt{2\pi}\sigma^2}\exp\left(-\frac{1}{2}\right).
\]
Як і у випадку з фільтром першої похідної, можемо нормалізувати фільтр другої похідної шляхом множення на $ σ ^ 2 $
\[
\sigma^2\frac{d^2}{dx^2}G_\sigma(x).
\]
В цьому випадку пікове значення від $ \sigma $ не залежать.
Таким чином, якщо проведемо фільтрацію ребра за допомогою нормализованої другої похідної Гаусіана (як визначено вище), то на місці ребра буде перетин з нулем,
і на відстані ± σ від краю будуть піки (додатні і від'ємні), але висота піків не залежить від σ.
Таким чином, щоб отримати справжню масштабну інваріантність, потрібно LoG помножити на $ σ ^ 2 $.
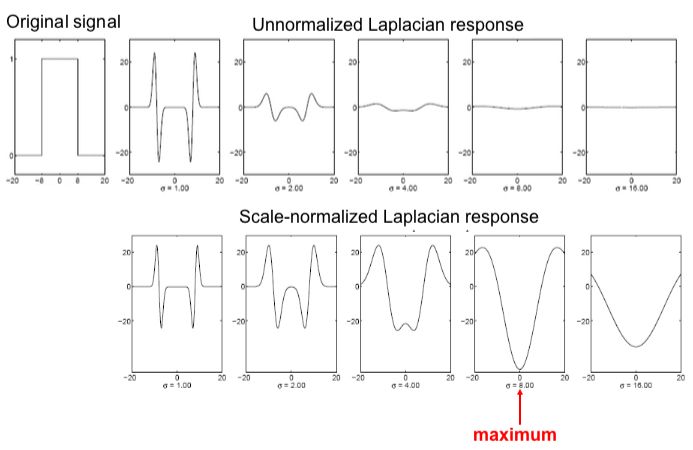
Ефект від нормалізації фільтру.
На практиці Лапласіан апроксимується з використанням різниці Гаусіанів (DoG-Difference of Gaussian).
Взаємозв'язок між DoG і $ σ ^ 2LoG $ можна зрозуміти з рівняння дифузії тепла:
\[
\frac{\partial G}{\partial\sigma}=\sigma\nabla^2G.
\]
Звідси
\[
\sigma\nabla^2G=\frac{\partial G}{\partial\sigma}\approx\frac{G(x,y,k\sigma)-G(x,y,\sigma)}{k\sigma-\sigma}.
\]
і
\[
G(x,y,k\sigma)-G(x,y,\sigma)\approx (k-1)\sigma^2\nabla^2G.
\]
Це показує, що коли функція DoG має шкали, що відрізняються сталим коефіцієнтом, вона вже включає нормалізацію шкали $ σ ^ 2 $,
що потрібно для масштабно-інваріантного Лапласіану.
Коефіцієнт (k - 1) в рівнянні є сталим для всіх масштабів і, отже, не впливає на місце розташування екстремумів.
Локалізація ключових точок (субпіксельна локалізація)
Після першого кроку виявляємо деякі ключові точки, які грубо локалізовані, в кращому випадку з точністю до найближчого пікселя, в залежності від того,
де в масштабному просторі були знайдені об'єкти. Вони погано локалізовані в масштабі, так як σ квантується на відносно невелику кількість кроків у масштабі
простору. Другий етап полягає в уточненні розташування цих характерних точок з точністю до субпікселя, одночасно усуваючи будь-які погані характеристики.
Локалізація субпікселя здійснюється шляхом використання часткової суми ряду Тейлора для побудови тривимірної квадратичної поверхні (по x, y і σ)
локальної області з метою інтерполяції максимумів або мінімумів.
Нехтуючи складовою більш високого ступеня точності, маємо DoG у вигляді, де похідні оцінюються в запропонованій точці $ z_0 = [x_0, y_0, σ_0] T $ і $ z = [δx, δy, δσ] $ $ T $ -
зрушення від цієї точки.
\[
D(z_o+z)\approx D(z_0)+\left(\left.\frac{\partial D}{\partial z}\right|_{z_0}\right)^Tz+\frac{1}{2}z^T\left(\left.\frac{\partial^2 D}{\partial z^2}\right|_{z_0}\right)z.
\]
Прирівняємо похідну нулю і знайдемо точку екстремуму $\hat{z}$
\[
\hat{z}=-\left(\left.\frac{\partial^2 D}{\partial z^2}\right|_{z_0}\right)\left(\left.\frac{\partial D}{\partial z}\right|_{z_0}\right).
\]
Використання різницевих апроксимацій від сусідніх точок вибірки в DoG, призводить до системи лінійних рівнянь 3 × 3, яка досить просто вирішується.
Значення екстремуму можна апроксимувати
\[
D(\hat{x},\hat{y},\hat{\sigma})=D(z_0+\hat{z})\approx D(z_0)+\frac{1}{2}\left(\left.\frac{\partial D}{\partial z}\right|_{z_0}\right)^T\hat{z}.
\]
і будь-які точки зі значенням нижче певного порогу відхиляються як точки з низьким контрастом.
Остаточний тест виконується для видалення будь-яких елементів, розташованих по краях зображення, оскільки якщо вони будуть використовуватися для зіставлення, то пік,
розташований на гребені в DoG (який відповідає краю на зображенні), буде мати більшу кривизну поперек гребеня і низьку уздовж нього,
тоді як чітко визначений пік (крапля) матиме велику кривизну в обох напрямках.
Для цієї мети оцінюється Гессіан характерної точки
\[H(f)={\begin{bmatrix}{\frac {\partial ^{2}D}{\partial x^{2}}}&{\frac {\partial ^{2}D}{\partial x\,\partial y}}
\\{\frac {\partial ^{2}D}{\partial y\,\partial x}}&{\frac {\partial ^{2}D}{\partial y^{2}}}\end{bmatrix}}.\]
Оцінка проводиться з використанням наближення локальної різниці, і відносини власних значень $ λ_1 $ і $ λ_2 $, що відповідають основним кривизнам, які
порівнюються з граничним значенням $ r $
\[
\frac{Tr^2(H)}{Det(H)}=\frac{(\lambda_1+\lambda_2)^2}{\lambda_1\lambda_2}\lt\frac{(r+1)^2}{r}.
\]
Звідки виходить така оцінка?
Покладемо
\[
Tr(H)=\frac {\partial ^{2}D}{\partial x^{2}}+\frac {\partial ^{2}D}{\partial y^{2}}=\alpha+\beta,\\
Det(H)=\frac {\partial ^{2}D}{\partial x^{2}}\frac {\partial ^{2}D}{\partial y^{2}}-\left(\frac {\partial ^{2}D}{\partial x\partial y}\right)^2=\alpha\beta.
\]
Нехай $r=\frac{\alpha}{\beta}$, тоді маємо
\[
\frac{Tr^2(H)}{Det(H)}\lt\frac{(r+1)^2}{r}.
\]
Можна привести геометричну інтерпретацію.
Припустимо, у нас є поверхня M в R³, яка задається графіком гладкої функції $ z = f (x, y). $
Припустимо, що M проходить через початок координат $ p $, і її дотична площина - це площина $ z = 0. $
Нехай N = (0,0,1), нормаль до M в точці $ p $.
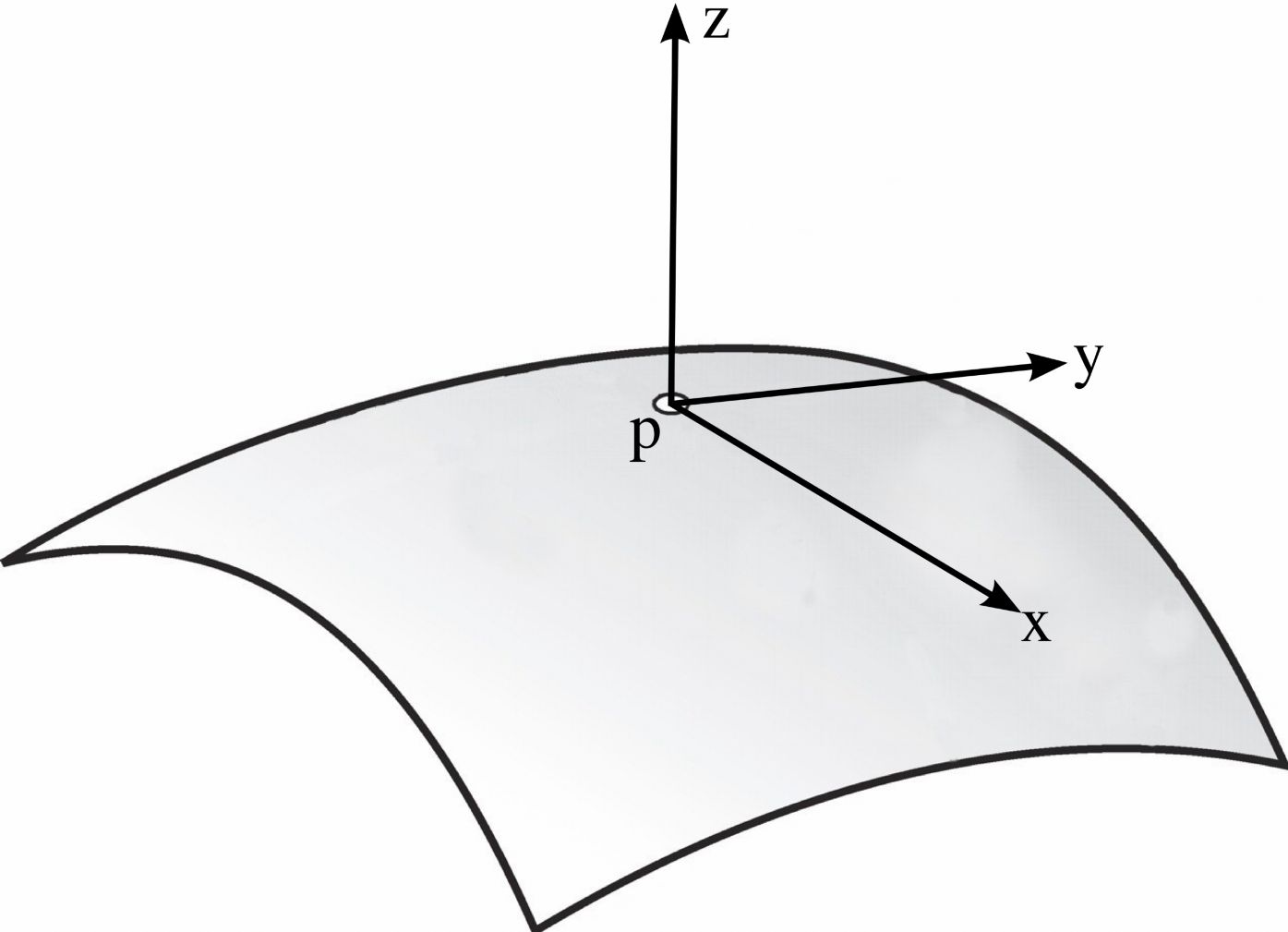
Нехай $ v $ - одиничний вектор, скажімо, $ v = (v_1, v_2,0) $ і $ c $ параметризована крива, задана розрізанням M через площину, натягнуту на $ v $ і $ N $:
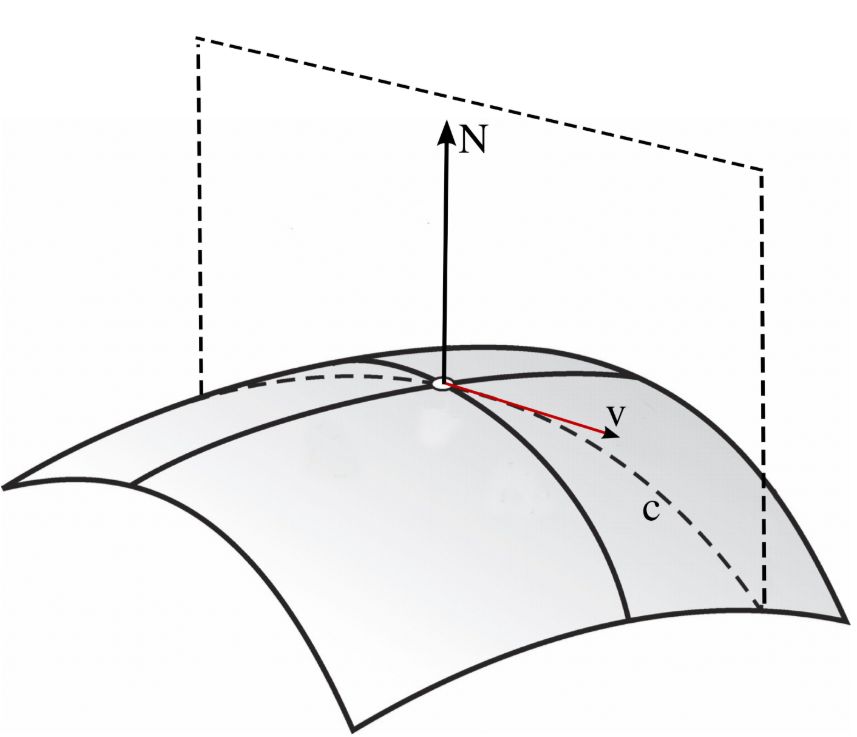
Тоді
\[
c(t)=(v_1t,v_2t,f(v_1t,v_2t)).
\]
Тепер можемо обчислити кривизну $ c $ вздовж напрямку $ v = (v_1, v_2,0) $. Як відомо з диференціальної геометрії, кривизна $ k_v $ є зворотною величиною радіуса
дотичного кола до $ c $ в $ p $.
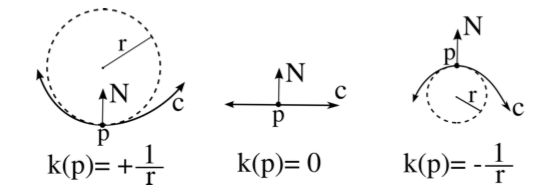
і
\[
k_v=f_{xx}(0,0)v_1^2+2f_{xy}(0,0)v_1v_2+f_{yy}(0,0)v_2^2.
\]
Кривизну можна записати через Гессіан
\[k_v=[v_1 v_2]{\begin{bmatrix}{\frac {\partial ^{2}f}{\partial x^{2}}}&{\frac {\partial ^{2}f}{\partial x\,\partial y}}
\\{\frac {\partial ^{2}f}{\partial y\,\partial x}}&{\frac {\partial ^{2}f}{\partial y^{2}}}\end{bmatrix}}
{\begin{bmatrix}{v_1\\\\v_2}\end{bmatrix}}.\]
Зауважимо, що головним кривизнам поверхні в точці $ p $ відповідатимуть найбільше та найменше значення $ λ_1, λ_2 $ для $ k_v $.
Інваріантність обертання.
Інваріантність обертання в алгоритмі SIFT забезпечується шляхом визначення орієнтації для кожної з виявлених ключових точок.
Це досягається шляхом дослідження градієнтів елемента зображення в області, навколо цього елементу.
Для кожної локалізованої характерної точки вибирається близьке оточення, зберігаючи незмінність масштабу.
З цього зображення, використовуючи апроксимацію градієнта різницею пікселів, отримуємо відповідну карту, що складається з величини градієнта і відповідного кута.
\[
m(x,y)=\sqrt{(L(x+1,y)-L(x-1,y))^2+(L(x,y+1)-L(x,y-1))^2},\\
\theta(x,y)=arctg\left(\frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)}\right).
\]
Для оцінки орієнтації (пучка напрямків) в характеристичній точці використовується гістограма орієнтованого градієнта (HOG-Histogram of Oriented Gradient).
Гістограма орієнтації формується з градієнтних орієнтацій точок вибірки в межах області навколо ключової точки.
Гістограма орієнтації має 36 блоків, що охоплюють 360-градусний діапазон орієнтацій.
Кожна вибірка, яка додається до гистограми, зважується за величиною її градієнта у круговому вікні Гаусіана з σ, який в 1,5 рази перевищує масштаб ключової точки.
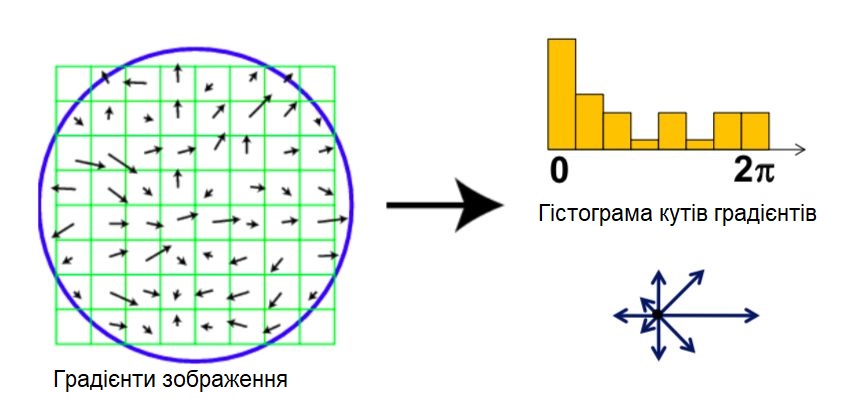
Потім гістограма згладжується фільтром змінного середнього:
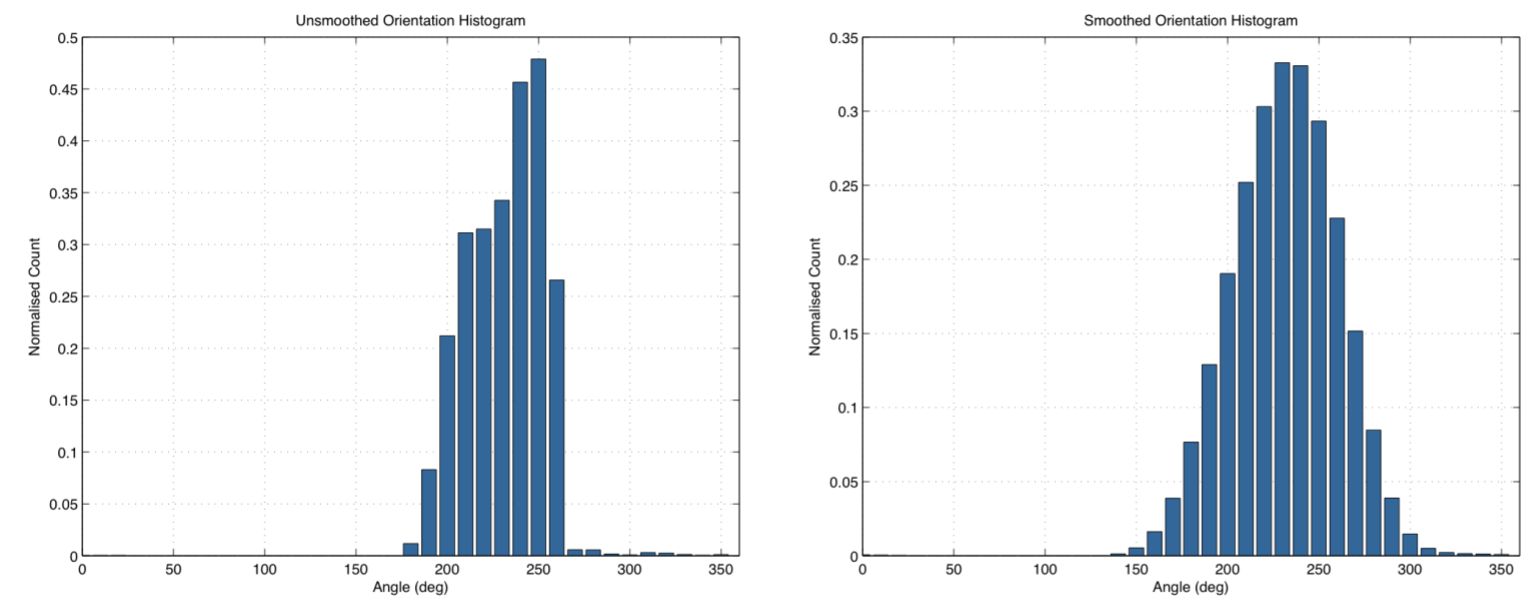
Оригінальна гістограма орієнтації і результат згладжування.
Якщо гістограма має більше одного виразного піку, то генерується кілька копій ключової точки, кожна з яких має одну з можливих орієнтацій.
Генерація дескриптора.
Завершальним етапом алгоритму SIFT є генерація дескриптора, який складається з нормалізованого 128-мірного вектора.
На цій стадії алгоритму формується список ключових точок, які описуються з точки зору розташування, масштабу і орієнтації.
Це дозволяє побудувати локальну систему координат навколо характерної точки, яка повинна бути однаковою для різних видів одного і того ж об'єкта.
Сам дескриптор є гистограмою, яка сформована з градієнта зображення в градаціях сірого.
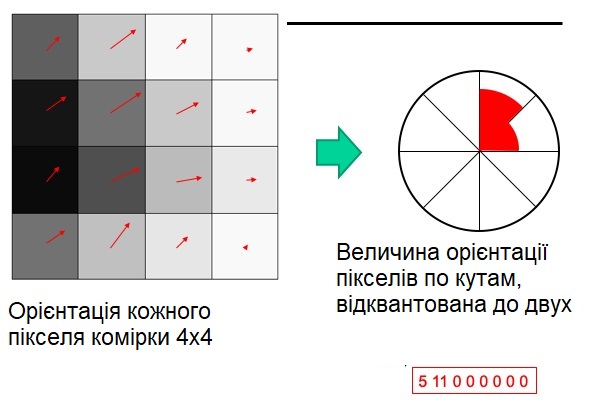
Використовується просторова сітка гістограм кута градієнта 4 × 4.
Розміри сітки залежать від масштабу точок інтересів, а сітка центрується по цій точці і повертається в напрямку, визначеному для точки.
Кожен з просторових елементів містить кутову гистограмму, розділену на 8 (128 = 4 × 4 × 8).
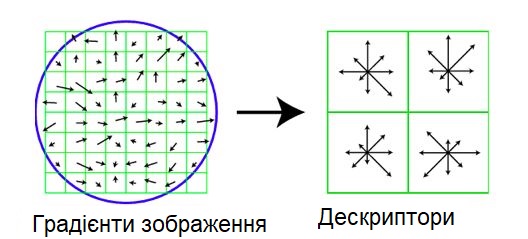
Вага кожного пікселя задається величиною градієнта, а також залежить від масштабу Гаусіана (σ, рівним половині ширини вікна дескриптора) з центром
в характерній точці, як показано синім колом.
Мета цього Гаусівського вікна полягає в тому, щоб уникнути раптових змін в дескрипторі з невеликими змінами в положенні вікна,
і приділяти менше уваги градиентам, які знаходяться далеко від центру дескриптора, оскільки вони найбільш схильні до помилок неправильної реєстрації.
Під час формування гістограми використовується трилінійна інтерполяція для уточнення кожного значення, тобто інтерполяції по x, y і θ.
Тобто, складається з інтерполяції ваги пікселя по сусіднім просторовим елементам на основі відстані до центрів елементів, а також інтерполяції по сусіднім
елементам кута.
Ця процедура використовується, щоб уникнути граничних ефектів, в яких дескриптор різко змінюється при плавному переході вибірки з однієї гістограми в іншу або з
однієї орієнтації в іншу. Таким чином, трилінійна інтерполяція використовується для розподілу значення кожної вибірки градієнта в суміжні комірки гістограми.
Іншими словами, кожен запис множиться на вагу 1 - d для кожного вимірювання, де d - відстань вибірки від центрального значення осередку, виміряний в
одиницях відстані між осередками гістограми.
Нарешті, вектор ознак змінюється, щоб зменшити ефекти зміни освітленості, для чого вектор нормалізується на одиницю довжини.
Зміна контрастності зображення, при якому кожне значення пікселя множиться на постійну, буде множити градієнти на одну і ту ж константу, тому ця
зміна контрастності буде скасована векторною нормалізацією. Зміна яскравості, при якому постійна додається до кожного пікселя зображення, не вплине на
значення градієнта, так як вони розраховуються на основі різниць пікселів. Отже, дескриптор інваріантний до афінних змін освітлення.
Однак нелінійні зміни освітлення також можуть відбуватися через зміни освітлення, які впливають в різній ступені на тривимірні поверхні з
різною просторовою орієнтацією. Ці ефекти можуть викликати великі зміни відносних величин для деяких градієнтів, але з меншою ймовірністю впливають
на орієнтацію градієнта. Тому зменшуємо вплив великих величин градієнта, встановлюючи граничні значення в векторі одиничних елементів, щоб кожний не
перевищував 0,2, а потім перенормуємо до одиничної довжини. Це означає, що зіставлення величин для великих градієнтів не так важливо, і що розподіл
орієнтацій має більший акцент. Значення 0,2 було визначено експериментально з використанням зображень, що містять різну освітленість для одних і тих же
тривимірних об'єктів.
На закінчення наведемо карту дескрипторів SIFT для використовуваних раніше зображень костелу св.Миколая (м.Кам'янське) для світлини XIX століття і сучасної.
Важливою сферою використання масштабно-незалежних дескрипторів є порівняння зображень. Алгоритм SIFT надає чудові можливості в цьому напрямку. порівнюючи ключові
точки обох зображень, можемо отримати карту порівняння, що показує зв'язок ключових точок на різних зображеннях.






































