Підходи до побудови детекторів.

Детектори ознак можна розділити на три категорії:

Одномасштабні детектори інваріантні до перетворень зображення, таких як обертання, переміщення, зміни в освітленні і додавання шуму. Однак вони не здатні впоратися з проблемою масштабування, тобто, два зображення однієї і тієї ж сцени, пов'язані зі зміною масштабу, можуть мати різні точки інтересу.
Багатомасштабні детектори, здатні надійно витягувати характерні ознаки при змінах масштабу.

Одномасштабні детектори.

Детектор Moravec

Детектор Moravec орієнтований на знаходження різних областей у зображенні, які можна використовувати для стабілізації послідовних кадрів зображення. Основною ідеєю є виявлення кута, для цієї мети вважається, що кут є точкою з низькою самоподібністю. Детектор перевіряє кожен піксель на заданому зображенні, щоб перевірити, чи присутній кут. Для цієї мети він розглядає локальні зміни зображення з центром у поточному пікселі, а потім визначає подібність між даними і сусідніми ділянками. Подібність вимірюється шляхом взяття суми різниць квадратів (SSD-sum of square differences) між центрованою плямою і іншими плямами зображення. Грунтуючись на значенні SSD, необхідно розглянути три випадки: Найменший SSD між плямою і його сусідами (горизонтальний, вертикальний і на двох діагоналях) використовується в якості міри кута повороту. Кут або точка інтересу виявляються, коли SSD досягає локальних максимумів.
Алгоритм реалізації детектора Моравека:
  1. Вхід: сіре зображення, розмір вікна, поріг T.
  2. Для кожного пікселя (x, y) в зображенні розраховують зміну інтенсивності V від зсуву (u, v) \[ V_{u, v} (x, y) =\sum_{∀a, b∈window} \left[I (x + u + a, y + v + b) - I (x + a, y + b)\right]^2. \]
  3. Побудувати карту кутів, розрахувавши міру кутів C (x, y) для кожного пікселя (x, y) \[C (x, y) = \min \{V_ {u, v} (x, y) \}. \]
  4. Встановити поріг карти кутів, замінити всі значення C (x, y) нижче заданого порогового значення T на нуль.
  5. Виконати придушення НЕ-максимальних значень, щоб знайти локальні максимуми. В результаті все ненульові точки, що залишаються на мапі кутів, є кутами.


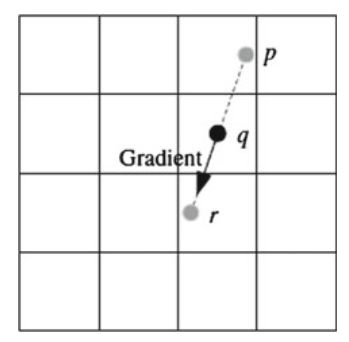
Виконання придушення НЕ-максимуму.  

Для виконання придушення НЕ-максимумів, зображення сканується в напрямку його градієнта, яке повинно бути перпендикулярно краю. Будь-який піксель, який не є локальним максимумом, пригнічується і встановлюється в нуль. Як показано на малюнку, p і r є двома сусідами вздовж напрямку градієнта q. Якщо значення пікселя q не більше значень пікселів як p, так і r, воно пригнічується.
Одна з переваг детектора Моравека полягає в тому, що він може виявляти більшість кутів. Однак він не є ізотропним, зміна інтенсивності розраховується тільки при дискретному наборі зрушень (тобто вісім основних напрямків). Таким чином, він не інваріантний до обертання, в результаті чого детектор має низьку повторюваність.

Детектор Harris

Harris і Stephens розробили комбінований детектор кутів і країв для усунення обмежень детектора Моравека. Отримуючи зміни автокореляції (тобто зміна інтенсивності) при всіх різних орієнтаціях, це призводить до більш бажаного детектору з точки зору виявлення і повторюваності. Отриманий детектор на основі матриці автокореляції, є найбільш широко використовуваним методом. Симетрична матриця автокореляції 2 × 2, яка використовується для виявлення особливостей зображення та опису їх локальних структур, може бути представлена ​​у вигляді \[ M(x, y) = \sum_{u,v}w(u,v) \left[ \begin{array}{cc} I^2_x(x,y)& I_xI_y(x,y) \\ I_xI_y(x,y) & I^2_y(x,y) \\ \end{array} \right], \] де \(I_x\) і \(I_y\) - локальні похідні зображення у напрямах x і y відповідно, а w (u, v) є вагове вікно (ваги) по області (u, v).
Якщо використовується кругле вікно, таке як при використання Гаусіану, то відклик буде ізотропним, а ваги будуть більше, чим ближче точка до центру.   Для знаходження точок інтересу, для кожного пікселя обчислюються власні значення матриці M. Якщо обидва власних значення великі, це вказує на наявність в цьому місці кута.


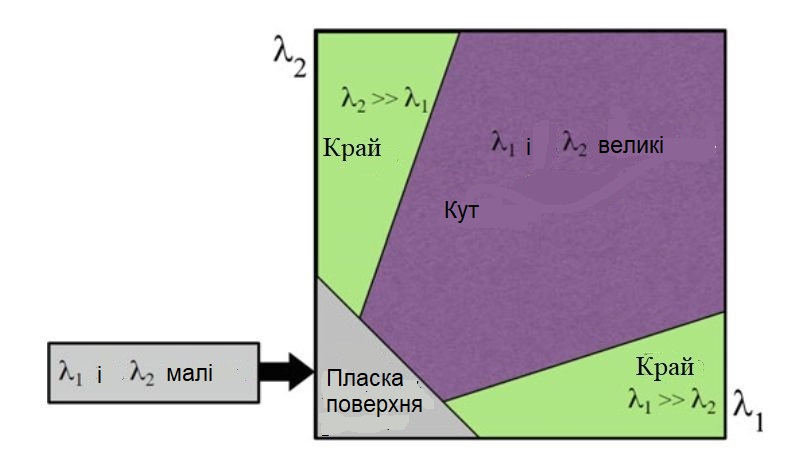
  Класифікація точок зображення на основі власних значень матриці автокореляції M  

  Побудову карти відклику можна виконати шляхом обчислення міри кута C (x, y) для кожного пікселя (x, y) \[ C (x, y) = det (M) - K (trace (M))^2, \] де \[ det (M) = λ_1 * λ_2 \hbox{ і } trace(M) = λ_1 + λ_2, \] K є коректуючим параметром і λ1, λ2 є власними значеннями матриці автокореляції.
Точне обчислення власних значень обчислювально дорого, оскільки вимагає обчислення квадратного кореня.  Тому Харріс запропонував використовувати цю міру кута, яка об'єднує два власних значення в одному числі.  Придушення НЕ-максимумів має бути проведено, щоб знайти локальні максимуми, і все ненульові точки, що залишаються в карті кутів, є шуканими кутами.  

SUSAN Detector

 Замість використання для обчислення кутів похідних зображень, Smith і Brady представили загальну низько рівневу техніку обробки зображень, так  звану SUSAN (Smallestм Univalue Segment Assimilating Nucleus). Крім того, що отримана характеристика є детектором кута, вона використовується для виявлення країв і  зменшення шуму зображення. Кут визначається шляхом накладення кругової маски фіксованого радіусу на кожен піксель зображення.  Центральний піксель називається ядром, де порівнюються пікселі в області під маскою з ядром, щоб перевірити, чи мають вони однакові або різні значення інтенсивності.  Пікселі, що мають майже ту ж яскравість, що і ядро, групуються разом, і результуюча область називається USAN (Univalue Segment Assimilating Nucleus).  Кут знаходиться в місцях, де кількість пікселів в USAN досягає локального мінімуму і нижче певного порогового значення T.  
 Для виявлення кутів функція порівняння C (r, r 0 ) між кожним пікселем в масці і ядром маски задається як \[ C(r,r_0)= \left\{ \begin{array}{ll} 1 & \hbox{ якщо } |I(r)-I(r_0)|\le T,\\ 0, & \hbox{ у зворотному випадку,} \end{array} \right. \] а размір регіону USAN дорівнює \[ n(r_0)=\sum_{r\in C(r_0)}C(r,r_0), \] де \(r_0\) і \(r\) - координати ядра і, відповідно, координати інших точок у масці. Ефективність детектора кута SUSAN в основному залежить від функції порівняння \(C (r, r_0) \), яка не захищена від певних факторів, що впливають на зображення (наприклад, сильної флуктуації яскравості і шумів).
Детектор SUSAN має деякі переваги, такі як: На жаль, він не інваріантний до масштабування і інших перетворень, при цьому, фіксований глобальний поріг не підходить для загальної ситуації. Кутовий детектор потребує адаптивного порогу, і зміни форми маски.

FAST Detector

FAST (Features from Accelerated Segment Test) - детектор кутів, спочатку розроблений Rosten і Drummondn. У цій схемі виявлення точки-кандидата проводиться шляхом застосування сегментного тесту до кожного пікселя зображення, розглядаючи коло з 16 пікселів навколо кутового пікселя-кандидата в якості основи обчислення. Якщо набір з n суміжних пікселів в колі Брезенхема з радіусом r яскравіше, ніж інтенсивність потенційного пікселя (позначається \(I_p \)) плюс граничне значення \(t, I_p + t \), або все темніше, ніж інтенсивність пікселя-кандидата мінус граничне значення \(I_p - t \), тоді p класифікується як кут.
Це тест має високу швидкість і може використовуватися для виключення дуже великої кількості некутових точок.
Для перевірки чотирьох пікселів 1, 5, 9 і 13, кут може існувати тільки в тому випадку, якщо три з цих тестових пікселів яскравіше, ніж \(I_p + t \) або темніше, ніж \(I_p-t \), а інші пікселі потім перевіряються для остаточного висновку.


Виявлення ознак в плямі зображення з використанням детектора FAST.  

Малюнок ілюструє процес, де виділені квадрати - це пікселі, які використовуються при визначенні кута. Піксель в точці p є центром можливого кута. Дуга позначена пунктирною лінією, що проходить через 12 суміжних пікселів, які по порогу яскравіше p. Найкращі результати досягаються при використанні кола з r = 3 і n = 9.
Хоча тест дає високу продуктивність, він страждає від декількох обмежень і недоліків. Усунення цих обмежень і слабких місць досягається за допомогою підходу машинного навчання. Порядок питань, використовуваних для класифікації пікселя, вивчається за допомогою добре відомого алгоритму дерева рішень (ID3), який значно прискорює цей крок. Так як перший тест видає багато суміжних відповідей навколо точки інтересу, для виконання придушення немаксимумів застосовуються додаткові критерії. Це дозволяє точно локалізувати особливості. Використовувана міра кута на цьому кроці має вигляд \[ C(x, y) = \max \left(\sum_{j ∈S_{bright}}| I_{p → j} - I_p | - t, \sum_{j ∈S_{dark}}| I_p - I_{p → j} | - t\right), \] де \(I_ {p → j} \) позначає пікселі, що лежать на колі Брезенхема. Таким чином, час обробки залишається коротким, тому що другий тест виконується тільки для частини точок зображення, які пройшли перший тест.
Іншими словами, процес працює в два етапи.
По-перше, виявлення кута для набору зображень виконується з перевіркою сегмента заданого n і відповідним порогом (переважно з цільової області). Кожен піксель з 16 місць на колі класифікується як більш темний, схожий або більш яскравий.
По-друге, використовуючи алгоритм ID3 в 16 місцях, щоб вибрати той, який дає максимальний виграш інформації.
Чи не максимальне обмеження застосовується до суми абсолютної різниці між пікселями в суміжній дузі і центральним пікселем. При цьому кути виявлені за використанням алгоритму ID3 можуть трохи відрізнятися від результатів, отриманих за допомогою детектора тестів сегмента, через те, що модель дерева рішень залежить від даних навчання, які не можуть охопити всі можливі кути. У порівнянні з багатьма існуючими детекторами кутовий детектор FAST дуже підходить для додатків обробки відео в реальному часі через його швидкодію. Але він не є інваріантним для масштабування змін і не стійкий до шуму, а також залежить від порогу, при цьому вибір адекватного порогу не є тривіальним завданням.

Детектор Гессіан

Цей детектор заснований на матриці 2 × 2 похідних другого порядку інтенсивності зображення I (x, y), так званої матриці Гессе. Ця матриця може бути використана для аналізу локальних структур зображення, і вона має вигляд \[ H (x, y, σ) = \left[ \begin{array}{cc} I_{xx} (x, y, σ) & I_{xy} (x, y, σ) \\ I_{yx} (x, y, σ) & I_{yy} (x, y, σ)\\ \end{array} \right] \] де \(I_{xx}, I_{xy}\) и \(I_{yy}\) - похідні зображення другого порядку, обчислені з використанням функції Гауса стандартного відхилення σ.
Для того, щоб виявити точки інтересу, він шукає підмножину точок, де відгуки похідних високі в двох ортогональних напрямках. Тобто детектор шукає точки, в яких визначник матриці Гессе має локальні максимуми \[ det (H) = I_ {xx} I_ {yy} - I ^ 2_ {xy}. \] Вибираючи точки, які максимізують визначник Гессіану, він виділяє довші структури, які мають невеликі другі похідні (тобто зміни сигналу) в одному напрямку. Далі йде застосування не-максимального придушення з використанням вікна розміром 3 × 3 по всьому зображенню зі збереженням лише пікселів, значення яких більше, ніж значення всіх восьми безпосередніх сусідів всередині вікна. Потім, детектор повертає всі місця розташування, що залишилися, значення яких перевищує заздалегідь визначений поріг T. Отримані відклики детектора в основному розташовані на кутах і сильно текстурованих областях зображення.
У той час як матриця Гессе використовується для опису локальної структури в околиці навколо точки, її детермінант використовується для виявлення структур зображення, які демонструють зміни сигналу в двох напрямках. У порівнянні з іншими операторами, такими як Лапласіан, детермінант Гессіану реагує тільки в тому випадку, якщо локальний шаблон зображення містить значні варіації уздовж будь-яких двох ортогональних напрямків. Однак використання похідних другого порядку в детекторі чутливо до шуму. Крім того, локальні максимуми часто виявляються поблизу контурів або прямих країв, де сигнал змінюється тільки в одному напрямку. Таким чином, ці локальні максимуми менш стабільні, так як на локалізацію впливають шум або невеликі зміни в сусідньому фрагменті.

Мультімасштабні детектори

Лапласіан Гауса (LoG)

Лапласіан Гауса (LoG), лінійна комбінація других похідних, є звичайним детектором, яким виділяються плями. Для заданого вхідного зображення I (x, y) отримуємо уявлення в масштабному просторі зображення, визначеного за допомогою L (x, y, σ), шляхом згортання зображення за допомогою Гаусова ядра змінного масштабу G (x, y, σ), де \[ L (x, y, σ) = G (x, y, σ) \otimes I (x, y) \] і \[ G (x, y, σ) =\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}. \] Для обчислення оператора Лапласа використовується наступна формула \[ \nabla ^ 2L (x, y, σ) = L_ {xx} (x, y, σ) + L_ {yy} (x, y, σ). \]  Це призводить до сильних додатних відкликів на темні плями і сильним від'ємним відгукам для яскравих плям розміром \(\sqrt {2σ} \).  Однак реакція сильно залежить від співвідношення між розміром структур плям в області зображення і розміром ядра Гауса.  Стандартне відхилення по Гаусу використовується для керування масштабом, шляхом зміни ступеня розмиття. Щоб автоматично захоплювати плями різного розміру в  області зображення. Використовується багатомасштабний підхід з автоматичним вибором масштабу за допомогою пошуку екстремумів масштабного простору  нормалізованого за масштабом оператора Лапласа  \[ \nabla_ {norm} ^ 2L (x, y, σ) = \sigma ^ 2 (L_ {xx} (x, y, σ) + L_ {yy} (x, y, σ)). \] Запропонований метод також може виявляти точки, які одночасно є локальними максимумами / мінімумами \(∇ ^ 2_ {norm} L (x, y, σ) \) щодо простору і масштабу. Оператор LoG є радіально-нормальним, симетричним, тому він природно інваріантний до обертання. Завдяки властивості кругової симетрії LoG добре пристосований до виявлення плям, але він також забезпечує хорошу оцінку для інших локальних структур, таких як кути, ребра, гребні і вузли. У цьому контексті LoG може застосовуватися для пошуку місця розташування заданої характеристики зображення або для безпосереднього виявлення областей, інваріантних до масштабу, шляхом пошуку екстремумів 3D (місце розташування + масштаб) функції LoG.


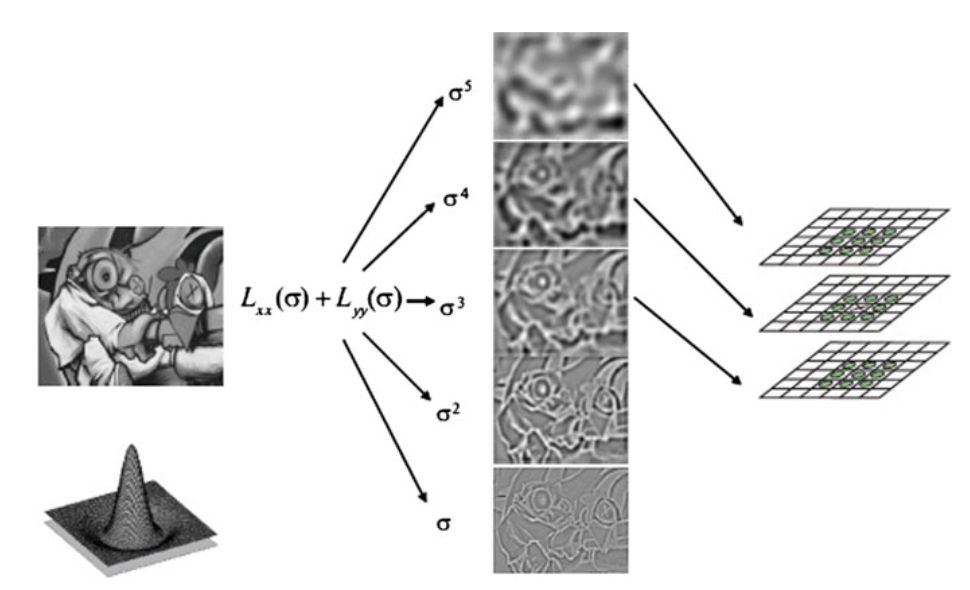
Пошук просторових екстремумів 3D-функції функції LoG.  

Різниця Гаусіанів (DoG)

Насправді обчислення операторів LoG займає багато часу. Для прискорення обчислень Lowe запропонував ефективний алгоритм, заснований на масштабно-просторовій піраміді, побудованої з використанням фільтрів різниці функцій Гауса (DoG). Цей підхід використовується в алгоритмі масштабно-інваріантного перетворення ознак (SIFT). У цьому контексті DoG дає близьке наближення до Гаусівського Лапласіану (LoG) і використовується для ефективного виявлення стабільних об'єктів з екстремумів масштабуючих просторів. Функція DoG D (x, y, σ) може бути обчислена без згортки шляхом вирахування суміжних масштабних рівнів Гаусової піраміди, розділених коефіцієнтом k. \[ D (x, y, σ) = (G (x, y, kσ) - G (x, y, σ)) \otimes I (x, y) = L (x, y, kσ) - L ( х, у, σ). \] Типи об'єктів, витягнуті DoG, можна класифікувати так само, як і для оператора LoG. Крім того, детектор області DoG виконує пошук екстремумів тривимірної функції DoG.


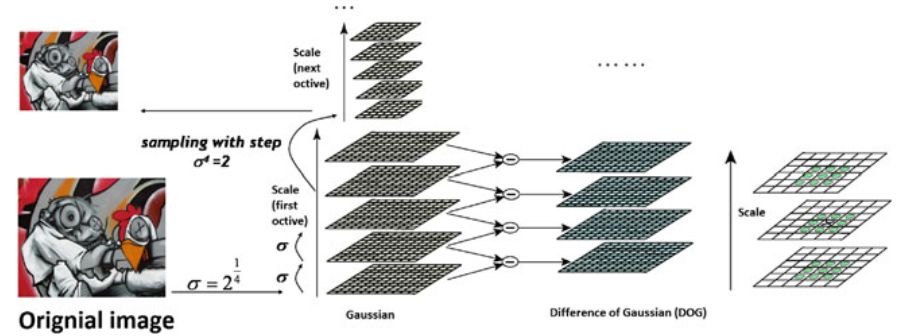
Пошук екстремумів тривимірного масштабу функції DoG  

 Загальним недоліком уявлень як LoG, так і DoG є те, що локальні максимуми також можна виявити в сусідніх контурах прямих країв, де зміна сигналу відбувається тільки в одному напрямку, що робить їх менш стійкими і більш чутливими до шуму або невеликих змін.

Harris-Laplace

Детектор Харріса-Лапласа - масштабно-інваріантний детектор кутів, запропонований Mikolajczyk і Schmid. Він заснований на комбінації кутового детектора Харріса і просторового представлення у Гаусівському масштабуючому просторі. Хоча кутові точки Харріса інваріантні до повороту і змін освітленості, точки не є інваріантними до масштабування. Тому матриця другого моменту, використовувана в цьому детекторі, модифікується таким чином, щоб вона не залежала від масштабу зображення. Адаптована за масштабом матриця другого моменту, використовувана в детекторі Харріса-Лапласа, представлена ​​як \[ M (x, y, σ_I,σ_D) = σ_D^2g(σ_I)\left[ \begin{array}{cc} I_{x}^2 (x, y, σ_D) & I_{x}I_y (x, y, σ_D) \\ I_{x}I_y (x, y, σ_D) & I_{y}^2 (x, y, σ_D)\\ \end{array} \right] \] де \(I_x\) и \(I_y\) - похідні зображення, розраховані в їх відповідному напрямку з використанням Гаусівського ядра з відхиленням \(σ_D \).  
 Параметр \(σ_I \) визначає поточний масштаб, при якому кутові точки Харріса виявляються у Гаусівському масштабуючому просторі.  Іншими словами, шкала похідних \(σ_D \) визначає розмір Гаусівських ядер, використовуваних для обчислення похідних,  в той час як інтегральний масштаб \(σ_I \) використовується для визначення середньозваженого значення похідних в околиці.  Багатовимірна міра кута Харріса обчислюється з використанням визначника і сліду адаптованої матриці другого моменту як \[ C (x, y, σ_I, σ_D) = det [M (x, y, σ_I, σ_D)] - α. trace^2 [M (x, y, σ_I, σ_D)]. \] Значення константи α знаходиться в діапазоні від 0,04 до 0,06. На кожному рівні представлення, точки інтересу витягуються шляхом виявлення локальних максимумів в  8-околі точки (x, y). Потім використовується порогове значення для відкидання максимумів малого кута, оскільки вони менш стійкі при довільних умовах  перегляду \[C (x, y, σ_I, σ_D)> Threshold_ {Harris} \]  Крім того, Лапласіан Гауса використовується, щоб знайти максимуми за масштабом, де приймаються тільки ті точки, для яких Лапласіан досягає максимуму чи його відклик  вище порога \[σ ^ 2_I | L_ {xx} (x, y, σ) + L_ {yy} (x, y, σ) | > Threshold_ {Laplacian}. \]  Підхід Харріса-Лапласа забезпечує репрезентативний набір точок, які характерні для зображення і при його масштабуванні.  Точки інваріантні до змін масштабу, обертання, висвітлення і додаванню шуму. Крім того, точки інтересів дуже повторювані.  Однак детектор Харріса-Лапласа повертає набагато меншу кількість точок в порівнянні з детекторами LoG або DoG.  Крім того, він зазнає невдачі в разі афінних перетворень.  

Hessian-Laplace

 Подібно детектуванню Харріса-Лапласа, та ж ідея може бути застосована і до детектора на основі Гессіану, що призводить до масштабно-інваріантного детектору, названому  Гессіаном-Лапласа. Спочатку будуємо уявлення в масштабі простору зображення, використовуючи фільтри Лапласа або їх наближені фільтри DoG.  Потім використовуємо визначник Гессіану, щоб витягти масштабні інваріантні об'єкти, схожі на плями.  
 Детектор Гессіана-Лапласа виділяє велику кількість функцій, які покривають всі зображення з дещо меншою повторюваністю в порівнянні з його аналогом  Харріса-Лапласа. Крім того, витягнуті розташування є більш придатними для оцінки масштабу через подібності фільтрів, використовуваних в  просторовій і масштабній локалізації, обидва на основі похідних другого порядку функції Гауса. Детектори на основі Гессіану більш  стабільні, ніж аналоги на основі детектора Харріса. Аналогічно, апроксимуючи для прискорення LoG за допомогою DoG, детермінант Гессіану апроксимується з використанням методу  інтегральних зображень, в результаті чого виходить швидкий Гессівський детектор.  

Детектор вейвлета Габора

Yussof і Hitam запропонували багатомасштабний детектор точок інтересу, заснований на принципі вейвлетів Габора.  Вейвлети Габора є ядрами згортки в формі пласких хвиль, обмежених функцією Гауса.  Вейвлети Габора приймають форму складної пласкої обвідної хвилі, модульованої за Гаусом \[ \psi_{u,v}(z)=\frac{\|K_{u,v}\|^2}{\sigma^2}e^{\frac{\|K_{u,v}\|^2\|z\|^2}{2\sigma^2}}\left(e^{izK_{u,v}}-e^{\frac{\sigma^2}{2}}\right), \] де \(K_ {u, v} = K_v e ^ {iφ_u}, z = (x, y), u \) і \(v \) визначають орієнтацію і масштаб вейвлетів Габора, \(K_v = K_ \max / f ^ v \) і \(φ_u = π u / 8, K_ \max \) -  максимальна частота, а \(f = \sqrt {2} \) - коефіцієнт відстані між ядрами в частотної області.  
 Відгук зображення I на вейвлет ψ розраховується як згортка \(G = I \otimes ψ \).  Коефіцієнти згортки представляють інформацію в локальній області зображення, яка повинна бути більш ефективною, ніж ізольовані пікселі.  Перевага вейвлетів Габора полягає в тому, що вони забезпечують одночасний оптимальний відклик як в просторових, так і в частотних  областях. Крім того, вейвлети Габора можуть посилювати низькорівневі функції, такі як піки, провали і гребені. Таким чином, вони використовуються для вилучення  точок з зображення в різних масштабах шляхом об'єднання кількох орієнтацій відгуків зображення.  
 Точки інтересу витягуються в декількох масштабах з комбінацією рівномірно розподіленої орієнтації. Доведено, що точки, витягнуті за допомогою вейвлет-детектора Габора мають високу точність і адаптованість до різних геометричних  перетворень.  

Афінні інваріантні детектори.

Детектори функцій, які обговорювалися досі, демонструють незмінність щодо переміщень,  обертань і рівномірного масштабування, припускаючи, що на локалізацію і масштаб не впливають афінні перетворення локальних структур зображення.  Таким чином, вони частково вирішують складну проблему повної інваріантності, маючи на увазі, що масштаб може бути різним у кожному напрямку,  а не рівномірним, що, в свою чергу, робить масштабно-інваріантні детектори невдалими в разі значних афінних перетворень.  Отже, створення детектора, стійкого до перспективних перетворень, вимагає інваріантності до афінних перетворень.  
 Афінно-інваріантний детектор можна розглядати як узагальнену версію масштабно-інваріантного детектора.

Масштабно-інваріантні перетворення ознак.

Після того, як був виявлений набір точок інтересу зображення у вигляді розташування $ p (x, y) $, масштабу $ s $ і орієнтації θ, їх вміст або структура зображення в околиці $ p $ повинні бути закодовані в потрібному дескрипторі для відповідності та нечутливого до локальних деформацій зображення. Дескриптор повинен бути вирівняний з θ і пропорційний зі шкалою s. У літературі є велика кількість дескрипторів ознак зображення, розглянемо деякі з них.

Масштабно-інваріантне перетворення ознак (SIFT)

Lowe запропонував алгоритм масштабно-інваріантного перетворення ознак (SIFT), де на зображенні виявляється ряд точок інтересу. Для цієї мети використовується оператор різниці Гаусіанів (DOG). Точки вибираються як локальні екстремуми функції DoG. З кожної точки інтересу витягується вектор об'єктів. По ряду масштабів і по околиці навколо характеристичної точки оцінюється локальна орієнтація зображення з використанням локальних властивостей зображення з метою забезпечення інваріантності щодо повороту. Потім для кожної виявленої точки обчислюється дескриптор на основі локальної інформації зображення.
Дескриптор SIFT будує гістограму градієнтних орієнтацій точок вибірки в області навколо ключової точки, знаходить найбільше значення орієнтації і будь-які інші значення, які знаходяться в межах 80% від найбільшого, після чого використовує ці орієнтації як домінуючу орієнтацію ключової точки.

Робота алгоритму SIFT починається з вибірки величин і орієнтацій градієнта зображення в області 16 × 16 навколо кожної ключової точки, використовуючи її масштаб для вибору рівня розмиття зображення по Гаусу. Потім створюється набір гістограм орієнтації, де кожна гістограма містить вибірки з 4 × 4 субрегіону сусідніх областей і має вісім бінів (комірок) орієнтації в кожній.

 Вагова функція Гауса з дисперсією σ, яка дорівнює половині розміру області, використовується для обчислення розміру ваги кожної точки вибірки і дає більш високі ваги градієнтам, розташованим ближче до центру області. Дескриптор формується з вектору, що містить значення гістограм орієнтації. Оскільки є 4 × 4 гістограми, кожна з 8 комірками, вектор ознак має 4 × 4 × 8 = 128 елементів для кожної ключової точки. Нарешті, вектор ознак нормалізується по довжині, що дорівнює одиниці, щоб отримати інваріантність до афінних змін освітлення. Ці зміни можна зменшити, встановивши порогове значення координат вектору об'єктів до максимального значення 0.2, після чого вектор знову нормалізується.


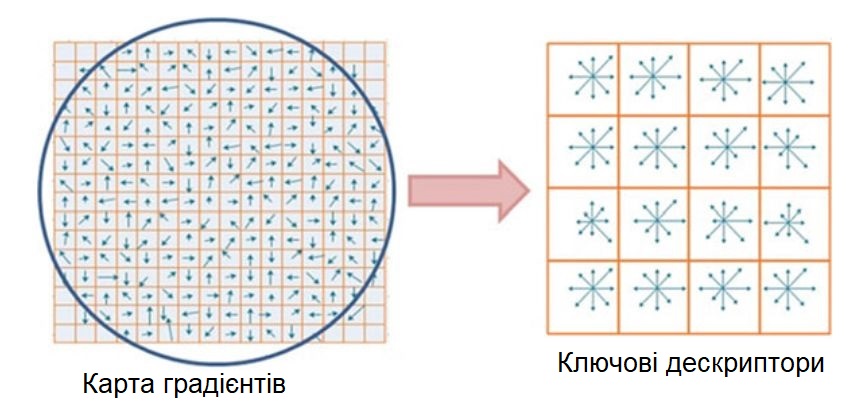
Схематичне представлення дескриптора SIFT для фрагмента 16 × 16 пікселів
і Гаусовій ваговій функції масиву дескрипторів розміру 4 × 4  

Малюнок ілюструє схематичне представлення алгоритму SIFT, де орієнтації і величини градієнта обчислюються для кожного пікселя, а потім кожному ставиться у відповідність вага за допомогою функції Гауса (позначено накладеним колом). Потім для кожного субрегіону обчислюється зважена гістограма градієнта орієнтації.

Стандартний опис дескриптора SIFT заслуговує на увагу в декількох аспектах:

Як доповнення до SIFT Ke і Sukthankar запропонували PCA-SIFT для зменшення розмірності вихідного дескриптора SIFT з використанням стандартної методики аналізу основних компонентів (PCA) нормалізованого градієнта.

 

Градієнтно-орієнтована гістограма (GLOH)

 Дескриптор GLOH дуже схожий на SIFT, де він замінює тільки декартову сітку розташування, використовувану SIFT, на лог-полярну (логарифм-полярну), \[ \displaystyle {\begin{cases}\rho =\log {\sqrt {x^{2}+y^{2}}},\\\theta =\rm{arctg } \frac{y}{x}{\hbox{, для }}x>0.\end{cases}} \] і застосовує PCA (метод головних компонент) для зменшення розміру дескриптора.  
 У GLOH використовується лог-полярна сітка з 3 осередками в радіальному напрямку (радіус встановлений в 6, 11 і 15) і 8 в кутовому напрямку, в результаті чого  отримано 17 місць розташування.   


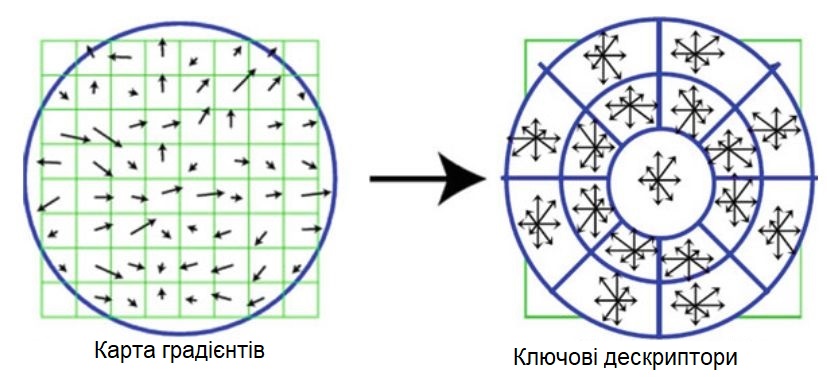
Схематичне представлення алгоритму GLOH з використанням лог-полярних бінів  

 Дескриптор GLOH створює набір гістограм, що використовують орієнтацію градієнта в 16 осередках, в результаті чого вектор ознак  становить 17 × 16 = 272 елементів для кожної ключової точки.  
 272-мірний дескриптор зменшується до 128-мірного дескриптора шляхом обчислення коваріаціоної матриці для PCA, і для  опису обрані найважливіші 128 власних векторів (що відповідають найбільшим власним значенням).  

Виявлено, що результати використання GLOH перевершують дескриптор SIFT і забезпечують найкращу продуктивність, особливо при змінах освітленості, але при цьому більш ресурсоємні.

Дескриптор SURF (Speeded-Up Robust Features Descriptor)

Детектор-дескриптор прискорених надійних функцій (SURF) розроблений в якості ефективної альтернативи SIFT. SURF набагато швидше і надійніше, ніж SIFT. На стадії виявлення точок інтересу, замість того, щоб покладатися на похідні Гауса, проводяться обчислення основані на простих 2D-фільтрах. Для цього використовується масштабно-інваріантний детектор, заснований на визначнику матриці Гессе, як для вибору масштабу, так і для визначення місць розташування. Його основна ідея полягає в тому, щоб ефективно апроксимувати похідні другого порядку згортки з функцією Гауса за допомогою згортки зображень з набором прямокутних фільтрів.


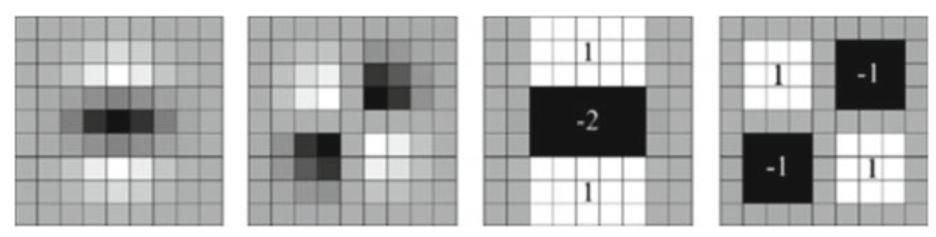
Похідні другого порядку від функції Гауса -по y (D yy ), змішана похідна -по xy (D xy ) і,
відповідно, їх апроксимації в тих же напрямках.  

Фільтри 9 × 9, зображені на малюнку, є наближенням Гаусіана з σ = 1.2 і представляють найнижчий масштаб. Ці наближення позначаються через D xx , D yy і D xy . Таким чином, можна апроксимувати визначник Гессіану, і може бути виражений як \[Det (H_ {approx}) = D_ {xx} D_ {yy} - (wD_ {xy}) ^ 2, \] де $ w $ - відносна вага відклику фільтра, і він використовується для врівноваження виразу для детермінанта Гессіану.
Апроксимація детермінанту Гессіану дає відклик точки на зображенні, а локальні максимуми виявляються і уточнюються за допомогою квадратичної інтерполяції, так само як в DoG. Після проведення пригнічення немаксімумов в околиці 3 × 3 × 3, отримуємо стійкі точки інтересу і шкалу значень. Дескриптор SURF починається з побудови квадратної області, центрованої навколо виявленої ключової точки і орієнтованої уздовж її основної орієнтації.
Розмір цього вікна 20s, де s - масштаб, на якому можна знайти характеристичну точку. Потім область додатково ділиться на менші 4 × 4 підобласті, і для кожної підобласті вейвлет-відклики Харра в вертикальному і горизонтальному напрямках (позначені d x і d y , відповідно), обчислюються для 5 × 5 точок вибірки, як показано на малюнку.


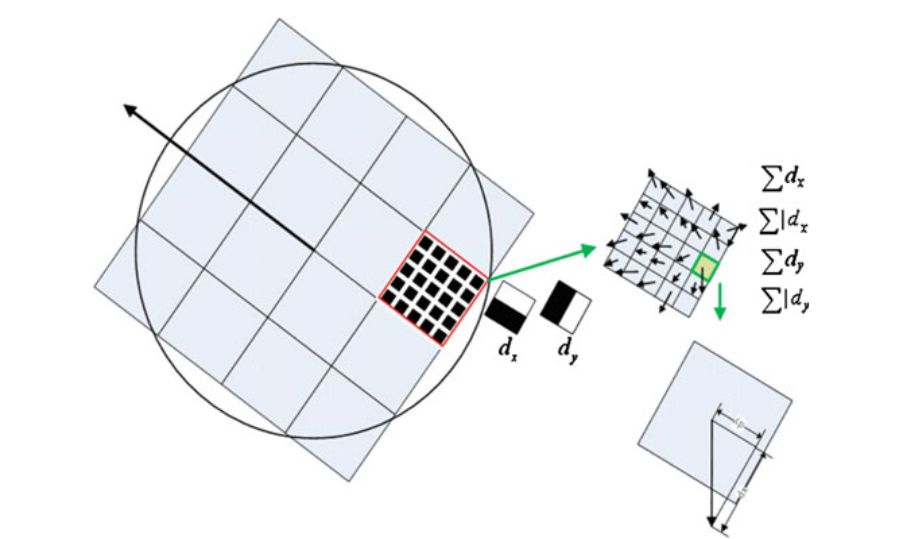
Поділ області інтересу на 4 × 4 підобласті для обчислення дескриптора SURF.  

На відклики навішуються вагові коефіцієнти за допомогою Гаусівського вікна з центром в точці інтересу, що підвищує стійкість до геометричних деформацій і помилок локалізації. Вейвлет-відклики d x і d y підсумовуються для кожної підобласті і заносяться в вектор ознак $ v $, де \[ v = \left (\sum {d_x}, \sum {| d_x |}, \sum {d_y}, \sum {| d_y |} \right). \] Обчислюємо $ v $ для всіх 4 × 4 підобластей, в результаті чого дескриптор ознаки має довжину 4 × 4 × 4 = 64 вимірювання. Нарешті, дескриптор об'єкта нормалізується до одиничного вектору, щоб зменшити ефекти освітлення.
Основною перевагою дескриптора SURF в порівнянні з SIFT є швидкість обробки, оскільки він використовує 64-мірний вектор ознак для опису локальної функції, в той час як SIFT використовує 128. Однак дескриптор SIFT більше підходить для опису зображень, на які впливають переміщення, поворот, масштабування і деформації освітлення. Хоча SURF демонструє свій потенціал в широкому спектрі додатків, він також має деякі недоліки, він не ефективний, якщо обертання є великим або кути огляду занадто різні.

Локальні бінарні шаблони (LBP)

Локальні бінарні шаблони (LBP-Local Binary Pattern) характеризують просторову структуру текстури і являють собою характеристики інваріантності монотонних перетворень рівнів сірого. Дескриптор кодує відношення упорядкування, порівнюючи сусідні пікселі з центральним пікселем, тобто він створює функцію на основі порядку для кожного пікселя, порівнюючи значення інтенсивності кожного пікселя із значенням його сусідніх пікселів.
Зокрема, сусіди, чиї характеристики перевищують центральні, позначені як «1», в той час як інші позначені як «0». Спільна поява результатів порівняння згодом записується рядком двійкових бітів. Після цього, ваги, визначаються з геометричної прогресії зі знаменником 2 і присвоюються бітам відповідно за їх індексами. Далі бінарний рядок із значень зважених бітів, перетворюється в десятковий індекс (двійковий шаблон).
У стандартній версії піксель $ c $ з інтенсивністю g (c) позначається як \[ \displaystyle {S(g_p-g_c)=\begin{cases}1, \hbox{ якщо }g_p\ge g_c,\\0, \hbox{ якщо }g_p\lt g_c.\end{cases}} \] де пікселі $ p $ належать околиці 3 × 3 з рівнями сірого $ g_p (p = 0, 1, ..., 7) $.
Потім шаблон LBP околиці пікселя обчислюється шляхом підсумовування відповідних порогових значень $ S (g_p - g_c) $, з вагами $ 2 ^ k $ \[ LBP = \sum_ {k = 0} ^ 7S (g_p-g_c) 2 ^ k. \] Після обчислення маркера для кожного пікселя зображення, в якості дескриптора ознаки для текстури використовується гістограма з 256 бінів отриманих міток. Приклад ілюстрації обчислення LBP для пікселя в околиці 3 × 3 і дескриптора орієнтації базової області зображення показаний на наступному малюнку.


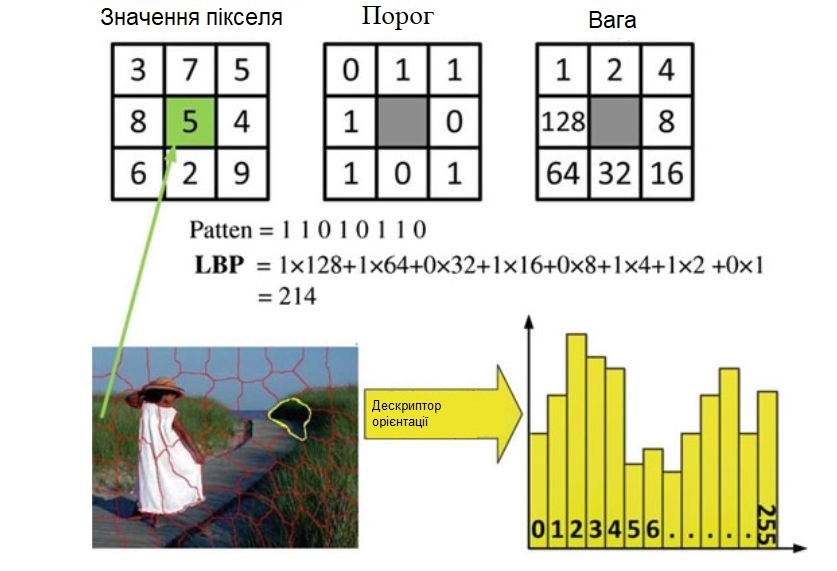
Обчислення дескриптора LBP для пікселя в околиці 3 × 3.  

Крім того, дескриптор LBP в його загальному вигляді обчислюється таким чином \[ LBP_ {RN} (x, y) = \sum_ {i = 0} ^ {N-1} S (n_i-n_c) 2 ^ i, \\ \displaystyle {S (x) = \begin {cases} 1, \hbox { якщо } x \ge g_c, \\0, \hbox { інакше, } \end {cases}} \] де $ n_c $ відповідає рівню сірого центрального пікселя локальної околиці, а $ n_i $ - це рівні сірого з N рівномірно рознесених пікселів на колі радіусу R.
Так як кореляція між пікселями зменшується зі збільшенням відстані між ними, то радіус R зазвичай залишається невеликим.
На практиці відмінності в околиці інтерпретуються як двійкове число з N-біт, що призводить до $ 2 ^ N $ різних значень для двійкового шаблону, як показано на малюнку.


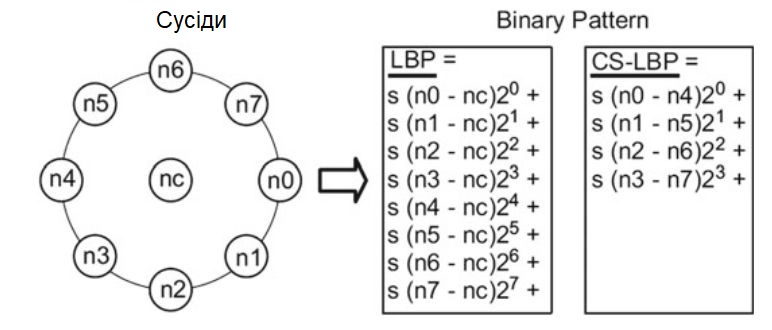
Обчислення LBP і CS-LBP для 8 пікселів.  

Бінарні шаблони називаються однорідними шаблонами, якщо вони містять найбільше два побітових переходу від 0 до 1. Наприклад, «11000011» та «00001110» - це дві однорідні структури, а «00100100» та «01001110» - неоднорідні структури. Було запропоновано кілька варіантів LBP, включаючи центрально-симетричні локальні двійкові структури (CS-LBP), локальний трійковий шаблон (LTP), центрально-симетричний локальний трійковий шаблони (CS-LTP) на основі CS-LBP, і ортогонально-симетричні локальні (OS-LTP). На відміну від LBP, дескриптор CS-LBP порівнює відмінності рівнів сірого центру симетричних пар. Фактично, LBP має перевагу у стійкості до змін освітлення і простоти обчислень. Крім того, LBP і його варіанти досягають великих успіхів в описі текстур. На жаль, особливість LBP в тому, що він створює більш об'ємні елементи і чутливий до Гаусового шуму.

Binary Robust Independent Elementary Features (BRIEF)

BRIEF- дескриптор з низькою швидкістю передачі бітів, введений для зіставлення зображень з випадковими класифікаторами типу лісу і дерев. Він належить до сімейства двійкових дескрипторів, таких як LBP і BRISK, виконує тільки простий двійковий тест порівняння з використанням відстані Хеммінга замість відстані Евкліда або Махалонобіса.
Для побудови двійкового дескриптора необхідно тільки порівняти інтенсивність між двома позиціями пікселів, розташованими навколо виявлених точок інтересу. Це дозволяє отримати репрезентативний опис при дуже низьких обчислювальних витратах. Крім того, зіставлення двійкових дескрипторів вимагає тільки обчислення відстаней Хеммінга, які можуть бути виконані дуже швидко за допомогою примітивів XOR.
BRIEF використовує порівняно невелику кількість тестів. Двійковий дескриптор для ділянки пікселів розміром S × S створюється шляхом об'єднання результатів наступного тесту \[ \displaystyle {\tau=\begin{cases}1, \hbox{ якщо }I(P_j)\ge I(P_i),\\0, \hbox{ інакше, }\end{cases}} \] де $ I (p_i) $ позначає згладжені значення інтенсивності пікселів $ p_i $, а вибір місця розташування всіх $ p_i $ однозначно визначає набір бінарних тестів. Точки відбору взяті з ізотропного Гаусівського розподілу з нульовим середнім і дисперсією, яка дорівнює $ \frac {1} {25} S ^ 2 $.
Для підвищення надійності дескриптора ділянка пікселів попередньо згладжується за допомогою Гаусівського ядра з дисперсією, яка дорівнює 2, і розміром, рівним 9 × 9 пікселів.
Дескриптор BRIEF має два параметра налаштування: кількість двійкових пар пікселів і двійковий поріг.
Експерименти показали, що 256 біт або навіть 128 біт досить для отримання дуже непоганих результатів зіставлення. Таким чином, BRIEF вважається дуже ефективним як для обчислення, так і для зберігання в пам'яті.
На жаль, BRIEF-дескриптор не є стійким до повороту, що перевищує приблизно 35°, отже, він не забезпечує інваріантність обертання.

Описані дескриптори не охоплюють всі детектори-дескриптори, існує велика кількість інших дескрипторів, і багато з них виявилися ефективними в додатках комп'ютерного зору.

Особливості відповідності

Зіставлення ознак або взагалі зіставлення зображень, що є частиною багатьох додатків комп'ютерного зору, таких як реєстрація зображень, калібрування камери і розпізнавання об'єктів, є завданням встановлення відповідності між двома зображеннями однієї і тієї ж сцени / об'єкта. Загальний підхід до співставлення зображень полягає в виявленні набору точок інтересу, кожна з яких пов'язана з дескрипторами даних зображень. Після того, як елементи і їх дескриптори витягнуті з двох або більше зображень, наступним кроком є ​​встановлення деяких попередніх збігів ознак між цими зображеннями, як, наприклад, проілюстровано нижче


Відповідність областей зображення на основі їх локальних дескрипторів об'єктів.  

Проблема зіставлення зображень може бути сформульована таким чином. Припустимо, що \(p \) - це точка, виявлена ​​детектором в зображенні, пов'язаному з дескриптором. \[ Φ (p) = \{φ_k (P) | k = 1, 2, ..., K \} \] де для всіх \(K \) вектор ознак, наданий \(k \) - м дескриптором, дорівнює \[ φ_k (p) = \left (f ^ k_ {1, p}, f ^ k_ {2, p}, ..., f ^ k_ {n_k, p} \right) \] Мета полягає в тому, щоб знайти найкращу відповідність $ q $ в іншому зображенні з набору $ N $ точок інтересу $ Q = \{q_1, q_2, ..., q_N \} $, порівнюючи вектор ознак \(φ_k (p) \) з точками набору $ Q $. З цією метою міру відстані між двома дескрипторами точок інтересу $ φ_k (p) $ і $ φ_k (q) $ можна визначити як \[ d_k (p, q) = | φ_k (p) - φ_k (q) | \] На основі відстані $ d_k $ точки $ Q $ сортуються в порядку зростання незалежно для кожного дескриптора, що створює множину \[ Ψ (p, Q) = \{ψ_k (p, Q) | k = 1, 2, ..., k \} \] де \[ ψ_k (p, Q) = \left \{\left (ψ_k ^ 1, ψ_k ^ 2, ..., ψ_k ^ N \right) ∈ Q | d_k (p, ψ_k ^ i) ≤ d_k (p, ψ_k ^ j), ∀i> j \right \} \] Збіг між парою точок інтересу $ (p, q) $ допускається, тільки якщо $ p $ є найкращим збігом для $ q $ по відношенню до всіх інших точок на першому зображенні, і $ q $ є найкращим збігом для $ p $ по відношенню до всіх інших точок на другому зображенні.
У цьому контексті дуже важливо розробити ефективний алгоритм для максимально швидкого виконання процесу зіставлення. Порівняння найближчих сусідів в просторі ознак дескрипторів зображень в евклідової нормі може використовуватися для зіставлення векторних ознак. Однак на практиці оптимальний алгоритм найближчого сусіда і його параметри залежать від характеристик набору даних. Крім того, для пригнічення кандидатів, для яких відповідність може розглядатися як неоднозначне, співвідношення між відстанями до найближчого і наступного найближчого дескриптора зображення повинно бути менше деякого порогового значення. Як окремий випадок, найбільш ефективними виявилися два алгоритму: рандомізований ліс k-d і метод найближчих сусідів.
З іншого боку, ці алгоритми не підходять для двійкових функцій (наприклад, FREAK або BRISK). Двійкові характеристики порівнюються з використанням відстані Хеммінга, розрахованого за допомогою операції побітового XOR з подальшим підрахунком бітів в результаті. Це включає тільки операції з бітами, які можуть бути виконані досить швидко.


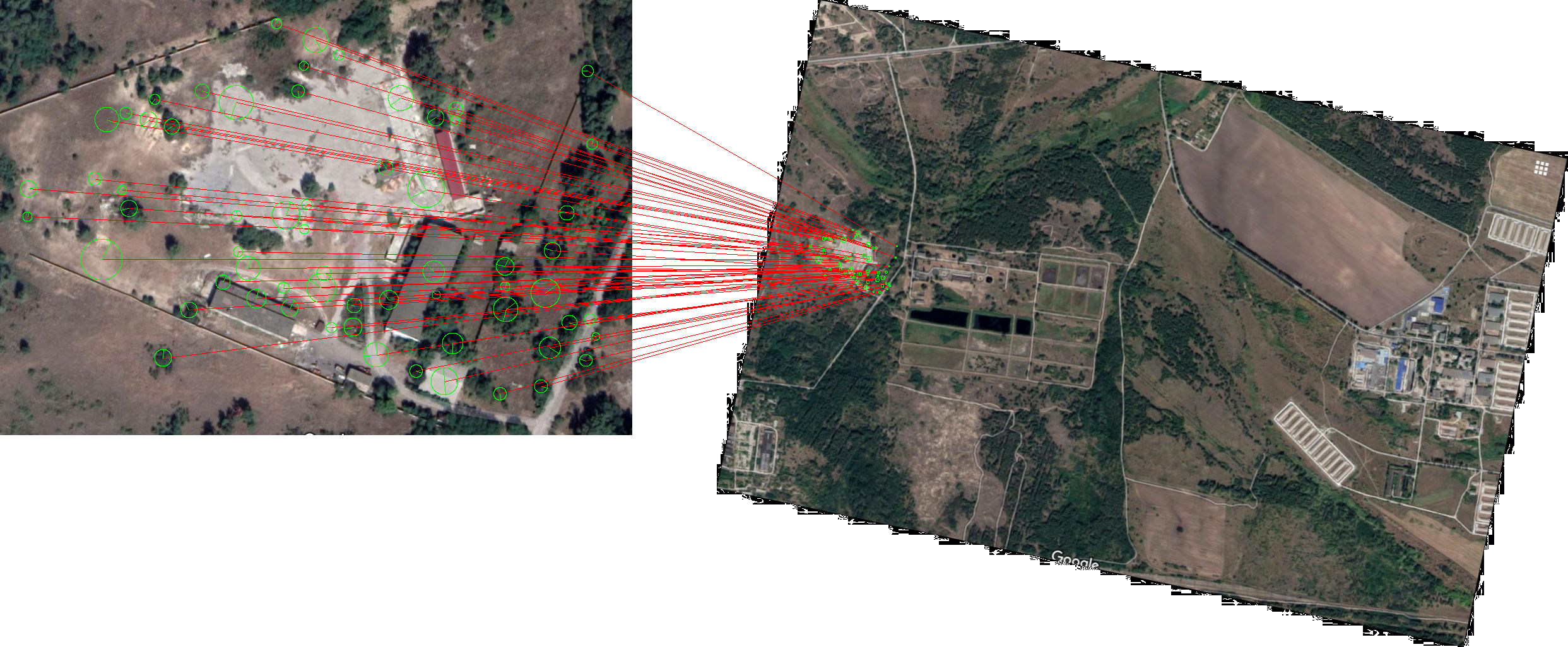
Приклад пошуку відповідностей на зображеннях (проммайданчик в околицях лівобережного масиву м.Кам'янське (мапи Google)).