Нечеткие модели ценообразования.

Оценка компанией нового продукта - довольно сложная задача. Требуются совместные усилия экспертов по финансам, маркетингу, продажам и управлению, чтобы рекомендовать начальную цену нового потребительского продукта. Желание получить большую прибыль через завышение цен может создать рынок для конкурента.
Рассмотрим модель основанную на правилах или целях (требованиях R_i), разработанных экспертами. Перечислим некоторые типичные требования:
\(R_1 \stackrel{\triangle}{=}\) продукт должен иметь низкую цену;

\(R_2 \stackrel{\triangle}{=}\) продукт должен иметь высокую цену;

\(R_3 \stackrel{\triangle}{=}\) продукт должен иметь цену, близкую к цене конкурента.

\(R_4 \stackrel{\triangle}{=}\) продукт должен иметь цену близкую к удвоенной себестоимости;

Дополнительные требования или правила, относящиеся к конкретной ситуации, можно добавить, например,

\(R_5 \stackrel{\triangle}{=}\) продукт должен иметь немного более высокую цену чем цена конкурентов.

Лингвистические значения "низкая цена", "высокая цена", "близкая цена" могут быть модифицированы, что приводит к изменению самих требований.
Противоречивые лингвистические значения "низкая цена" и "высокая цена" могут быть описаны правыми и левыми треугольными или трапециевидными числами на множестве альтернатив, являющемся подмножеством \(R^+\). Лингвистическая значение "близкая цена" может быть описана треугольными числами.

Модель ценообразования с тремя правилами

Модель 1.

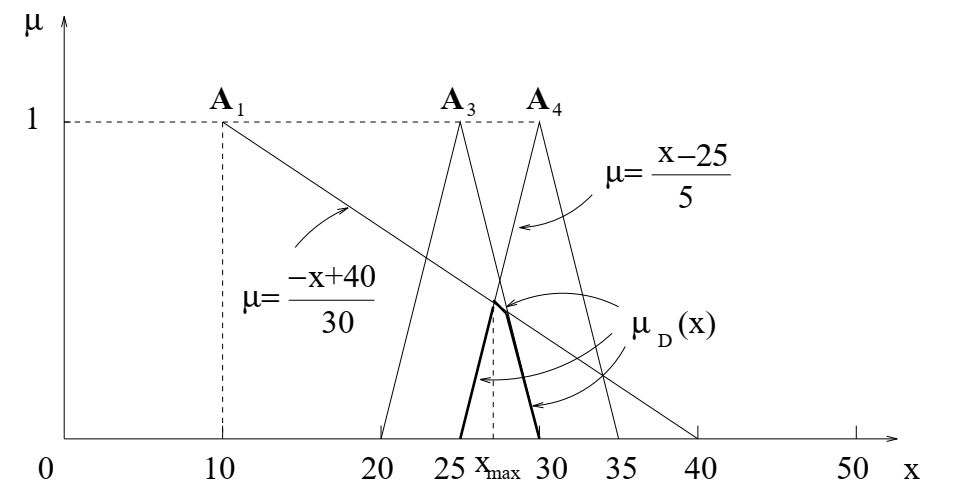
Рассмотрим модель ценообразования, состоящую из трех правил R₁, R₃ и R₄ приведенных ранее.
Предположим, что конкурентная цена равна 25, а удвойная стоимость изготовления - 30. Кроме того, множество альтернатив \(A_{alt}\) представляет собой интервал [10, 50], означающий, что цена товара должна лежать в этом интервале.
Лингвистические переменные этих правил описываются нечеткими числами следующим образом: R₁ представлено треугольным числом A₁ (низкая цена), R₃ и R₄ представлены треугольными числами A₃ (близко к конкурентной цене) и A₄ (близко к удвоенной себестоимости). \[ A_1\stackrel{\triangle}{=}\mu_{A_1}(x)= \left\{ \begin{array}{lll} \frac{-x+40}{30}, & \hbox{ для } 10\le x\le 40,\\ 0, & \hbox{ иначе } \end{array} \right. \] \[ A_3\stackrel{\triangle}{=}\mu_{A_3}(x)= \left\{ \begin{array}{lll} \frac{x-20}{5}, & \hbox{ для } 20\le x\le 25,\\ \frac{-x+30}{5}, & \hbox{ для } 25\le x\le 30,\\ 0, & \hbox{ иначе}. \end{array} \right. \] \[ A_4\stackrel{\triangle}{=}\mu_{A_4}(x)= \left\{ \begin{array}{lll} \frac{x-25}{5}, & \hbox{ для } 25\le x\le 30,\\ \frac{-x+33}{5}, & \hbox{ для } 30\le x\le 35,\\ 0, & \hbox{ иначе}. \end{array} \right. \]

Модель ценообразования с использованием правил R₁, R₃ и R₄.

Тогда решение D лежит в интервале [25; 30] \[ D\stackrel{\triangle}{=}\mu_{D}(x)=\min\left(\mu_{A_1}(x),\mu_{A_3}(x),\mu_{A_4}(x)\right). \] Совместное решение \(µ = \frac{−x +40}{30}\) и \(µ = \frac{x − 25}{5}\) дает максимальное решение \[ x_\max = 27.14, \] что интерпретируется как цена на товар. Эксперты принимают эту цену в качестве рекомендации.
Из рисунка видно, что треугольное число A₃ (близкие к конкурентной цене) способствует нечеткому решению D, но не оказывает никакого влияния на максимизирующее решение x_max. Только треугольные числа A₄ (близкое к удвоенной себестоимости) и A₁ (низкая цена) вносят вклад в x_max. Основную роль играет А₄, чей пик с максимальным уровнем членства 1 составляет х = 30, что является удвоенной стоимостью производства. Из-за влияния А₁ максимальная цена составляет 27,14.

Модель 2.

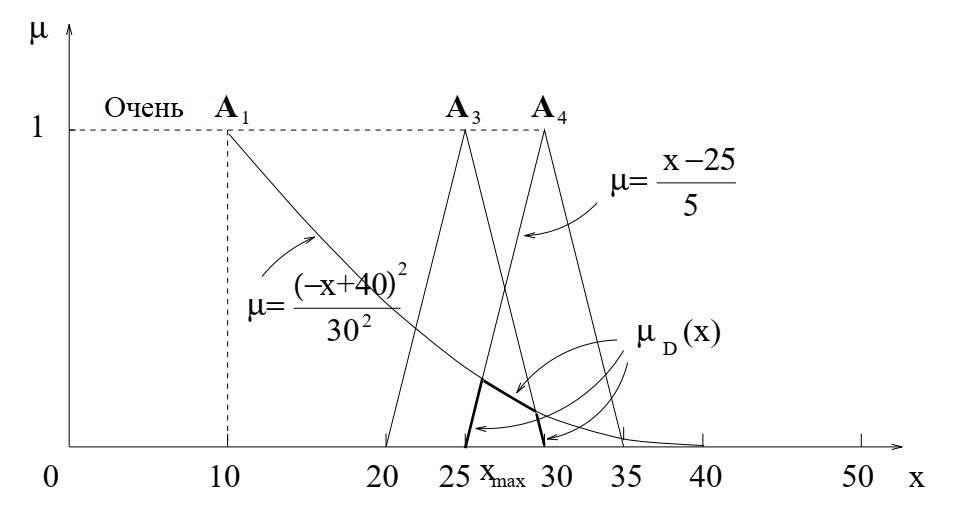
Рассмотрим модель ценообразования, в случае, если требование R₁, определенное A₁, модифицируется модификаторами: (a) очень; (б) немного.
(а) Модифицированное правило R₁ "очень" читается так

очень R₁ \(\stackrel{\triangle}{=}\) продукт должен иметь очень низкую цену.

Модификацию функции принадлежности "очень" A₁ проведем следующим образом \[ \mu_{very A_1}(x)=\mu^2_{A_1}(x)= \left\{ \begin{array}{lll} \left(\frac{-x+40}{30}\right)^2, & \hbox{ для } 10\le x\le 40,\\ 0, & \hbox{ иначе}. \end{array} \right. \] Это парабола на отрезке [10, 40]

Модель ценообразования с использованием правил "очень" R₁, R₃ и R₄.

Решение D имеет функцию принадлежности \(µ_D (x)\) из интервала [25; 30] \[ \mu_{D}(x)=\min\left(\mu_{very A_1}(x),\mu_{A_3}(x),\mu_{A_4}(x)\right). \] Чтобы найти x_max, нужно решить совместно \(µ = \left(\frac{−x +40}{30}\right)^2\) и \(µ =\frac{х-25}{5}\), что приводит к квадратному уравнению \(x^2 - 260x + 6100 = 0\) и, соответственно, к решению 26.08 и 233.92. Находя решение из промежутка [25, 30], получаем \(x_\max = 26.08 ≈ 26\), что и дает предлагаемую цену продукта.
Модификатор "очень" придает больше значения переменной. В данном случае мы получаем 26, то есть, меньшую цену, чем 27,14, то есть, ту, которую получали при условии одинакового влияния функций принадлежности.
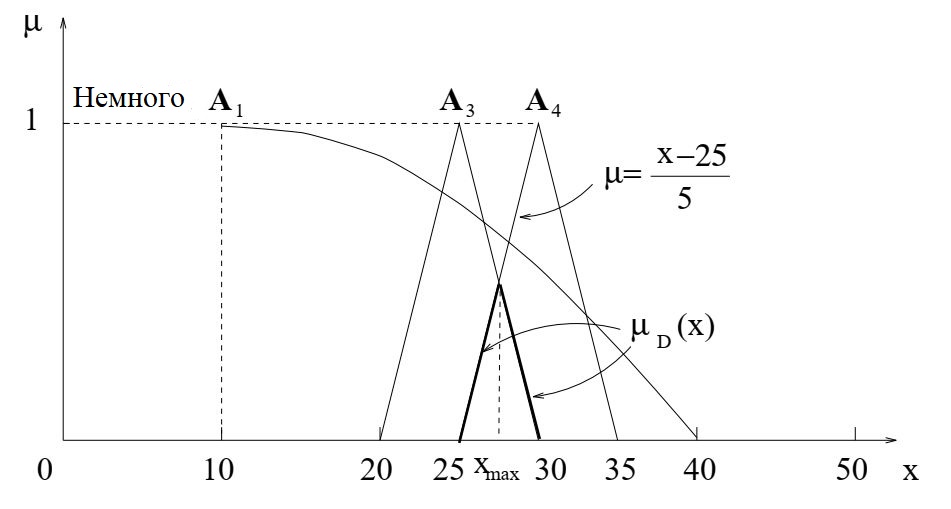
Рассмотрим случай не усиления влияние переменной, а ее ослабления.
(b) Модифицированное правило R₁ "немного" читается так

немного R₁ \(\stackrel{\triangle}{=}\) продукт должен иметь цену немного ниже.

\[ \mu_{fairly A_1}(x)=\sqrt{\mu_{A_1}(x)}= \left\{ \begin{array}{lll} \sqrt{\left(\frac{-x+40}{30}\right)}, & \hbox{ для } 10\le x\le 40,\\ 0, & \hbox{ иначе}. \end{array} \right. \] Это также параболическая функция на отрезке [10, 40]

Модель ценообразования с использованием правил "немного" R₁, R₃ и R₄.

Как видно, правило R₁ (довольно низкая цена) не способствует нечеткому решению D с функцией принадлежности µ_D (x) в области D = [25; 30]. Только правила R₃ и R₄, т.e. A₃ и A₄, вносят вклад в D. Максимальное решение - это середина [25, 30], x_max = 27.5.

Модель калькуляции цен

Рассмотренные модели ценообразования позволяют получать максимальные решения на основе низкой цены и удвоенной себестоимости, но не отражая конкурентную цену, которая участвует в модели. Компания с такой ценовой политикой может создать рынок с благоприятными условиями для участника. Как следствие, компания может понести убытки, ведущие к таким действиям, как снижение цен, изменение дизайна продукта или его уход с рынка. Для компании может быть важнее серьезно рассматривать конкурентную цену, чем пытаться быстро получить прибыль от премиальных цен.
Единственный надежный способ определения цены - это начать с того, что рынок готов заплатить, и, таким образом, оценить конкуренцию. Модель калькуляции цен иллюстрирует это предложение.
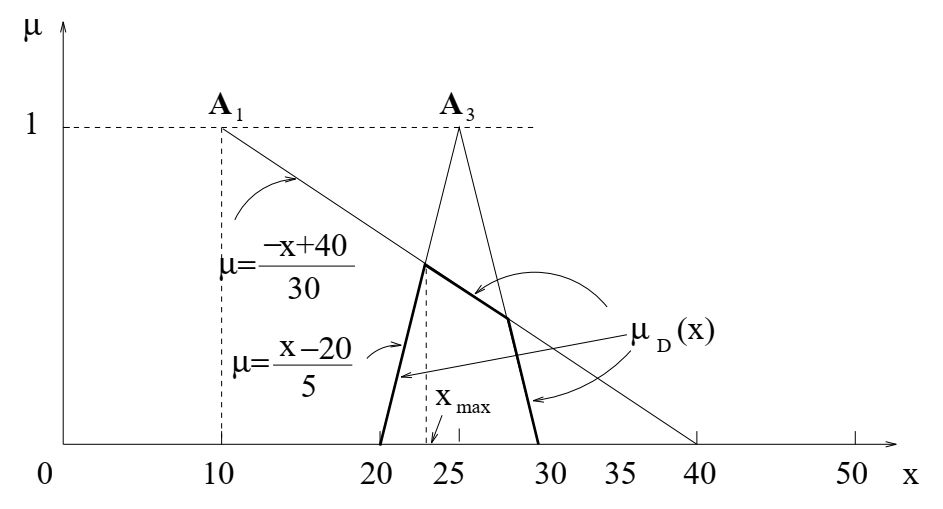
Простая модель для отражения «затрат на основе цены» состоит из двух правил: R₁ (низкая цена) и R₃ (близко к конкурентной цене). R₁ и R₃ описываются треугольными числами A₁ и A₃ , определенными в модели 1.

Модель расчета цены с правилами R₁ и R₃.

Выпишем нечеткое решение D в области D = [20; 30] \[ D\stackrel{\triangle}{=}\mu_{D}(x)=\min\left(\mu_{A_1}(x),\mu_{A_3}(x)\right). \] Максимизирующим решением в [20, 30] является совместное решение уравнений \(µ =\frac{х-20}{5}\) и \(µ = \frac{-x +40}{30}\), это \(x_\max = 22.66\), что ниже конкурентной цены (как следствие требования низкой цены).
Эта модель ценообразования, в отличие от моделей, описанных ранее, не включает требования в отношении стоимости производства. Цену 22,66 следует рассматривать как предложение. Продукт должен разрабатываться, производиться и продаваться, чтобы обеспечить получение прибыли, если цена продукта составляет 22,66 или близка к ней.
Если продукт является новым на рынке и нет конкуренции, то следует предложить разумную цену, которую потребители готовы платить. Возможная модель может быть основана на правилах R₁, R₂ и R₄.
Если продукт превосходит продукт конкурента, это должно быть отражено в модели путем включения правила R₅. Более изощренная и общая модель может содержать вместо R₅ правила типа:

Если продукт превосходит продукт конкурентов, цена продукта должна быть выше, чем у конкурентов.

Как видно из рассмотренных моделей ценообразования, существуют правила, которые не способствуют принятию решения.
Корень проблемы лежит в процедуре принятия решения на основе пересечения, что не всегда обеспечивает вклад от всех правил, которые участвуют в модели. В этих случаях принятие решения на основе пересечения может быть не самым подходящим методом для использования.
Другой подход к принятию решений, который учитывает все цели и ограничения (или правила), основан на нечетком усреднении.