Fuzzy PERT для Project Management.

Управление проектами - сложное мероприятие, включающее планирование различных действий, которые должны быть выполнены в процессе разработки нового продукта или технологии. Проекты имеют фиксированные начало и конец. Для удобства они подразделяются на виды деятельности, которые также имеют указанные начало и завершение. Более того, как правило, действия должны быть выполнены в некотором порядке, хотя некоторые могут выполняться одновременно. Время, необходимое для завершения каждого действия должно быть оценено.

Классический PERT и CPM

Два важных классических метода были разработаны, чтобы облегчить планирование и контроль проектов, это "Project Evaluation and Review Technique" (PERT) и "Critical Path Method" (CPM).
PERT был разработан военно-морским флотом США при планировании производства атомной подводной лодки Polaris.
CPM был разработан в то же время исследователями из Remington Rand и DuPont для технического обслуживания химического завода. Есть некоторые сходства между PERT и CPM и часто они используются вместе как одна технология.
Чтобы проиллюстрировать PERT и CPM, представляем упрощенную и модифицированную версию реального проекта.
Проект под названием "Проектирование системы обработки материалов" включает в себя проектирование, изготовление, сборку и испытания. Проект подразделяется на восемь мероприятий, обозначенных A, B, C, D, E, F, G, H.

	Описание деятельности	Предшествующая активность	Параллельная активность	Последующая активность	Время завершения (в днях)
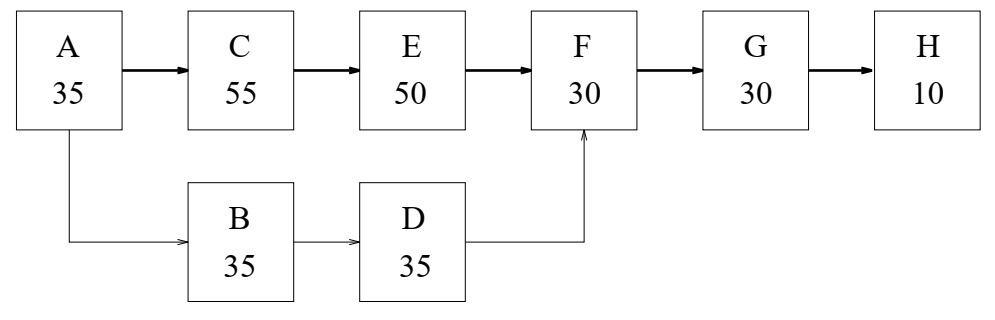
А	Проектирование механической части	-	-	B,C	35
B	Проектирование электрической части	A	C	D	35
C	Изготовление механизмов	A	B	E	55
D	Изготовление электрической части	B	C,E	F	35
E	Сборка механизмов	C	D	F	50
F	Проводка и установка электической части	D,E	-	G	30
G	Монтаж трубопроводов	F	-	G	30
H	Пуск, тестирование, сдача продукта	F	-	-	10

PERT и CPM создают модель сетевого планирования. Каждая деятельность представлена квадратом, прямоугольником или кругом, внутри которого метка и время завершения в днях.

Модель сетевого планирования для системы обработки материалов.

Модель сетевого планирования дает четкое представление о последовательной взаимосвязи между действиями.

Критический путь (Critical path)

Критический путь определяется как путь связанных в последовательности действий от начала до конца проекта, который требует наибольшего времени завершения. Следовательно, общее время для завершения проекта, это время, необходимое для завершения деятельности на критическом пути.
Модель сетевого планирования помогает определить критический путь. Критический путь на рисунке показан жирными стрелками, связывающими действия A, C, E, F, G и H. Общее время для завершения проекта
35+ 55 + 50 + 30 + 30 + 10 = 210 дней.
Из рисунке также видно, что деятельность B и D лежит не на критическом пути. Они могут быть не завершены как планируется, но задержка должна быть не более чем 35 дней. В противном случае деятельность F на критическом пути будет отложена.

Вероятностный PERT

Оценка времени или прогнозирование завершения работ по своей сути является неопределенной. Чтобы справиться с неопределенностью, исследователи расширили возможности PERT, используя статистику и вероятность.
PERT требует от эксперта три оценки для каждого времени завершения деятельности: оптимистичный прогноз - t₁, время, необходимое для завершения действия, если все идет очень хорошо; наиболее вероятное время t_M, время, необходимое для завершения активность, если все идет по плану; пессимистическое время t₂, время для завершения, если есть трудности или что-то пошло не так.
Как правило, время для завершения деятельности рассчитывается взвешенным средним значением \[t_e=\frac{t_1+4t_M+t_2}{6},\] которое применяется для каждого вида деятельности.
Три временные оценки t₁, t_M и t₂ для каждого вида деятельности приходят от экспертов, которые используют свои знания, опыт и любую доступную соответствующую информацию; они субъективны, но не произвольны, следовательно характер неопределенностей, связанных с этими типами проблем, довольно нечеткий, но не вероятностный. PERT не предлагает методику поиска t₁, t_M и t₂, только утверждает, что они должны быть оценены и объединены.

Нечеткий PERT для прогнозирования времени выполнения проекта

В данном разделе улучшим PERT, используя Fuzzy Delphi из предыдущего раздела для оценки t₁, t_M и t₂ для каждого вида деятельности. Эксперты каждый раз представляют завершение деятельности треугольными числами типа (t₁, t_M, t₂). Для каждого вида деятельности рассчитывается среднее число треугольников. Чтобы найти четкое значение времени активности мы должны использовать дефаззификацию. Для этого можем взять максимальное значение или прибегнуть к различным средним.

Прогнозирование времени для управления проектами

Рассмотрим "Проектирование системы обработки материалов" и отбросим оценки времени, полученные классическим путем. Теперь каждый раз активность должна оцениваться тремя экспертами. Менеджер проекта может принимать участие во всех групповых сметах. Экспертов просят оценить оптимистично, скорее всего, и пессимистическое время завершения деятельности А, B,..., H, выраженное в виде треугольных чисел $T^A_i,T^B_i,...,T^H_i,i=1,2,3$.
Предположим, что эксперты привели оценки времени завершения этапа для вида деятельности А

Эксперт	Описание деятельности	Оптимистический прогноз	Ожидаемый прогноз	Пессимистический прогноз
$E_1$	$T^A_1$	33	35	38
$E_2$	$T^A_2$	33	35	38
$E_3$	$T^A_3$	33	35	38
Всего	$\sum_{i=1}^3T^A_i$	98	105	114

Расчетное время завершения для деятельности А.

Агрегированные мнения экспертов дают среднее время \[ T^A_{ave}=\left(\frac{98}{3},\frac{105}{3},\frac{114}{3}\right)=\left(32.67,35,38\right)\approx \left(33,35,38\right). \] Чтобы найти четкое время для завершения, проведем дефазификацию $T^A_{ave}$.

Дефаззификация нечеткого среднего.

Оценки нечетких вычислений реализуются, как правило, треугольными или трапециевидными числами, но при принятии решений, полученную числовую характеристику очень часто приходится выражать через четкое значение, которое наилучшим образом представляет соответствующее среднее. Эта операция называется дефаззификацией.
Рассмотрим дефаззификацию треугольного числа $A_{ave} = (m_1, m_M, m_2)$. Для этой цели представляется вероятным выбрать значение m_M в интервале поддержки $[m_1; m_2]$ величины $A_{ave}$ так, чтобы значение $m_M$ имело высшую степень соответствия $A_{ave}$. Другими словами, $A_{ave}$ достигает максимума в \begin{equation}\label{df0} x_\max = m_М. \end{equation} Однако операция дефаззификации не может быть определена однозначно.
Здесь представлены три варианта дефаззификации $A_{ave} = (m_1, m_M, m_2)$, которые являются по существу статистическими средними формулами: \begin{equation}\label{df1} x^{ (1)}_\max = \frac{m_1 + m_M + m_2}{3}, \end{equation} \begin{equation}\label{df2} x^{ (2)}_\max = \frac{m_1 + 2m_M + m_2}{4}, \end{equation} \begin{equation}\label{df3} x^{ (3)}_\max = \frac{m_1 + 4m_M + m_2}{6}. \end{equation} В отличие от вершины треугольного числа, эти значения учитывают вклад $m_1$ и $m_2$, но придают различный вес $m_M$.
Если треугольное число $A_{ave}$ близко к центральному треугольному числу, то есть, $m_M$ находится почти в середине $[m_1; m_2]$, то хорошее четкое значение дает $x_\max = m_M$. При это все приведенных три средних значения, также дают числа (максимизирующие значения) близкие к $m_M$.
Процедура дефаззификации может быть представлена в виде блок-схемы

Дефаззификация нечеткого среднего $A_{ave}=(m_1,m_M,m_2)$.

Дефаззификация среднего трапециевидного $A_{ave} = (m_1, m_{M_1},m_{M_2},m_2)$ может быть получена обобщением полученных соотношений с использованием вместо $m_М$ средней точки плоского сегмента $m_{M_1}m_{M_2}$. Максимальные значения можно выбрать следующим образом \[ x_\max =\frac{m_{M_1}+m_{M_2}}{2}, \] а также \[ x^{(1)}_\max =\frac{m_{1}+\frac{m_{M_1}+m_{M_2}}{2}+m_{2}}{3}, \] \[ x^{(2)}_\max =\frac{m_{1}+m_{M_1}+m_{M_2}+m_{2}}{4}, \] \[ x^{(3)}_\max =\frac{m_{1}+2(m_{M_1}+m_{M_2})+m_{2}}{6}. \] Для дефаззификации $A^w_{ave} = (m^w_1, m^w_{M_1}, m^w_{M_2}, m^w_2)$ значения $m^w_1, m^w_{M_1}, m^w_{M_2}, m^w_2$ должны быть заменены на $m_1, m_{M_1}, m_{M_2}, m_2$.

Вернемся к нашей задаче.
Замечая, что $Т_{ave}$ является почти центральным треугольным числом (средняя точка промежутка [32.67, 38] составляет 35,335, что близко к 35, используем соотношение (1), что дает $t_\max = 35.$
Для сравнения, проведем дефаззификацию в соответствии с (2)-(4) \[ t^{(1)}_\max=\frac{32.67+35+38}{2}=35.22, \] \[ t^{(2)}_\max=\frac{32.67+2\times 35+38}{4}=35.17, \] \[ t^{(3)}_\max=\frac{32.67+4\times 35+38}{2}=35.11, \] видим, что все полученные значения близки к 35.
Точно так же другие семь групп экспертов могут дать оценки и построить соответствующие таблицы. В результате получим среднее время для завершения работы над проектом.

Этап	Среднее время выполнения	Оптимистический прогноз $t_1$	Ожидаемый прогноз $t_M$	Пессимистический прогноз $t_2$
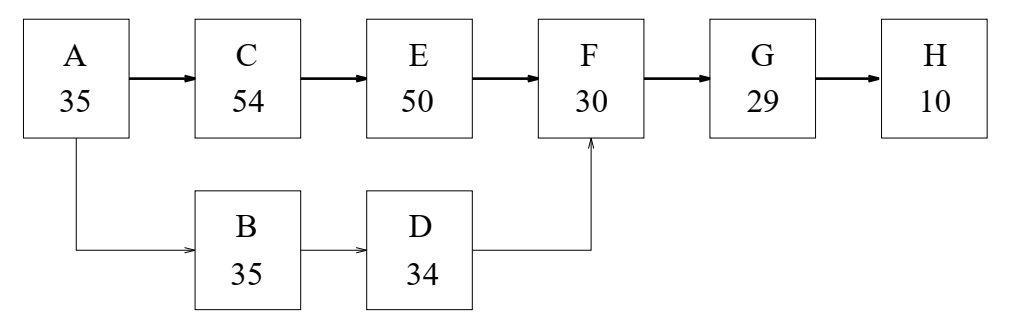
A	$T^A_{ave}$	33	35	38
B	$T^B_{ave}$	32	35	38
C	$T^C_{ave}$	51	54	58
D	$T^D_{ave}$	32	34	36
E	$T^E_{ave}$	46	50	53
F	$T^F_{ave}$	27	30	33
G	$T^G_{ave}$	27	29	32
H	$T^H_{ave}$	7	10	12

Каждое треугольное число, представляющее среднее время выполнения этапа проекта, должно быть дефаззифицировано для получения четкого числа, обозначающего время завершения деятельности над соответствующим этапом, так как это было сделано ранее. Дефаззифицированные значения могут быть представлены в улучшенной модели сетевого планирования:

Улучшеная модель сетевого планирования с использованием Fuzzy PERT.

Общее время для завершения проекта по критическому пути выраженно треугольным числом Т.
Использование чисел, исключая те, которые относятся к видам деятельности B и D, дает \[ T=T^A_{ave}+T^C_{ave}+T^E_{ave}+T^F_{ave}+T^G_{ave}+T^H_{ave}=(192,208,226). \] Следовательно, продолжительность работы над проектом будет между 192 и 226 днями, скорее всего 208 дней. Последнее число 208 является результатом дефаззификации T с использованием (1). Применение формул (2)-(4) для дефазификации дает четкие числа $T^{(1)}_\max = 208.67, T^{(2)}_\max = 208.5$ и $T^{(3)}_\max = 208.33$, все они близки к 208. В качестве вывода прогнозируется, что срок завершения проекта составит 208 дней.

График распределения ресурсов.

Время выполнения проекта находится в тесной взаимосвязи с распределением ресурсов, как материальных, так и человеческих.
Общепринятой практикой является то, что до выделения ресурсов для проекта необходимо установить сеть критических путей. Прогнозирование времени завершения проекта подразумевает, что проект продолжался без перерыва, то есть, что все необходимые ресурсы доступны и могут быть выделены на требуемые действия с эффективной скоростью. В реальности могут возникать различные трудности, которые усложняют работу. Иногда руководство имеет возможность применить дополнительные ресурсы и, тем самым, сократить время завершения деятельности над тем или иным этапом. Понятно, что этот шаг может увеличить цену работы. Сокращение продолжительности проекта может быть желательным из-за бонусов, а позднее завершение может быть оштрафовано.
PERT помогает анализировать проблемы, подобные упомянутым выше, и решать другие задачи, связанные с планированием ресурсов. Для вопросов, требующих оценки, PERT может быть объединен с Fuzzy Delphi способом, подобным оптимизации времени работы над проектом и поиском критического пути.
Следуя PERT, мы вводим обозначения: $t_n$ нормальное время для завершения действия над этапом, так как и запланировано, $t_c$ время сбоя (сокращение времени) для завершение операции, $C_n$ нормальная стоимость завершения операции, $C_c$ стоимость сбоя (увеличение стоимости) для завершения действия во время сбоя. Каждый вид деятельности, $t_c, t_n, C_n$ и $C_c$ должен быть оценен.
Проиллюстрируем Fuzzy PERT для сокращения продолжительности проекта на том же примере, что и ранее.
Сократить продолжительность проекта означает сократить время на завершение критического пути, то есть сократить общее время $T_\max = 208$ дней. Заметим, что сокращение продолжительности времени деятельности не на критическом пути (B и D) не уменьшит $T_\max$. Тем не менее, некоторые ресурсы, выделенные для B и D могут быть перераспределены на действия над этапами C и D, чтобы сократить время их завершения (внутреннее перераспределение). Рассмотрим сокращение времени активности на критическом пути без внутреннего перераспределения ресурсов.
Нормальное время $t_n$ для каждого вида деятельности уже оценено - это время $t_\max = t_M$. Время сбоя $t_c$, обычная стоимость $C_n$ и стоимость сбоя $C_c$ для каждого этапа можно прогнозировать аналогично обычному времени выполнения проекта.
После дефазификации по формуле (1), получаем, соответственно, $t_{c \max}, C_{n \max}$ и $C_{c \max}$.
Таким обраом, получена оценка нормальной стоимости $C_n$ для операции A, $t_c$ и $C_c$ могут быть оценены аналогично.
Далее, три эксперта проводят оценку нормальной стоимости для завершения активности на этапе A в виде треугольного числа $ C_n = (C_{n_1}, C_{n_M}, C_{n_2})$, где $C_{n_1}$ - самая низкая стоимость, $C_{n_M}$ - наиболее вероятная стоимость, а $C_{n_2}$ - самая высокая стоимость.

Эксперт	Наименьшая стоимость $C_{n_1}$	Ожидаемая стоимость $C_{n_M}$	Наибольшая стоимость $C_{n_2}$
$E_1$	18.000	20.000	22.000
$E_2$	19.500	21.000	22.000
$E_3$	17.000	19.000	21.000
Всего	54.500	60.500	65.000

Отсюда найдем среднюю нормальную стоимость выполнения этапа А \[ C^A_{n ave}=(18.000,20.000,21.500). \] Дефаззификация $C^A_{n ave}$ приводит к величине 20.000. Аналогично получаем $t_c, C_n$ и $C_c$ для других этапов на критическом пути.
Для выбора действия для сокращения продолжительности этапов, PERT использует понятие ценового наклона \[ k=cost slope=\left|\frac{C_{n \max}-C_{c \max}}{t_{n \max}-t_{c \max}}\right|. \]

Наклон затрат для сокращения времени активности над этапом проекта.

Как видно на рисунке, по мере уменьшения нормального времени, то есть, когда $t_{n \max}$ приближается к времени сбоя $t_{c \max}$, нормальная стоимость $C_{n \max}$ увеличивается, приближаясь к стоимость аварийной ситуации $C_{c \max}$.
Приведем дефаззифицированные значения.

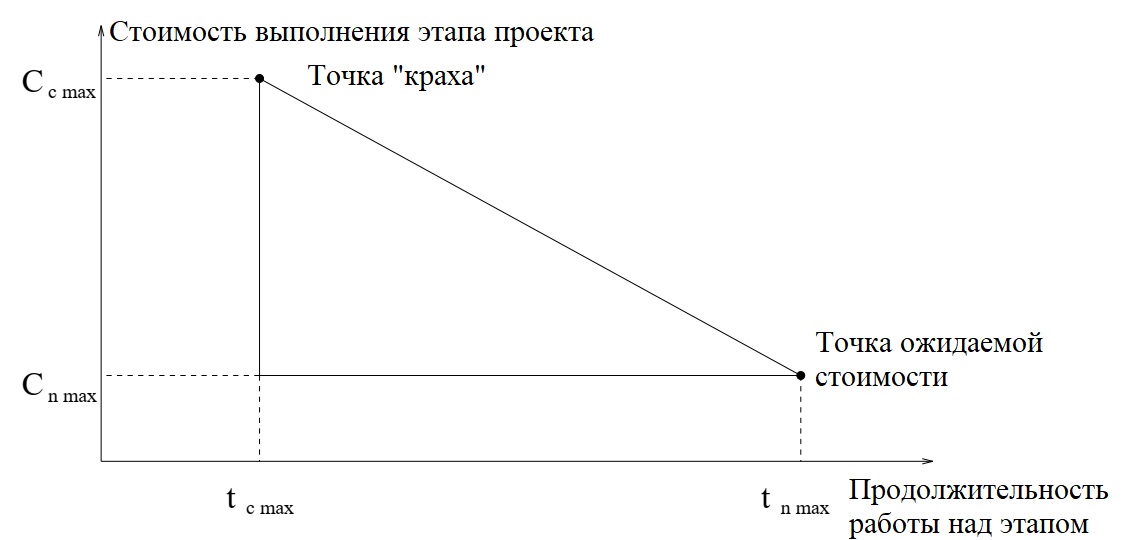
Этап	Ожидаемое время $t_{n \max}$	Время аварийной ситуации $t_{c \max}$	Ожидаемая стоимость $C_{n \max}$	Cтоимость "краха" $C_{c \max}$	Наклон затрат на день
A	35	25	20.000	26.000	600
C	54	30	30.500	40.500	417
E	50	32	28.000	35.000	389
F	30	22	18.500	25.000	813
G	29	20	15.000	19.000	444
H	10	8	7.000	8.000	600

Приведем вычисление наклона затрат для этапа А \[ k_A=\left|\frac{C_{n \max}-C_{c \max}}{t_{n \max}-t_{c \max}}\right|=\left|\frac{20.000-26.000}{35-25}\right|=\left|\frac{-6.000}{10}\right|=600. \] Коэффициенты наклона стоимости для других этапов рассчитываются аналогично.
Как правило, дополнительные ресурсы должны быть применены в первую очередь к деятельности над этапами с наименьшим наклоном стоимости.

Ранжирование	Этап	Сокращение временных затрат $t_{n \max}-t_{c \max}$	Дополнительная стоимость $C_{c \max}-C_{n \max}$	Наклон затрат на день
1	E	18	7.000	389
2	C	24	10.000	417
3	G	9	4.000	444
4	H	2	1.000	500
5	A	10	6.000	600
6	F	8	6.500	813

Ранжированные действия над этапами в соответствии с наклоном стоимости

Предположим, что руководство хочет сократить продолжительность работы над проектом от 208 дней до 180 дней, то есть, провести сокращение на 28 дней. В соответствии с критическим путем, работа над этапом E занимает первое место при наименьшем k, и имеет оценку стоимости 389$ в день. Вложив 7000 долларов, продолжительность для этапа E может быть сокращена на 18 дней. Для дальнейшего сокращения хорошим кандидатом является этап С, занимающий второе место. 10-дневное сокращение будет стоить 10 × 417 = 4170 долларов. Заметим, что рассмотренные варианты не являются единственными. Если есть некоторые причины против сокращения времени выполнения этапов E или C, могут быть рассмотрены другие варианты.

Прогнозирование спроса

Концепция спроса является основной в бизнесе и экономике. По существу, спрос состоит из двух компонентов, выражающих:

количество продукта, требуемого по определенной цене и времени;
желание и возможность приобрести продукт.

Спрос на новый продукт должен прогнозироваться. Прогнозирование успешнее, когда доступна история спроса на аналогичный продукт. Если продукт не является инновационным, даже в сегодняшней быстро меняющейся среде присутствуют некоторые основные связи между прошлым и будущим. Спрос на данный товарный запас подразделяется на независимый и зависимый спрос. Спрос является независимым, если он не связан или не вытекает из спроса на другие товары или товары. В противном случае спрос называется зависимым. Независимый спрос должен быть спрогнозирован, в то время как зависимый спрос должен быть определен на основе спроса на соответствующие товары.
Пусть пятерых экспертов просят спрогнозировать годовой спрос на новый продукт. Как уже было показано ранее, применение техники Fuzzy Delphi требует использования треугольных чисел $A_i = \left(a^{(i)}_1,a^{(i)}_M,a^{(i)}_2\right), i = 1,..., 5$. Здесь $a^{(i)}_1$ является наименьшим количество единиц продукции, которые будут произведены, $a^{(i)}_M$ является наиболее вероятным числом единиц, и $a^{(i)}_2$ - самое большое количество единиц.

Эксперт	$A_i$	Наименьшее количество $a^{(i)}_1$	Ожидаемое количество $a^{(i)}_M$	Наибольшее количество $a^{(i)}_2$
$E_1$	$A_1$	10 000	12 000	13 000
$E_2$	$A_2$	11 500	13 000	15 000
$E_3$	$A_3$	10 000	11 000	14 000
$E_4$	$A_4$	12 000	13 000	14 000
$E_5$	$A_5$	11 000	12 000	13 000
Всего		54 000	61 000	69 000

Отсюда получаем \[ A_{ave} = \left(\frac{54 000}{5},\frac{61 000}{5},\frac{69 000}{5}\right)=(10800,12200,13800). \] Дефаззифицированное значение $A_{ave}$ равно 12200. Следовательно, это число и может быть принято в качестве прогноза годового спроса на новый продукт.

Эксперт	Описание деятельности	Оптимистический прогноз	Ожидаемый прогноз	Пессимистический прогноз
\(E_1\)	\(T^A_1\)	33	35	38
\(E_2\)	\(T^A_2\)	33	35	38
\(E_3\)	\(T^A_3\)	33	35	38
Всего	\(\sum_{i=1}^3T^A_i\)	98	105	114

Этап	Среднее время выполнения	Оптимистический прогноз \(t_1\)	Ожидаемый прогноз \(t_M\)	Пессимистический прогноз \(t_2\)
A	\(T^A_{ave}\)	33	35	38
B	\(T^B_{ave}\)	32	35	38
C	\(T^C_{ave}\)	51	54	58
D	\(T^D_{ave}\)	32	34	36
E	\(T^E_{ave}\)	46	50	53
F	\(T^F_{ave}\)	27	30	33
G	\(T^G_{ave}\)	27	29	32
H	\(T^H_{ave}\)	7	10	12

Эксперт	\(A_i\)	Наименьшее количество \(a^{(i)}_1\)	Ожидаемое количество \(a^{(i)}_M\)	Наибольшее количество \(a^{(i)}_2\)
\(E_1\)	\(A_1\)	10 000	12 000	13 000
\(E_2\)	\(A_2\)	11 500	13 000	15 000
\(E_3\)	\(A_3\)	10 000	11 000	14 000
\(E_4\)	\(A_4\)	12 000	13 000	14 000
\(E_5\)	\(A_5\)	11 000	12 000	13 000
Всего		54 000	61 000	69 000