Оценка политики экспертных систем.

Анализ сложных проблем требует усилий и мнений многих специалистов, выступающих в роли экспертов. Мнения экспертов выражаются словами из естественного языка и профессиональных терминов, которые можно рассматривать как лингвистические переменные, в этом качестве они описываются и обрабатываются нечеткими множествами и нечеткой логикой. Мнения экспертов либо близки, либо в той или иной степени конфликтуют. Для окончательного принятия решений все мнения должны быть объединены или согласованы. Это разрешение конфликта, если мнения противоречивы или агрегация, в противном случае.
В качестве иллюстрации использования нечетких методов для принятия решений группой экспертов приведем два примера, касающихся политики индивидуального планирования инвестиций, предложенной экспертами, мнения которых близки, а во втором случае - противоречивы.

Экспертная политика близкой оценки инвестиционной модели.

Рассмотрим упрощенную модель индивидуального инвестиционного планирования, которая создает агрессивную или консервативную политику в зависимости от того, снижаются или повышаются процентные ставки.
Слова агрессивный и консервативный являются лингвистическими переменными, то есть нечеткими понятиями. Финансовые эксперты, работающие с инвестиционной моделью, соглашаются описывать агрессивную (агрессивную инвестиционную политику) подходящим левым трапециевидным числом по шкале от 0 до 100 (универсальный набор {интервал [0, 100]) и консервативную - правым трапециевидным числом на шкала от −100 до 0 (универсальный набор [−100; 0]). Числа в объединенной шкале от -100 до 100 имеют определенное значение, принятое экспертами. Например, 50 и -50 можно интерпретировать как индикаторы для умеренно агрессивных инвестиций и умеренно консервативных инвестиций, соответственно; 70 и −70 как агрессивные и консервативные вложения и т.д.
Предположим, что процентные ставки падают и три эксперта \(E_i,i=1,2,3\) имеют мнение, что инвестиционная политика должна быть агрессивной. Их агрессивное описание дано в виде левых трапециевидных чисел

A₁ = (40, 70, 100, 100), A₂ = (45, 80, 100, 100); A₃ = (70, 85, 100, 100).

Агрегирование близких мнений экспертов (предполагаемых одинаковой важности) в соответствии с трапециидальным средним дает \[ A_{ave} = \frac{A_1 + A_2 + A_3}{3}=\frac{(40, 70, 100, 100) + (45, 80, 100, 100) + (70, 85, 100, 100)}{3}= \frac{(155, 235, 300, 300)}{3}=(51.66, 78.33,100, 100). \]

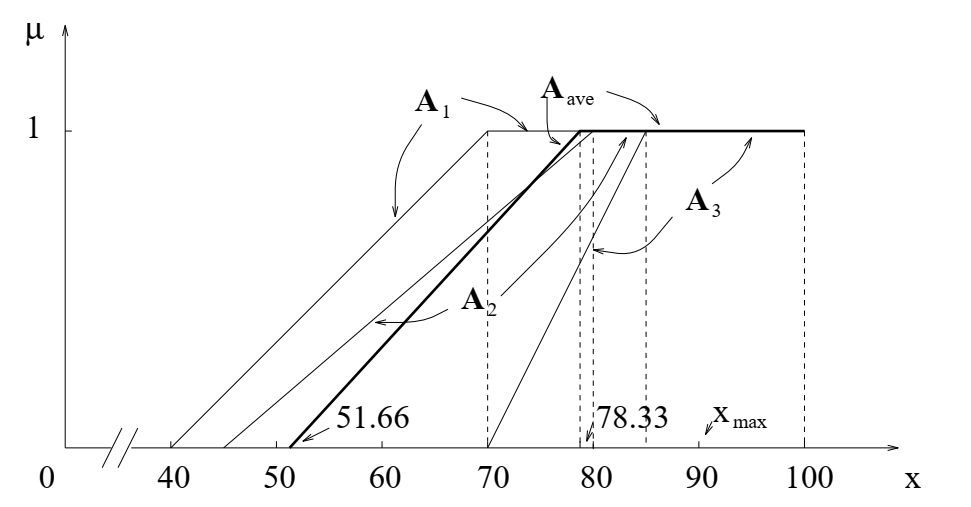
Политика инвестиционного планирования: мнение трех близких экспертов. Агрегированное решение A_ave, максимизирующее решение x_max.

Дефаззификация A_ave дает максимальное значение \(\frac{78.33 + 100}{2} = 89.16 ≈ 90\). Интерпретация этого числа - очень агрессивная инвестиционная политика.

Предположим теперь, что три эксперта по-разному оцениваются своими коллегами. По шкале от 0 до 10: r₁ = 6 - рейтинг эксперта E₁, r₂ = 10 - рейтинг эксперта E₂, а r₃ = 4 - рейтинг эксперта E₃. Веса \(w_i, i = 1, 2, 3\), которые выражают относительную важность E_i, можно рассчитать следующим образом \[ w_i =\frac{r_i}{r_1 + r_2 + r_3}, w_1 =\frac{6}{20}= 0.3, w_2 =\frac{10}{20}= 0.5, w_3 =\frac{4}{20}= 0.2 \] Используя эти веса, выпишем средневзвешенное трапециевидное среднее \[ A^w_{ave}= 0.3A_1 + 0.5A_2 + 0.2A_3 = (12,21, 30, 30) + (22.5, 40, 50, 50) + (14, 17, 20, 20) = (43.5, 78, 100, 100). \] Дефаззификация приводит к значению \(\frac{78 + 100}{ 2} = 89\). Это число говорит об очень агрессивной инвестиционной политике.
Существует небольшая разница между \(A_{ave}\) и \(A^w_{ave}\), а также между максимальными значениями 89.16 и 89. Следовательно, в этом случае для окончательного вывода, ранжирование экспертов не имеет значения. Это, в основном, связано с тем, что мнения экспертов более или менее близки, а также с тем, что второй эксперт \(E_2\), мнение которого ближе всего к \(A_{ave}\), было оценено как лучшее (\(r_2 = 10\)).

Инвестиционная модель при противоречивых мнениях экспертов

Рассмотрим инвестиционную модель в случае, если процентные ставки падают, но теперь предположим, что эксперты имеют противоречивые мнения. Это означает, что некоторые эксперты рекомендуют агрессивную политику (шкала от 0 до 100), в то время как другие рекомендуют консервативную политику (от −100 до 0). Также существует вероятность того, что некоторые эксперты могут высказывать мнения, которые находятся почти посередине между агрессивной и консервативной политикой.
Предположим, что три эксперта представили свое мнение:

A₁ = (-100, -100, -50, -30), A₂ = (-10, 10, 30), A₃ = (60, 90, 100, 100).

Здесь A₁ (описывающиее консервативность) - это правое трапециевидное число, A₂(описывающее слегка агрессивное) - треугольное число, а A₃(описывающее агрессивное) - левое трапециевидное число.
Для проведения каких-либо действий над числами А₁, A₂ и A₃, число A₂ должно быть представлено в виде трапециевидного числа,\[A_2 = (-10; 10; 10; 30).\] Результат будет иметь вид \[ A_{ave} = A_1 + A_2 + A_3=\frac{(-100, -100, -50, -30) + (-10, 10, 10, 30) + (60, 90, 100, 100)}{3}= \frac{(-50, 0, 60, 100)}{3}= (-16.67, 0, 20, 33.33). \]

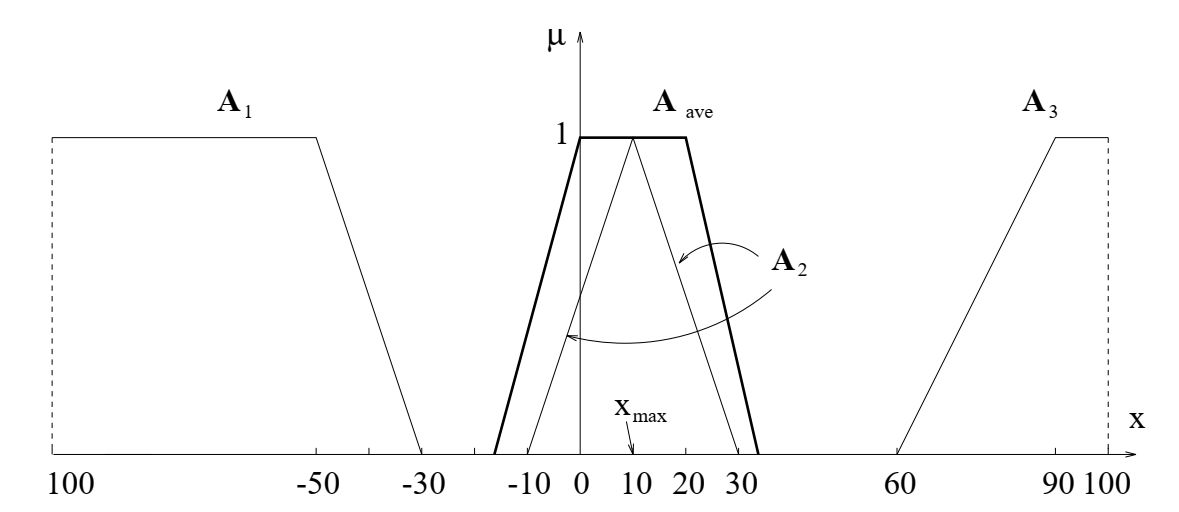
Политика инвестиционного планирования при противоречивых мнениях экспертов. Агрегирующее решение A_ave, максимизирующее решение x_max.

Максимальное значение равно \(\frac{0 + 20}{ 2} = 10\). Это предполагает политику на агрессивной стороне шкалы.

Теперь рассмотрим случай, когда мнения трех конфликтующих экспертов имеют разное значение по шкале от 0 до 10. Рейтинги \(\lambda_i, i=1,2,3\) экспертов E₁, Е₂ и Е₃ предполагаются равными 4, 6 и 10 соответственно.
Веса \(w_i\) для \(E_i\), равны \[ w_i=\frac{\lambda_i}{λ_1 + λ_2 + λ_3}, w_1 =\frac{4}{20}= 0.2, w_2 =\frac{6}{20}= 0.3, w_3 =\frac{10}{20}= 0.5, \] и, соответственно, \[ A^w_{ave} = 0.2A_1 + 0.3A_2 + 0.5A_3 = (-20, -20, -10, -6) + (-3, 3, 3, 9) + (30, 45, 50, 50)= (7, 28, 43, 53). \] Максимальное значение равно \(x_\max = \frac{28 + 43}{ 2} = 35.54\). Это указывает на то, что инвестиционная политика должна быть осторожно агрессивной.
Существует некоторая разница между \(A_{ave}\) и \(A^w_{ave}\), а также между значениями 10 и 35.5, из-за высокого рейтинга эксперта E₃, который выступает за агрессивную инвестиционную политику.