Оценка времени для технической реализации инновационного продукта.
|

|
Группу из 15 компьютерных экспертов просят дать оценку для технической реализации нового продукта - компьютера для обработки когнитивной информации.
Мнения экспертов имеют одинаковый вес.
Треугольные числа \(A_i, i = 1,2,...,15\), представляющие собой оценки экспертов, приведены в таблице.
| Ei | Ai | Оптимистический прогноз (a1) | Реалистический прогноз (aM) | Пессимистический прогноз (a2) |
|---|
| E1 | A1 | 2020 | 2024 | 2032 |
| E2 | A2 | 2022 | 2025 | 2030 |
| E3 | A3 | 2024 | 2030 | 2036 |
| E4 | A4 | 2020 | 2022 | 2024 |
| E5 | A5 | 2026 | 2034 | 2042 |
| E6 | A6 | 2023 | 2026 | 2030 |
| E7 | A7 | 2021 | 2025 | 2028 |
| E8 | A8 | 2025 | 2029 | 2033 |
| E9 | A9 | 2022 | 2026 | 2031 |
| E10 | A10 | 2021 | 2023 | 2030 |
| E11 | A11 | 2020 | 2025 | 2033 |
| E12 | A12 | 2020 | 2023 | 2032 |
| E13 | A13 | 2026 | 2029 | 2032 |
| E14 | A14 | 2022 | 2024 | 2030 |
| E15 | A15 | 2023 | 2030 | 2036 |
Найдем средние значения Aave. Вначале найдем суммы каждого столбца прогноза, то есть
\(\sum_{i=1}^{15}a^{(i)}_1=\),
\(\sum_{i=1}^{15}a^{(i)}_M=\),
\(\sum_{i=1}^{15}a^{(i)}_2=\).
Поделив, каждое из полученных чисел на число экспертов, то есть, на 15, получаем Aave=(, , ).
Таким образом, примерно получаем Aave=(, , ).
Найдем отклонения Aave-Ai прогнозов от полученных средних значений.
Эта таблица показывает расхождение мнений каждого эксперта со средним значением.
Какие-то эксперты имеют мнение близкое к средним, какие-то нет. Заметим, что понятие "близко" в данной постановке нечетко, поэтому оно требует некоторого
уточнения. Это может быть основано на концепции расстояния di,j между двумя треугольными числами Ai и Aj .
Если все di,j рассчитаны и записаны в таблице (в нашем случае, состоящей из 15 строк и столбцов), то можно
будет лучше понять, насколько близки различные пары Ai и Aj.
Предположим, что менеджер не удовлетворен средним (, , ).
Тогда отклонение (mi-a1,mM-aM,m2-a2) задается
каждому эксперту Ei для уточнения прогноза. Эксперты предлагают новые треугольные числа Bi, которые представлены в таблице
| Ei | Bi | Оптимистический прогноз (b1) | Реалистический прогноз (bM) | Пессимистический прогноз (b2) |
|---|
| E1 | B1 | 2021 | 2025 | 2032 |
| E2 | B2 | 2022 | 2025 | 2030 |
| E3 | B3 | 2021 | 2028 | 2033 |
| E4 | B4 | 2022 | 2024 | 2028 |
| E5 | B5 | 2024 | 2030 | 2032 |
| E6 | B6 | 2021 | 2026 | 2031 |
| E7 | B7 | 2021 | 2025 | 2030 |
| E8 | B8 | 2023 | 2028 | 2032 |
| E9 | B9 | 2021 | 2026 | 2031 |
| E10 | B10 | 2021 | 2026 | 2030 |
| E11 | B11 | 2021 | 2025 | 2033 |
| E12 | B12 | 2020 | 2025 | 2032 |
| E13 | B13 | 2021 | 2028 | 2032 |
| E14 | B14 | 2022 | 2024 | 2032 |
| E15 | B15 | 2021 | 2028 | 2033 |
Тогда Bave=(, , )
и приблизительно получаем Bave=(, , ).
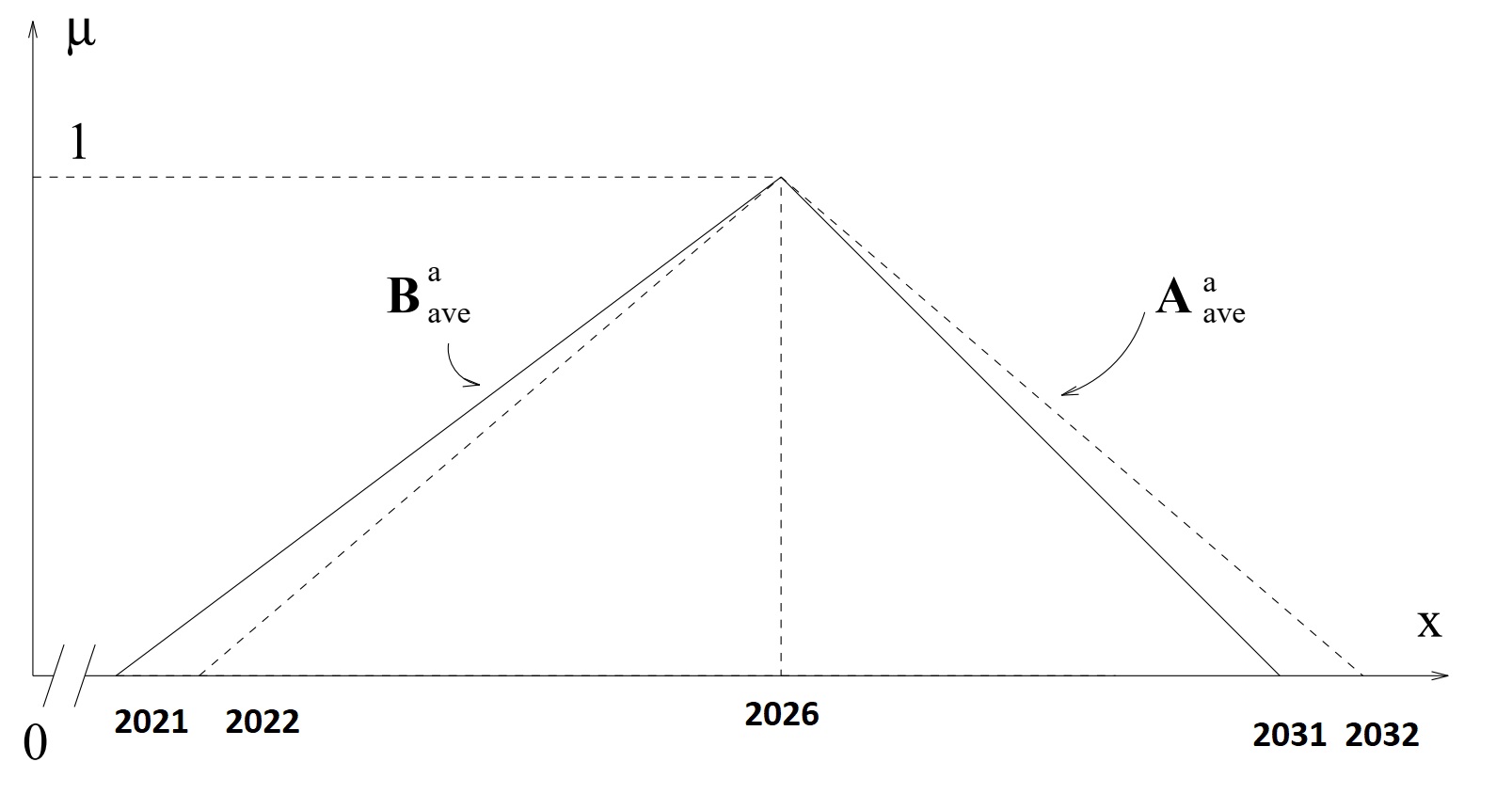
Если менеджер удовлетворен тем, что Aave и Bave лежат друг от друга достаточно близко, он останавливает нечеткий процесс и принимает
треугольное число Bave как совокупный вывод мнений экспертов.
В бизнесе, финансах, управлении, как и в науке, опыт и знания некоторых экспертов более предпочтительны знаниям,
опыту и экспертизе других экспертов. Это выражается весами, которые назначены экспертам.
В приведенном ранее примере эксперты были признаны одинаково важными, поэтому не было необходимости вводить веса.
Теперь рассмотрим случай, когда экспертные суждения или мнения имеют различный вес.
Это приводит к взвешенному нечеткому методу Дельфи.
Предположим, что каждому эксперту \(E_i, i = 1,2,...,15\) поставлен в соответствие вес \(w_i, i = 1,...,n; w_1 + · · · + w_n = 1.\)
Для предыдущей задачи, как и ранее, эксперты представляют свои мнения, выраженные треугольными числами \(A_i\). Теперь предположим, что
эксперты E1, E3, E5, Е8 и Е13 оцениваются выше (вес 0,1), чем остальные (вес 0.05).
| Ei | wi | wi×a1 | wi×aM | wi×a2 |
|---|
| E1 | 0.1 | | | |
| E2 | 0.05 | | | |
| E3 | 0.1 | | | |
| E4 | 0.05 | | | |
| E5 | 0.1 | | | |
| E6 | 0.05 | | | |
| E7 | 0.05 | | | |
| E8 | 0.1 | | | |
| E9 | 0.05 | | | |
| E10 | 0.05 | | | |
| E11 | 0.05 | | | |
| E12 | 0.05 | | | |
| E13 | 0.1 | | | |
| E14 | 0.05 | | | |
| E15 | 0.05 | | | |
| Всего | | | | |
|---|
и приблизительно получаем Aave=(, , ).
Остальные шаги такие же, как и в предыдущем случае.


