Принятие решений в нечетких условиях.
|

|
Принятие решений - это процесс решения проблем, который приводит к действию. По сути, это выбор между различными способами достижения цели.
Принятие решений играет важную роль в бизнесе, финансах, управлении, экономике, социальных и политических науках, технике и информатике, биологии и медицине.
Процесс этот достаточно сложный из-за таких факторов, как неполная и неточная информация, субъективность, которые, как правило, представлены в реальных ситуациях в меньшей или
большей степени. Эти факторы указывают на то, что процесс принятия решений происходит в нечеткой среде.
Рассмотрим два метода принятия решений на основе нечетких множеств и нечеткой логики.
Согласно первому подходу (Беллман-Заде (1970)), принятие решений определяется как пересечение целей и ограничений, описываемых нечеткими множествами.
Второй подход к принятию решений объединяет цели и ограничения с использованием нечеткого усреднения.
Применяется для различных реальных ситуаций, требующих выбора или оценки.
Принятие решений путем пересечения нечетких целей и ограничений
Принятие решений характеризуется выбором из доступных альтернатив, если они найдены или обнаружены.
В процессе принятия решений должны быть достигнуты определенные цели и соблюдены определенные ограничения.
Рассмотрим простую модель принятия решений, состоящую из цели, описываемой нечетким множеством G с функцией принадлежности µG (x), и ограничения, описываемого нечетким
множеством C с функцией принадлежности µC (x), где x является элементом четкого множества альтернатив Aalt.
По определению (Bellman и Zadeh (1970)) решение представляет собой нечеткое множество D с функцией принадлежности µD (x), выраженной как пересечение G и С.
\begin{equation}\label{3.1}
D=G\cap C=\left\{\left(x,\mu_D(x)\right)|x\in [d_1,d_2],\mu_D(x)\in [0,h\le 1]\right\}.
\end{equation}
Множество решений, приводящее к выбору четкого набора \([d_1; d_2]\) из множества альтернатив \(A_{alt}; µ_D (x)\) указывает степень, до которой любое \(x \in [d_1; d_2]\)
принадлежит решению D. Схематически это представлено на рисунке, когда \(x \in A_{alt} \subset R\), а также G и C имеют монотонные непрерывные функции
принадлежности.
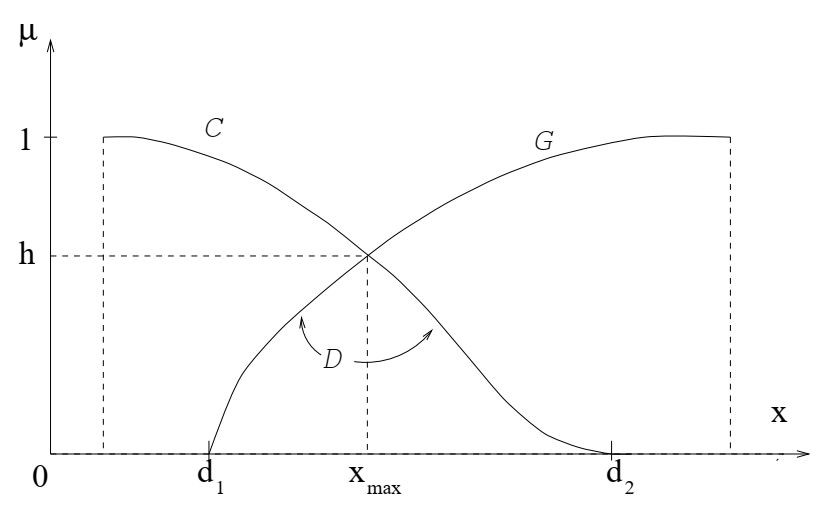
Нечеткая цель G, ограничение C, решение D, максимальное решение x
max.
Используя функции принадлежности и пересечение операций, получаем
\begin{equation}\label{3.2}
µ_D (x) = \min (µ_G (x); µ_C (x)), x \in A_{alt}. \end{equation}
Пересечение является коммутативной операцией, поэтому цель и ограничение можно формально поменять местами, то есть D = G \ C = C \ D.
На самом деле, существуют реальные ситуации, в которых цель может рассматриваться как ограничение и наоборот.
Иногда нет необходимости указывать цель или ограничение, тогда просто называем их целями или аспектами проблемы.
Обычно лицо, принимающее решения, желает получить четкий результат, то есть, значение среди элементов набора \([d_1; d_2] \subset A_{alt}\), которое наилучшим образом
или адекватно представляет нечеткий набор D. Для этого требуется провести дефаззификацию D.
Для этой цели естественно принять значение x из выбранного набора \([d_1; d_2]\) с наивысшей степенью принадлежности к множеству D.
Такое значение x максимизирует \(µ_D (x)\) и называется максимизирующим решением, что может быть выражено следующим образом
\begin{equation}\label{3.3}
x_\max = \left\{x|\max µ_D (x) = \max \min (\mu_G (х),\mu_C (х)) \right\}.\end{equation}
Процесс принятия решения показан в виде блок-схемы
Процесс принятия решения в нечетких условиях.
Формулы (\ref{3.1})-(\ref{3.3}) можно обобщить для моделей принятия решений со многими целями и ограничениями (Bellman и Zadeh (1970)).
Для n целей \(G_i, i=1,...,n\) и m ограничений \(C_j; j = 1,...,m\) решением является
\begin{equation}\label{3.4}
D = G_1\cap ...\cap G_n \cap C_1\cap ...\cap C_m,
\end{equation}
функция принадлежности к D
\begin{equation}\label{3.5}
µ_D (x) = \min (µ_{G_1} (x),..., µ_{G_n} (x),µ_{C_1} (x),...,µ_{C_m} (x)), x \in A_{alt}. \end{equation}
и максимизирующее решение
\begin{equation}\label{3.6}
x_\max = \{x|µ_{D}\to \max\}. \end{equation}
В качестве иллюстрации, рассмотрим на множестве альтернатив \(A_{alt} = \{1, 2, 3, 4, 5, 6\}\)
цели G и ограничения C, заданные дискретными нечеткими множествами.
\[
G=\{(1,0),(2,0.2),(3,0.4),(4,0.6),(5,0.8),(6,1))\}\\
C=\{(1,1),(2,0.9),(3,0.7),(4,0.6),(5,0.2),(6,0))\}.
\]
Следуя (\ref{3.2}), получаем
\[
D=G\cap C=\{(1,\min(0,1)),(2,\min(0.2,0.9)),(3,\min(0.4,0.7)),(4,\min(0.6,0.6)),(5,\min(0.8,0.2)),(6,\min(1,0))\}=\\
\{(1,0),(2,0.2),(3,0.4),(4,0.6),(5,0.2),(6,0)\}.
\]
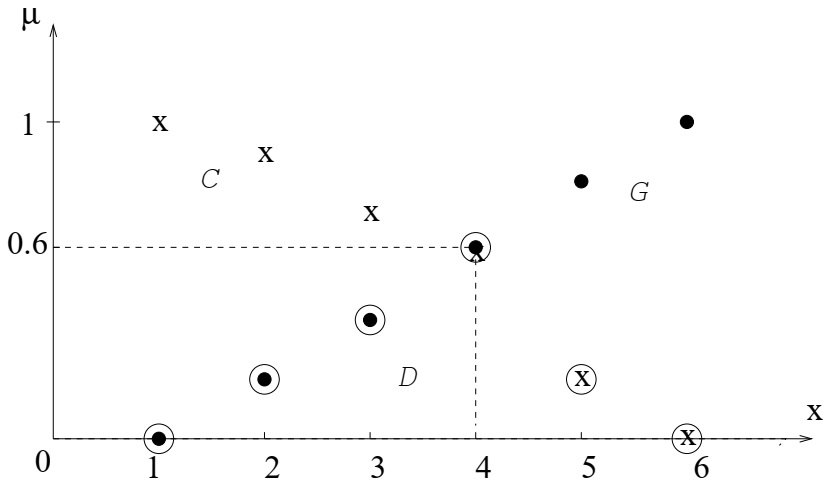
Цели G (точки), ограничения С (крестики) и нечеткое решение D (кружочки).
Здесь \([d_1; d_2] = \{1, 2, 3, 4, 5, 6\}, h = 0.6\) и максимальное решение - это \(x_\max = 4\) с наивысшей степенью принадлежности к D, равной 0,6.
Идея Беллмана и Заде может быть сформулиролвана следующим образом "Решение = Слияние Целей и Ограничений".
Распределение дивидендов
В компании совет директоров, с одной стороны, готов платить привлекательным дивиденды акционерам, а с другой стороны, они должны быть скромными.
Привлекательный дивиденд рассматривается как цель G, описываемая нечетким множеством, определенным для некоторого набора альтернатив
\(A_{alt} = \{x|0 \lt x \le a\}\), где x измеряется в некоторых денежных единицах. Функция принадлежности \(µ_G (x)\) возрастающая на интервале \(A_{alt}\).
Скромный дивиденд - это ограничение C, описываемое нечетким множеством \(A_{alt}\) с убывающей функцией принадлежности \(µ_C (x)\).
Предположим, что цель нечеткого множества G, привлекательный дивиденд, определенный на множестве альтернатив \( A_{alt} = \{x|0 \lt x \le 8\}\) как
\[
G\stackrel{\triangle}{=}\mu_G(x)=
\left\{
\begin{array}{lll}
0, & \hbox{для} & 0\lt x\le 1,\\
\frac{x-1}{4}, & \hbox{для} & 1\le x\le 5,\\
1, & \hbox{для} & 5\le x\le 8,
\end{array}
\right.
\]
и ограничение нечеткого множества C, соответствуюшее скромному дивиденду, задается на \(A_{alt}\)
\[
C\stackrel{\triangle}{=}\mu_C(x)=
\left\{
\begin{array}{lll}
1, & \hbox{для} & 0\lt x\le 2,\\
-\frac{x-6}{4}, & \hbox{для} & 2\le x\le 6,\\
0, & \hbox{для} & 6\le x\le 8,
\end{array}
\right.
\]
Согласно (\ref{3.1}) решение D нечеткого множества представляется его функцией принадлежности, что показано на рисунке
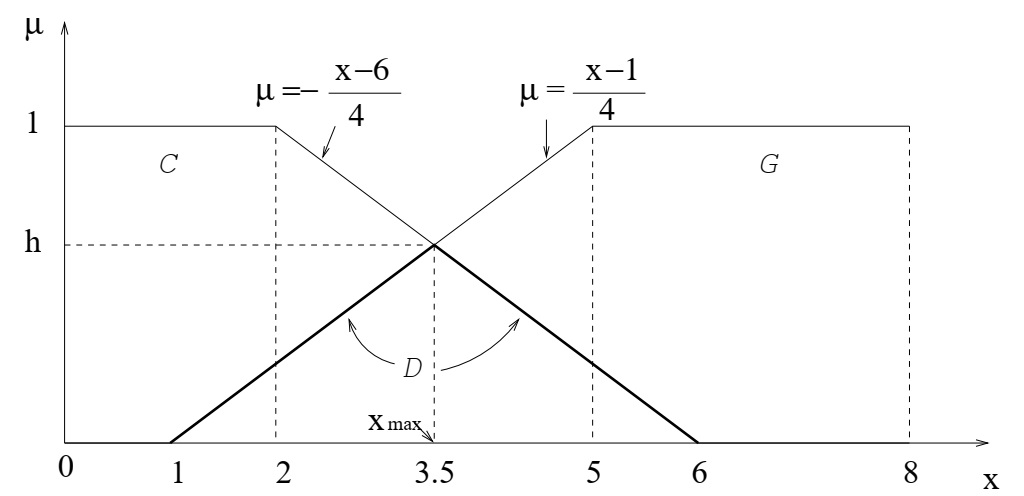
Нечеткая цель G, ограничение C, решение D, максимальное решение x
max.
Здесь \([d_1; d_2]= [1; 6]\), точка пересечения прямых \(µ =\frac{x-1}{4}\) и
\(µ = -\frac{x-6}{4}\) равна (3.5, 0.625), то есть \(x_\max = 3.5; h =\max µ_D (x) = 0.625\).
Дивиденды, подлежащие выплате, составляют 3,5 денежных единиц.
Политика приема на работу
Компания рекламирует позицию, на которую претендуют кандидаты \(x_k, k = 1,...,р\). Претенденты образуют дискретный набор альтернатив
\(A_{alt} = \{x_1,...,x_p\}\). Менеджер по кадрам требует от кандидатов обладания определенными качествами, такими как опыт, знания в определенных областях и т.д.,
которые рассматриваются как цели \(G_i; i = 1,...,n\). Кроме того, он хочет наложить некоторые ограничения \(C_j, j = 1,...,m\), например, скромная зарплата и тд.
В конце процесса собеседования каждый кандидат \(x_k\) оценивается с точки зрения как целей, так и ограничений по шкале от 0 до 1. Оценка, присвоенная кандидату \(x_k\)
относительно целей \(G_i\), обозначается \(a_{k_i}\), а оценка ограничений C обозначается через \(b_{k_j}\).
Используя оценки, получаем дискретные нечеткие множества \(G_i\) и \(C_j\) на множестве альтернатив \(A_{alt}\):
\[
G_i=\{(x_1,a_{1_i}),...,(x_p,a_{p_i})\},i=1,...,n,\\
C_j=\{(x_1,b_{1_j}),...,(x_p,b_{p_j})\},j=1,...,m.
\]
Тогда, в соответствии с (\ref{3.4}) решение можно записать в виде
\[D = G_1\cap ...\cap G_n \cap C_1\cap ...\cap C_m,\]
и с учетом (\ref{3.5})
\begin{equation}\label{3.8}
D=\{(x_1,\mu_1),...,(x_p,\mu_p),\}
\end{equation}
где
\[
\mu_k=\min\{a_{k_1},...,a_{k_n},b_{k_1},...,b_{k_m}\},k=1,...,p.
\]
Кандидат с наивысшей оценкой членства среди \(µ_1,...,\mu_p\) будет считаться лучшим кандидатом на работу.
Предположим, что компания хочет заполнить должность, на которую есть пять кандидатов \(x_i, i = 1,...,5\), которые образуют множество альтернатив,
\(A_{alt} = \{x_1, х_2, x_3, x_4, x_5\}\). Менеджер по кадрам имеет три цели, которым кандидаты должны удовлетворить:
- опыт,
- умение работать на компьютере,
- молодой возраст.
Также у HR-менеждера есть ограничение - предлагаемая зарплата должна быть скромной. После серьезного обсуждения каждый кандидат оценивается с точки зрения целей и
ограничений. HR-менеждер строит нечеткие множества на множестве альтернатив ( n = 3 и m = 1):
\[
G_1=\{(x_1,0.8),(x_2,0.6),(x_3,0.3),(x_4,0.7),(x_5,0.5)\}\\
G_2=\{(x_1,0.7),(x_2,0.6),(x_3,0.8),(x_4,0.2),(x_5,0.3)\}\\
G_3=\{(x_1,0.7),(x_2,0.8),(x_3,0.5),(x_4,0.5),(x_5,0.4)\}\\
C =\{(x_1,0.4),(x_2,0.7),(x_3,0.6),(x_4,0.8),(x_5,0.9)\}.
\]
Здесь \(G_1\) представляет опыт, \(G_2\) знание компьютера, \(G_3\) молодой возраст и C определяет готовность кандидатов принять скромную зарплату.
Используя (\ref{3.8}), получаем решение
\[
D =\{(x_1,0.4),(x_2,0.6),(x_3,0.3),(x_4,0.2),(x_5,0.3)\}.
\]
Кандидат \(x_2\) имеет наивысшую оценку членства 0.6, следовательно, является лучшим кандидатом на работу.
Выбор для строительства
Строительная компания планирует возвести в городе четыре здания. Ресурсов на одновременное строительство нет, поэтому их можно построить только по очереди.
Строительная компания хочет выбрать здание, которое будет построено первым. Здания \(b_i,i= 1,...,4\), формируют множество альтернатив \(A_{alt}\).
Компания предпочитает (имеет цель) построить здание, которое не очень важно для города, но его сооружение очень прибыльно, а время строительства довольно длительное,
при этом, компания также знает, что городской совет предпочитает, чтобы первое здание было очень важным для города, с коротким временем строительства и разумной стоимостью строительства.
Эти условия формируют ограничения для компании. Руководство компании описывает цели и ограничения с помощью нечетких множеств:
\[
G_1\stackrel{\triangle}{=} \hbox{не очень важно } b = \{(b_1,0), (b_2, 0.4), (b_3, 0.3), (b_4, 0.8) \},
\]
\[
G_2\stackrel{\triangle}{=} \hbox{высокодоходный } b = \{(b_1,0.5), (b_2, 0.6), (b_3, 0.7), (b_4, 0.3) \},
\]
\[
G_3\stackrel{\triangle}{=} \hbox{длительное время строительства } b = \{(b_1,0.8), (b_2, 0.7), (b_3, 1), (b_4, 0.2) \},
\]
\[
C_1\stackrel{\triangle}{=} \hbox{очень важно } b = \{(b_1,1), (b_2, 0.6), (b_3, 0.7), (b_4, 0.2) \},
\]
\[
C_2\stackrel{\triangle}{=} \hbox{короткое время строительства } b = \{(b_1,0.3), (b_2, 0.4), (b_3, 0.5), (b_4, 0.7) \},
\]
\[
C_3\stackrel{\triangle}{=} \hbox{разумная стоимость } b = \{(b_1,0.3), (b_2, 0.4), (b_3, 0.7), (b_4, 0.2) \}.
\]
В соответствии с соотношением (\ref{3.8}) выпишем решение
\[
D = G_1 \cap G_2 \cap G_3 \cap C_1 \cap C_2 \cap C_3
= \{ (b_1, 0), (b_2, 0.4), (b_3, 0.3), (b_4, 0.2) \}.
\]
Решение руководства компании заключается в предложении по строительству здания \(b_2\), которое имеет в наборе D максимальное значение, равное
0,4. Это решение наилучшим образом соответствует целям и ограничениям.
Если предложение не будет принято городским советом, то управление готово предложить для строительства здание \(b_3\), которое является вторым выбором
(значение 0,3 в D).
Заметим, что \(G_1\stackrel{\triangle}{=} \hbox{не очень важно } b\) является дополнением к \(C_1\stackrel{\triangle}{=} \hbox{очень важно } b\), то есть
\(µ_{C_1} (b) = 1 - µ_{G_1} (b)\). Тем не мение,
\(C_2\stackrel{\triangle}{=} \hbox{короткое время строительства } b \) близка, но не равна дополнению
\(G_3\stackrel{\triangle}{=} \hbox{длительное время строительства } b\), т.е. \(µ_{C_2} (b) ≈ 1 - µ_{G_3} (b)\).
Лингвистические конструкции "короткий" и "длинный" как слова имеют противоположное значение и могут быть описаны
нечеткими множествами, которые почти дополняют друг друга, т. е. короткие - не длинные \(µ_{short} (x) ≈ 1 - µ_{long} (x) = µ_{notlong} (x)\).
Однако нужно быть осторожным с толкованием слов с противоположным смыслом.
Жилищная политика для семей с низким доходом.
Городской совет проводит жилищную политику для семей с низким доходом, проживающих в старом многоквартирном доме, который расположеннен на большом участке.
Обсуждаются три альтернативных проекта: p1 (ремонт и управление жильем), p2 (программа передачи прав собственности) и p3 (новое строительство).
Множество альтернатив \(A_{alt} = \{p_1, p_2;=,p_3\}\). Проекты \(p_1\) и \(p_3\) потребуют частичного и полного переселения семей.
Городской совет, используя анализ экспертов и различных заинтересованных групп, после долгих обсуждений устанавливает три цели и одно ограничение,
описываемое нечеткими множествами на \(A_{alt}\) следующим образом:
\[
G_1\stackrel{\triangle}{=} \hbox{улучшенное качество жилья } = \{(p_1,0.2), (p_2, 0.4), (p_3, 0.8)\},
\]
\[
G_2\stackrel{\triangle}{=} \hbox{увеличение размеров жилья } = \{(p_1,0.1), (p_2, 0), (p_3, 0.9)\},
\]
\[
G_3\stackrel{\triangle}{=} \hbox{улучшение жизненной среды } = \{(p_1,0.4), (p_2, 0.5), (p_3, 0.8)\},
\]
\[
С_1\stackrel{\triangle}{=} \hbox{разумные затраты } = \{(p_1,0.8), (p_2, 0.9), (p_3, 0.4)\},
\]
Согласно (\ref{3.1}) решение будет иметь вид
\[
D = \{ (p_1, 0.1), (р_2,0), (р_3, 0.4) \}.
\]
Проект \(p_3\) с наибольшей степенью участия 0,4 предпочтительнее, чем \(p_1\) и \(p_2\).
Это лучше, когда речь идет о целях, но не достаточно удовлетворяет ограничению на стоимость.
Стратегия выбора работы.
Пусть некий профессионал в своей области, скажем Мария, выбирает среди вакансий нескольких компаний \(c_1,...,c_n\). Этот набор образует множество альтернатив
\(A_{alt} = \{c_1,...,c_n\}\).
Мария, имея цель получить высокую зарплату, также имеет в виду определенные требования, такие как интересная работа, место работы на близком расстоянии от дома,
компания с будущим, возможность быстрого карьерного продвижения и т. д. Эти требования являются аспектами проблемы и могут рассматриваться как ограничения.
Мария определяет цель высокой зарплаты на основании набора G с функцией принадлежности µG (x), которая является возрастающей в наборе зарплат,
расположенном в \(R^+\). Она также строит множество ограничений на множестве альтернатив \(A_{alt}\), придавая каждой компании значение принадлежности в соответствии с ее мнением.
Здесь цель определяется на \(R^+\), в то время как ограничения определяются на дискретном множестве компаний, поэтому необходима корректировка алгоритмов,
рассмотренных ранее. Набор заработной платы может быть преобразован в множество из \(A_{alt}\). Для этого размер зарплаты \(s_1,...,s_n\), предлагаемой компаниями
\(c_1,...,c_n\), соответственно, подставляются в µG (x) и значения \(µ_G (s_1),...,µ_G (s_n)\), ассоциированные с \(c_1,...,c_n\),
формируют множество зарплат на \(A_{alt}\):
\[
G_{alt} = \{ (c_1, µ_G (s_1)),...,(c_n, µ (s_n)) \}.
\]
Предположим, что Мария должна выбрать одну из трех работ, предложенных ей тремя разными компаниями c1, с2 и с3, следовательно,
множество альтернатив \(A_{alt} = \{c_1, c_2, c_3\}\). Заработная плата в приведена таблице
| Компания | c1 | c2 | c3 |
|---|
| Зарплата | 40 000 | 35 000 | 30 000 |
|---|
У Марии есть цель - работать на высокую зарплату с учетом ограничений: - интересная работа,
- место работы на близком расстоянии от дома,
- компания с будущим.
Мария использует свое субъективное суждение, чтобы определить цель и описывает ограничения с помощью дискретных нечетких множеств
\[
C_1 = \{ (c_1, 0.5), (с_2, 0.7), (с_3, 0.8)\},
\]
\[
C_2 = \{ (c_1, 0.3), (с_2, 0.8), (с_3, 1)\},
\]
\[
C_3= \{ (c_1, 0.3), (с_2, 0.7), (с_3, 0.5)\},
\]
на множестве альтернатив (это универсальный набор для \(C_1, C_2\) и \(C_3\)) и цели G высокой заработной платы с помощью функции принадлежности
\[
G\stackrel{\triangle}{=}\mu_G(x)=
\left\{
\begin{array}{lll}
0, & \hbox{ для } 0\lt x\lt 25000,\\
\frac{x-25000}{20000}, & \hbox{ для } 25000\le x\le 45000,\\
1, & \hbox{ для }x \ge 45000.
\end{array}
\right.
\]
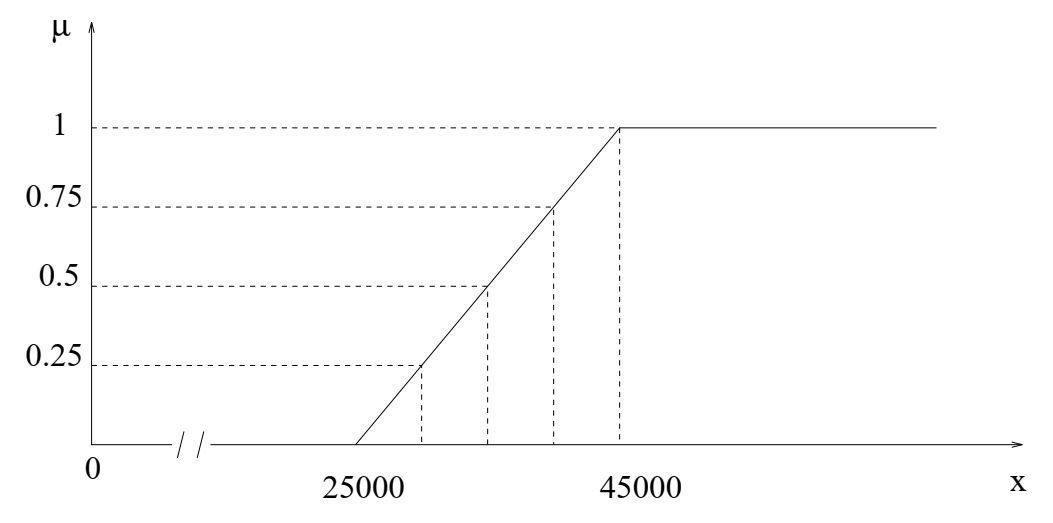
Нечеткая цель G- высокая зарплата.
Чтобы применить формулу принятия решения, Мария должна иметь дело с одним универсальным набором - набором альтернатив.
Для этого она создает значения функции принадлежности, подставляя в \(\mu_G(x)\) вместо х, зарплаты, соответствующие альтернативам,
\[
\mu_G(40 000) = 0.75, \mu_G(35 000) = 0.5, \mu_G(30 000) = 0.25.
\]
Как следствие, цель нечеткого множества G на \(R^+\) теперь заменяется целью нечеткого множества \(G_{alt}\) на множестве альтернатив,
\[
G_{alt} = \{ (c_1, 0.75), (с_2, 0.5), (с_3, 0.25) \}.
\]
Тогда решение будет иметь вид
\[
D = G_{alt} \cap C_1 \cap C_2 \cap C_3 = \{ (c_1, 0.3), (с_2, 0.5), (с_3, 0.25)\}.
\]
Максимальное значение функции принадлежности в D составляет 0,5, поэтому если Мария хочет наилучшим образом выполнить свои цели,
она должна устроиться на работу в компании \(c_2\).
Оценка успеваемости
Руководство компании Ноосфера учредило ежегодную стипендию для учащихся старших классов с отличными достижениями в области естественных наук (математика, физика, химия) и
знания английского языка. Критерием являются лингвистические переменные, которыми руководство описало по 100-бальной шкале, отдельно уровень знаний для естественных наук (ES) и
отдельно знание английского языка (EE), используя трапециевидные числа на промежутке [0; 100].
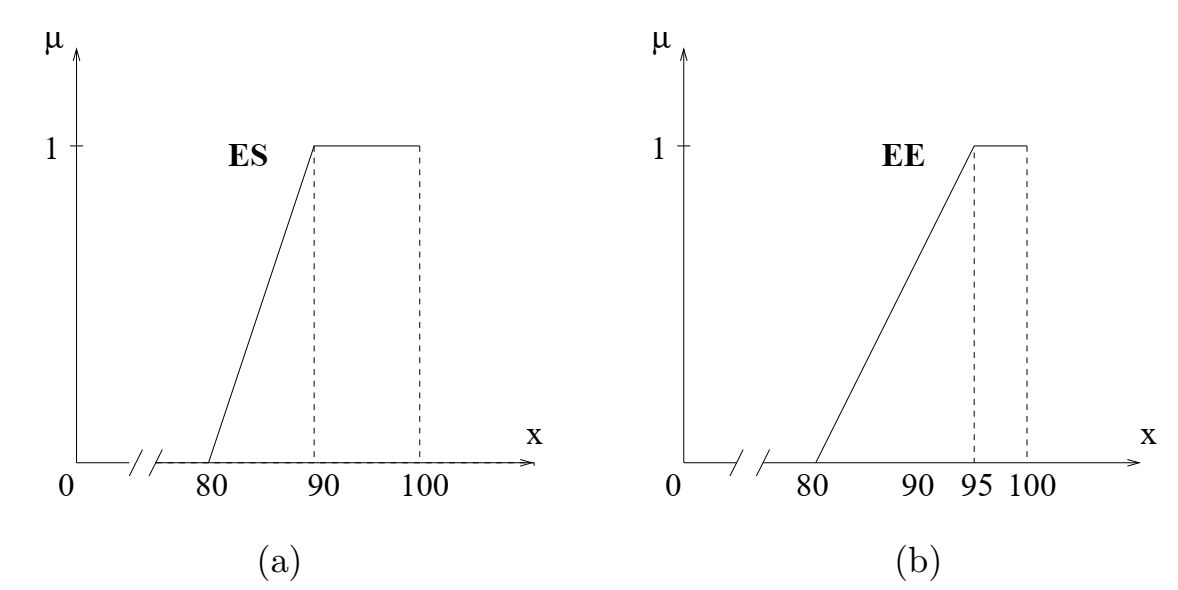
(а) Отлично в естественных науках. (b) Отлично по английскому языку.
Их использование дает функции принадлежности
\[
ES\stackrel{\triangle}{=}\mu_{ES}(x)=
\left\{
\begin{array}{lll}
0, & \hbox{ для } 0\le x\le 80,\\
\frac{x-80}{10}, & \hbox{ для } 80\le x\le 90,\\
1, & \hbox{ для } 90\le x \le 100.
\end{array}
\right.
\]
\[
EE\stackrel{\triangle}{=}\mu_{EE}(x)=
\left\{
\begin{array}{lll}
0, & \hbox{ для } 0\le x\le 80,\\
\frac{x-80}{15}, & \hbox{ для } 80\le x\le 95,\\
1, & \hbox{ для } 95\le x \le 100.
\end{array}
\right.
\]
Оценка ученика по естественным наукам в 90 баллов приводит к значению принадлежности ES в 1 в то время как тот же балл по английскому языку имеет значение принадлежности
EE только 0,67.
Пять студентов являются кандидатами на стипендию, х1 = Саша, х2 = Таня, х3 = Женя, х4 = Костя, х5 = Маша.
| Математика | Физика | Химия | English |
|---|
| Саша (х1) | 86 | 91 | 95 | 93 |
|---|
| Таня (х2) | 98 | 89 | 93 | 90 |
|---|
| Женя (х3) | 90 | 92 | 96 | 88 |
|---|
| Костя (х4) | 96 | 90 | 88 | 89 |
|---|
| Маша (х5) | 90 | 87 | 92 | 94 |
|---|
Оценки учащихся по естественным наукам и английскому языку
Получаем множество альтернатив \(A_{alt} = \{x_1, х_2, x_3, x_4, x_5\}\).
Используя функции принадлежности, получаем
| Математика | Физика | Химия | English |
|---|
| Саша (х1) | 0.6 | 1 | 1 | 0.87 |
|---|
| Таня (х2) | 1 | 0.9 | 1 | 0.67 |
|---|
| Женя (х3) | 1 | 1 | 1 | 0.53 |
|---|
| Костя (х4) | 1 | 1 | 0.8 | 0.60 |
|---|
| Маша (х5) | 1 | 0.7 | 1 | 0.93 |
|---|
Уровень знаний учащихся по естественным наукам и английскому языку
Отсюда получаем нечеткие множества уровня знаний в науках и английском языке, которые формируют цели или аспекты проблемы:
\[
\hbox{успехи в математике }\stackrel{\triangle}{=}G_1,=\{(x_1,0.6),(x_2,1),(x_3,1),(x_4,1),(x_5,1)\},
\]
\[
\hbox{успехи в физике }\stackrel{\triangle}{=}G_2,=\{(x_1,1),(x_2,0.9),(x_3,1),(x_4,1),(x_5,0.7)\},
\]
\[
\hbox{успехи в химии }\stackrel{\triangle}{=}G_3,=\{(x_1,1),(x_2,1),(x_3,1),(x_4,0.8),(x_5,1)\},
\]
\[
\hbox{Excellent in English }\stackrel{\triangle}{=}G_4,=\{(x_1,0.87),(x_2,0.67),(x_3,0.53),(x_4,0.6),(x_5,0.93)\}.
\]
Выпишем решение
\[
D = G_1 \cap G_2 \cap G_3 \cap G_4= \{ (x_1, 0.6), (x_2, 0.67), (x_3, 0.53), (x_4, 0.6), (x_5, 0.7)\}.
\]
Отсюда вывод - \(х_5\), т.е. Мария со степенью членства 0,7 в D - учащаяся с лучшими показателями.