Нечеткое бюджетирование с нулевой базой
|

|
Традиционно бюджетирование с нулевой базой определяется как метод составления бюджета, при котором планируемые расходы определяются с нуля, то есть каждый период (например, год)
бюджет составляется так, как будто текущая программа затрат только что начинается.
Поскольку доступная информация обычно неточна и неоднозначна, более реалистично использовать нечеткие данные вместо четких.
Метод бюджетирования на основе нечеткого нуля использует треугольные числа для построения модели нечеткости при планировании бюджета.
А поскольку нечеткое бюджетирование на основе нуля использует сложение треугольных чисел, то с этой точки зрения, оно близко к
нечеткому усреднению. Это и будет проиллюстрировано для конкретной ситуации.
Рассмотрим компанию с несколькими центрами принятия решений, скажем, A, B, и C.
Предположим, что лица, принимающие решения, согласны с некоторыми предварительными бюджетами, использующими для каждого центра определенное количество уровней бюджета в зависимости
от его важности. Бюджеты выражаются в виде треугольного нечеткого числа, полученного по определенной процедуре (это может быть нечеткий Delphi или другой способ).
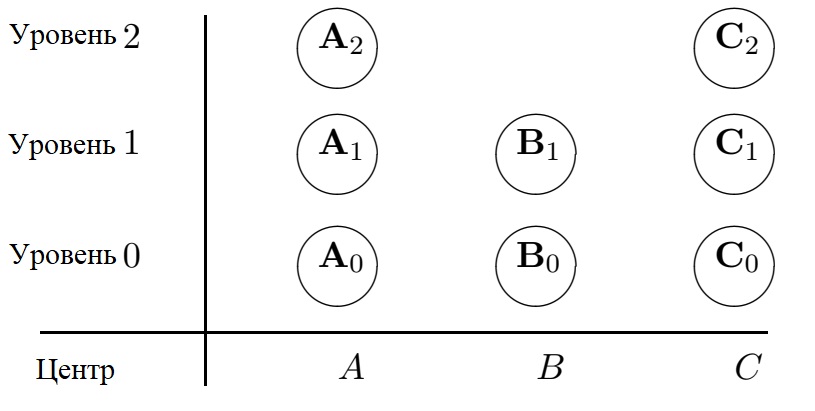
Были предложены следующие возможные уровни бюджета:
для центра А, A0 < A1 <A2;
для центра B, B0 <B1;
для центраC, C0 <C1 <C2.
Бюджет с нулевым индексом (уровень 0) представляет собой минимальный бюджет, если центр получает этот бюджет, он может быть закрыт.
Бюджеты с индексом один (уровень 1) - нормальные бюджеты, позволяющие функционирование на предыдущем уровне, бюджеты индексом два или
более двух (уровень 2 или более высокий уровень, если таковой существует) улучшают состояние и позволяют развиваться.
Общий бюджет, доступный для компании, ограничен, но он гибок и может быть выражен правым трапециевидным числом L с функцией принадлежности
\[
\mu_L(x)=\left\{
\begin{array}{lll}
1, & \hbox{ для }& 0\lt x\le l_1,\\
\frac{x-l_2}{l_1-l_2} & \hbox{ для }& l_1\le x\le l_2,\\
0, & \hbox{ иначе.}
\end{array}
\right.
\]
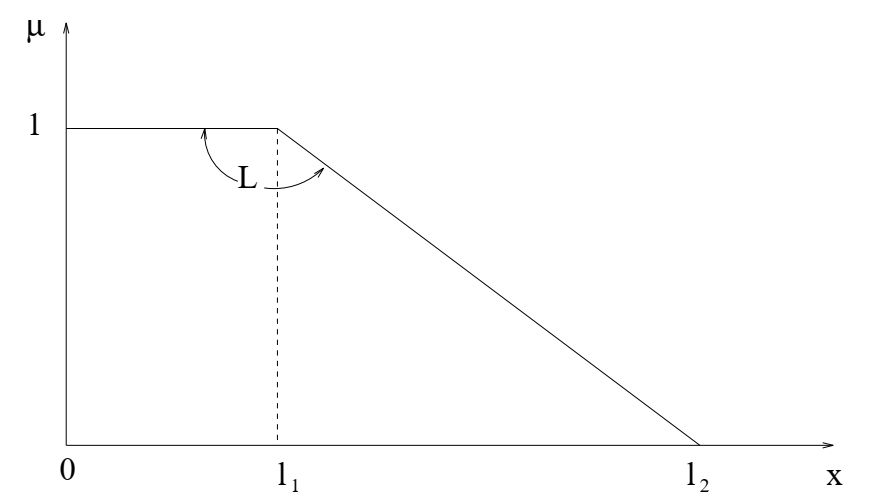
Общий бюджет компании.
Лица, принимающие решения, следуют пошаговой процедуре распределения бюджета в соответствии с важностью (по их мнению) каждого центра.
Вначале выбирается выбирают бюджет для центра, который начинается с нулевого уровня и продолжается до тех пор, пока не будут использованы все бюджеты.
Бюджет более высокого уровня включает бюджет более низкого уровня для того же центра.
Процедура показана на следующей схеме

Схема построения бюджета.
Выбранные бюджеты представлены заштрихованной областью. Из представленной схемы видно, что сначала (шаг 1) начальный бюджет C0 выделяется центру C,
который считается наиболее важным.
После этого (шаг 2) центр A получает поддержку A0.
Затем снова (шаг 3) выбирается центр C, его бюджет увеличен с C0 до C1, прежде чем будет выбран центр B.
Очевидно, что центр B является последним приоритетом. Процедура отбора последовательная.
Шаг 7, например, указывает, что, хотя центры C и A выбраны для распределения на уровне 2, центру B предоставляется бюджет на уровне 0, только в последнем шаге 8 этот центр
получает бюджет на уровне 1.
Совокупные бюджеты, перечислены шаг за шагом:
S1 = C0;
S2 = A0 + C0;
S3 = A0 + C1;
S4 = A0 + C2;
S5 = A0 + B0 + C2;
S6 = A1 + B0 + C2;
S7 = A2 + B0 + C2;
S8 = A2 + B1 + C2:
Бюджеты Si, i = 1,...,8 представляют собой треугольные числа, так как это суммы треугольных чисел. Они могут быть представлены
в виде \(S_i = \left(s^{(i)}_1, s^{(i)}_M, s^{(i)}_2\right)\).
Компания хочет иметь оптимальный бюджет \(S_{opt} = (s_1, s_M, s_2)\) с пиком \((s_M; 1)\) в соответствии с имеющимся бюджетом L. Следовательно, разумно требовать
\begin{equation}\label{1}
S_{opt} = (s_1, s_M, s_2)\subseteq L,\end{equation}
где
\begin{equation}\label{2}
s_M=\max s^{(i)}_M\le l_1, s_2=\max s^{(i)}_2\le l_2,
\end{equation}
Включение интерпретируется как требование, что бюджет \(S_{opt}\) не превышает доступный бюджет L и по сути означает, что \(S_{opt}\) влечет за собой L.
Если нужен четкий бюджет, компания может принять максимальное значение \(x_\max = s_M\).
Условие (\ref{1}) вместе с (\ref{2}) подходит для консервативного бюджета.
Компания, ожидающая дополнительного финансирования, которое может или не может быть реализованым, или готовая пойти на риск, может решить ослабить включение (\ref{1}) и
заменить его на \(S_{opt} ≈ L.\)
В таком случае требуется первое условие (\ref{2}), а второе отброшено или наоборот, или же оба условия (\ref{2}) отбрасываются, но вместо этого подставляется
\(s_M = \min s^{(i)}_M\gt l_1\).
Применение нечеткого бюджетирования с нулевой базой
Пусть имеется ограниченный доступный бюджет L, определеннный следующим образом
\[
\mu_L(x)=\left\{
\begin{array}{lll}
1, & \hbox{ для }& 0\lt x\le 40000,\\
\frac{x-46000}{60000} & \hbox{ для }& 40000\le x\le 46000,\\
0, & \hbox{ иначе.}
\end{array}
\right.
\]
и восемь проектов бюджетов
A0 = (10000, 11000, 12000),
A1= (12000, 13000, 15000),
A2 = (14000, 15000, 17000),
B0 = (7000, 9000, 11000),
B1 = (11000, 12000, 13000),
С0 = (7000, 9000, 12000),
C1 = (11000, 13000, 15000),
С2 = (15000, 18000, 19000).
Для совокупного бюджета используется сложение треугольных чисел
S1 = C0 = (7000, 9000, 12000),
S2 = A0 + C0 = (17000, 20000, 24000),
S3 = A0 + C1 = (21000, 24000, 27000),
S4 = A0 + C2 = (25000, 29000, 31000),
S5 = A0 + B0 + C2 = (32000, 38000, 42000),
S6 = A1 + B0 + C2 = (34000, 40000, 45000),
S7 = A2 + B0 + C2 = (36000, 42000, 47000),
S8 = A2 + B1 + C2 = (39000, 45000, 49000).
Бюджеты S1, S2, S3 и S4 слишком малы по сравнению с
ограничивающим бюджетом L. Следовательно, компания отбрасывает их и рассматривает S5, S6, S7 и S8, что показано на рисунке вместе с L.
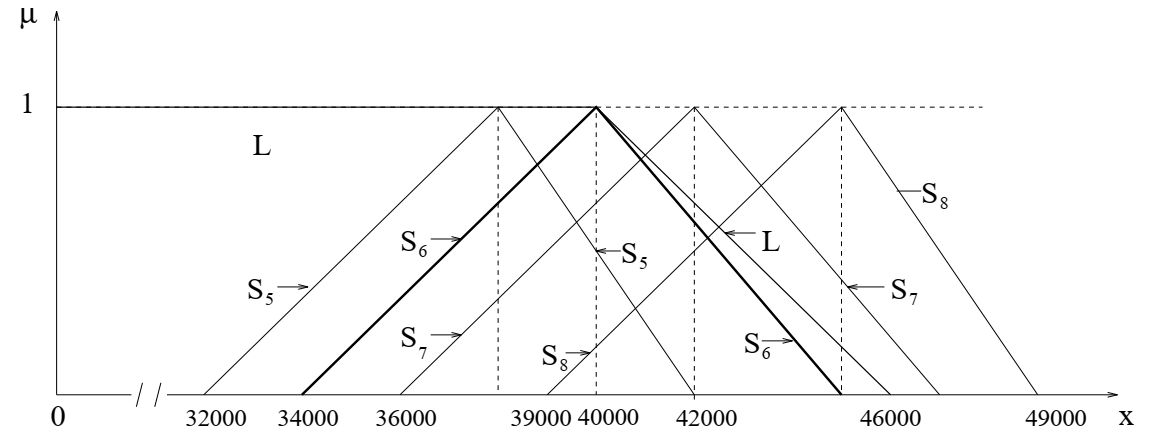
Совокупные бюджеты.
Однако бюджеты S7 и S8 нарушают условие (\ref{2}).
Бюджеты S5 и S6 имеют пик 1 для \(s^{(5)}_M = 38000\) и \(s^{(6)}_M =40000\) соответственно, но так как \(s^{ (5)}_M \lt s^{ (6)}_M = l_1 = 4000\)
и \(s^{(5)}_2 \lt s^{(6)}_2 \lt l_2 = 4600\), оптимальный бюджет равен \(S_6 =(34000, 40000, 45000)\), а четкий бюджет равен \(x_\max = s^{(6)}_M = 40000\).
Если компания принимает этот бюджет, учитывая, что \(S_6 = A_1 + B_0 + C_2\), центр A получает бюджет \(A_1\) (четкий 13000), центр B получает бюджет \(B_0\)
(четкий 9000), и центр C получает бюджет \(C_2\) (четкий 18000).
Бюджет центра B находится на уровне 0 (меньше, чем обычно), лица, принимающие решения, могут рассмотреть возможность закрыть этот центр и перераспределить деньги в два других
центра, которые являются более важными.
Если руководство компании хочет быть более гибким и иметь причины быть более оптимистичным, тогда следует принять бюджет \(S_7 = (36000; 42000; 47000)\) и
можно было бы рассмотреть четкое значение 42000. Этот бюджет удовлетворяет условию, что \(s^{(7)}_M\) наименьшее среди \(s^{(i)}_M\gt l_1=4000\).