Нечеткое усреднение для принятия решений.

Далее для принятия решений рассмотрим метод нечеткого усреднения. Пусть цели и ограничения или требования (правила) описываются треугольными или трапециевидными числами. Если они ранжируются в соответствии с важностью, то применяется взвешенное нечеткое усреднение.
Результатом (вывод, агрегация) является треугольное или трапециевидное число D, интерпретируемое как решение. Будем называть этот подход усредняющим принятием решений. Чтобы найти максимизирующее решение, рассматриваем значение на вспомогательном интервале D, на котором µ_D (x) имеет максимальную степень принадлежности (она равна единице). Также могут быть использованы статистические средние.

Распределение дивидендов с помощью нечеткого усреднения и взвешенного нечеткого усреднения

Применим метод нечеткого усреднения для задачи распределения дивидендов, рассмотренной ранее. Итак, цель G (привлекательный дивиденд) и ограничение C (умеренный дивиденд) - это правое и левое трапециевидные числа, например, такие

G = (1, 5, 8, 8), С = (0, 0, 2, 6).

Используя прямые вычисления (или формулу среднего для трапеции), получим трапециевидное число \[ D = A_{ave} = \frac{G + C}{2}=\frac{(1,5,8,8)+(0,0,2,6)}{2}=\frac{(1,5,10,14)}{2}=(0.5,2.5,5,7). \]

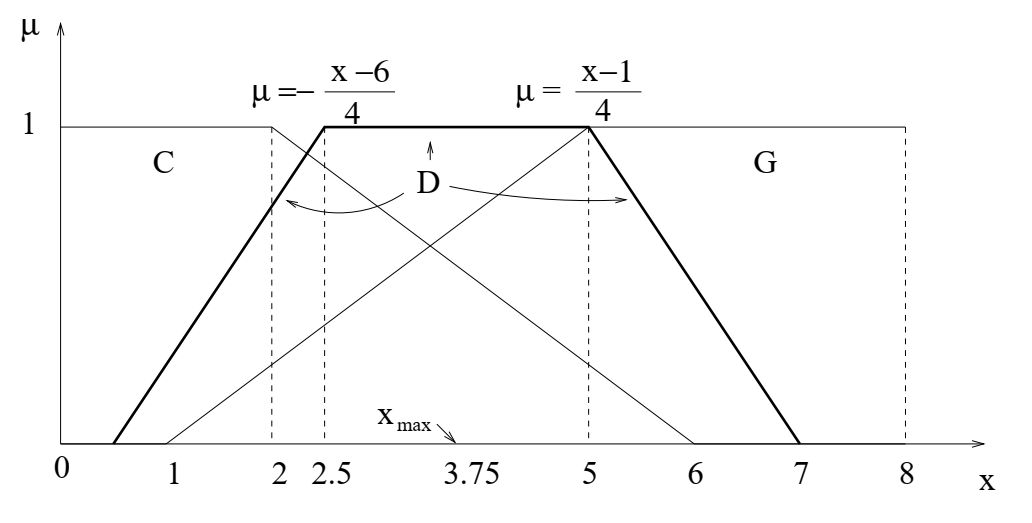
Решение D и x_max=3.75.

Функция принадлежности µ_D (x) решения имеет плоский сегмент, проекция которого на ось x является интервалом [2.5, 5]. Числа в этом интервале имеют наибольшую степень принадлежности к D. Определим максимизирующее решение как середину плоского интервала, т.е. \[ x_\max =\frac{2.5+5}{2}= \frac{7.5}{2}=3.75. \] Заметим, что максимальное решение, полученное методом пересечения, равно 3,5.
Окончательное решение принимает совет директоров, который определяет, какой критерий выбирать.
Предположим теперь, что совет директоров дает разный вес к G и C, например, \(w_G = 0.4\) и \(w_C = 0.6\), то есть, ограничение (скромный дивиденд) немного важнее цели (привлекательный дивиденд). Тогда получаем решение \[ D = A^w_{ave} = 0.4 G + 0.6 C = 0.4(1, 5, 8, 8) + 0.6 (0, 0, 2, 6) = (0.4, 2,3.2, 3.2) + (0, 0, 1.2, 3.6) = (0.4, 2, 4.4, 6.8) \] которое выражается в виде трапециевидного числа с плоским интервалом [2, 4.4], середина которого дает максимизирующее решение \[ x_\max =\frac{2+4.4}{2}= \frac{6.4}{2}=3.2 \] что, как ожидается, меньше, чем для случая без предпочтений - 3,75.

Рассмотрим еще один пример.

Использование нечеткого усреднения в задаче ценообразования.

Модель 1.

Пусть имеем модель ценообразования, рассмотренную ранее - правила R₁, R₃ и R₄ описаны треугольными числами

A₁ = (10, 10, 40), A₃ = (20, 25, 30), А₄ = (25, 30, 35).

Используя формулу треугольного среднего, получаем решение \[ D=A_{ave}=\frac{A_1+A_3+A_4}{3}=\frac{(10, 10, 40) + (20, 25, 30) + (25, 30, 35)}{3}=\frac{(55, 65, 105)}{3}= (18.33, 21.67, 35). \]

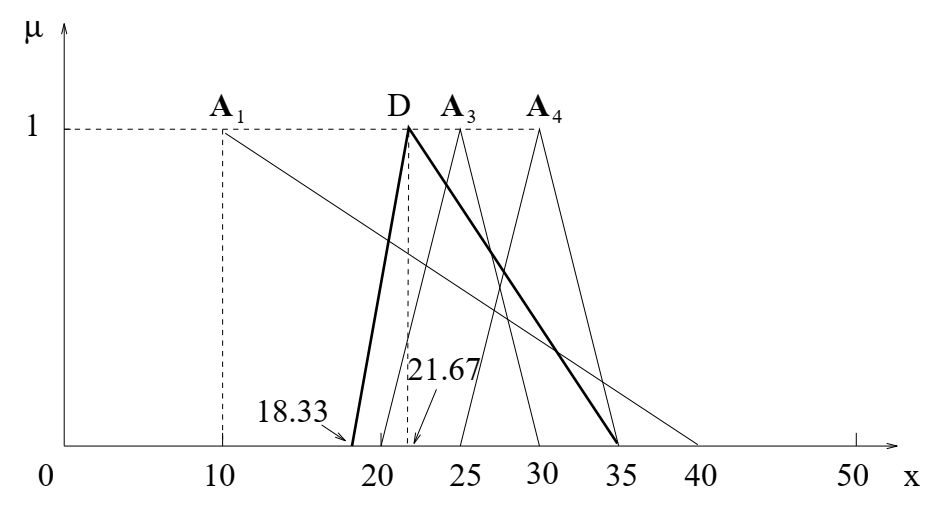
Модель ценообразования с правилами R₁, R₃,R₄.

Решением будет x_max = 21.67, поскольку при этом значении функция принадлежности µ_D (x) максимальна. Максимальное решение для модели 1, полученное в предыдущем разделе, составляет 27.14. Разница между двумя решениями не маленькая. Тогда какое значение является правильным? На этот вопрос нет однозначного ответа. Оба решения должны рассматриваться как предложения. Окончательное решение должны принять эксперты.
Значение 27.14 слишком высоко и не отражает конкурентную цену, представленную А₃. С другой стороны, значение 21.67 выглядит слишком маленьким, это не около А₄, хотя и зависит от него.
Компромиссом может быть принятие числа (среднего) между 21.67 и 27.14, которое составляет 24.405 ≈ 24.4.

Модель 2.

Опишем правило R₁ в модели 1 немного иначе, а остальное оставим без изменений.
Пусть новое треугольное число описывающее правило R₁ равно A₁ = (10, 10, 25).
Тогда треугольное усреднение дает \[ D = A_{ave} =\frac{(10, 10, 25) + (20, 25, 30) + (25, 30, 35)}{3}=\frac{(55, 65, 90)}{3}= (18.33, 21.67, 30). \] Максимальное решение: x_max = 21.67, такое же, как в модели 1.

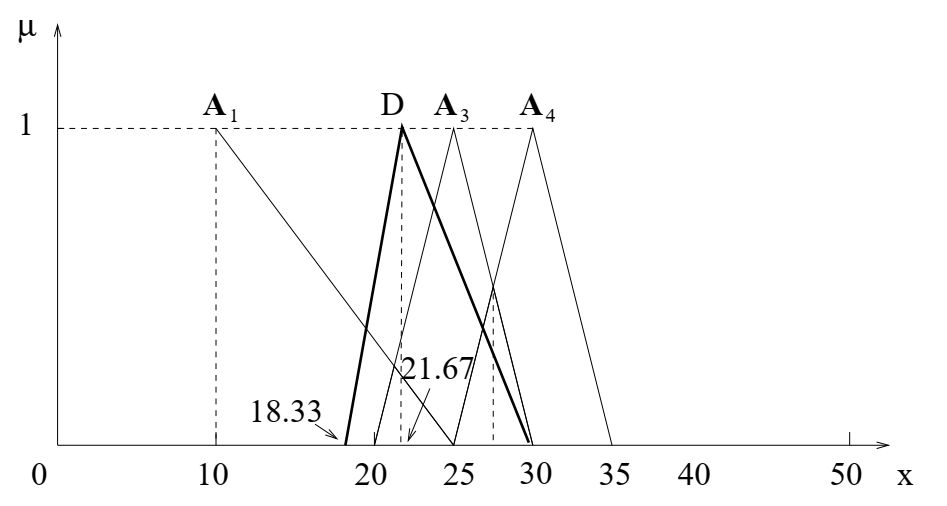
Модель ценообразования с правилами R₃, R₄ и немного другой R₁

Просто для сравнения, применим метод пересечения решений к той же модели.
Заметим, что A₁ пересекает A₃, но не имеет точек пересечения с A₄, тогда решение D, \[ D\stackrel{\triangle}{=}\mu_{D}(x)=\min\left(\mu_{A_1}(x),\mu_{A_3}(x),\mu_{A_4}(x)\right) \] вырождается в точку (25,0).
Число 25 выглядит как максимизирующее решение, но поскольку степень его членства равна нулю, то метод пересечения решений в этом случае не является подходящим инструментом.