Результаты этого раздела любезно предоставлены С.Л. Сотником
(тех. директор Iveonik Systems, г.Каменское).
Введение в мягкие вычисления.
Термин "мягкие вычисления" ввел в 1994 году основоположник направления нечеткой логики - Лотфи Заде. Под этим термином подразумевалась совокупность эмпирических, нечетких, приближенных методов решения задач, не имеющих точных алгоритмов решения за полиномиальное время (время работы которых полиномиально зависит от размера входных данных). В настоящее время, к мягким вычислениям принято относить следующие методы:
- Нейронные сети;
- Эволюционные стратегии;
- Нечеткая логика;
- Многоагентные системы (интеллект стаи);
- Различные эвристические алгоритмы поиска решений;
- Теория хаоса и др.
Многие алгоритмы, используемые в данных направлениях, относят к разряду интеллектуальных. Но термин интеллект (и искусственный интеллект) сейчас настолько размылись, что хотелось бы остановиться на нем подробнее.
Под термином "интеллект" мы будем понимать свойство чего-либо решать
интеллектуальные задачи. Интеллектуальной задачей назовем такую задачу, для решения которой еще не придумано чёткого алгоритма. Другими словами, интеллект - это свойство человека, компьютера или чего-то еще, позволяющее создавать новые алгоритмы.
Такое определение позволяет нам сразу же отсечь множество маркетинговых (в плохом смысле этого слова) определений интеллекта, привязанных к стиральным порошкам, лекарствам и т.п. Интересно также применить данное определение к человеческим профессиям.
- Программист.
- Продуктом деятельности программиста является программа - алгоритм в чистом виде. Не думаю, что найдется кто-то, кто сможет утверждать, что данная профессия неинтеллектуальна, хотя\ldots есть и здесь подводные камни. К примеру, в программе есть кусок кода, решающий уже
готовую проблему. Программист берет его, меняет несколько символов
(констант) и получает дублированный код, адаптированный к новой предметной
области. Речь идет о типичном грехе copy/paste. Не будем здесь рассуждать о
недостатках такого подхода - взглянем на это с другой стороны. Новый
алгоритм не был рожден. Значит, интеллектуальность такого результата близка
к нулю.
- Мошенник.
- Есть типичные схемы, когда преступления совершаются по накатанной
технологии. Здесь не нужно большого интеллекта. Такие мошенники обычно
попадаются рано или поздно. Но есть и "звезды", которые каждый раз
изобретают необычные ходы, не повторяются. Фактически, каждый раз пишется
новый алгоритм. Интеллект налицо.
- Сыщик.
- Пожалуй, можно сказать, что профессия сыщика и мошенника составляет
синергетическую пару. Чем более интеллектуален мошенник, тем больше
интеллекта нужно сыщику, чтобы разоблачить преступника, изобретая ответные
нестандартные методы поиска.
- Кассир (банк, магазин и т.п.).
- В этой профессии изобретение нового алгоритма
- зло. Все нужно делать тщательно, аккуратно и одинаково. Ни в коем случае
не хочу сказать, что кассиры - неумные люди. Для того чтобы научиться
данной работе, интеллект необходим. Зачастую немалый. Но во время самой
работы "блок" алгоритмизации необходимо отключать. Поэтому не могу назвать
эту профессию интеллектуальной согласно принятому определению.
- Водитель.
- Сочетание заранее алгоритмизированной деятельности (соблюдение
правил дорожного движения, стандартные приёмы управления автомобилем) и
постоянный поиск алгоритмов решения возникающих проблем. Это распознавание
дорожной ситуации при большом количестве участвующих объектов, движущихся в
разных направлениях с разными скоростями, поиск (суб-) оптимального маршрута
при движении в незнакомом месте, реагирование на изменившиеся условия
движения в уже знакомых местах (ямы, ремонт дороги, новые дорожные знаки).
Неудивительно, что эту деятельность еще не автоматизировали до конца, есть
только отдельные компоненты, помогающие в решении отдельных задач, например,
GPS-навигаторы.
Думаю, на этом перечисление интеллектуальных особенностей профессий можно
завершить - читатель без труда может сам проанализировать интересующие его
направления. Также, у нас появился дополнительный критерий оценки
интеллектуальности деятельности - чем тяжелее это направление
автоматизируется, тем интеллектуальнее оно (это временный критерий, пока
человек является самым интеллектуальным "устройством" на Земле). Кстати,
это и подсказка тем, кто пытается автоматизировать сложную деятельность -
можно не только повышать интеллект машины, но и снижать степень
интеллектуальности задачи. Например, полностью автоматизировать выращивание
и сбор урожая на произвольном поле на открытой местности достаточно сложно
- слишком много неизвестных. Но если предварительно подготовить поле "по
линейке", поместить все растения в теплицу, то сложность задачи уменьшится.
Решить её станет проще. А ваш интеллект проявится в подготовке алгоритме
такого упрощения.
Возвратимся к методам, называемым "мягкими вычислениями". То, что они
ассоциируются с интеллектуальными задачами, связано, скорее всего, с тем,
что они обладают высокой универсальностью и могут быть применены до того,
как будет разработан хороший специализированный метод решения задачи.
Другим важным общим свойством мягких вычислений является свойство
адаптивности - подстройки под задачу. Это вносит в решение задачи этап
обучения (также часто связываемый с интеллектуальной деятельностью) и
уменьшает для исследователя сложность задачи. Теперь он может работать с
задачей как с черным (система с неизвестным алгоритмом, о сути которого
можно только догадываться по внешним проявлениям) или серым ящиком (система
с возможностью ограниченной настройки пользователем), не вникая до конца в
тонкости работы управляемой системы, в надежде, что эти тонкости будут
скомпенсированы "интеллектом" метода.
Именно поэтому владение перечисленными выше методами является большим плюсом
для любого исследователя, программиста, ученого, инженера, аналитика.
Следствием универсальности методов, являются также их хорошие комбинаторные
способности. Часто можно встретить системы, где нейронная сеть обучается при
помощи генетического алгоритма. Нечеткие классификаторы являются основой
индивидуумов в многоагентных системах.
Эволюционные вычисления.
Краткая история.
Эволюционные методы придуманы и используются очень давно (уже больше
миллиарда лет). Разумеется, речь идет о естественной эволюции. Именно этот
процесс, по мнению большинства ученых, в конце концов дал нам HomoSapience,
используемый как эталон интеллектуальности. Разумеется, есть люди, которые
не согласны с этой точкой зрения. Что ж, не будем с ними спорить. Даже, если
правы они, алгоритмы, которые получены в результате моделирования этих
"неправильных" процессов показывают свою эффективность во многих задачах.
И только, исходя из этого, они уже имеют право на использование.
Первым ученым, предложившим стройную теорию происхождения новых видов,
явился Чарльз Дарвин. Именно он в своей работе "Происхождение видов",
вышедшей в 1859 году, показал, что основой эволюции являются следующие
процессы:
- Изменчивость - новые особи популяции практически всегда немного (а иногда
сильно) отличаются от своих родителей.
- Отбор - естественный или искусственный отбор отсеивают неудачные варианты
изменений. Жить остаются только удачные (более приспособленные).
- Наследственность - изменения, произошедшие в одном из поколений,
наследуются потомками.
Совокупность этих движущих сил и позволяет видам приспосабливаться к
изменяющейся окружающей среде, совершенствоваться и выживать. Но во времена
Дарвина ясен был только механизм отбора. То, как появлялись новые признаки и
как они передавались потомкам, стало ясно гораздо позже. В 1944 году, О.
Эйвери, К. Маклеод и М. Маккарти опубликовали результаты своих исследований.
В них доказывалось, что за наследственные процессы в организмах отвечает
"кислота дезоксирибозного типа". Что это за кислота, мир узнал еще позже
- 27 апреля 1953 года в журнале "Nature" была опубликована знаменитая
статья Уотсона и Крика, а мир впервые услышал о двухцепочечной спирали ДНК.
С тех пор прошло уже более полувека, но до сих пор нельзя сказать, что о
механизме функционирования ДНК мы знаем все. Мы постоянно узнаем все новые и
новые детали. Что разные участки ДНК мутируют с разной частотой. Что многие
гены могут присутствовать в ДНК в разном количестве экземпляров
(copynumbervariation), и от этого может зависеть продукция того или иного
белка, чувствительность к различным заболеваниям.
Несмотря на продолжающийся процесс познания естественных процессов, они с
самого начала привлекали исследователей, которые хотели повторить
аналогичный процесс с использованием вычислительной техники. К сегодняшнему
дню накопилось огромное количество различных алгоритмов. Перечисление
основных направлений, конечно же, хочется начать с генетических алгоритмов и
классификационных систем Холланда. Впервые они были опубликованы в начале
60-х годов, но основное свое распространение получили после выхода книги,
ставшей классикой - "Адаптация в естественных и искусственных системах". На территории бывшего СССР также работали в данном направлении,
несмотря на то, что сразу после войны по идеологическим соображениям был
введен лозунг "генетика и кибернетика - продажные девки империализма". А
ведь эволюционные вычисления объединяли эти два направления. Тем не менее,
Л.А. Расстригиным в 70-е годы в рамках теории стохастического поиска был
предложен ряд алгоритмов, моделировавших различные стороны поведения живых
организмов. Эти идеи получили дальнейшее развитие в посвященных
эволюционному моделированию работах И. Л. Букатовой. Ю. И. Неймарком было
предложено осуществлять поиск глобального экстремума на основе множества
независимых автоматов, при этом моделировались процессы рождения, развития и
смерти особей. Также большой вклад в развитие эволюционных вычислений внесли
Уолш и Фогел.
Каждая из этих школ взяла из известных на то время принципов эволюции что-то
свое. После этого оно было упрощено до такой степени, что процесс можно было
провести (промоделировать) на компьютере.
Как и многие эмпирические алгоритмы, эволюционные алгоритмы не гарантируют
нахождения хорошего результата. Также они бывают сложны в настройке. При
неправильных параметрах может проявляться склонность к вырождению, плохая
поисковая способность. В этом случае не стоит сразу забрасывать эволюционные
алгоритмы - стоит попытаться помочь им своим, естественным интеллектом
("поиграться" с настройками, например). Здесь можно вспомнить, что если
какого-то вида осталось очень мало - меньше десятка особей, то в природе он
обречен на вымирание из-за вырождения. Но лучше вспоминать чудные по
конструкции тела птиц, и их крылья, обтекаемых мант, эхолокаторы дельфинов и
летучих мышей, черную плесень, использующую энергию излучения разрушенного
реактора Чернобыльской АЭС.
Генетический алгоритм.
Генетический алгоритм (далее ГА) является одним из самых известных
эволюционных алгоритмов. Он прост в принципах работы, но имеет большой
потенциал для развития, что и попытаемся показать в данном разделе.
По своей сути, ГА является алгоритмом для поиска глобального оптимума
многоэкстремальной функции. Для этого он использует, с определенной степенью
приближения, модель размножения живых организмов. Для того, чтобы решить
проблему, нам нужно представить её в виде так называемой фитнесс-функции от
многих переменных (также называемой оценочной):
\[
f(x_1,x_2,\ldots,x_N).
\]
Для решения задачи нам необходимо найти глобальный максимум или минимум (это
не принципиально, поскольку поиск максимума легко заменяется поиском
минимума этой же функции, взятой со знаком минус, и наоборот). При этом на
значения входных переменных обычно налагаются определенные ограничения, как
минимум по диапазону их изменения.
Перед тем, как мы рассмотрим работу ГА, нам необходимо представить все
входные переменные в виде хромосом. Под хромосомами в ГА подразумеваются
цепочки символов, с которыми и производятся дальнейшие операции. Для
кодирования параметров чаще всего применяют следующие два метода:
- двоичный формат;
- формат с плавающей запятой.
При использовании двоичного формата, под параметр выделяется \(N\) бит (для
каждого параметра это N может быть различным). Поскольку для каждого из этих
параметров имеются ограничения MIN и MAX, то взаимный переход между
значениями параметров в формате с плавающей запятой и их бинарным
представлением можно записать в следующем виде:
\[
g=(r-MIN)/(MAX-MIN)\cdot (2^N-1),
\]
\[
r=g\cdot(MAX-MIN)/(2^N-1)+MIN,
\]
здесь \(g\) - бинарное представление параметра, помещенное в \(N\) бит, \(r\) - значение параметра в формате с плавающей запятой. Часто используют последующее преобразование полученного бинарного представления в код Грея - это позволяет уменьшить разрушительную силу мутаций (тут мы немного забегаем вперед).
Полученные бинарные представления каждого параметра выкладывают в цепочку (строку) бит, которая дальше называется хромосомой.
При работе с параметрами в формате с плавающей запятой, их значения также выкладываются в цепочку бит, но без указанного выше преобразования, прямо в том представлении, с которым работает процессор компьютера.
После того, как мы закодировали все необходимые параметры в виде хромосомы, можем приступать к основному циклу генетического алгоритма:
- Генерация первоначальной случайной популяции.
- Генерация следующего поколения.
- Отбраковка худших решений во вновь сгенерированном поколении.
- Если не достигнут критерий окончания, переходим на шаг 2.
- Окончание работы. Экземпляр, у которого самое лучшее значение фитнесс-функции, является искомым решением.
Ключевым здесь, конечно же, является этап 2. Его можно детализировать
следующим образом:
- Сортируем родительское поколение в соответствии со значением фитнесс-функции для каждого экземпляра.
- Пока не сгенерировано достаточное количество экземпляров новых поколений:
- Отбираем двух родителей.
- Объединяем их хромосомы (кроссовер).
- Применяем другие генетические операторы.
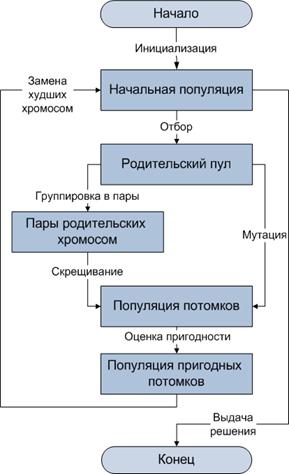
Схема основного цикла генетического алгоритма.
Опишем немного подробнее каждый из шагов генерации.
(a) Для отбора используются различные стратегии. Например, просто случайным образом выбираем из \(N\) самые лучшие экземпляры.
Другим распространенным подходом является турнирный. Он заключается в том, что для каждого из родителей выбирается случайная пара (или больше)
претендентов. Из них используется тот, у которого значение фитнесс-функции лучше. Таким образом, более приспособленные особи чаще будут
родителями, но менее приспособленные также имеют шанс пройти.
Для ускорения сходимости также часто используется стратегия элитизма - в следующее поколение решений проходят без изменений самые лучшие
из имеющихся решений предыдущего поколения (элита). Но с этим подходом нужно быть крайне осторожным - при недостаточном размере популяции, она очень быстро становится похожей на элиту и поиск новых решений практически прекращается.
(b) и (c) - применение генетических операторов. Основой ГА являются два оператора: кроссовер, который объединяет решения родителей, и мутация, которая обеспечивает поисковые способности. Кроме этих основных операторов могут также применяться дополнительные операторы, например, инверсия.
Оператор кроссовера работает с битовыми строками двух родительских хромосом. Наиболее простым вариантом является одноточечный кроссовер. В этом случае каждая из родительских хромосом перерезается в одной, случайно выбранной точке. Хромосома потомка формируется из "головы" хромосомы одного предка и "хвоста" второго:
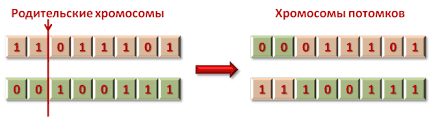
Иллюстрация работы одноточечного кроссовера.
Оператор кроссовера может быть и более сложным - двухточечным, или даже использовать совершенно иные принципы (к этому мы еще вернемся). Главное, чтобы он объединял решения предков, и потомку не было необходимости находить удачные решения заново.
Оператор мутации - это просто случайное изменение хромосомы в одном или большем количестве бит.
Мутация - разрушительный оператор. В большинстве случаев, он нарушает
решение или даже приводит особь к неработоспособному состоянию. Поэтому
вероятность его применения не должна быть чрезмерно высокой. Но отсутствие
мутаций сводит на нет способность ГА к поиску глобального оптимума во всем
пространстве решений.

Иллюстрация мутации.
Приведенный в качестве примера дополнительных операторов, оператор инверсии
заключается в циклической перестановке бит в хромосоме случайное количество
раз:

Иллюстрация инверсии.
Теперь у нас есть все составные части генетического алгоритма, и мы можем
закрепить их на практике. В приложении есть архив программ, среди которых реализация простейшего ГА SimpleGA
на языке программирования C#.
Программа является консольной, что позволяет не концентрироваться на интерфейсной части, а сразу же переходить к алгоритмизации. Из-за
этого, и в связи с учебной направленностью этого и других примеров, основные настройки задаются в тексте программ в виде констант. На сленге
программистов, параметры данной программы являются «захардкожеными». Однако минусом это будет в том случае, если пользователю программы не нужно иметь доступа к коду программы. Мы же обращаемся, скорее
к разработчикам, поэтому правку параметров в тексте программы вполне можно считать своеобразным интерфейсом для программиста. Таким образом, в качестве интерфейса пользователя к изменению параметров, можно
использовать IDE.
Простой пример реализации ГА.
Попробуем найти глобальный экстремум одной из тестовых функций. Она известна
под названием DeJong 2:
\[
f(x,y) = \frac{100}{100 \cdot \left( {x^2 - y} \right)^2 + \left( {x - 1}
\right)^2 + 1}.
\]
Данная функция является овражной с достаточно малым наклоном в районе максимума. Максимум функции равен \(100\) при значении \(x=y=1\).
Конечно же, сделаем вид, что нам это неизвестно, только известно, что максимум находится при значениях параметров (как \(x\) так и \(y\))
где-то между \(-1.28\) и \(+1.28\).
Определимся, как мы будем представлять геном. В первом примере применим бинарный способ кодирования генома, без использования кода Грея.
Цепочку бит будем хранить в типе int, причем, старшие 16 бит будут отвечать за параметр x, а младшие - за параметр y.
Поскольку к каждому геному также привязано значение фитнесс-функции, по которому придется производить отбор наиболее приспособленных
экземпляров (сортировкой), то удобно геном и это значение объединить в одной записи. Используем для этого уже готовый класс из .NET
Framework - KeyValuePair <int, double>. При этом в поле Key у нас будет находиться геном, а в Value - f(x, y).
В новых версиях для этого удобно использовать шаблон Taple<>, но данный код написан так, чтобы не требовать установки чего-то более
нового, чем .NET Framework 3.5.
Определим поля и константы, используемые далее:
private static Random _rnd = new Random();
const int GenerationSize = 10000;
const int GenerationNumbers = 200;
constdoubleMutationProbability = 0.2;
Основной цикл работы программы сосредоточен в методе Main:
public static void Main(string[] args)
{
// Инициализируем нулевое поколение.
List<KeyValuePair<int, double>> generation = GenerateRandom();
SortGeneration(generation);
// Основной цикл генерации
for (int genNum = 1; genNum < GenerationNumbers; ++genNum)
{
generation = GenerateNewGeneration(generation, true);
SortGeneration(generation);
Console.WriteLine("Лучшая особь = " +
Weight(generation[0].Key));
Console.WriteLine("Generation " + genNum);
}
Console.WriteLine("x = " + GetX(generation[0].Key));
Console.WriteLine("y = " + GetY(generation[0].Key));
Console.WriteLine("Genome = {\{}0:X{\}}", generation[0].Key);
Console.Write("Press any key to continue . . . ");
Console.ReadKey(true);
}
Здесь мы видим вызов случайной инициализации стартового поколения и
генерацию последовательности дочерних поколений. Критерием остановки
генерации поколений у нас является номер поколения. В конце цикла мы выводим
параметры лучшего экземпляра в консольном выводе. Поскольку коллекция
экземпляров у нас отсортирована по убыванию приспособленности, то самым
лучшим будет экземпляр с номером 0.
Пройдемся теперь по вызываемым методам. Генерация первого, случайного
поколения:
private static List<KeyValuePair<int, double>> GenerateRandom()
{
List<KeyValuePair<int, double>> result = new List<KeyValuePair <int,double>>();
for (int i = 0; i < GenerationSize * 2; ++i)
{
int genome = _rnd.Next();
result.Add(new KeyValuePair(genome,
Weight(genome)));
}
return result;
}
Здесь, и в процедуре генерации нового поколения, мы генерируем в 2 раза
больше особей, чем будет потом участвовать в турнире. Таким образом, мы
отбраковываем самые неприспособленные особи ("уродцев"), которые
совершенно "нежизнеспособны". Этой начальной отбраковкой занимается
следующий метод:
privatestaticvoidSortGeneration(List<KeyValuePair<int,double>>generation)
{
generation.Sort((x, y) => y.Value.CompareTo(x.Value));
if (generation.Count > GenerationSize)
generation.RemoveRange(GenerationSize,
generation.Count - GenerationSize);
}
Здесь происходит сортировка коллекции с геномами (используются достаточно
краткие в записи лямбда-выражения). После этого оставляется уже необходимое
количество наиболее приспособленных особей.
Немного остановимся на процедуре "взвешивания" - вычисления
фитнесс-функции. Она выполняется методом Weight, который в качестве
параметра принимает цепочку бит генома:
private static double GetY(int genome)
{
int y = genome {\&} 0xffff;
return y * (1.28 + 1.28) / (0x10000 - 1.0) - 1.28;
}
private static double GetX(int genome)
{
int x = (genome >> 16) {\&} 0xffff;}=
return x * (1.28 + 1.28) / (0x10000 - 1.0) - 1.28;
}
private static double Sqr(double x)
{
return x * x;
}
private static double Weight(int genome)
{
double x = GetX(genome);
double y = GetY(genome);
return 100 / (100 * Sqr(Sqr(x) - y) + Sqr(1 - x) + 1);
}
Немного остановимся на методах GetX и GetY. Они извлекают из генома (32 бита) часть, ответственную за хранение параметров x и y,
соответственно, после чего преобразуют её в формат с плавающей запятой. При этом используется формула преобразования представления из
предыдущего раздела, где \(MIN=-1.28, MAX=1.28, N=16\) (бит на параметр), \(2^{N}=0\times 10000\).
И, наконец, процедура генерации нового поколения:
private static List<KeyValuePair<int, double>>
GenerateNewGeneration(
List<KeyValuePair<int, double>> parents, bool useElitism)
{
List<KeyValuePair<int, double>> result =
new List<KeyValuePair<int,double>>();
// Реализация элитизма
if (useElitism)
result.Add(parents[0]);
while (result.Count < GenerationSize * 2)
{
// Tурнирный выбор предков}
int parent1a = _rnd.Next(GenerationSize);
int parent1b = _rnd.Next(GenerationSize);
int parent2a = _rnd.Next(GenerationSize);
int parent2b = _rnd.Next(GenerationSize);
int parent1 = Math.Min(parent1a, parent1b);
int parent2 = Math.Min(parent2a, parent2b);
// Генерация с кроссовером
int mask = ($\sim \(0 << _rnd.Next(32));
int child = parents[parent1].Key {\&} mask \(\vert \(
parents[parent2].Key {\&} \(\sim \(mask;
// Мутация
if (_rnd.NextDouble() > MutationProbability)
child ^= 1 << _rnd.Next(32);
result.Add(new KeyValuePair<int, double>
(child, Weight(child)));
}
return result;
}
В данном методе сосредоточена демонстрация отбора с элитизмом, турнирный
выбор предков, кроссовер (одноточечный) и мутация. Как и при генерации
нулевого поколения, данный метод генерирует в два раза больше потомков, чем
будет использовано при генерации нового поколения дальше. Этим излишком
опять займется наш метод (уже рассмотренный выше) SortGeneration. При тех
настройках, которые указаны в программе, будет использован вариант,
называемый ГА с элитизмом. В нашем случае, он заключается в том, что один
наиболее приспособленный индивидуум гарантированно попадает в новое
поколение. Такой подход гарантирует неухудшение показателей самого лучшего
решения из поколения в поколение, часто обеспечивает более высокую стартовую
скорость поиска решения. В то же время, может мешать более полному
исследованию пространства решений и ускорению вырождения популяции. Читатель
может самостоятельно поэкспериментировать с разными настройками и
понаблюдать, как они влияют на качество и скорость поиска решений.
Запустив программу с приведенными настройками, довольно часто можно получить
вот такую картину:
....
Поколение 197
Лучшая особь = 99,9999998156313
Поколение 198
Лучшая особь = 99,9999998156313
Поколение 199
x = 0,999995727473869
y = 0,999995727473869
Геном = E3FFE3FF
Нажмите "Ввод" для выхода . . .
Указанные параметры x и y - это наиболее близкий к числу 1.0 узел из множества узлов, которые получаются при разбиении промежутка \([-1.28\ldots +1.28]\) на \(2^{16}\) отрезка. Этот результат можно наблюдать не всегда - мы ведь работаем с вероятностным (ну хорошо, псевдовероятностным) процессом, поскольку используем генератор случайных чисел (класс Random). А пространство решений, которые нужно исследовать достаточно велико.
Конечно, пример не самый сложный. Его вполне можно решить различными аналитическими и градиентными методами. Но \(\ldots\) если для вас не составляет труда привести параметры в цепочку бит и закодировать фитнесс-функцию, а также устроит субоптимальное значение, то вы вполне можете обойтись без анализа функции на экстремум или выбора того или иного градиентного метода. Если у вас этих знаний нет, то такой подход сэкономит затраты, связанные с вызовом специалиста или с самостоятельным более глубоким изучением предметной области. Конечно, не бесплатно - за счет вас как специалиста по программированию и крайне нерациональному использованию вычислительной
техники. Что лучше, в каждом случае решается индивидуально. Но наличие в вашем арсенале такого интеллектуального помощника, как ГА, не будет мешать - это точно.
Приведем пример работы генетического алгоритма для подбора строк с целью восстановления надписи "Hello, World!". Для запуска скрипта, щелкните мышкой на надписи.
a
a
О влиянии генератора случайных чисел на работу ГА.
Одним из факторов, которые могут влиять на работу ГА, является способ получения случайных чисел. Приведем иллюстрацию работы ГА
для поиска глобального экстремума двух тестовых функций Гривонка и Розенброка, с одновременным проведением исследования влияния на работу ГА различных алгоритмов генерации «псевдослучайных» чисел.
- Функция Гривонка (Griewangk’s function). Пусть n − натуральное число, тогда
\[
F(x_1,x_2,\ldots,x_n)=1+\sum_{i=1}^n\frac{x_i^2}{4000}-\prod_{i=1}^n\cos\frac{x_i}{\sqrt{i}},
(-6000\le x_i\le 6000,i=1,2,\ldots,n).
\]
Функция Гривонка близка по виду на функцию Растригина. Она
имеет триллион локальных экстремумов. Однако эти локальные экстремумы регулярно распределены по всей поверхности функции. Глобальный
минимум, равный 0, достигается в точке \(x_1=x_2=\ldots=x_n=0\). При \(n =10\)
существует еще 4 локальных минимума, которые равны \(0,0074\), и достигаются приблизительно в точке \((\pm \pi,\pm \sqrt{2}\pi,0,\ldots,0)\).
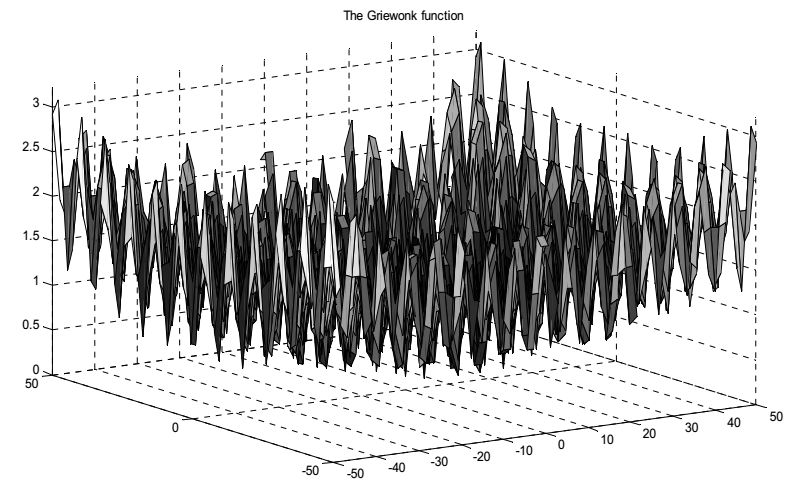
Функция Гривонка для случая двух переменных.
- Функция Розенброка (Rosenbrock's saddle или second function of De Jong). Функция Розенброка входит в набор тестовых функций De Jong и
носит второе название De Jong 2. Пусть \(n\) − натуральное число, тогда
\[
f(x)=\sum_{i=1}^{n-1}\left(100\left(x_{i+1}-x_i^2\right)^2+\left(x_i-1\right)^2\right).
\]
Интервал, которому принадлежит переменная: \(−5.12 \lt x_i \lt 5.12, i =1,2,..., n \).
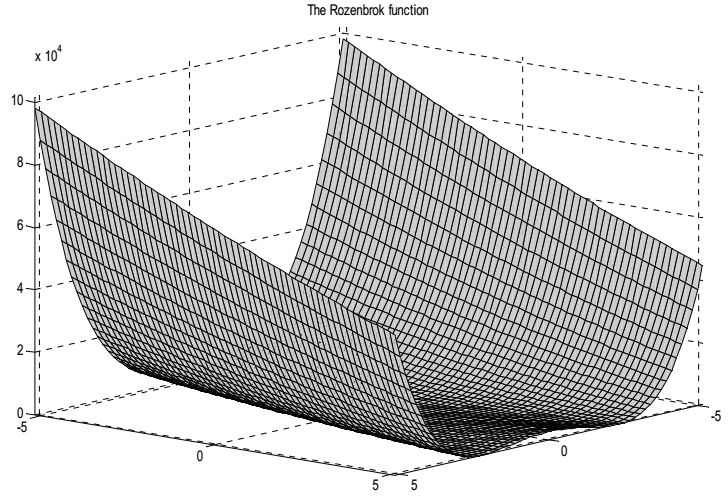
Функция Розенброка для случая двух переменных.
Данная функция была предложена Ховардом Розенброком в 1960 году. Эта функция имеет крайне пологий изогнутый овраг, который очень
усложняет поиск минимума (значения аргументов в точке минимума очевидны: \(\bar{x}_1=\ldots =\bar{x}_n=1\)(при этом \(f(\bar{x})=0\)).
Для случая двух переменных функция создает небольшое плато с двумя «крыльями» по обеим сторонам.
Точка минимума (1,1) находится на одной стороне плато, в то время как поисковые алгоритмы часто «застревают» на другой стороне. Благодаря
сложным для методов поиска особенностям экстремума функция Розенброка часто используется для тестирования сходимости разных оптимиза
ционных алгоритмов и для их сравнения.
Для исследования влияния на работу ГА алгоритмов генерации «псевдослучайных» чисел программно реализовано 3 вида генераторов
- генератор Мерсена (стандартный);
- линейный конгруэнтный генератор (ЛКГ);
- генератор Фибоначчи с запаздыванием.
Указанные генераторы, а также отдельно исследованный линейный конгруэнтный генератор (Urand) были использованы для работы генетического
алгоритма (ГА).
В то же время исследовалось влияние на работу ГА хаотических чисел, для реализации которых использовались генераторы Лоренца с
параметрами \(\sigma =10, \rho = 28, \beta = 8 / 3\) и Чуа с параметрами \(\alpha = 4,91667, \beta = 3,642\) и
\[
\left\{
\begin{array}{ll}
-0.07x-1.57, & x\lt -1, \\
-0.07x+1.43, & x\gt 1, \\
1.5x, & x\in [-1,1].
\end{array}
\right.
\]
Ниже в таблицах приведены результаты работы ГА на тестовых многоэкстремальных функциях Гривонка и Розенброка. Для каждого из
генераторов псевдослучайных чисел, а также для хаотических генераторов было проведено по 100 экспериментов.
В 50-ти случаях из них вероятность мутации выбиралась на уровне 0,1, а в остальных 50 – на уровне 0,3.
В каждом эксперименте брало участие по 100 индивидуумов, эксперимент длился в течении 100 поколений. Для удобства напомним значения
глобального минимума рассмотренных функций:
- функция Гривонка – 0;
- функция Розенброка – 0;
| Функции | Генератор псевдослучайных чисел | Генераторы хаоса |
| Мерсен | ЛКГ | Фибоначчи | Urand | Лоренц | Чуа |
| Гривонка | 0,0123216 | 0,0098595 | 0 | 0,252528 | 0,00739627 | 0,0297598 |
| Розенброка | 0,00221527 | 1,54568e-05 | 0,000954742 | 1,08383 | 0,00109675 | 7,19038e-09 |
Минимизация функций ГА со стандартным оператором мутации (коэффициент мутации равен 0,1)
| Функции | Генератор псевдослучайных чисел | Генераторы хаоса |
| Мерсен | ЛКГ | Фибоначчи | Urand | Лоренц | Чуа |
| Гривонка | 0 | 0,00739618 | 0 | 0,697938 | 0,00986468 | 0,0239592 |
| Розенброка | 0,0112275 | 0,00799863 | 0,000689653 | 1,21357 | 0,0764429 | 0,0875793 |
Минимизация функций ГА со стандартным оператором мутации (коэффициент мутации равен 0,3)
Ближе к реальности, или пространственный кроссовер.
Задачи, похожие на решаемую в предыдущем разделе, проблему поиска экстремума
тестовой функции DeJong 2, любят приводить в учебных пособиях по ГА. Понятно
почему - проблема обозрима, ответ известен, легко проверить. В то же время,
такие примеры оставляют двойственное впечатление. Ведь их часто нетрудно
решить и другими, тоже простыми методами - от случайного перебора (метод
Монте-Карло) до градиентных методов типа покоординатной оптимизации. Либо,
наоборот, трудно любыми методами.
Мощь ГА раскрывается в примерах, в которых моделируемая система разделяется
на подсистемы, решения в которых могут быть найдены параллельно. Часто для
эффективности работы в конкретной задаче, приходится адаптировать
классические генетические операторы, изобретать новые.
Другим важным моментом является то, что в реальных задачах зачастую наиболее
трудоемкой частью процесса просчета является не генерация нового поколения,
а оценка приспособленности каждой особи. Поэтому некоторое усложнение схемы
генерации новых поколений не сильно увеличивает интегральную трудоемкость
алгоритма, а вот увеличение "выхода" хороших потомков - очень даже
уменьшает её.
Попробуем показать это все на примере решения задачи, приближенной к
реальной. Итак, задача:
Воюем. У нас есть войска противника, расположенные неравномерно на
определенной территории, и оружие - 10 боеголовок ядерного оружия.
Известно, что при взрыве боеголовки в радиусе поражения KillingRadius, не
остается ничего живого. Упрощенно будем считать, что за пределами данного
радиуса, боевые единицы противника остаются живыми. Нашей задачей будет
найти такие координаты для каждой боеголовки, чтобы у противника после удара
осталось как можно меньше войск.
Конечно, если у вас более пацифистские настроения, эту же задачу можно
представить и иначе - есть средства на постройку 10 магазинов в
определенном районе города. Люди готовы ходить в магазин, расположенный не
далее, чем за M (аналог KillingRadius) метров от дома. Люди проживают
неравномерно по выбранному району. Необходимо расположить магазины таким
образом, чтобы покрыть сервисом наибольшее количество жителей.
Далее, в тексте программы, названия идентификаторов выбраны исходя из первой
формулировки задачи, но это не будет означать специализации только на первом
варианте постановки проблемы.
В качестве входных данных для тестового приложения будут поступать
изображения в формате PNG. Данный формат используется, поскольку он сжимает
без потери информации, а для определения яркости точек это важно. Боевая
единица противника кодируется черной точкой (яркости цветовых компонент в
RGB - 0, 0, 0). Территории, накрытые взрывами, будем показывать
"томатным" цветом. Такой способ подачи входных данных дает возможность
наглядно увидеть полученный результат, а также задействовать при решении
графическую карту компьютера, поскольку для оценки полученного результата
можно его просто нарисовать: поверх исходного изображения нарисовать залитые
окружности с радиусом поражения.
В этот раз программа будет представлять собой WinForms-приложение с
единственным окном, поскольку довольно любопытно наблюдать за динамикой
работы генетического алгоритма. А оценить её только по числам, бегущим в
консоли, в данном случае не очень удобно. Различные же параметры приложения,
как и в прошлом примере, можно изменить прямо в тексте программы, используя
в качестве редактора IDE.
Прежде всего, решим, какой вариант кодирования пространственной информации в хромосомы мы будем использовать.
Самый простой вариант - последовательно закодировать координаты в битовую строку так, как это было показано в предыдущем разделе.
После этого, применить обычные операторы кроссовера и мутации. Но, практика показывает, что в таких случаях очень часто возникают различные
проблемы - проблема конкурирующих решений, слабое качество синтезируемых решений.
Один из возможных вариантов решения этих проблем - кроссовер, основанный на пространственном положении точек решения.
Далее будем сокращенно его называть пространственным кроссовером.
Итак, будем хранить данные, относящиеся к одной точке в виде неразделяемого набора данных.
В биологии такие признаки называются сцепленными из-за того, что передаются потомкам, как правило, вместе.
Т.е., в нашем случае это будут координаты на плоскости по осям X и Y.
В программе одному "взрыву", соответствует следующий класс:
public class Explosion
{
public float X { set; get;}
public float Y { set; get;}
public Explosion Clone()
{
Explosion copy = new Explosion()
{
X = this.X,
Y = this.Y,
};
return copy;
}
static Random rnd = new Random();
public static Explosion GenerateRandom(TaskSpecification spec)
{
return new Explosion()
{
X = (float)(rnd.NextDouble() * spec.Bound.Width
+ spec.Bound.Left),
Y = (float)(rnd.NextDouble() * spec.Bound.Height
+ spec.Bound.Top),
};
}
}
В этом классе хранятся координаты взрыва (X, Y), а также представлено несколько вспомогательных методов.
Упомянутый в одном из методов класс TaskSpecification хранит некоторые ограничения и начальные условия задачи:
public class TaskSpecification
{
public RectangleF Bound {get; set;}
public int ExplositionsNumber {get; set;}
public float KillingRadius {get; set;}
public Bitmap OriginalField {get; set;}
}
Здесь представлены (по порядку) координаты границ, за которые не следует выходить при расположении взрывов (свойство Bound),
количество боеголовок (фактически, это длина генома), радиус поражения каждой боеголовки и оригинальное поле (карта) сражения,
на котором отмечены войска противника.
Перед тем, как привести код класса, ответственного за хранение генетической информации особи и работы с ней, посмотрим,
что собой представляет пространственный кроссовер.
Как уже было сказано выше, если к списку пространственных координат двух хороших, но разных родителей, применить обычный одно- или двухточечный
кроссовер, мы, скорее всего, получим нежизнеспособного потомка. Основных причин тут две. Прежде всего, у разных особей одна и та же точка может
храниться в разных местах генома, и, при обмене генетической информацией, мы можем поместить почти рядом геометрически две точки, находящиеся в
разных местах генома родителей. При этом оголится какой-то другой участок. Поначалу, генетический алгоритм будет тратить всю свою мощь на то,
чтобы отобрать удачный способ кодирования координат, и, только потом, если к этому моменту еще не произойдет вырождения популяции, начнет собственно
поиск удачного решения. Это и есть проблема конкурирующих решений - когда одному и тому же решению может соответствовать множество способов
кодирования этого решения, что очень увеличивает разрушающее свойство кроссовера.
Второй проблемой является то, что если обращать внимание только на место, где расположена точка в геноме, то кроссовер будет случайным образом
брать точки из одного родительского решения и из другого. Эти точки будут разбросаны по всему пространству поиска. Однако понятно, что часто точки,
расположенные вблизи друг от друга, образуют своеобразные подкомплексы решений, которые поддерживают друг друга. И случайное изъятие или добавление
точек в такой ансамбль точек существенно нарушает качество решений.
Обе эти проблемы решает пространственный кроссовер. В своей работе он ориентируется на положение точек в пространстве решаемой задачи.
На следующем эскизе показана схема объединения двух родительских геномов.
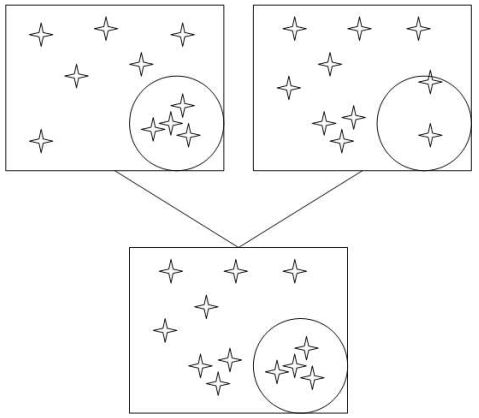
Схема пространственного кроссовера.
Пространственный кроссовер состоит из следующих шагов:
- Выбираем в пространстве решаемой задачи произвольную (случайную) точку.
- У обоих родителей вырезаем одинаковую (по координатам центра и радиусу) окружность (сферу или гиперсферу для пространств с размерностью более 2-х).
- У одного родителя берем точки, которые лежат внутри окружности, у другого -
снаружи.
- Объединяем взятые точки в одно решение.
- Корректируем количество точек в потомке - удаляем (случайным образом), если есть лишние, либо добавляем еще не использованные точки родителей.
Такой подход позволяет сохранить уже сложившиеся локальные ансамбли точек с большей вероятностью (по сравнению с обычным кроссовером и способом кодирования).
Теперь, после краткого рассмотрения схемы пространственного кроссовера, мы можем рассмотреть избранные места класса Individual (особь). При этом мы пропустим, не связанные непосредственно с ГА места прорисовки изображений,
вспомогательные небольшие методы.
Прежде всего, генотип хранится в виде списка точек взрывов. Также есть поле, в которое заносится степень приспособленности особи. У нас это количество оставшихся после взрыва черных точек.
publicList<Explosion>Explosions = newList<Explosion>();
public double Fitness = Double.MaxValue;
Первое поколение генерируется случайным образом при помощи статического
метода GenerateRandom:
public static Individual GenerateRandom(TaskSpecification spec)
{
var result = new Individual();
for (int i = 0; i < spec.ExplositionsNumber; ++i)
result.Explosions.Add(Explosion.GenerateRandom(spec));
return result;
}
Теперь рассмотрим реализацию генетических операторов. Мутация проста. Произвольная точка решения заменяется случайным образом. Для нашего случая этого хватает, но для большого количества точек (сто, тысячи взрывов) может понадобиться расширить реализацию, чтобы единомоментно могло изменяться большее количество точек.
public void Mutate(TaskSpecification spec)
{
Explosions[rnd.Next(Explosions.Count)] =
Explosion.GenerateRandom(spec);
}
Более длинным является код пространственного кроссовера.
public void SpatialCrossoverWith(Individual parent2,
TaskSpecification spec)
{
float x0 = (float)(rnd.NextDouble() * spec.Bound.Width
+ spec.Bound.Width);
float y0 = (float)(rnd.NextDouble() * spec.Bound.Height
+ spec.Bound.Height);
float radius = (float)(rnd.NextDouble()
* Math.Max(spec.Bound.Width, spec.Bound.Height));
List<Explosion> newGenome = new List<Explosion>();
bool[] used1 = new bool[spec.ExplositionsNumber];
bool[] used2 = new bool[spec.ExplositionsNumber];
bool[] deleted = new bool[spec.ExplositionsNumber * 2];
// Добавляем точки из первого решения
for (int i = 0; i < spec.ExplositionsNumber; ++i)
{
Explosion sp = this.Explosions[i];
if (radius > Math.Abs(sp.X - x0) + Math.Abs(sp.Y - y0))
{
newGenome.Add(sp.Clone());
used1[i] = true;
}
}
// Добавляем точки из второго решения
for (int i = 0; i < spec.ExplositionsNumber; ++i)
{
Explosion sp = parent2.Explosions[i];
if (radius <= Math.Abs(sp.X - x0) + Math.Abs(sp.Y - y0))
{
newGenome.Add(sp.Clone());
used2[i] = true;
}
}
// Приводим количество точек нового решения к необходимому
if (newGenome.Count > spec.ExplositionsNumber)
{
// Удаляем лишние точки
int num = newGenome.Count - spec.ExplositionsNumber;
for (int i = 0; i < num; ++i)
{
int delNum;
do
{
delNum = rnd.Next(newGenome.Count);
}
while (deleted[delNum]);
deleted[delNum] = true;
}
List<Explosion> tmpGenome = new
List<Explosion>(spec.ExplositionsNumber);
for (int i = 0; i < newGenome.Count; ++i)
if (!deleted[i])
tmpGenome.Add(newGenome[i]);
newGenome = tmpGenome;
}
else if (newGenome.Count < spec.ExplositionsNumber)
{
// Добавляем недостающие из первого решения
while (newGenome.Count < spec.ExplositionsNumber)
{
int addNum;
do
{
addNum = rnd.Next(spec.ExplositionsNumber);
}
while (used1[addNum]);
used1[addNum] = true;
newGenome.Add(this.Explosions[addNum]);
}
}
// Копируем полученное решение в геном первого родителя
Explosions = newGenome;
}
Здесь мы видим все те шаги, которые были описаны для пространственного кроссовера. Но есть и особенность. При добавлении точек из предков,
расстояние до точки мы измеряем в пространстве \(L_{1}\) (метрика улиц). Это можно заметить, проанализировав фрагмент
radius>Math.Abs(sp.X - x0) +Math.Abs(sp.Y - y0).
Принципиально это ничего не меняет, просто из пространства родителей будут вырезаться квадраты (повернутые на 45 градусов), а не окружности.
Также, при первоначальном тестировании примера, оказалось, что после первоначального прогресса и нахождения наиболее перспективных конфигураций
решений, далее идет крайне медленный процесс адаптации полученных решений, в основном за счет мутации. Но мутация, в том виде, в котором она была
приведена выше, является достаточно грубым средством - ведь вместо одного взрыва получаем случайным образом другой. И вероятность того, что он лишь
слегка подкорректирует предыдущий, очень мала. Поэтому в пример был добавлен еще один оператор, названный степпингом (Stepping). Фактически это тоже
мутация, но мягкая, которая лишь немного смещает взрыв, к которому она применяется:
public void Stepping(TaskSpecification spec)
{
int indexOfChange = rnd.Next(Explosions.Count);
float shiftX = (float)((rnd.NextDouble() - 0.5) *
spec.KillingRadius * 0.25);
float shiftY = (float)((rnd.NextDouble() - 0.5) *
spec.KillingRadius * 0.25);
Explosion explosition = Explosions[indexOfChange];
explosition.X = Limit(explosition.X + shiftX, spec.Bound.Left,
spec.Bound.Right);
explosition.Y = Limit(explosition.Y + shiftY, spec.Bound.Top,
spec.Bound.Bottom);
}
private float Limit(float x, float min, float max)
{
if (x < min)
return min;
if (x > max)
return max;
return x;
}
Один шаг ГА выглядит следующим образом (файл MainForm.cs, там же можно поменять вероятности применения генетических операторов и другие настройки
алгоритма):
private List<Individual> NewGeneration(List<Individual> generation)
{
var result = new List<Individual>(GenerationSize);
if (UseElitism)
result.Add(generation[0].Clone());
while (result.Count < GenerationSize)
{
Individual parent1 = GetTournamentResult(generation);
Individual newIndividual = parent1.Clone();
if (rnd.NextDouble() < CrossoverProb)
{
Individual parent2 = GetTournamentResult(generation);
newIndividual.SpatialCrossoverWith(parent2, spec);
}
if (rnd.NextDouble() < MutationProb)
newIndividual.Mutate(spec);
if (rnd.NextDouble() < SteppingProb)
newIndividual.Stepping(spec);
result.Add(newIndividual);
}
return result;
}
Посмотрим, что у нас получилось. Изначально на изображении 5910 черных пикселов, которые мы и
должны максимально "накрыть взрывами".

Исходная область для поражения.
Радиус области поражения - 12 пикселов, количество взрывов - 10. Размер
популяции - 1000 особей. Использовался элитизм, турнирный отбор из 500
лучших особей. Вероятность применения пространственного кроссовера - 0.4,
мутации - 0.1, степпинга - 0.3. Конечно же, при каждом запуске результаты
будут несколько отличаться - ведь мы имеем дело с вероятностным процессом.
Работа с программой происходит следующим образом - запускаем приложение, загружаем нужную картинку (кнопка "Loadsample"), запускаем эволюцию
(нажимаем кнопку "Start"). Текущий результат эволюции отражается в главном окне программы, а промежуточные результаты записываются в том же каталоге,
из которого была загружена картинка (файл с таким же именем и расширением TXT, а также png-картинки).
 |
 |
 |
 |
 |
| лучший представитель нулевого (случайного) поколения. Качество 3435. |
лучший представитель 5-го поколения. Качество 3170. |
лучший представитель 20-го поколения. Качество 2688. |
лучший представитель 100-го поколения. Качество 2214. |
лучший представитель 500-го поколения. Качество 2153. |
Результаты применения эволюционного алгоритма.
В приведенном примере мы показали лишь одну из возможных адаптаций ГА к практике. Природа является только первоначальным образцом для подражания, но мы не обязаны копировать все детали. Достаточно соблюдать только базовые принципы и руководствоваться здравым смыслом. Перечислим некоторые принципы, позволяющие добиться более быстрой сходимости процесса эволюции, либо улучшить качество исследования предметной области:
| Ускорение сходимости решения | Улучшение качества работы (поисковые способности) ГА |
|---|
- Увеличение прессинга естественного отбора
- Уменьшение количества особей, допускаемых к размножению
- Использование элитизма
- Уменьшение общего количества генерируемого потомства
- Выполнение алгоритма параллельно на нескольких компьютерах (процессорах)
|
- Уменьшение прессинга естественного отбора
- Увеличение объема генетического материала
- Диплоидия (также увеличивает количество генетического материала)
- Разбиение популяции на части. Это также является и способом легко распараллелить алгоритм
|
Генетическое программирование.
Рассмотренный выше генетический алгоритм, работал с закодированной в генах информацией. Что это за информация, в общем-то, не важно.
Это вполне могут быть и команды какой-то вычислительной машины - программа, а качество получаемой особи будет зависеть от того, насколько
хорошо эта программа выполняет поставленную задачу. Основным минусом будет то, что длина программы будет фиксирована.
Да и классические генетические операторы не способствуют высокой вероятности появления работоспособных потомков.
Поэтому для эволюционного составления программ были разработаны иные (по сравнению с ГА) методы хранения генома и других реализации генетических
операторов. Хронологически, первой формой, была древообразная форма хранения генома, предложенная Н.Крамером и Дж.Коза.
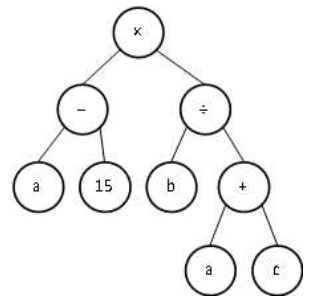
Алгоритм вычисления значения функции \((a-15)(b/(a+c))\), представленный в виде дерева.
В качестве других форм, которые также часто используются, можно назвать
линейную и сетевую (или графовую) формы.
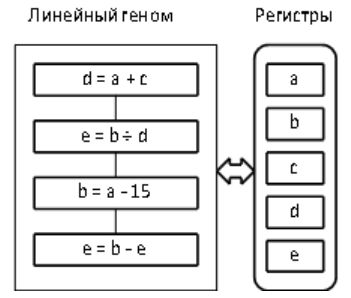
Алгоритм значения функции \((a-15)(b/(a+c))\), представленный в линейном виде (код какого-то виртуального процессора).
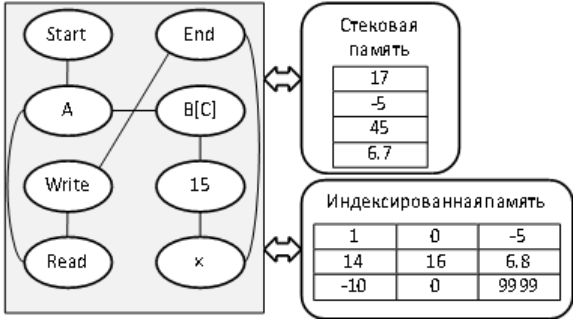
Геном небольшой программы для виртуального процессора, представленный в сетевом (графовом) виде.
Операция мутации, в случае генетического программирования (ГП), похожа на аналогичную операцию у ГА, но добавляется разнообразие изменений,
которые она может внести в геном. Для линейного генома, например, к случайному изменению произвольной команды, добавляются операции вставки
случайной команды или удаления в случайном месте.
Несколько сложнее также выглядит и операция обмена генетическим материалом у предков - кроссовер, хотя основной принцип остается тем же -
берется часть генома одного родителя и часть второго. Приведем примеры кроссовера для линейного и древовидного представления генома.
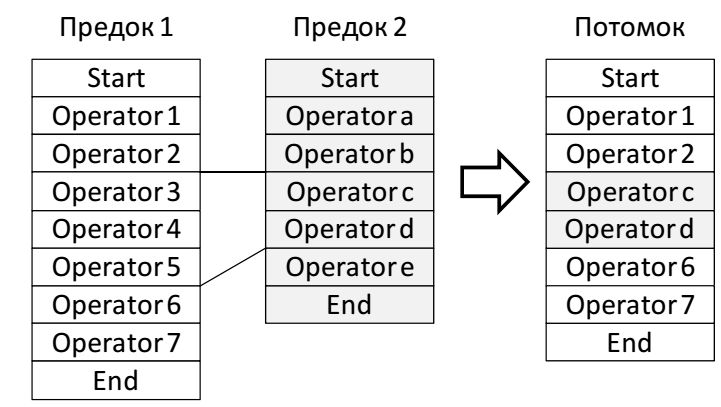
Кроссовер для линейного представления генома.
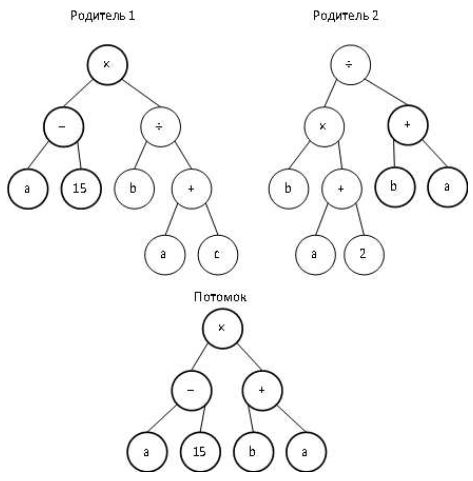
Кроссовер при древовидном представлении генома.
Операция кроссовера чрезвычайно разрушительна для обычных программ и подавляющее количество потомков после такой операции становятся
нежизнеспособными. Поэтому, в систему команд часто вводят необычные операции, например, перехода по комплементарным меткам,
автоопределяемые функции (ADF), и много других усовершенствований.
Сами программы также "борятся" с тем, что их разрушает. Например, путем увеличения количества интронов - кусков кода, которые содержат ничего не
делающие операции:
(NOT (NOT X))
(AND \ldots (OR X X))
(+ \ldots (- X X))
(+ X 0)
(* X 1)
(* \ldots (DIV X X))
(MOVE-LEFT MOVE-RIGHT)
(IF (2=1) \ldots X)
(A := A)
Такой способ защиты (как и дублирование самых важных участков генома) не является изобретением ГП.
Похожие механизмы имеются и в геномах обычных клеток. Рассмотрение всех тонкостей генетического программирования может послужить темой
отдельной книги (и не одной). Поэтому предложим заинтересованному читателю далее изучать данное направление по специализированной литературе.
А ниже мы рассмотрим относительно простой пример поиска решения для генома переменной длины.
To be, or not to be...
Как говорилось в известном советском фильме - "друзья, а не замахнуться ли
нам на Вильяма нашего Шекспира?" Попробуем и мы погреться в лучах славы
бессмертных. Причем способом, который наверняка бы оценил Джонатан
Свифт. (Имеется в виду произведение "Путешествия Гулливера", в
котором описывается изобретатель, построивший машину, выдававшую случайные
сочетания всех существующих слов. Осмысленные же предложения записывались,
чтобы составить полную энциклопедию всех наук и искусств. Конечно же, Свифт
в данном случае критиковал данное направление - но он тогда ничего не знал
о генетическом программировании.).
Рассмотрим следующую задачу. Нам необходимо отгадать некоторую фразу. Для
того, чтобы узнать, отгадали мы фразу или нет, мы показываем любую строку, а
нам говорят число (фитнесс-функцию), которая представляет собой разность
количества букв, которые стоят на своих местах, с теми, что занимают не свою
позицию:
\[
f(a,b) = \sum\limits_{i = 0}^{\max \left( {length\left( a \right),length(b)}
\right) - 1} {c(a,b,i),}
\]
\[
c(a,b,i) = \left\{ {{\begin{array}{*{20}c}
{1,} \hfill & {i \lt length(a) \cap i \lt length(b) \cap a[i] = b[i],} \hfill
\\
{ - 1,} \hfill & {\mbox{иначе.}} \hfill \\
\end{array} }} \right.
\]
Здесь a - строка-образец. Она известна только вычислителю фитнесс-функции, b - строка, которую мы предъявили для оценки,
length() - функция, вычисляющая длину переданной строки. Индексация символов начинается с нулевой позиции.
Имея только такие скудные данные и приблизительный размер текста, попробуем отгадать фразу из бессмертного произведения.
А именно, монолог Гамлета, начало которого вынесено в заголовок данной главы.
Приложение SimpleGP) является консольным, все данные и настройки забиты в код, поэтому для того, чтобы их поменять, нужно использовать IDE и
перекомпилировать программу. Начнем с точки входа в программу - файл Program.cs:
classProgram
{
static void Main(string[] args)
{
GPWorld world = new GPWorld();
for (int g = 0;
world.Generation[0].Genome != GPWorld.SecretPattern; ++g)
{
WriteWorldState(g, world);
world.Next(true);
}
WriteWorldState("last", world);
Console.WriteLine("The solution found!");
Console.ReadLine();
}
private static void WriteWorldState(object generation, GPWorld
world)
{
Console.WriteLine("Best individual {0}:", generation);
Console.WriteLine(" Genome=" + world.Generation[0].Genome);
Console.WriteLine(" Length=" + world.Generation[0].Genome.Length);
Console.WriteLine(" Fitness=" + world.Generation[0].Fitness);
Console.WriteLine("----------");
}
}
Метод Main включает в себя генерацию нулевого поколения и основной цикл -
генерацию новых поколений. Цикл прерывается тогда, когда будет найдена
точная фраза - она хранится в константеSecretPattern класса GPWorld. Но
это место хранения выбрано только для упрощения примера. На самом деле,
исходный текст может храниться где угодно, хоть на другом компьютере.
Главное, чтобы была возможность выполнить с ним две операции: сравнение (как
условие окончания цикла) и оценку похожести (вычисление fitness-функции).
Метод WriteWorldState выводит на консоль лучшего представителя текущей
популяции.
В классе Program) используются еще два класса - Individual (инкапсулирует
особь) и GPWorld (инкапсулирует популяцию и операции над ней и отдельными
особями). Рассмотрим их подробнее. Individual.cs:
public class Individual
{
public string Genome = "";
publicdoubleFitness = 0;
}
Класс прост - в своих полях он хранит только геном (строку) и кешированное
значение fitness-функции (в основном для сортиртировки особей в популяции).
Основная логика генетических операций сосредоточена в файле GPWorld.cs:
publicclassGPWorld
{
privatestaticchar[] _possibleLetters =
"abcdefghijklmnopqrstuvwxyz' ABCDEFGHIJKLMNOPQRSTUVWXYZ,;.-?
\(\backslash
\(r$\backslash \(n".ToCharArray();
private Random _rnd = new Random();
private StringBuilder _sb = new StringBuilder();
Имеет смысл прокомментировать перечисленные выше поля.
Поле _possibleLetters задает перечень возможных символов, которые нам
могут встретиться в искомой фразе. В данном случае мы ограничились
английским алфавитом, знаками препинания, пробелом и переводом строки. Поля
_rnd и _sb хранят объекты, которые не хочется создавать каждый раз -
на это тратятся ресурсы процессора (выделить память, освободить память). В
данном случае это небольшая оптимизация, рассчитанная на то, что программа
выполняется в однопоточном режиме.
public const string SecretPattern =
@"To be, or not to be, that is the question;
...
Здесь мы сократим многострочный строковый литерал. Полностью его можно
увидеть в исходных файлах, прилагаемых к книге, либо можно просто запустить
программу и дождаться её окончания.
...
And lose the name of action.";
public List Generation;
public const int GenerationSize = 100000;
public const double CrossoverProbability = 0.4;
public const double MutationProbability = 0.2;
Именно этот блок констант служит для настройки параметров примера.
publicGPWorld()
{
Generation = GenerateRandomGeneration();
SortGeneration(Generation);
}
Конструктор генерирует новую случайную популяцию, после чего она сортируется
по убыванию fitness-функции.
private void SortGeneration(List<Individual> generation)
{
generation.Sort((y, x) => x.Fitness.CompareTo(y.Fitness));
}
private List<Individual> GenerateRandomGeneration()
{
List<Individual> result = new List<Individual>();
for (int i = 0; i < GenerationSize; ++i)
{
int length = _rnd.Next(1, SecretPattern.Length * 2);
_sb.Length = 0;
for (int l = 0; l < length; ++l)
{
_sb.Append(RandomPossibleChar());
}
result.Add(new Individual()
{
Genome = _sb.ToString(),
}
);
result[i].Fitness = CalcFitness(result[i].Genome);
}
return result;
}
Вспомогательный метод RandomPossibleChar() выполняет то, что и сказано в его
названии - возвращает случайно выбранный символ из числа возможных.
private char RandomPossibleChar()
{
return
_possibleLetters[_rnd.Next(_possibleLetters.Length)];
}
Метод CalcFitness() вычисляет fitness-функцию в соответствии со словесным
описанием, заданным нами в начале раздела.
public double CalcFitness(string genome)
{
double result = 0;
int maxLength = Math.Max(SecretPattern.Length, genome.Length);
int minLength = Math.Min(SecretPattern.Length, genome.Length);
for (int i = 0; i < maxLength; ++i)
{
if (i >= minLength){
result -= 1;}
else if (genome[i] != SecretPattern[i]){
result -= 1;
else{
result += 1;
}
}
return result;
}
Метод Next() выполняет генерацию нового поколения. Принимаемый параметр
булевого типа указывает, используется ли стратегия элитизма. Если
используется - один самый лучший экземпляр предыдущего поколения
гарантированно переходит в следующее без изменений. Отбор производится
турнирным методом из представителей наиболее приспособленной половины
популяции. Таким образом, несколько усиливается давление отбора.
public void Next(booluseElitism)
{
List<Individual> newGeneration = new List<Individual>();
if (use Elitism)
newGeneration.Add(Generation[0]);
while (newGeneration.Count<GenerationSize)
{
// Tурнирный выбор предков из более приспособленной половины
int parent1a = _rnd.Next(GenerationSize / 2);
int parent1b = _rnd.Next(GenerationSize / 2);
int parent2a = _rnd.Next(GenerationSize / 2);
int parent2b = _rnd.Next(GenerationSize / 2);
int parent1 = Math.Min(parent1a, parent1b);
int parent2 = Math.Min(parent2a, parent2b);
string newGenome = (_rnd.NextDouble() < CrossoverProbability)
Crossover(Generation[parent1].Genome,
Generation[parent2].Genome) :
Generation[parent1].Genome;
if (_rnd.NextDouble() < MutationProbability)
newGenome = Mutate(newGenome);
Individual individual = new Individual()
{
Genome = newGenome,
};
individual.Fitness = CalcFitness(individual.Genome);
newGeneration.Add(individual);
}
SortGeneration(newGeneration);
Generation = newGeneration;
}
Метод Mutate() с равной вероятностью выполняет операции вставки случайного
символа, удаления или замены.
private string Mutate(string genome)
{
// Случайная вставка
if (_rnd.NextDouble() < 0.33)
{
int pos = _rnd.Next(genome.Length + 1);
_sb.Length = 0;
for (int i = 0; i < pos; ++i)
_sb.Append(genome[i]);
_sb.Append(RandomPossibleChar());
for (int i=pos; i<genome.Length; ++i)
_sb.Append(genome[i]);
genome = _sb.ToString();
}
// Случайное удаление
if (genome.Length > 0 {\&}{\&} _rnd.NextDouble() < 0.33)
{
int pos = _rnd.Next(genome.Length);
genome = genome.Remove(pos, 1);
}
// Случайное изменение
if (genome.Length > 0 {\&}{\&} _rnd.NextDouble() < 0.33)
{
int pos = _rnd.Next(genome.Length);
_sb.Length = 0;
for (int i = 0; i < genome.Length; ++i)
if (i != pos)
_sb.Append(genome[i]);
else
_sb.Append(RandomPossibleChar());
genome = _sb.ToString();
}
return genome;
}
Операция кроссовера похожа на одноточечный кроссовер у обычного ГА, но приспособлена для обработки геномов переменной и неравной длины.
Результирующий геном имеет длину, равную genome1. Если второй геном оказывается короче, то к строке добавляются случайные символы из
множества допустимых. Если длиннее - то используется только часть символов в пределах длины первого генома.
private string Crossover(stringgenome1, stringgenome2)
{
int pos = _rnd.Next(genome1.Length);
_sb.Length = 0;
for (int i = 0; i < genome1.Length; ++i)
if (i > pos)
_sb.Append(genome1[i]);
else
if (i < genome2.Length)
_sb.Append(genome2[i]);
else
_sb.Append(RandomPossibleChar());
return_sb.ToString();
}
}
В данной реализации кроссовера отсутствуют операции, которые приводят к сдвигу фрагментов строк к началу или к концу.
Это связано с тем, что оценочная функция оценивает только символы, точно попавшие в свою позицию.
Поэтому любые сдвиги приведут практически в каждом случае к тому, что геном будет "испорчен". Подобные операции можно реализовать самостоятельно
вместе с модификацией fitness-функции. В этом случае fitness-функция должна добавлять очки геному, если в нем имеются общие с образцом подстроки,
пусть даже они стоят не на своих местах.
Итак, у нас все готово для запуска. Запускаем программу и наблюдаем за работой алгоритма. Здесь приведем фрагменты работы:
Поколение 0:
Genome=EA-B;-gOcLaRGGhjaQonoAFaHWz
S?QlBBQs;UaoUIpGBUJYLoUeUpd-.eEh?g.XqfYWpoPaLm
...
;u,sW.rAFbkYs
Length=1409
Fitness=-1350
Поколение 500
Genome=TE be, or notGto b?, tpan .' Ghe eBeJtiln;
WhetRer Vpis irblgrBgT tfekqi dxto iuWdIrw
The SliJ?sLaIn Ao
...
ADd losG theonCme of a-tikn.
Length=1442
Fitness=182
Поколение 1000:
Genome=To be, or not to be, that is the qBestion;
Whether 'tis nobler in the mind to sufder
The Slings ann Arrmws of outrageous
...
ADd lose the name of action.
Length=1442
Fitness=1066
Поколение 1426:
Genome=To be, or not to be, that is the question;
Whether 'tis nobler in the mind to suffer
The Slings and Arrows of outrageous Fortune
...
And lose the name of action.
Length=1442
Fitness=1442
Интеллект стаи.
Многие методики, относящиеся к мягким вычислениям, эксплуатируют идею того,
что множество относительно простых объектов, работающих по вполне понятным
правилам, объединяясь, демонстрируют поведение, намного превышающее по
интеллектуальности поведение отдельного индивидуума. Сюда можно отнести и
нейронные сети и эволюционные алгоритмы. Про нейронные сети в данном пособии
мы подробно рассказывать не будем - о них нужно говорить либо много (что
выливается в отдельный курс), либо ничего. К счастью, теория нейронных сетей
проработана и описана достаточно хорошо для читателя любого уровня, поэтому
при желании несложно найти именно то учебное пособие, которое позволит
вникнуть в данную тематику более глубоко. С эволюционными алгоритмами мы
познакомились в предыдущем разделе. Но, видимо, наиболее ярко и явно идея
суммирования индивидуальных интеллектов, воплощается в таком направлении
исследований, как "Интеллект стаи" (swarm intelligence).
Не хотелось бы давать какое-то скучное определение направления, поэтому
давайте познакомимся с ним, используя фрагмент фантастического произведения
Станислава Лема - "Непобедимый".
Небольшая преамбула. Большой космический корабль землян "Непобедимый"
садится на планету, которая кажется безжизненной. Обнаружены только очень
простые "растения" и "насекомые" на основе полупроводников и металлов.
Но постепенно начинают происходить странные вещи - люди теряют память,
погибают, технике кто-то наносит сильнейшие удары. Начинается более
подробное изучение "простейших":
"Пленники" занимали во времясовещаниях почетное место в закрытом стеклянном сосуде, стоявшем посреди стола. Их осталось всего десятка полтора, остальные были уничтожены в процессе изучения. Все эти создания обладали тройственной симметрией и напоминали формой букву Y, с тремя остроконечными плечами, соединяющимися в центральном утолщении...
Каждый кристаллик соединялся с тремя; кроме того, он мог соединяться концом плеча с центральной частью любого другого, что давало возможность образования многослойных комплексов. Соединение не обязательно требовало соприкосновения, кристалликам достаточно было сблизиться, чтобы возникшее магнитное поле удерживало все образование в равновесии...
Кроме цепи, заведующей такими движениями,каждый черный кристаллик содержал в себе еще одну схему соединений, вернее ее фрагмент,так как она, казалось, составляла часть какой-то большой структуры. Это высшее целое, вероятно возникающее только при объединении огромного количества элементов, и было истинным мотором, приводящим тучу в действие. Здесь, однако, сведения ученых обрывались. Они не ориентировались в возможностях роста этих сверхсистем, и уж совсем темным оставался вопрос об их "интеллекте". Кронотос допускал, что объединяется тем больше элементарных единиц, чем более трудную проблему им нужно решить. Это звучало довольно убедительно, но ни кибернетики, ни специалисты по теории информации не знали ничего соответствующего такой конструкции, то есть "произвольно разрастающемуся мозгу", который свои размеры примеряет к величине намерений.
Часть принесенных Роханом "насекомых" была испорчена. Остальные демонстрировали типовые реакции. Единичный кристаллик мог подпрыгивать, подниматься и висеть в воздухе почти неподвижно, опускаться, приближаться к источнику импульсов либо удаляться от него. При этом он не представлял абсолютно никакой опасности, не выделял, даже при угрозе уничтожения. \ldots Зато объединившись даже в сравнительно небольшую систему, "насекомые" начинали, при воздействии на них магнитным полем, создавать собственное поле, которое уничтожало внешнее, при нагревании стремились избавиться от излишка тепла инфракрасным излучением - а ведь ученые располагали лишь маленькой горсточкой кристалликов.
Чем закончилось противостояние людей и этой интеллектуальной стаи, описывать
не будем - если вас заинтересовало само произведение, прочтите его. Оно
того стоит. Нас же оно заинтересовало как описание практически идеальной
системы "интеллекта стаи".
Почему это направление так привлекает исследователей? Наверное, потому, что
в окружающем мире все мы видим примеры таких "интеллектов":
Животные (человек как высшее проявление) - уже понятно, что за все очень
сложное поведение отвечает система относительно простых (но все еще не до
конца изученных) элементов, нейронов.
Группы ученых чаще всего могут решать более сложные в интеллектуальном
отношении задачи, чем одиночки. Хотя, очень часто здесь происходит не
параллельное объединение, а последовательное - научные школы,
учителя-ученики.
Производство компьютеров (и любой сложной современной техники) - рискнем
утверждать, что ни один из ныне живущих людей не знает полностью цикл
производства компьютера во всех деталях. Начиная с добычи нефти для
производства пластика и металла для производства проводов, заканчивая
вопросами дизайна рекламных буклетов для магазинов. Тем не менее, множество
людей, объединяясь, успешно производят и продают всю эту технику.
Муравьи и пчелы - рой пчел или муравьиная стая для стороннего наблюдателя
производят впечатление чего-то гораздо более интеллектуального, чем
отдельные особи. Например, когда наблюдается процесс поиска пищи и
оптимизация пути, по которому муравьи приносят найденное в муравейник.
Именно последний пример моделируется в "Муравьиных алгоритмах", на примере
которых мы хотим раскрыть направление Интеллекта Стаи.
Оригинальный алгоритм (AntColonyOptimization) возник в процессе наблюдения
за тем, как живые муравьи вида ArgentineAnt обследуют территорию вокруг
муравейника, находят пищу и несут её в муравейник, постоянно оптимизируя
(сокращая) путь, который проходит каждый из муравьев. Эти исследования
проводились в 1989-м году Госсом и в 1990-м Денеборгом. Первая
математическая формализация алгоритма предложена в 1992-м году Марко Дориго.
Живые муравьи во время поисков пищи ходят вокруг муравейника случайным
образом по тропам, которые не являются физическими дорожками,
"протоптанными" поколениями насекомых. Основная ориентация у муравьев
происходит за счет феромонов, к которым они очень чувствительны и которыми
они помечают все вокруг. Более того, каждый муравейник имеет свой
индивидуальный запах и муравей того же вида но из другого муравейника, будет
воспринят как враг. Существуют слепые муравьи, которые в пространстве
ориентируются только за счет запаха и осязания.
Найдя пищу, муравей-разведчик возвращается домой, используя одну из троп.
При этом весь его путь помечается особым феромоном. По возвращении в
муравейник, этот муравей "зовет" (назовем это действие таким образом,
чтобы не усложнять описание) за собой других, рабочих муравьев, и начинается
процесс переноса пищи в муравейник.
Рабочие муравьи идут, ориентируясь на запах, оставленный
муравьем-разведчиком. При этом, они усиливают запах, оставляя свои следы на
дорожке в том случае, если находят пищу. Таким образом, тропинки становятся
все более и более заметными. Но они не всегда идут одним и тем же путем -
иногда муравьи сбиваются с пути и тогда случайным образом ищут место,
помеченное феромоном. Иногда это приводит к нахождению более короткого пути.
Также, в это время происходит процесс испарения феромонов. Если бы его не
было, то первоначальный путь всегда имел бы самый сильный запах и процесс
поиска более короткого пути не происходил бы.
Представим этот процесс графически.
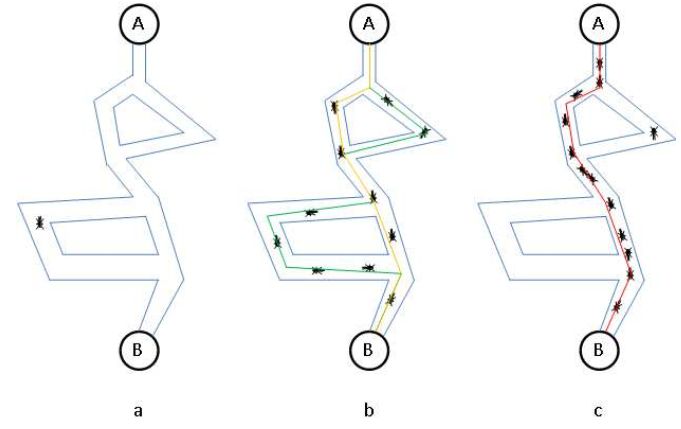
Процесс оптимизации пути при переносе найденной пищи (А) в муравейник (В).
На иллюстрации
a) муравей разведчик находит еду, после чего произвольным путем возвращается домой.
b) - рабочие муравьи переносят пищу в муравейник, прокладывая феромонные
тропы. По более короткому пути муравьи успевают пройти в большем количестве,
поэтому постепенно этот путь становится все более "пахнущим".
c) - большая часть муравьев движется по самому короткому пути и только
отдельные особи используют другие пути.
Опишем простейший муравьиный алгоритм более формально. Лабиринт задан графом
(вершины и ребра). Считаем, что муравьи ищут оптимальный путь (самый
короткий) между двумя вершинами (муравейник и еда).
Пока (не выполнены условия выхода)
- Создаем муравьев.
- Муравьи ищут решения.
- Обновление уровня феромона.
Рассмотрим каждый из шагов цикла более подробно.
- Начальные точки, куда помещаются муравьи, зависят от ограничений задачи. В простейших случаях, мы можем их всех поместить в одну точку, либо случайно распределить по площади лабиринта. На этом же этапе каждое ребро лабиринта помечается небольшим положительным числом, характеризующим запах феромона. Это нужно для того, чтобы на следующем шаге у нас не было нулевых вероятностей.
- Определяем вероятность перехода из вершины i в вершину j по следующей формуле:
\[
P_{i,j} (t) = \frac{\tau _{i,j} (t)^\alpha \left( {d_{i,j} } \right)^{ -
\beta }}{\sum\nolimits_{j \in connected\mbox{ nodes}} {\tau _{i,j}
(t)^\alpha \left( {d_{i,j} } \right)^{ - \beta }} }.
\]
Здесь \(\tau _{i,j} (t)\) - уровень феромона, \(d_{i,j}\) - эвристическое расстояние, \(\alpha ,\beta \) - константы.
Если \(\alpha =0\), то наиболее вероятен выбор ближайшего соседа, и алгоритм становится "жадным".
В случае \(\beta =0\), наиболее вероятен выбор только на основе уровня феромона, что приводит к застреванию на уже "протоптанных" путях.
Как правило, используется некоторое компромиссное значение этих величин, подбираемое экспериментально для каждой задачи.
- Обновление уровня феромона производится следующим образом:
\[
\tau _{i,j} (t + 1) = (1 - \rho )\tau _{i,j} (t) + \sum\nolimits_{k \in
usededge(i,j)} {\frac{Q}{L_k (t)}.}
\]
Здесь \(\rho \)- параметр, задающий интенсивность испарения, \(L_k (t)\)- цена текущего решения для \(k\)-го муравья, а \(Q\) характеризует
порядок цены оптимального решения. Таким образом, выражение \(\frac{Q}{L_k (t)}\) определяет количество феромона, которым \(k\)-й муравей
пометил ребро \((i,j)\).
Задача коммивояжера и муравьиный алгоритм.
Чтобы проверить способность муравьиных алгоритмов решать серьезные задачи,
часто используют известную задачу коммивояжера - есть набор городов, которые
должен посетить коммивояжер, побывав в каждом из них по одному разу и
вернувшись в тот город, из которого путешествие было начато. Задачей здесь
является оптимизация пути таким образом, чтобы пройденное расстояние было
наименьшим. Это одна из самых простых постановок задачи и именно её мы
попробуем решить.
Задачи, связанные с графами, неудобно показывать в консоли, поэтому для этой
задачи мы выберем обычное приложение WinForms. Читатель может самостоятельно
изменить, откомпилировать, запустить пример, взяв проект из приложения к
данному курсу. Но вся логика сосредоточена в файле AntOptimizer.cs, его и
рассмотрим подробнее.
Прежде всего, в классе AntOptimizer определены два класса - обертки, не несущие особого функционала:
public class AntOptimizer
{
class Town
{
public double X {set; get; }
public double Y {set; get; }
}
class RouletteSector
{
public double Start = 0;
publicintTown = -1;
}
Класс Town хранит координаты "городов", а RouletteSector используется при
имитации рулетки с секторами разного размера.
Далее идут определения приватных полей.
_towns - список городов.
_distanses - таблица расстояний между городами, чтобы не нужно было их
вычислять каждый раз. Но, в принципе, при недостатке памяти, вполне может
быть заменена функцией, вычисляющей эти значения на лету.
Town[] _towns = null;
Random _rnd = new Random();
double[,] _distanses = null;
double[,] _scents = null;
double GetScent(int town1, int town2)
{
return _scents[Math.Min(town1, town2), Math.Max(town1, town2)];
}
void AddScent(int town1, int town2, double scent)
{
_scents[Math.Min(town1, town2), Math.Max(town1, town2)] +=scent;
}
Таблица, хранящая феромонные пометки (запах) - _scents, используется не полностью, а только нижняя треугольная часть
(если первый индекс принять за \(x\), а второй за \(y\) координаты). Поэтому введены вспомогательные методы GetScent и AddScent,
которые приводят индексы в нужный порядок.
Далее следуют описания публичных полей, которые используются для вывода числовых результатов в GUI.
Функции полей соответствуют их названиям.
publicAntBestWay = null;
publicdoubleBestWayLength = Double.MaxValue;
publicintStepCount = 0;
Конструктор. Имеет 3 основных функциональных блока (не считая проверки входящих параметров).
Прежде всего, инициализируется случайными значениями список координат городов. Координаты мы берем из промежутка \(0\ldots 1\).
Выбор диапазона для алгоритма не важен - просто нам так удобнее.
Далее, инициализируются таблицы расстояния между городами и таблица запахов.
Таблицу запахов мы инициализируем отличными от нуля значениями, чтобы начальная вероятность выбора той или иной дорожки была положительной.
public AntOptimizer(int townNumber)
{
// Проверяем параметры.
if (townNumber < 3)
throw new ArgumentOutOfRangeException("townNumber", townNumber,
"'townNumber' should be more then 2");
// Инициализируем города случайными координатами.
_towns = newTown[townNumber];
for (int t = 0; t < townNumber; ++t)
{
_towns[t] = new Town()
{
X = _rnd.NextDouble(),
Y = _rnd.NextDouble()
};
}
// Заполняем таблицу расстояний между городами.
_distanses = new double[townNumber,townNumber];
for (int t1 = 0; t1 < townNumber; ++t1)
{
Town town1 = _towns[t1];
for (int t2 = 0; t2 < townNumber; ++t2)
{
Town town2 = _towns[t2];
_distanses[t1, t2] = Math.Sqrt(Sqr(town1.X -
town2.X) + Sqr(town1.Y - town2.Y));
}
}
// Инициализируем таблицу запахов.
_scents = new double[townNumber, townNumber];
for (int i = 0; i < townNumber; ++i)
for (int j = i + 1; j < townNumber; ++j)
_scents[i, j] = 1.0;
}
Метод Step несет в себе логику одного шага оптимизации при помощи
муравьиного алгоритма. Из каждого города пускается по муравью, которые
обходят все города, ориентируясь по феромонным следам и модифицируя их.
public void Step(double alpha, double beta, double q)
{
StepCount++;
int townNumber = _towns.Length;
// По очереди пускаем муравьев. Проверяем, какой маршрут наилучший.
for (int a = 0; a < townNumber; ++a)
{
Ant ant = new Ant(this, a);
double wayLength = ant.Move(alpha, beta, q);
if (wayLength < BestWayLength)
{
BestWay = ant;
BestWayLength = wayLength;
}
}
// Испаряем ферромоны
for (int i = 0; i < townNumber; ++i)
for (int j = i + 1; j < townNumber; ++j)
_scents[i, j] = _scents[i, j] * 0.9;
}
Вспомогательные методы Sqr и DrawMap мы опустим - в них нет алгоритмически сложных моментов.
Последний оставшийся класс - Ant. Он инкапсулирует "поведение" отдельного муравья. Поле _pathHash, которое можно увидеть в списке
приватных полей, служит для быстрого определения, присутствует ли определенный город в списке пройденных.
Сам список, упорядоченный по порядку посещения, находится в поле Path.
public class Ant
{
private AntOptimizer _owner;
private int _townNumber = -1;
private int _startTown;
private Dictionary<int, int> _pathHash = new Dictionary<int,int>();
public List<int> Path = new List<int>();
Конструктор принимает в качестве входных параметров экземпляр класса-владельца (из которого берутся координаты городов,
расстояния между ними) и номер города, из которого необходимо стартовать процесс оптимизации.
public Ant(AntOptimizer owner, int startTown)
{
_owner = owner;
_startTown = startTown;
_townNumber = _owner._towns.Length;
}
Метод Move производит поиск пути, ориентируясь на запах и расстояния. В процессе движения производится маркировка использованных "дорожек"
свежей порцией ферромонов. В качестве параметров принимает параметры алгоритма α, β и q.
public double Move(double alpha, double beta, double q)
{
double pathLength = 0;
Path.Add(_startTown);
_pathHash.Add(_startTown, _startTown);
int currentTown = _startTown;
for (int i = 1; i < _townNumber; ++i)
{
currentTown = FindNextTown(currentTown, alpha, beta);
Path.Add(currentTown);
_pathHash.Add(currentTown, currentTown);
}
Path.Add(_startTown);
for (int i = 0; i < _townNumber; ++i)
pathLength += _owner._distanses[Path[i], Path[i + 1]];
for (int i = 0; i < _townNumber; ++i)
_owner.AddScent(Path[i], Path[i + 1], q / pathLength);
return pathLength;
}
Метод FindNextTown имитирует рулетку с неравными секторами.
private int FindNextTown(int currentTown, double alpha, double beta)
{
// Заполняем "рулетку" с неравными секторами
List<RouletteSector> rouletteSectors = new List<RouletteSector>();
double sum = 0;
for (int i = 0; i < _townNumber; ++i)
{
if (!_pathHash.ContainsKey(i))
{
rouletteSectors.Add(
new RouletteSector()
{
Start = sum,
Town = i,
});
sum +=
Math.Pow(_owner.GetScent(currentTown, i), alpha) /
Math.Pow(_owner._distanses[currentTown, i], beta);
}
}
// Выбираем на "рулетке" случайный сектор бинарным поиском
double val = _owner._rnd.NextDouble() * sum;
int a = 0; int b = rouletteSectors.Count;
while (b - a > 1)
{
int c = (a + b) / 2;
if (rouletteSectors[c].Start < val)
a = c;
else
b = c;
}
return rouletteSectors[a].Town;
}
}
Итак, мы рассмотрели код, который реализует алгоритм муравьиного алгоритма.
Посмотрим, как это выглядит графически. Запустим программу, установим
количество городов равным 100, а параметр бета равным 2. Далее следуют
скриншоты начала работы алгоритма, середина и установившийся процесс.
Поскольку при каждом запуске города имеют случайные координаты, то у
читателей будут свои картинки, отличные от приведенных.
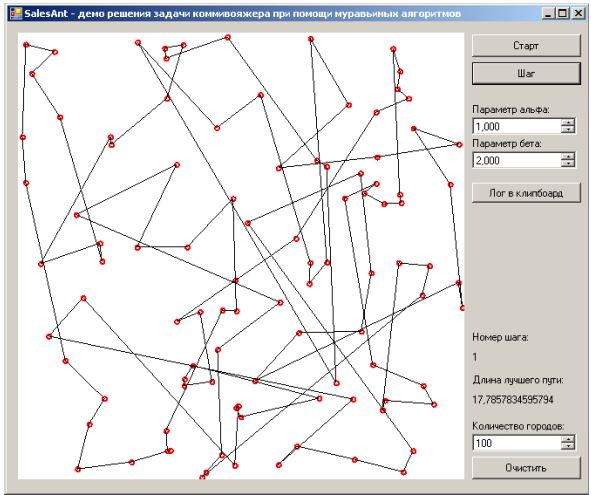
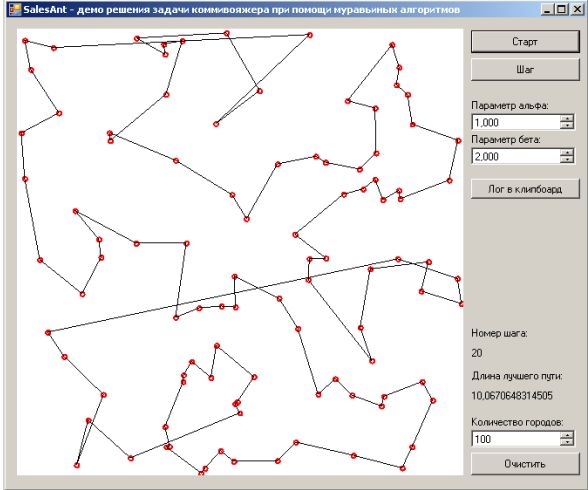
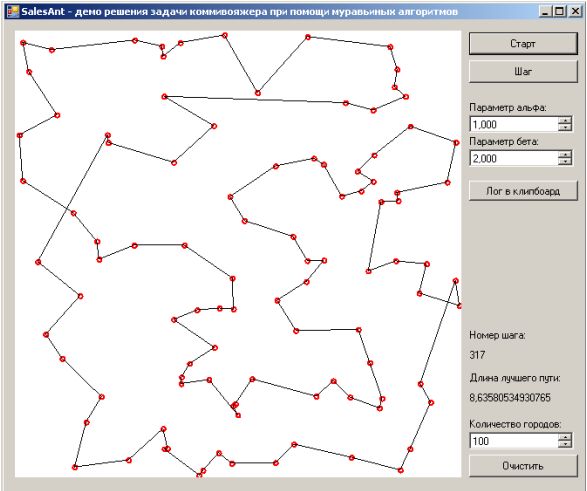
Скриншоты решения задачи коммивояжера.
Видно, что в установившемся решении есть еще петли в пути, что говорит о
некоторой неоптимальности, но она не столь велика, как вначале.
Можно поиграться с настройками алгоритма. Например, если при данном
количестве городов мы выберем параметр бета равным 10, то решение найдется
быстрее. Но поиск замрет быстрее. Также, можно попытаться убрать мелкие
петли, добавив элитных муравьев. Пробуйте! Наблюдать искусственную жизнь
всегда занятно - чувствуешь себя чуть-чуть богом...
В заключение приведем несколько интересных примеров использования генетического программирования.
и многие другие.
Задача 1.
Используя генетические алгоритмы, найти решение уравнения \(a + 2b + 3c + 4d = 30\) в целых числах.
Задача 2.
Используя ГА решить следующую задачку:
Есть 10 карточек с номерами от 1 до 10, нужно их разделить на две пачки так, чтобы сумма чисел на карточках в первой стопке была как можно ближе
к 36, а произведение со второй пачки, как можно ближе к 360.
Задача 3.
Реализовать алгоритм поведения светлячка.
Считаем, что целью вспышки света светлячка является привлечение других светлячков.
Тогда, будем считать, что
- Каждый светлячек будет привлечен ко всем другим светлячкам;
- Степень привлечения пропорциональна их яркости, и для любых двух светлячков, тот, у которого свет менее яркий будет двигаться к более яркому,
однако интенсивность света уменьшается по мере увеличения расстояния между светлячками;
- Если нет светлячков ярче, чем данный светлячок, то он будет перемещаться случайным образом.
Вспомогательная информация: интенсивность света зависит от расстояния \(r\) между светлячками - \(I(r)=\frac{I_0}{r^2}\), если \(\gamma -\)
коэффициент поглощения среды, то интенсивность света можно записать в виде \(I(r)=I_0\exp\left(-\gamma r^2\right)\), таким образом, функция привлекательности
равна \(\beta=\beta_0\exp\left(-\gamma r^2\right)\). Если светлячок \(i\) менее яркий, чем светлячок \(j\),
движение светлячка \(i\) описывается уравнением:
\(x_{ik}=x_{ik}+\beta_0\exp\left(-\gamma r^2\right)(x_{ik}-x_{jk})+\alpha S_k(rand_{ik}-0.5)\),
где \(k = 1,2,3, ... , D\) (\(D\) - размерность рассматриваемой задачи). Величина \(\alpha\) называется параметром рандомизации, \(S_k\) - параметр масштабирования над областью задачи.
Полезная литература. Книги.
- Hassanien A.E. Swarm intelligence. Principles, Advances, and Applications / A.E.Hassanien, E.Emary .— Broken Sound Parkway NW: CRC Press Taylor & Francis Group, 2016 .— 220 p.
- Venugopal K.R. Soft Computing for Data Mining Applications / K.R.Venugopal, K.Srinivasa, L.M.Patnaik .— Berlin Heidelberg: Springer-Verlag, 2009 .— 354 pp.
- Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности / [Г.К. Вороновский, К.В. Махотило,
С.Н. Петрашев, С.А. Сергеев]. – Харьков: Основа, 1997. – 112 с.
- Михалев А.И. Компьютерные методы интеллектуальной обработки данных: учебное пособие / А.И.Михалев, Е.А.Винокурова, С.Л.Сотник .— Днепропетровск: НМетАУ, ИК "Системные технологии", 2014 .— 209 с.
- Растригин Л.А. Адаптация сложных систем. — Рига: Зинатне, 1981. — 375 с.
- Рутковская Д. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. / Рутковская Д., Пилиньский М., Рутковский
Л. – М.: Горячая линия–Телеком, 2004. – 452 с.
- Шумейко А.А. Интеллектуальный анализ данных (Введение в Data Mining) / А.А.Шумейко, С.Л.Сотник .— Днепропетровск: Белая Е.А., 2012 .— 212 с.
Полезная литература. Статьи.
- Holland J.H. Complex adaptive systems / J.H.Holland // A New Era in Computation (Winter, 1992) .— 1992 .— Vol. 121, No. 1 .— P.17-30.
- Заде Л. Роль мягких вычислений и нечеткой логики в понимании,
конструировании и развитии информационных интеллектуальных систем /Заде Л.А. – Новости Искусственного Интеллекта. – №2-3, 2001. – с. 7–11.
Вопрос-ответ.
Задать вопрос: