Використання масштабно-інваріантних дескрипторів для реєстрації зображень.
Реєстрація зображень (зіставлення, накладання) - це процес трансформації різних наборів даних в одну координатну систему.
Даними можуть бути серія фотографій, дані з різних сенсорів, моментів часу, глибини, або точок спостереження.
Алгоритми реєстрації зображень використовуються в комп'ютерному зорі, методах медичної візуалізації, у військовій справі для автоматичного розпізнавання цілей,
і для упорядкування та аналізу зображень супутникових даних.
Реєстрація необхідна для того, мати можливість порівнювати або інтегрувати дані, отримані з різних пристроїв.
Для цієї мети було запропоновано і розроблено безліч методів виявлення локальних ознак.
Набір відповідних ознак або точок зіставлення між двома зображеннями використовується щоб дізнатися, як вони пов'язані один з одним.
Класичний процес реєстрації зображень в якості першого кроку включає в себе виявлення ознак із зображень.
Ці ознаки класифікуються на локальні і глобальні і можуть бути представлені точками, ребрами, кутами і контурами або іншими дескрипторами.
Як тільки об'єкти вилучені з зображень, починається другий етап або процес зіставлення шляхом порівняння відповідних дескрипторів витягнутих ключових точок.
Третій і четвертий етапи процесу реєстрації включають оцінку моделі перетворення, повторну вибірку і складання зареєстрованої версії.
У літературі автоматичне вирівнювання і зшивання зображень можна розділити на дві категорії: пряме і засноване на ознаках.
Прямі методи використовують всі дані зображення, які можуть забезпечити дуже точну реєстрацію, засновану на близькій ініціалізації,
що забезпечує надійне зіставлення незважаючи на різні можливі перетворення (наприклад, обертання, масштабування та ін.).
Основні етапи автоматичного зшивання зображень:
- витягти інваріантні об'єкти з усіх вхідних зображень,
- знайти кількість найближчих сусідів для кожного об'єкта,
- для кожного зображення вибрати кандидатів відповідного зображення, які мають більшість збігів ознак з цим зображенням,
- пошук геометрично узгоджених збігів ознак,
- перевірка збігів зображень шляхом знаходження компонентів збігів зображень,
- застосувати багатосмугове змішування для отримання вихідного зшитого зображення.
Локальна особливість розглядається як зразок зображення, який відрізняється від його прямих околиць і зазвичай представлений точками, краями, кутами або іншими дескрипторами.
На основі таких уявлень було запропоновано багато детекторів ознак, наприклад, Harris і FAST працюють на основі виявлення кутів, в той час як SIFT і SURF працюють на
основі точок або плям (латок). Останні два детектора показали хорошу ефектівность проти обертання, масштабування і розмиття.
Концепції
Роль детектора ознак полягає в ідентифікації точок інтересу (тобто областей інтересу), в той час як дескриптор функції відповідає за обчислення вектора ознак,
описує ці пункти інтересів (області).
Процес зіставлення визначає відповідність між обчисленими дескрипторами.
Наочним прикладом є алгоритм SIFT, запропонований Девідом Лоу в 2004 році.
Звичайною практикою є використання детектора SIFT і дескриптора SIFT незалежно.
Ключові точки можуть вилучатись без дескрипторів (використовуючи тільки детектор SIFT), або дескриптор SIFT можна використовувати для опису користувацьких ключових точок.
Кожен детектор (наприклад, SIFT) використовується разом зі своїм власним відповідним дескриптором.
Реєстрація зображення - це процес визначення геометричного перетворення, яке вирівнює точки або пікселі в одному зображенні з відповідними точками в іншому
зображенні, що має ту ж сцену. Успішна реєстрація зображень є обов'язковою для об'єднання зображень і інтеграції даних.
Як правило, основні етапи процесу реєстрації зображень:
- ідентифікація об'єкта,
- зіставлення об'єкта,
- просторове перетворення
- і, нарешті, етап повторної вибірки.
Ідентифікація об'єкта включає в себе виявлення необхідних дескрипторів, таких як ключові точки або опорні точки, з вхідних зображень.
Як тільки об'єкти вилучені з зображень, починається процес зіставлення шляхом порівняння дескрипторів, заснований на виявлених ключових точках,
щоб отримати набір відповідностей між цими дескрипторами.
Існують різні методи для виконання таких перетворень і можуть бути класифіковані як жорсткі і нежорсткі перетворення зображень.
У жорстких перетвореннях форма і розмір об'єктів не змінюються, на відміну від нежорстких перетворень, таких як афінне перетворення і перетворення подібності.
На основі моделі перетворення використовуються методи передискретизации, такі як лінійна інтерполяція.
Реєстрація зображень може бути класифікована наступним чином:
- Мультимодальна реєстрація: інтегрується додаткова інформація для мультисенсорних зображень.
Зображення однієї і тієї ж сцени отримують з різних датчиків.
Мета полягає в тому, щоб об'єднати інформацію, отриману з різних вхідних потоків, щоб отримати більш складний і детальний опис сцени.
Наприклад, об'єднання інформації, одержуваної від датчиків з різними характеристиками, таких як панхроматичні зображення, кольорові / мультиспектральні зображення з різним
спектральним розрішення або радіолокаційні зображення, незалежні від хмарного покрову і сонячного освітлення.
- Реєстрація декількох видів: зображення однієї і тієї ж сцени, які отримують з різних точок огляду. Мета полягає в тому, щоб отримати збільшений 2D-вид або
тривимірне представлення відсканованої сцени.
- Тимчасова реєстрація. Зображення однієї і тієї ж сцени отримуєм в різний час, часто на регулярній основі і, можливо, в різних умовах.
Мета полягає в тому, щоб оцінити зміни в сцені, які з'явилися між послідовними зображеннями.
Існує безліч програм для реєстрації зображень в медичній візуалізації, дистанційного зондування та супутникових знімках.
На ці зображення впливає ряд ефектів, заснованих на несучої частоті електромагнітних хвиль.
З іншої сторони, оптичні датчики при отриманні інформації про спостережувані об'єкти, на Землі блокуються хмарами.
Навіть тіні хмар або нічний перехід над областю впливають на інтерпритуємість зображень.
Крім того, радар з синтезованою апертурою (SAR) залежить від геометричних спотворень, які основані на його геометрії (укладання, ракурс і тінь).
Щоб подолати цей вплив, можна об'єднати різні зображення, отримані одним і тим же або різними інструментом, для отримання одного зображення, що має
більше інформації, ніж ми отримуємо від одного датчика.
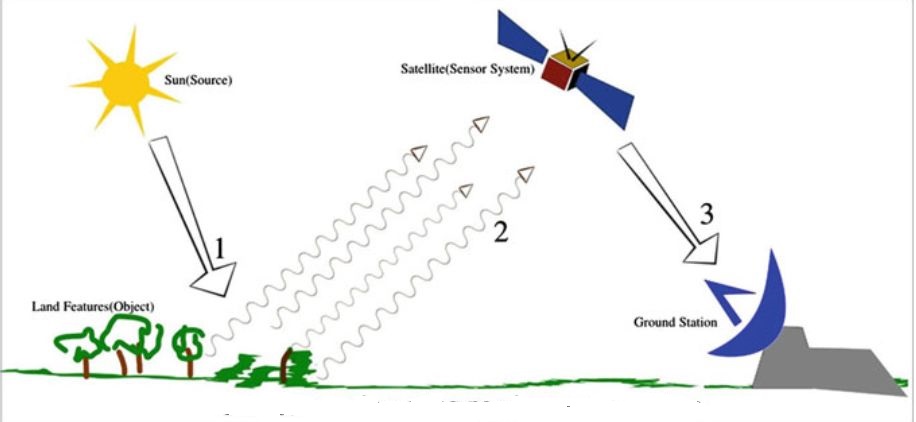
Дистанційне зондування з використанням пасивної сенсорної системи
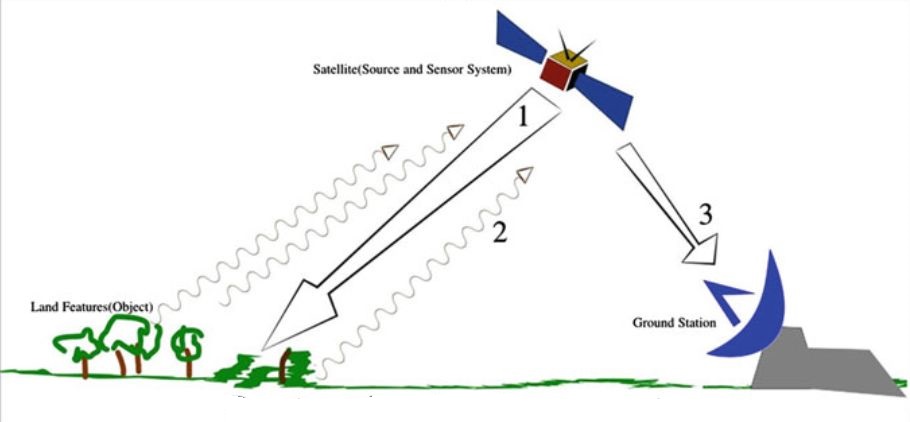
Дистанційне зондування з використанням активної сенсорної системи
Розглянемо найбільш популярні детектори.
SIFT (Scale Invariant Feature Transform) складається з чотирьох основних етапів:
- виявлення екстремумів в різних масштабах простору,
- локалізація ключових точок,
- визначення орієнтації,
- і, нарешті, створення дескриптора ключових точок.
На першому етапі ключові точки визначаються шляхом сканування місця розташування, для різного масштабу зображення.
Для виконання цього кроку використовується різниця по Гаусу (DoG), потім кандидати в ключові точки локалізуються з точністю до субпікселя.
Потім обчислюється орієнтація для кожної ключової точки в локальних напрямках градієнта зображення для отримання інваріантності до обертання.
На останньому кроці створюється 128-бітовий дескриптор або вектор об'єктів, готовий до процесу зіставлення.
SIFT дає гарну продуктивність, але все ж має деякі обмеження проти сильних змін освітлення і великого обертання.
SURF (Speeded-Up Robust Features) є локальним інваріантним детектором точок інтересу або BLOB-об'єктів.
Він частково заснований на дескрипторі SIFT і використовується також для статичного зіставлення і пошуку сцен.
Цей дескриптор інваріантний для більшості перетворень зображення, таких як зміна масштабу і освітленості, на додаток до невеликих змін в точці огляду.
Він використовує проміжне представлення для зображення і містить суму значень пікселів зображення в градаціях сірого.
SURF добре справляється з серйозним розмиванням і поворотом зображення і погано справляється зі змінами точки огляду і зміною освітленості.
Harris - це комбінований детектор кутів і країв, заснований на локальної функції автокореляції.
Він не залежить від обертання, зміщення або афінної зміни інтенсивності.
Цей детектор розширює принцип кутового детектора Моравека, враховуючи локальну енергію автокорреляции.
Кути, як правило, є хорошими характеристиками, щоб відповідати змінами точки огляду.
Star Feature Detector отриманий з детектора CenSurE (Center Surround Extrema).
CenSurE обчислюваною альтернативою колу використовує багатокутники, такі як квадрат, шестикутник і восьмикутник,
Star імітує коло двома квадратами, що перекриваються: один вертикальний, а другий повернутий на 45 градусів.
CenSurE визначає великомасштабні об'єкти на всіх масштабах і вибирає екстремуми за масштабом і розташуванню.
Він використовує спрощені дворівневі ядра в якості фільтрів центрального оточення.
Основна увага приділяється пошуку ядер, інваріантних щодо обертання.
FAST (Features from Accelerated Segment Test) - це метод визначення кута, важливість якого полягає в його обчислювальній ефективності,
оскільки він швидше, ніж багато відомих методи вилучення ознак (наприклад, DoG, SIFT, Harris).
Він використовує коло Брезенхема радіуса 3, щоб дізнатися, чи є обрана точка кутом.
Кожному пікселю в колі за годинниковою стрілкою присвоюється число від 1 до 16.
Якщо набір суміжних пікселів всередині кола яскравіше або темніше, ніж піксель-кандидат, то він класифікується як кут.
FAST вважається детектором ознак високої якості, але все ж не стійкий до шуму і залежить від порогового значення.
BRISK (Binary Robust Invariant Scalable Keypoints) залежить від шаблону кругової вибірки, з якого він обчислює порівняння яскравості для формування рядка бінарного
дескриптора, що швидше, ніж SIFT і SURF.
ORB (Oriented BRIEF-Binary Robust Independent Elementary Features) - локальний детектор ознак і дескриптор, заснований на бінарних рядках.
Залежить від відносно невеликої кількості тестів різниці в інтенсивності, щоб представити ділянку зображення у вигляді двійкового рядка.
Побудова і узгодження цієї локальної особливості відбувається швидко і працює добре, поки не потрібна інваріантність до великих поворотів.
Однією з проблем, яка не була належним чином вирішена, є масштабна інваріантність.
GFTT (Good Features to Track) виділяє найбільш помітні кути на зображенні, де розраховується показник якості кутів для кожного пікселя.
Потім застосовується обмеження по порогу - кути нижче певного порогу відхиляються, а інші кути упорядковані відповідно до значень у порядку спадання.
Нарешті, кожен кут, для якого є більший кут на відстані менше порогового значення, відкидається.
Метод показує, що функції з хорошими текстурними властивостями можуть бути знайдені шляхом оптимізації точності трекера.
MSER (Maximally Stable Extremal Regions) схожий на SIFT, оскільки він виділяє коваріантні області з зображення.
Використовуються екстремальні області, які мають деякі важливі властивості.
MSER має майже лінійну складність і швидко виявляє афінно-інваріантну стійку підмножину екстремальних областей.
Показники порівняння
Показники схожості зображень оцінюють ступінь відповідності між парами зображень або так званими дескрипторами ознак.
Розглянемо найбільш часто використовувані інструменти подібності:
Середньоквадратична помилка (RMSE)
Відповідність може бути виміряна як різниця суми квадратів між інтенсивностями пікселів.
Це може бути інтерпретовано як функція помилки, де нульове значення представляє ідеальний збіг:
\[
RMSE =\sqrt{\frac{1}{MN}\sum_{i=1}^M\sum_{j=1}^N(x_{i,j}-y_{i,j})^2},
\]
де М ×N - розміри зображення, (х, y) - список точок з еталонного і перетвореного зображення.
Пікове співвідношення сигнал / шум (PSNR)
Це відношення максимально можливої потужності сигналу до потужності, що спотворює, шуму, яке впливає на точність представлення.
Його діапазон широкий, тому він виражається у вигляді логарифмічної шкали.
Максимальне значення PSNR вказує на хорошу відповідність між двома зображеннями і може бути виражено як
\[
PSNR = 10 \log_ {10} \frac{(2 ^ n-1) ^ 2} {MSE}.
\]
Нормалізована взаємна кореляція (NCC)
NCC є загальною мірою подібності і може бути математично визначена наступним чином
\[
NCC (A, B) = \frac {1} {N} \sum_ {x, y} \frac {(A- \mu_A) (B- \mu_B)} {\sigma_A \sigma_B}
\]
де N загальна кількість пікселів на зображенні A і B, \(μ_A, μ_B \) представляють собою середнє значення зображень A і B, відповідно, а \(σ_A, σ_B \)
позначають стандартне відхилення зображень A, B.
Взаємна інформація (MI)
Взаємна інформація - це надійний метод для вимірювання показника подібності між двома зображеннями в градаціях сірого.
Метод вимірює статистичні кореляції між двома зображеннями на основі ентропії Шеннона.
Якщо кожен піксель в зображенні розглядається як випадкова подія, інформація, що міститься в зображенні, може бути виміряна за допомогою ентропії Шеннона.
Це можна розглядати як міру невизначеності або кількості інформації, що міститься в зображенні.
Для двох зображень A і B взаємна інформація MI (A, B) обчислюється таким чином:
\[
MI (A, B) = H (A) + H (B) - H (A, B)
\]
Інтерпретація даного рівняння полягає в тому, що вимірюється відстань між спільним розподілом значень пікселів зображення і спільним розподілом в
випадку незалежності зображень A і B. H (A) і H (B) є ентропія A і B відповідно, а H (A, B) представляє собою спільну ентропію A з B.
H (A) і H (A, B) можна розрахувати:
\[
H (A) = - \sum_ {i = 1} ^ {L_a} P_i (a) \log P_i (a),
\]
\[
H (A, B) = \sum_ {i = 1} ^ {L_a} \sum_ {j = 1} ^ {L_b} P_ {i, j} (a, b) \log \frac {P_ {i, j } (a, b)} {P_i (a) P_j (b)},
\]
де $ L_a $ і $ L_b $ - кількість різних кольорів в зображеннях A і B відповідно, $ P_i (a) $ - ймовірність появи значення кольору $ i $ в зображенні A, а $ P_ {i, j} (a, b) $
- ймовірність появи пари кольорів $ i $ і $ j $ на зображеннях A і B.
Індекс структурної подібності (SSIM)
SSIM -Показник якості одного зображення, яке порівнюється з іншим зображенням, які мають можливості для покращення якості.
Це покращена версія універсального індексу якості зображення (UIQI). Значення SSIM дорівнює одиниці, коли два зображення однакові.
На відміну від RMSE і PSNR, SSIM не оцінює виявлені помилки, і навпаки, SSIM розглядає погіршення зображення як сприймається зміна в структурних даних,
мають сильні взаємозалежності (важлива інформація про структуру об'єкта), особливо коли вони просторово близькі.
SSIM-індекс є розвитком традиційних методів, таких як PSNR (peak signal-to-noise ratio) і метод середньоквадратичної помилки MSE, які виявилися несумісні з фізіологією людського сприйняття.
SSIM метрика розрахована на різні розміри вікна. Для різниці між двома вікнами $ \displaystyle x $ і $ \displaystyle y $ мають однаковий розмір N × N
SSIM розраховується наступним чином:
\[
SSIM = \frac {(2 \bar {x} \bar {y} + C_1) (2σ_ {xy} + C_2)} {σ_x ^ 2 + σ_y ^ 2 + C_2) (\bar {x} ^ 2 + \bar {y} ^ 2 + C_1)}
\]
де $ x_ {i, j} $ і $ y_ {i, j} $ - еталонне і перетворене зображення відповідно, $ \bar {x}, \bar {y} $ - середні значення для еталонного і перетвореного зображень
відповідно, $ σ x ^ 2 $ і $ σ y ^ 2 $ - дисперсія зображення $ x $ і $ y $, а $ C_1 $, $ σ_ {xy} $ їх коваріація і $ C_2 $ - константи, визначені як:
\[
C_1 = (k_1 * L) ^ 2, C_2 = (k_2 * L) ^ 2
\]
де $ k_1 = 0.01 $ і $ k_2 = 0.03 $ і $ L = 2 ^ N - 1 $.
Наведена формула застосовна тільки для яскравості зображення, по якій і відбувається оцінка якості.
Отриманий SSIM-індекс лежить в межах від -1 до +1. Значення +1 досягається тільки при повній автентичності зразків.
Як правило, метрика розрахована на вікно розміром 8 × 8 пікселів.
Співвідношення однорідності (однаковості) зображення (RIU)
Коефіцієнт однорідності зображення (RIU) заснований на перетворенні, яке мінімізує стандартне відхилення відносини інтенсивностей зображення.
Це співвідношення обчислюється на основі вокселів по перетвореному зображенню і вхідному зображенню і використовується для вирівнювання медичних зображень.
Обчислюється таким чином:
\[
RUI = \frac {1} {\bar {R}} \sqrt {\frac {1} {N} \sum \left \{\left (R (X_ {I_1 (i, j)}) - \bar { R} \right) ^ 2 \left | X_ {I_1 (i, j)} \in \Omega ^ T_ {I_1 (i, j), I_2 (x + 1, y + j)} \right. \right \}}
\]
де $ R (X_ {I_1 (i, j)}) $ вокселі проміжного способу оригінального зображення $ I_1 (i, j) $, $ \bar {R} $ - середнє проміжного зображення,
$ N $ - число вокселів.
Вокселі $ R (X_ {I_1 (i, j)}) $ проміжного зображення обчислюються наступним чином
\[
R(X_{I_1(i,j)})=\frac{\left\{I_1(i,j)\left|\Omega^T_{I_1(i,j),I_2(x+1,y+j)}(X_{I_1(i,j)})\right.\right\}}
{\left\{I_2(x+i,y+j)\left|\Omega^T_{I_1(i,j),I_2(x+1,y+j)}(X_{I_1(i,j)})\right.\right\}},
\]
\[
\bar{R}=\frac{1}{N}\sum\left\{R(X_{I_1(i,j)})\left|X_{I_1(i,j)}\in \Omega^T_{I_1(i,j),I_2(x+1,y+j)}\right.\right\}
\]
$ I_1 (i, j) $ оригінальне зображення, $ I_2 (x + i, y + j) $ зображення після трансформації, $ X_ {I_2 (x + i, y + j)} $ воксель зображення $ I_2 (x + i , y + j) $,
$ \Omega ^ T_ {I_1 (i, j), I_2 (x + 1, y + j)} $ - домен перекриття.
RIU знаходиться в діапазоні від 0 до 1. Якщо RIU прагне до 0, відхилення помилок мінімальні і максимізують однорідність, коли прагнуть до 1, це максимізує
нормалізоване стандартне відхилення і мінімізує однорідність.
Геометричні перетворення.
Операції попередньої обробки (pre-processing), іноді звані відновленням і виправленням зображення, призначені для виправлення конкретних радіометричних і
геометричних спотворень даних.
Радіометричні поправки можуть бути необхідні через відмінності в освітленні сцени і геометрії огляду, атмосферних умов, а також шуму і відклики датчика.
Кожен з них буде варіюватися в залежності від конкретного датчика і платформи, що використовується для збору даних, і умов під час збору даних.
Крім того, може бути бажано перетворити і / або відкалібрувати дані у відомі (абсолютні) одиниці вимірювання випромінювання або відображення,
щоб полегшити порівняння між даними.
Однакові умови освітлення і геометрії огляду між зображеннями (для оптичних датчиків) можна виправити шляхом моделювання геометричного
взаємозв'язку. Це часто потрібно для більш простого порівняння зображень, зібраних різними датчиками в різні дати або час, або для мозаїчного зображення декількох
зображень з одного датчика при збереженні однорідних умов освітлення від сцени до сцени.
Всі зображення дистанційного зондування за своєю природою схильні до геометричних спотворень.
Ці спотворення можуть бути викликані декількома факторами, в тому числі перспективою сенсорної оптики, рухом системи сканування, рухом платформи, висотою платформи,
орієнтацією і швидкістю, рельєфом місцевості, а також викривленням і обертанням Землі. Геометричні поправки призначені для компенсації цих спотворень,
щоб геометричне предствлення зображень було якомога ближче до реального світу.
Багато з цих змін носять систематичний або передбачуваний характер і можуть бути пояснені точним моделюванням руху датчика і платформи та
геометричних взаємозв'язків платформи з Землею.
Інші несистематичні або випадкові помилки не можуть бути змодельовані і виправлені таким чином.
Отже, необхідно виконати геометричну реєстрацію зображень певною системою координат.
Процес геометричної реєстрації включає в себе визначення координат декількох чітко помітних точок (опорних точок) у спотвореному зображенні і зіставлення їх з
істинними положеннями в наземних координатах (наприклад, широтою і довготою).
Як тільки кілька добре розподілених пар опорних точок були ідентифіковані, інформація про координати обробляється для визначення правильних рівнянь перетворення,
застосовуваних до вихідних координат зображення, щоб зіставити з їх новими координатами.
Геометрична реєстрація також може бути виконана шляхом реєстрації одного (або кількох) зображень в іншому зображенні замість географічних координат.
Це називається реєстрацією зображення до зображення і часто виконується перед виконанням різних процедур перетворення зображення або для порівняння кадрів відеопотоку.
Модель перетворення визначає, який тип геометричного перетворення можна застосувати до зображення сцени для реалізації моделі.
Крім того, це дозволяє зрозуміти які геометричні властивості (наприклад, розмір, форма, положення, орієнтація і т.д.) зберігаються в процесі знімання інформації.
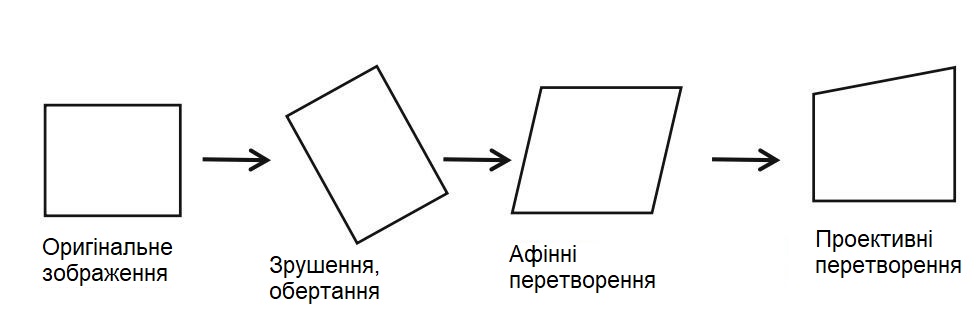
Геометричні перетворення.
Перетворення ізометрії
Перетворення ізометрії відображає елементи в тому ж або іншому метричному просторі, так що відстань між елементами зображення в новому метричному просторі дорівнює
відстані між елементами у вхідному метричному просторі і може бути записана у матричної формі:
\[
\left(
\begin{array}{c}
x'\\
y' \\
1 \\
\end{array}
\right)=
\left(
\begin{array}{ccc}
\cos (θ) & - \sin (θ)& dx \\
\sin (θ)& \cos (θ) & dy \\
0 & 0& 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
x\\
y \\
1 \\
\end{array}
\right),
\]
де $ (x ', y') $ - перетворена координата $ (x, y), dx $ і $ dy $ - переміщення уздовж осі x і y відповідно.
Перетворення подібності
Це перетворення враховує обертання, зрушення і масштабування, його можна записати в матричній формі:
\[
\left(
\begin{array}{c}
x'\\
y' \\
1 \\
\end{array}
\right)=
\left(
\begin{array}{ccc}
S_x\cos (θ) & - \sin (θ)& dx \\
\sin (θ)& S_y\cos (θ) & dy \\
0 & 0& 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
x\\
y \\
1 \\
\end{array}
\right),
\]
де $ (x ', y') $ - перетворена координата $ (x, y), dx $ і $ dy $ - переміщення уздовж осі x і y відповідно, $ S_x, S_y $ -масштабуючі коефіцієнти.
Для визначення 4 параметрів потрібно мінімум дві відповідні точки на зображеннях.
При перетворенні подібності кути зберігаються, і це корисно при реєстрації зображень пласких сцен.
Афінні перетворення
Афінне перетворення представляє спотворення співвідношення сторін і зсуву зображення.
При цьому паралельні лінії залишаються паралельними, а прямі залишаються прямими.
Афінне перетворення представляється в матричної формі з використанням однорідних координат (з шістьма невідомими параметрами) у вигляді:
\[
\left(
\begin{array}{c}
x'\\
y' \\
1 \\
\end{array}
\right)=
\left(
\begin{array}{ccc}
a_{1,1} & a_{1,2}& dx \\
a_{2,1}& a_{2,2} & dy \\
0 & 0& 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
x\\
y \\
1 \\
\end{array}
\right),
\]
У афінних перетвореннях зв'язок між двома відповідними точками (x ', y') і (x, y) може бути сформульована як:
\[
x' = m_1 + m_2x + m_3y,\\
y' = n_1 + n_2x + n_3y,
\]
де $ m_i $ і $ n_i $ - коефіцієнти перетворення.
Поліноміальне перетворення
Поліноміальна деформація першого порядку включає член взаємодії $ xy $, який допускає зрушення зображення:
\[
x' = m_1 + m_2x + m_3y+m_4xy,\\
y' = n_1 + n_2x + n_3y+n_4xy.
\]
Проективне перетворення
Проективне перетворення має вісім ступенів свободи, воно зберігає прямолінійність ліній і площинність поверхонь, а вигнуті перетворення - ні.
Проективні перетворення можуть бути представлені в однорідних координатах в матричному вигляді:
\[
\left(
\begin{array}{c}
x'\\
y' \\
1 \\
\end{array}
\right)=
\left(
\begin{array}{ccc}
a_{1,1} & a_{1,2}& a_{1,3} \\
a_{2,1}& a_{2,2} & a_{2,3} \\
a_{3,1} & a_{3,2}& a_{3,3} \\
\end{array}
\right)
\left(
\begin{array}{c}
x\\
y \\
1 \\
\end{array}
\right).
\]
Приклад.
Одні і ті ж зображення датчиків зазвичай знімаються в різний час або з різних точок зору.
Крім того, якщо мова йде про віддалене зондування Землі, то інформація надходить від різних супутників з різною орбітою руху, тобто одна і таж ділянка сканується під
різними кутами.
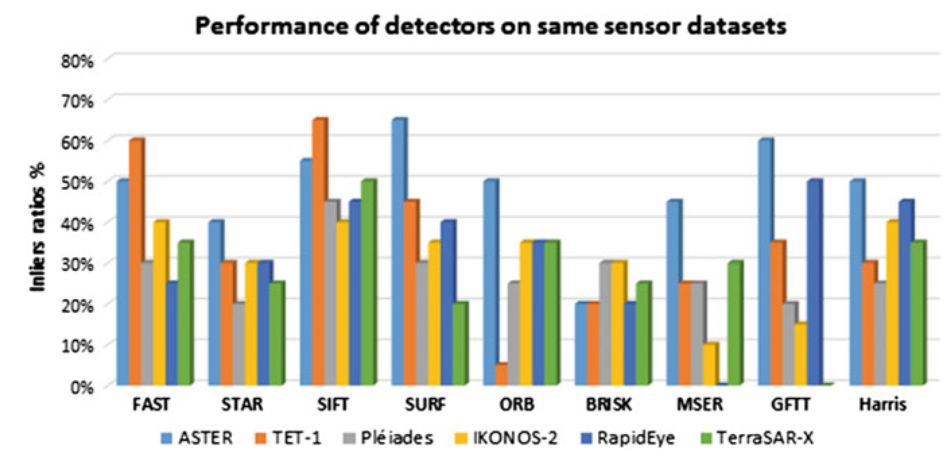
На наступній діаграмі представлені оцінки якості реєстрації даних, отриманих від різних супутників і оброблені з використанням різних дескрипторів -
джерело http://www.ccrs.nrcan.gc.ca