Глобальні і локальні особливості зображення
Одним із завдань обробки зображень і комп'ютерного зору є необхідність виділення із зображення деяких значень, що характеризують або зображення в цілому, або
якусь його частину, яка цікава для дослідника.
При описі глобальної ознаки, зображення може бути представлено одним вектором якоїсь багатовимірної характеристики, що описує інформацію про зображення в цілому.
Іншими словами, метод глобального представлення створює один вектор зі значеннями, які вимірюють різні аспекти зображення, такі як колір, текстура або форма.
Таким чином, два зображення можуть порівнюватися шляхом порівняння векторів їх ознак.
Наприклад, якщо хтось хоче розрізнити зображення моря (синього кольору) та лісу (зеленого кольору), глобальний дескриптор кольору буде давати зовсім різні вектори для кожної
категорії. У цьому контексті глобальні особливості можуть бути інтерпретовані як особливі властивості зображення за участю всіх пікселів.
Ця властивість може бути гістограмами кольору, текстурою, наявністю країв або навіть певним дескриптором, витягнутим з деяких фільтрів, що застосовуються до зображення.
З іншого боку, основна мета уявлення локальних об'єктів полягає в тому, щоб чітко уявляти зображення на основі деяких особливих характеристик,
які залишаються незмінними щодо зміни точки огляду і освітлення.
Таким чином, зображення представлене на основі його локальних структур набором дескрипторів локальних ознак, виділених з набору областей зображення, які називаються областями
інтересу (тобто ключовими точками). Більшість локальних особливостей представляють текстуру частини зображення.
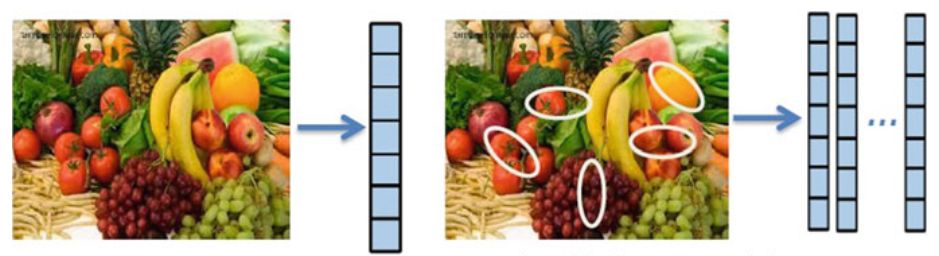
Представлення глобальних і локальних характеристик зображень.
Як правило, використання того чи іншого типу характеристик може сильно залежати від розв'язуваної задачі.
Наприклад, для дуже великих наборів даних при індексуванні зображень, доцільно враховувати глобальні характеристики,
в цілому, глобальні характристики корисні в додатках, де необхідна груба сегментація об'єкта, що нас цікавить.
Переваги глобальних значень полягають в тому, що вони набагато компактніше, а також прості в обчисленні та, як правило, вимагають невеликих обсягів пам'яті і обчислювальних
можливостей.
Це може бути актуальним, наприклад, у деяких додатках, таких як виявлення копій зображень. Більшість нелегальних копій дуже схожі на оригінал, вони тільки зазнали змін від
стиснення, масштабування або обрізання фрагментів зображення, в цьому випадку використання локальних характеристик є пріоритетним інструментом.
Більш того, використання локальних характеристик для великомасштабного пошуку зображень має набагато більш високу продуктивність, ніж використання глобальних.
Оскільки локальні структури досить помітні і стабільні, вони більш корисні для зіставлення зображень і розпізнавання об'єктів.
Як вирішення цієї проблеми можна об'єднувати локальні дескриптори зображень в дуже компактне векторне представлення та оптимізувати зменшення розмірності цих векторів.
Характеристики детекторів ознак
Місцева особливість визначається як «фрагмент зображення, який відрізняється від його безпосередніх сусідів».
Таким чином, метою локальних інваріантних характеристик є надання уявлення, яке дозволяє ефективно зіставляти локальні структури
зображень. Тобто, результатом є отримання розрідженого набору локальних характеристик, які відображають сутність вхідних зображень і кодують
виявлення, опис та зіставлення тих чи інших цікавих особливостей зображень.
Для досягнення цієї мети детектори і дескриптори повинні мати властивості, які визначаються розв'язуваною задачею.
Наведемо деякі властивості, важливі при використання детектора в комп'ютерному зорі, це
- - Надійність. Алгоритм знаходження ознак повинен дозволяти виявляти одні і ті ж місця розташування елементів незалежно від масштабування, повороту, зсуву,
фотометричних деформацій, артефактів стиснення і шуму.
- - Повторюваність. Алгоритм знаходження ознак повинен бути здатний виявляти одні і ті ж ознаки однієї і тієї ж сцени або об'єкта неодноразово в різних умовах перегляду.
- - Точність. Алгоритм знаходження ознак повинен точно визначати місце розташування елементів зображення (в тих же точках розташування пікселів), особливо для задач зіставлення
зображень, де оцінка геометричних характеристик потребує точної відповідності.
- - В цілому, алгоритм знаходження повинен бути здатний виявляти ознаки, які можна використовувати в різних додатках.
- - Ефективність. Алгоритм знаходження ознак повинен бути здатний швидко виявляти особливості в нових зображеннях для підтримки додатків реального часу.
- - Алгоритм знаходження ознак повинен виявляти всі або більшість особливостей на зображенні,
при цьому щільність виявлених ознак повинна відображати інформаційний зміст зображення для забезпечення його компактного представлення.
Масштабування і афинна інваріантність.
Пошук відповідностей на основі порівняння областей фіксованої форми, таких як прямокутники або кола, не є надійним при наявності деяких геометричних і
фотометричних деформацій, оскільки вони впливають на форми областей. Також об'єкти на цифрових зображеннях з'являються по-різному в залежності від масштабу спостереження.
Отже, при аналізі вмісту зображення, зміна масштабу має важливе значення. Існують різні методи вирішення проблеми виявлення та вилучення ознак
інваріантних для цих умов. Деякі з них призначені для обробки змін масштабу, а інші - для афінних перетворень.
Для того, щоб отримати незалежність від зміни масштабу ці методи припускають, що зміна масштабу однакова в усіх напрямках (тобто рівномірно),
і далі знаходимо елементи, стабільні при всіх можливих масштабах. Для цієї мети використовується згортка зображення з деяким безперервним ядром для різного кроку сітки,
по якій проводиться згортка.
Як правило, в якості ядра згортки використовується фільтр Гауса. Результат згортки називається масштабним або масштабуючим простором.
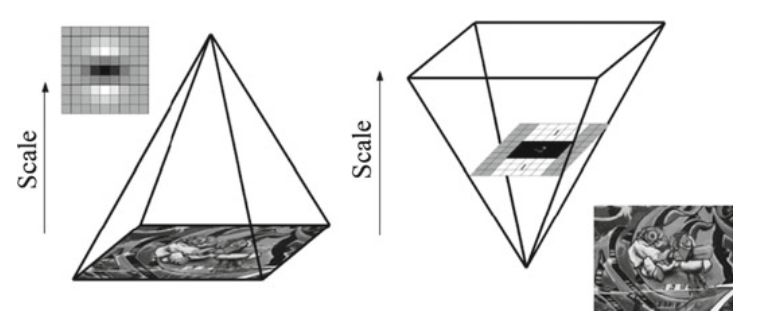
Побудова масштабної просторової структури
З іншого боку, в разі афінного перетворення, масштабування може бути різним у різному напрямку. Нерівномірне масштабування впливає на локалізацію,
масштаб і форму локальної структури. Отже, масштабно-інваріантні детектори неефективні в разі значних афінних перетворень.
Отже, детектори, розроблені для виявлення особливостей зображення при рівномірному масштабування, повинні бути узагальнені, щоб бути аффінно
інваріантними, які можуть визначати афінну форму локальних структур зображень. Таким чином, ці афінно-інваріантні детектори можна розглядати як узагальнення
масштабно-інваріантного детектора.
Як правило, афінне перетворення створюються з використанням послідовностей масштабування, поворотів, обертань і зрушень. Афінне перетворення (афінність) -
це будь-лінійне відображення, яке зберігає колініарність і відносини відстаней. У цьому сенсі афінність вказує на особливий клас проективних перетворень,
що не переміщують який-небудь об'єкт з афінного простору \(R ^ 3 \) в площину на нескінченності або навпаки. Якщо коротко, афінне перетворення \(R ^ n \) є
відображенням \(f: R ^ n → R ^ n \) виду
\[F (Y) = AY + B \]
для всіх \(Y \in R ^ n \), де A - лінійне перетворення \(R ^ n \).
У деяких особливих випадках, якщо det (A)> 0, перетворення називається таким, що зберігає орієнтацію, а якщо det (A) < 0,
то це призводить до зміни орієнтації.

